自动武器在连发射击过程中,枪管经历着火药燃气高温、高压、弹头高速、高加速度的高频热压耦合冲击、机械冲击等作用,这种工况严重影响了枪管寿命。自动武器内弹道学是研究弹头在膛内运动规律的科学,是枪械和弹药设计的理论基础,而弹头挤进时期是影响内弹道初始条件的重要因素,研究弹头与内膛的受力关系对研制新型枪弹以及改进膛线结构,从而达到提高枪管寿命有重要意义。
弹头挤进经历的时间极短,难以用实验准确测量,因此经典内弹道学中通常假设在达到挤进压力瞬间弹头才开始运动,忽略了弹头挤进这一重要过程。近年来国内外对此进行了多方面的研究,孙全兆对某大口径榴弹炮弹带挤进过程数值模拟研究[1],王鹏基于Johnson-Cook本构模型对弹带挤进过程进行了数值模拟[2],上述研究主要针对含有弹带的大口径炮弹,本文采用仿真方法模拟了枪弹弹头的挤进过程,着重对枪管与弹头挤进过程中的应力以及变形情况进行了分析,并考虑了铬层的影响。
本文基于步枪枪管开展弹头挤进枪管过程仿真研究,对比分析挤进过程不同膛线结构、不同厚度铬层厚度条件下的枪管应力情况,为高寿命枪管设计提供强有力的技术支撑。
1 弹头挤进过程力学理论分析
枪弹挤进过程中,弹头受到枪管阳线、阴线和导转侧的作用力,分别为坡膛阻力Fc,阴线阻力Fs和导转阻力Fd,这三部分的合力构成了挤进阻力,对挤进过程弹头受力分析如图1所示,其中为η缠角,β为坡膛角,α为导转侧角度[3-4]。
F=Fc+Fs+Fd
(1)
在接触面上产生的接触应力分别为:σc、τc,σs、τs和σd、τd,其中法向应力和切向应力通过摩擦因数ν呈正比关系,即
(2)
(3)
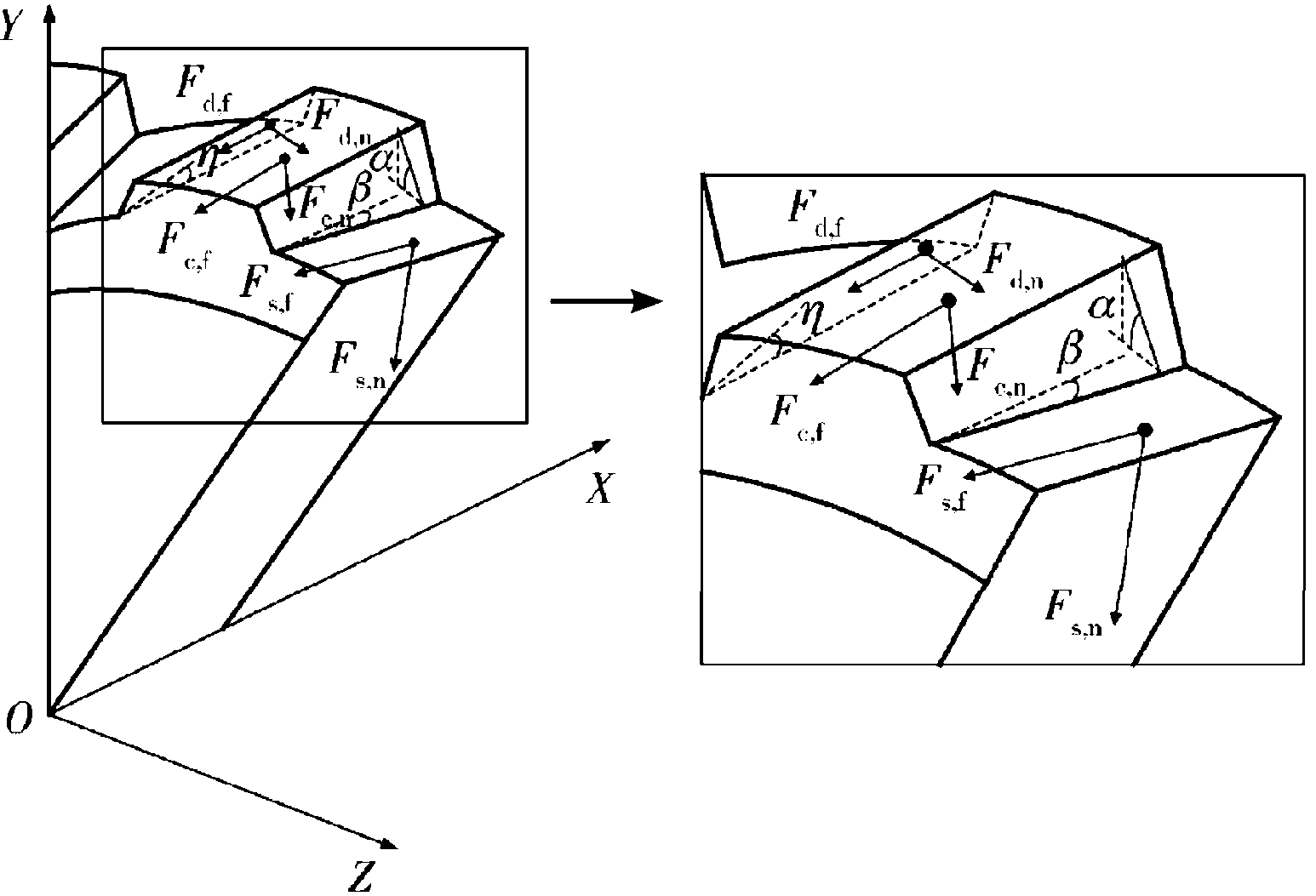
图1 挤进过程膛线受力分析
2 步枪弹挤进枪管仿真建模
基于梯形膛线、弧形膛线两种膛线结构开展研究,暂不考虑枪管内壁铬层的影响,如图2所示。
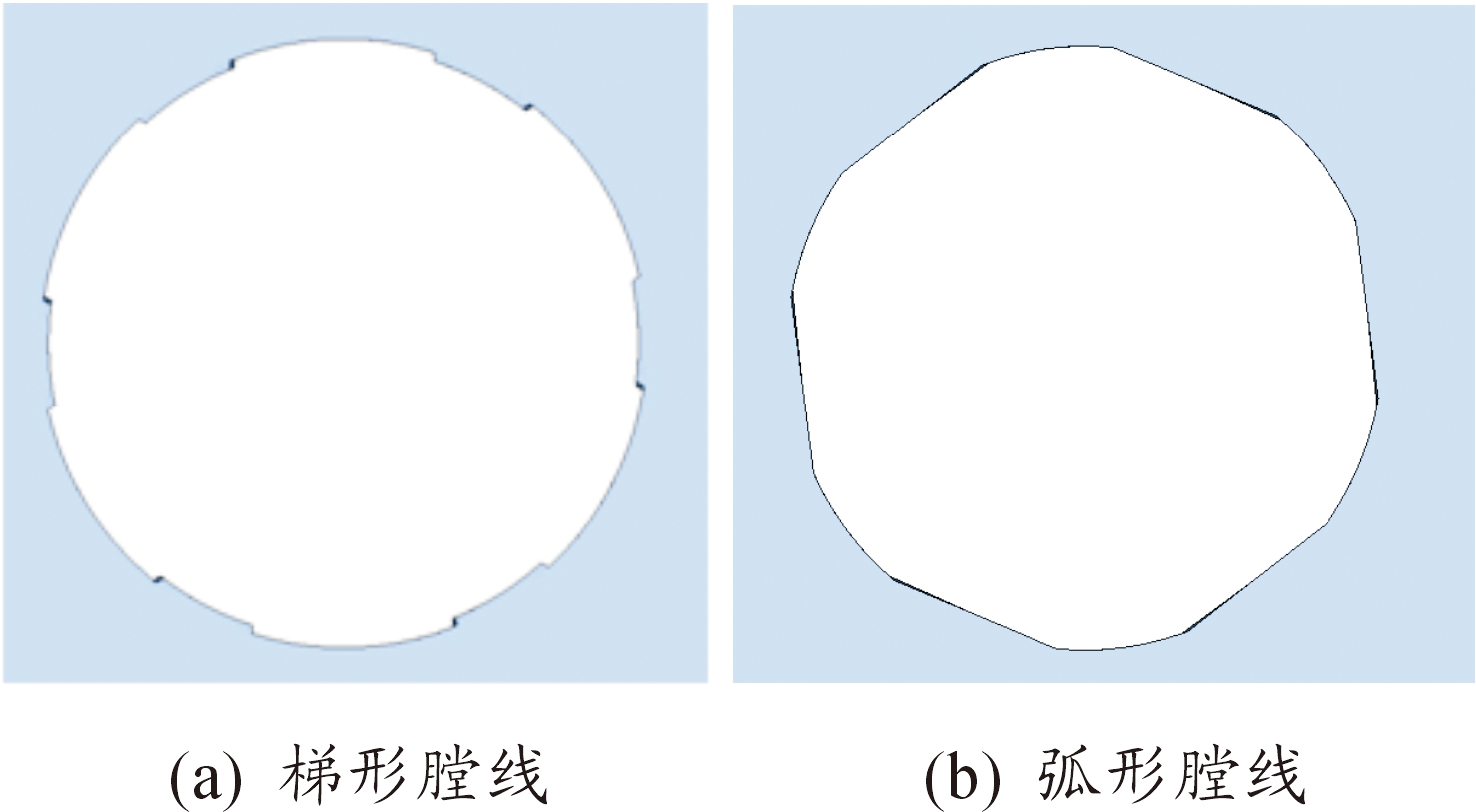
图2 两种不同膛线结构示意图
软件弹头枪管基于Hypermesh软件全部划分成六面体网格,其中坡膛均为15°,梯形膛线厚度方向两个网格,弧形膛线由于没有明显凸起网格与枪管一起划分(见图3、图4),在弹头与枪管实际装配位置,弹头底部及尾锥部施加膛压曲线(见图5),在此基础上采用LS-DYNA软件进行仿真计算。
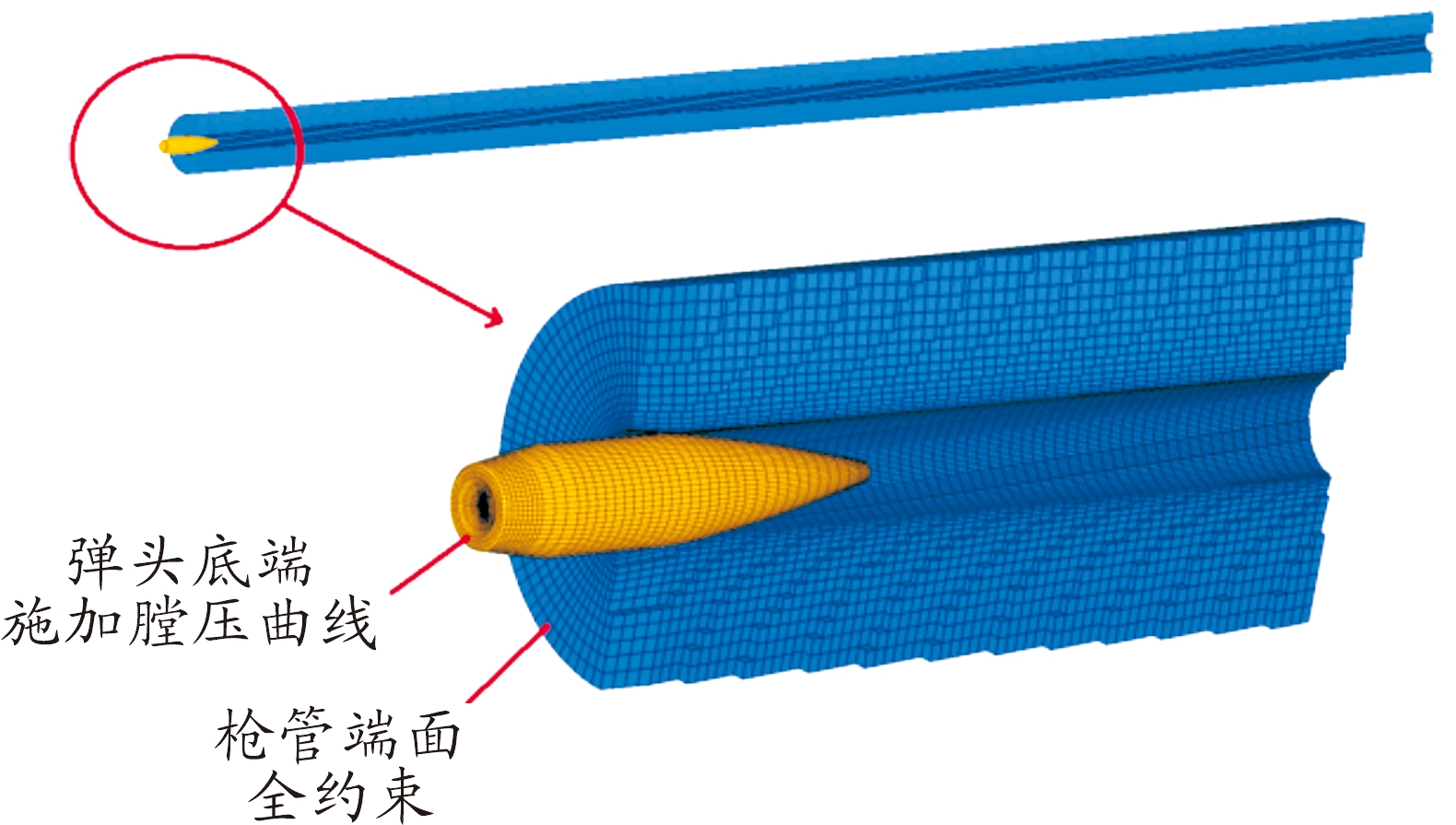
图3 挤进过程网格模型示意图
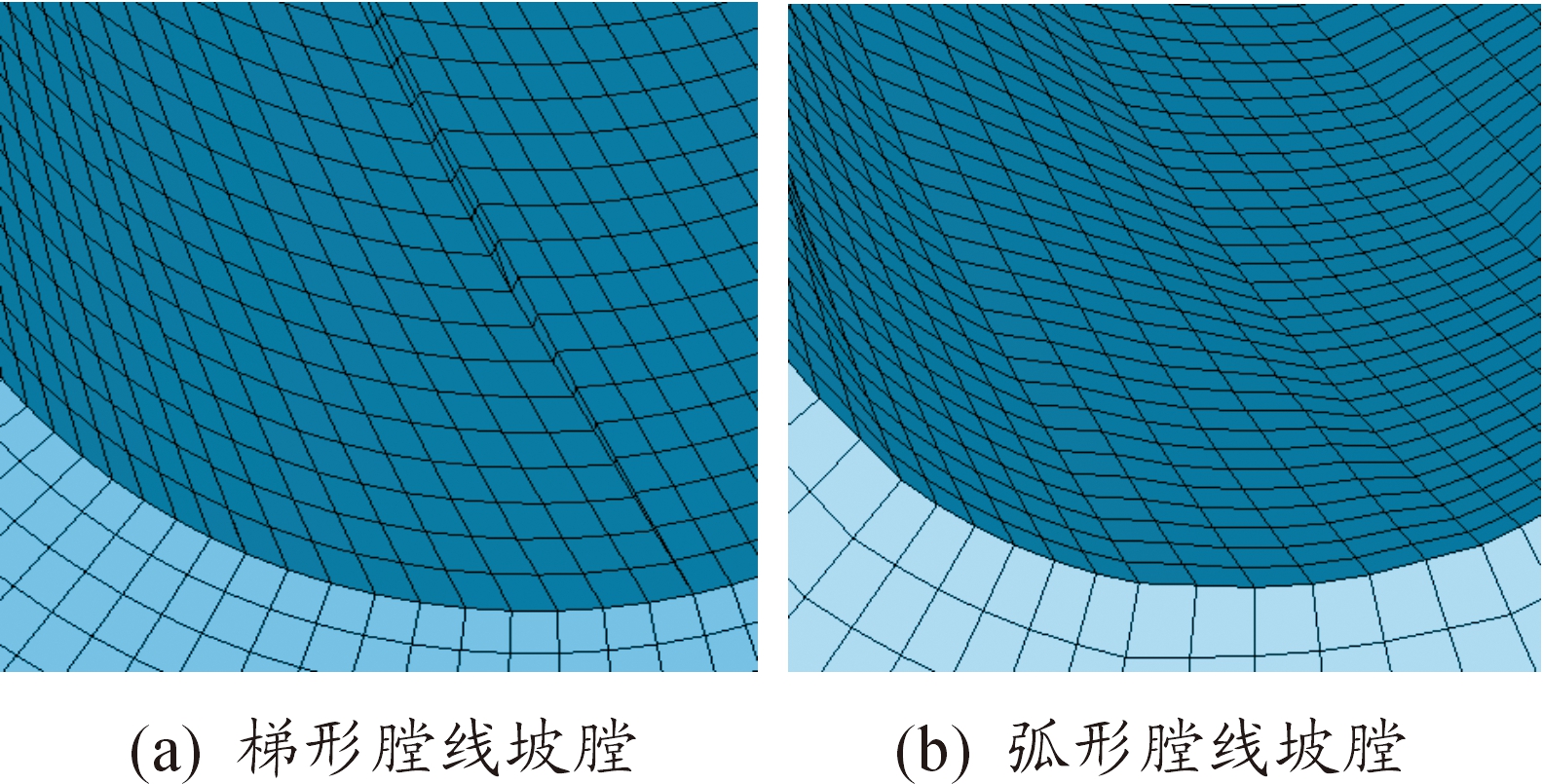
图4 两种不同膛线坡膛结构网格示意图
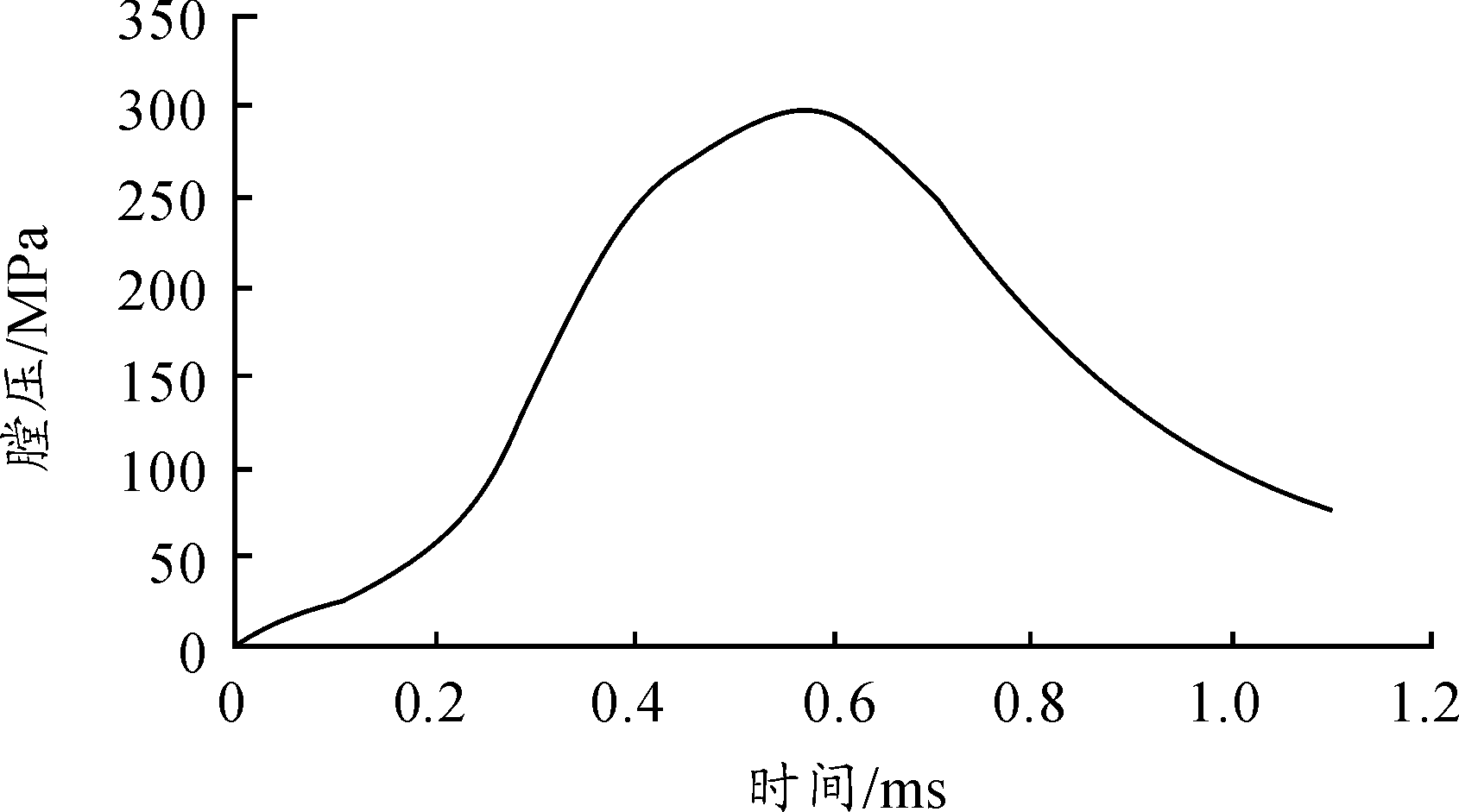
图5 步枪弹膛压曲线
弹头挤进过程时间极短,膛线受力过程快,存在应变率效应,强度随应变率增加而提高,因此材料使用考虑应变率,对于模型材料的本构关系,步枪弹由钢心、铅套、弹头壳三部分构成,均属于各向同性材料,使用Jonnson-Cook材料模型来描述该材料特性,由于挤进过程弹头发生塑性变形,需考虑损伤失效[5-6]。
Jonnson-Cook材料模型及失效模型公式是基于实验得到的。Jonnson-Cook模型中,流动应力(flow stress)可以表示为以下形式
σ = [A + Bεn][1 + Clnε*][1 - T*m]
(4)
式中:σ为 等效应力;ε为等效塑性应变;ε*为 法向等效塑性应变率。
T* =(T-298)/(Tmelt-298)
(5)
材料的强度是应变、应变率和温度的函数。式(1)中的 A、B、C、n来自实验数据,对于大变形问题,可以假设在变形过程中,塑性功的任意百分比在变形材料中产生热量。对于许多材料,90%~100%的塑性功作为热量在材料中散失[7-9]。因此,式(1)中使用的温度可以根据下面的表达式从温度上升中导出:
![]()
(6)
式中:ΔT为温度增量; α为塑性功作为热量百分比;c为热熔; ρ为密度。
枪管、枪弹各部分具体材料参数如表1所示。
表1 某步枪弹的Jonnson-Cook材料参数

类别密度ρ/(kg·m-3)屈服强度A/MPa应变硬化常数B/MPa应变硬化指数n应变率系数C枪管7 8301 0107540.220.011弹头壳8 9004202920.310.025铅套11 34050170.6850.035钢芯7 8309615110.260.014
3 步枪弹挤进枪管仿真结果分析
3.1 梯形六条膛线仿真结果
重点提取弹头变形量,弹头与膛线贴合情况,被甲、铅套、钢芯的最大应力,坡膛与膛线的最大应力,具体见图6~图13(图中的为105 MPa),并对不同膛线结构应力进行分析,如表2。

图6 步枪弹形变图

图7 步枪弹被甲应力云图

图8 步枪弹铅套应力云图

图9 步枪弹钢芯应力云图
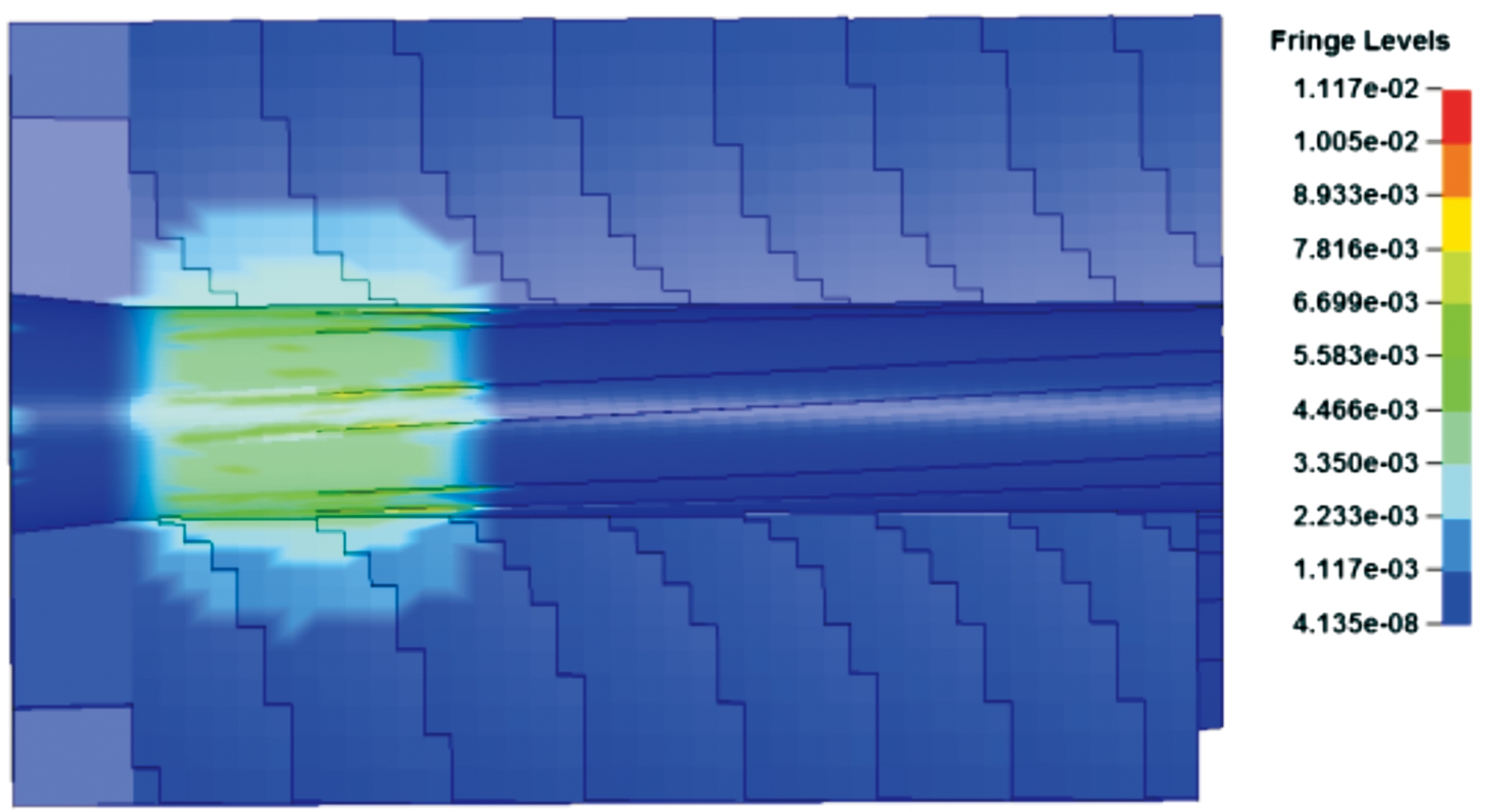
图10 步枪枪管梯形膛线坡膛应力云图

图11 步枪枪管梯形膛线应力云图
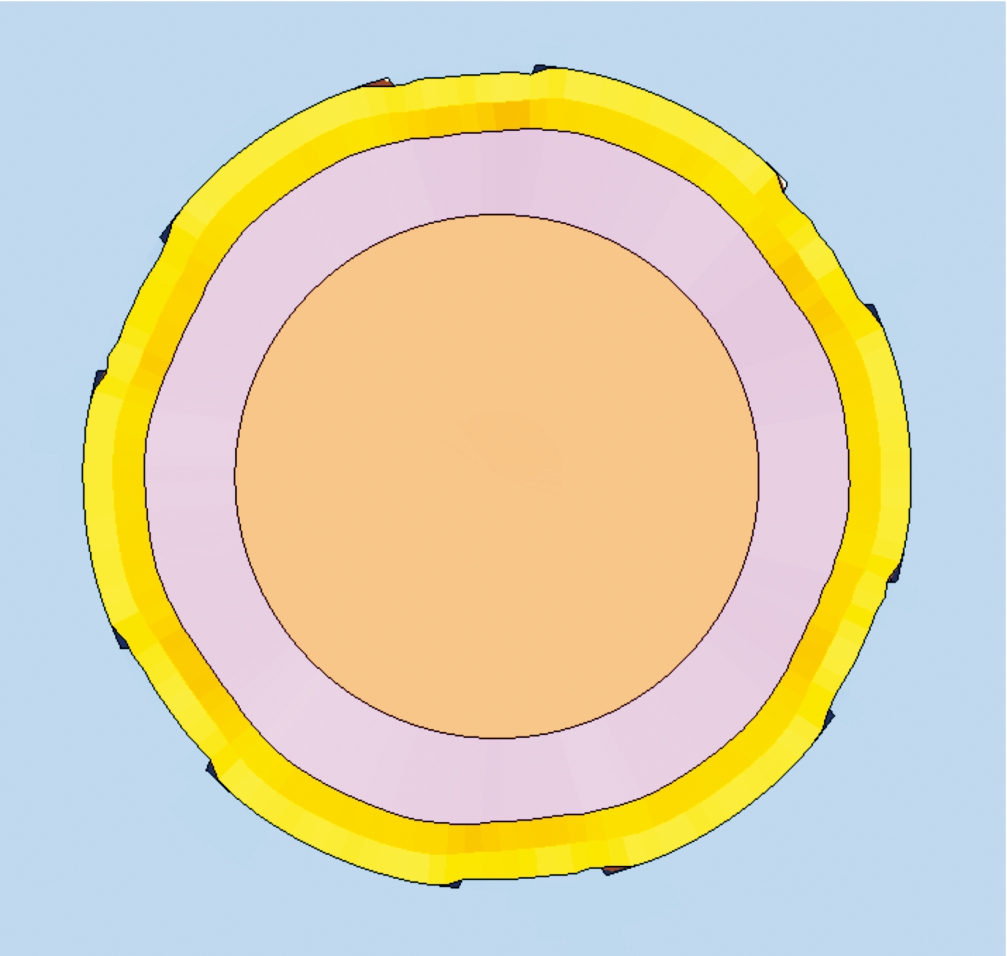
图12 步枪弹挤进枪管截面图

图13 梯形膛线枪管应力径向传递云图
3.2 弧形六条膛线仿真结果
重点提取弹头变形量,弹头与膛线贴合情况,被甲、铅套、钢芯的最大应力,坡膛与膛线的最大应力,具体见图14~图21,并对数据进行分析,如表2。

图14 步枪弹形变图
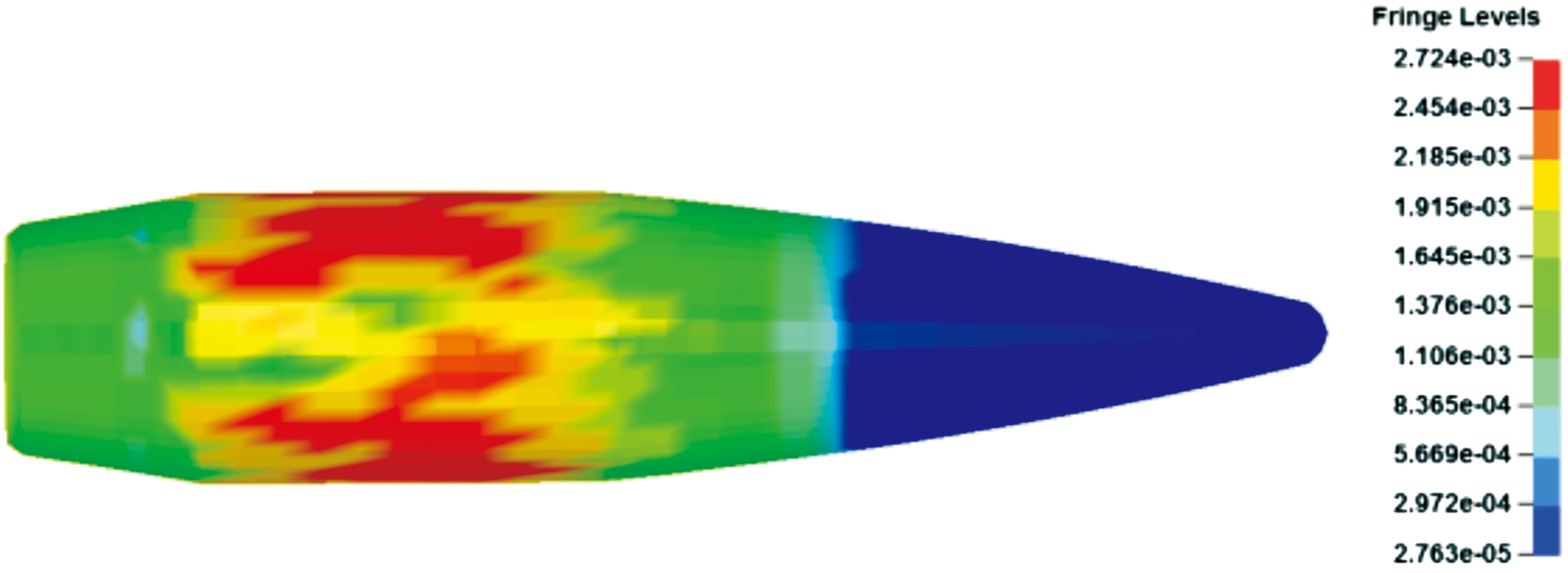
图15 步枪弹被甲应力云图

图16 步枪弹铅套应力云图

图17 步枪弹钢芯应力云图

图18 步枪枪管弧形膛线坡膛应力云图
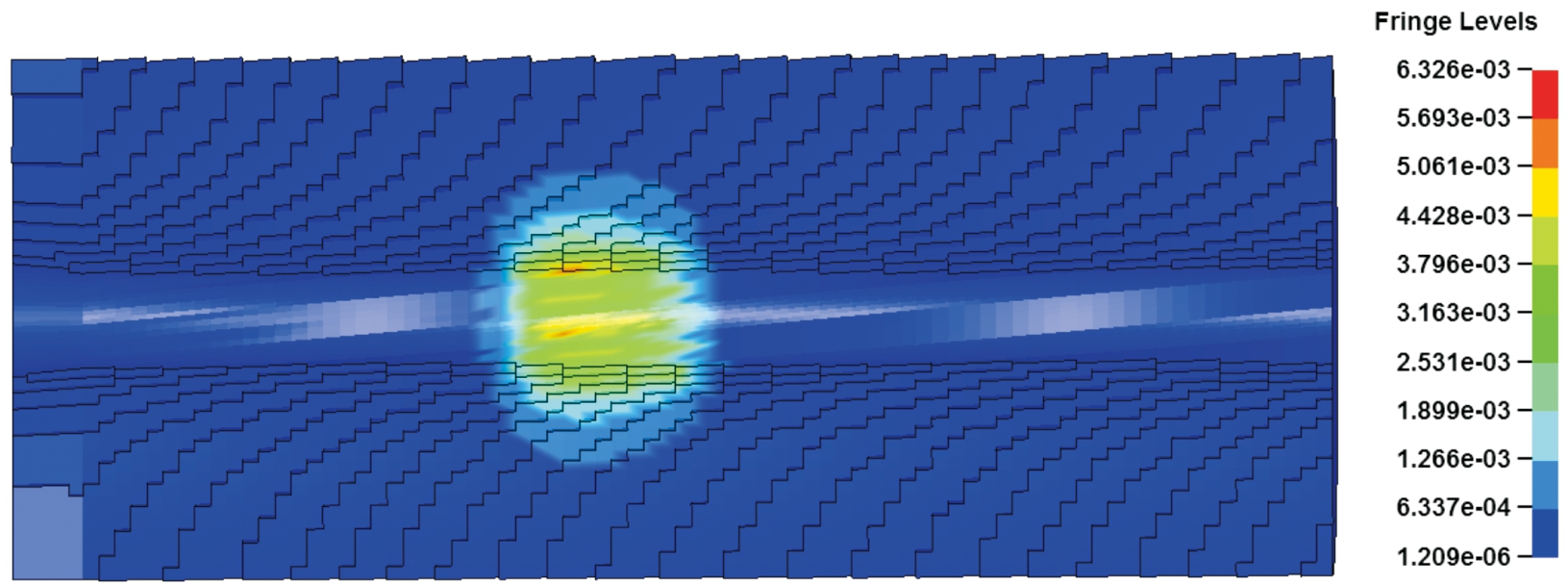
图19 步枪枪管弧形膛线应力云图
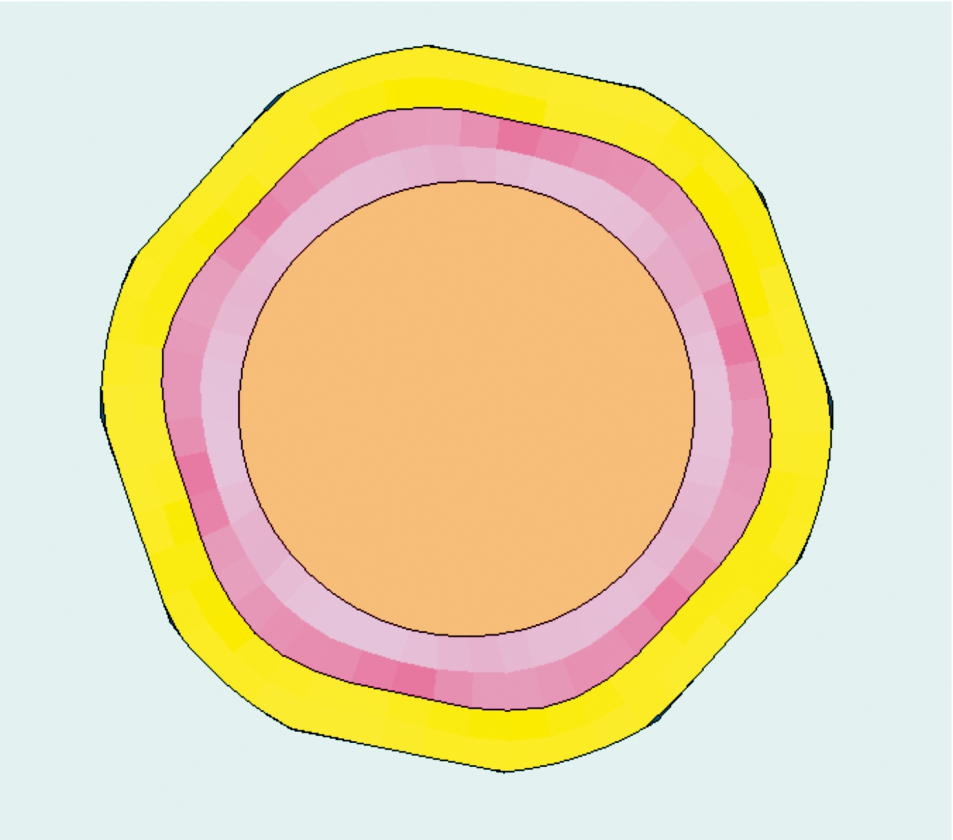
图20 步枪弹挤进枪管截面图
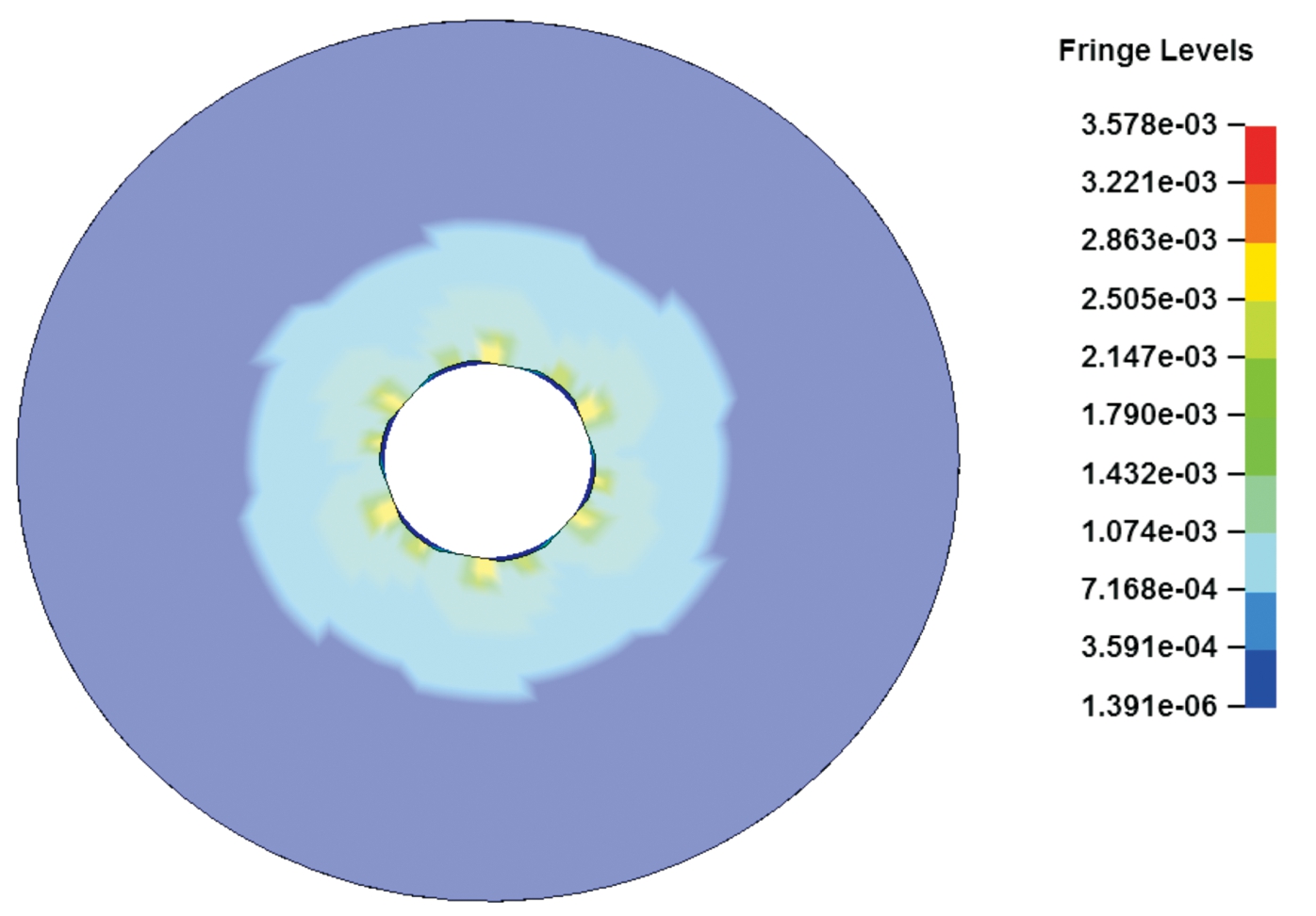
图21 弧形膛线枪管应力径向传递云图
3.3 仿真结果分析
步枪弹挤进枪管后,通过两种膛线结构截面图11和图19可以看出,弧形膛线结构可使弹头与枪管阴线阳线贴合的更加紧密,起到较好的闭气效果,有利于弹头初速提高;通过两种膛线枪管应力径向传递云图图12和图20可以看出,由于梯形膛线存在应力集中,应力向枪管外壁传播距离较短,而弧形膛线结构过渡平滑,应力向枪管外壁传播距离较远,对提高枪管寿命有利。
从表2可以看出弧形膛线应力值与传统梯形膛线应力值,被甲应力降低3.5%,铅套应力增大5.5%,钢芯应力降低20.2%,坡膛应力降低45%,膛线应力降低55.6%。仿真结果表明,弹头挤进弧形膛线时,弹头没有损坏,而且降低了膛线应力,提高了枪管寿命。
表2 不同膛线结构应力
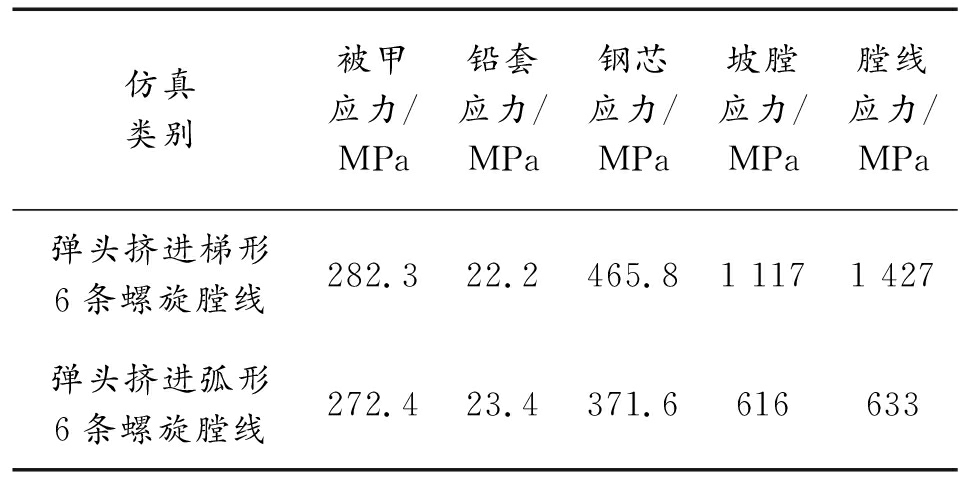
仿真类别被甲应力/MPa铅套应力/MPa钢芯应力/MPa坡膛应力/MPa膛线应力/MPa弹头挤进梯形6条螺旋膛线282.322.2465.81 1171 427弹头挤进弧形6条螺旋膛线272.423.4371.6616633
4 挤进含铬层枪管仿真初探
4.1 枪管及铬层有限元建模
前文仿真建模未考虑铬层的影响,本节初步建立枪管铬层模型如图22所示。铬层和枪管是紧密结合在一起的,在挤进变形过程中铬层一般不会脱落,铬层的厚度远远小于枪管的厚度,在枪管内壁表面直接进行 Thin Shell 163壳单元网格划分,并设置不同厚度,这样两种网格单元属于共节点方式,自动紧密结合在一起,这与实际情况相符合[10-11]。
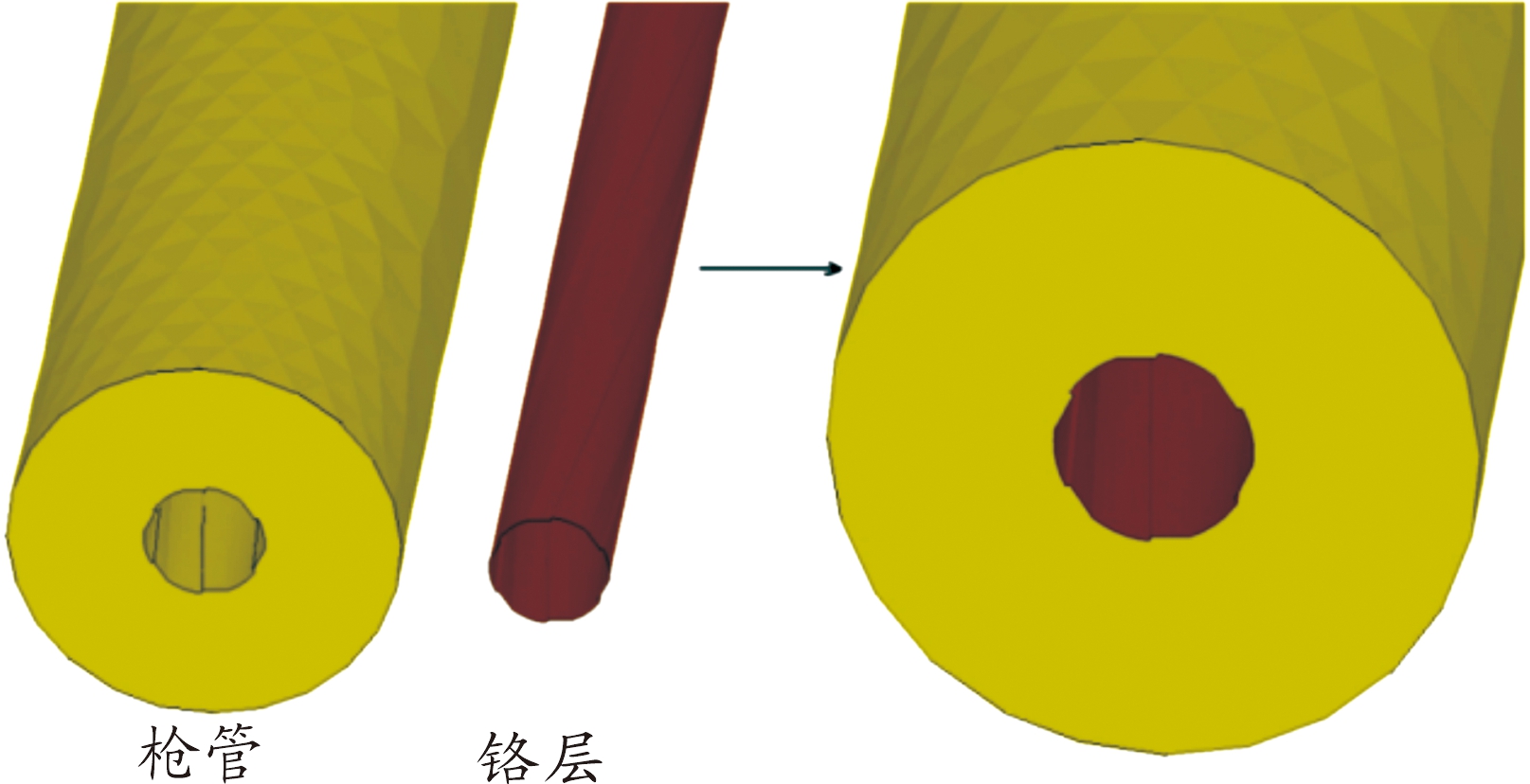
图22 枪管及铬层模型示意图
4.2 建立接触模型
对于铬层与枪管的接触,二者网格单元本身就属于共节点方式,无需再设置接触方式。
对于铬层与弹头的接触,受力情况比较复杂,影响因素众多,是一个弹头与铬层之间的接触,润滑与摩擦,大位移及大变形的过程,采用ONE-WAY CONTACT(单向接触)。
4.3 仿真结果分析
铬层厚度10丝时仿真结果可以看到膛线最大应力972.6 MPa,分布较为均匀,铬层最大应力944.8 MPa。如图23、图24所示。
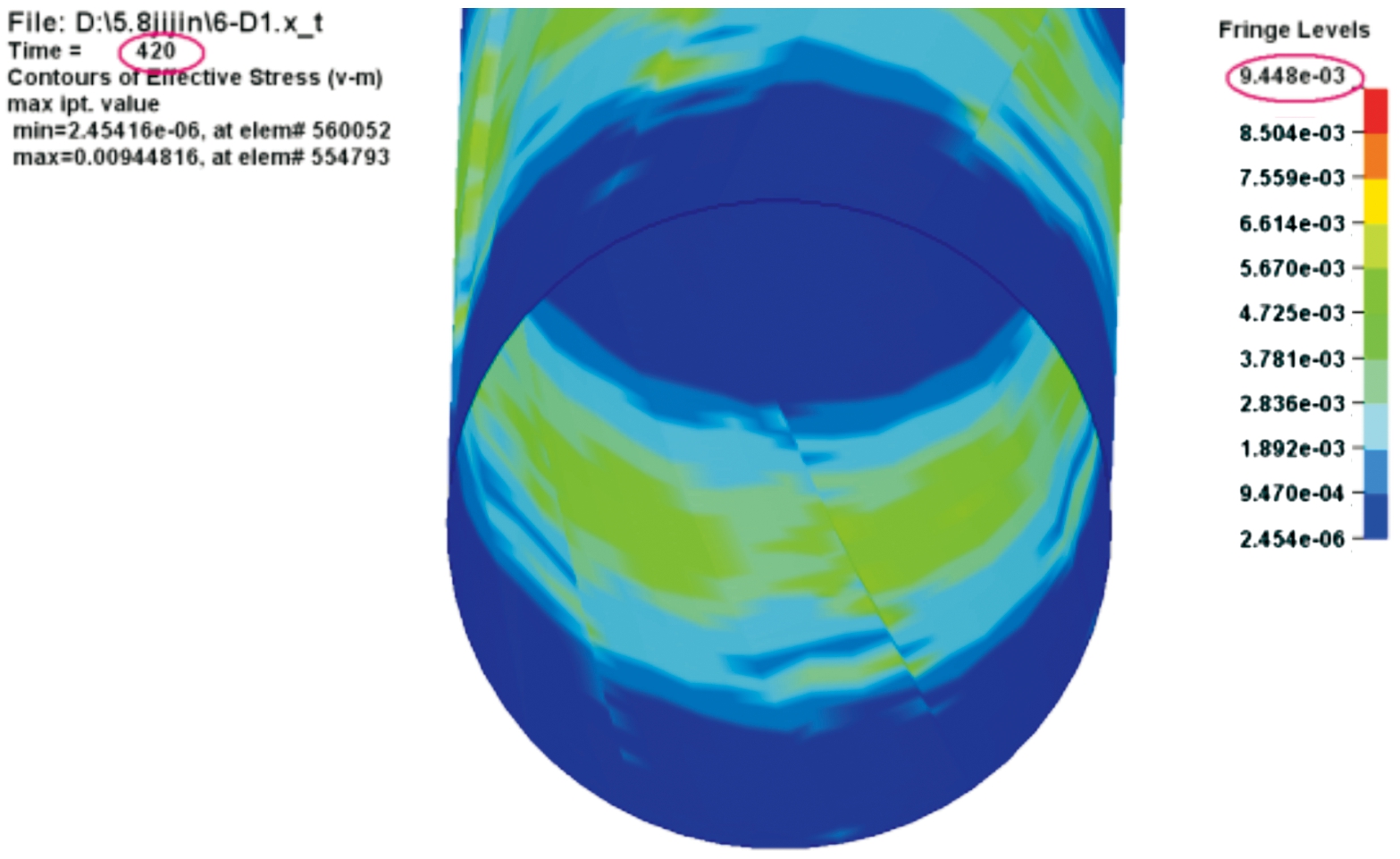
图23 铬层应力云图
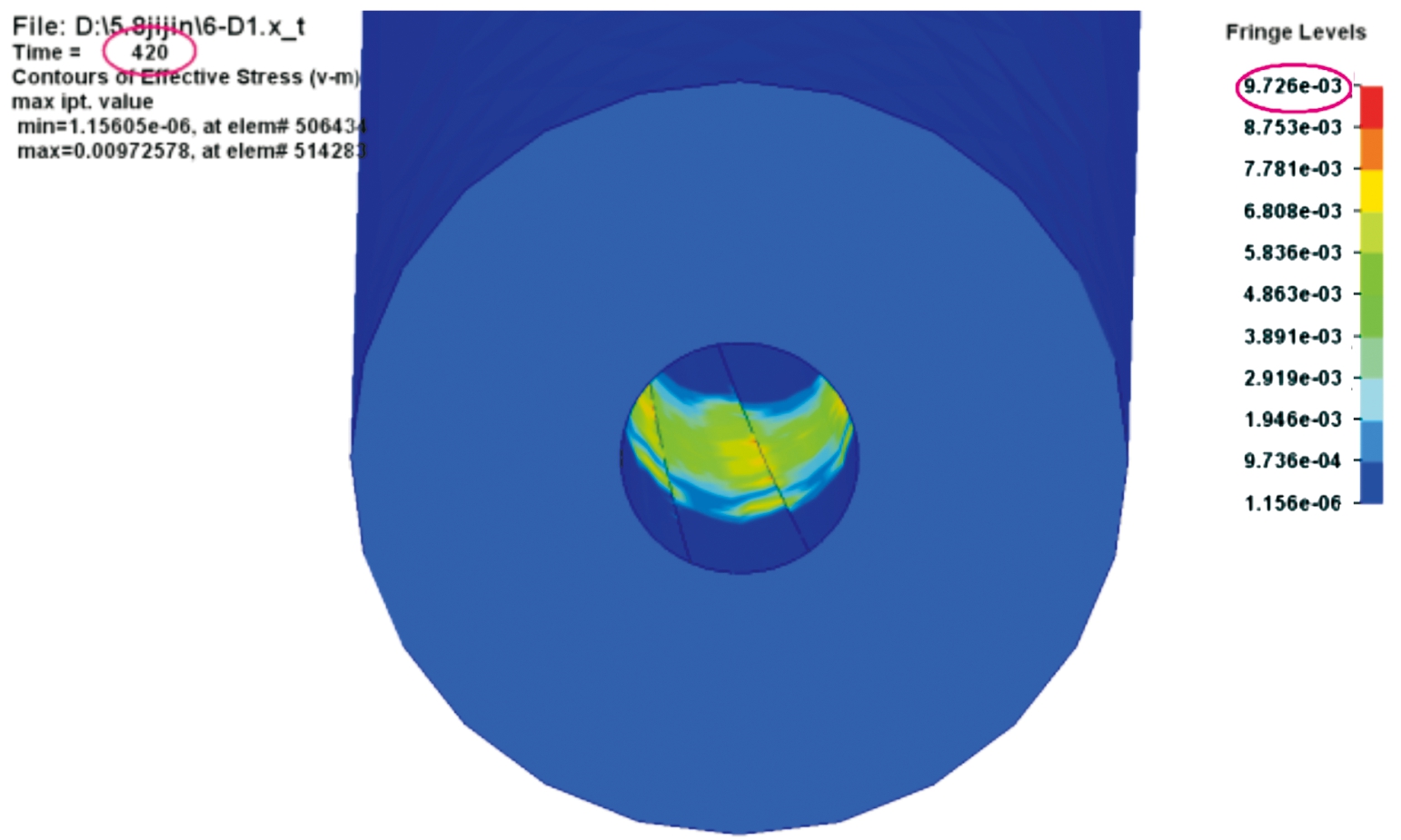
图24 膛线应力云图
由于铬层和枪管的弹性模量不同且二者厚度差别太大,在挤进变形过程中铬层和枪管所受应力的大小也不同,在二者结合面上也产生了应力差,即层间切应力。不同厚度铬层仿真结果如表3所示,由表3可以见到铬层与其他最大应力的关系。较厚时,铬层和膛线应力较小,但层间切应力较大,挤进时容易铬层脱落,而铬层较薄时,铬层和膛线应力较大,但层间切应力仍然较大,更不利于提高寿命,因此铬层的厚度需要综合考虑,厚0.1 mm时较为合适。
不同厚度铬层的应力曲线见图25。
表3 不同厚度铬层应力仿真结果
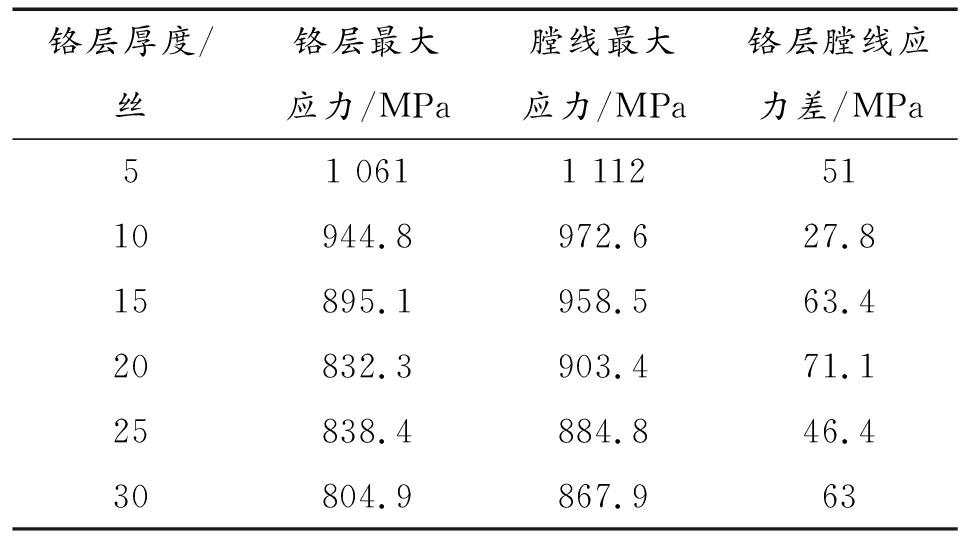
铬层厚度/丝铬层最大应力/MPa膛线最大应力/MPa铬层膛线应力差/MPa51 0611 1125110944.8972.627.815895.1958.563.420832.3903.471.125838.4884.846.430804.9867.963

图25 不同厚度铬层应力曲线
5 结论
1) 弹头挤进弧形膛线结构的枪管时所受应力较小,弹头可正常运动,被甲表面损伤程度较小,可明显减少挂铜现象,有利于射击精度的提高。
2) 枪管弧形膛线结构均比传统梯形膛线应力下降45%以上,为优选膛线结构和枪管寿命提升提供强有力的技术支撑。
3) 铬层较厚时,膛线应力较小,但层间切应力较大;铬层较薄时,层间切应力较小,但膛线应力较大,都不利于提高枪管寿命,与实际情况相符。
[1] 孙全兆,杨国来,王鹏.某大口径榴弹炮弹带挤进过程数值模拟研究[J].兵工学报,2015,36(2):206-212.
[2] 王鹏,杨国来,葛建立,等.基于Johnson-Cook本构模型的弹带挤进过程数值模拟[J].弹道学报,2015,27(2):55-61.
[3] 陆野,周克栋,赫雷.坡膛结构参数对枪械内弹道挤进时期的影响研究[J].兵工学报,2015,36(7):1363-1369.
[4] 陆野,周克栋,赫雷.某大口径枪械内弹道挤进时期的数值仿真与分析[J].弹道学报,2014,26(2):67-71.
[5] 丁传俊,张相炎.基于热力耦合有限元模型的弹带挤进过程及内弹道过程的仿真研究[J].兵工学报,2015,36(12):2254-2260.
[6] 丘尔巴诺夫 E B.挤进时期内弹道学与挤进压力计算[J].杨敬荣,译.北京:国防工业出版社,1997:115-121.
[7] 樊黎霞,何湘玥.弹头挤进过程的有限元模拟与分析[J].兵工学报,2011,32(8):963-968.
[8] 韩文祥.弹头挤进变形模拟问题研究[D].南京:南京理工大学,2009.
[9] 彭涛,王学军,黄善文.基于ANSYS的弹带挤进变形及应力分析[J].舰船电子工程,2009,29(11):156-158.
[10] 殷军辉,郑坚,倪新华,等.弹头膛内运动过程中弹带塑性变形的宏观与微观机理研究[J].兵工学报,2012,33(6):677-681.
[11] 伍杰.镍镀层金属薄板冲压成形的失效分析[D].湘潭:湘潭大学,2012.