伴随武器装备可靠性水平不断提高，受试验周期等保障条件制约，传统基于被试品故障个数和故障时间的高可靠性评定方法逐渐不相适应。传统的可靠性评估是基于产品只有正常、失效两种状态，分析手段主要是通过大量的试验数据得到产品的失效数据，然后应用统计原理，选择合适的分布模型，得到产品的可靠性。但对于复杂的高可靠度装备而言，这种基于一定失效数据的可靠性分析评估理论在工程应用实践中存在着一定的局限，主要表现在：一是针对高可靠性产品，在进行评估时所得到的可靠性试验数据往往有限，无法应用传统的可靠性理论建立精确的评估模型，难以进行有效的可靠性评估；二是在产品的性能验证各阶段，积累的大量可靠性综合测试数据，不能在可靠性分析工作中被深度挖掘运用，最终验证试验评估往往只记录和采用故障数和故障时间，评估结果不能体现可靠性的变化趋势。故本文引用产品性能可靠性[1]和性能失效特征量的概念以及分析方法，对复杂电子装备性能可靠性评估进行了分析，特别是提出了基于性能失效特征量随机漂移的装备可靠性评估方法，为高可靠性产品评估提供了新的途径。
1 性能失效特征量的确定
由于受使用环境和条件的影响，装备在使用或贮存过程中，其性能往往会随着时间的延长而逐渐的变化，原因可能是由于零部件之间磨损、电器件性能衰退等造成的机械公差范围变大、电阻值超差等。而上述这些表征产品工作能力的参量，我们称其为“性能失效特征量”。而性能可靠性是指产品在规定的条件和时间内，性能失效特征量保持在规定指标范围内的概率[2]。
性能失效特征量是表征产品性能变化的参数，应根据产品规定的功能来确定。确定前，应先明确产品的失效标准，失效标准是判断产品工作状态好坏的依据，其值又称为失效阈值，某种情况下它可能是一个随机变量，具体由工程实际问题决定，失效标准往往按照产品的设计指标要求来确定。总之，性能失效特征量的选择通常有如下的考虑：一是性能失效特征量一般选取产品技术文件中规定的性能指标参数；二是性能失效特征量必须能够通过试验等测量手段得到；三是性能失效特征量应有较为明显的变化趋势，能真实表征映产品的工作状态；四是为更加准确描述产品失效特征，可以选择多种不同特征量参数，构建复合特征量[3-4]。
2 基于性能失效特征量参数随机漂移的性能可靠性评估
产品在外界复杂环境综合作用下，其性能或状态通常会发生变化。通常来说，性能会随时间增加而逐渐退化，但在退化过程中可能会出现短时间内不稳定的情况，进而表征产品性能特征量参数会出现随机漂移。基于性能失效特征量随机漂移的可靠性评估方法优点是：对于试验测量数据没有规律性要求，并且可依据实时获得的性能失效特征量参数评估任意时刻的性能可靠度结果[5-6]。
2.1 评估一般流程
步骤1：收集产品性能失效特征量数据，依据产品的定型文件规定的技术指标要求确定失效标准。
步骤2：随机选取m个子样，在不同的时间点t1,t2,…,tn(t1<t2<…<tn)分别测量得到特征量数据zij(i=1,2,…,m; j=1,2,…,n)，之后进行假设检验，得到不同时刻特征量的分布，据此估计参数值[7]。
步骤3：将上一步估计结果代入分布函数中，根据已知的失效阈值，进一步计算求得不同时刻产品的性能可靠度Rj(j=1,2,…,n)。
步骤4：利用数据{(tj,Rj); j=1,2,…,n}求可靠度分布中的未知参数估计。若服从指数分布，则
步骤5：通过适当的算法对参数
和
进行估计，求得相应分布的性能可靠寿命tR。
2.2 基于特征量参数漂移的随机过程建模分析
假设特征量漂移的原因是由于元器件受到了强度λ的泊松分布流的冲击[8]，且在(0，t)的时间内受到N(t)次冲击的概率pi(t)服从泊松分布：
(1)
假如第i次冲击后性能特征量产生的漂移量为Xi且相互独立，依据大数定理，当观测的值足够多时，则Xi服从于正态分布。而且各Xi和N(t)独立，X(0)≡0，从而总的漂移量X(t)有[9-11]：
(2)
显然，经过i次冲击的漂移量满足Xi(t)～N(iμ,iσ2)，则X(t)的分布函数为[12-13]
(3)
式中: pi(t)为出现i次冲击的概率; Fi(X)为i次冲击的漂移量。
则X(t)的概率密度函数为
(4)
由正态分布的数学期望
x·fN(iμ,iσ2)dx=iμ和泊松分布的数学期望
可推导出X(t)的数学期望为E(X(t))=μλt，方差D(X(t))=(σ2+μ2)λt[14]。
由X(t)的数学期望和方差，X(t)服从E(X(t))=μλt，D(X(t))=(σ2+μ2)λt的正态分布，因此下式成立：
F(x)=Φ((x-μλt)/d)
(5)
式中d2=(σ2+μ2)λt。
2.3 可靠度评估
如果系统性能失效特征量漂移量的容差范围为(a,b)，则发生故障前的性能可靠度可定义为[14]
R(t)=P{a<X(t)<b}， t>0
(6)
由式(5)得到性能可靠度的计算公式为
(7)
在实际应用中，通常a和b的值是已知的，而λ,μ,σ是估计得到，设X1(τ),X2(τ),…,Xn(τ)是在(0,τ)时间内一组样本量为n的观测值，进而由式(7)得到可靠度的估计算式为[15]
(8)
其中， 
3 应用示例
假设某装备正常运行时，其性能特征漂移量的容差范围为(-3.0,3.0)，30 d内实际测得的性能特征量漂移量数据见表1所示，问该装备运行90 d后的可靠度是否满足95%的指标要求。
依已知条件计算得到：
故有：
根据可靠度估计计算式(8)，计算得到不同时间可靠度估计值如表2所示，可靠度变化趋势见图1所示。
表1 性能特征量漂移量数据
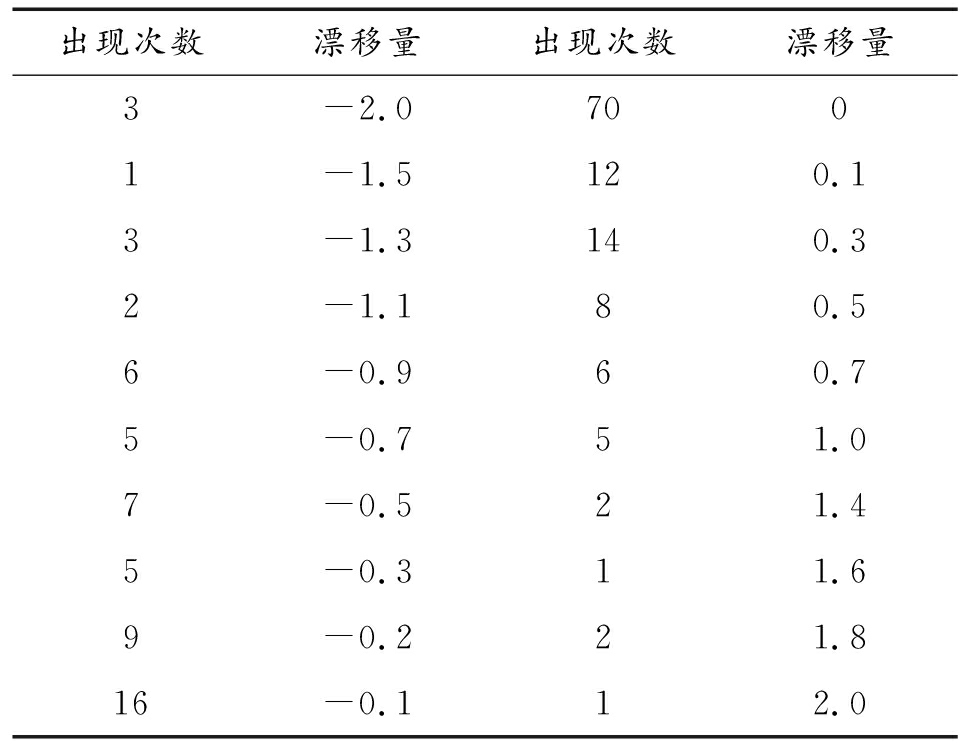
出现次数漂移量出现次数漂移量3-2.07001-1.5120.13-1.3140.32-1.180.56-0.960.75-0.751.07-0.521.45-0.311.69-0.221.816-0.112.0
表2 不同时间可靠度估计值
t51015202530354045R110.999 90.999 90.999 80.999 70.998 30.997 90.995 2t5560657075808590100R0.991 20.988 20.980 00.975 10.970 20.961 10.957 80.946 00.936 6
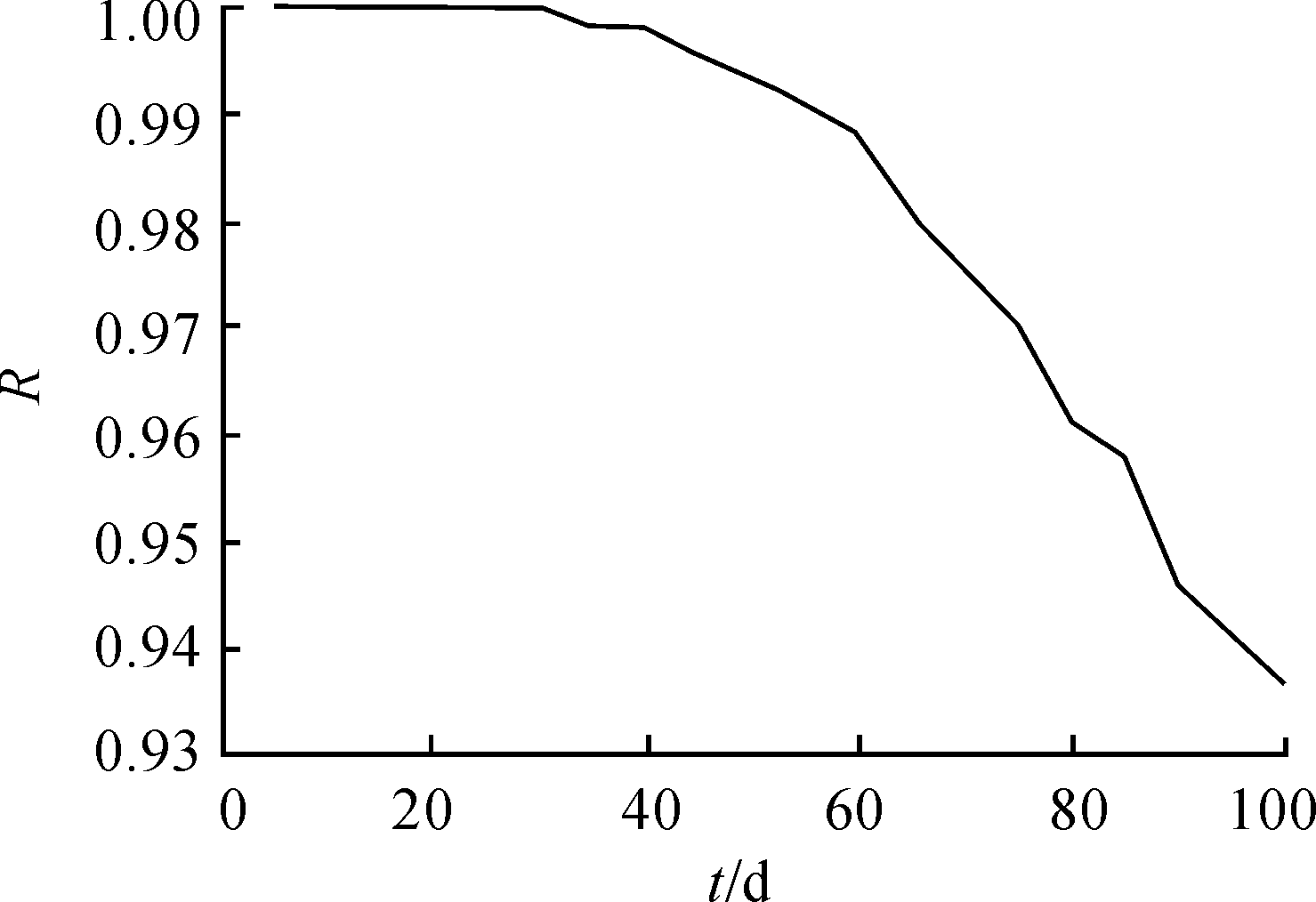
图1 装备可靠度曲线
由表2和图1可以看到，该装备随着工作时间的增加，失效发生的概率随之增加，即性能可靠性随时间增加呈下降趋势。装备正常工作90 d的可靠度估计值为94.6%，不满足指标要求。若采用传统的基于故障数和时间可靠性评估方法，一般只给出可靠性的点估计值，不能充分反应可靠性随时间的变化趋势。
通过上例分析过程，可及时掌握装备经过长期工作或贮存后的性能变化情况。同时，按照规定的可靠度下限，可及时确定装备预防性维护的时间期限，以便更好的开展装备延寿工作。
4 结论
提出了基于性能失效特征量随机漂移的电子装备性能可靠性评估方法，明确了其一般步骤及具体分析过程，并通过应用实例验证了该方法的可行性，此方法在预测装备预防性维护周期、使用寿命及潜在故障时间等方面具有工程应用价值。
[1] 胡超斌.性能可靠性评价指标的初步探讨[J].电子产品可靠性与环境试验，2004(6)：27-30.
[2] 黄建新，边亚琴，张胜涛,等.新型雷达装备系统性能可靠性评估[J].空军工程大学学报，2008，9(5):57-61.
[3] 盖炳良，滕克难，夏菲,等.整机级装备贮存延寿试验技术[J].火力与指挥控制.2018(01):169-174.
[4] 李晓阳，姜同敏，黄涛，等.微波电子产品贮存状态的SSADT评估方法[J].北京航空航天大学学报，2008，34(10):1135-1138.
[5] 王卓健，虞健飞，王礼沅.国内生存分析在可靠性数据分析中的应用进展[J].火力与指挥控制,2015,40(1):1-4.
[6] WANG X L,JIANG P,GUO B,et al.Real-Time Reliability Evaluation Based on Damaged Measurement Degradation Data[J].Journal of Central South University,2012,19(11)：3162-3169.
[7] 吴晗平.多阶段任务系统的可靠度研究[J].现代防御技术，1995(1):17-20.
[8] 孙青，庄弈棋.电子元器件可靠性工程[M].北京：电子工业出版社，2002.
[9] 金碧辉.系统可靠性工程[M].北京：国防工业出版社，2004.
[10] 库明阳，郭建英.基于故障树的系统可靠性仿真分析[J].计算机仿真，2007，24(08):78-81.
[11] 陆廷孝，郑鹏洲，何国伟.可靠性分析与设计[M].国防工业出版社，1995.
[12] CILLEN K T,CELINA M,BEMSTEIN R.Review of The Ultrasensitive Oxygen Consumption Method for Making More Reliable Extrapolated Predictions of Polymer Lifetimes[J].Ann Tech Conf Soc Plast.Eng,2004,62(2)：2289-2293.
[13] 韩松臣.导弹武器系统效能分析的随机理论方法[M].北京:国防工业出版社，2006.
[14] 李晓阳，姜同敏.基于加速退化模型的卫星组件寿命与可靠性评估方法[J].航空学报，2007，28(增):100-103.
[15] 尤琦，赵宇，马小兵.产品性能可靠性评估的时序分析方法[J].北京航空航天大学学报，2009，35(5):644-648.