为了满足现代战争的需要,世界各国竞相研制和装备各种口径的高精度狙击步枪,为此,我国开展了相应的狙击步枪高精度发射术研究,欲进一步提高狙击步枪的射击精度。枪管是高精度狙击步枪的重要部件,它的结构在很大程度上决定了射击精度,为了提高身管的多个性能指标,除了在身管的制造方法和加工工艺方面改进外,通过结构优化设计的方法来提高身管的性能指标也非常重要[1-2]。
然而,传统优化方法利用有限元分析软件对弹丸在枪管的膛内运动过程进行一次仿真分析需要将近48小时,若对枪管模型进行优化分析,不仅需要精细模型,而且需要进行近万次的寻优计算,少则需要几年时间,且容易陷入局部最优解[3];若采用数值计算方法,对于弹丸在膛内运动的复杂过程,考虑因素众多,计算量庞大,难以精确编程求解。随着神经网络、遗传算法等兴起,迫切需要一种高效、高质量的多目标优化方法[4-5]。
1 枪管结构优化方法
为了提高优化效率和质量,将多岛遗传算法、近似建模技术和有限元计算三者相结合,形成一种新的优化方法。
近似建模技术对解决过于复杂而费时的优化问题具有十分重要的意义,其基本思想是采用原始弹丸在枪管膛内运动有限元模型有限次计算得出的输入与输出数据,构造出精度满足要求、计算代价小的近似模型模拟原始模型的输入输出关系,然后用该近似模型代替弹丸在枪管膛内运动有限元模型进行寻优计算,大幅提高复杂模型的优化效率[6-7]。
遗传算法(GA,Genetic Algorithm)是Holland在20世纪60年代提出的,主要借助生物进化过程中“适者生存”的规律,模仿生物进化过程中的遗传繁殖机制,对优化问题解空间的个体进行编码(二进制或其他进制),然后对编码后的个体种群进行遗传操作(如:选择、交叉、变异等),通过迭代从新种群中寻找含有最优解或较优解的组合[8]。
多岛遗传算法(MIGA)本质上是日本Doshisha大学知识工程系的M.Kaneko,M.MiKi,T.Hiroyasu等对并行分布遗传算法(Parallel Distributed Genetic Algorithms)的改进,它具有比传统遗传算法更优良的全局求解能力和计算效率[9-11]。
在此通过多学科优化软件ISIGHT,集成三维建模软件Solidworks和有限元分析软件ABAQUS,对枪管结构参数进行优化,基于多岛遗传算法,实现对12.7 mm高精狙枪管结构多目标参数优化。
优化过程中,ISIGHT通过Solidworks组件对弹丸在膛内运动的参数化模型中枪管结构参数进行修改,然后采用构建好的近似模型进行计算,并将近似型计算出的弹丸速度矢量表征数值弹丸初速、弹丸横向摆动角和弹丸纵向摆动角输入到优化目标函数中,如此循环往复进行寻优计算。其基本流程图如图1所示。
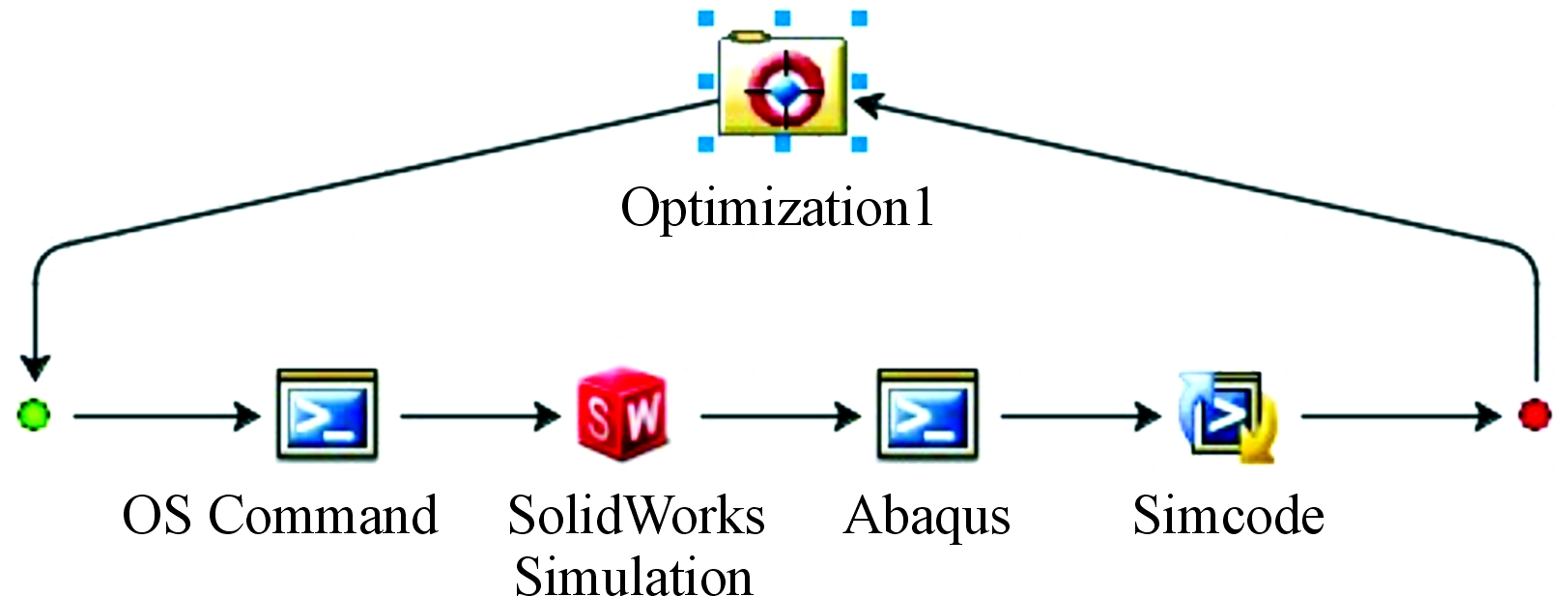
图1 枪管结构优化基本流程框图
2 有限元模型建立
进行结构优化前首先要建立有限元模型,利用SolidWorks建立12.7 mm弹丸和枪管的实体三维模型并导入ABAQUS中,设置各个零件的材料参数、相互作用和载荷参数,对各个零件进行网格划分并设置输出参数。在建立枪管的有限元模型时,抑制对武器动态特性影响不大的零部件的微小特征,如:螺纹、小导角等,并对一些对发射特性影响不大的零部件进行了简化处理,保留了枪管的实际结构形状特征。
枪管材料为30CrMnMoTiA,弹丸被甲材料为紫铜,弹芯材料为铝,设置模型各部分的材料参数[12]如表1所示。
表1 模型材料参数
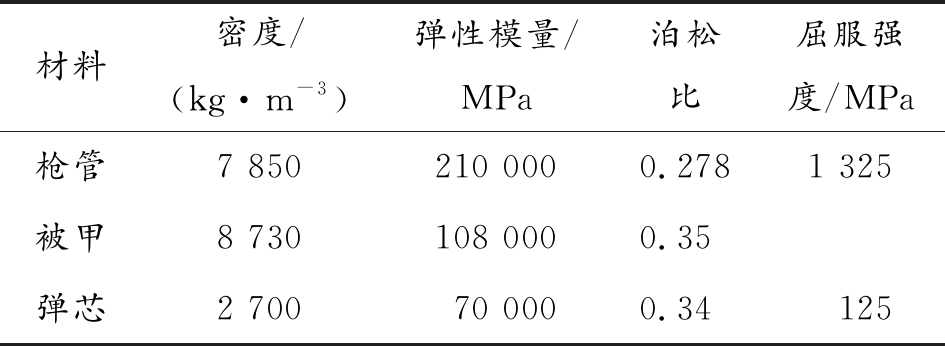
材料密度/(kg·m-3)弹性模量/MPa泊松比屈服强度/MPa枪管7 850210 0000.2781 325被甲8 730108 0000.35弹芯2 70070 0000.34125
在设置材料属性时铜被甲用Johnson-Cook本构方程法设置,Johnson-Cook本构方程法是由Johnson和Cook提出的一种经验模型,这种经验模型较为综合的考虑了应力强化、应变率强化和温度软化对材料力学性能的影响,能够更为清晰直观的描述弹丸嵌入枪管膛线的过程[13],具体的材料参数如表2所示。
表2 Johnson-Cook本构方程法被甲材料参数

A/MPaBmNTr/℃Tm/℃1125050.421.6801 058
为了真实地模拟出枪管在弹丸发射过程中的实际情况,考虑了武器其他部件如膛口装置等对枪管的作用,对枪管添加了外载荷力,模拟真实约束条件,在枪管尾部圆柱端约束了全部自由度,为了真实地反映弹丸的挤进过程及在膛内运动情况,对弹丸施加火药燃气在膛内的压力载荷。
ABAQUS软件中的求解器一般分为Standar求解器和Explicit求解器[14]。Standar求解器适于模拟静态、准静态的各种非线性问题,但弹丸的挤进过程和膛内运动过程伴随着材料的塑性变形、材料之间的摩损以及材料表面的热交换与热对流,本质上是一系列的复杂接触问题。因此,在对仿真分析的求解器的选择中,需要考虑处理复杂的弹塑性应变的能力,在计算非线性问题的过程中,为了保证网格在激变的情况下而不发生扭曲变形而导致计算失败,选择ABAQUS/Explicit求解器,可以使仿真分析结果更快、更加精确。
根据实际的情况,结合分析计算的客观条件,选择六面体网格作为划分类型。单元类型分为减缩积分与完全积分[28]。对于减缩积分的线性单元只在单元的中心有一个积分点,减缩积分的二次单元在每一个方向上有2个积分点;对于全积分的线性单元在每一个方向上采用2个积分点,完全积分的二次单元在每一个方向上采用3个积分点。
为了减少计算时间,单元类型选择减缩积分,同时为了保证精度,枪管膛线处和弹丸被甲的网格大小为0.1~0.5 mm,枪管和铝芯为0.1~2 mm。
完成后的弹丸与身管耦合作用有限元模型如图2,能有效满足有限元分析和参数优化需求。
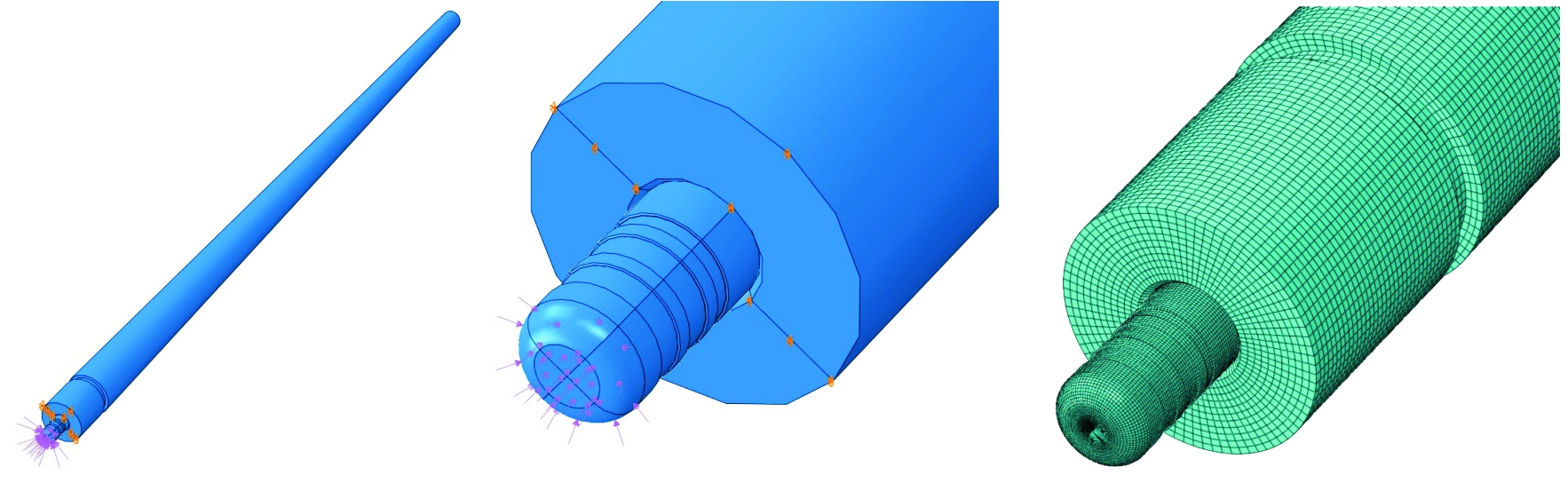
图2 弹丸与身管耦合作用有限元模型
3 优化过程及优化结果
以12.7 mm高精狙的身管结构参数为设计变量,利用多岛遗传算法(MIGA),以优化弹丸出膛口时刻的速度矢量为目标,对枪管结构参数进行优化计算,并将参数优化后的结果代入原始弹丸在枪管内运动的有限元模型进行有限元分析,评估验证优化结果。
3.1 优化过程
在进行结构优化前通过最优拉丁超立方试验设计方法对枪管结构参数进行了灵敏度分析,根据灵敏度分析的结果,选取对弹丸起始扰动影响较大的4个枪管结构参数作为优化设计变量,分别为膛线条数n、膛线深度h、膛线导程L、阴阳线宽度比t,具体参数取值范围如表3所示。
表3 枪管结构参数设计变量及取值范围
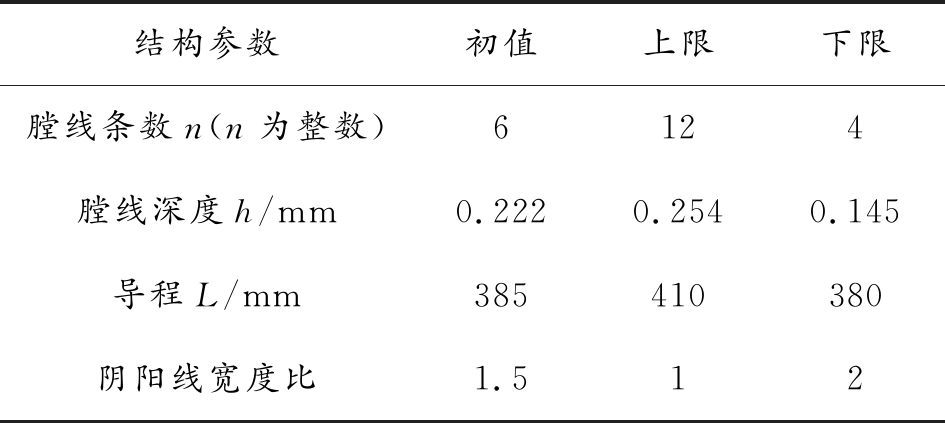
结构参数初值上限下限膛线条数n(n为整数)6124膛线深度h/mm0.2220.2540.145导程L/mm385410380阴阳线宽度比1.512
以4个枪管结构参数作为优化设计变量,同时以弹丸出膛口时刻速度矢量目标函数达到最大值为优化目标,对应弹丸速度矢量优化数学模型如下:
MAX F(Xi)=f(f1,f2)
XLi≤Xi≤XUi 1≤i≤5
其中,F(Xi)为弹丸起始扰动目标函数;Xi为结构参数设计变量,共5个,XLi、XUi分别为设计变量的取值下限和取值上限。以弹丸运动的摆角和速度为目标函数建立优化目标函数数学模型如下:
f=f1-f2
其中,f1为弹丸运动速度大小目标函数; f2为弹丸运动的摆角目标函数;θx和θy为弹丸横向和纵向摆动角;v为弹丸的速度大小;v0、θx0、θy0为弹丸相应参数的初始值;c1、c2、c3为各弹 丸参量的影响程度来确定的经验值,且c1+c2+c3=0。
釆用多岛遗传算法(MIGA),在每个岛上运用传统的遗传算法进行子种群进化,同时MIGA算法每隔一定的代数会进行迁移操作,保证了群体的多样性,避免局部最优解,提高了达到全局最优解的机会[15]。经过多次试算验证,弹丸速度矢量优化算法的参数设置如表4所示。
3.2 优化结果分析
将膛线条数n、膛线深度h、膛线导程L和阴阳线宽度比t这4个枪管结构参数的优化结果和最初值进行对比如表5所示。
表4 优化算法的参数设置

参数值子种群规模10岛的个数10总群体规模100总进化代数200交叉概率0.9迁移的间隔代数5保留到下一代的精英个体数量1
表5 枪管结构参数优化前后值对比
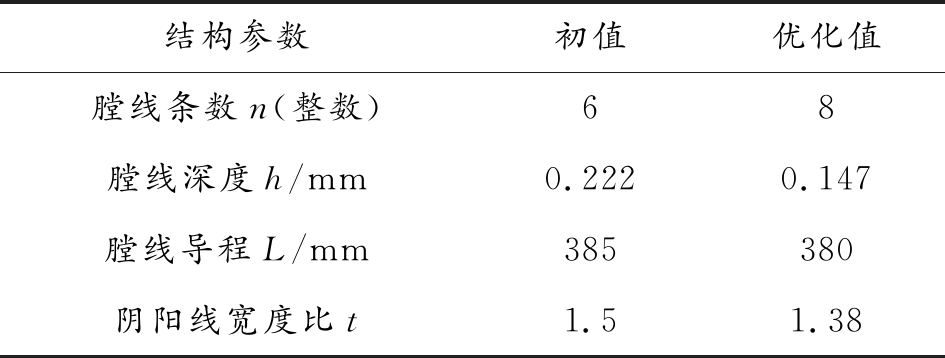
结构参数初值优化值膛线条数n(整数)68膛线深度h/mm0.2220.147膛线导程L/mm385380阴阳线宽度比t1.51.38
根据表5可以看出:膛线条数n、膛线深度h、膛线导程L和阴阳线宽度比t这4个参数均在给定的取值范围内取适中值,考虑到矩形膛线成本较低且闭气性较好,弹丸在膛内运动时也能较为平稳的挤进,因此选择矩形膛线。优化后的枪管横截面图如图3所示。
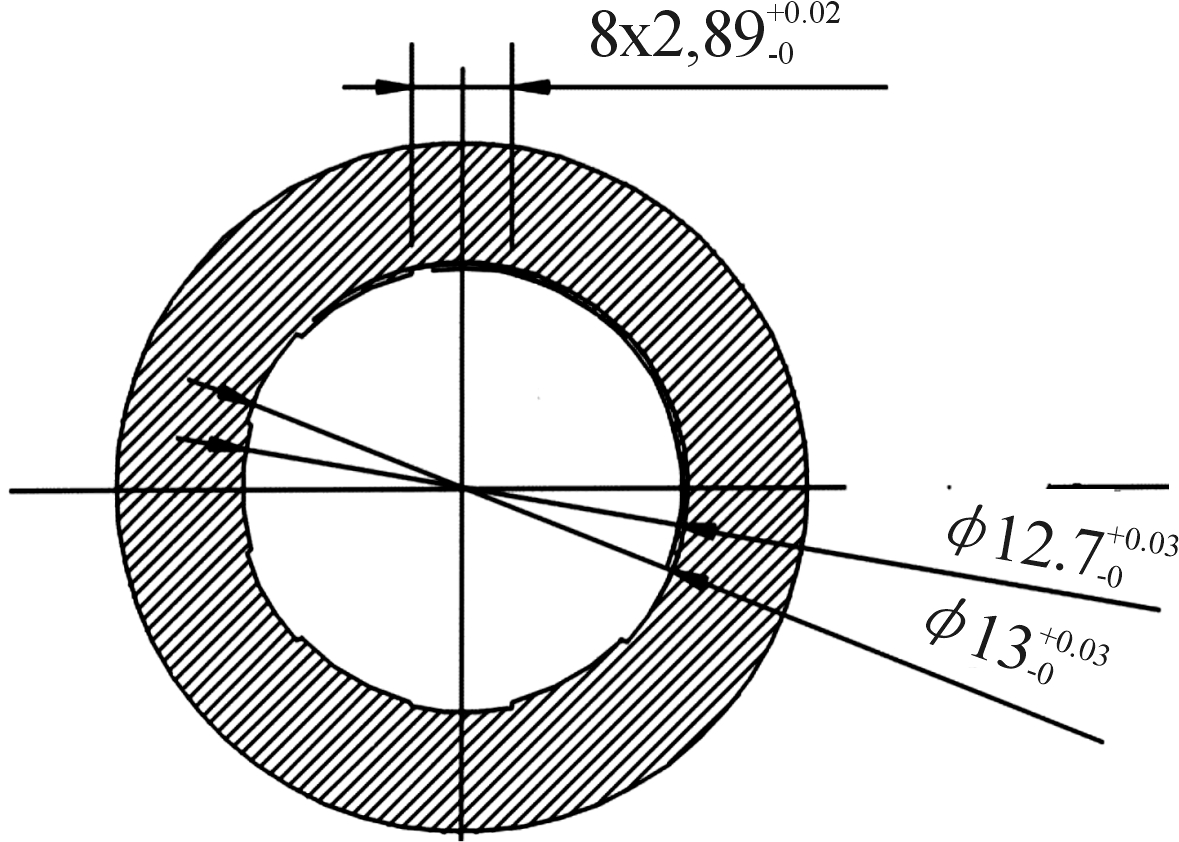
图3 优化后的枪管横截面图
通过与工厂专家的交流和探讨,优化后的身管可通过精锻和电镀工艺进行制造,身管参数具备工程实现可行性,并对优化前后的身管结构进行了仿真对比分析。
优化前后弹丸在膛内运动的速度、角度对比如图4~6所示。
从图4~图6可以看出:优化后在膛内运动时期,弹丸摆动幅度大幅减小,,其中弹丸攻角偏差变化幅度尤为明显,达到了对弹丸膛内稳定运动优化的效果。优化后弹丸出膛口时刻攻角偏差由1.6°下降至0.5°,降幅为1.1°;章动角由0.5°下降至0.3°,降幅0.2°;弹丸初速由939 m/s提升至966.3 m/s。优化效果明显,达到了对弹丸出膛口时刻速度矢量优化的目的。

图4 优化前后弹丸运动速度

图5 优化前后弹丸攻角偏差
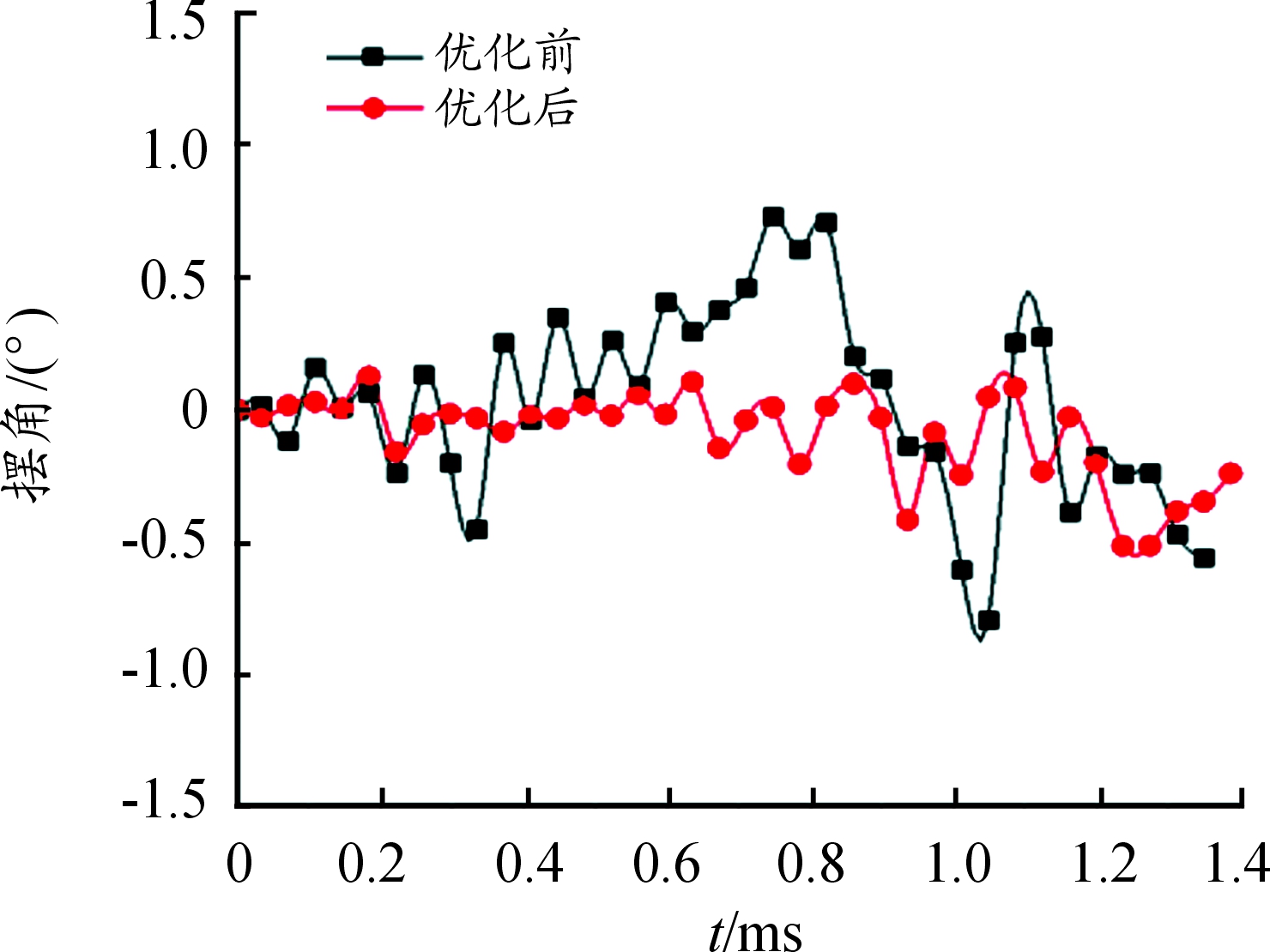
图6 优化前后弹丸章动角
4 结论
在膛线条数为8、膛线深度0.147 mm、膛线导程380 mm和阴阳线宽度比1.38的情况下:
1) 弹丸在膛内运动时摆动幅度大幅减小,出膛口时刻攻角偏差下降1.1°,章动角下降0.2°,有利于提高稳定性;
2) 弹丸初速增加了27.3 m/s。
采用此优化方法,优化参数区间大,优化效率较高,质量较好,达到了12.7 mm高精狙枪管结构参数优化设计的目的,为提高武器射击精度的武器结构参数高效优化设计提供了技术途径参考,同时对其他的工程设计也具有应用价值。
[1] 萧辉,杨国来,孙全兆,等.基于自适应神经网络的火炮身管结构优化研究[J].兵工学报,2017(10):4-11.
[2] GESKIN E S,PETRENK O P,RUSANOVA O A,et al.Strength analysis and optimization of the barrel nozzle of a powder water cannon[J].Strength of Materials,2006,38(02):206-213.
[3] 李林林.自行火炮身管优化方法及应用研究[D].南京:南京理工大学,2013:15-20.
[4] 方峻,李林林,徐诚.基于神经网络和遗传算法的身管多目标优化[J].机械设计与制造,2013(08):110-112.
[5] 徐志远,葛建立,杨国来.影响炮口扰动的火炮总体结构参数灵敏度分析与优化[J].兵器装备工程学报,2016,37(06):45-48.
[6] 宋浩展.基于高斯随机过程的高精度近似建模及其在车身声学结构特性优化中的应用[D].重庆:重庆大学,2019:20-30.
[7] 王强,苏小平,尹振华.基于响应面近似模型的汽车后桥桥壳优化[J].郑州轻工业学院学报(自然科学版),2019,34(01):71-78.
[8] 刘国强,陈维义,陈华东,等.舰炮身管的模态分析与多目标优化[J].国防科技大学学报,2020,42(02):150-155.
[9] 赵山杉,张雯,李晶,等.基于多岛遗传算法的小型有效载荷分离装置质量优化设计[J].导弹与航天运载技术,2017(02):16-19.
[10] 郭映华,朱文芳,赵娜,等.基于多岛遗传算法的膛压动态加载实验装置参数优化[J].火炮发射与控制学报,2019,40(03):90-93,110.
[11] SABULSKY D O,JUNCA J,LEFEVRE G,et al.A fibered laser system for the MIGA large scale atom interferometer[J].Pubmed,2020,10(1):10-15.
[12] 王鹏,杨国来,葛建立,等.基于Johnson-Cook本构模型的弹带挤进过程数值模拟[J].弹道学报,2015,27(02):55-61.
[13] BOISSON D,RIGOLLET F,LEGREAT Q.Raditiative Heat Transfer in A Gun Barrel[C]//Proceedings of 17th International Symposium on Ballistics,1998:338-341.
[14] 石亦平,周玉蓉.ABAQUS 有限元分析实例详解[M].北京:机械工业出版社,2006.
[15] SHI X,MENG X,DU X,et al.Application of MIGA to optimal disposition of sensors in active vibration control[J].Zhendong Ceshi Yu Zhenduan/Journal of Vibration,Measurement and Diagnosis,2008,28(01):62-65.