零件制造质量由设计公差和制造公差共同决定，影响成品的几何特征和功能特征。工程师通常需要选择适当的模型来描述公差，这样，一方面可以根据设计图估计公差，另一方面，公差可以分配到设计图的每个部分，以满足目标公差要求[1]。传统上，公差建模主要有两种类型：极值法和概率统计法[2-3]。概率统计法通过考虑公差的分布来校核或设计公差，从而使每个公差都与其对应的分布相关联。通过统计规则对相关公差进行总结，可以实现公差的传播。统计分析模型描述了对目标公差分布范围的估计，而不是计算极值法中描述的极值[4]。本文在枪械尺寸链设计中引入了一种新的基于统计变量的公差建模方法，以及在该模型上进行公差合成操作。基于统计规则建立的公差模型，不仅适用于公差估计，而且也适用于公差分配。
目前，我国自动武器行业在实际加工和装配中，很难达到预定的设计目标，往往要通过“人工修锉”，即通过手工修配不合格零件尺寸，以达到最终产品的总装合格[5]。“人工修锉”严重影响轻武器的生产效率，降低了部件的互换性。增加了次品率。产品零部件之间的互换性差成为制约自动武器产品设计、加工、装配周期的一大难题。
在装配过程中，产生大量修锉问题的重要原因之一就是公差分配不合理。在我国，传统的分析方法是以二维尺寸链图为基础的数值计算(如极值法、统计法)，以及设计人员的经验来进行尺寸公差和形位公差的分析与分配[6-7]。同时自动武器典型机构的装配尺寸链计算项目繁多，常规计算手段与分析方法计算效率低、工作量大、校核困难[8]。
1 理论分析
1.1 概率统计法
运用极值法进行尺寸链的计算时，是按照各组成环的极限尺寸进行计算，即构成封闭环的所有组成环同时达到最大极限尺寸或最小极限尺寸。但在实际制造中几乎不可能出现工件的各个尺寸同时是极限尺寸的情况，所以封闭环出现极值的概率也极小。因此，采用概率论的原理从各组成环的实际分布特性出发，所得的封闭环公差更合理、更符合实际。在大批量的生产制造中，传统的概率统计法假定各组成环尺寸都是相互独立的随机变量，这样就可以应用正态分布理论来进行公差分析。通过大量的实际测量数据，任何组成环都有以下两个重要参数：
1) 平均尺寸，表示实际尺寸的集中分布位置；
2) 标准差，表示实际尺寸的分布相对于算术平均值的离散程度。
图1是依据正态分布原理绘制的尺寸误差分布图。
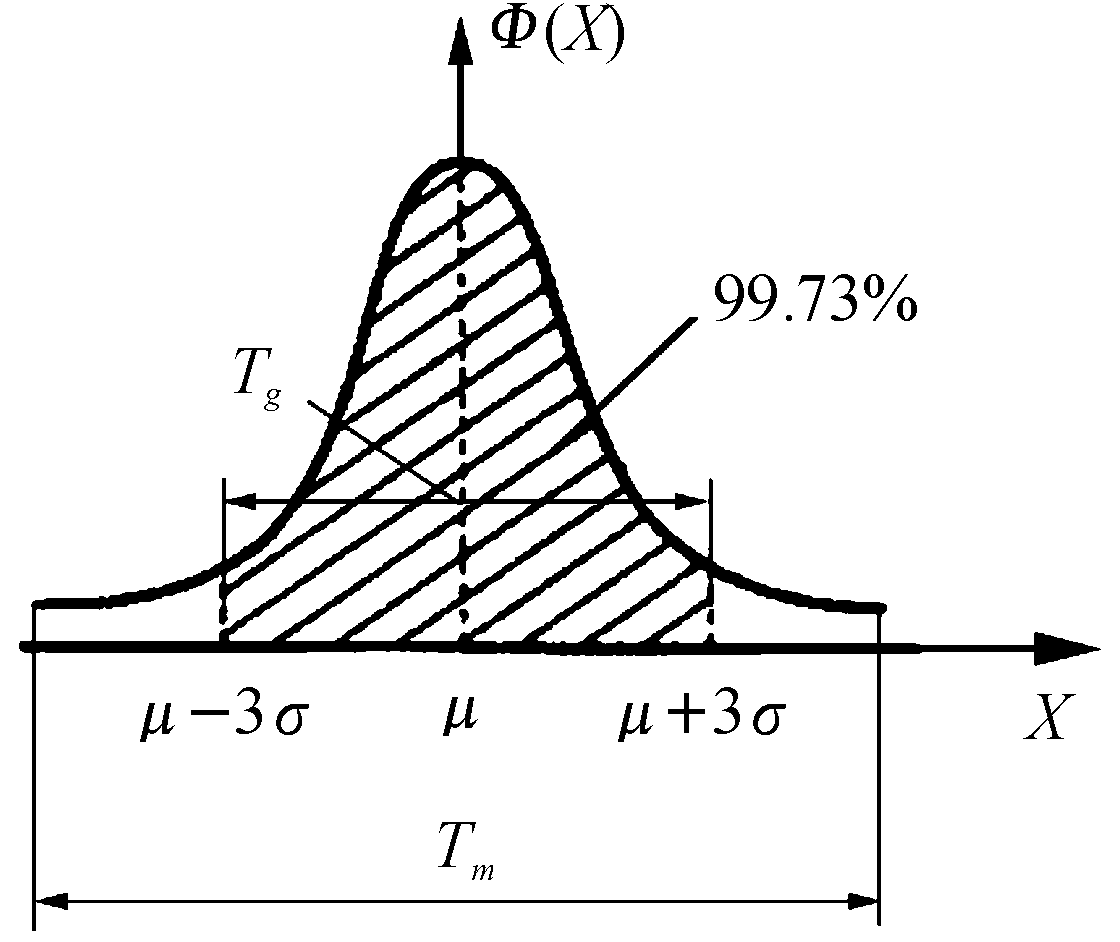
图1 尺寸误差分布图
其中，横坐标表示尺寸偏差范围，纵坐标表示在此偏差范围内的概率密度。Tm表示极值法所求得的极限尺寸公差；Tg表示概率统计法所求的处于±3σ内的尺寸公差，显然Tm>Tg。
统计概率计算法基本方程为：
1) 封闭环的平均值
为：
(1)
2) 封闭环的方差σx为：
(2)
式中，ξi为封闭环与组成环的传递比;
为各组成环的平均值; Ti为各组成环的尺寸公差，
是封闭环X对各组成环Ai的偏导数。
概率统计法相比极值法来说考虑了实际加工情况，既能在装配时确保大数互换又可以降低加工制造精度，降低成本提高效率。
传统的公差统计方法多采用蒙特卡罗模拟方法[9-10]，并将统计规则应用于公差估计。本文运用了一种新的统计公差几何模型，将传统统计公差分析中复杂的解析计算分解为一系列简单的几何计算，而不失去固有的统计意义。
首先使用多元统计模型来表示或近似系统中单个部件的公差分布，该模型与描述零件特征的多个维度相关联。对于置信值，可以确定一个描述公差区域的几何区域，这些区域通常被椭圆或椭球所包围。可以在统计模型上进行一系列操作，使来自不同部分的几何区域可以联系起来，公差可以沿着公差图传播。此外还可以从高自由度表示中提取低自由度信息的方法，以便于公差估计。新模型不仅能采用统计法计算公差，而且还考虑了尺寸之间的相关性，并对传统的尺寸公差带定义了几何形状。
1.2 多元统计分析[11]
在这一部分，使用多元正态分布来近似公差的分布，并且使用χ2分布来生成公差的几何表示。
假设存在一个n维向量μ，μ∈Rn，并假定各自由度之间的相关性由协方差矩阵ξ来表示。可以用多元正态分布来表示向量正态分布的不确定性区域.用一个概率密度函数来描述这个区域，若给出变量x的μ和σ的估计值。则可由下式求得：
(3)
其中x服从xN的正态分布，则可以得到多元正态分布服从χ2分布：
(4)
其中
表示p自由度的卡方分布，给定概率值α后，就可以求出在置信率(1-α)下x的分布区域。多元正态分布的这个置信区的形状通常是高维椭球。椭球体的中心由中心决定，椭球轴的方向和长度由协方差矩阵ξ决定。其中，二维正态分布的置信区域在平面的投影是一个椭圆。
1.3 多元正态分布的可加性
对于具有多元正态分布的随机变量X，具有以下性质：
1) X的分量的线性组合是正态分布;
2) X的分量的所有子集有一个(多元)正态分布;
3) 零协方差意味着相应的分量是相互独立的;
4) 分量的条件分布是(多元)正态的[11]。
以上4个多元正态分布的性质为以下方差的传递与合成提供了理论依据。
如果已知尺寸公差数据，就可以很容易地得到协方差矩阵ξ。通过对随机变量之间的相关关系的计算，可以得到构成相关矩阵的随机向量元素间的相关系数。
联系到实际公差设计，根据多元概率统计法原理，二维尺寸公差分布的置信区域示意图如图2。
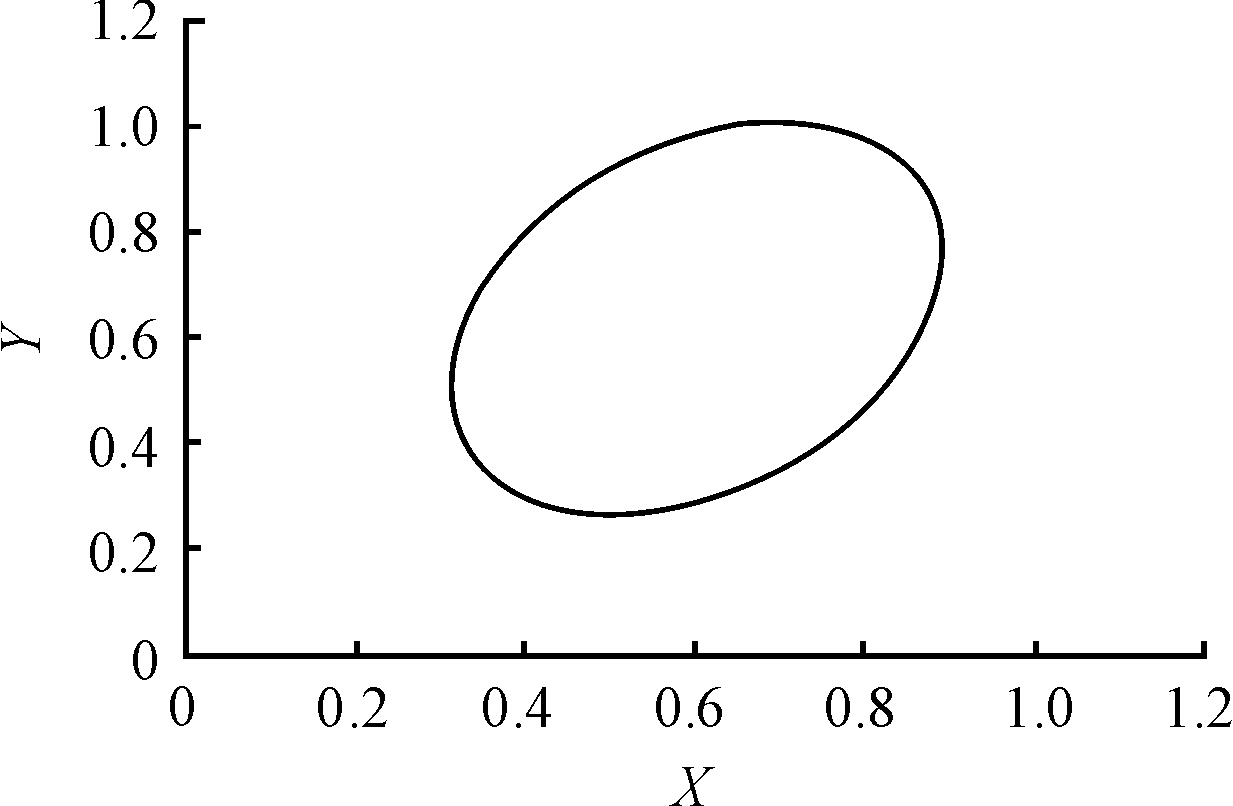
图2 置信椭圆图
在求得协方差矩阵后，运用式(2)可得到二元统计分布的置信椭圆图，椭圆内包含的区域表示在在置信度水平1-α情况下的置信区域，坐标点在给定的置信区域内的概率为置信度，通常情况下按照6σ的制造标准，α取0.002 7。其中椭圆中心点代表待求未知量的均值。
如果尺寸A和B之间的相关系数为正，则尺寸A取概率极值时尺寸B也取概率极值；对比于尺寸A和B相对独立的情况下尺寸A和B同时取极值的概率，显然尺寸A和B成正相关的情况下的概率更大，所以成正相关的尺寸会使计算结果比传统概率统计法偏大。反之负相关系数会使结果偏小。
在绘出零件的公差尺寸链图并确定相关系数ρ后，可以预测到相对于传统概率统计法的计算结果的大小：
1) 若公差尺寸链中只存在正相关尺寸，则二元统计公差计算结果会偏大；
2) 若公差尺寸链中只存在负相关尺寸，则二元统计公差计算结果会偏小；
3) 若公差尺寸链中同时存在正负相关尺寸，则计算结果相对大小都有可能。
2 公差合成
2.1 尺寸链串联叠加
只要给出零件的尺寸公差的参数，可以得到二元统计分布的一般形式
P(x; μ1, μ2, σ1, σ2,ρ)∝
(6)
其中: μ1、μ2为尺寸均值; σ1、σ2为方差; ρ为相关系数。
这种组合有两个假设。一个是变量x和y在空间中使用相同的基准坐标系,另一个是变量x和y都有相同的自由度。如果满足这些假设，就可以串联公差。也就是将变量x和y的协方差矩阵进行矩阵的加法运算。
然而在大多数情况下，在公差合成时既不能确保公差尺寸链图不同的部分使用相同的基准坐标系，也不能确保它们有相同数量的自由度数。当第一个假设无效时，可以使用坐标系转换来调整；当第二个假设无效时，可以使用简单的矩阵操作将所有变量x和y的协方差矩阵的自由度保持一致。
2.2 坐标系变换
当两个公差不具有相同的坐标系时，可以采用转换坐标系操作。基本上，可以对一组协方差矩阵进行旋转，并计算出为这组旋转的协方差矩阵提供最佳匹配的分布。如图3所示的公差链，公差a→b的基准坐标系不同于b→c，这是进行坐标系旋转操作的根本动机。设a→b的公差区遵循分布P(X)～N(μx，ξx)，b→c的公差区分布为P(Y)～N(μy，ξy)。假设两个公差带的传播方向是一致的。这时需要一个旋转矩阵R来对齐这两个基础坐标系。在不损失概括性的情况下，首先可以把P(X)的基看作静态参考。P(Y)的概率对齐为
其中R是旋转P(Y)基使其与P(X)一致的旋转矩阵。
图3 坐标系转置图
因为与多个自由度相关的零件的公差可以用多元正态分布建模，因此可以利用坐标系的旋转操作将两个具有不同自由度基的公差区域串联起来。坐标系的旋转运算保持了自由度的相关性，使得公差估计比传统的分解方法更精确。
2.3 协方差矩阵的对位
当将不同自由度数的两个公差区域合成时，可以运用一些矩阵的操作运算将它们结合在一起。设P(X)～N(μx，ξx)有x个自由度，P(Y)～N(μy，ξy)有的y个自由度，其中x>y。假定P(X)和P(Y)使用相同的基集，即的基是的一个子集。串联P(X)和P(Y)的过程可分3步完成。首先，将矩阵ξy重新排序为ξy1，使所用基的阶与的阶相同。其次，将矩阵ξy1扩展到ξy2，使其具有与x相同的自由度数，空位上填充零，以便两个矩阵的相应行指示相同的自由度。最后，使用公差的串联规则合并ξx和ξy2。由于这个运算将P(Y)的基对位到相应的P(X)基，所以称之为对位。
3 实例分析
闭锁机构是武器发射时关闭弹膛，承受火药燃气压力并防止后逸的机构。本文研究的是闭锁机构的装配间隙量X，其中闭锁机构装配产生的间隙会影响装配的质量，对自动武器工作的可靠性和射击准确性都有重要的影响。图4是闭锁机构的部分二维装配示意图，机构由枪管、弹壳、枪机、节套等组成，其零件尺寸及公差如表1所示。
图4 闭锁间隙示意图
表1 闭锁机构的零件尺寸及公差表
零件名称尺寸符号名义尺寸上偏差下偏差枪管H18.740.050H229.50.20H334.90.390弹壳D133.00-0.20D28.570-0.22D333.410枪机节套G5.50-0.048T430.10
运用二元统计公差的方法求解间隙X的公差。图5是闭锁间隙的公差尺寸链图，图中箭头方向表示公差传递的方向。从公差X的左端点开始进行公差的逐级串联。根据公式统计公差的分布规律有T=6σ，其中T是公差，σ为正态分布的标准差。在已知各组成环的公差情况下，根据协方差矩阵的一般形式可以写出各组成环的具体协方差矩阵。
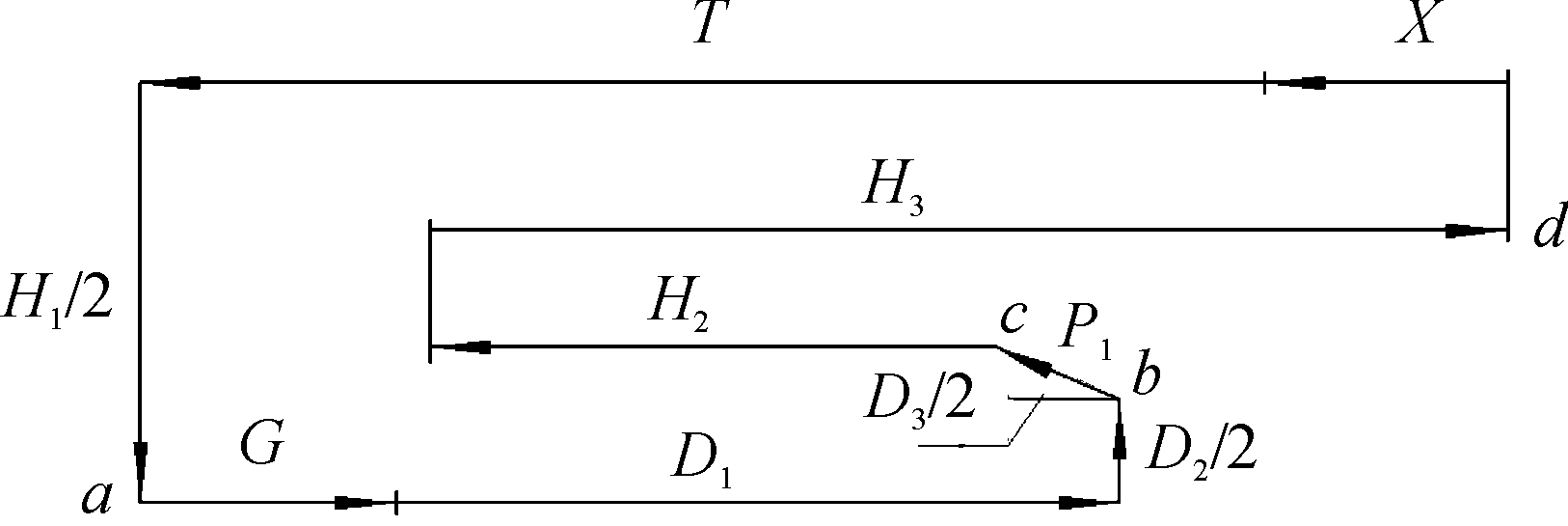
图5 公差尺寸链图
根据公差尺寸链的关系图5得到a、b、d的协方差矩阵，并按照对位操作扩展至二阶，其中尺寸D1和D2/2的相关系数为-1，分别为：
C点的变动范围由角度公差所确定，T1=L(1-cosθ), T2=Lsinθ, T1为X轴方向的变动范围，T2为Y轴方向的变化范围，σ1=T1/6, σ2=T2/6, ρ=1进一步转化为协方差矩阵可得
可旋转坐标系使C点的坐标系与其保持一致，根据矩阵的相关知识可以得到β=RTαR,其中α、β分别为为旋转前后的坐标系，R为旋转矩阵，θ为旋转角度值，在本例中θ=D3/2
(7)
求得c点的协方差矩阵：
在得到a、b、c、d四点变化的协方差矩阵后，最后可由串联规则将四点的协方差矩阵相加，求得总协方差矩阵为：
运用矩阵的求逆矩阵的方法进一步求得其逆矩阵为：
由公差尺寸链图可得封闭环X计算式：
(8)
可以计算得到X的理论平均值μ=0.537 680，又因为
在置信率99.73%即α=0.002 7的情况下运用式(5)得到：
可求出X的公差为T= 0.493 133。
图6是从Matlab程序中导出的间隙量X的置信椭圆图，表示其在平面上尺寸的分布区域。
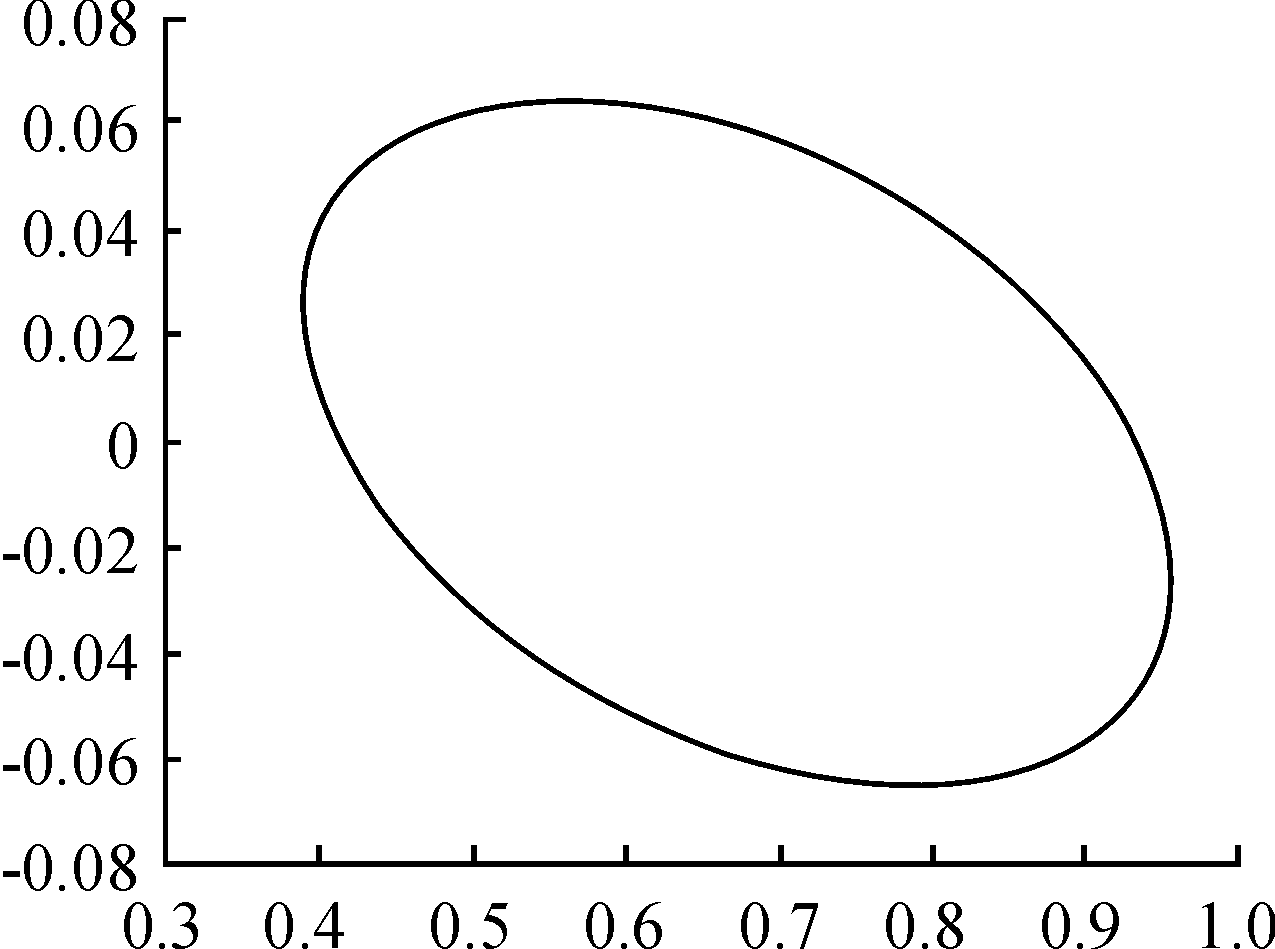
图6 闭锁间隙置信椭圆图
闭锁间隙置信椭圆图的意义：传统概率统计法求得的尺寸公差是一个封闭区间值，此置信区间相当于是由封闭环一元正态分布在置信率99.73%的区域投影到X轴所求的；而对于二元正态分布，对应其置信率99.73%下所投影得到的是封闭椭圆区域，它表示尺寸值在封闭椭圆内的合格率是99.73%。实际零件的封闭环尺寸在平面内的变动几乎不会体现在一维直线上变化，显然二元概率统计法的置信区间更具有代表性。
结合式(8)并运用线性尺寸链统计公差的计算式(2)，可以求得T1=0.507 105。
4 结论
运用二元统计公差的方法对闭锁间隙进行公差分析，在考虑到尺寸之间相关性的情况下求得的闭锁间隙的公差值为0.493 133，对比概率统计公差的计算结果0.507 105，得到在相同的尺寸公差水平下，二元统计公差比一维统计公差小，如果要达到相同的封闭环公差，二元统计公差的计算方法要求的组成环公差宽松，加工经济性好。该方法的应用有助于提高装配成功率。
[1] ISABEL GONZ
LEZ,ISMAEL SNCHEZ.Statistical tolerance synthesis with correlated variables[J].Mechanism & Machine Theory,2009,44(6):1097-1107.
[2] 龚鑫，黄美发，孙永厚,等.基于极值法与统计公差法的不同尺寸公差分配方法的研究[J].组合机床与自动化加工技术,2015(3):5-8.
[3] 姬舒平,孙贤会,马玉林.一种基于制造环境的统计公差分析方法[J].中国机械工程,1999,10(3):249-252.
[4] XU S, KEYSER J.Statistical geometric computation on tolerances for dimensioning[J].Computer-Aided Design,2015:193-201.
[5] 彭和平,刘晓军.考虑形位公差的二维装配公差分析[J].机械传动,2008,32(3):75-77.
[6] 王洋，徐诚，郭胜，等.三维公差分析技术在机枪脱链机构公差设计中的应用[J].兵器装备工程学报，2017(10):36-39.
[7] 罗少敏,王亚平,邹衍.某型手枪击发机构装配公差分析与信息化集成研究[J].机械设计与制造,2014,12:132-136.
[8] 常方圆,方峻,罗少敏.自动武器闭锁机构三维装配精度分析技术研究[J].机械设计与制造,2018(03):255-259.
[9] 张岩,莫蓉.基于低偏差序列样本的装配公差分析方法[J].计算机集成制造系统,2014,20(3):579.
[10] 姚寿文，黄德智，王瑀.虚拟装配下车辆传动装置的公差分析与设计[J].兵器装备工程学报，2017(6):7-12.
[11] 理查德A.约翰逊,迪安W.威克恩.实用多元统计分析[M].陆璇，葛余博，赵衡秀，等译.北京：清华大学出版社,2008:119.