在技术的推动与市场的召唤下,无人机以其零伤亡、效费比高、机动灵活、起降方便等诸多优点在军民两用领域得到了迅速发展。概括起来,无人机从军事应用起步,逐步扩展到民事领域,以消费级无人机的身份被大众熟知[1]。目前工业级无人机正以行业改革者的姿态广泛应用于多个领域,例如:森林防火、资源勘探、农林植保、公安消防、电力巡检、航拍测绘、快递投送等[2]。
无人机按照升力原理不同大致可分为旋翼无人机、扑翼无人机和固定翼无人机[3](Fixed Wing Unmanned Aerial Vehicle,UAV),后者往往造价更高且在无人机大家族中扮演着重要角色,多应用于速度快、距离远、续航久的场景,因此在使用时面临着更严峻的安全风险。对UAV状态进行预测分析,及时了解飞机自身可靠性,可有效减免损失降低任务风险,以此具有重要实用意义和研究价值。
国内外众多学者就无人机状态预测进行了深入研究,按照方法不同大体可分为模型的方法和基于统计的方法两种。前者,如Xiong等[4]设计了基于全局快速动态终端模型控制算法,实现了无人机的姿态跟踪控制和预测。Liu[5]通过动力学特性推导出无人机姿态角及对应位置状态空间方程,设计出了基于模型预测控制算法的姿态角控制器,进一步构建了轨迹跟踪控制系统。Wang[6]提出了基于轨迹线性化将无人机纵向非线性动力学模型转化为线性变参数模型,总结了鲁棒预测控制器的局限性,进一步提高了模型预测的准确性。
基于统计的方法包括扩展卡尔曼滤波、无色卡尔曼滤波、粒子滤波、支持向量机及神经网络等方法。Zhao等[7] 提出一种基于运行状态识别的无人机高斯过程-无味卡尔曼滤波的混合估计方法,以确定无人机实时状态并提高预测模型的适应性。Koops等[8]提出了一种多传声器机器学习数据融合方法来精确预测多旋翼无人机在飞行中的上升、悬停、下降状态。Zhao等[7]提出了一种基于高斯回归过程的无味卡尔曼滤波的无人机状态预测方法,结合状态识别机制提升了预测的适宜性。Wang等[9]提出了一种基于粒子滤波的无人机姿态估计算法,通过建立状态空间方程,运用粒子滤波算法实现对无人机姿态估计,最终实现航迹预测。Gao等[10]利用核学习相关向量机的方法,预测电子设备的未来状态,并通过在线数据来更新模型,提高了预测效率与精度。Wu[11]提出了基于RVFLNN模型RVFLNN短时轨迹预测算法,在利用无人机历史轨迹数据进行训练后,RVFLNN能较好把握无人机的飞行趋势,实现对无人机下一采样时刻位置信息进行精度较高的快速实时预测。Zhang等[12]提出了基于Elman神经网络的战斗机空战轨迹预测方法,该方法与传统粒子滤波算法相比预测误差更小、预测效果更好。
文献调研发现,尽管众多学者使用不同技术实现了无人机状态预测,但都将飞机飞行全过程视为一种工况并使用单一模型对飞机状态进行描述。该方法只适用于飞机处于稳态、准稳态的特定情况,与UAV实际飞行情况并不相符。实际应用中仅从典型飞行过程来看,UAV包含起飞、巡航、遂行任务、返航、回收等多个阶段,且各工况间各传感器和执行机构工作状态存在较大差异,可见UAV飞行属于典型的多工况过程。本文以UAV纵向控制回路状态为预测目标,提出了“聚类分析-模式识别-回归预测”相结合的技术路线。该技术使用了基于共享近邻相似性的密度聚类算法,能够结合数据本身规律从抽象层面对无人机历史飞行数据进行合理分组,以算法分组结果代表各个工况数据。基于各工况数据训练工况识别模型和回归预测模型,前者用于判断测试数据工况类别,后者用于预测测试数据状态。通过“分而治之”的数据分组与建模策略,进一步贴合了UAV多工况特征,有效提高了预测准确度。
1 UAV纵向控制原理与多工况分析
1.1 UAV纵向控制与状态表征
UAV具有自驾系统,其核心控制回路包括纵向控制回路、横向控制回路等。其中纵向控制回路受机载飞行控制计算机控制,飞行控制计算机一方面接收机载数据链终端送达的高度调整指令、姿态角调整指令和空速调整指令,另一方面接收姿态角传感器、高度传感器、发动机转速传感器实时采集飞机状态信息。飞行控制计算机输出控制指令控制执行机构(升降舵机和油门杆舵机)运动,改变飞机状态直到负反馈回路达到稳定,如图1所示。
从图1中可以看出,俯仰角(θ)、升降舵偏角(δZ)、缸温(T)、发动机转速(V)、高度(H)等5个传感器/执行机构输出数据可基本表征UAV纵向控制回路工作状态,其中高度(H)直观反映了纵向控制回路的最终状态,属于自变量,故可作为被预测变量,其他4个输出量的波动会引起高度(H)的变化,属于因变量,故可作为预测变量。本文将以上5个数据的单次采样构成向量,记作x=[θ,δz,T,V,H]∈R5,令采样次数为m,则UAV纵向控制回路飞行数据构成的矩阵可表示为D=[x1,x2,…,xm]T∈Rm×5。
1.2 UAV多工况分析
UAV工况数据是飞机在某种状态下的数据集合,各工况内数据高度相似,工况间数据差异较大。由于UAV纵向控制回路飞行数据为高维数据(五维),无法进行直观展示,本文使用t分布随机邻居嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)技术和平行坐标可视化技术探究UAV工况特征。
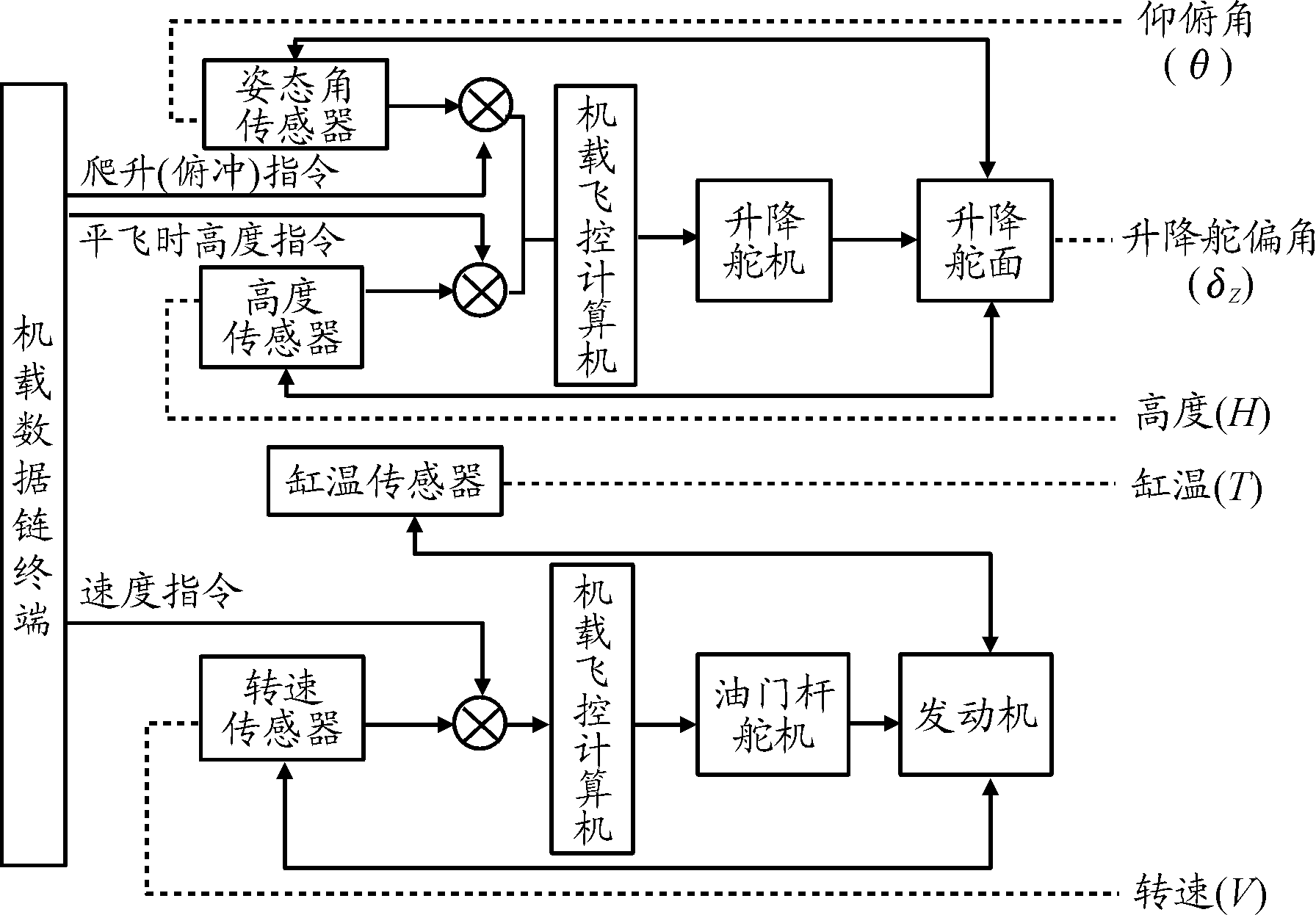
图1 UAV纵向控制回路框图
t-SNE是一种将高维数据可视化的流形降维算法,其基本思想是用条件概率表示两个数据间的相似性,若两个数据分布相近则相似性高,反之亦然。通过对比高低维数据间的KL散度评价降维效果,最终使高维数据间的相似性在低维体现出来。故可以通过观察经t-SNE降维的低维数据聚成簇的情况推断数据在高维的分布规律。t-SNE一般包含以下几个过程:1) 计算每两个高维数据点之间的距离;2) 计算高维数据的相似度矩阵;3) 初始化一组低维(二维或三维)数据点;4) 迭代更新低维点,最小化高维空间中的高斯分布与低维空间中的t分布之间的KL散度(Kullback-Leibler divergence)。文章第3部分用于算法建模的3 195组训练数据(traindata)的二维t-SNE映射图如图2所示,从图2中可以看出低维数据聚成大小不等的多个簇,故推断原始高维数据应划分为多个工况。
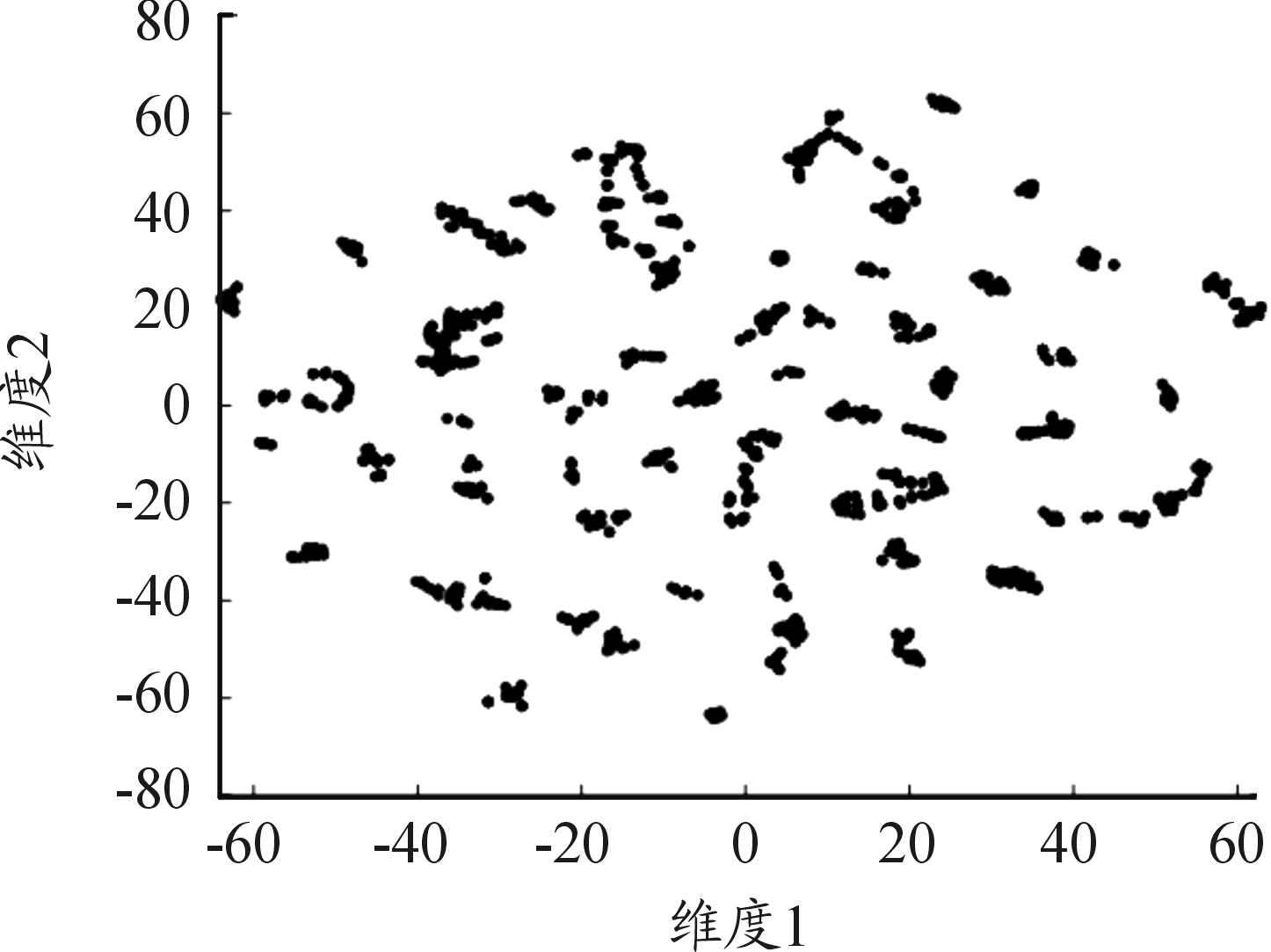
图2 飞行数据二维映射图
平行坐标绘图法是另外一种将高维数据可视化的方法。该方法通过构建一种特殊的二维坐标系,将高维数据转化为该坐标系中的折线。该坐标系中横轴为维度,纵轴为幅度,一条连接各维度幅值的折线表示一个高维数据点,折线的走势代表高维数据的特征。如图3所示,图3中折线表示的5维数据点为:[θ,δz,T,V,H]=[0.8,0.97,0.05,0.75,0.025]。将多次采样数据对应折线绘制在一张图上,即可得到该数据集对应平行坐标图。图4展示了训练数据(traindata)的平行坐标法可视化结果。观察可知,折线走势复杂并不呈现统一的变化规律,故推断该数据集包含多个工况。
为应对UAV的多工况现象,同时考虑不依赖先验知识,后文将使用数据挖掘领域的非监督聚类分析算法对UAV工况进行分析。
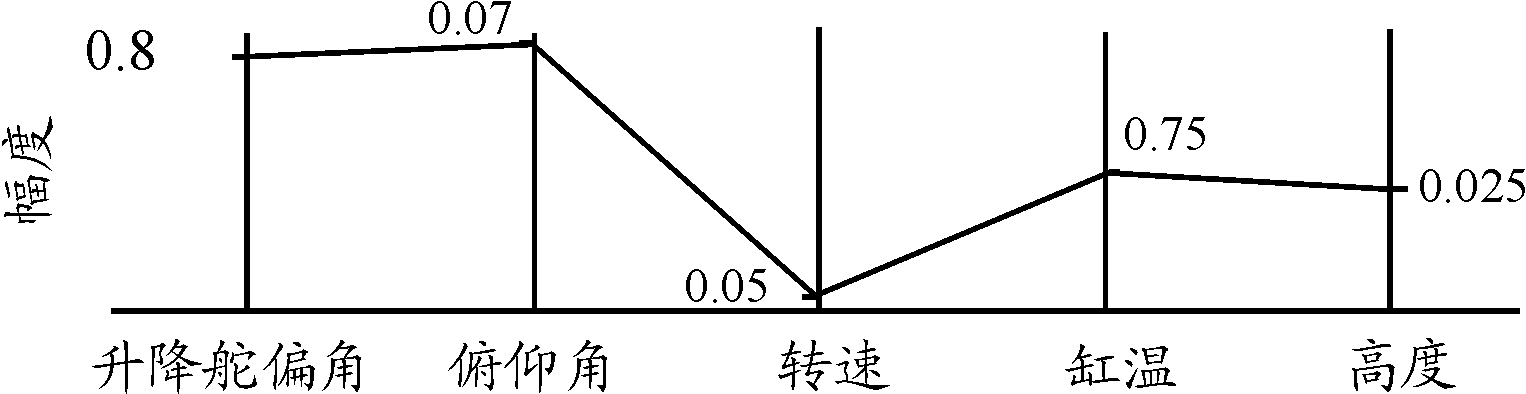
图3 UAV某次采样数据平行坐标可视化折线
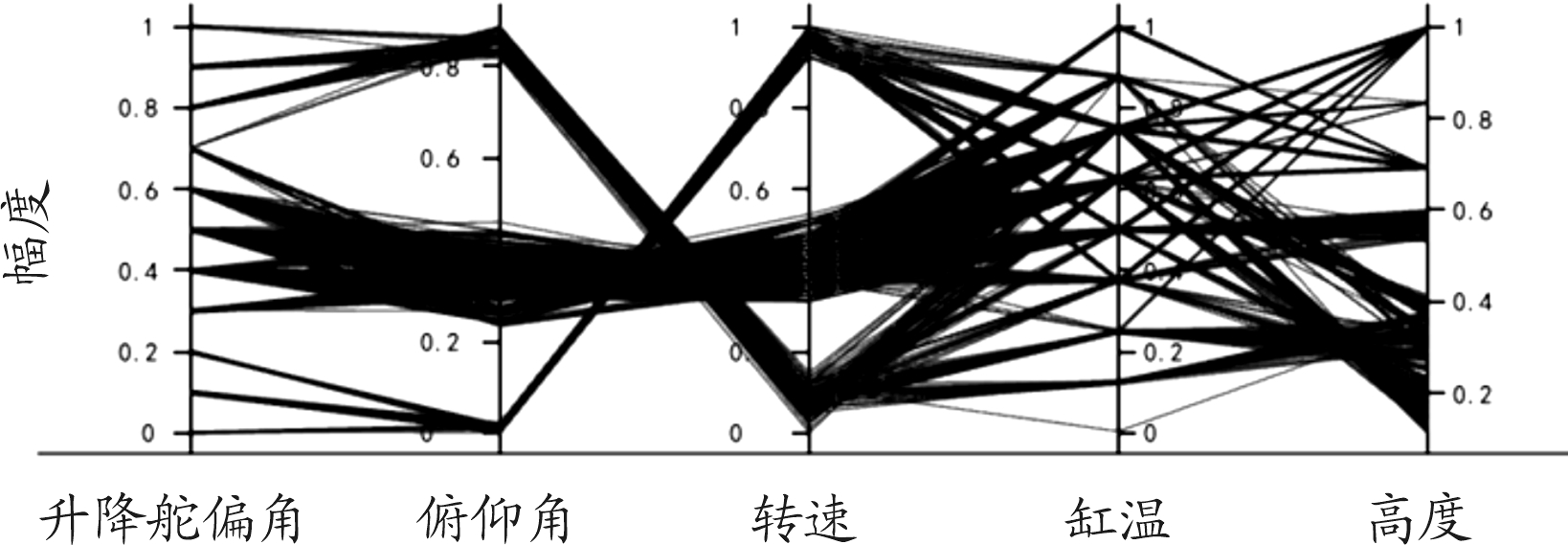
图4 飞行数据平行坐标可视化折线
2 多工况状态预测算法
2.1 总体路线
UAV纵向控制回路多工况状态预测算法分为两个阶段:离线建模阶段与在线预测阶段。前者完成对数据的聚类分析与ANN、KGPR建模,后者利用离线建模结果对测试数据进行在线工况识别与状态预测。
如图5所示,在离线建模阶段首先使用聚类算法对UAV纵向控制回路历史飞行数据进行分析,得到各工况飞行数据及对应工况标签。之后分别将聚类得到的各工况数据与对应标签作为神经网络分类器输入与输出数据训练ANN工况分类器模型。将聚类得到的各工况数据作为KGPR输入数据训练多个KGPR回归预测模型。
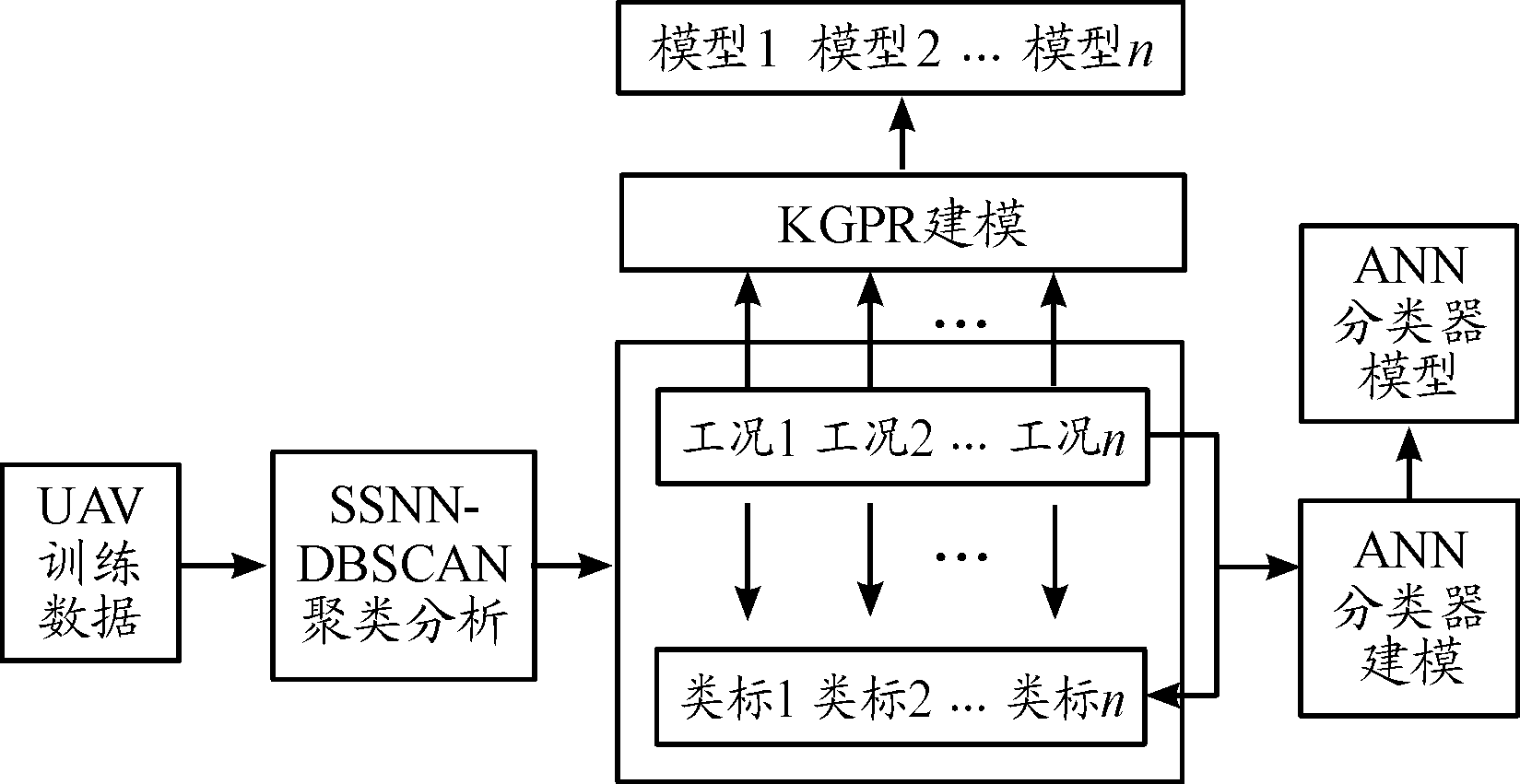
图5 离线建模框图
如图6所示,在线预测阶段首先使用离线建模得到的ANN分类器模型对当下在线测试数据所属工况进行辨识。然后根据工况辨识结果提取对应的KGPR回归预测模型,使用该模型对当下测试数据高度值进行预测,重复以上过程即可完成对测试数据的在线预测。
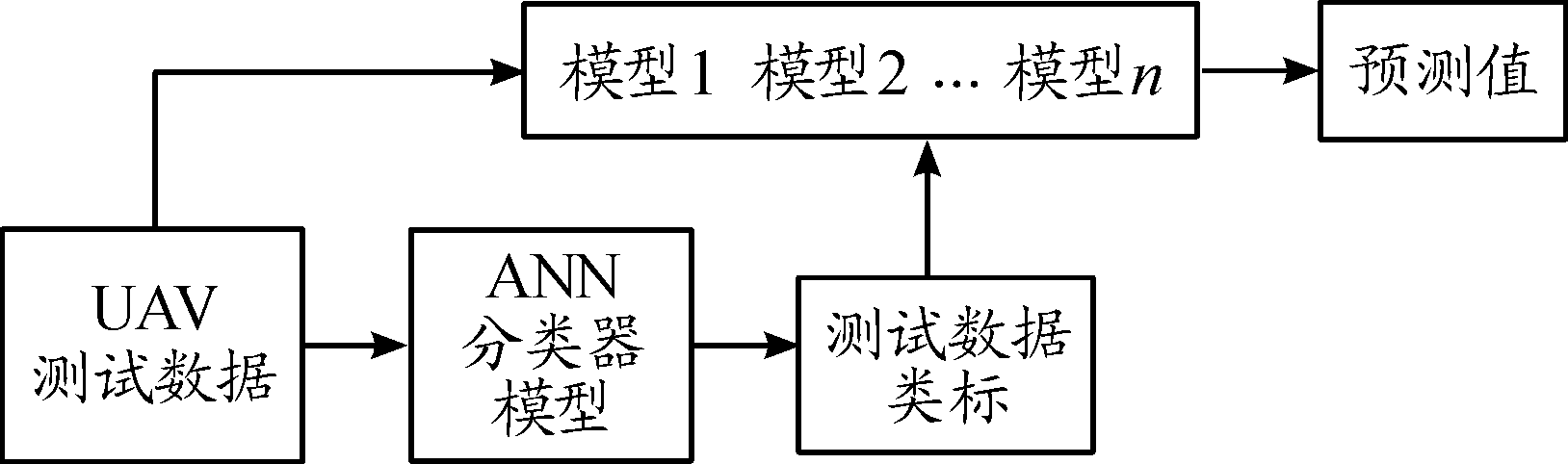
图6 在线预测框图
2.2 相关技术与算法实现
UAV纵向控制回路多工况状态预测算法涉及到聚类分析、回归预测、模式识别等三种技术。本文结合UAV数据特点,具体使用基于共享近邻相似性的密度聚类(Similarity of Shared Nearest Neighbor-Density Based Spatial Clustering of Applications with Noise,SSNN-DBSCAN)算法对UAV飞行数据作聚类分析;使用核高斯过程回归[14](Kernel Gaussian Process Regression,KGPR)算法对各工况数据进行回归建模与预测;使用人工神经网络[15](Artificial Neural Network,ANN)算法对各工况数据进行建模和工况辨识。UAV多工况状态预测算法的伪代码为:

Algorithm:predictData= UAV_MC_Predict(testData,trainData,Eps,Minpts,k)Input:(1)trainData:训练数据(2)testData:测试数据(3)Eps:DBSCAN算法中邻域半径(4)Minpts:DBSCAN算法中核心点近邻阈值(5)k:SNN算法中近邻数量Output:clusterPrdictValue:预测输出的高度值1.%使用SSNN-DBSCAN算法对训练数据聚类分析[clusteredData,clusterID]=SSNN-DBSCAN(trainDa-ta,k,Eps,Minpts)2.%使用聚类结果及其类标训练神经网络分类器。ANNClassifierModel=trainANN([clusteredData,clusterID])%使用各个聚类簇数据训练多个KGPR回归模型3.For i=1:| clusterID |4. KGPRModel(i)=TrainKGPR(clusteredData(i,1:4),clusteredData(i,5))5.End For%对测试数据中的每个采样数据进行工况识别,调取对应GPR模型预测高度值6.For i=1:length(testData)7. clusterID=ANNClassifierModel(testData(i,∶))8. selectedTrainedModel=KGPRModel(clusterID)9. clusterPrdictValue(i)=selectedTrainedModel(testData(i,1∶4))10.End For11.testDataValue=testData(∶,5);%测试数据的真实值12.clusterRMSE=RMSE(testDataValue,clusterPredi-ctValue)%预测值与真实值均方根误差
2.2.1 聚类分析
DBSCAN是一种基于密度聚类的算法,该算法通过引入邻域半径(Eps)和近邻阈值(Minpts)概念将数据划分为核心点、边界点和离群点,并以核心点为主导构建各个簇。DBSCAN能够基于数据自主推测聚类个数,可发现任意形状和大小的簇并且对噪声有较强的鲁棒性,因此被广泛应用于光谱分析、社会科学、生物医学等多个领域。
DBSCAN算法中以距离描述两个数据点之间的相似性,常用的距离度量方式为欧氏距离。这种度量方式对数据集的密度和维度敏感,难以适应变密度、高维度的UAV数据集。因此本文使用共享近邻相似性(Similarity of Shared Nearest Neighbor,SSNN)度量方式对经典DBSCAN算法进行改良,记为SSNN-DBSCAN。
共享近邻相似性源自共享近邻距离(Shared Nearest Neighbor Distance,SNND)。SNND首先寻找数据集D中P、Q两点的前k个近邻组成的近邻集,记为Pk与Qk,若P、Q的近邻集中有SNNDP,Q个近邻是共享的,则P、Q点的共享近邻距离记为SNNDP,Q,即SNNDP,Q= Pk∩Qk。为适应距离越近相似度越高的习惯,这里进一步定义共享近邻相似性概念,并规定SSNNP,Q=k-SNNDP,Q。
图7展示了SSNN的变密度适应能力,图7中左侧数据集合的密度明显大于右侧数据集合,但两组数据对“P,Q”与“P′,Q′”的共享近邻相似度相同(k=9),即SSNNP,Q=SSNNP′,Q′=6。图7说明SSNN能够根据局部数据的分布密度自动调整领域半径,具备密度缩放能力,适合用来分析具有变密度数据分布特征的UAV数据。
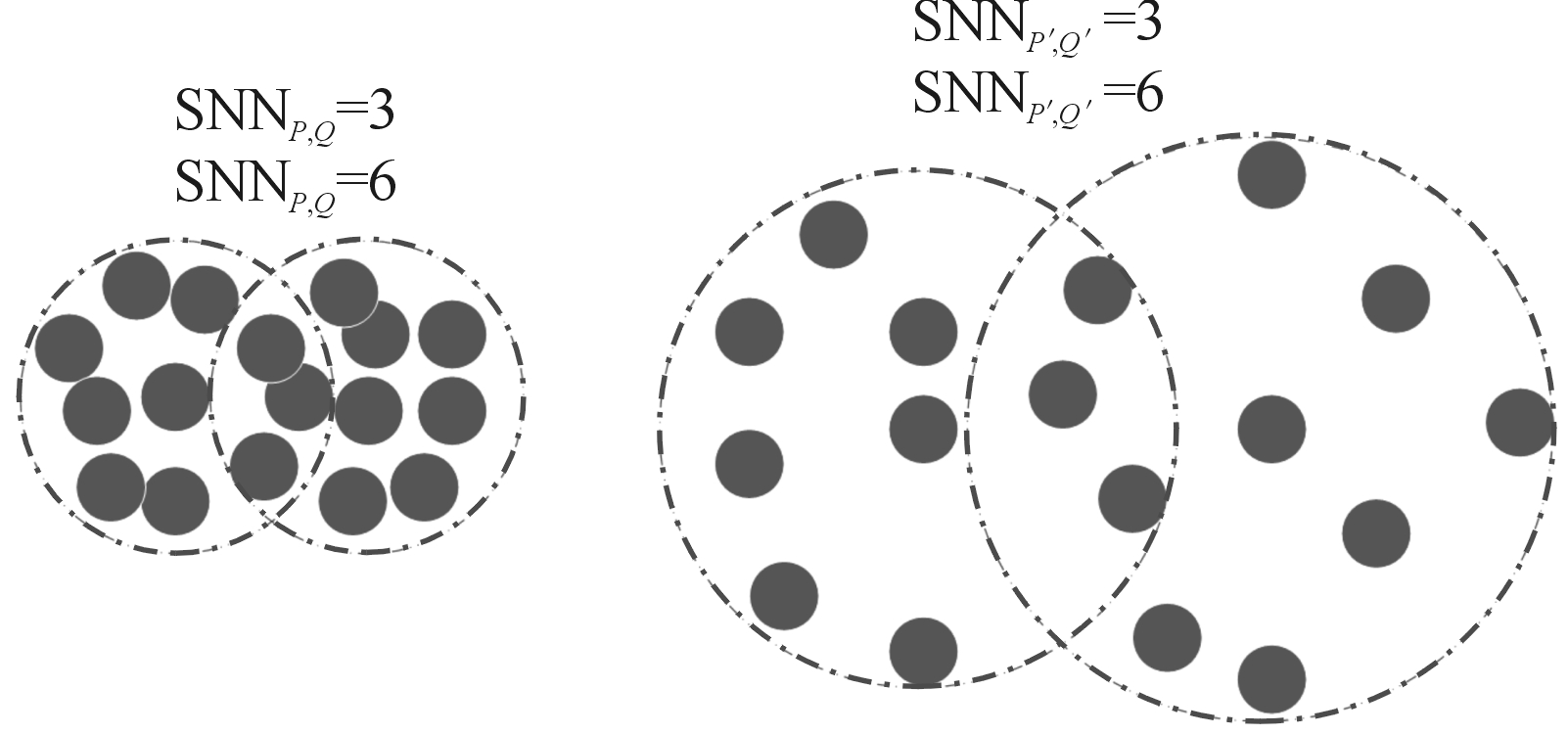
图7 SSNN的变密度适应能力示意图
2.2.2 回归预测
聚类分析阶段已将UAV数据D划分为多个工况,在此基础上本文使用MATLAB回归学习工具箱训练多个UAV回归预测模型。
将各工况飞行数据的前4维(θ、δZ、T、V)作为输入数据,第5维(H)作为输出数据,根据模型优劣评价标准:均方根误差(RMSE)、绝对误差均值(MAE)、可决系数(R-Squared),择优选取适合UAV状态预测的模型。
2.2.3 模式识别
UAV被有效划分为多个工况后,在线故障诊断首先要完成工况匹配。鉴于UAV各维度数据与类别标签之间的非线性关系,本文使用能够处理多变量输入与输出间非线性关系的多隐层神经网络分类器对UAV进行工况匹配。
ANN分类器需要先训练再使用,训练ANN分类器需要指定输入数据与输出类标。本文将SSNN-DBSCAN聚类得到的各工况飞行数据作为输入数据,对应的工况标签作为输出数据训练神经网络分类器。
使用训练好的分类器对测试数据进行在线测试,输出类别标签,将类别标签视为测试数据的工况标签。基于SSNN-DBSCAN的ANN分类器工作流程如图8所示。
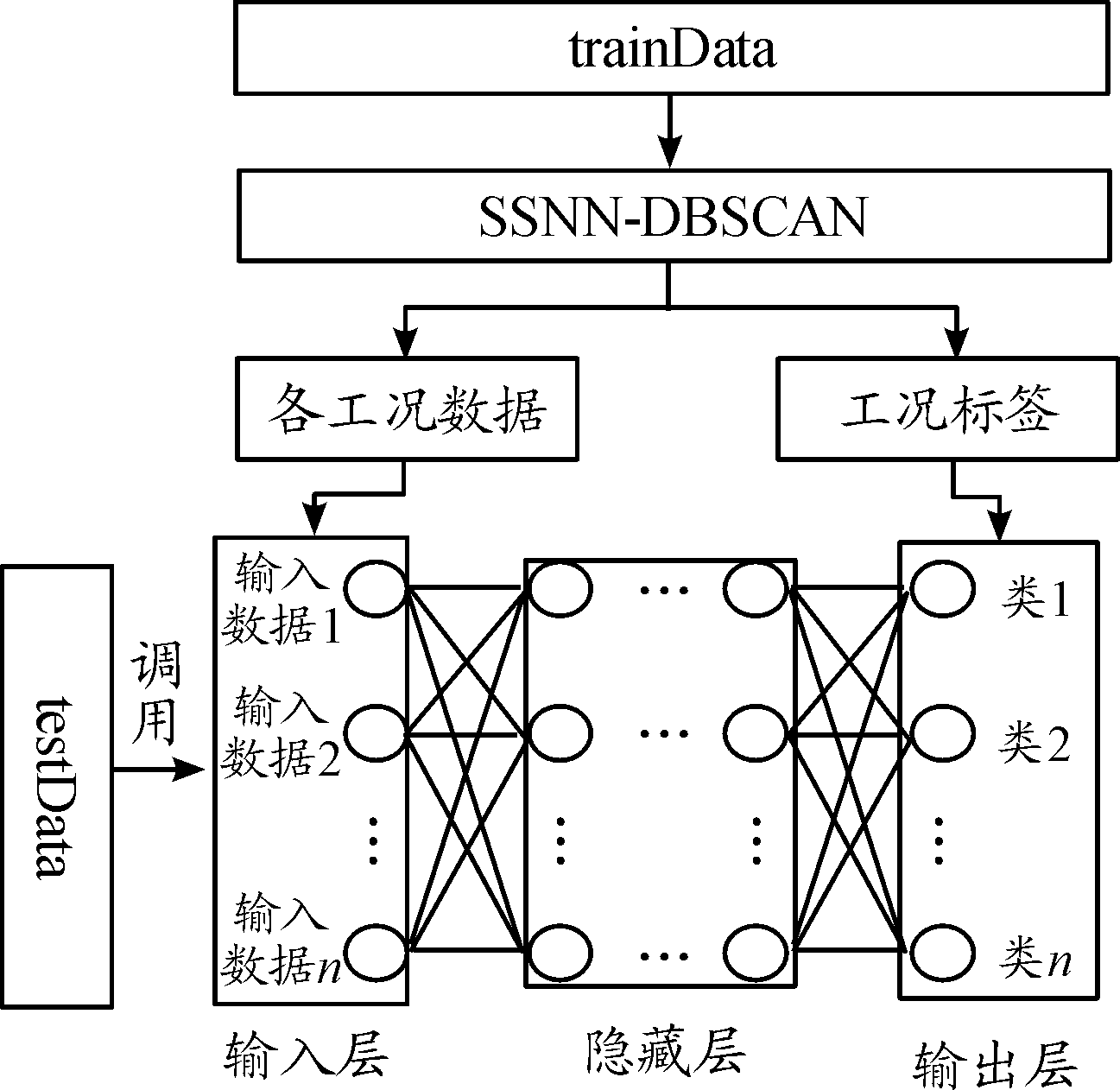
图8 基于SSNN-DBSCAN的ANN分类器工作流程框图
3 验证
为验证本文提出的技术方案,分别取某侦察型UAV执行近程、中程、中远程、远程任务4种情境下的实飞数据作为测试数据与训练数据。
远程任务数据包含了最多的数据量,各工况数据丰富,适合用来做训练数据。本文在对该数据进行采样、去除离群值、归一化、无偏差抽样后得到了3 195组训练数据(trainData)。测试数据分别从近程、中程、中远程任务数据中抽样得到,数据量分别为100组、200组、500组。这3种情境能够较好反映UAV的典型用途,具有一定的代表性。图9、图10展示了训练数据与测试数据变量趋势曲线。
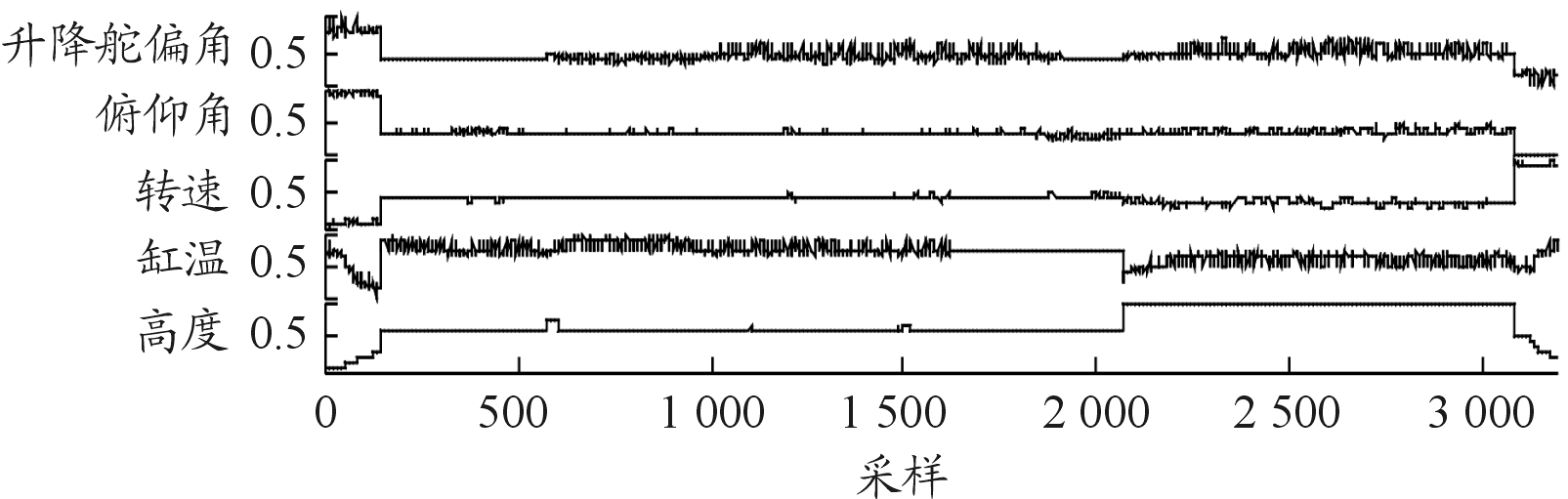
图9 训练数据变量趋势曲线
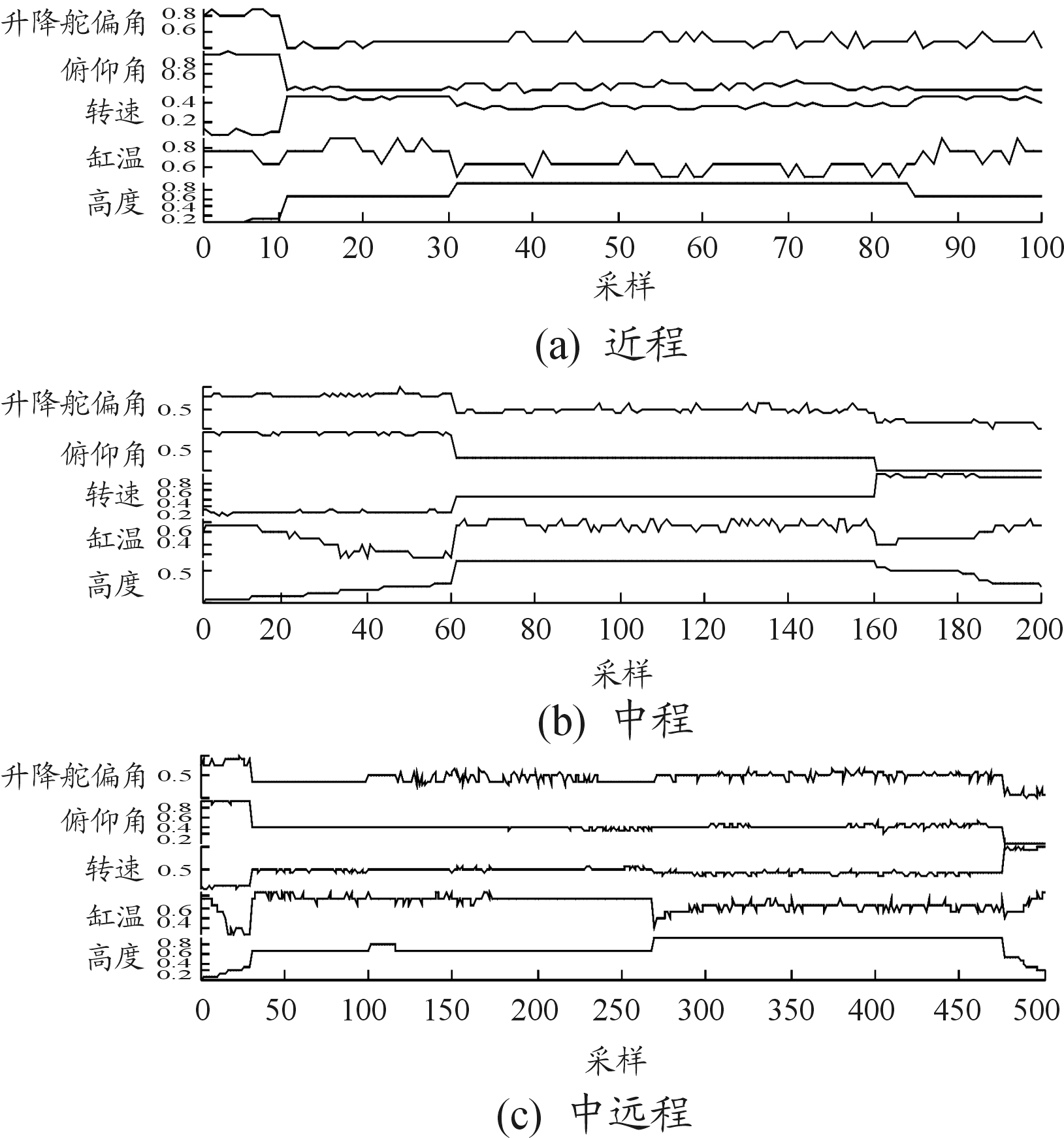
图10 测试数据变量趋势曲线
为了方便区分,将本文中提出的方案称为“多工况模型”,将不区分工况的常规技术称为“单一模型”。为对比两种技术手段预测效果的优劣,提出了图11所示的试验验证技术路线。图11中,trainData被复制为两份,即trainData1、trainData2。使用trainData1在Matlab2019a回归学习工具箱中训练多个回归模型,建模结果如表2所示。结合模型评估指标RMSE、R-Squared、MAE,选择在单一模型下19种模型中建模最优的核高斯过程回归(KGPR)模型分别对短程、中程、中近程testData进行预测分析。分别将短程、中程、中近程testData与trainData2代入表1算法,得到多工况模型预测结果。
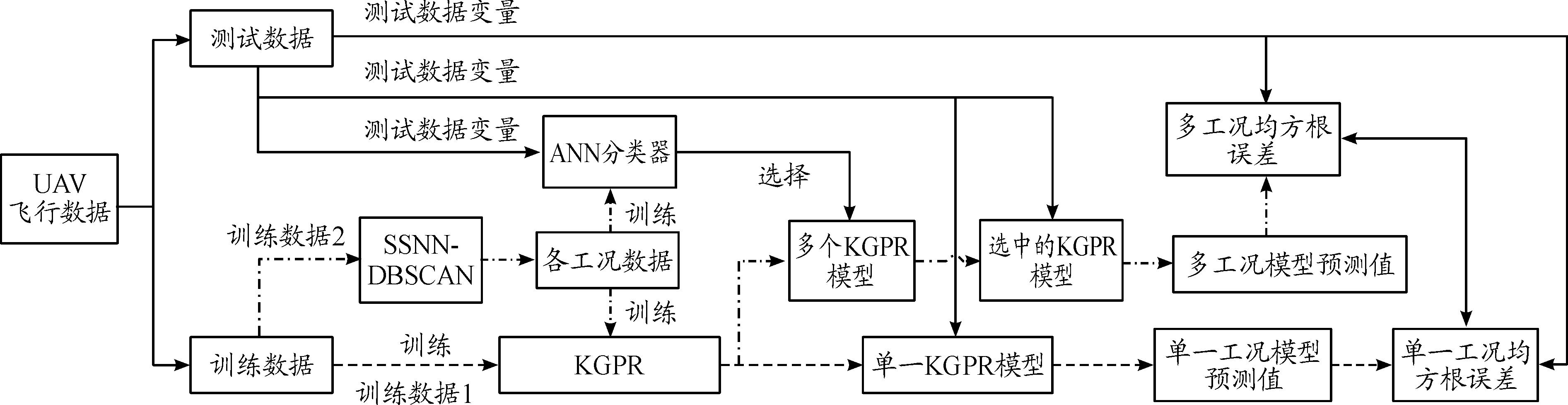
图11 试验验证阶段技术路线框图
表2 回归模型建模结果
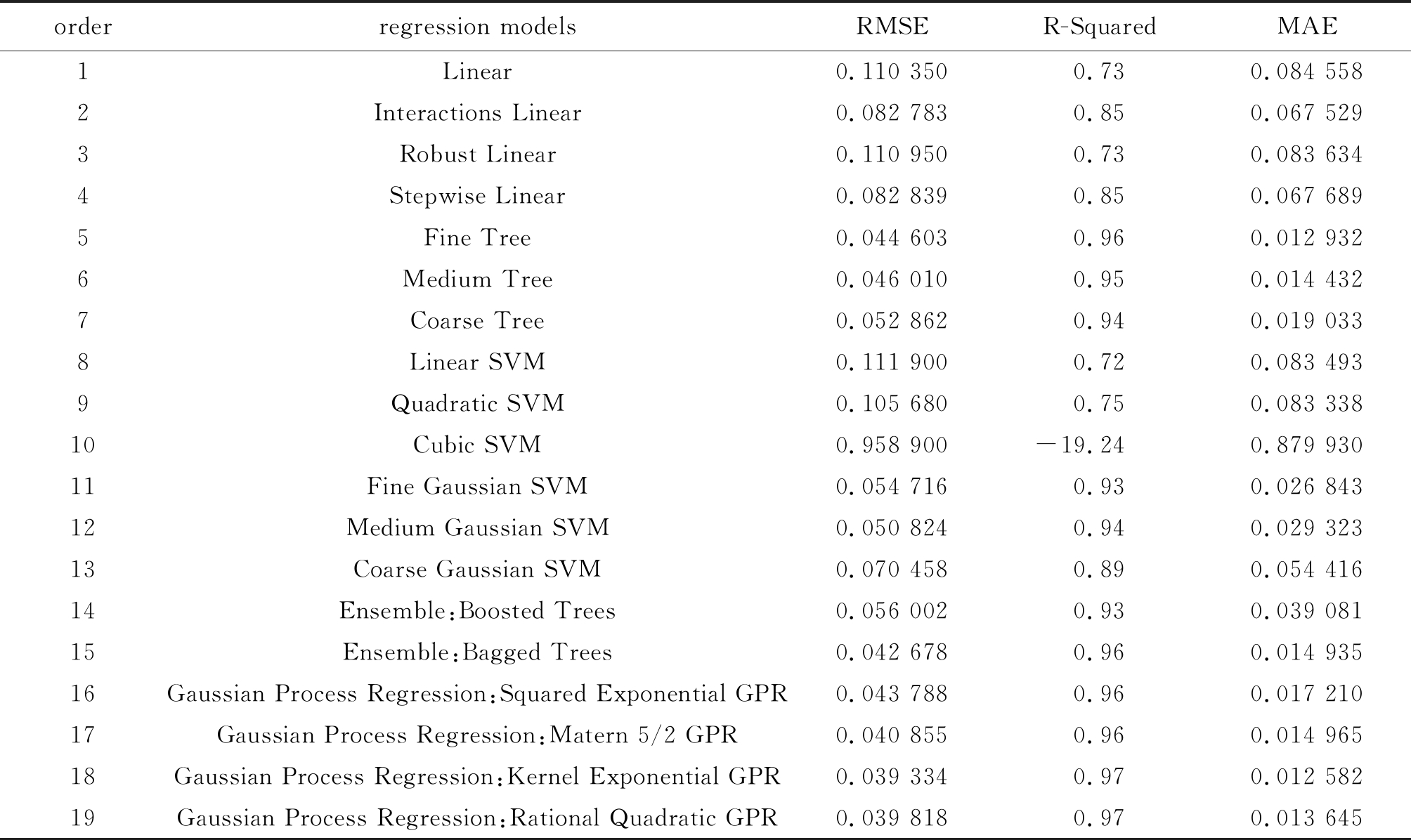
orderregression modelsRMSER-SquaredMAE1Linear 0.110 350 0.730.084 558 2Interactions Linear 0.082 783 0.850.067 529 3Robust Linear 0.110 950 0.730.083 634 4Stepwise Linear0.082 839 0.850.067 689 5Fine Tree0.044 603 0.960.012 932 6Medium Tree0.046 010 0.950.014 432 7Coarse Tree0.052 862 0.940.019 033 8Linear SVM0.111 900 0.720.083 493 9Quadratic SVM0.105 680 0.750.083 338 10Cubic SVM0.958 900 -19.240.879 930 11Fine Gaussian SVM0.054 716 0.930.026 843 12Medium Gaussian SVM0.050 824 0.940.029 323 13Coarse Gaussian SVM0.070 458 0.890.054 416 14Ensemble:Boosted Trees0.056 002 0.930.039 081 15Ensemble:Bagged Trees0.042 678 0.960.014 935 16Gaussian Process Regression:Squared Exponential GPR0.043 788 0.960.017 210 17Gaussian Process Regression:Matern 5/2 GPR0.040 855 0.960.014 965 18Gaussian Process Regression:Kernel Exponential GPR0.039 334 0.970.012 582 19Gaussian Process Regression:Rational Quadratic GPR0.039 818 0.970.013 645
图12(a)、图12(b)、图12(c)中上图分别展示了单一模型和多工况模型对近程、中程、中远程testData预测结果与真实值分布,下图为预测值与真实值的误差分布曲线。
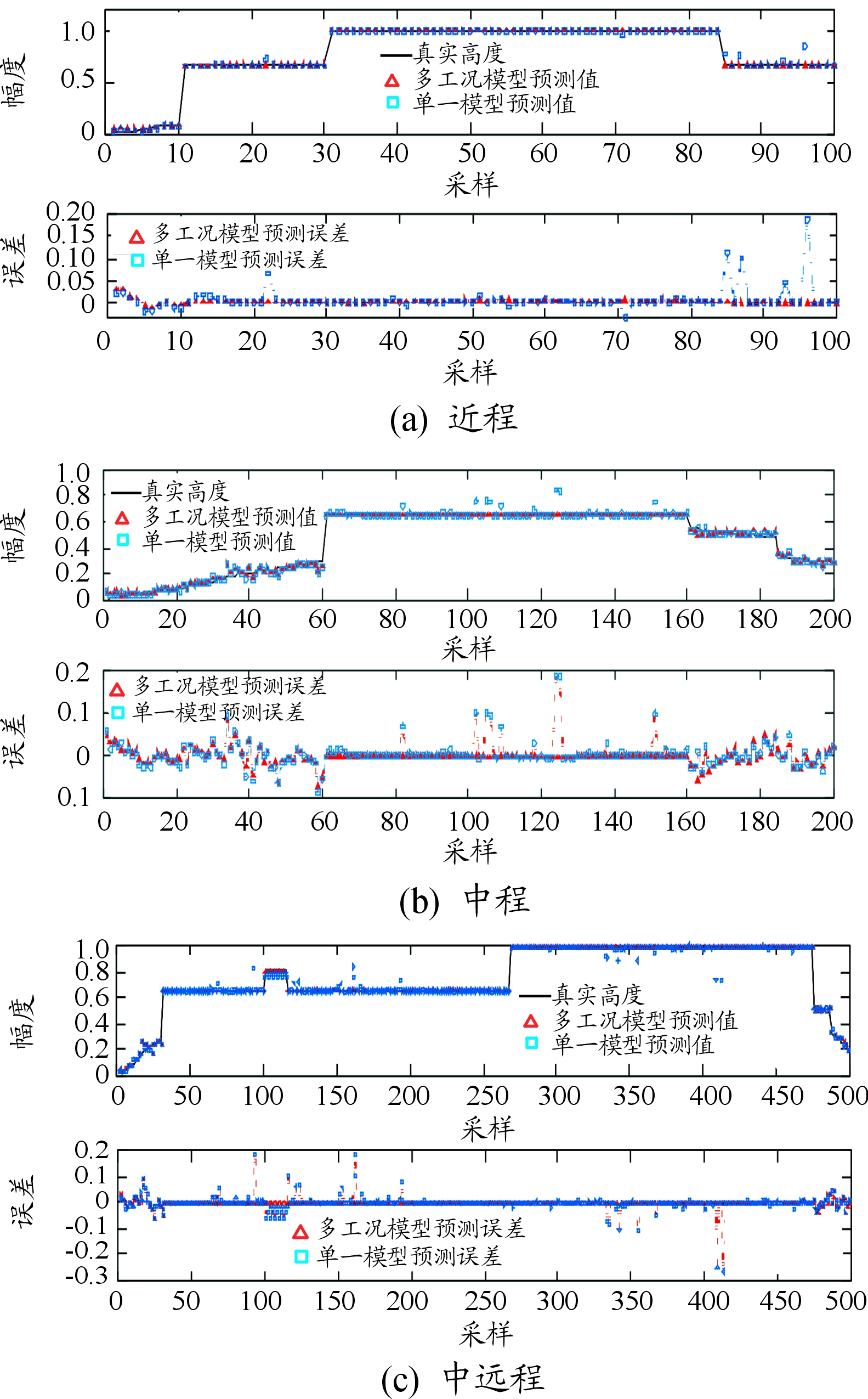
图12 预测结果与误差分布曲线
从图12中可以看出,多工况模型预测值更逼近真实值,误差波动更小,相比单一模型有明显优势。
表3统计了两种模型在3种情境测试数据下的预测均方根误差(RMSE)和平均绝对误差(MAE)。由于测试数据为归一化后数据,即分布区间为[0,1],因此RMSE与MAE为相对值。从结果来看,多工况模型在3种情境下的RMSE与MAE值均小于单一模型对应值,各情境下多工况模型RMSE与MAE均值小于单一模型对应值的1/2。
综上所述,本文提出的多工况模型比最优的单一工况预测模型方案更适应UAV数据多工况特征,能够取得更好的预测效果。
表3 预测结果
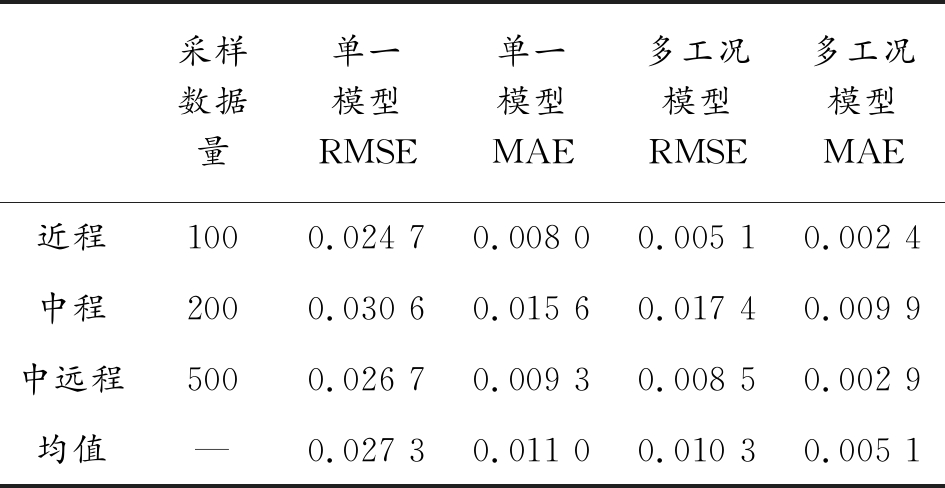
采样数据量单一模型RMSE单一模型MAE多工况模型RMSE多工况模型MAE近程1000.024 70.008 00.005 10.002 4中程2000.030 60.015 60.017 40.009 9中远程5000.026 70.009 30.008 50.002 9均值—0.027 30.011 00.010 30.005 1
4 结论
本文首先介绍了UAV纵向控制回路控制原理,指出了可以使用5个传感器/执行机构输出数据表征该回路整体状态,解决了数据源问题。之后借助两种高维可视化方法直观展示了UAV实飞数据的分布规律,证实了UAV的多工况特征。为解决多工况下UAV状态预测难题,提出了基于SSNN-DBSCAN聚类算法自动分析UAV工况,基于ANN算法实现测试数据多工况模式识别,使用KGPR算法完成状态预测的技术路线。相比单一工况预测模型本文提出的多工况模型能进一步提高预测准确度,更适合UAV数据的多工况特征。
本文提出的“聚类分析-模式识别-回归预测”的技术路线还可用于其他多工况工业流程状态预测中,也可以推广到多工况故障诊断等场景。
[1] 丁宇,李书文.民用固定翼无人机发展现状以及未来展望[J].电子技术与软件工程,2018(23):107-108.
[2] 邵瑰玮,刘壮,付晶,等.架空输电线路无人机巡检技术研究进展[J].高电压技术,2020,46(01):14-22.
[3] 孔德胜.某型固定翼无人机飞控系统的设计与仿真[D].北京:北京理工大学,2015.
[4] XIONG Jingjing,ZHANG Guobao.Global fast dynamic terminal sliding mode control for a quadrotor UAV[J].ISA Transactions,2017,66:233-240.
[5] 刘斐.基于模型预测控制的无人机轨迹跟踪方法研究[D].武汉:湖北工业大学,2017.
[6] 吴卿刚.面向任务的合作类无人机轨迹预测技术研究[D].南京:南京航空航天大学,2019.
[7] 赵嶷飞,杨明泽.基于运行状态识别的无人机航迹预测[J].科学技术与工程,2019,19(23):304-309.
[8] KOOPS H V,GARG K,KIM M,et al.Multirotor UAV state prediction through multi-microphone side-channel fusion[C]//2017 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI).IEEE,2017.
[9] 王义平,王佳辉,薛雅丽.基于流水线高斯粒子滤波的无人机姿态估计算法及FPGA实现[J].电光与控制,2019,26(02):66-70,75.
[10] 高明哲,许爱强,许晴.基于aRVM的电子设备状态在线预测方法[J].兵器装备工程学报,2017,38(11):108-113.
[11] 吴卿刚.面向任务的合作类无人机轨迹预测技术研究[D].南京:南京航空航天大学,2019.
[12] 张涛,郭基联,徐西蒙,等.基于Elman神经网络的战斗机空战轨迹预测[J].飞行力学,2018,36(05):86-91.
[13] WANG Y,ZHANG H,HAN D.Neural Network Adaptive Inverse Model Control Method for Quadrotor UAV[C]//Proc.of the Control Conference(CCC),2016 35th Chinese.IEEE,2016:3653-3658.
[14] LV Y H,MA T H,TANG M L,et al.An efficient and scalable density-based clustering algorithm for datasets with complex structures[J].Neurocomputing,2016,171:9-22.
[15] YE X,SAKURAI T.Spectral clustering using robust similarity measure based on closeness of shared Nearest Neighbors[J].ETRI Journal,2016,38(3):540-550.