在实际应用中,受工作器具、人员操作、环境等影响,图像的获取、传输与转换过程不可避免地伴随着图像质量降低的情况,此类情况大多为不可逆过程,主要表现为清晰度退化、局部失真以及噪声干扰等[1]。因此,如需获取高质量的图像,则需要通过图像复原算法抑制退化,降低噪声干扰。然而图像的退化过程多由成像系统与目标物体间的相对位移引起,很难通过技术手段消除,因此提升运动模糊图像的复原效果具有极为重要的现实及经济意义[2]。
模糊图像的退化过程可以等效为原始图像与点扩散函数的卷积计算过程,因此抑制退化的过程也可以等效为对模糊图像反卷积的过程[3]。对于退化图像的复原,目前常用的方法有维纳滤波法、卡尔曼滤波法以及R-L算法等[4-7]。然而这几类方法均存在着振铃效应以及受点扩散函数准确度影响较大两个固有缺陷[8-10],而且,在对含噪图像进行复原时,会严重影响整体复原质量[11-12]。基于此,Tony F.Chan提出了一种基于全变差(Total Variation,TV)的图像复原算法,对振铃效应有一定的抑制作用。然而该算法只能有效针对拍摄散焦所导致的图像退化,对运动模糊图像的复原效果较差[13]。由于实际图像的退化过程可以简化为原始图像和点扩散函数的卷积以及噪音的添加过程[14],因此如何准确估算出点扩散函数的系数是图像退化模型复原的关键。
针对传统复原方法的固有缺陷,本文提出了一种基于二次变换的点扩散函数系数估计方法,并选择对噪声有一定抑制作用的R-L算法完成后续的反卷积过程。然后,选取均方根误差、峰值信噪比以及灰度平均梯度三个无量纲特征量作为评价系数,在无噪声和有噪声的两个条件下与传统图像复原方法进行了量化对比。实验结果表明,二次变换估计方法可以有效提升点扩散函数的估算精度;将二次变换估计方法与R-L算法相结合,可以显著提升算法的复原精度,同时对含噪图像也能保持较高的稳定性。
1 运动模糊图像模型
对于某一理想退化模型,设其原始图像为f(x,y),对应的运动模糊图像为g(x,y),点扩散函数为h(x,y)、加性噪声为n(x,y),其图像的运动退化模型如图1所示。
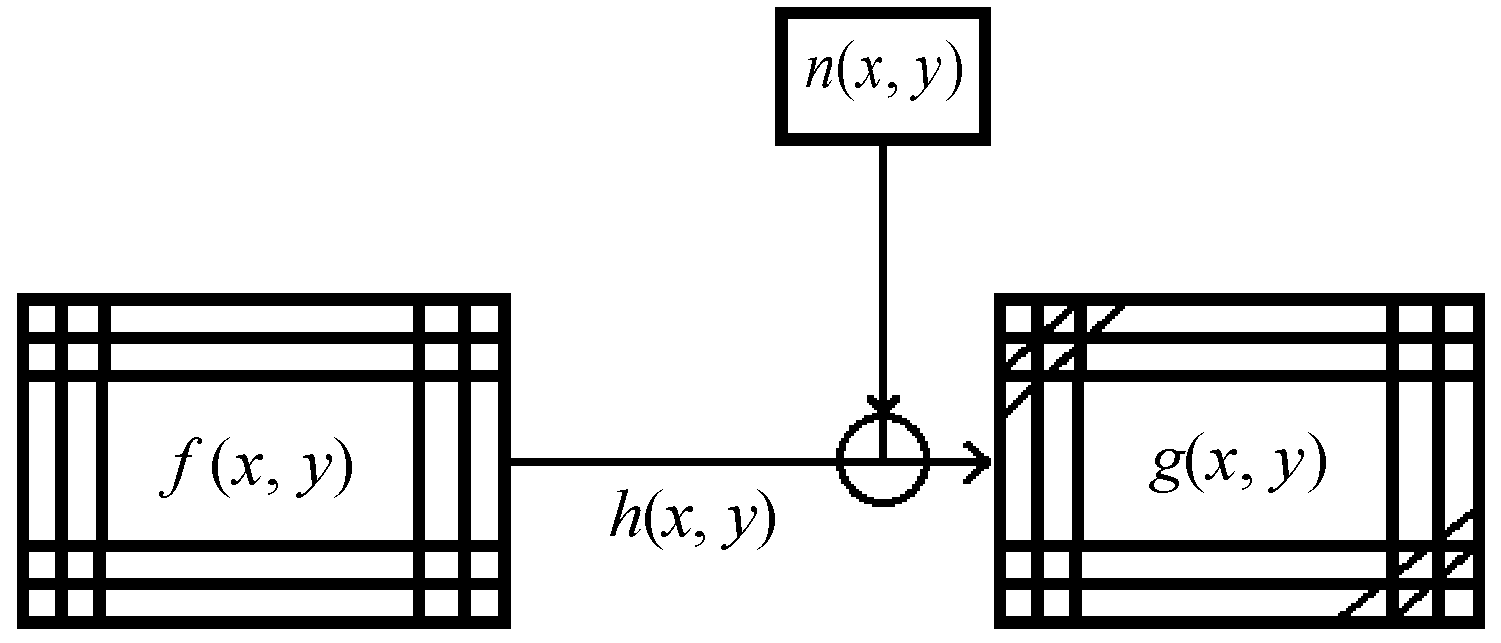
图1 图像运动退化模型示意图
对于任一线性空间不变的退化系统,其运动模糊图像的计算过程可由以下卷积计算及噪声添加表示,即:
g(x,y)=f(x,y)*h(x,y)+n(x,y)
(1)
式(1)中,“*”表示空间卷积运算。
对式(1)的左右同时进行傅里叶变换,即可获取其频率模型为:
G(x,y)=H(x,y)F(x,y)+N(x,y)
(2)
由于实际拍摄时相机的曝光时间较短,在此期间目标物体的速度变化可以忽略不计,因此可以将相机曝光期间的物体运动视为匀速直线运动,即L=vT。相应地,在曝光过程中,点扩散函数h(x,y)可通过以下形式表示为[15]:
(3)
式(3)中:θ为运动模糊方向与x正轴的夹角;L为退化过程的模糊尺度;v为相机曝光期间物体运动的速度;T为相机曝光时间。
在实际图像的复原过程中,对于上述退化模型的复原,关键在于对于模糊角度θ的准确估量以及尽可能减小图像中加性噪声的影响。因此本文提出了一种基于二次变换的估计方法,可以在传统估计方法的基础上进一步提高点扩散函数系数估算的准确性以及鲁棒性。
2 基于二次变换的系数估计方法
对于第1节中提到的线性空间不变退化模型,将式(3)代入式(1)中,然后进行傅里叶变换,可得:
G(u,v)=H(u,v)·F(u,v)+N(u,v)=
![]()
(4)
由式(4)可知,G(u,v) 中存在与运动方向垂直的条纹。由于式(4)中分子sin(πuL)存在等于零的情况,因此可知G(u,v) 中可能出现一系列同向平行条纹,且这些条纹的位置与sin(πuL)=0的位置一一对应,即![]() 由此可见平行条纹的方向与退化系统的相对运动方向垂直,且当图像退化过程中存在其他方向的运动时,同样可以使用该方法以确定模糊方向。对式(4)两侧进行同态变换,可得:
由此可见平行条纹的方向与退化系统的相对运动方向垂直,且当图像退化过程中存在其他方向的运动时,同样可以使用该方法以确定模糊方向。对式(4)两侧进行同态变换,可得:
log(|G(u,v)|)=log(|F(u,v)|)+log(|H(u,v)|)
(5)
经过上述变换后可发现,图像的退化过程可以改由F(u,v)以及H(u,v)两者自身的同态变换线性相加表示出来,而通过进行对数运算可以将傅里叶变化后的范围进一步压缩,从而在不更改条纹间隙的前提下得到更为明亮的条纹。选择标准图cameraman作为原始样本,在相同运动模糊长度条件下,进行模糊角度分别为10°、50°以及90°的模糊仿真,然后对其进行傅里叶变换后,原始图像、经模糊处理和傅里叶变换后的频谱图像如图2所示。

图2 不同模糊角度的运动模糊频谱图像
不难发现,在图2中各条纹以中央条纹为中心,呈对称渐弱分布,且中央条纹的角度随着运动模糊角度的变化呈规律性分布。然而所得图像虽与运动模糊角度变化有所关联,但图像中干扰特征较多,难以准确判断出原始图像的运动模糊角度。
此时,为了更好地获取图像运动模糊退化过程中的角度特征,对图2所得的频谱图像进行二次变换,然后对所得图像进行二值化处理以凸显图像有效特征,如图3所示。经过二次变换以及二值化处理后,原始运动模糊图像已经转化为了一条明亮条纹。此时,只需选取相应的阈值,对二次变换后的图像进行Radon变换,获取各角度所对应的极大值,其对应的极大值曲线角度即为模糊方向角度。通过这一关系,即可准确地估计出退化图像的运动模糊角度。

图3 运动模糊图像经二次变换后的图像
为了验证二次变换参数估计法的可行性,分别在无噪声以及有噪声条件下对Cameraman图像进行模糊长度为20像素的不同模糊方向仿真并使用二次变换参数估计法对模糊方向进行估计,然后与传统的基于方向微分的估计方法进行对比,对比结果如表1所示。
从表1中可以发现,本文提出的二次变换参数估计法相比具有更高的准确性,更适用于匀速直线运动导致的图像退化模型参数估计,同时对有噪声的图像进行估计时也可以保持较高的稳定性。
表1 不同估计方法对运动模糊角度的估计结果
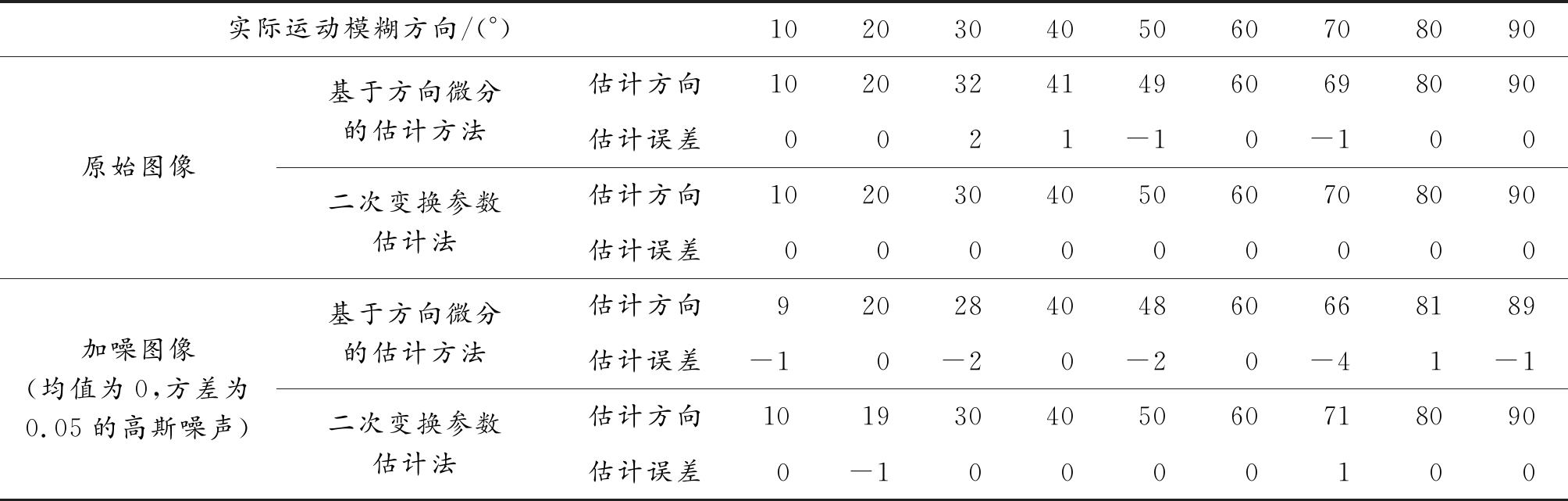
实际运动模糊方向/(°)102030405060708090原始图像基于方向微分的估计方法二次变换参数估计法估计方向102032414960698090估计误差0021-10-100估计方向102030405060708090估计误差000000000加噪图像(均值为0,方差为0.05的高斯噪声)基于方向微分的估计方法二次变换参数估计法估计方向92028404860668189估计误差-10-20-20-41-1估计方向101930405060718090估计误差0-10000100
3 基于二次变换改进的R-L复原算法
3.1 Richardson-Lucy算法原理
对于以式(1)为主要退化形式的模糊图像,当其服从泊松分布时,通过最大似然法对其进行迭代,即可逐步完成图像的复原过程,其方程为[16]:
(6)
式(6)中,f(x,y)k为完成k次迭代后的复原图像。
通过式(6)不难发现,随着迭代次数k的不断增加,所得到的复原图像会逐步收敛于原始图像,从而得到一个相对清晰的图像。然而,原始噪声也会随着迭代进程不断被放大,影响最终迭代所得的图像质量。因此在使用R-L算法还原图像时,只需要控制迭代次数并搭配以准确的系数估计方法,即可在减小噪声影响的同时更为精确地完成对原始图像的复原。
3.2 二次变换改进的R-L算法复原效果验证
为验证上述仿真效果的有效性,采用加州大学洛杉矶分校图像通信实验室提供的Lena灰度图像(像素为512×512,263kByte的8位BMP图像)作为复原目标图像进行仿真验证,其原始图像如图4(a)所示。

图4 图像复原效果
将模糊角度θ设定为35,模糊长度L设定为10,通过高斯滤波器模拟原始图像的退化过程,经退化后的图像如图4(b)所示。由于本次复原对比未添加噪声干扰项,因此将去模糊参数DAMPAR设定为0,分别使用原始R-L算法以及二次变换改进的R-L算法对模糊图像进行复原。
由于R-L算法的固有特性,随着迭代次数的增加,复原图像的质量也会随之变化,噪声的影响也会逐渐增大。选取峰值信噪比作为对比指标,两种算法迭代次数与峰值信噪比的关系如图5所示。其中,峰值信噪比越高,图像清晰度越高。从图5中可以发现,两种算法在进行前30次迭代时,峰值信噪比均有明显提升,在迭代40次后变化逐步趋于平缓,在迭代60次后甚至出现负增长现象。将复原效果以及噪音扩散等因素综合考虑,最终选择将两种复原算法迭代50次后的结果进行复原,其复原结果如图4(c)、图4(d)所示。其中,未改进R-L算法复原图像的峰值信噪比为26.457 0,改进算法的峰值信噪比为34.786 2,提升约31.5%。
为进一步验证改进R-L算法的优越性,向原始图像中添加均值为0,方差为0.05的高斯噪声,将去模糊参数DAMPAR 设定为噪声标准差的5倍,即0.25。使用两种方法对退化图像进行复原,加噪原始图像、运动模糊图像以及改进前后算法的复原效果如图6所示。

图5 两种算法峰值信噪比随迭代次数的变化曲线

图6 加噪图像复原效果
分别选择均方根误差、峰值信噪比以及灰度平均梯度3个无量纲特征量作为评价系数,对复原效果进行量化。3个评价系数中,图像复原的效果越好,均方根误差越低、峰值信噪比以及灰度平均梯度越高,在不同噪声条件下,两种算法的量化结果如表2所示。
表2 图像复原效果量化结果

图像质量复原算法评价系数均方根误差MSE峰值信噪比PSNR灰度平均梯度GMG原始图像R-L算法41.632 826.457 013.747 3改进的R-L算法30.105 234.786 217.812 7加噪图像R-L算法126.473 224.145 57.889 2改进的R-L算法96.548 228.763 69.635 1
由表2可以看到,在无噪音条件下,相比于未改进算法,改进R-L算法复原图像的MSE降低约27.7%,PSNR提升约31.5%,GMG提升约24.9%。在含噪条件下,改进的R-L算法MSE降低约23.6%,PSNR以及GMG均提升约20%,算法的稳定性有效增加。
4 结论
1) 二次变换估计方法可以有效提升点扩散函数的估算精度,相比于传统的点扩散函数系数估计方法误差显著降低,更具优越性,而且在对含噪样本的系数估计时具有更高的稳定性;
2) 基于二次变换改进的R-L算法可以显著提升退化图像的复原精度,有效降低复原图像的均方根误差,提高峰值信噪比以及灰度平均梯度,同时对含噪图像的复原具有更高的鲁棒性。
[1] 张玉叶,李明珠,王春歆,等.运动模糊图像复原技术研究[J].中国设备工程,2017(6):182-183,185.
[2] 刘桂雄,王博帝,黄坚,等.运动模糊图像复原技术研究进展与展望[J].激光杂志,2019(4):1-8.
[3] 胡伏原,王振华,吕凡,等.一种基于显著性边缘的运动模糊图像复原方法[J].苏州科技学院学报(自然科学版),2017,34(1):77-82.
[4] LI T J,YUAN Y,SHUAI Y,et al.Joint method for reconstructing three-dimensional temperature of flame using Lucy-Richardson and nearest neighbor filtering using light-field imaging[J].Science China Technological Sciences,2019,62(7):1232-1243.
[5] 王灿,杨帆,李靖.基于l1/l2的高低阶全变差运动模糊图像盲复原方法[J].激光与光电子学进展,2018(4):197-205.
[6] 赵惠,夏晶晶,张凌,等.改进矢量外推Richardson-Lucy算法在波前编码图像复原中的应用[J].光子学报,2019,48(6):20-30.
[7] 刘鹏飞,赵怀慈,曹飞道.多尺度卷积神经网络的噪声模糊图像盲复原[J].红外与激光工程,2019(4):300-308.
[8] 全蕾.结合图像恢复的方块编码压缩图像防篡改方法[J].兵器装备工程学报,2019,40(10):136-141,155.
[9] 周炜,关洪军.基于GF-2卫星影像的冲积扇地貌识别方法[J].兵器装备工程学报,2018,39(10):188-192.
[10] 刘微.运动模糊图像恢复算法的研究与实现[D].长春:中国科学院研究生院(长春光学精密机械与物理研究所),2006.
[11] CHAN T F,ESEDOGLU S,NI K.Histogram Based Segmentation Using Wasserstein Distances[C]//International Conference on Scale Space and Variational Methods in Computer Vision.2007:697-708.
[12] 李喆,李建增,王哲.基于先验优化的一致性模糊盲复原算法[J].北京邮电大学学报,2019(2):63-69.
[13] 黄绿娥,吴禄慎,陈华伟.融合LSTM的DCNN及其图像模糊类型和参数识别[J].应用基础与工程科学学报,2018(5):1092-1100.
[14] 杨爱萍,王南.基于结构-纹理分层的夜间图像去雾算法[J].激光与光电子学进展,2018,55(06):101-108.
[15] 许兵朝,杨天成,杨一.考虑泊松比的HTPB推进剂贮存老化反应速率研究[J].兵器装备工程学报,2017(02):168-171.