排爆机械手是用来排除未爆弹药的主要作业工具,主要由机械臂和手爪组成,大型排爆机械手的控制由于其本身作业环境特殊、结构重量较大,导致控制精度较低,调整时间较长,因此,合理优化排爆机械手的控制策略一直是研究的重点。排爆机械手的驱动方式有液压驱动、电机驱动和气压启动,作业时,控制器输出信号控制驱动装置,驱动装置直接带动各关节到达相应位置,通过各关节联合运动,使机械手末端达到指定位置,实现排爆过程。由于排爆机械手本身重量较大,使其在作业过程中会产生较大的滞后性和惯性,并且关节驱动需要的力矩较大,因此PID成为目前排爆机械手控制的主流算法,然而,PID控制时存在初始参数确定困难、超调量较大、响应时间较长等问题,因此,开发新的控制方法,或在原有PID算法上加以改善,具有非常重要的研究价值和应用前景。
为提高排爆机械手等大型机械手的控制精度,国内外学者为此进行了广泛的研究。宁煜[1]设计了一种单神经元来优化机械臂PID控制方法,使关节误差减小,鲁棒性更强,但微分跟踪器参数难以确定; Indrawanto[2]考虑到机械臂动力学具有的强非线性等特点,因此采用具有强鲁棒性特点的滑模控制进行关节控制内的运动控制。Aly[3]结合模糊和PID控制策略,推出了一个新型的模糊PID算法,用以大型电液机械臂轨迹控制,与传统PID方法对比,此方法可实现更快的收敛以及具有更优的鲁棒性能。沈玲[4]研究了大型送料机械手夹紧模糊PID控制系统,采用二维模糊控制器,根据模糊规则建立模糊推理系统,搭建模糊PID控制系统仿真模型,缩短了机械手反应时间。倪骁骅等[5]研究了机械手自适应滑模控制系统,建立机械手运动数学模型,设计了滑模控制系统,对控制系统的稳定性进行证明,通过仿真验证滑模控制效果,降低了机械手角速度跟踪误差。
本文基于排爆机械手关节PID控制参数初始值确定困难、超调量较大等问题,设计一种排爆机械手关节BP+PID伺服电机控制系统,运用BP神经网络优秀的学习能力和非线性求解能力对其参数进行整定,加快PID控制的收敛速度,提升控制精度。通过建立直流伺服电机模型、BP+PID算法模型,并与传统PID控制进行对比,验证了该控制系统的实用性与可行性。
1 排爆机械手关节控制系统分析
1.1 排爆机械手系统参数
某排爆机械手采用六自由度的结构,其最大臂展为2 m,最大夹持力为20 kg,机械手本身重189 kg,采用伺服电机直接带动关节进行运动,其结构简化模型如图1所示。其机械参数如表1所示。

图1 某排爆机械手结构示意图
表1 排爆机械手机械参数

名称旋转底座大臂中臂小臂手爪长度/mm100300400600200重量/kg4844413224
某排爆机械手关节控制系统原理如图2所示。

图2 排爆机械手关节伺服电机控制系统原理框图
系统采用位置直流伺服电机直接驱动机械手关节运动,并通过角度传感器采集机械手关节运动的角度反馈给电机进行实时调整。
1.2 关节控制系统数学模型
直流伺服电机工作时,其工作转矩等于负载转矩与负载惯性系统加、减转矩之和,即:
(1)
式(1)中,T(t)为电动机输出转矩(N·m);TL(t)为负载转矩(N·m);w(t)为电动机角速度(rad/s); Ja为电动机电枢转动惯量,Ja=2.2×10-3 kg·m2;J1为负载的转动惯量,需将机械手关节的惯性转换到电机轴上,取5×10-3 kg·m2; h为丝杠螺距; mz为工作台质量。
当电机电路处于动态过程中时,电机内部线圈施加的电源电压Ua(t)和电枢线圈内通过的电流Ia(t)的关系为:
![]()
(2)
式(2)中,Ra为电机电枢线圈内阻,Ra=20 Ω;La为电机电枢线圈的电感,La=2H;eb(t)为电机电枢线圈在钉子磁场中运动时产生的反电动势。
电机输出转矩M(t)应与通过电枢线圈的电流大小成正比,则M(t)=kTIa(t)[6]。其中,kT为电机输出扭矩常数,kT=9.2 N·m·A-1。电机电枢线圈产生的反电动势eb(t)与电枢的工作角速度w(t)成正比[7],故有:
eb(t)=kbw(t)
(3)
式(3)中,kb为电机电枢反电动势系数,kb=0.024 4 V·rad-1。
对上述式子进行拉普拉斯变换,并令初始条件为0,则有:
M(s)=ML(s)+(Ja+J1)s·Ω(s)
(4)
Ua(s)=(Rs+sLa)Ia(s)+Eb(s)
(5)
M(s)=kTIa(s)
(6)
Eb(s)=kbΩ(s)
(7)
对上式进行综合,得:
(8)
在不考虑外部干扰负载ML(s)时,直流伺服电机的传递函数为:
![]()
(9)
式(9)中,Tm为直流电机的时间常数。
假设kφ为关节角度对应电压转换系数,此处取kφ=0.07 V·rad-1。
直流伺服电机的闭环控制系统如图3所示。

图3 直流伺服电机闭环控制系统框图
1.3 关节控制系统稳定性分析
系统稳定性是指控制系统在使它偏离平衡状态的扰动消失后返回原来平衡状态的能力[8]。在设计控制系统时,首先要求系统是稳定的。对于本排爆机械手关节电机伺服控制系统,依据以上系统传递函数模型推导出系统的开环传递函数为:
(10)
系统零-极点分布图如图4,系统零-极点主要在s右半平面内,因此该系统为最小相位系统。系统奈奎斯特图如图5,系统是稳定的。系统响应曲线如图6,
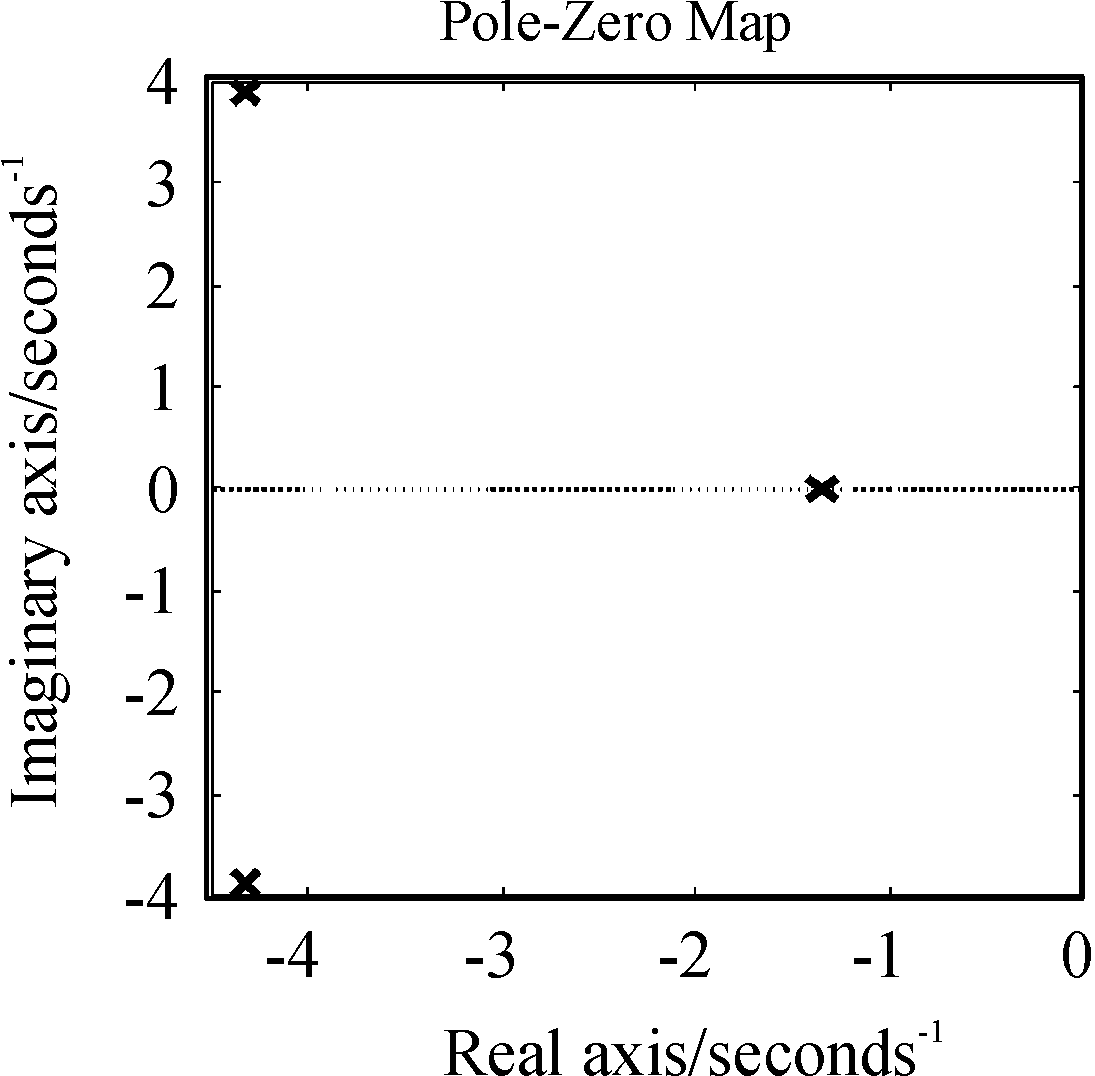
图4 电机伺服控制系统零-极点分布图
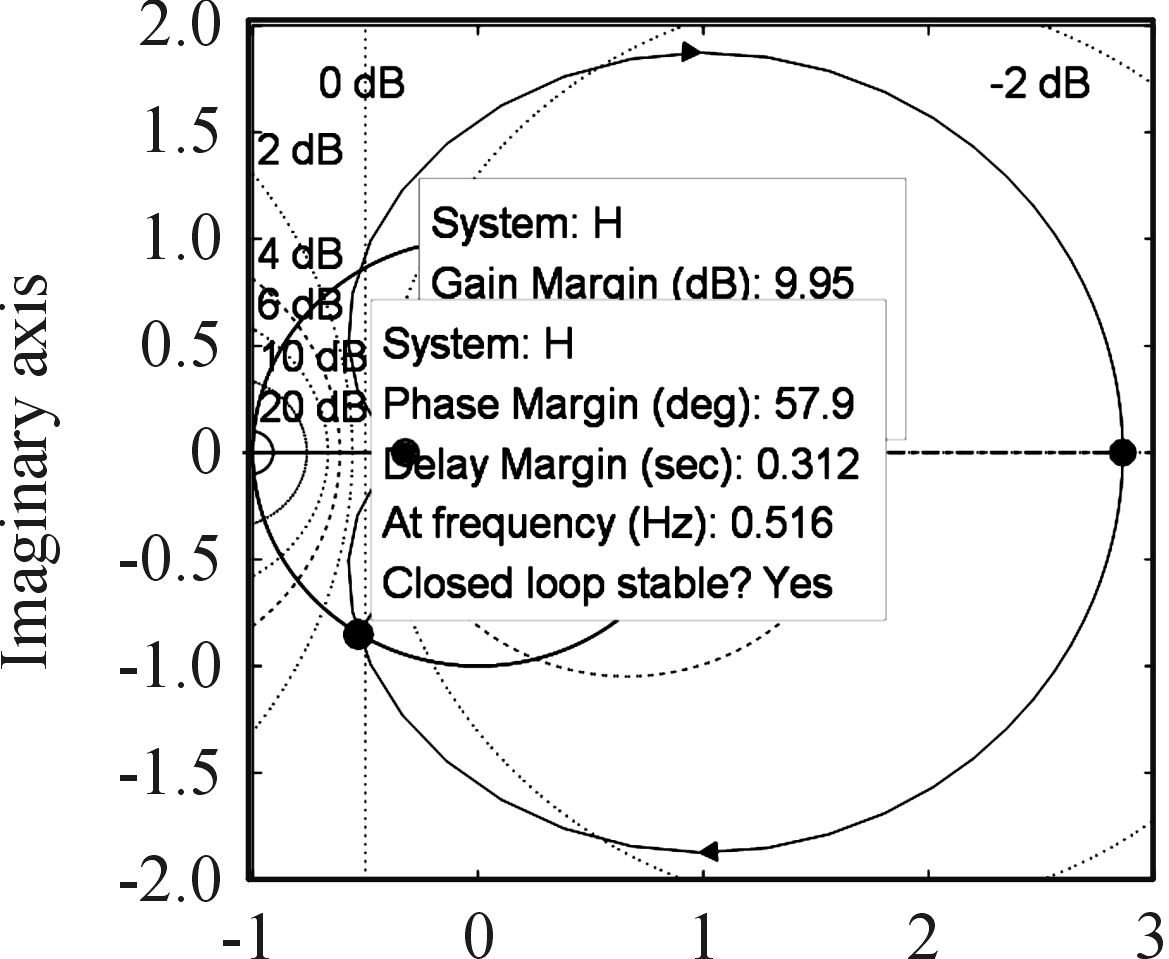
图5 电机伺服控制系统奈奎斯特图
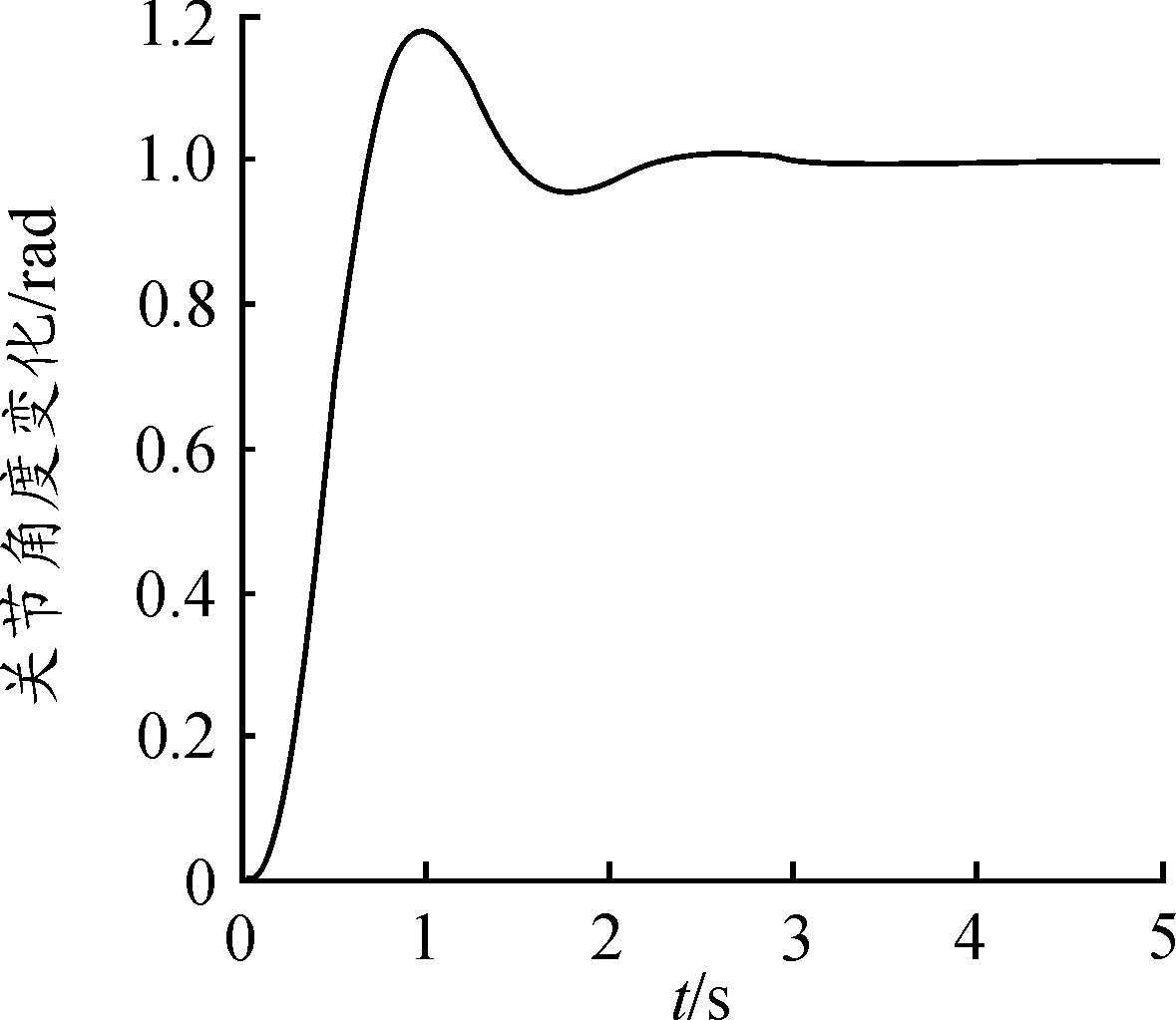
图6 电机伺服控制系统响应曲线
可以看出,系统受到冲击时响应时间大约为0.5 s,调节时间大约为2.7 s,超调量大约为0.2 rad。该伺服电机控制系统虽能趋于稳定但系统调整时间过长、超调量过大。由此,本文提出的BP+PID控制来优化电机伺服控制系统,以提高机械手关节控制的响应速度和调整精度。
2 BP神经网络PID控制设计
经典增量式数字PID的控制计算公式为:
u(k)=u(k-1)+Kp[e(k)-e(k-1)]+Kie(k) +
Kd[e(k)-2e(k-1)+e(k-2)]
(11)
式(11)中,Kp、Ki、Kd分别为比例、积分、微分系数;e(k)为当前采样时刻的期望输出与实际输出之差;u(k)为当前采样时刻的控制量[9]。
将Kp、Ki、Kd视为以来于系统运行状态的可调参数时,可将上式描述为:
u(k)=f(u(k-1),Kp,Ki,Kd,e(k),e(k-1),e(k-2))
(12)
式(12)中, f(·)是与Kp、Ki、Kd、u(k-1)、u(k)等有关的非线性函数。
通过BP神经网络训练和学习来找到此函数最佳的一个控制规律。BP神经网络结构如图7所示。

图7 BP网络结构示意图
BP神经网络输出层的3个输出分别对应PID控制器的3个可调参数Kp、Ki、Kd。由于Kp、Ki、Kd不能为负,所以输出层神经元的激活函数取非负的Sigmoid函数,而隐含层神经元的激活函数可取正负对称的tanh函数[10-12]。BP神经网络的输入为(M为输入变量的个数):
(13)
隐含层的输入输出为:
(14)
(15)
![]()
式(14)、(15)中,上标(1)、(2)、(3)分别代表输入层、隐含层、输出层;![]() 为隐含层加权系数;
为隐含层加权系数;![]() 为阈值,
为阈值,![]() 取双曲正切函数[12-14],即
取双曲正切函数[12-14],即
(16)
网络输出层的输入输出为:
![]()
(17)
![]()
(18)
则有:
式(17)中,![]() 为输出层的加权系数,输出层神经元的激活函数为:
为输出层的加权系数,输出层神经元的激活函数为:
(19)
![]() 为阈值,且
为阈值,且![]()
采用输出误差二次方为网络的损失函数:
![]()
(20)
按照梯度下降法修正网络的加权系数,并附加一个使搜索快速收敛全局极小的惯性项,则有BP神经网络输出层的加权系数修正计算公式为:
(21)
(22)
同理可得隐含层加权系数的修正计算公式为:
![]()
(23)
![]()
(24)
式(22)中,g′[x]=g(x)[1-g(x)],式(24)中, f′[x]=[1-f2(x)]/2。
其系统结构如图8所示。

图8 BP+PID控制系统结构框图
BP神经网络PID控制算法流程可总结为图9。
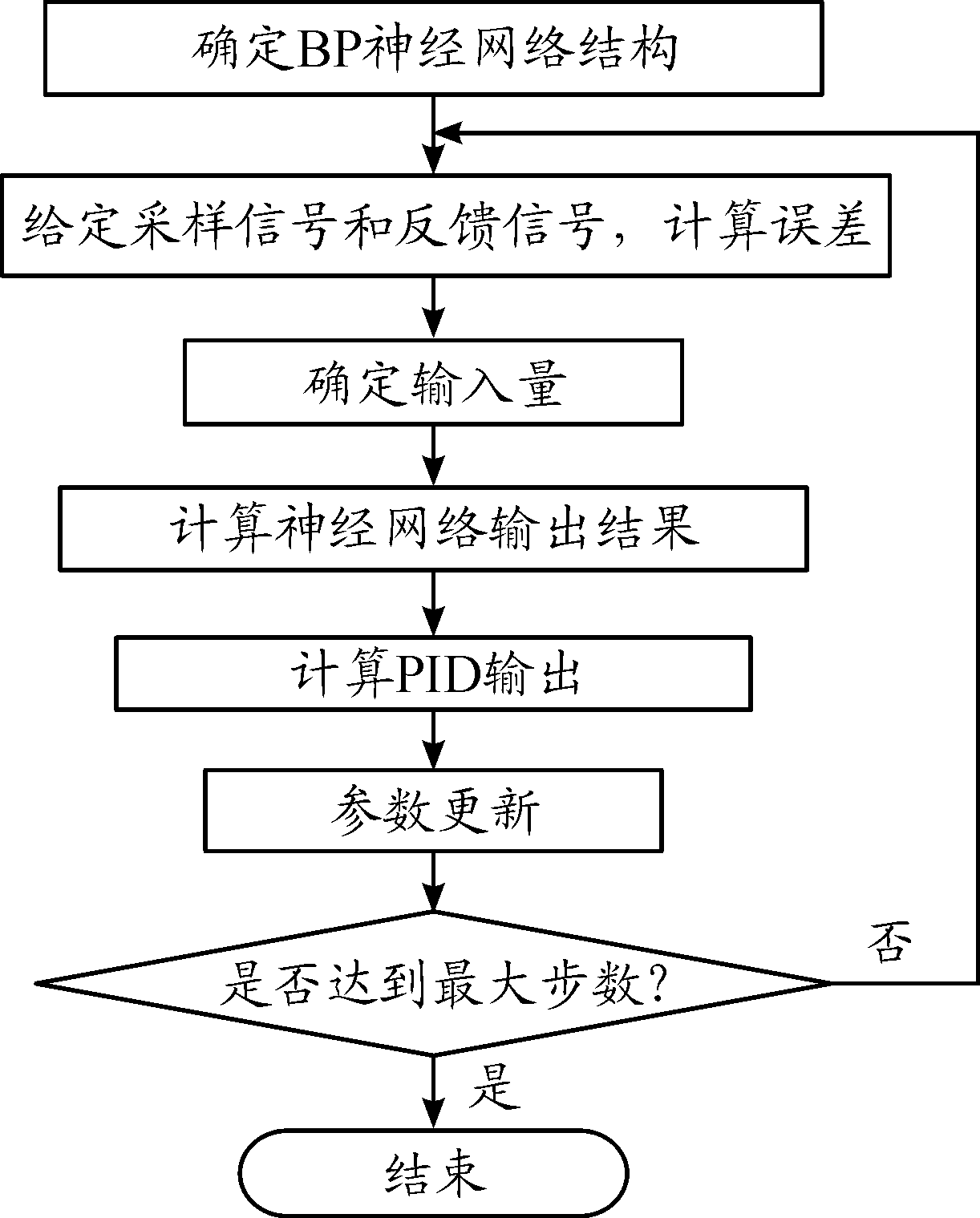
图9 BP+PID程序控制算法流程框图
3 系统仿真实验及结果分析
根据以上数学模型在Matlab/Simulink中进行建模与仿真,Simulink模型如图10所示。在建立的排爆机械手关节控制系统进行模拟仿真,假定在某一作业过程中,机械手视觉系统定位了某一目标,中心处理器根据逆运动学计算,排爆机械手大臂关节的期望角度为1 rad,因此在系统的输入接口输入信号为1 m/s的关节信号进行仿真,查看该关节运动情况[15-16]。当控制系统输入1 m/s的关节信号时,关节角度运动如图11所示。
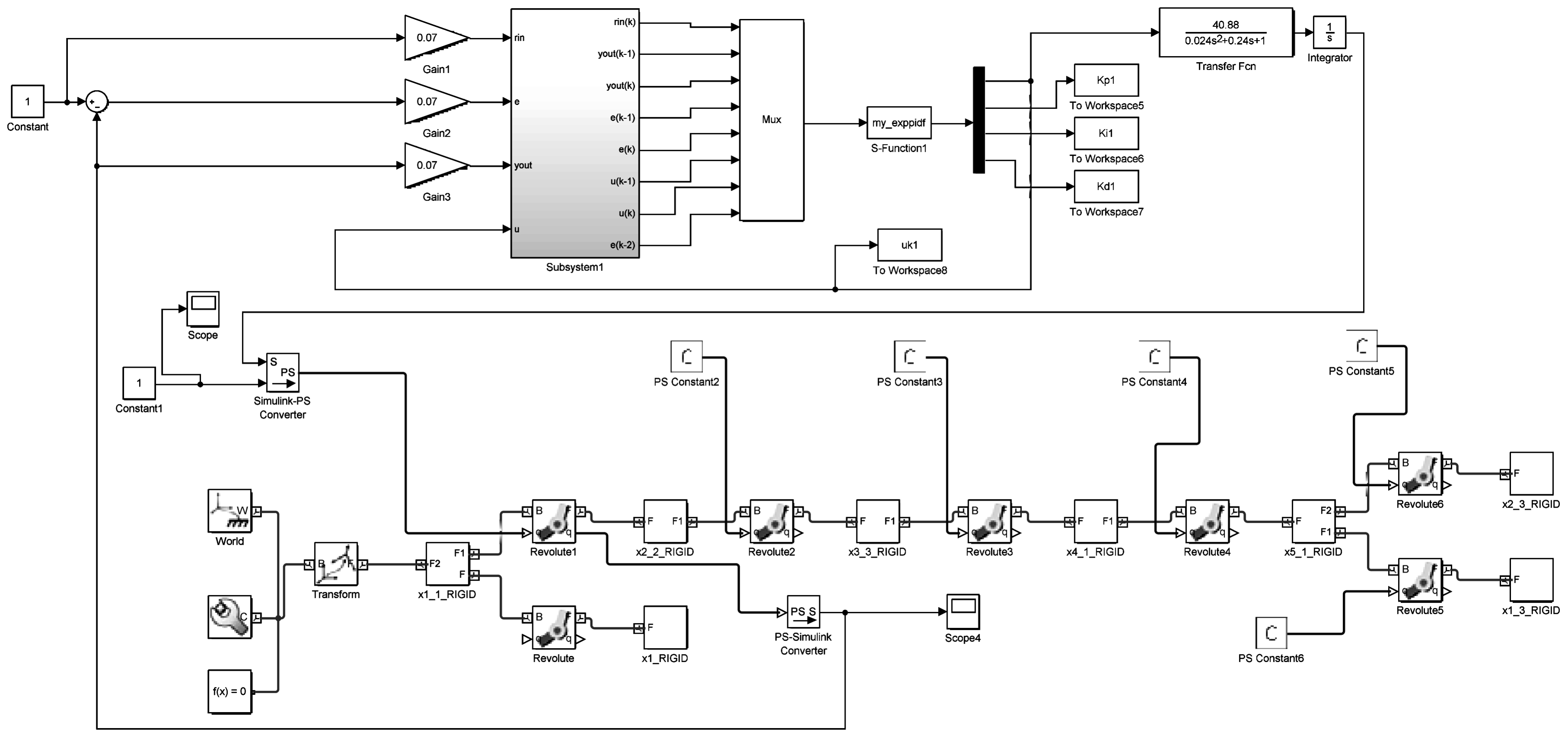
图10 排爆机械手关节BP+PID伺服电机控制系统Simulink仿真模型示意图

图11 排爆机械手关节运动效果图
由以上仿真结果可以看出,该排爆机械手关节控制方案可行。为证明该控制方案与传统PID机械手控制相比具有一定的先进性与实用性,在Simulink中建立相同系统采用PID控制进行仿真,PID排爆机械手关节伺服电机控制Simulink模型如图12所示,其中,PID控制参数Kp=0.94、Ki=0.04、Kd=0.40,并输入相同关节信号进行仿真。将两次仿真结果进行对比,两个系统控制参数Kp、Ki、Kd参数变化如图13所示,得Kp=0.222、Ki=0.54、Kd=0.245关节角响应如图14所示,误差如图15所示。
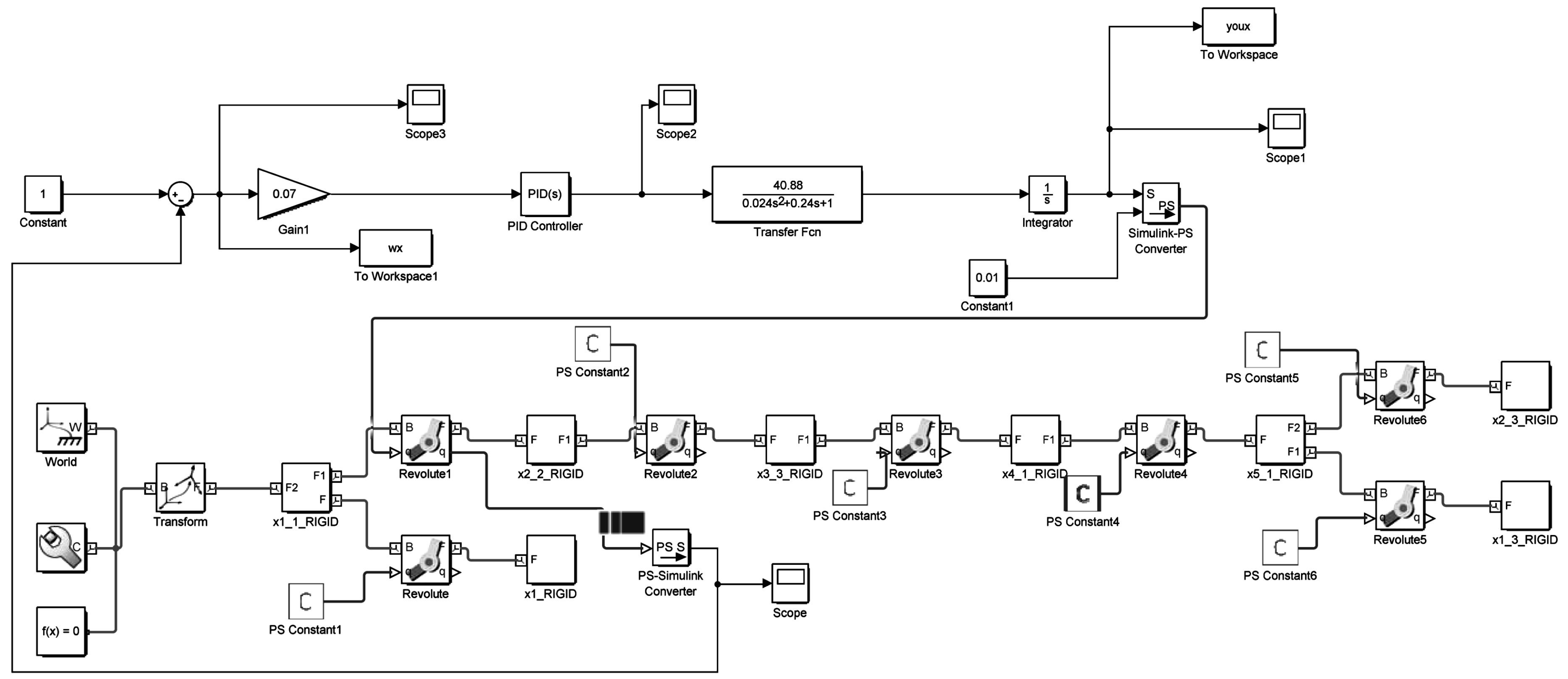
图12 排爆机械手关节传统PID伺服电机控制系统Simulink仿真模型示意图
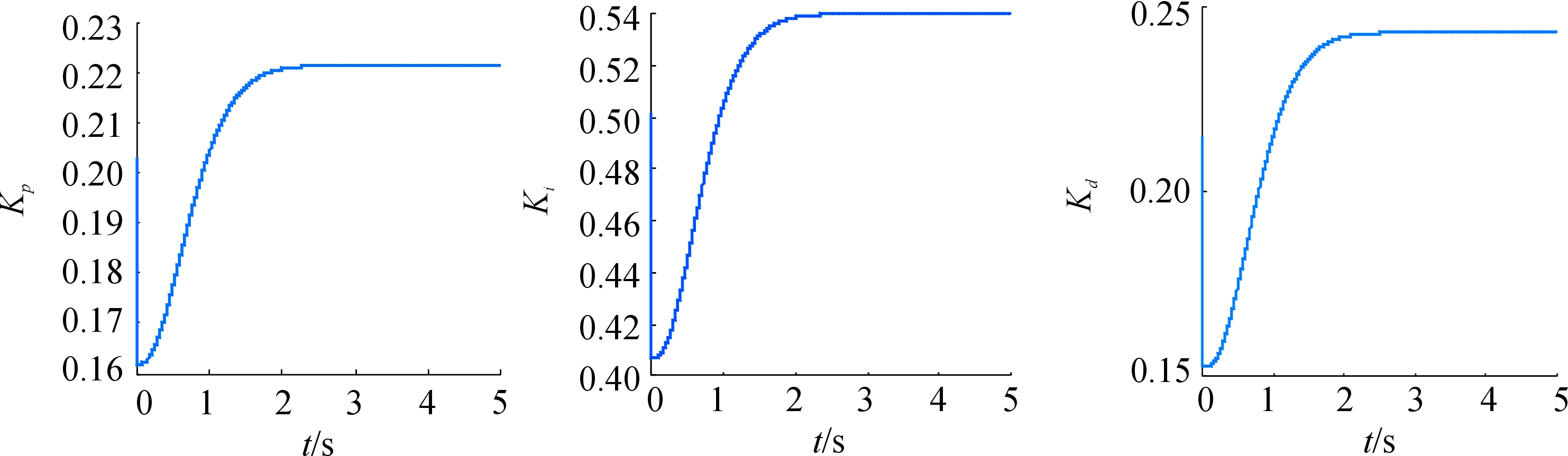
图13 Kp、Ki、Kd参数曲线
根据图14、图15,BP+PID伺服控制系统响应时间约为1.2 s,系统调整时间约为2 s,系统误差约为0.01 rad,系统稳定上升至目标角度,无超调量;PID伺服控制系统响应时间约为0.7 s,系统调整时间约为2.5 s,系统误差约为0.04 rad,系统初期存在波动,波动角度约为0.1 rad;原伺服电机控制系统响应时间约为0.6 s,调整时间约为2.9 s,超调量约为0.2 rad,误差约为0.03 s,系统波动较大。

图14 排爆机械手关节角度曲线

图15 关节角度误差曲线
由此可知,1)原系统由于加入了控制环节导致系统响应时间相比较原系统稍慢,但系统调整时间和误差变小,超调量变小,因此在原系统中加入控制环节具有一定的必要性;2) 相比较传统PID控制,由于自身参数学习过程导致BP+PID伺服电机控制系统的响应时间稍慢,但系统整体超调量变小,抗干扰能力更强,能够根据系统误差和期望迅速调整Kp、Ki、Kd参数。3) BP+PID伺服电机控制系统可以根据系统整体性能得出最优Kp、Ki、Kd参数,解决了传统PID系统控制参数初始化难以确定的问题,且调整时间相比较其他两个系统较短。由此验证了本文提出的排爆机械手关节控制系统的有效性和实用性。
5 结论
1) 引入PID进行机械手关节控制优化,并且通过应用BP神经网络调整传统PID的控制参数Kp、Ki、Kd。
2) 本文提出的排爆机械手关节BP+PID伺服控制系统与传统PID系统相比控制精度更高,且抗干扰能力较强、鲁棒性较强。
3) 本文提出的排爆机械手关节BP+PID伺服电机控制系统仿真,给排爆机械手控制提供了新的算法,可为更加精确的控制研究提供参考。
[1] 宁煜.基于改进PID控制的三关节机械臂运动轨迹跟踪误差研究[J].机械设计与制造工程,2018,47(08):107-110.
[2] INDRAWANTO I.Sliding mode control of a singles rigid hydraulically actuated manipulator[J].International Journal of Mechanical & Mechatronics Engineering,2011,11(5/14).
[3] ALY A A,EI LAIL A S A,SHOUSH K A,et al.Intelligent PI fuzzy control of an electro-hydraulic manipulator[J].International Journal of Intelligent Systems and Applications,2012,4(7):43-50.
[4] 沈玲.机械手夹紧控制系统基于模糊PID控制的研究[J].内燃机与配件,2018(15):5-7.
[5] 倪骁骅,刘青.基于MIMO系统的机械手自适应模糊滑模控制[J].中国农机化学报,2015,36(02):265-268.
[6] 章细福.基于串励电机的跑步机控制器设计[D].哈尔滨:哈尔滨工业大学,2010.
[7] 刘国平.机械系统中的摩擦模型及仿真[D].西安:西安理工大学,2007.
[8] 周文军.基于自适应算法的无刷直流电机控制器的研究与设计[D].上海:东华大学,2014.
[9] 吴文铁,宋曰聪,李敏.蚁群优化神经网络的网络流量混沌预测[J].计算机工程与应用,2012,48(34):97-101.
[10] 杜峰.基于神经网络和高斯过程的机械手抓取策略与仿真研究[D].武汉:武汉科技大学,2018.
[11] 岳光,潘玉田,张华君.一种多神经元智能算法的GURV伺服控制系统研究[J].兵器装备工程学报,2019,40(02):125-130.
[12] 王琪,丁柏文,陈萍.苹果采摘机器人控制系统设计[J].机械制造与自动化,2019,48(05):150-152.
[13] Mohanty.Zeng.G.Nagamani,Young Hoon Joo,G.Soundararajan,Reza Mohajerpoor.Robust event-triggered reliable control for T-S fuzzy uncertain systems via weighted based inequality[J].Information Sciences,2020,512-520.
[14] YE C S.Indrawanto G.Nagamani,Young Hoon Joo,G.Soundararajan,Reza Mohajerpoor.Robust Event-Triggered Reliable Control for T-S Fuzzy Uncertain Systems via Weig-hted Based Inequality[J].Information Sciences,2019.
[15] Ignacio Carlucho,Mariano De Paula,Gerardo G.Double Q-PID algorithm for mobile robot control[J].Expert Systems With Applications,2019,137-141.
[16] 陈涛.遥操作排爆机器人研制及其运动控制研究[D].济南:山东大学,2019.