现代信息技术正在迅速发展，并且以无线通信，卫星通信和船舶通信为代表的电子设备的小型化和小型化的需求正在增加。天线作为通信设备中的前端部件，对通信质量起着至关重要的作用[1-2]。
在光栅耦合器的研究中，2010年，香港中文大学Xia Chen等[3]为降低耦合损耗，提出了一种啁啾光栅结构，实验结果表明，该光栅的耦合能量损耗仅有1.2 dB。2011年，国防科技大学杨俊波等[4]设计了一种双周期垂直耦合光栅结构。实验表明，当光波波长为1 550 nm时，该耦合器的耦合效率达到80%。2014年，西班牙C.Alonso-Ramos等[5]提出了一种光栅耦合结构，耦合方向性不受光波导各层厚度、光栅高度等因素的影响，耦合效率达到-1.05 dB。
虽然结构层出不穷的光栅结构使耦合效率不断提高，但其结构设计相对复杂，由于制作工艺和制作成本等因素限制，目前应用于芯片式光学天线的光栅耦合器还是以传统直线型为主[6-10]。
在光学天线接收端与光纤耦合的过程中，传统直线型光栅耦合器的最优横向宽度一般在，通常硅基单模波导的宽度在 左右，两者之间的宽度差异很大[11]。为了匹配单模光纤的横向尺寸，通常在两者之间添加一个线性变化的模斑转换器。这可以降低失配损耗，但会导致整个光栅耦合器的尺寸过大[12-13]，成了天线芯片的体积负担。
为了减小光栅耦合器的尺寸，基于现有的传统直线型光栅耦合器的结构参数，提出了一种将现有直线型光栅耦合器改良设计成会聚形光栅耦合器的方法，将样品优化设计后，仿真得到在耦合效率比直线型高的同时，尺寸减小到原来的1/4。优化光栅结构参数并制作实物进行实验，理论计算，模拟仿真与实验测试结果吻合良好，实现高效耦合和低损耗模式的改变，它可用作芯片式光学天线接收端，以减小天线的尺寸。
1 会聚型光栅耦合器工作原理
会聚型光栅耦合器[13-14]的基本结构如图1(a)所示，它的刻槽与传统光栅耦合器不同，采用弧形刻槽，每段圆弧是圆心角相等，半径等差排列的同心圆弧，其构成的扇形结构对耦合进光栅的光波有会聚作用，光波可直接进入波导，因此可以在不需要模斑转换器的情况下，实现模斑转换。这允许使光栅耦合器的尺寸大大减小，从而进一步减小了光学天线接收端的尺寸。
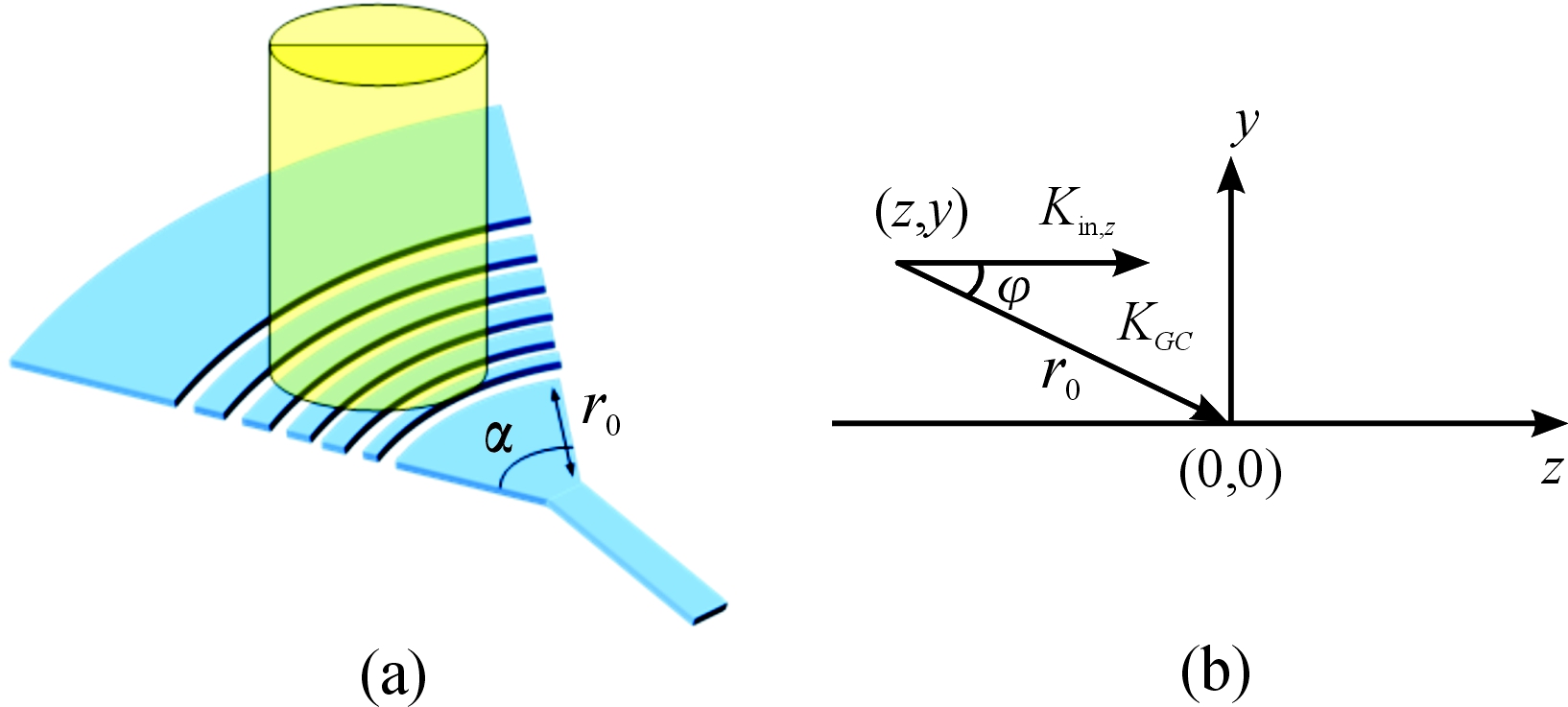
图1 会聚型光栅耦合器的基本结构(a)和会聚型光栅耦合器波矢图(b)
通过分析，耦合进光栅区域的光，只有在圆弧刻槽满足特定条件时，才能恰好会聚到波导中去。如图1(b)所示为会聚型光栅耦合器上在点(z,y)的波矢，圆弧圆心的坐标(0,0)，即光波会聚到单模波导的初始坐标。入射波矢Kin沿xz平面倾斜入射，并且在yz平面中有一个平行于z轴的投影分量Kin，z。如果想光栅耦合器上的每个点到圆心处的相位都是相长干涉，需要满足：
Kincosφr+2πn=KGCr
(1)
其中：KGC为波导的波矢；φ为点(z,y)与圆心(0,0)的连接矢量与z轴的夹角；
为点(z,y)到圆心(0,0)的距离；n为一个整数，在光栅平面中入射波矢的投影分量大小可以表达为Kin，z=(2πn1sinθ)/λ，n1为入射介质的折射率，θ为耦合角度， λ为真空波长，光栅波导的波矢大小可以表达为 KGC=(2πneff)/λ，neff 为光栅波导的有效折射率。当点在z轴上时，φ=0，r=-z，代入Kin，z=(2πn1sinθ)/λ和KGC=(2πneff)/λ可得：
(2)
因此，xz截面上光栅耦合器的周期p为：
(3)
有效折射率neff可用周期p表达为：
(4)
在以上分析以后，可以计算会聚型光栅耦合器的横向结构分布。
2 会聚型光栅耦合器的结构设计
2.1 对样品直线型光栅耦合器结构参数仿真
如图2所示为直线型光栅耦合器沿xz平面的截面，使用常用的SOI结构，顶硅层的厚度为220 nm，BOX层的厚度为2 μm。可以看出刻蚀深度e,刻蚀宽度w，周期p以及入射耦合角度θ是影响其性能的主要参数。
图2 直线型光栅耦合器示意图
选择现有的直线型光栅耦合器作为参照样品[15]，其光栅参数为：入射波长λ=1 550 nm，刻蚀深度e=70 nm,刻蚀宽度w=300 nm，周期p=630 nm,横向宽度d0=16 μm,入射耦合角θ=14°。
将以上直线型光栅参数代入FDTD软件进行三维仿真，得到耦合谱线如图3，峰值耦合效率为-3.3 dB,1 dB带宽为43 nm。
2.2 会聚型光栅耦合器的结构参数的设计和优化
1) 选取和优化起始半径r0和会聚角α
如图4(a)所示，决定光栅耦合器性能的结构参数除了刻蚀深度e,刻蚀宽度w，周期p以及入射耦合角度θ之外，还应考虑的起始半径r0和会聚角α。从图4(b)可以看出，在xz截面中的会聚型光栅耦合器与传统光栅耦合器结构相同，选用与传统直线型光栅耦合器相同的xz平面参数：刻蚀深度e=70 nm,刻蚀宽度w=300 nm，周期p=630 nm。考虑到两种光栅耦合器在yz平面中的结构分布不一样，还要确定的参数为起始半径r0和会聚角α。
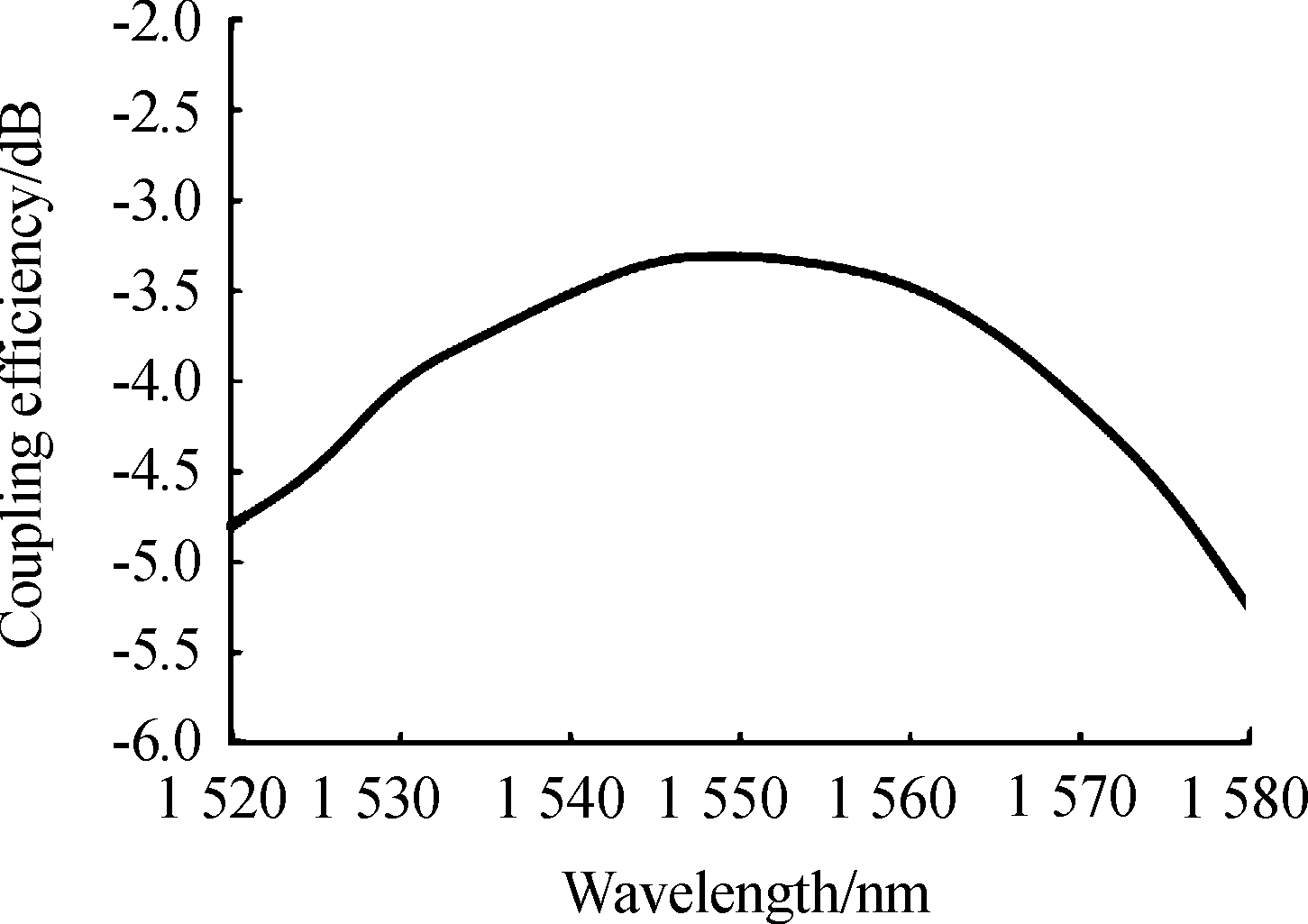
图3 仿真耦合谱线
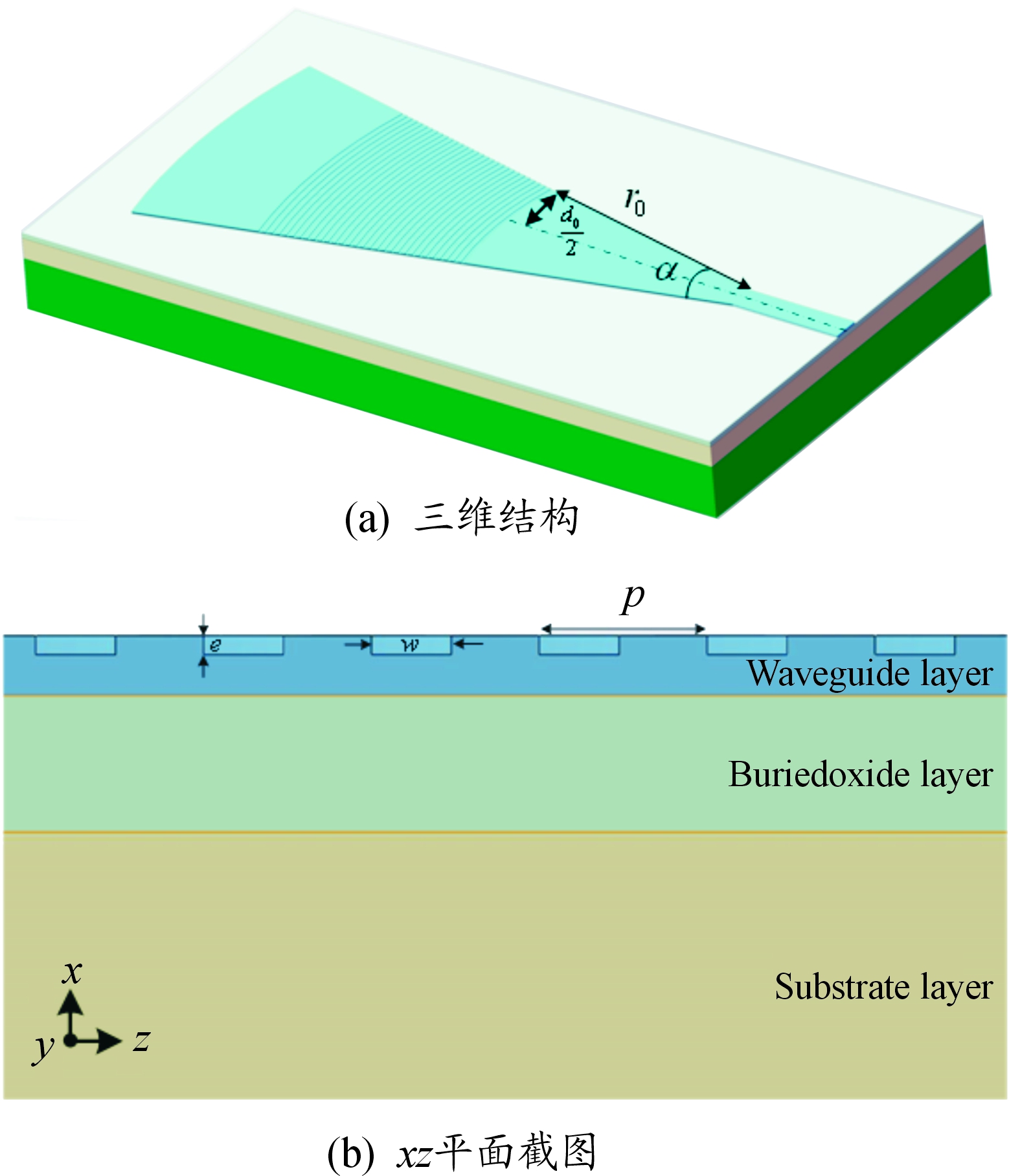
图4 会聚型光栅耦合器结构示意图
横向宽度d0由起始半径r0和会聚角α决定。假设光栅耦合器起始周期的中心点是(z=-r0,y=0),其对应的宽度d0可近似表达为：
(5)
根据前面的仿真，获得了直线型光栅耦合器的最佳横向宽度d=16 μm，代入会聚型光栅耦合器，可以得到最佳起始半径r0为(μm):
(6)
再将起始半径r0用起始周期数来表达，即r0=n0p。当α=35°时，根据式(6)可得最佳起始周期数，再仿真计算了不同n0从25到39到时，光栅耦合器的效率如图5所示，获得了最优的起始周期数n0=31，小于理论计算值。这是由于在理论计算最优起始周期时，将呈高斯分布的圆形入场光源看作是以其直径为边长的正方形入射光源，导致仿真值比理论值小一些。根据n0=31可以得到r0=n0p=31×0.63=19.53 μm，取r0=19.5μm，则d0=12.4 μm。
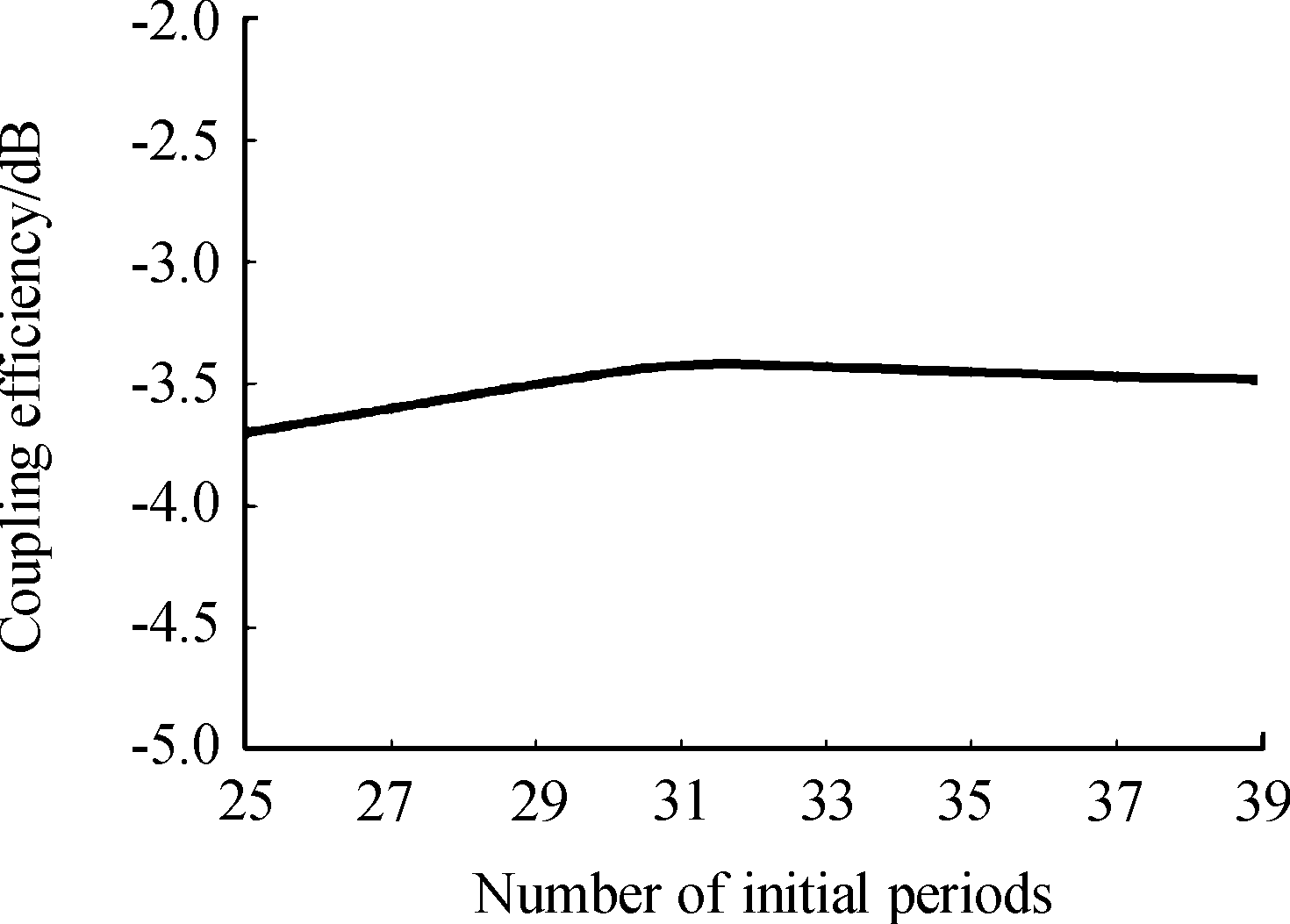
图5 当α=35°时，不同起始周期数n0对应的耦合效率曲线
根据式(6),会聚角α越大，起始半径r0越小，光栅耦合器的尺寸也越小。对于会聚型耦合器，最佳起始半径r0=19.5 μm,分别对不同会聚角α=25°，30°，35°，40°，45°进行模拟计算，如图6所示，它们的耦合峰值分别为-3.39 dB, -3.40 dB, -3.41 dB, -3.45 dB， -3.46 dB。
图6 当α=25°，30°，35°，40°，45°时，不同起始周期数n0对应耦合效率曲线
由于光栅耦合器扇形区域的边缘在实际成品中不是完全光滑的，因此粗糙的边缘会造成一定的散射损耗。当最佳起始宽度d0选定时，若会聚角α选择过大，扇形区域的粗糙边缘部分就更多，散射损耗增大；若会聚角α选择过小，则对应的起始半径r0变大，致使光栅耦合器的尺寸变大。因此，会聚角的选择是一个尺寸和耦合效率之间的权衡。
根据仿真结果，当会聚角α=30°时，耦合效率与α=25°几乎一样，并且起始半径小了6.83 μm，综合考虑后，选择会聚角α=30°，其起始周期n0=36，起始半径r0=23.14 μm，其耦合峰值为-3.40 dB,1 dB带宽43 nm。
2) 优化光栅周期p
周期直接影响布拉格条件的光栅矢量,因此耦合效率对周期很敏感。保持会聚角α=30°，起始半径r0=23.14 μm，刻蚀深度e=70 nm刻蚀宽度w=300 nm，和入射耦合角θ=14°不变。在仿真模型中，将光栅周期p由610 nm增加到650 nm,可以得到光栅耦合效率随周期变化的关系曲线如图7所示。
图7 不同光栅周期对应的耦合效率曲线
从图7可知，周期p在610～634 nm时，耦合效率随光栅周期的增加而增加，在周期p=634 nm时达到峰值耦合效率-3.32 dB，而后耦合效率下降，故选择p=634 nm。
3) 优化刻蚀宽度w
刻蚀宽度影响到入射介质折射率，进而改变有效折射率，间接影响模式在波导中的传播常数。保持会聚角α=30°，起始半径r0=23.14 μm，刻蚀深度e=70 nm，光栅周期p=634 nm和入射耦合角θ=14°不变。在仿真模型中，将刻蚀宽度w由280 nm增加到380 nm,可以得到光栅耦合效率随刻蚀宽度变化的关系曲线如图8所示。
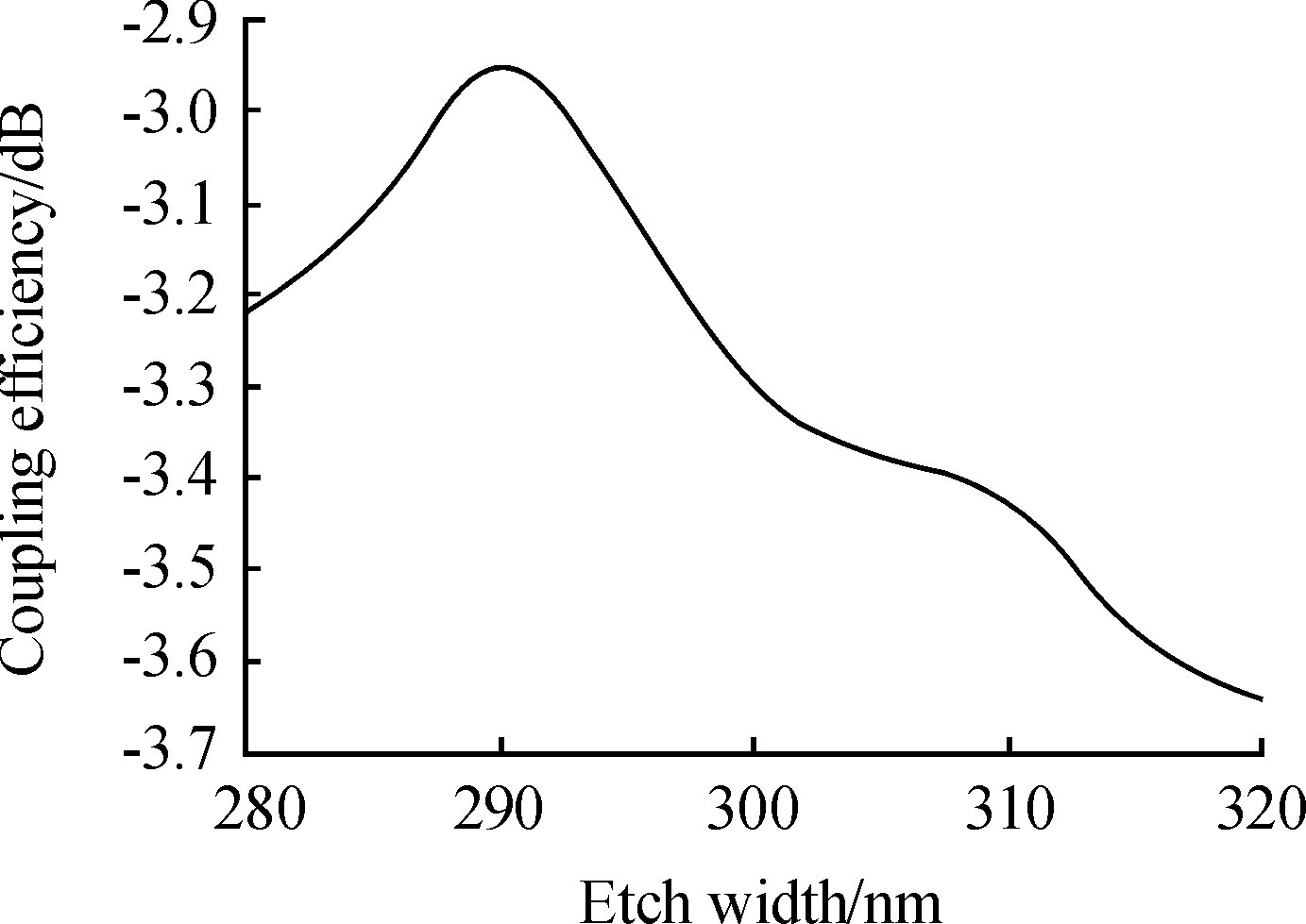
图8 不同刻蚀宽度对应的耦合效率曲线
从图8可知，刻蚀宽度w在280～291 nm时，耦合效率随刻蚀宽度的增加而增加，在刻蚀宽度w=291 nm时达到峰值耦合效率-2.9 dB，而后下降。故选择w=291 nm。
4) 优化刻蚀深度e
刻蚀深度和宽度一样，都改变了入射介质折射率，因此，两者对耦合效率的影响相似。保持会聚角α=30°，起始半径r0=23.14 μm，刻蚀宽度w=291 nm，光栅周期p=634 nm和入射耦合角θ=14°不变。在仿真模型中，将刻蚀深度e由60 nm增加到80 nm,可以得到光栅耦合效率随刻蚀宽度变化的关系曲线如图9所示。
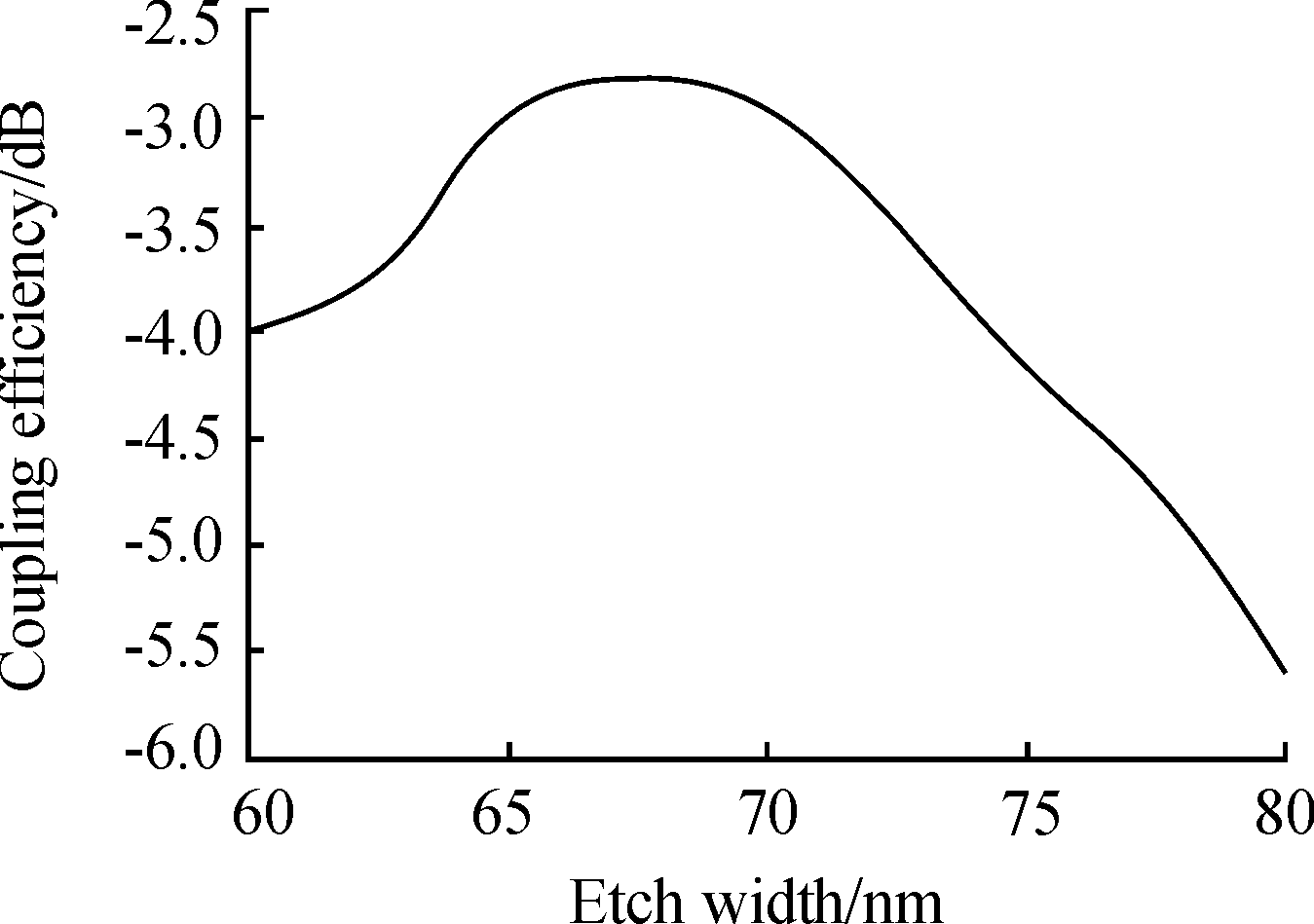
图9 不同刻蚀深度对应的耦合效率曲线
从图9可知，刻蚀深度e在60～67 nm时，耦合效率随刻蚀宽度的增加而增加，在刻蚀宽度e=67 nm时达到峰值耦合效率-2.8 dB，而后下降。故选择e=67 nm。结构参数经过优化后，场强分布图如图10，可以看出，耦合到光栅耦合器的光会自动会聚到输出单模波导中，从而减小了由光栅区域和波导的横向宽度失配导致而引起的传输损耗，提高耦合效率，达到了预期目标。
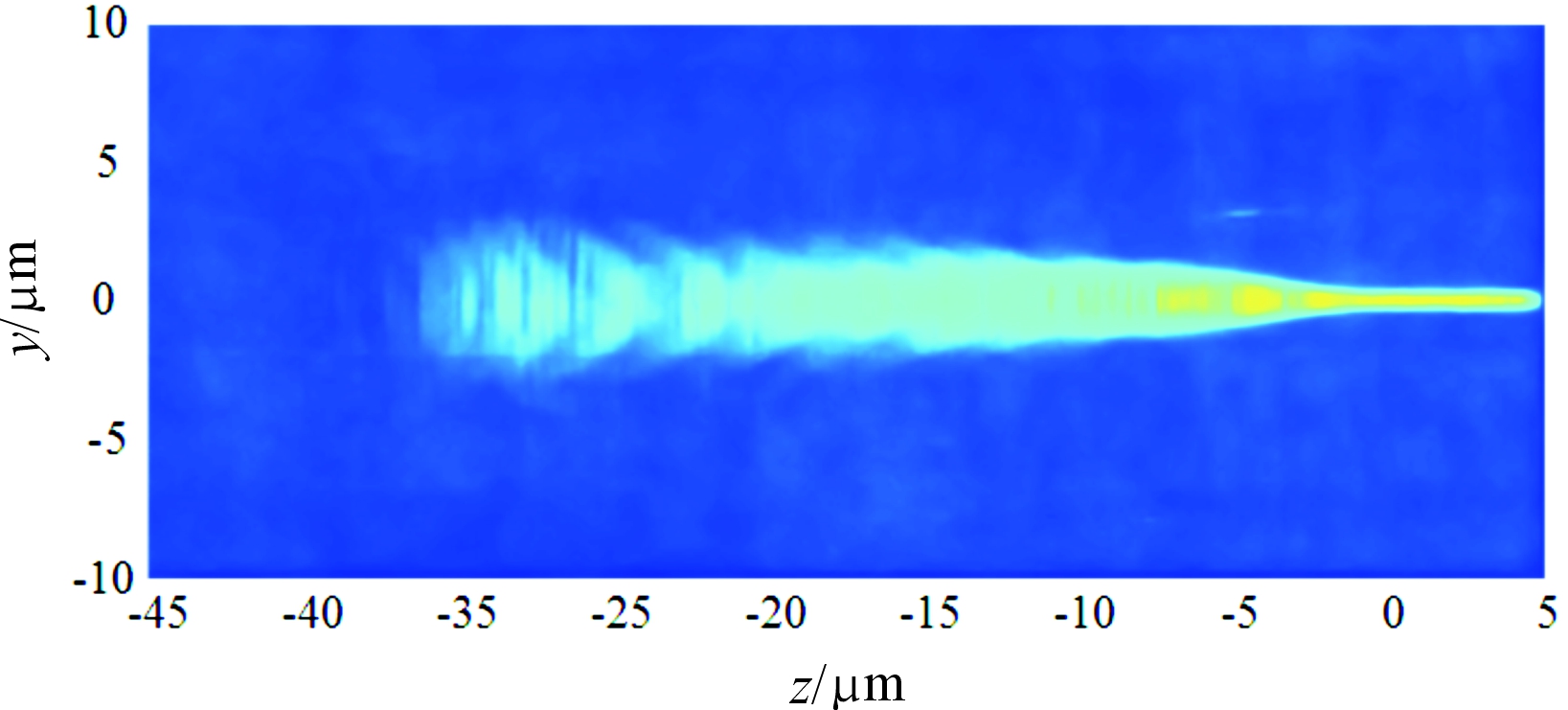
图10 会聚型光栅耦合器的场强分布图
此时，耦合谱线如图11(a)所示，会聚型光栅耦合器的峰值耦合效率为-2.8 dB，1 dB带宽46 nm,耦合效率比传统直线型高了0.5 dB，并且传统光栅耦合器还有模斑转换器的损耗，即使250 μm长的线性锥形模斑转换器，其损耗也有0.3 dB。所以设计会聚型光栅耦合器的耦合效率比传统光栅耦合器高，并且尺寸减小到原来的约1/4，如图11(b)所示。
3 制作与实验测试
3.1 制作会聚型光栅耦合器样品
据以上的理论计算和仿真设计，制定了如下方案对样片进行制备。因为器件在实际制作过程中会存在一定的工艺误差，导致实际制作出来的器件尺寸和设计尺寸不能完全一致。根据加工难度和工艺水平，最终选择制作的参数如下
1) 材料：SOI片，顶硅为250 nm，SiO2氧化层为2 μm；
2) 波导：500 nm(宽)×250 nm(高)；
3) 光栅区域：光栅周期p=630 nm，刻蚀深度e=65 nm，会聚角α=30°，起始半径r0=25 μm；
经过加工得到光栅区域的结构示意图如图12所示。
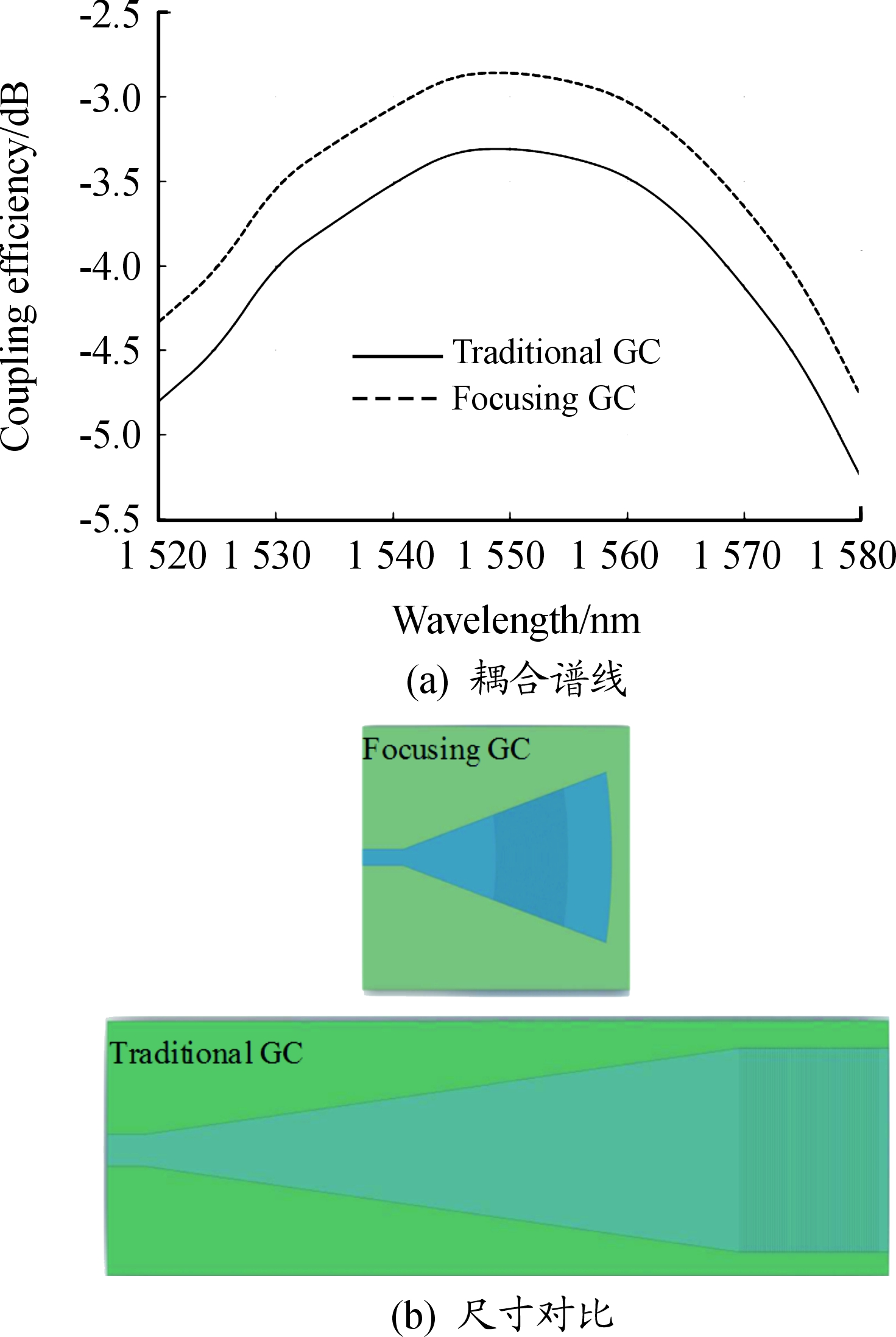
图11 会聚型和直线型光栅耦合器的耦合谱线(a)和尺寸(b)
图12 光栅区域在电子显微镜下的结构示意图
3.2 实验测试与结果分析
通过OSA测试，得到了样片测试的耦合谱线，再与传统光栅仿真结果进行对比，可以得到如图13所示的耦合谱线对比图。
由图13可知，经过改良设计制作成会聚型光栅耦合器后，实验测试耦合谱线与理论结果走势吻合良好；当波长为1 557 nm时，峰值耦合效率为57%，比之前提高了16%。
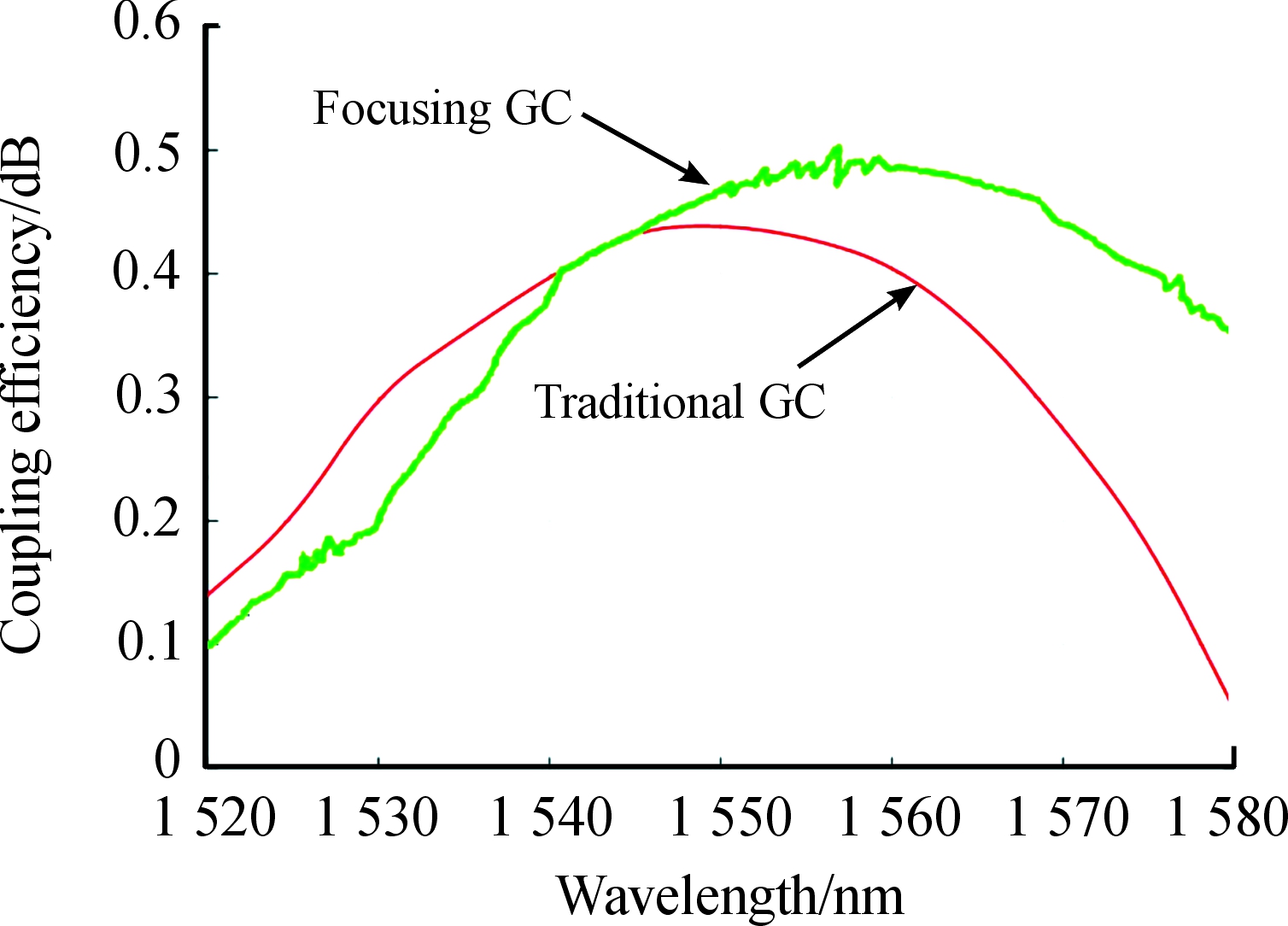
图13 汇聚型光栅的测试耦合谱线和传统光栅的仿真耦合谱线
实际测试的耦合效率降低，是由于以下3个因素：① 实际制作的光栅边缘粗糙，造成散射损耗；② 光纤和光栅耦合器之间模式匹配存在反射；③ 仿真中采用高斯光与实际光纤模式会有误差。
4 结论
针对当前芯片式天线中传统光栅耦合器尺寸过大，在现有光栅结构的基础上，提出将现有直线型光栅耦合器设计成会聚形光栅耦合器，仿真优化了结构参数，且尺寸显著减小；制作实物进行实验后，理论计算，模拟仿真与实验测试结果吻合良好，光栅耦合器经过测试，峰值耦合效率提高16%，可为进一步减小光栅耦合器尺寸及其在芯片式天线中的研究与应用提供参考。
[1] MOORE C I,BURRIS H R,RABINOVICH W S,et al.Lasercomm demonstration during US navy trident warrior 06 forcenet exercise[C]//Antennas and Propagation Society International Symposium.IEEE,2007:17-20.
[2] 李少辉,陈小梅,倪国强.高精度卫星激光通信地面验证系统[J].光学精密工程,2017,25(05):1149-1158.
[3] CHEN X,LI C,FUNG C K Y,et al.Apodized Waveguide Grating Couplers for Efficient Coupling to Optical Fibers[J].IEEE Photonics Technology Letters,2010,22(15):1156-1158.
[4] YANG J,ZHOU Z,JIA H,et al.High-performance and compact binary blazed grating coupler based on an asymmetric subgrating structure and vertical coupling[J].Optics Letters,2011,36(14):2614～2617.
[5] ALONSORAMOS C,CHEBEN P,ORTEGAMO
UX A,et al.Fiber-chip grating coupler based on interleaved trenches with directionality exceeding 95[J].Optics Letters,2014,39(18):5351.
[6] MERLO J M,NESBITT N T,CALM Y M,et al.Wireless communication system via nanoscale plasmonic antennas[J].Scientific Report,2016,6:31710.
[7] 毛强,唐雄贵,孟方,等.基于亚波长光栅结构的微流控可调窄带滤波器设计与分析[J].激光与光电子学进展,2019,56(4):042301.
[8] 赵彪,杜鹏飞,沃江海,等.基于啁啾光纤布拉格光栅的可调谐双通带微波光子滤波器[J].激光与光电子学进展,2019,56(3):030605.
[9] SUN Y,YANG M,SONG C,et al.Experimental research on silicon carbide photoconductive semiconductor switch[J].Microwave and Optical Technology Letters,2015,57(8):1946-1948.
[10] BENEDIKOVIC D,CHEBEN P,SCHMID J H,et al.Subwavelength index engineered surface grating coupler with sub-decibel efficiency for 220 nm silicon-on-insulator waveguides[J].Optics Express,2015,23(17):22628-35.
[11] LI X,LIAO J,NIE Y,et al.Unambiguous demonstration of soliton evolution in slow-light silicon photonic crystal waveguides with SFG-XFROG[J].Optics Express,2015,23(8):10282.
[12] MORICHETTI F,GRILLANDA S,MELLONI A.Breakthroughs in Photonics 2013:Toward Feedback-Controlled Integrated Photonics[J].IEEE Photonics Journal,2014,6(2):1-6.
[13] YANG B,LI Z Y,YU Y D,et al.High-efficiency focusing grating coupler with optimized ultra-short taper[J].Chinese Physics B,2014,23(11):348-351.
[14] 周阔.硅基光栅耦合器和波导分束器的研究[D].长沙： 国防科学技术大学,2013：13-15.
[15] YU L,LIU L,ZHOU Z,et al.High efficiency binary blazed grating coupler for perfectly-vertical and near-vertical coupling in chip level optical interconnections[J].Optics Communications,2015,355:161-166.