步枪、机枪、狙击步枪是轻武器装备体系中的重要骨干武器,提高其射击精度一直是世界各国的研究重点。近年来,随着我国对外交流的加深,对西方高精度武器在城市作战中发挥的特殊作用,以及在反劫持、反恐怖作战中的精确打击效果有了清晰认识,针对我国枪械实现高精度发射开展了相关研究。
提高轻武器的射击精度是一个复杂的系统工程,影响因素非常多,涉及到理论基础、检测试验基础、制造水平等等,其中高精度步枪系统枪械动力匹配技术、高精度步枪系统枪械人机工效技术、高精度步枪系统设计理论和设计规范等是研制高精度步枪和高精度狙击步枪的基础,我国目前尚未掌握相关知识和技术,导致高精度步枪和狙击步枪设计的盲目性较大[1-5]。
步枪、机枪、狙击步枪等枪械的精度水平在实际作战中的效能发挥最终是由射手完成和体现,与射手操控有关的任何误差因素都会极大影响到射击结果。步枪在使用中多采用抵肩射击姿势,根据作战时的具体情况可取立姿无依托、跪姿无依托、卧姿有依托等多种形式。其中立姿无依托是实战中采用较多的姿势,该姿势便于在行进中射击,有利于把握作战时机,但相对于其他几种射击姿势而言,射击时的稳定性较难控制,人枪系统中人的特性对于步枪的射击精度有极大的影响[6-8]。
现有的针对射击精度的仿真分析和结构优化设计重点考虑枪和弹的因素,而忽略了人体因素的影响,并缺乏精准高效的优化设计。所以,从人枪系统的角度出发,寻求一种多参数动态优化设计方法,对提高武器的射击精度和人机工效具有重要意义。
1 ISIGHT多参数优化理论
ISIGHT是美国Engineous公司出品的过程集成、优化设计和稳健性设计软件,可以将数字技术、推理技术和设计探索技术有效融合,并把大量的需要人工完成的工作由软件实现自动化处理,从而代替工程设计人员进行重复性的、易出错的数字处理和设计处理工作,该软件可以集成仿真代码并提供智能设计支持,从而对多个设计可选方案进行评估研究,大大缩短产品的设计周期[9],故本文基于ISIGHT对人枪系统进行多参数动态优化设计。
对于现代优化设计而言,设计变量、目标函数和约束条件是优化问题数学模型的3个基本要素,大部分的优化问题的就是通过修改设计变量求解目标函数的极值问题,因此在建立数学模型时,一般将目标函数的求解表示为求极大或极小值。设优化设计模型共含有维设计变量,个等式约束条件,个不等式约束条件,其数学模型为
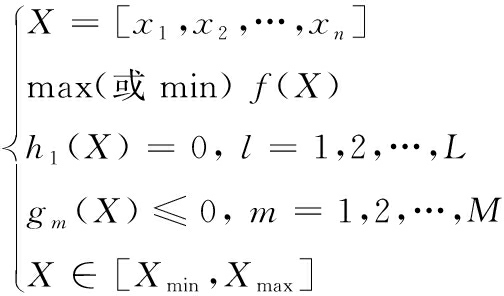
式中:X为设计变量组成的维向量; f(X)为目标函数;hl(X)=0是第l个等式约束条件;gm(X)≤0是第m个不等式约束条件;Xmin、Xmax—设计变量的边界向量。
ISIGHT集成功能强大,可以集成多种大型通用有限元软件及计算机辅助设计软件,集成优化过程如图1所示。
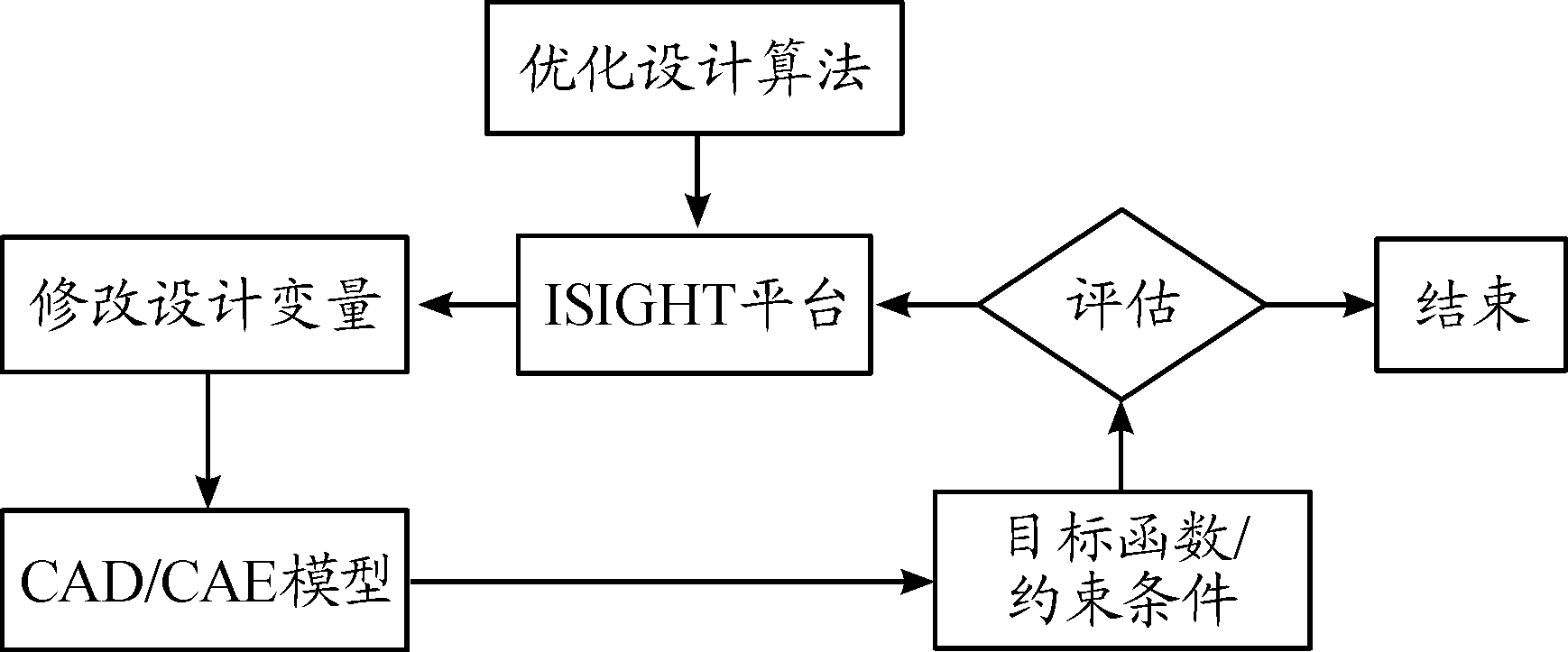
图1 ISIGHT集成优化过程框图
利用ISIGHT优化平台便捷的集成方法,综合考虑人枪系统在射击过程中各个影响因素,建立了以抵肩部位所受载荷和枪口垂直角位移为目标函数,以导气孔直径、气室初始容积、活塞直径、复进簧刚度、击锤簧刚度、枪机框质量为设计变量,融合ADAMS和MATLAB与一体的优化分析系统[10-11]。如图2所示。
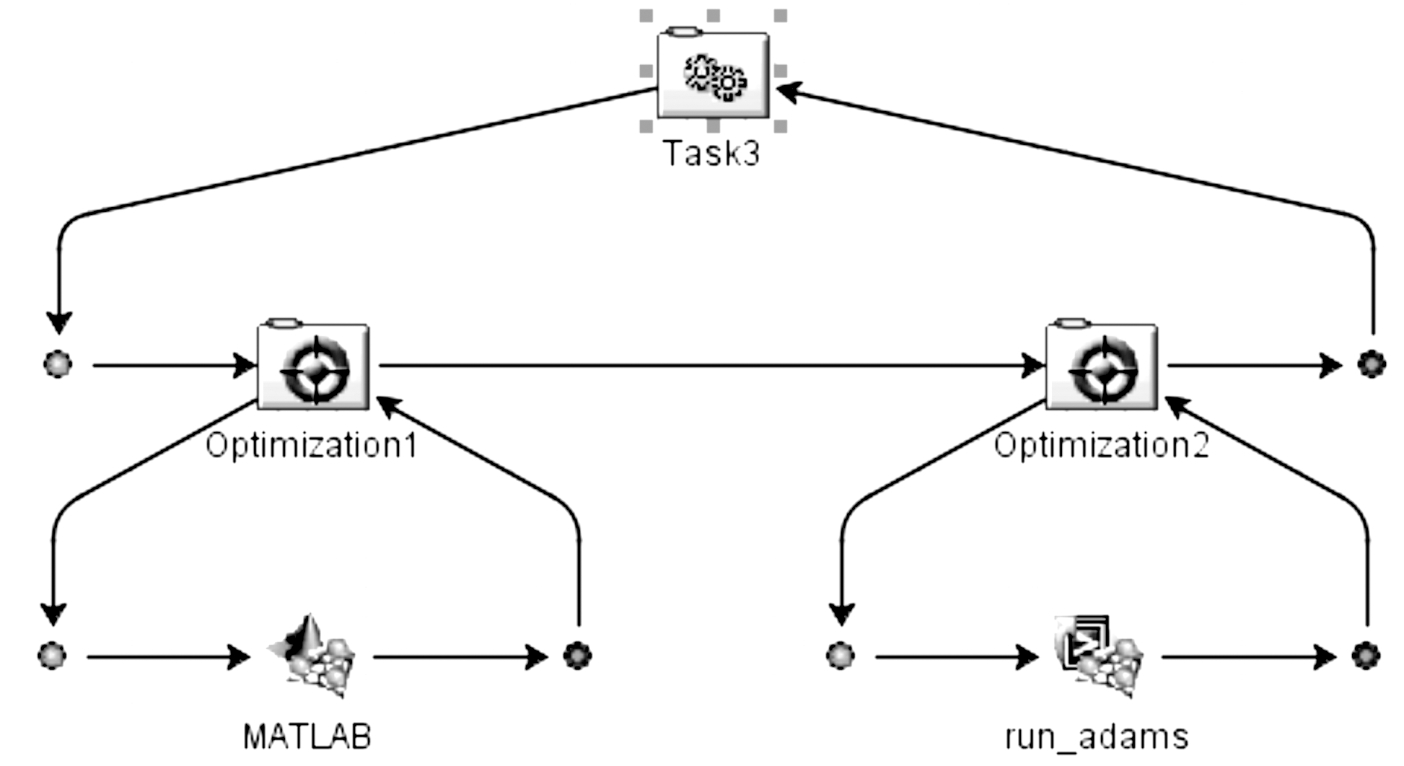
图2 人枪系统多参数优化设计系统集成
该系统通过自适应模拟退火算法(ASA)循环计算,无需人工修改仿真模型即可得出最优设计变量,达到对目标函数的最大优化的同时,可有效减少人力成本和时间成本。
2 人枪系统虚拟样机的建立
在进行人枪系统多参数动态优化设计时,需要建立刚柔耦合的人枪系统虚拟样机。
依照立姿射击时人体的姿态[12-14],确立人体各部分具体姿势、装配关系和约束关系,利用UG建立的人枪系统组成,如图3所示,三维模型,如图4所示。各球节的质量与各坐标轴的转动惯量的具体数据见表1。
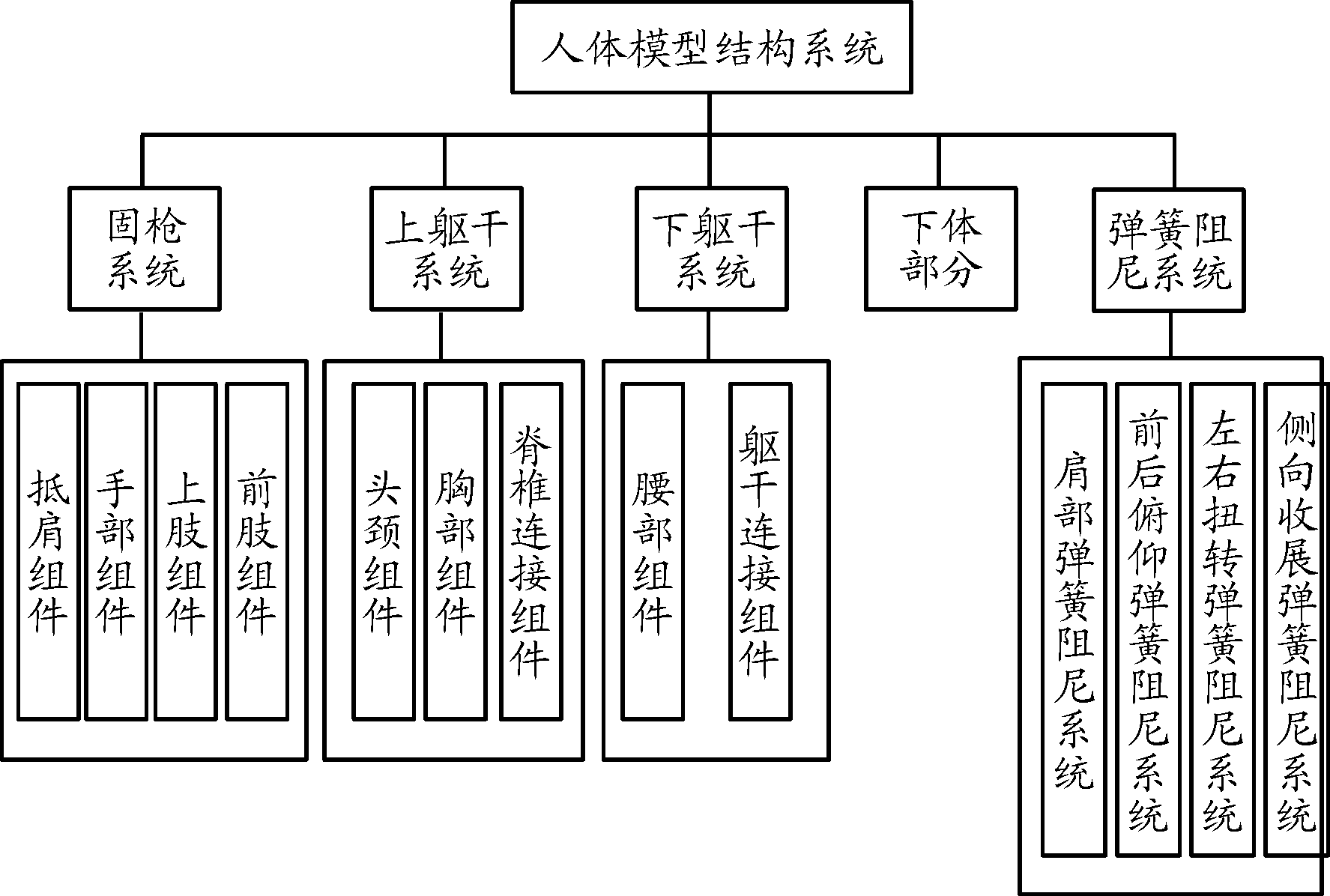
图3 人枪系统组成框图
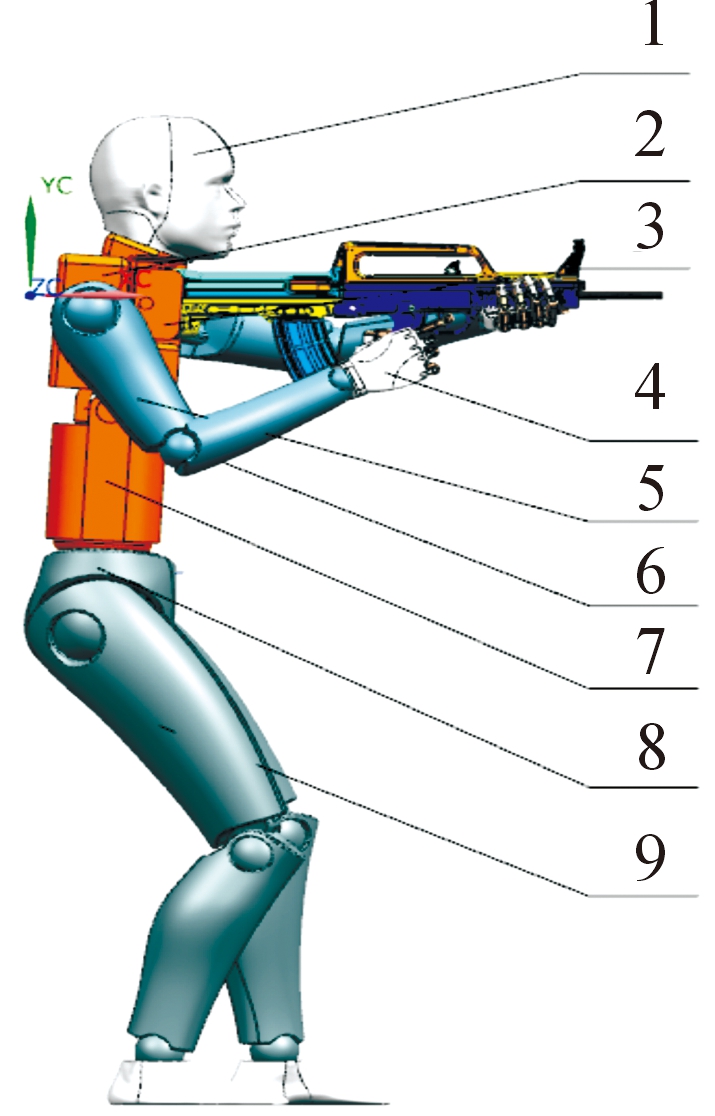
1.头颈;2.胸部组件;3.抵肩组件;4.手部组件;5.上肢体组件;6.躯干连接组件;7.腰部组件;8.臀部组件;9.下体组件
图4 人枪系统三维模型示意图
表1 人体模型各环节的质量与各坐标轴的转动惯量
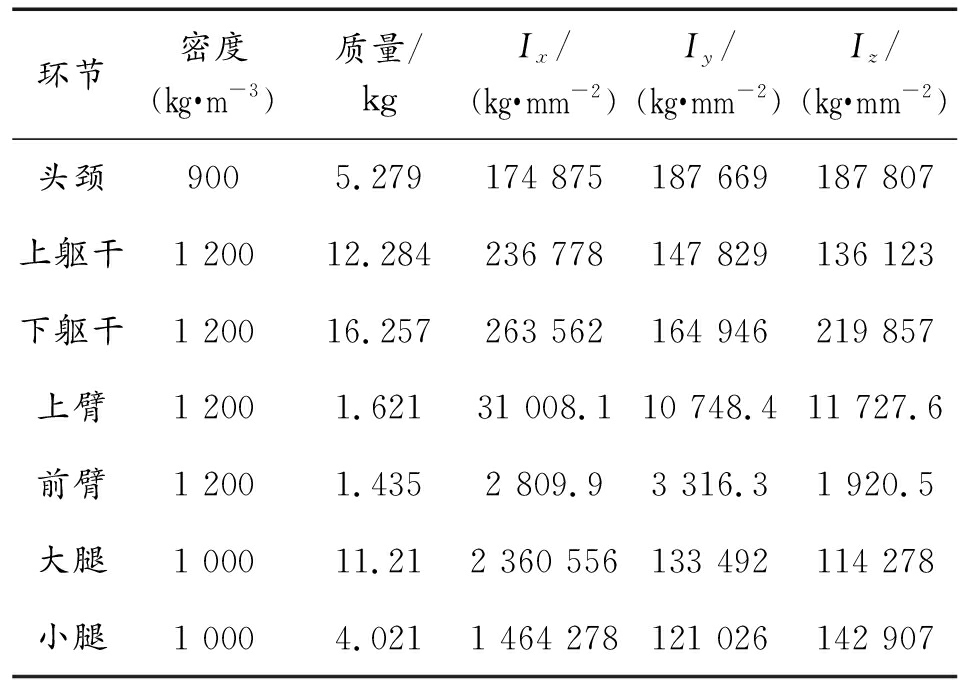
环节密度(kg·m-3)质量/kgIx/(kg·mm-2)Iy/(kg·mm-2)Iz/(kg·mm-2)头颈9005.279174 875187 669187 807上躯干1 20012.284236 778147 829136 123下躯干1 20016.257263 562164 946219 857上臂1 2001.62131 008.110 748.411 727.6前臂1 2001.4352 809.93 316.31 920.5大腿1 00011.212 360 556133 492114 278小腿1 0004.0211 464 278121 026142 907
注:人体的前臂、上臂、大腿、小腿均为单侧质量。
将三维模型导入ADAMS动力学仿真软件中,结合ANSYS 对人体躯干部分进行柔性化,建立5个运动自由度的立姿抵肩无依托人枪系统模型,主要为武器沿肩部转轴的上扬运动、武器沿肩部转轴的左右偏转运动、上躯干系统沿下躯干系统的左右扭转运动、上躯干系统沿下躯干系统的前后俯仰运动以及上、下躯干系统沿髋部的侧向收展运动,为此需要添加相应的运动副,如表2、表3所示。
表2 人体关键部件之间的约束关系

自由度运动约束副类型构件1构件2武器偏转旋转副夹具座胸部组件武器上仰接触副枪托枪托夹具旋转副枪托夹具夹具座左右扭转旋转副十字转轴轴承座1固定副轴承座1胸部组件前后俯仰旋转副十字转轴轴承座2固定副轴承座2腰部组件侧向伸展旋转副连接轴腰部组件旋转副连接轴臀部组件
表3 人体其他部位之间的约束关系

约束副部件1部件2约束副部件1部件2固定副头颈胸部固定副左脚左腿固定副左手下护盖球副左上臂胸部固定副右手下护盖球副右上臂胸部固定副腿部臀部球副左上臂左前臂固定副左脚地面球副右上臂右前臂固定副右脚右腿接触副枪托体枪托球副左手左前臂接触副机匣枪托球副右手右前臂接触副枪托枪托
建立弹簧阻尼系统来模拟标准射手的肌肉对上躯干、下躯干、2个手臂等运动的约束作用,作用于模拟人枪系统中的5个主要运动自由度,其具体参数如表4所示。
火药气体作用力是人枪系统中的主要载荷,本文所考虑的火药气体作用力主要包括:膛内火药气体作用于枪身上的作用力和导气室内的火药气体作用于自动机上的作用力。
根据武器射击时膛内火药燃气压力的变化特点,可将火药燃气压力作用的全过程分为静力燃烧时期、内弹道时期和后效期3个时间段本文主要考虑内弹道时期和后效期2个时间端的人枪系统运动特性。
表4 人体各弹簧阻尼系统参数
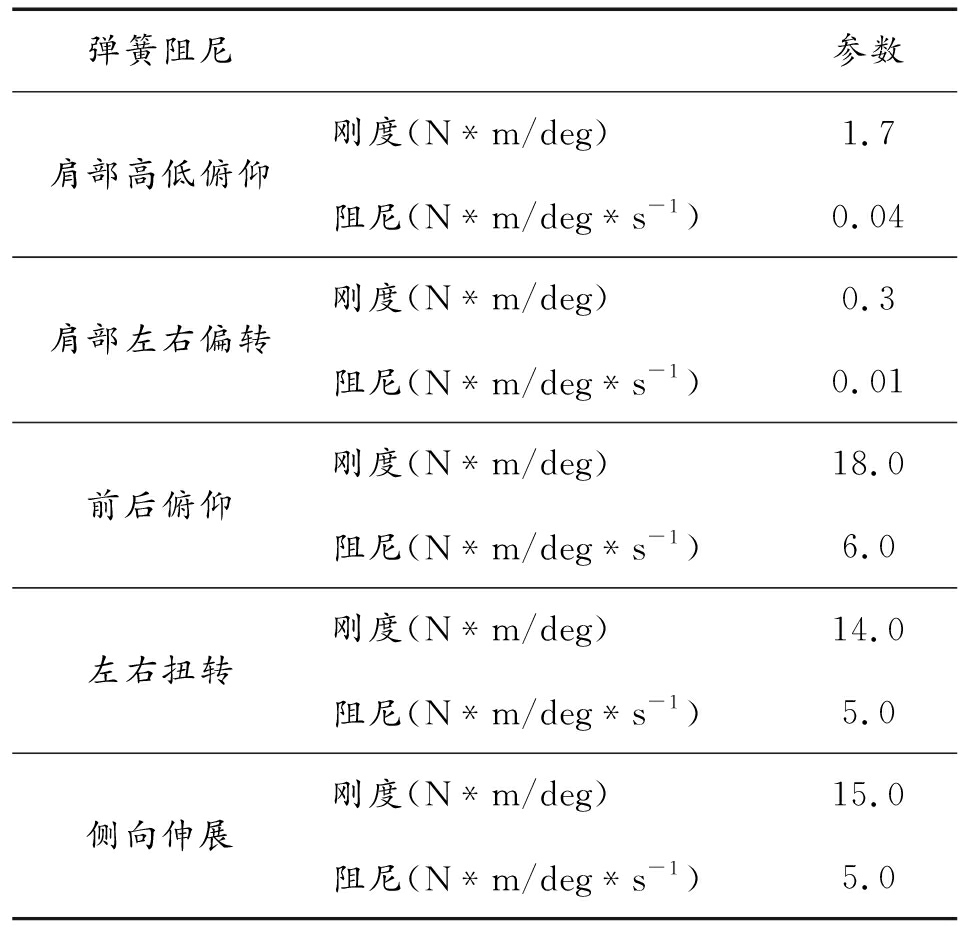
弹簧阻尼 参数肩部高低俯仰刚度(N*m/deg)1.7阻尼(N*m/deg*s-1)0.04肩部左右偏转刚度(N*m/deg)0.3阻尼(N*m/deg*s-1)0.01前后俯仰刚度(N*m/deg)18.0阻尼(N*m/deg*s-1)6.0左右扭转刚度(N*m/deg)14.0阻尼(N*m/deg*s-1)5.0侧向伸展刚度(N*m/deg)15.0阻尼(N*m/deg*s-1)5.0
气室内火药燃气压力的变化规律与膛内火药燃气压力的变化规律有关,也与导气装置的结构参数有关;后者包括导气孔在枪管上的位置、导气孔的横断面面积、导气管道的长度、气室初始容积、气室壁与活塞间间隙的大小、活塞横断面面积和活塞及与其联接的枪机框等零件的质量等,对于导气式武器,目前采用较多的是勃拉文的经验公式:
导气室内火药燃气对活塞作用力FS以及对导气室前壁作用力F′分别为
Fs=SsPs
其中:ps为气室压力;pd为弹丸经过导气孔瞬间的膛内平均压力;e为自然对数的底数t为导气室压力工作时间;b为与膛内压力冲量有关的时间系数;α为与导气装置结构参数有关的系数;Fs为导气室火药燃气作用力;Ss为导气室活塞面积;ηs为导气室冲量效率;i0为膛内压力的单位全冲量。
利用ADAMS进行动力学仿真分析时,导气室压力和膛底压力无法直接加载到人枪系统虚拟样机上。故根据导气室自动步枪的运动特性,可将两者分别转化成施加在活塞杆前端面上的力和枪机弹底窝镜面上的膛底合力,其中作用于活塞杆上的力,简化为气室压力乘以活塞杆前端面面积。利用MATLAB计算所得的膛底合力曲线和导气活塞杆的受力曲线如图5所示。
完成后刚柔耦合的人枪系统虚拟样机如图6所示。
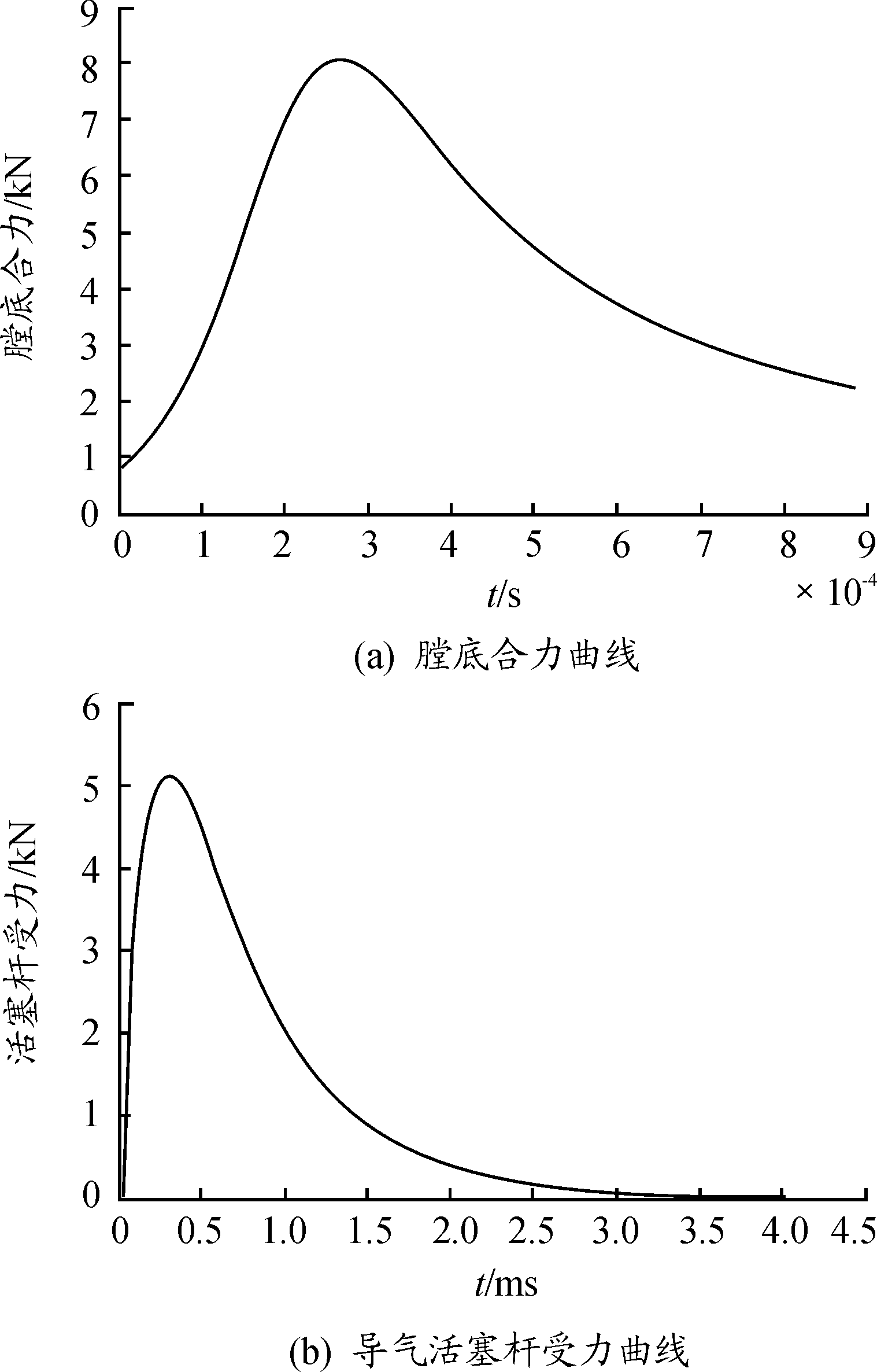
图5 加载的载荷曲线

图6 刚柔耦合的人枪系统虚拟样机
3 优化过程及优化结果分析
3.1 确定设计变量和目标约束条件
在建立刚柔耦合的人枪系统虚拟样机后,需要确定设计变量和目标约束条件,在进行结构优化前通过最优拉丁超立方试验设计方法对枪管结构参数进行了灵敏度分析,根据灵敏度分析的结果,本文选取复进簧刚度(DV_1)、击锤簧刚度(DV_2)、枪机框质量(DV_3)、导气孔直径(d_d)、气室初始容积(V_0s)和活塞杆直径(d_h)为设计变量,枪口垂直角位移(DF_Angle)、活塞杆受力(fs1)和抵肩部位受力(DF_2)为目标函数。
其中,复进簧刚度(DV_1)、击锤簧刚度(DV_2)和枪机框质量(DV_3)的取值范围在保证不超过后坐性能指标和自动机循环时间允许值得前体下进行选取。导气孔直径(d_d)、气室初始容积(V_0s)和活塞杆直径(d_h)的取值范围在保证不影响弹丸初速和后坐性能指标允许的条件下进行选择。
设计变量及其取值范围如表5所示,目标函数及其约束条件和表6所示。
表5 设计变量及其取值范围

代号定义初始值下限上限DV_1复进簧刚度211(N/m)180240DV_2击锤簧刚度170(N/m)150190DV_3枪机框质量0.2 kg0.170.26d_d导气孔直径0.2 cm0.180.22V_0s气室初始容积1.28 cm31.11.5d_h活塞杆直径1.2 cm1.11.4
表6 目标函数及其约束条件

代号定义初始值约束条件DF_Angle枪口垂直角位移1.954°小于3.0°fs1活塞杆受力5 109 N 5 000 N≤fs1≤5 500 NDF_2抵肩部位受力269 N小于300 N
3.2 建立优化系统数学模型
人枪系统问题属于高度非线性问题,并把全局目标作为主要工作,自适应模拟退火算法(ASA)非常适用,这种算法能以最小成本获得优化设计的最优解,并自动地辨认识别不同局部最优解[15-16],数学模型如下:Min f(fs1,DF_2,DF_Angle),0.18≤d_d≤0.22,1.15≤d_h≤1.32,1.18≤V_0s≤1.408,0.189≤DV_1≤0.232,0.153≤DV_2≤0.187,0.177≤DV_3≤0.226。
3.3 ISIGHT参数设置
在Optimization模块中设置设计变量的约束范围及优化算法的相关参数,如前文表1和表2所示。选择ASA算法作为优化求解的基本方法,优化算法参数如表7所示。
表7 参数设置

参数值种群大小80迭代次数200
3.4 优化结果分析
经过优化系统计算得出最优设计方案的结果如表8所示。
表8 优化前后结果对比
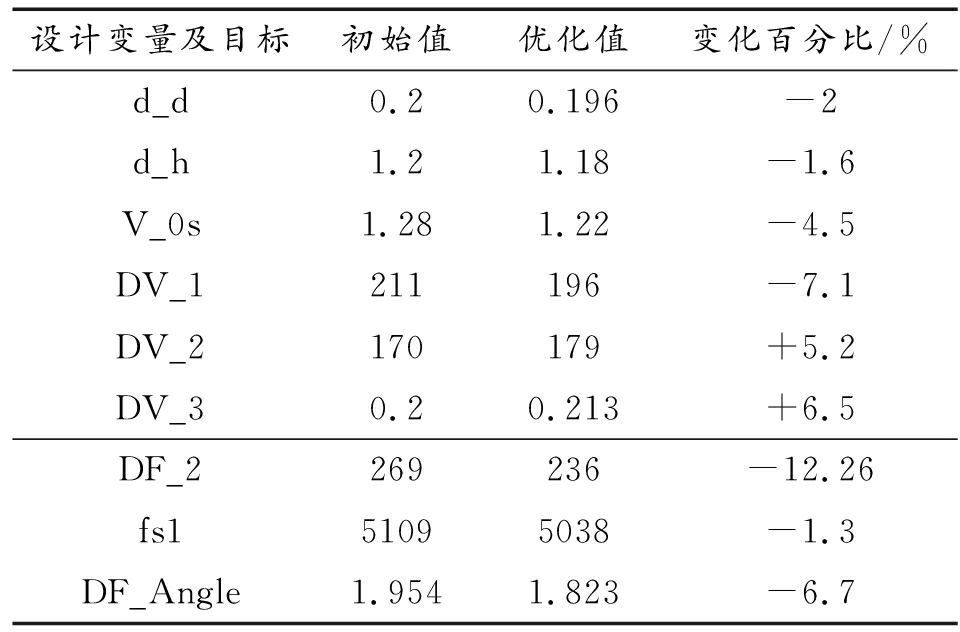
设计变量及目标初始值优化值变化百分比/%d_d0.20.196-2d_h1.21.18-1.6V_0s1.281.22-4.5DV_1211196-7.1DV_2170179+5.2DV_30.20.213+6.5DF_2269236-12.26fs151095038-1.3DF_Angle1.9541.823-6.7
从表8中可知通过设计变量优化,活塞杆受的最大力值降低了1.3%,弹丸出膛口时的枪口角位移降低了6.7%,抵肩部位受的最大力值降低了8.5%。活塞杆受力的降低,有利于减小自动机的初始能量,使其后坐到位时对抵肩部位的冲击载荷减小。抵肩部位的受力减小,有利于降低人枪系统振动特性,从而提高步枪连发射击精度。
3.5 优化结果验证
为了验证该优化系统的优化结果,分别对3个目标进行了验证。在ADAMS和Matlab中分别按照原始设计变量及优化设计变量导入虚拟样机和程序,然后对每一对优化模型与原始模型在保证约束施加、载荷施加、材料参数定义等均一致的前提下,进行动力学仿真分析。其仿真结果如图7~图10所示。
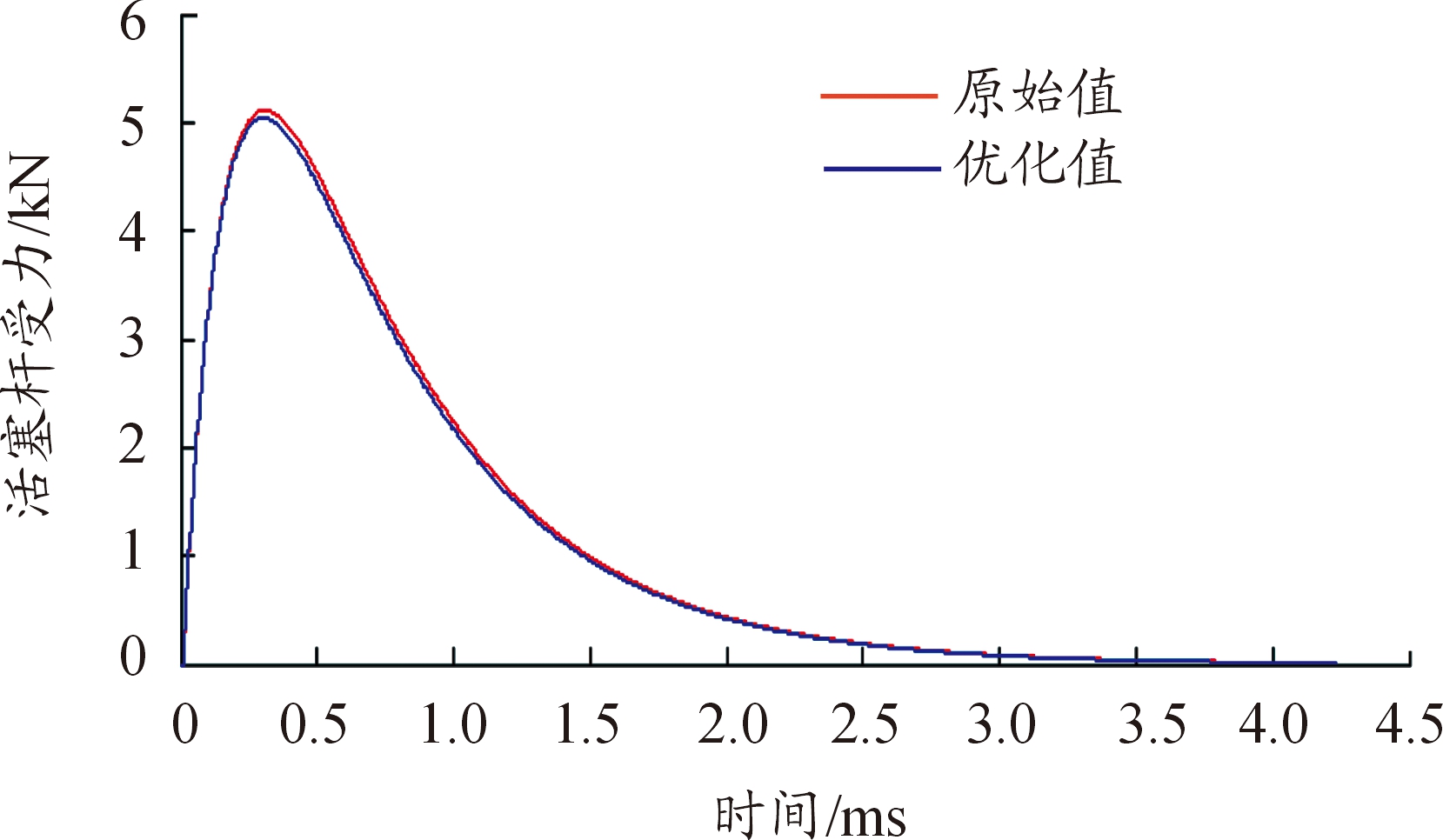
图7 活塞杆受力曲线

图8 枪机框位移曲线
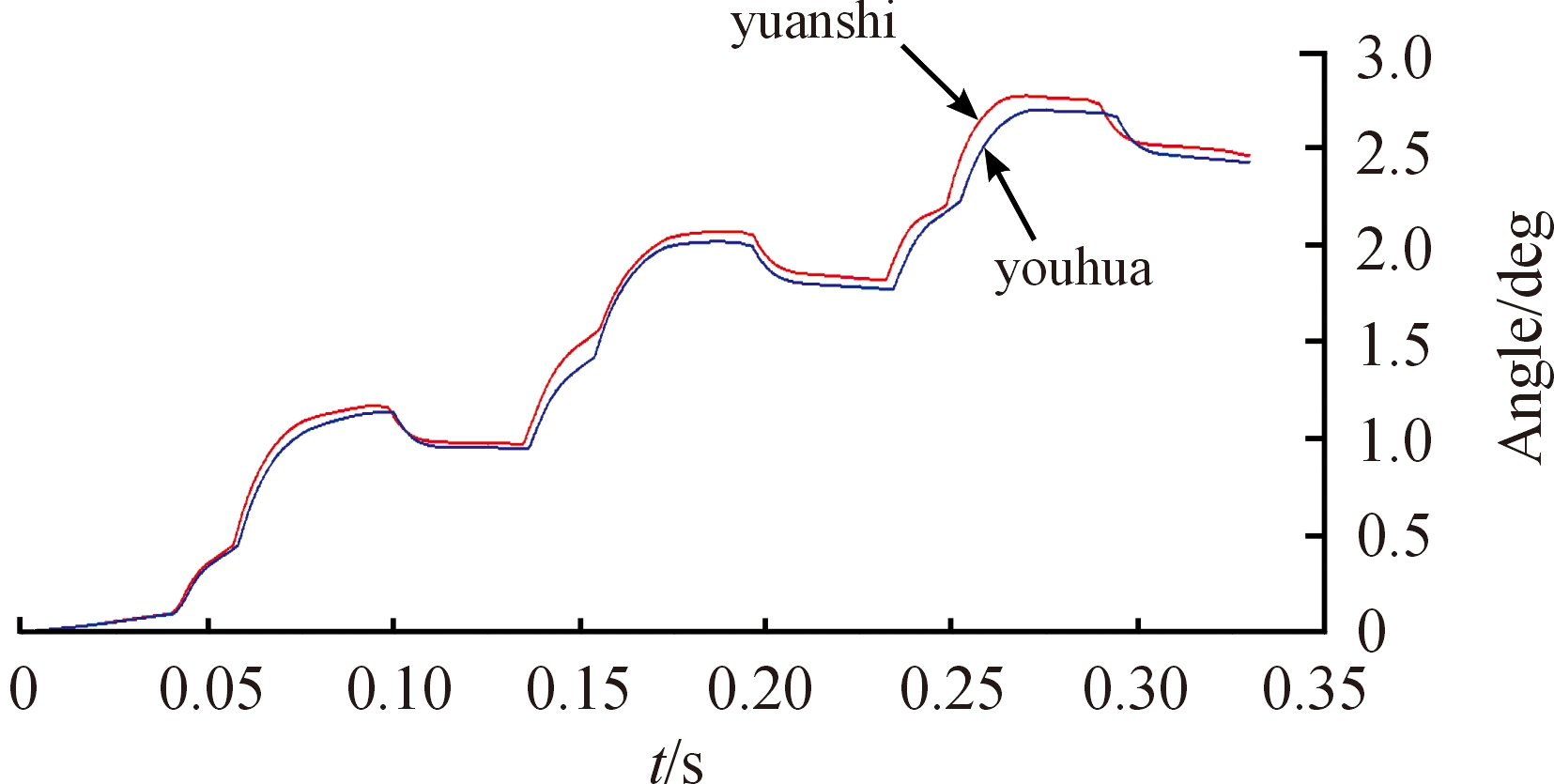
图9 枪口垂直角位移曲线

图10 抵肩部位受力曲线
由图7~图10可知,导气室压力对活塞杆的作用时间基本不变,活塞杆所受的最大力降为5 038 N,且自动机的速度略有减小,弹丸在出膛口时的枪口垂直角位移降为1.823°,抵肩部位所受的最大力降为236 N,其结果符合优化预期。
4 结论
本文基于ISIGHT建立了人枪系统多参数优化设计模型通过集成ADAMS和Matlab软件进行并行优化设计,利用自适应模拟退火算法(ASA)算法求解,得到了设计变量的优化值,并对优化结果进行了仿真验证,验证结果表明:
优化后活塞杆所受的最大力下降1.3%,弹丸在出膛口时的枪口垂直角位移减少6.7%,抵肩部位所受的最大力也下降12.26%,提高了步枪的连发射击精度。
采用此优化设计方法,可同时对多个设计变量进行多目标优化,且优化效率较高,质量较好,达到了提高射击精度的目的,为武器系统的优化设计提供了技术途径和参考价值,同时对其他工程优化设计也具有应用价值。
[1] 欧学炳,殷仁龙,王学颜.自动武器结构设计[M].北京:北京理工大学出版社,1995.
[2] 包建东,王昌明,孔德仁,等.连发射击人枪系统机械导纳测量与分析[J].南京理工大学学报(自然科学版),2006(04):521-524.
[3] 包建东,王昌明,孔德仁,等.人枪运动对射击精度影响的实验研究[J].仪器仪表学报,2006(S2):1274-1276.
[4] 孙海波,孔德仁,李永新,等,柳光辽.枪械的点射精度与模拟试验枪架[J].弹道学报,2000(04):86-90.
[5] 包建东,王昌明,孔德仁,等.连发射击人枪系统机械导纳测量与分析[J].南京理工大学学报(自然科学版),2006(04):521-524.
[6] HUTCHINGS T D,RAHE A E.Study of Man-Weapon Reaction Forces Applicable to the Fabrication of A Standard Rifle Firing Fixture[J].Simulation,1975,86(1):1-95.
[7] BASDOGAN I,ROYSTON T J.A Theoretical and Experimental Study of the Vibratory Dynamics of High-Precision Optical Positioning Systems[J].Journal of Vibration and Control,2006,45(7):15-20.
[8] LEE C H,et al.NDLA International Infantry & Joint Services Small Arms Systems Symposium[J].Experimental Performance Analysis on Eecoil Pad for Reducing Firing Shock Force,2013,6(2):19-22.
[9] 赖宇阳.Isight参数优化理论与实例详解[M].北京:北京航空航天大学出版社,2012.
[10] PEI H,LIU C,CHEN Y,et al.Influence of Nozzle Structure on The Consumption of Shielding Gas in The Gas Metal Arc Welding Process[J].Simulation,2020,1(2):10-12.
[11] CUI G,ZHOU H,WANG N,et al.Multi-Objective Optimization of 3-UPS-S Parallel Mechanism Based on Isight[J].Nongye Jixie Xuebao/Transactions of the Chinese Society of Agricultural Machinery,2013,44(9):261-266.
[12] 党建滨.跪姿射击状态人-枪相互作用研究[D].上海:华东工学院,1987.
[13] 蔡周斌.卧姿射击状态人-枪相互作用研究[D].上海:华东工学院,1987.
[14] 李永新.人枪相互作用模型与实验研究[D].南京:南京理工大学,1993.
[15] 杨庆新,安金龙,马振平,等.基于最小二乘支持向量机和自适应模拟退火算法的电磁场逆问题全局优化方法[J].电工技术学报,2008,23(11):1-7.
[16] 何庆,吴意乐,徐同伟.改进遗传模拟退火算法在TSP优化中的应用[J].控制与决策,2018,33(02):219-225.