目前国内的救援车辆,其底盘结构大多采用轮式结构,只适用于在路况较好的道路上快速行驶,存在越野行驶速度慢、复杂地形适应性差、轮胎容易发生打滑等问题。整体履带式车辆虽然可以更好地适应复杂地形与特殊环境,但它过于笨重,难以满足多种地形的切换且速度较低;同时,整体式履带一般采用钢制履带,振动噪声大,容易损伤路面,造价和维护成本比较高[1-2]。三角履带轮是结合了轮胎和履带行走机构的相关特点而研发的新型履带行走装置[3]。
三角履带轮与轮式行走装置相比,具有牵引性能好、复杂地面通过性好等优点[4-5],且能够快速实现轮履互换,减小了天气和地面条件对车辆的限制,极大扩展了救援车辆的应用范围[6-8]。救援车辆行驶系统所使用的三角履带轮的性能直接影响救援车辆的复杂地形适应能力,而履带作为三角履带轮的关键部件受力情况复杂,对履带进行受力分析是新型三角履带样机研制的重要基础。
1 救援车辆三角履带行驶系统力学分析
本文研究的三角履带救援车辆满载质量32 t,最大行驶速度不小于50 km/h,该车行驶系统采用4个三角履带轮驱动单元,三角履带轮单元包括1个驱动轮、1个导向轮、1个张紧轮、4个负重轮,其参数示意图如图1。本节通过救援车辆水平路面行驶时履带各段拉力进行受力分析,为后续动力学仿真奠定基础。
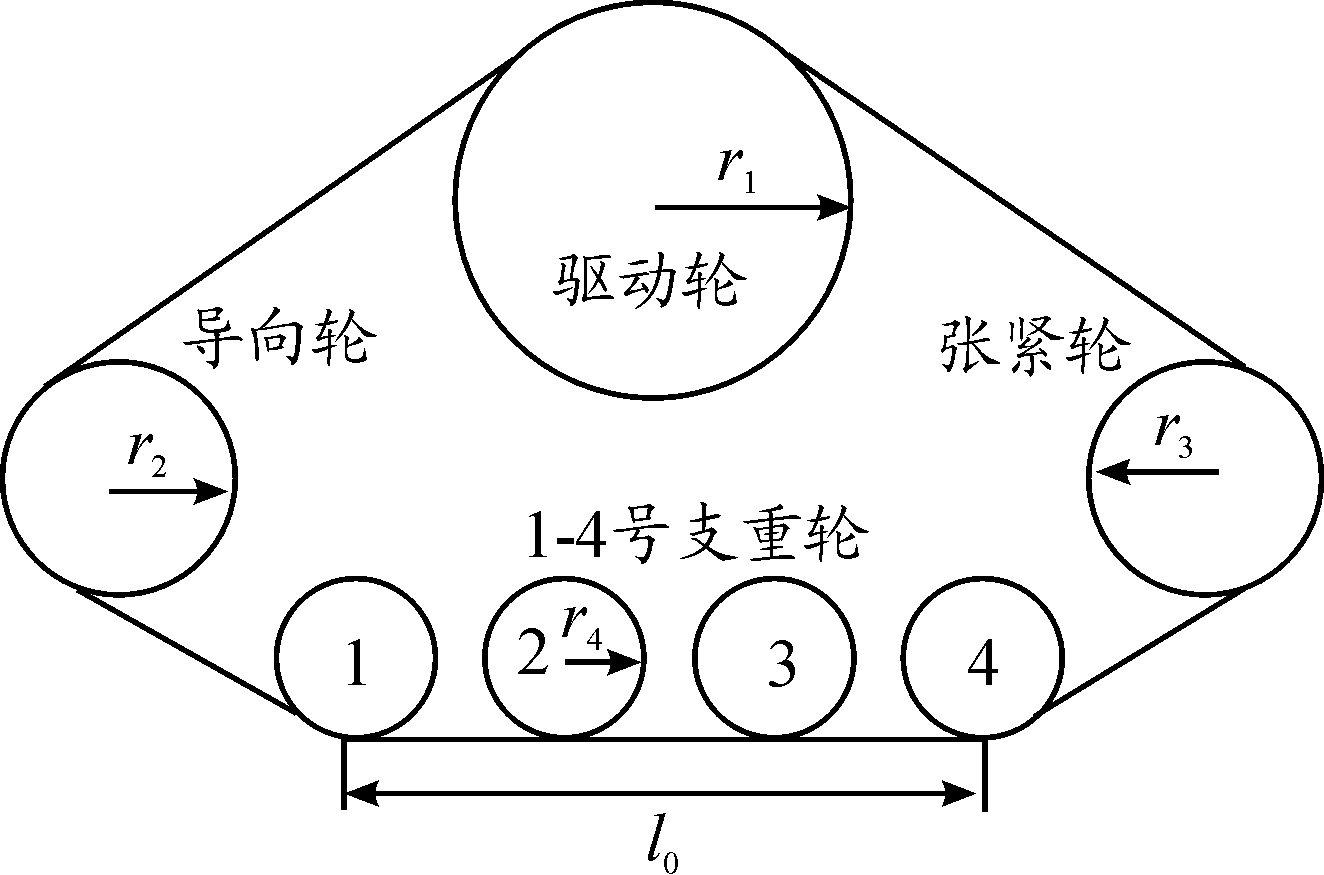
图1 三角履带轮结构参数示意图
车辆行驶时,发动机输出的扭矩T使驱动轮转动,为履带车辆前进提供牵引力,牵引力克服一系列阻力带动履带车辆向前运动。由于运行阻力的存在,各段履带受力不同[9],分别为F1~F7,如图2所示。
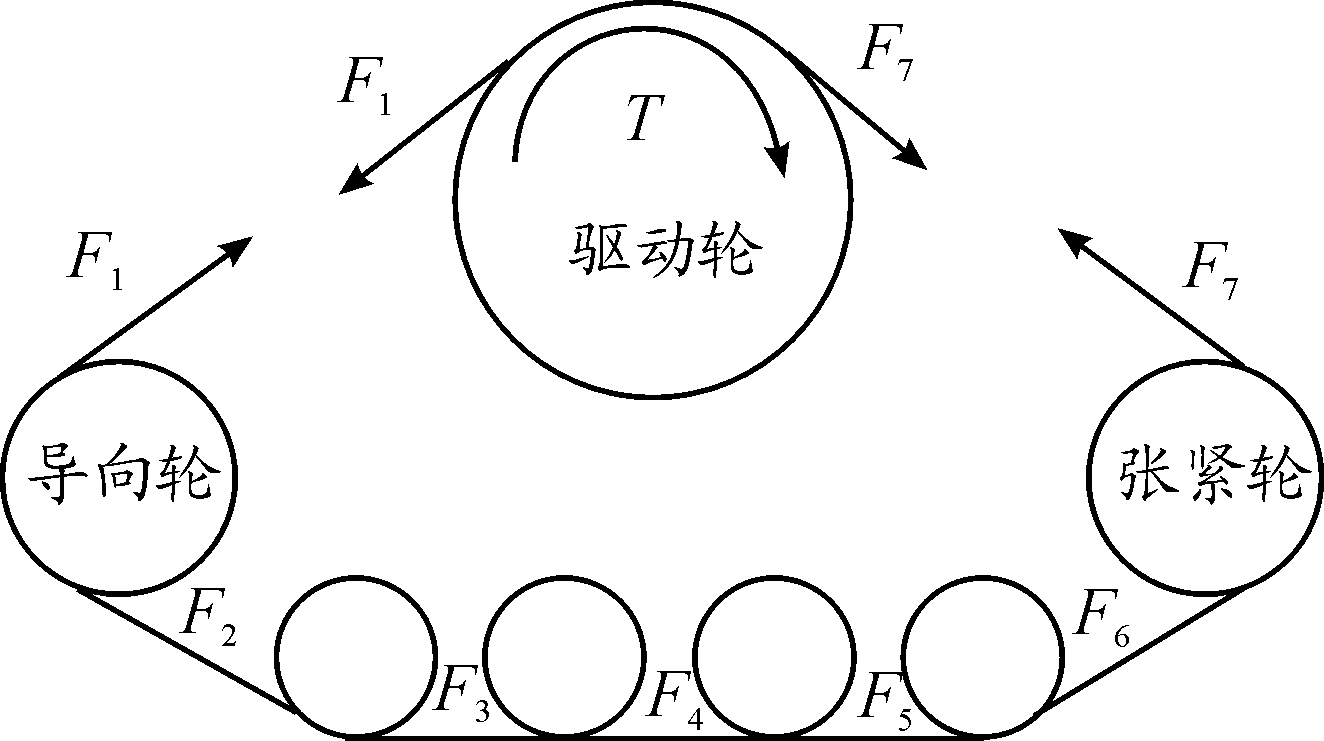
图2 三角履带轮系统各段履带受力示意图
以驱动轮为研究对象,忽略与驱动轮接触履带质量及履带厚度,驱动轮受到两侧的履带拉力、机架的支撑力、重力作用,将驱动轮受到的各作用力分解到直角坐标系,受力如图3所示。
根据力平衡方程得到驱动轮的力学方程见式(1):
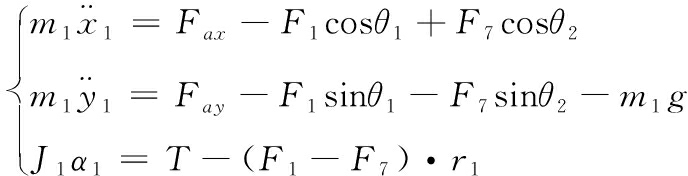
(1)
式中: F1、F7为驱动轮两侧履带拉力;Fax、Fay为驱动轮受到机架的支撑力; θ1、θ2为两侧履带拉力与水平方向夹角;T为驱动轮受到的驱动力矩;m1为驱动轮质量;J1为驱动轮转动惯量;α1为驱动轮转动角加速度;r1为驱动轮半径。

图3 驱动轮受力分析
导向轮的作用是使三角履带行走机构具有一定的离去角,其质心位置决定着履带轮离去角大小,导向轮受到两侧的履带的拉力、机架支撑力、重力的作用,导向轮受力如图4所示。
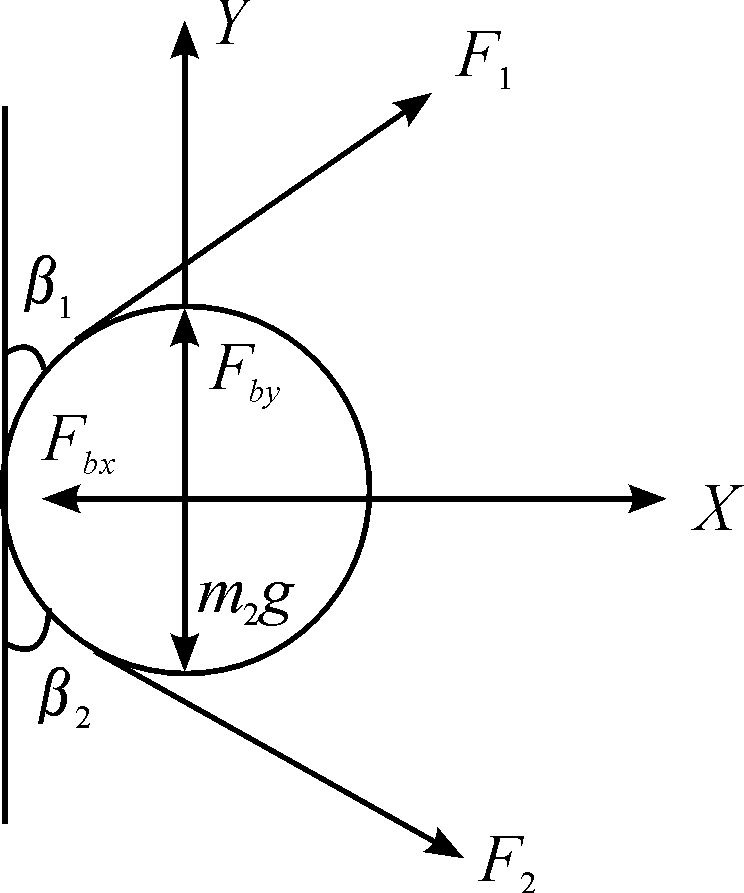
图4 导向轮受力分析
根据力平衡方程得到导向轮的力学方程见式(2):

(2)
式中:F1、F2为导向轮两侧履带拉力;Fbx、Fby为导向轮受到机架的支撑力; β1、β2为两侧履带拉力与竖直方向夹角;m2为导向轮质量;J2为导向轮转动惯量;α2为导向轮转动角加速度;r2为导向轮半径。
张紧轮是三角履带行走机构张紧装置中的关键部件,通过摆动实现对履带的张紧以适应复杂地面。张紧轮受到两侧的履带拉力、张紧杆的反作用力、重力的作用,张紧轮受力如图5所示。
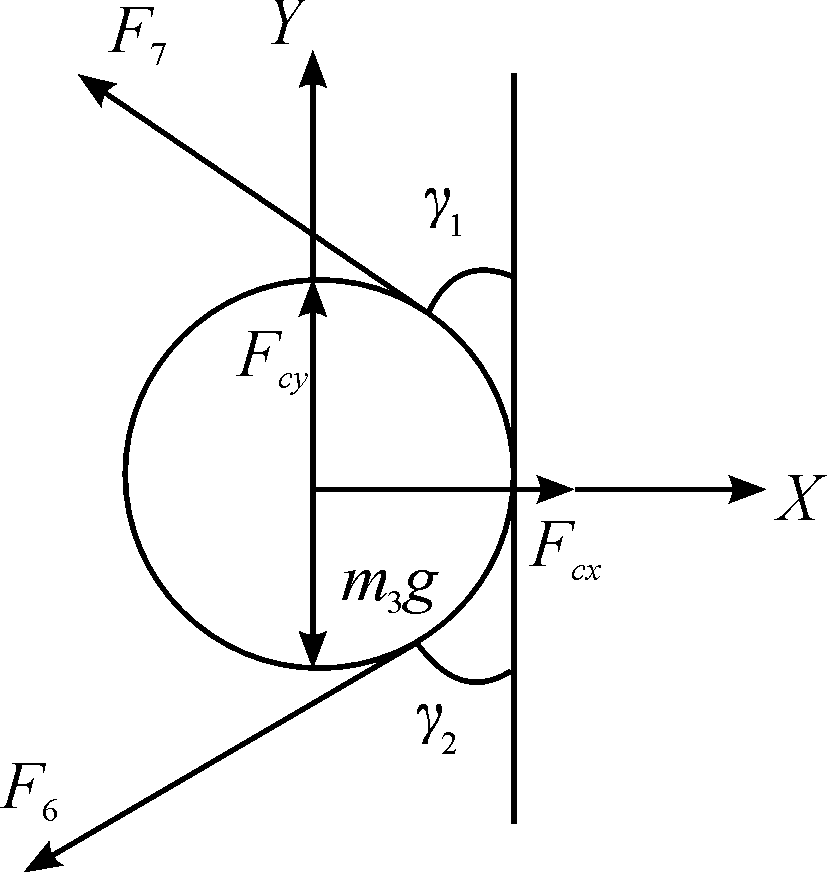
图5 张紧轮受力分析
根据力平衡方程得到张紧轮的力学方程见式(3):
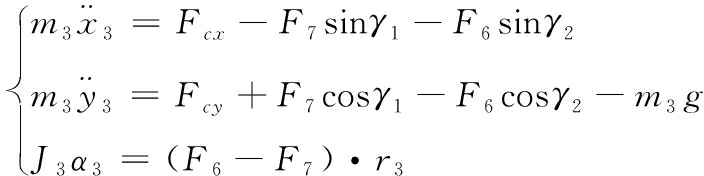
(3)
式中:F6、F7为张紧轮两侧履带拉力;Fcx、Fcy为张紧轮受到张紧杆的反作用力; γ1、γ2为两侧履带拉力与竖直方向夹角;m3为张紧轮质量;J3为张紧轮转动惯量;α3为张紧轮转动角加速度;r3为张紧轮半径。
负重轮主要起着传递载荷的作用,按照工作位置的不同将负重轮依次编号为1、2、3、4,其中1、4负重轮参与形成三角履带行走机构的接近角与离去角,其受力状态相似,2、3负重轮位于中间的位置,其受力状态相似,因此只针对1、2负重轮进行受力分析。
负重轮1受到支撑悬臂作用力、两侧履带的拉力、路面支撑力、重力的作用,其受力如图6所示。

图6 负重轮1受力分析
根据力平衡方程得到负重轮1的受力方程见式(4):

(4)
式中:F2、F3为负重轮1两侧履带拉力;Fdx、Fdy为负重轮1受到支撑悬臂作用力; FN1为左侧履带拉力与水平方向夹角;φ为左侧履带拉力与水平方向夹角;m4为负重轮1质量;J4为负重轮1转动惯量;α4为负重轮1转动角加速度;r4为负重轮半径。
负重轮2受到机架传递的车体载荷、与其接触履带对其的作用力,竖直方向上受到履带的支持力和重力,其受力如图7所示。

图7 负重轮2受力分析
根据力平衡方程得到负重轮2的受力方程见式(5):

(5)
式中:F3、F4为负重轮2两侧履带拉力;Fex、Fey为负重轮2受到支撑悬臂作用力; FN2为左侧履带拉力与水平方向夹角;m4为负重轮2质量;J4为负重轮2转动惯量;α5为负重轮2转动角加速度;r4为负重轮半径。
车辆静止时,设置履带预张紧力为F0,当驱动轮受到转矩T作用时,假设驱动轮两侧履带拉力的变化幅度相同,则可得到式(6):

(6)
根据前文对履带轮系受力分析及驱动轮受转矩作用时两侧履带拉力与预张紧力的关系式,当三角履带轮结构参数及车辆行驶初始条件确定时,联立方程组即可求得各段履带拉力。
2 救援车辆三角履带行驶系统建模
Recurdyn软件中的Track-HM工具包是针对高速履带车辆开发的,它具有丰富的履带系统组件,可参数化调节各部件的几何形状。工具箱由驱动轮、路面车轮、履带链接、橡胶衬套等组成[10]。可以方便快捷的构建履带子系统模型,实现高速履带车辆的运动学、动力学仿真模拟。三角履带救援车辆模型的建立主要分为3个部分:三维几何模型的建立、约束的添加和路面模型的建立。
2.1 几何模型的建立
三角履带轮相关结构参数的值可以根据有关设计原则进行确定,如表1所示。
表1 三角履带轮部分结构参数

结构参数参数名称计算公式设计值p履带节距厂家标准规格152 mmb履带宽度厂家标准规格635 mmr1驱动轮半径轮式车辆直径的23[11]490 mmz驱动轮齿数r1=p2sin(180/z)21r2导向轮半径基于履带轮整体结构选取 200 mmr3张紧轮半径基于履带轮整体结构选取200 mmr4负重轮半径r4=1.5p~2.5p150 mml0接地履带长度0.24≤b2l0≤0.281 143 mm
根据表1的参数,用Track-HM模块建立三角履带轮模型,每个三角履带轮履带包括42块履带板,驱动轮高置,履带结构采用单销履带,负重轮采用双轮缘式结构。张紧轮上通过线性弹簧(Spring)模拟液压张紧装置,以调整履带的张紧度。三角履带轮重1.7 t,其中机架以Pro/E软件建模后倒入。三角履带轮模型如图8所示。
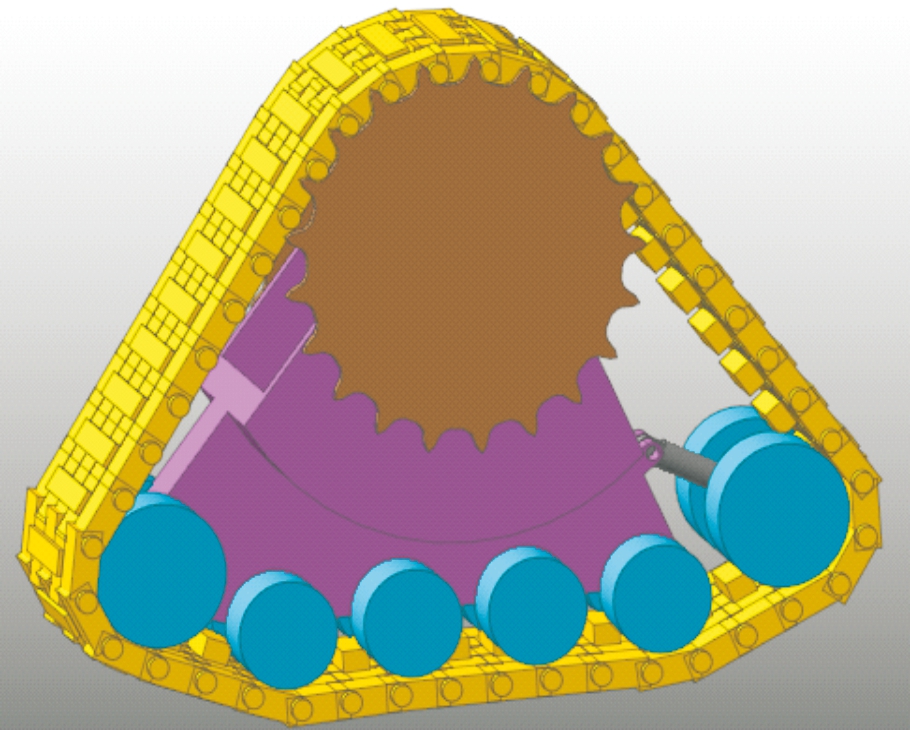
图8 三角履带轮模型示意图
救援车辆车体以质量块进行简化,质量为24 t,前后轮轴距为4 230 mm,左右轮轮距为2 076 mm。通过4个平动约束和4个线性弹簧模拟车辆减振系统。减振系统及三角履带轮张紧装置线性弹簧参数设置以实验获得的数据进行设置,这里不再赘述,整车行驶系统简化模型如图9所示。
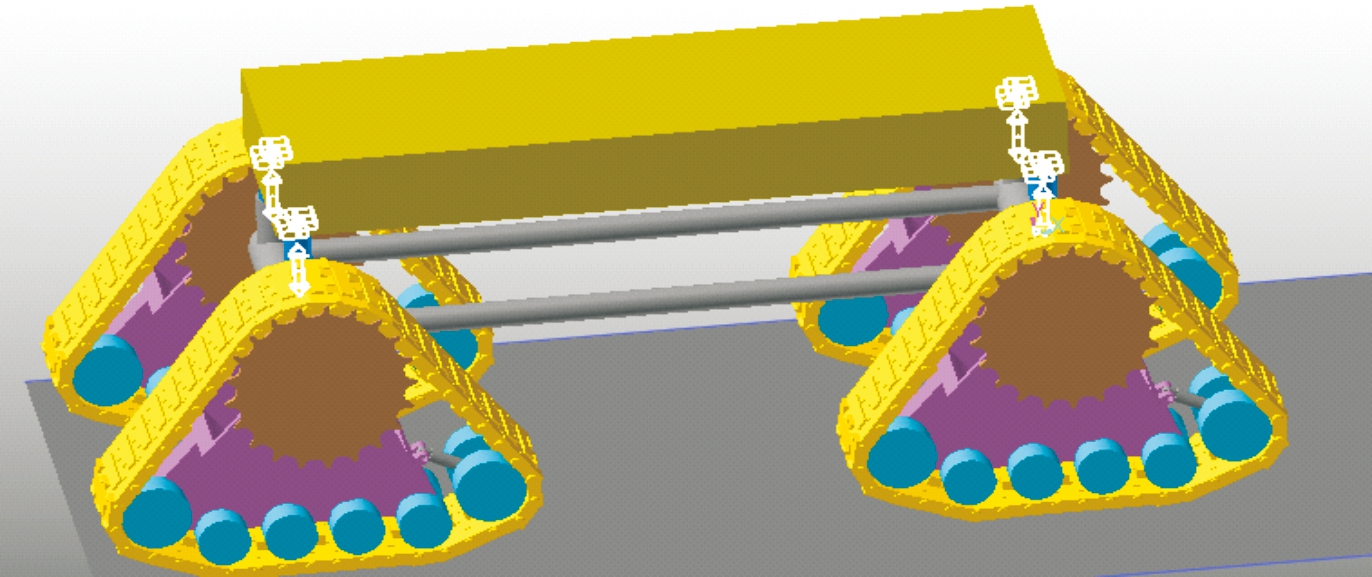
图9 救援车辆行驶系统模型示意图
2.2 约束的施加
为了如实反映整车各个部件的连接关系,需要添加相应的约束关系,才能进行正确的仿真[12],利用Joint命令对部件之间添加约束关系,救援车辆各部件约束关系如表2所示。
表2 救援车辆约束关系
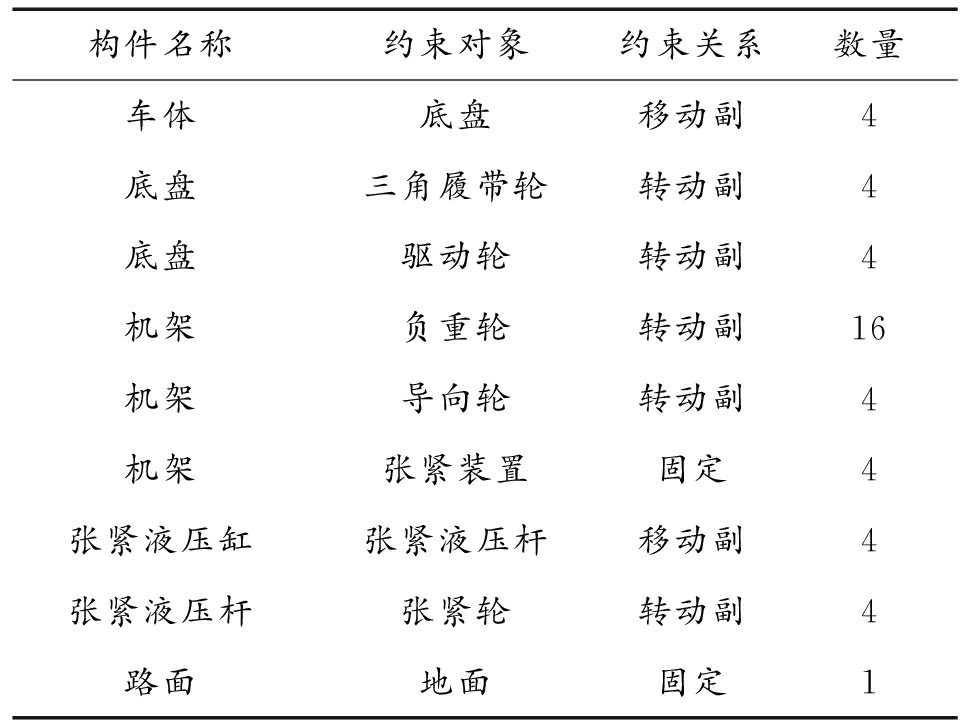
构件名称约束对象约束关系数量车体底盘移动副4底盘三角履带轮转动副4底盘驱动轮转动副4机架负重轮转动副16机架导向轮转动副4机架张紧装置固定4张紧液压缸张紧液压杆移动副4张紧液压杆张紧轮转动副4路面地面固定1
2.3 路面模型的建立
以履带与地面间的接触压力为依据,路面模型可利用软件自带的Ground模块建立,通过Outline Geometry生成法来生成水平路面、上坡路面(坡度60%)和含障碍的路面(路面上有300 mm高障碍及1.7 m宽,400 mm深的沟)。本文不考虑土壤的不同所造成的影响,统一采用默认的硬质路面进行仿真分析。3种路面的示意图如图10。
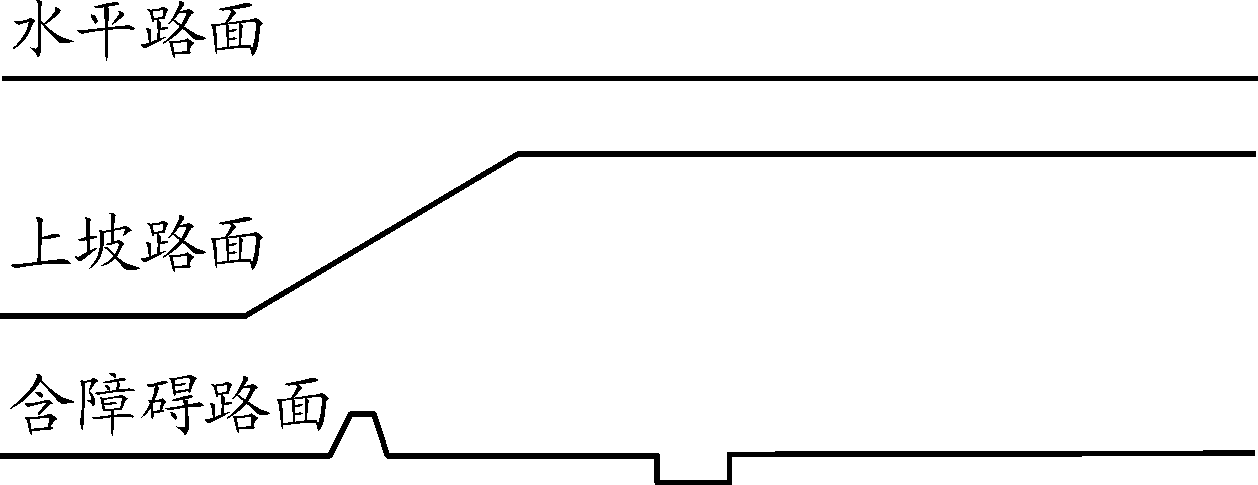
图10 3种路面示意图
3 不同工况力学性能仿真分析
将三角履带救援车辆设置为四轮驱动,整个系统单位制设置为MKS,仿真时间为15 s,步数为600。为了便于研究,只选取右前侧三角履带轮某个链节的受力曲线分析履带受力。
3.1 不同行驶速度对履带拉力的影响
履带车辆的动力是通过驱动轮实现的,驱动轮驱动履带环,进而驱动车体前进[13]。驱动轮的转动通过在驱动轮与底盘之间的转动副上添加step驱动函数实现。step函数可以通过3次多项式逼近的方式定义一个光滑的阶跃函数,其表达式为:step(time,x1,h1,x2,h2)[14]。
其中:time为时间自变量;x1为step函数的起点自变量初值;h1为step函数的起点处函数初值;x2为step函数的终点自变量的值;h2为step函数的终点处函数值。
保持预张紧力为60 kN,路面为水平路面,根据20 km/h、35 km/h、50 km/h三种车辆行驶速度和驱动轮半径计算驱动轮角速度并进行验证,得到对应的驱动函数分别为:STEP(TIME,3,0,6,10.5);STEP(TIME,3,0,6,18.4);STEP(TIME,3,0,6,26.2)。不同行驶速度下履带拉力曲线如图11所示。

图11 不同速度工况下三角履带受力曲线
从图11可以看出:0~3 s车辆达到静平衡状态,此阶段3条曲线基本重合,履带拉力为预张紧力60 kN,救援车辆从第3 s开始加速,第6 s加速到仿真速度然后匀速行驶,单个履带板行驶过程中周期进入履带紧边和松边,当进入紧边时履带拉力出现极大值,当进入松边时履带拉力出现极小值,因此6 s之后的匀速行驶阶段,3条曲线中履带板受力呈现周期性变化,周期为履带板循环一周的时间,通过履带总长与速度的换算,3种速度下受力循环周期分别为1.16 s、0.657 s、0.46 s。从图11受力曲线虚框所示位置提取不同速度下2个周期履带拉力曲线如图12~图14。

图12 20 km/h匀速行驶2个周期履带拉力曲线

图13 35 km/h匀速行驶2个周期履带拉力曲线
从图12~图14可以看出,履带受力周期与计算值吻合。履带最大拉力和平均拉力均随着车辆行驶速度的增大而增大,主要是由于行驶速度的增大,会导致履带离心力的增大,为克服因离心力导致的履带向外运动的趋势,履带拉力会相应的增大。总体而言履带受力虽然随速度增大而增大,但是速度对履带拉力的影响并不大,3种速度工况下履带平均拉力分别在预张紧力的基础上增大了2.4 kN、2.9 kN、4.8 kN。
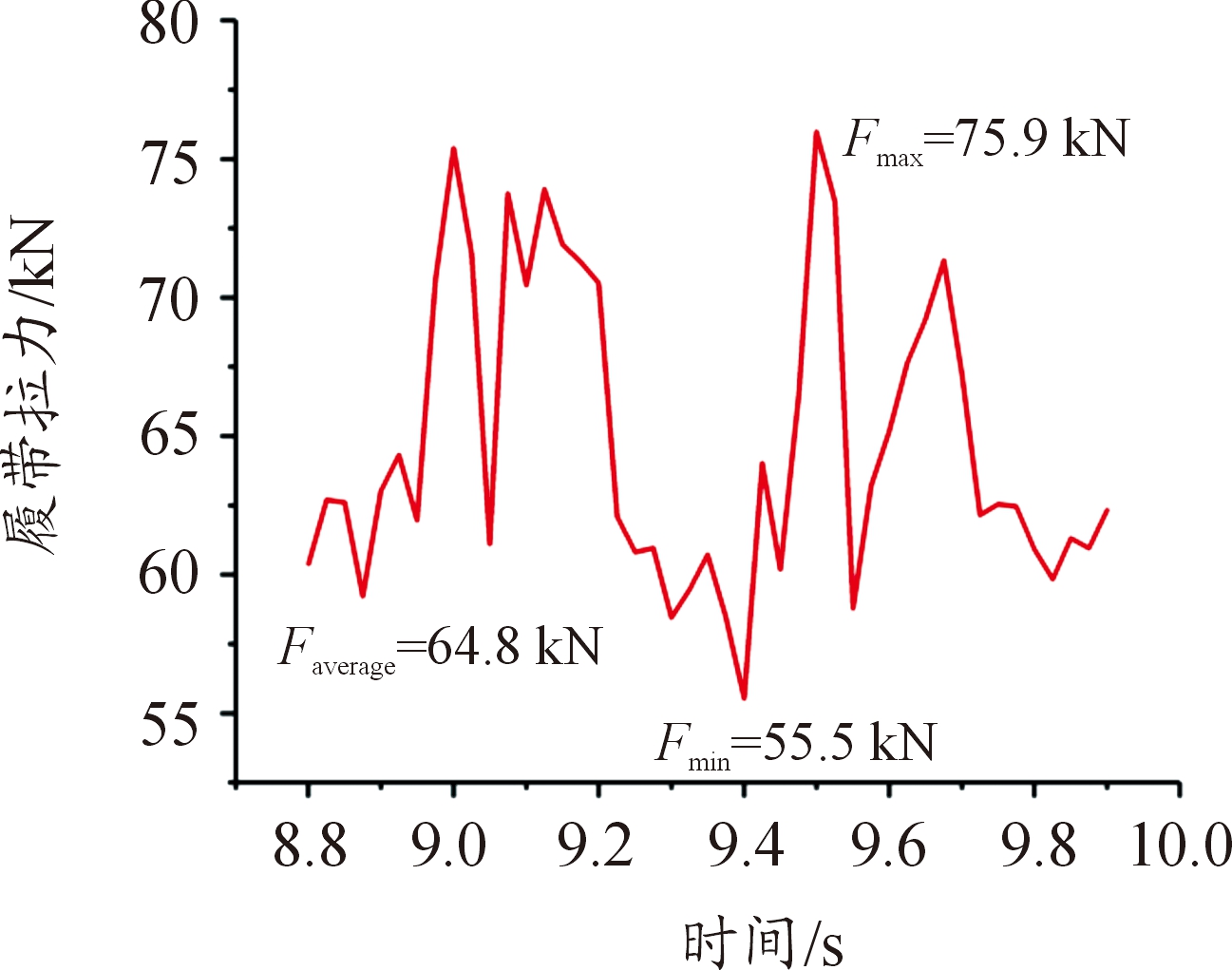
图14 50 km/h匀速行驶2个周期履带拉力曲线
3.2 不同预张紧力对履带拉力的影响
保持车速为20 km/h,路面为水平路面,预张紧力分别设置为40 kN、60 kN、80 kN。不同预张紧力下履带拉力曲线如图15。

图15 不同预张紧力下三角履带拉力曲线
从图15可以看出,0~3 s车辆达到静平衡状态,此阶段履带拉力基本与预张紧力一致,3~6 s车辆从静止加速到20 km/h,6 s后速度维持在20 km/h。由于车辆行驶速度相同,履带受力周期基本一致。从图15受力曲线中虚框所示位置提取不同预张紧力下2个周期的履带拉力曲线如图16~图18所示。
从图16~图18可以看出:不同预张紧力时,履带平均拉力分别为:39.5 kN、62.4 kN、82.3 kN,均与预张紧力基本一致;履带最大拉力与最小拉力的差值分别为:17.55 kN、20 kN、17.3 kN,该差值是驱动力矩引起的,由此可知虽然履带拉力随预张紧力增大显著增大,但由于行驶条件没有变化,所需的驱动力矩变化不大。

图16 40 kN预张紧力下2个周期履带拉力曲线

图17 60 kN预张紧力下2个周期履带拉力曲线
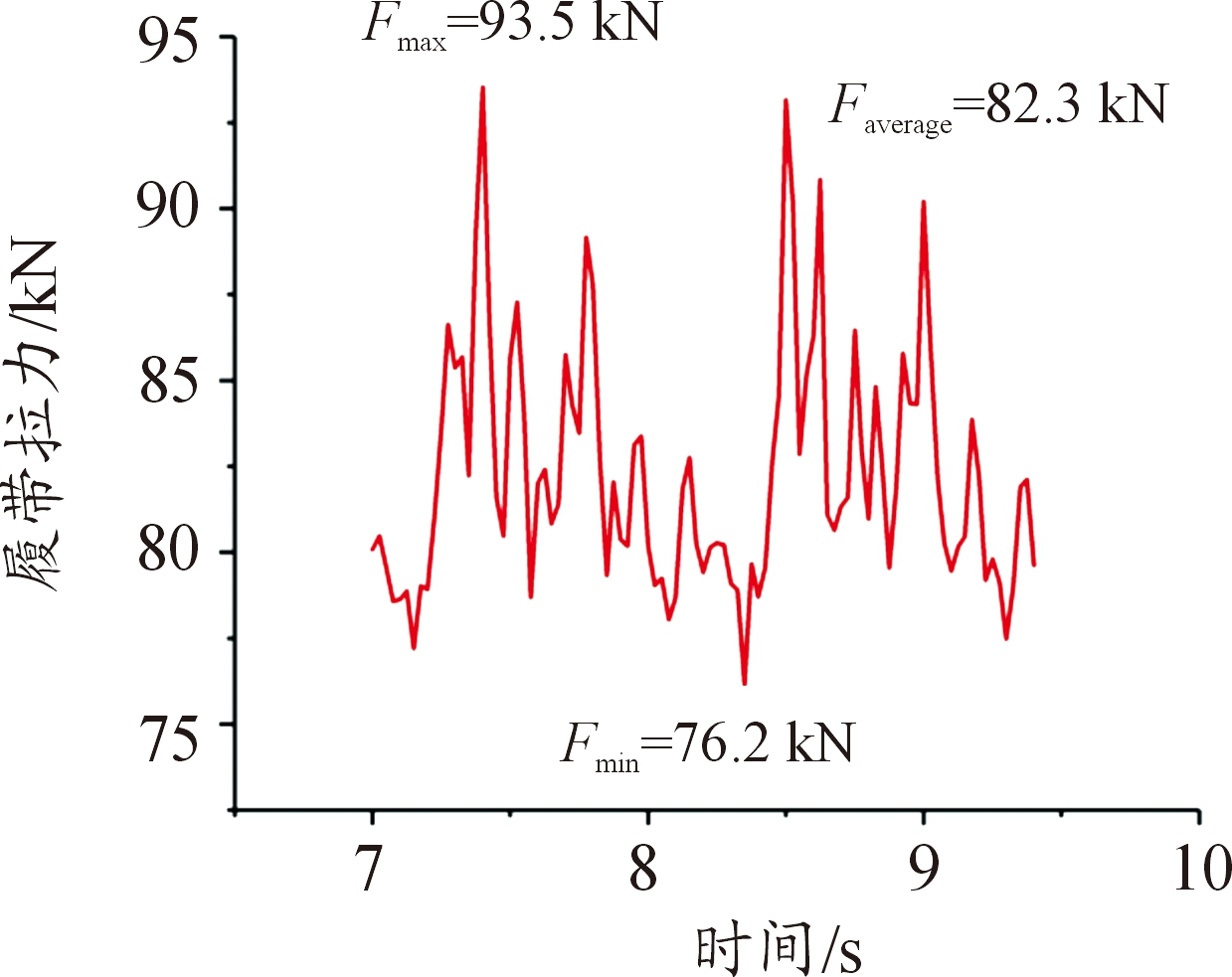
图18 80 kN预张紧力下2个周期履带拉力曲线
3.3 不同路况对履带拉力的影响
设置仿真条件使车辆从静止加速至10 km/h,并以此速度上坡和通过障碍,坡道结束及通过障碍后,车辆再加速至35 km/h,预张紧力为60 kN,分别对水平路面行驶、上坡、通过障碍进行仿真,履带拉力曲线如图19。
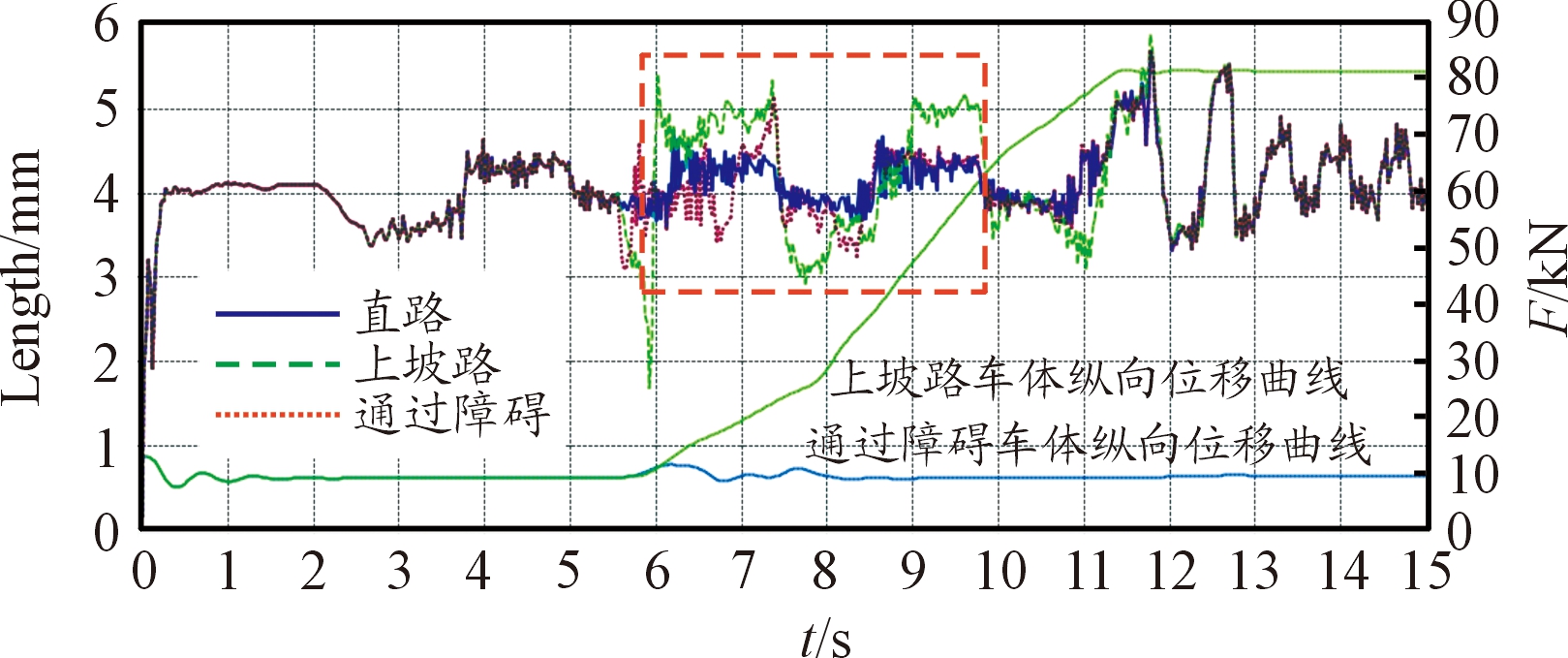
图19 不同路面条件下三角履带受力曲线
从图19可以看出:0~2 s车辆达到静平衡状态,此阶段履带拉力与预张紧力一致为60 kN,3~5 s车辆加速至10 km/h并匀速行驶,上坡及通过障碍前3条曲线基本重合。从车体纵向位移曲线可以看出,第6 s开始上坡及通过障碍,通过坡道及障碍后11~13 s加速至35 km/h,提取虚框所示履带拉力曲线进行分析,如图20~图22所示。
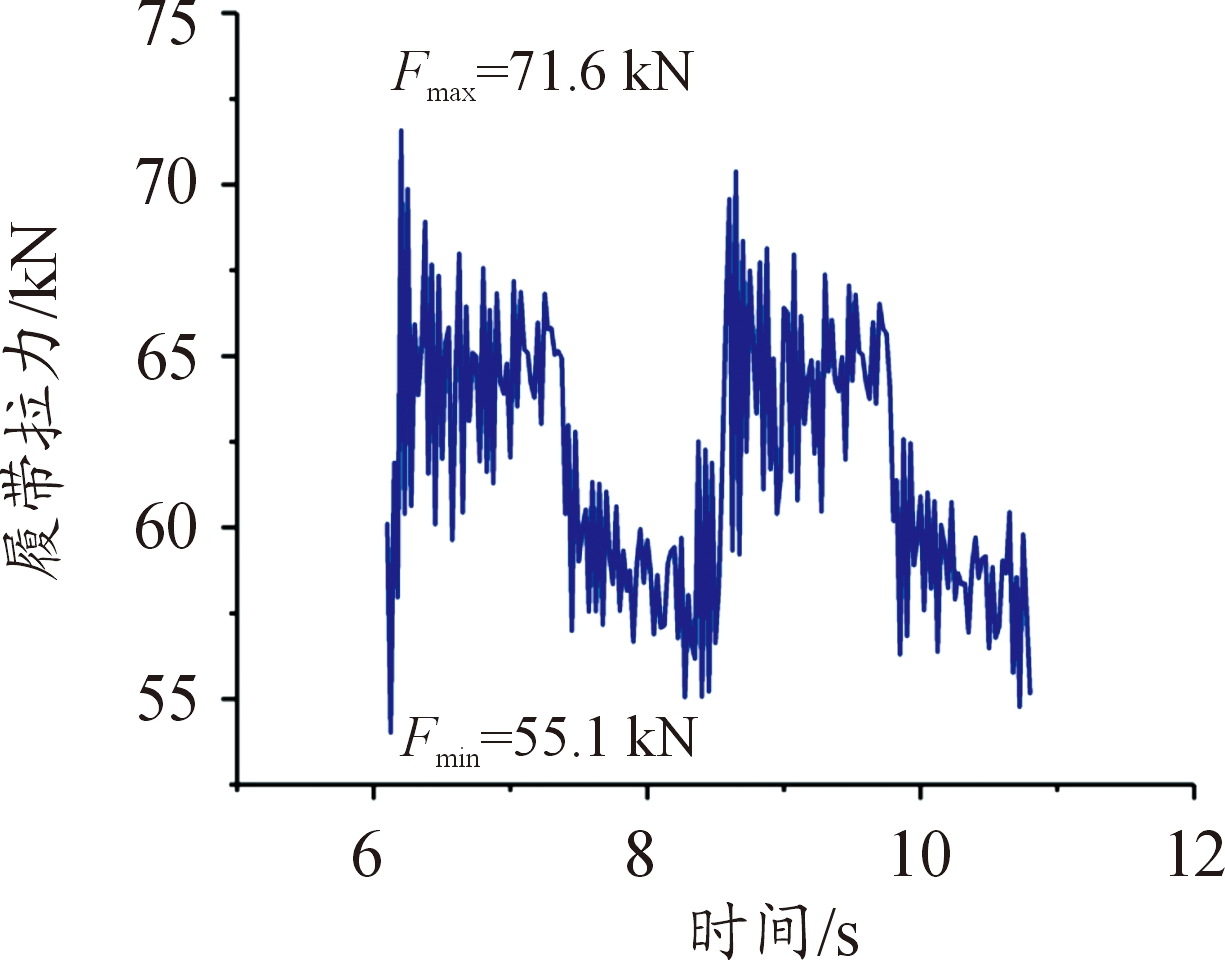
图20 水平路面行驶时履带受力曲线
从图20可以看出:此时车辆以10 km/h匀速行驶,履带受力周期明显,且与受力周期计算值2.32 s吻合较好,上坡时,履带受力也基本上保持相同的周期,通过障碍时,由于障碍的冲击作用,履带受力周期性不明显。对比图20~图22,3种路况下履带受力最大值与最小值的差值分别为 16.5 kN、36.7 kN、28.6 kN,通过前文理论分析,该差值是由驱动转矩导致的,差值越大说明驱动转矩越大,即上坡和通过障碍时,动力源需要输出的转矩成倍增大,同时上坡及通过障碍时履带的最大拉力分别比水平路面行驶时高出8.8 kN、5.5 kN。
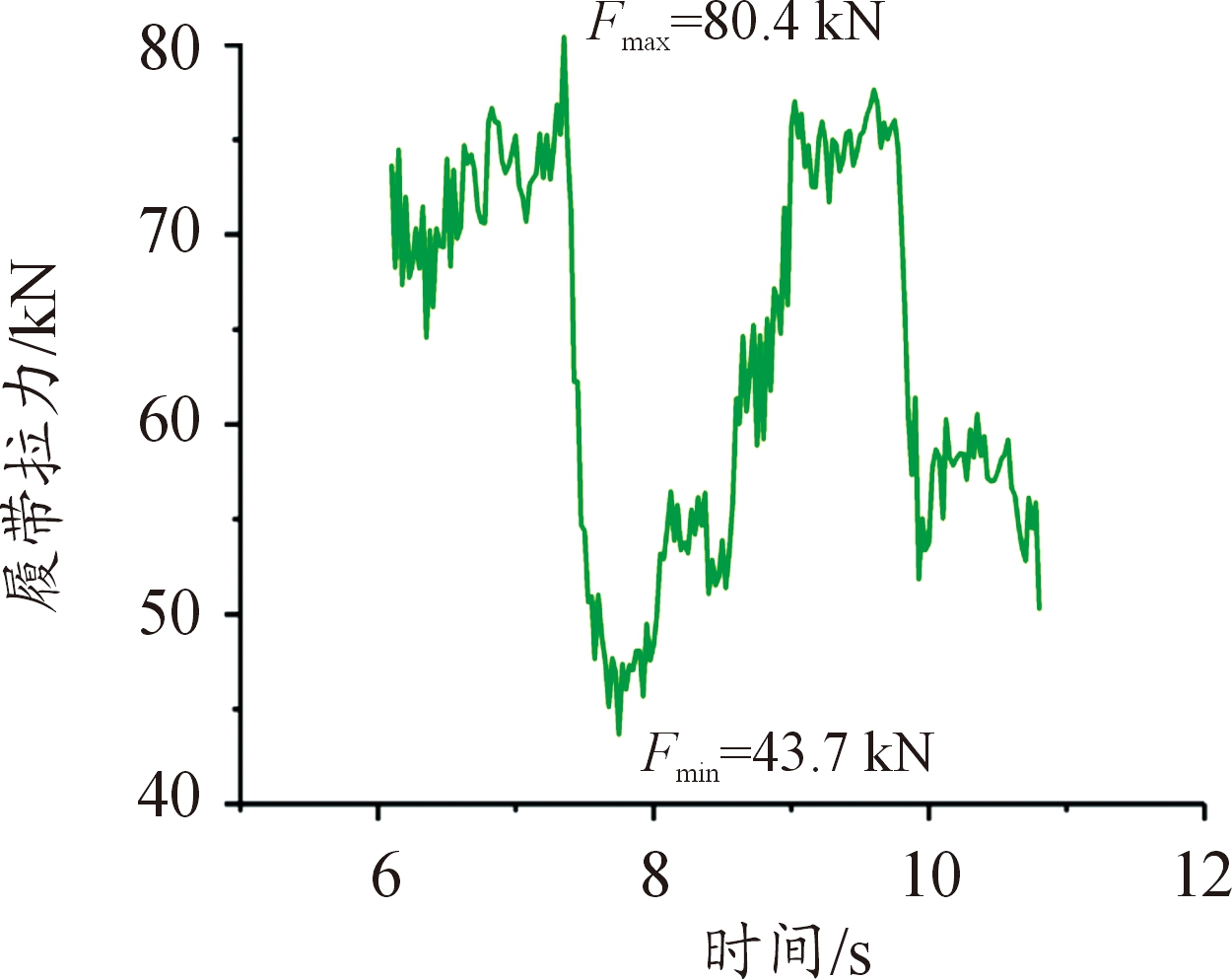
图21 上坡时履带受力曲线

图22 通过障碍时履带受力曲线
4 结论
1) 救援车辆履带拉力随着车辆行驶速度的增大而增大,但行驶速度对拉力大小的影响并不显著,不同行驶速度下的履带拉力平均值在预张紧力上下小幅度波动。
2) 救援车辆履带拉力随着预张紧力增大而显著增大,拉力过大会导致三角履带轮系与履带摩擦力增大,功率损耗及零部件磨损都会加大,拉力过小会导致履带松弛,行驶过程中可能导致履带剧烈振动,甚至履带脱落,因此应结合车辆行驶工况及三角履带轮结构,合理选择预张紧力。
3) 不同路面条件,对履带拉力影响较大,上坡、通过障碍时,履带拉力会较大幅度增大,根据应急救援车辆机动性能设计要求,应考虑履带受力最大的工况,即最大爬坡度工况的履带载荷进行履带的设计。
[1] 黄玉河.轮式挖掘机的市场现状及发展趋势[J].工程机械与维修,2005(15):82-84.
[2] 谢霞,康少华,侍才洪.复杂地形移动底盘技术研究[J].工程机械,2015,46(03):45-52.
[3] 吕凯,穆希辉,杜峰坡,等.重载三角橡胶履带轮设计关键问题综述[J].装甲兵工程学院学报,2016,30(01):29-38.
[4] 杨斗明.军用某50型装载机可更换三角履带轮的设计与仿真分析[D].哈尔滨:哈尔滨工业大学,2016.
[5] 潘晓春,姚凯.履带轮转换技术设计研究[J].机电产品开发与创新,2012(04):41-43.
[6] 沈仙法,周宏平,许林云.高射程履带喷雾车偏驶仿真与试验[J].中国农机化学报,2015,36(06):100-103,111.
[7] 印祥,禹泽栋,俞康,等.农业通用履带底盘控制系统研制[J].中国农机化学报,2018,39(12):77-81.
[8] 王涛,柳国光,楼婷婷,等.Development and test of fruit tree branches grinder in hilly area[J].中国农机化学报,2019,40(03):88-94.
[9] 张苏远.三角履带轮的设计及动力学仿真分析[D].秦皇岛:燕山大学,2019:31.
[10] 张燕,陈伦军,罗卫东.基于Recurdyn的高速履带车辆脱轮问题的仿真分析[J].煤矿机械,2014,35(02):49-51.
[11] 侯捷建.集材机可更换三角形履带主参数优选及动力学仿真分析[D].哈尔滨:东北林业大学,2015:20.
[12] 徐国英,薛大兵,姚新民.高机动履带车辆悬挂系统RecurDyn建模与实验验证[J].现代机械,2017(05):45-51.
[13] 王克运,张相洪,史力晨,等.履带车辆越障过程的动力学仿真[J].兵工学报,2005,26(05):577-583.
[14] 白钰,潘冠廷,刘志杰,等.山地履带拖拉机纵向坡地越障性能仿真分析及试验验证[J].安徽农业大学学报,2017(03):52-58.