线性调频连续波(linear frequency-modulated continues wave,LFMCW)雷达具有大的时宽带宽积,理论上具有较高的测量精度和距离分辨率,且平均发射功率较低,常用于目标近距离测量,如汽车防撞和异物探测。良好的距离分辨率对多目标探测和分辨至关重要。作为雷达发射机子系统中产生线性调频连续波的核心器件的频率源,由于器件非理想特性的影响,输出信号不可能是完全线性的,且非线性度会导致距离分辨率的恶化,因此分析非线性度对距离分辨率的影响显得尤为重要。当信号为理想线性调频时,线性调频连续波雷达的目标探测性能又受限于接收机频率分辨率及FFT(fast Fouier transform)变换时的加窗处理,因此需要对上述参数进行综合分析以满足系统距离分辨率要求[1]。
本文根据LFMCW雷达回波差频信号特性,从应用角度分析了扫频线性度和接收机频率分辨率对距离分辨率的影响,并根据理论分析结果设计了中心频率10 GHz,带宽125 MHz的频率源。X波段频率源作为雷达系统的核心模块,确保了LFMCW雷达最终能够达到0.3 m的高距离分辨率。最后根据所设计的X波段频率源扫频实测数据进行扫频线性度误差函数拟合验证了理论推导的正确性[2-5]。
1 LFMCW雷达信号模型分析
对于一个线性调频锯齿波信号,其数学表达式是一个理想线性调频信号加上一个非线性频率误差,频率与时间关系表达式为:
(1)
式(1)中:f0是射频中心频率;ΔF是扫频带宽;Tm是调制时间。
幅度为a0的发射信号可表示为:
![]() fe(τ)dτ], 0<t<Tm
fe(τ)dτ], 0<t<Tm
(2)
假设目标距离为R,则回波延迟时间为![]() 和幅度衰减到b0的信号为:
和幅度衰减到b0的信号为:
![]()
(3)
即:
(4)
在零拍调频连续波雷达中,接收信号和发射信号混频输出差频信号sb(t)为:
![]()
td<t<Tm
(5)
化简为:
![]() fe(τ)dτ], td < t < Tm
fe(τ)dτ], td < t < Tm
(6)
差频频率和相位分别为:
(7)
(8)
由此得到,目标距离雷达距离R为:
(9)
在目标和雷达相对静止条件下,即不考虑多普勒效应,上述结论对零差频FMCW信号普遍适用。在LFMCW雷达中,带宽和调制周期一定的情况下,差频正比于测量距离。在本系统中,信号带宽是500 MHz,调制时间为1 000 μs,根据式(9)计算可得150 m的测量距离对应的最大差频为500 kHz[6-8]。
2 扫频线性度误差及接收机分辨率对距离分辨率的影响
2.1 距离分辨率和接收机频率分辨率的关系
对式(9)取微分可到:
![]()
(10)
式(10))中,Δfb是差频信号的分辨率。
因为差频信号的分辨率是目标差频信号与接收机频率分辨率的卷积,差频信号的分辨率通过式(11)计算可得:
(11)
式(11)中:Δft是目标差频信号频谱宽度为一定值,等于调频时间的倒数;Δfr是接收机频率分辨率。
由式(11)可以看出,距离分辨率并不是单纯由目标频谱决定的,同时和接收机频率分辨率相关,即等效频谱被接收机频率分辨率展宽,距离分辨率相应下降。根据雷达设计需求,由采样率和带宽等可计算出接收机频率分辨率为1 kHz。当接收机频率分辨率为一定值时,只能通过降低线性度误差来提高距离分辨率。
2.2 距离分辨率与扫频线性度误差的关系
差频信号的瞬时频率fb为:
fb(t)=fb0+fe(t)+fe(t-td)
(12)
式(12)中,fe(t)是由频率源非理想扫频特性引起的扫频线性度误差。根据式(6)可知,sb(t)是一个以fb0为中心的调相信号,其频谱将被展宽。
由卡森公式可得,展宽后的频谱带宽Δf为:
(13)
式(13)中,a为非线性误差函数的形状参数,一般取3.5-5。由于频谱将被展宽,与理想线性调频时相比,频谱展宽的倍数n为[10]:
(14)
因此分辨率将下降n倍频ΔR为:
![]()
(15)
线性度定义为扫频线性误差函数的最大值与信号带宽的比值为:
(16)
3 X波段频率源设计概述
根据上述理论分析可知,设计频率源时必须保证良好的线性度,从而保证雷达系统距离分辨率。
LFMCW雷达系统采用如图1所示的数字锁相环结构作为线性频率源。根据锁相环工作原理,线性源首先产生如图1所示的步进式调谐电压,经过环路滤波器平滑后变为调谐电压信号,进而调节压控振荡器(voltage controlled oscillator,VCO)输出调频连续波。由于VCO每次变化的频率 fstep对应一个调谐电压Vstep值,且锁相环是闭环补偿系统,因此只要控制好调谐电压的变化值就能保证VCO端的线性调频频电压的输出。
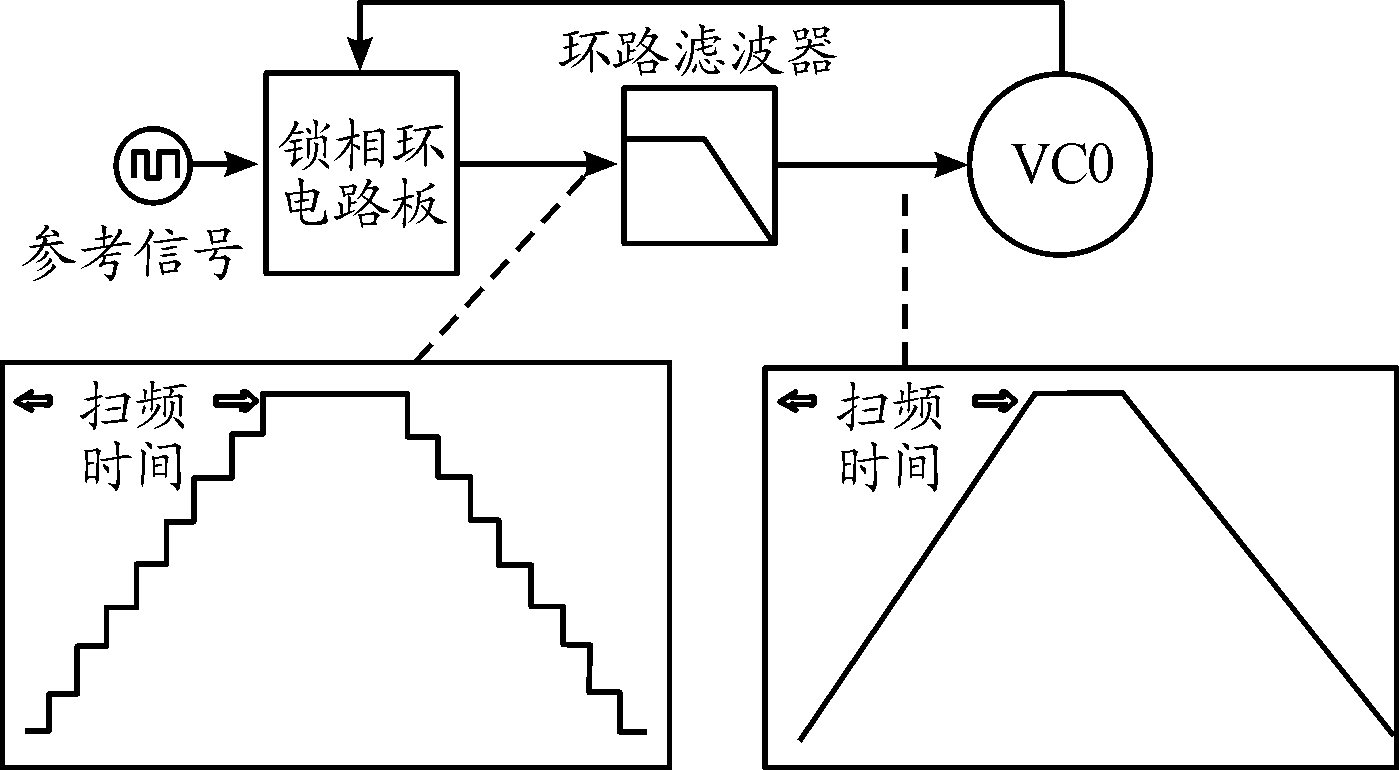
图1 频率源设计结构与原理分析示意图
如图2所示,最小非线性扫频误差 fe(t)min为0,最大非线性扫频误差fe(t)max可以认为是VCO端最大的频率变化值fstep。当所需分辨率为0.3 m时,根据式(15)计算出 fstep=12 kHz,依据这种量化关系设计中心频率为10 GHz,带宽125 MHz的锁相环电路,经4倍频变为中心频率为40 GHz,带宽为500 MHz的信号源。

图2 频率源非线性误差示意图
4 测试数据仿真结果与分析
4.1 实测扫频线性度误差函数的拟合
利用信号分析仪E5052B对设计频率源进行测试,对f-t测试数据进行与理想线性调频信号进行对比,从而拟合得到三角函数形式的扫频线性度误差函数fe(t)。对于扫频线性度误差函数fe(t)进行傅里叶级数展开(取前五项),有:
(17)
Ω=2π×103rad/s,Ωk=kΩ;
扫频线性度误差函数最大值为12 kHz,与第3节理论计算一致。误差函数 fe(t)在一个扫频周期(1 ms)内的拟合曲线如图3所示。

图3 扫频线性度误差函数曲线
4.2 单个目标探测性能的分析及加窗必要性
得到实际频率源扫频线性误差函数模型后,对差频信号进行FFT变换,可进行频谱分析,并通过瑞利判据验证频率源非线性度对距离分辨率的影响。根据雷达基本性能,仿真参数设置如表1所示[9-10]。
表1 零差频调频连续波雷达仿真参数
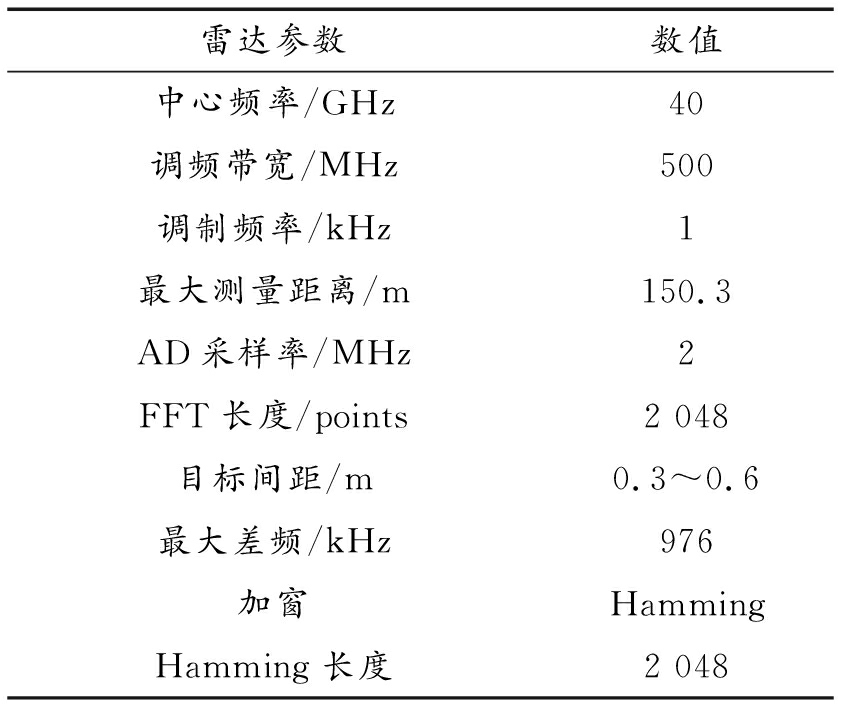
雷达参数数值中心频率/GHz40调频带宽/MHz500调制频率/kHz1最大测量距离/m150.3AD采样率/MHz2FFT长度/points2 048目标间距/m0.3~0.6最大差频/kHz976加窗HammingHamming长度2 048
扫频线性度约为10-5、扫频线性度误差函数最大值为12 kHz、150 m处目标回波进行FFT变换后的频谱如图4所示。从图4仿真结果可以看出,主瓣比旁瓣高出将近14 dB,在测量单一目标时,可以很容易从噪声中甄别出单个目标的存在,因此对单目标探测,此频率源的设计满足雷达系统需求。横坐标为探测距离(雷达距离目标的距离),纵坐标为差频信号归一化电平。
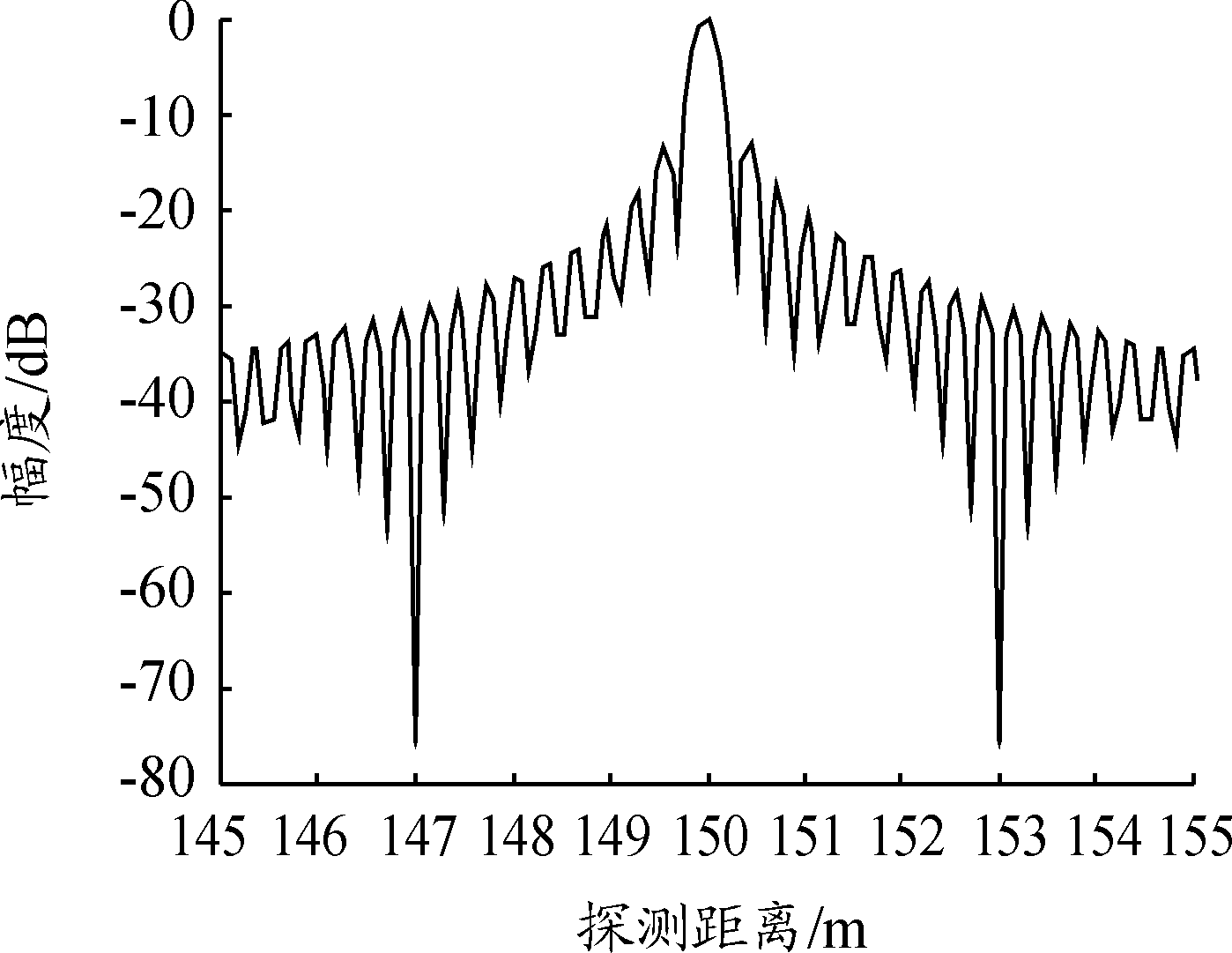
图4 单个目标频谱(扫频线性度误差函数
最大值12 kHz,扫频线性度约为10-5)
信号处理过程加窗有助于降低旁瓣电平。扫频线性误差函数最大值为12 kHz、 150 m处目标回波进行FFT变换时加Hamming窗处理后的频谱如图5所示。从图5仿真结果中可以看出,旁瓣电平相对于图4所示的旁瓣电平,降低了将近20 dB,主瓣比旁瓣高出将近40 dB。说明加窗处理对于整个旁瓣电平的降低有非常明显的效果,对于噪声中甄别出单个目标的存在更加容易。

图5 单个目标频谱(扫频线性度误差函数
最大值12 kHz,加汉明窗处理)
4.3 雷达距离分辨率的综合分析及最优信号处理参数小结
扫频线性度误差函数最大值为12 kHz,相同的2个目标分别位于150 m和150.3 m处目标回波进行FFT变换后的频谱(信号处理过程添加Hamming窗)如图6所示。从图6可以看出主瓣与旁瓣相比高出17 dB以上,依据瑞利判据,能够区分出2个目标。根据2.2节理论分析误差函数最大值在12 kHz时能够满足距离分辨率时0.3 m的要求,说明频率源的设计对于完成多目标探测没有问题。图7为相同条件下信号处理不添加Hamming窗的频谱,主瓣与旁瓣相比高出15 dB。从两图对比可以看出,Hamming窗能够压低旁瓣提高探测效果[11]。
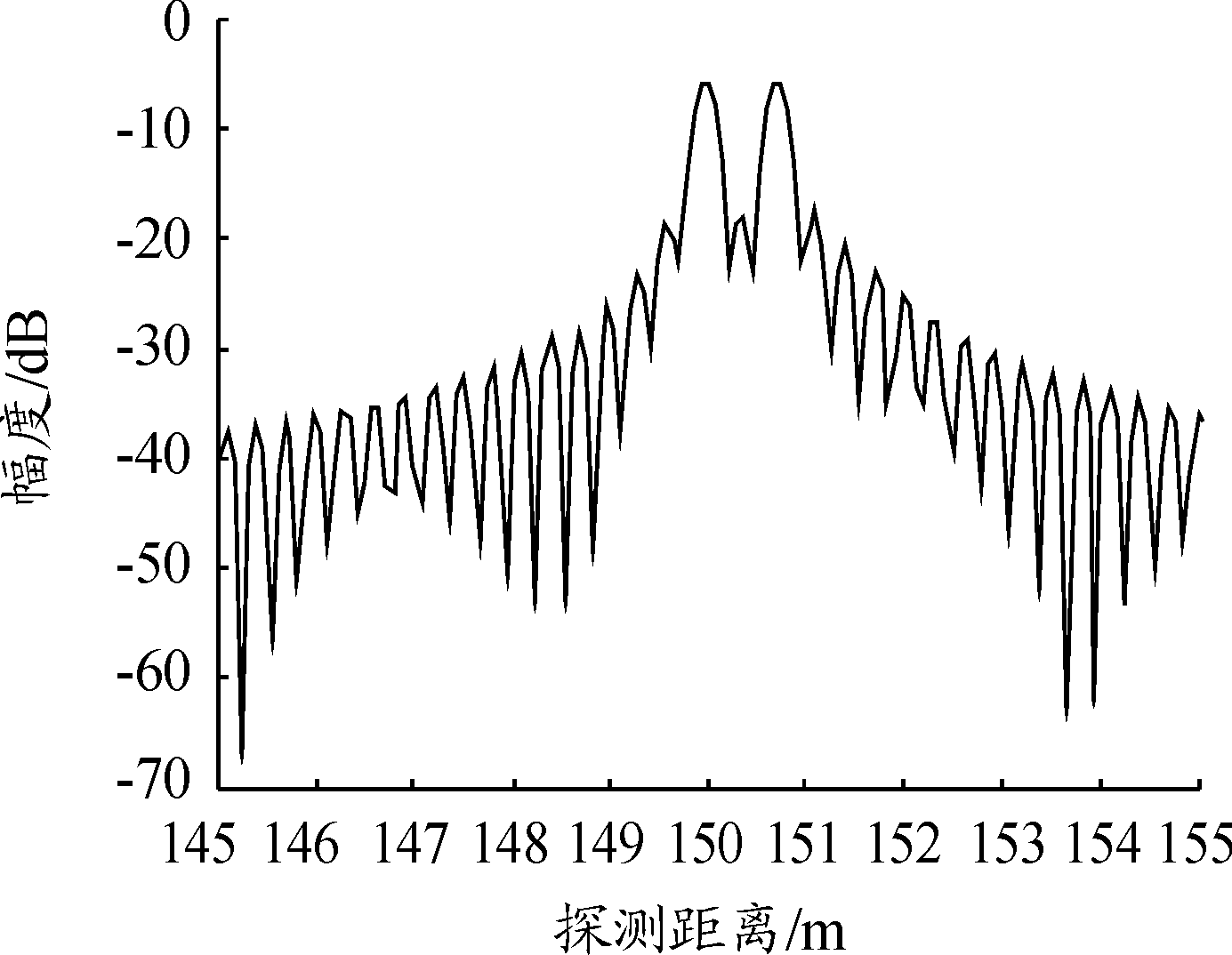
图6 相距0.3 m的两目标频谱
(信号处理过程添加Hamming窗)

图7 相距0.3 m的两目标频谱
(信号处理过程不添加Hamming窗)
进一步进行仿真,由理论分析可知,当扫频误差函数最大值过大时,频谱将被展宽,多目标测量将受到影响,修改扫频线性误差拟合函数,将误差最大值改为120 kHz。图8为扫频线性度约为10-4、扫频线性度误差函数最大值设置为120 kHz、相同的2个目标分别位于150 m和150.3 m处目标回波进行FFT变换后的频谱。与图7相比较,频谱明显要杂乱很多,从图8无法判断出目标是否存在,因此当扫频非线性误差过大时,距离分辨率将无法满足指标要求[12-16]。
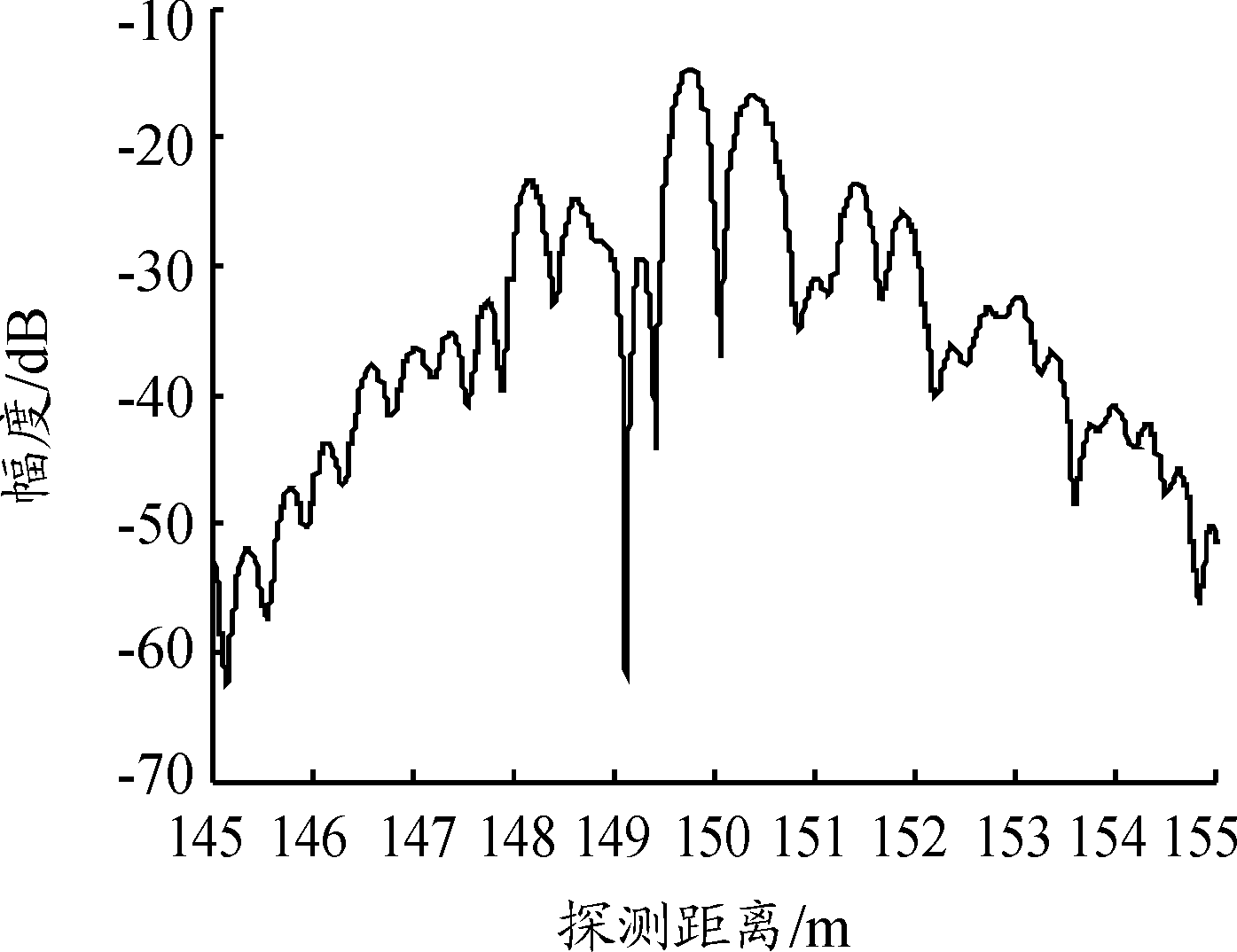
图8 相距0.3 m的两目标频谱分析
(扫频线性度约为10-4,扫频线性度误差函数最大值120 kHz)
通过以上仿真分析,总结仿真结果如表2所示。
表2 仿真小结
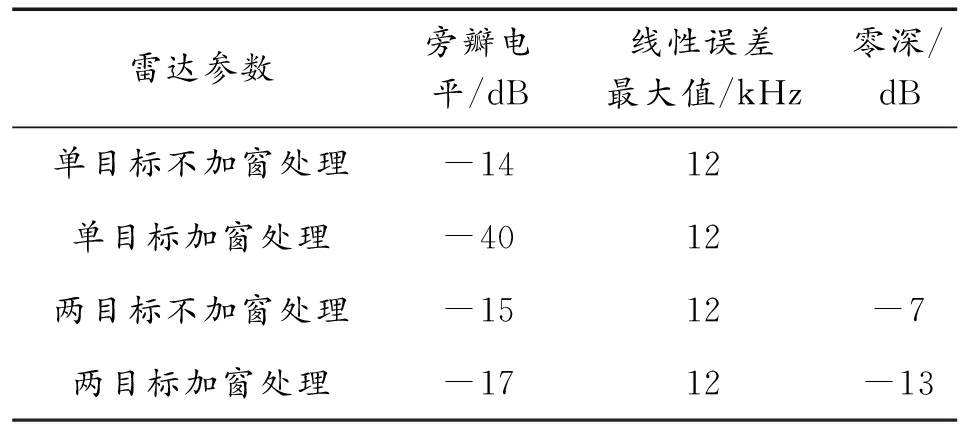
雷达参数旁瓣电平/dB线性误差最大值/kHz零深/dB单目标不加窗处理-1412单目标加窗处理-4012两目标不加窗处理-1512-7两目标加窗处理-1712-13
以上仿真实验结论可为后续的判别算法提供定量的指导意义。
5 结论
高距离分辨率是LFMCW雷达的优势,在调频带宽和接收机频率分辨率一定的情况下,扫频线性度误差的幅值决定着频谱边带的幅度,当扫频线性度误差过大时,频谱带宽明显变宽,距离分辨率将无法满足指标要求。FFT变换时加窗处理对压低频谱旁瓣有明显的作用,对目标探测和区分有改良作用。通过仿真实验可知,根据扫频线性度对距离分辨率影响理论设计的X波段频率源,当其扫频线性度误差为12kHz时,能够满足0.3 m距离分辨率的指标要求。
[1] 吴义中.60 GHz LFMCW雷达信号处理研究[D].杭州:浙江大学,2011.
[2] PATOLE S,TORLAK M,WANG K,et al.Automotive Radars:A Review of Signal Processing Techniques[J].IEEE Signal Processing Magazine,2017,34(02):22-35.
[3] STOVE A G.Linear FMCW Radar Techniques[J].IEEE Proceedings-F,1992,139(05):343-350.
[4] HADERER A,WAGNER C,FEQER R.A 77 GHz FMCW frontend with FPGA and DSP support[J].International Radar Symposium,2008,33(06):22-26.
[5] GRIFFITHS H D.New ideas in FM radar[J].Electronics Communications Engineering Journal,1990,2(05):185-203.
[6] 黄杨帆,谭晓衡,王保华.LFMCW雷达距离分辨力的分析及改善[J].重庆大学学报,2012,35(08):139-143.
[7] M.I.斯科尔尼克.雷达系统导论[M].北京:国防工业出版社,1992:74-72.
[8] 宋景唯.线性度对线性调频雷达距离分辨力的影响[J],电子科技大学学报,1992,12(02):121-126.
[9] PIPER S O.Homodyne.FMCW radar range resolution effects with sinusoidal nonlinearities in the frequency sweep[C] //Proc.Of the IEEE International Radar Conference,1995:563-567.
[10] CANDAN C.A Method for Fine Resolution Frequency Estimation from Three DFT Samples[J].IEEE Signal Processing Letters,2011,18(06):351-354.
[11] 汪学刚,袁湘辉,向敬成,等.调频线性度与零差拍线性调频连续波雷达的距离分辨力[J].系统工程与电子技术,1997(10):19-24.
[12] 周刚,苏宝平,傅佑麒.LFMCW雷达数字化测距测速的工作参数设计[J].电光与控制,2007,14(03):29-31.
[13] 潘世伟,葛俊祥,金良.基于FPGA的LFMCW雷达信号算法及实现[J].雷达科学与技术,2017,15(04):392-396.
[14] 孙峰,朱莉,张超,等.毫米波LFMCW雷达测距关键算法研究[J].微波学报,2015(S2):197-202.
[15] 李鹏.基于FPGA的LFMCW雷达信号处理机研究[J].火控雷达技术,2010,39(01):33-36.
[16] 赵宏图,郭昕,邵楠,等.锥扫LFMCW雷达信号处理方法的研究[J].北京理工大学学报,2006(06):528-531.