转管武器主要利用其高射速、高密集度、高可靠性应用于现代空战及近程防空反导作战。机心作为转管武器的一个重要部件在工作时反复承受膛底火药燃气的压力，其工作环境恶劣，容易出现强度破坏和疲劳破坏。因此分析机心强度和疲劳寿命对于武器可靠性和安全性很有必要。
很多学者对武器机心进行了强度和疲劳寿命分析。文献[1]利用有限元分析软件Ansys，建立了机芯应力分析的有限元仿真模型，通过仿真得到了机芯在膛压最大时的应力分布云图。文献[2]中应用解析与数值模拟方法，对闩体裂纹形成阶段的寿命和扩展阶段的寿命进行了分析计算并对闩体疲劳裂纹形成的影响因素进行了分析。文献[3]中在仿真载荷谱和有限元静应力分析的基础上，结合材料的S-N曲线，建立了抽筒子疲劳损伤与寿命预测模型，得到其危险部位的最小寿命。文献[4]中基于闭锁齿切向力和径向力的载荷谱、静强度结果和45CrNiMoVA材料的S-N疲劳寿命曲线，由Designlife进行协同仿真预测小闭锁齿的疲劳寿命。文献[5]中对影响自动武器关键要素的闭锁机构的动态应力进行了研究和分析。
学者们对于回转式机心研究较多，但对于闭锁块偏转式机心研究较少。本研究利用有限元分析软件对某闭锁块偏转式机心进行强度分析，提出减小应力集中程度的结构改进方法，并对改进结构进行强度校核和疲劳寿命分析，得出一套切实可行的分析闭锁块偏转式机心的方案，为闭锁块偏转式机心的结构设计提供一定参考。
1 闭锁块偏转式机心
闭锁块偏转式机心三维模型如图1所示。机心由主滚轮、导杆头、导杆头销、导杆、侧滚轮轴、闭锁块、闭锁块轴、侧滚轮、机体组成。主滚轮绕导杆头转动，导杆头销将导杆和导杆头连在一起，闭锁块轴将导杆和闭锁块连在一起，闭锁块圆弧端与机体下方的圆弧端为面接触且两圆弧面轴线同轴。炮膛合力作用方向平行于自动机回转中心同时垂直于抓壳钩弹底窝镜面。
开锁凸轮与闭锁凸轮均固定在炮箱上。开闭锁动作示意图如图2：机心沿凸轮曲线槽运动完成推弹入膛动作至前直线段部分，在自动机回转过程中，闭锁凸轮下压导杆头并通过主滚轮和导杆使闭锁块向下进入节套的闭锁槽中，使机心处于闭锁状态，闭锁状态示意图如图3。闭锁完成后，击发机构击发炮弹，膛压降为安全开锁压力后，开锁凸轮提起主滚轮并通过导杆提起闭锁块，闭锁块退出闭锁槽使机心开锁，继续完成抽壳动作。
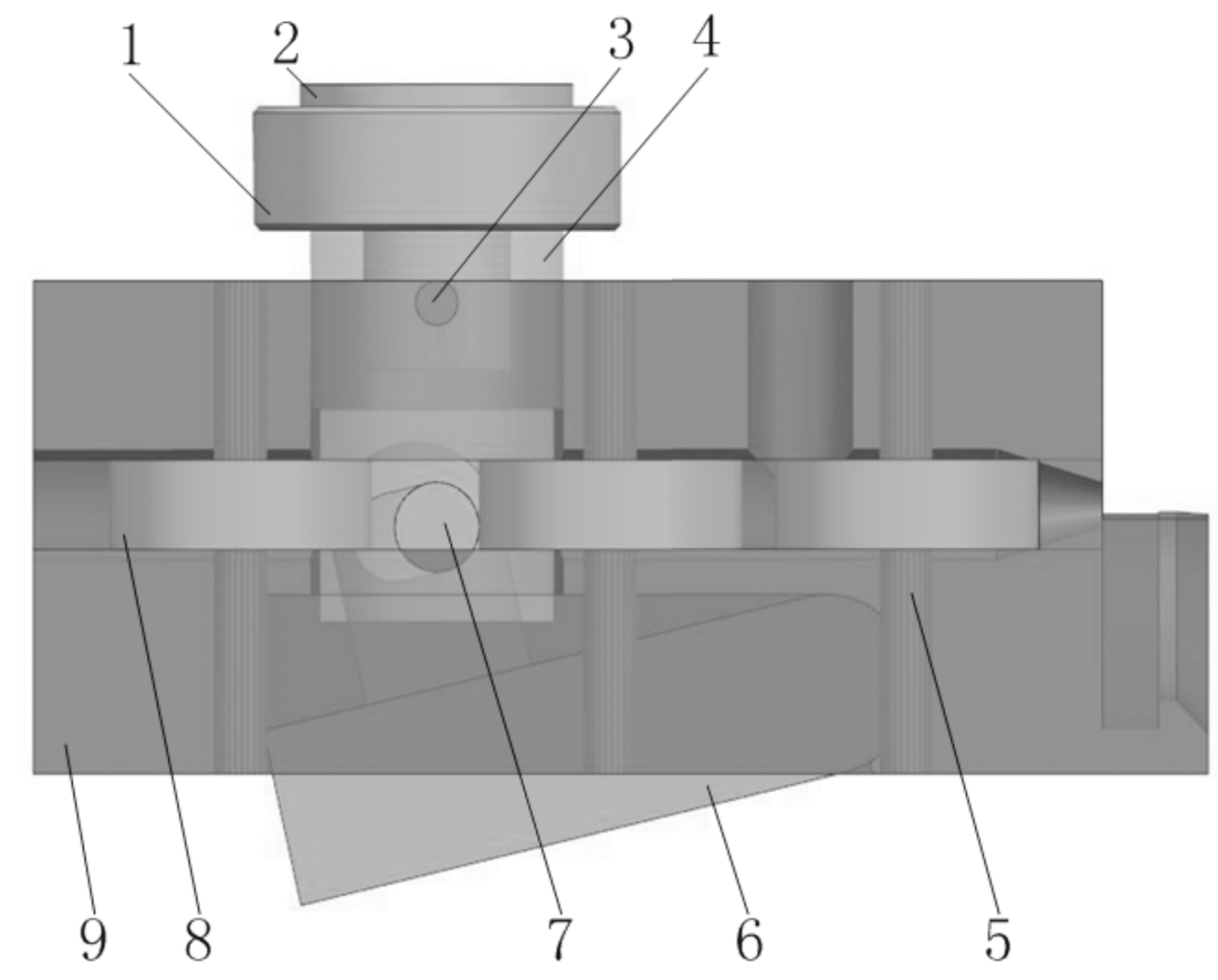
1.主滚轮；2.导杆头；3.导杆头销；4.导杆；5.侧滚轮轴；
6.闭锁块；7.闭锁块轴；8.侧滚轮；9.机体
图1 闭锁块偏转式机心三维模型示意图
1.开锁凸轮；2.闭锁凸轮
图2 开闭锁动作示意图
在闭锁状态时，机心承受较大的载荷，尤其是闭锁块和节套上的闭锁槽，更容易出现强度破坏，且多次工作容易发生疲劳破坏。因此对机构进行强度的校核、评估和疲劳寿命分析，进而进行合理设计，使其能够可靠、安全地工作。
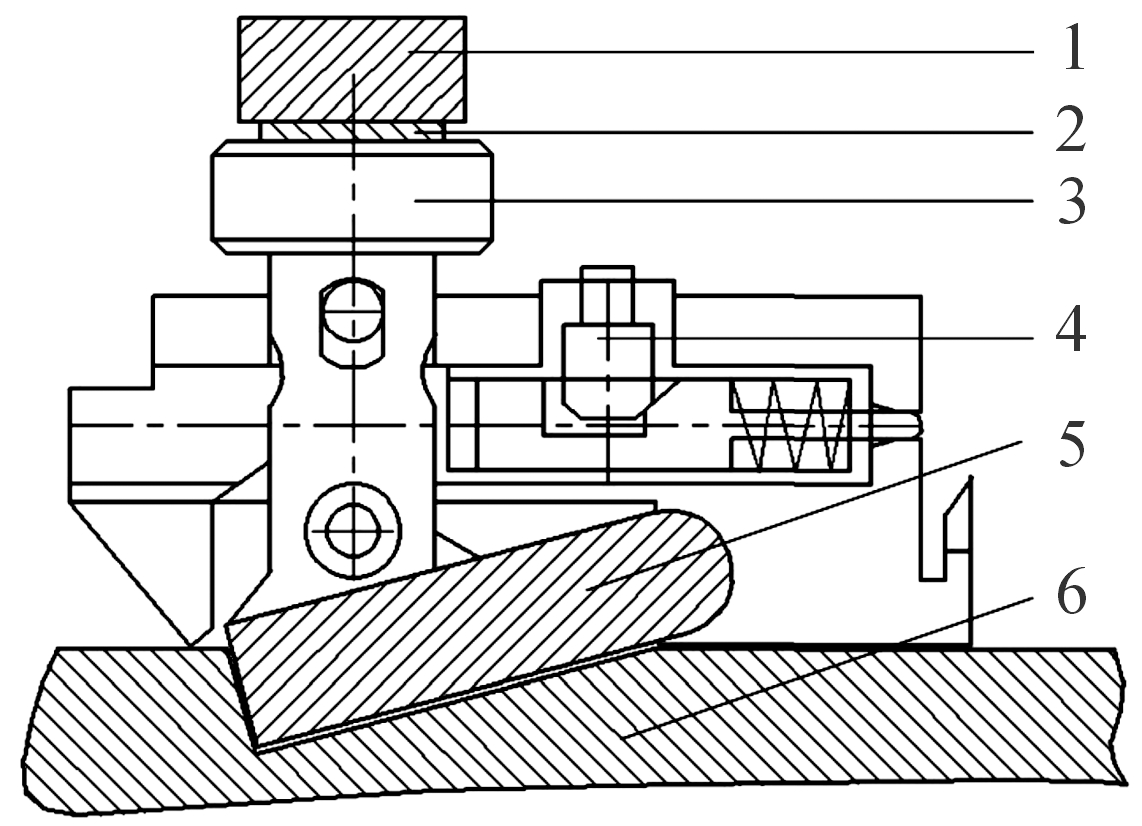
1.闭锁凸轮；2.导杆头；3.主滚轮；4.击发机构；5.闭锁块；6.节套
图3 闭锁状态示意图
2 有限元静强度分析
静力学分析是有限元分析的重要基础，是指在载荷不随时间变化的情况下，分析结构刚度和强度的问题。
2.1 有限元模型的建立
有限元模型的建立是有限元分析的基础。本文建立的有限元模型的分析对象、材料参数、网格划分方法及边界条件如下：
1) 在本文中，节套和机心采用炮钢材料45CrNiMoVA，材料参数如表1所示。
表1 45CrNiMoVA基本参数
温度密度/(kg·m-3)屈服极限/MPa拉伸极限/MPa 弹性模量/MPa泊松比室温7 8301 3251 4702.14×1050.29
2) 为了有效地进行有限元建模并减小计算量，取一组机心和其对应的节套闭锁槽为研究对象。
3) 对节套和闭锁块进行处理，划分为多部件体，便于后续网格划分；为了保证网格的质量，主要选择六面体网格，考虑到机体几何模型的复杂性，机体采用了四面体网格。
4) 由内弹道参数、内弹道理论公式和炮膛合力计算公式，编程得到炮膛合力曲线如图4所示。
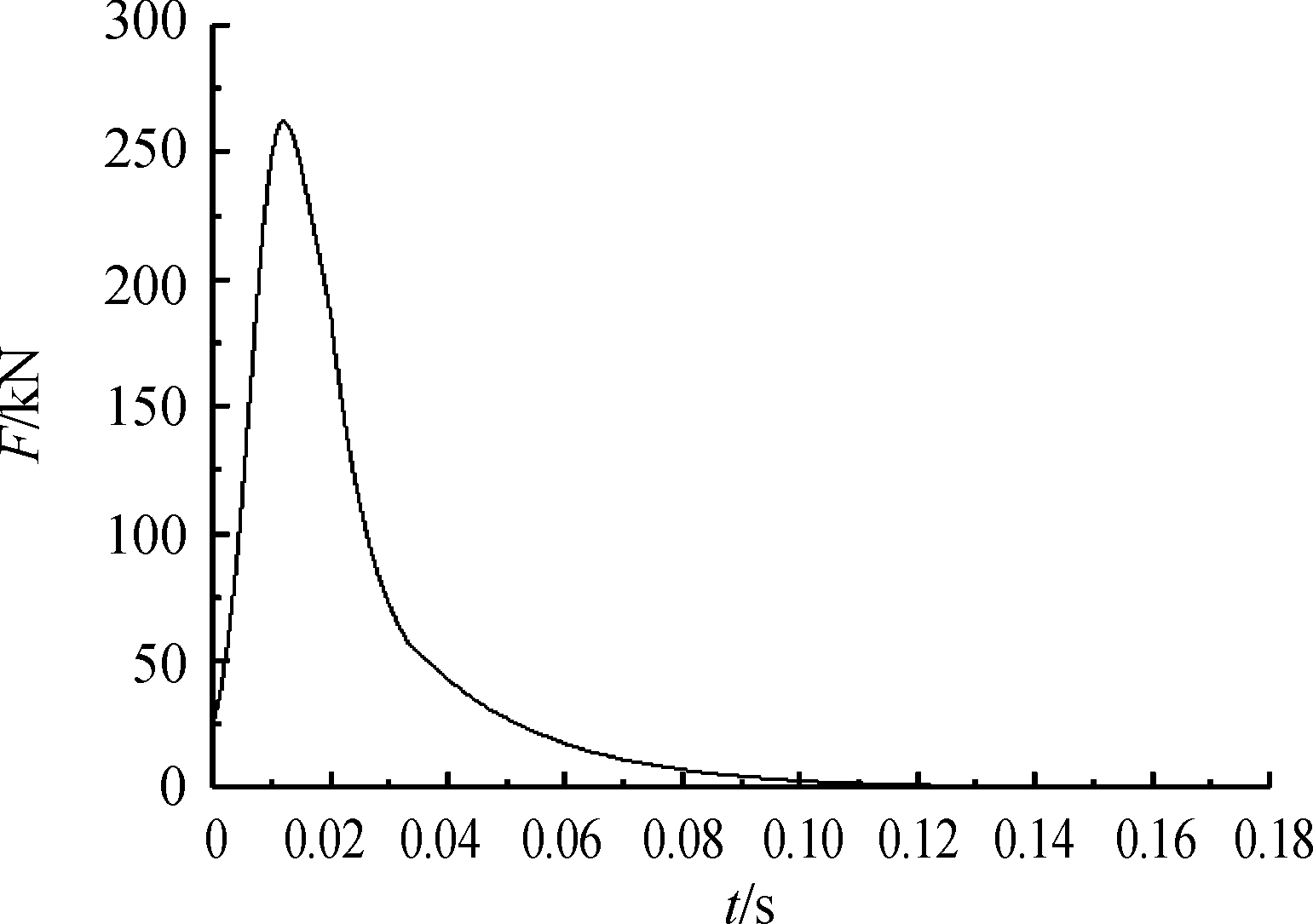
图4 炮膛合力曲线
火药燃气作用的时间非常短，在采用静力学分析时，只考虑把最大炮膛合力作为载荷加在机体受力面上，分析在最大炮膛合力作用下的节套和机心。
2.2 仿真结果与分析
对节套和机心有限元模型进行仿真求解，得到节套应力云图如图5所示，闭锁块应力云图如图6所示。
从图5可以看出，最大应力出现在闭锁槽受力面尖角处，且超过了材料的屈服极限；从图6可以看出，最大应力出现在闭锁块受力面直角边处，也超过了材料的屈服极限。在闭锁槽受力面尖角和闭锁块受力面直角边出现了较严重的应力集中现象，需要对结构进行改进来减小应力集中程度。
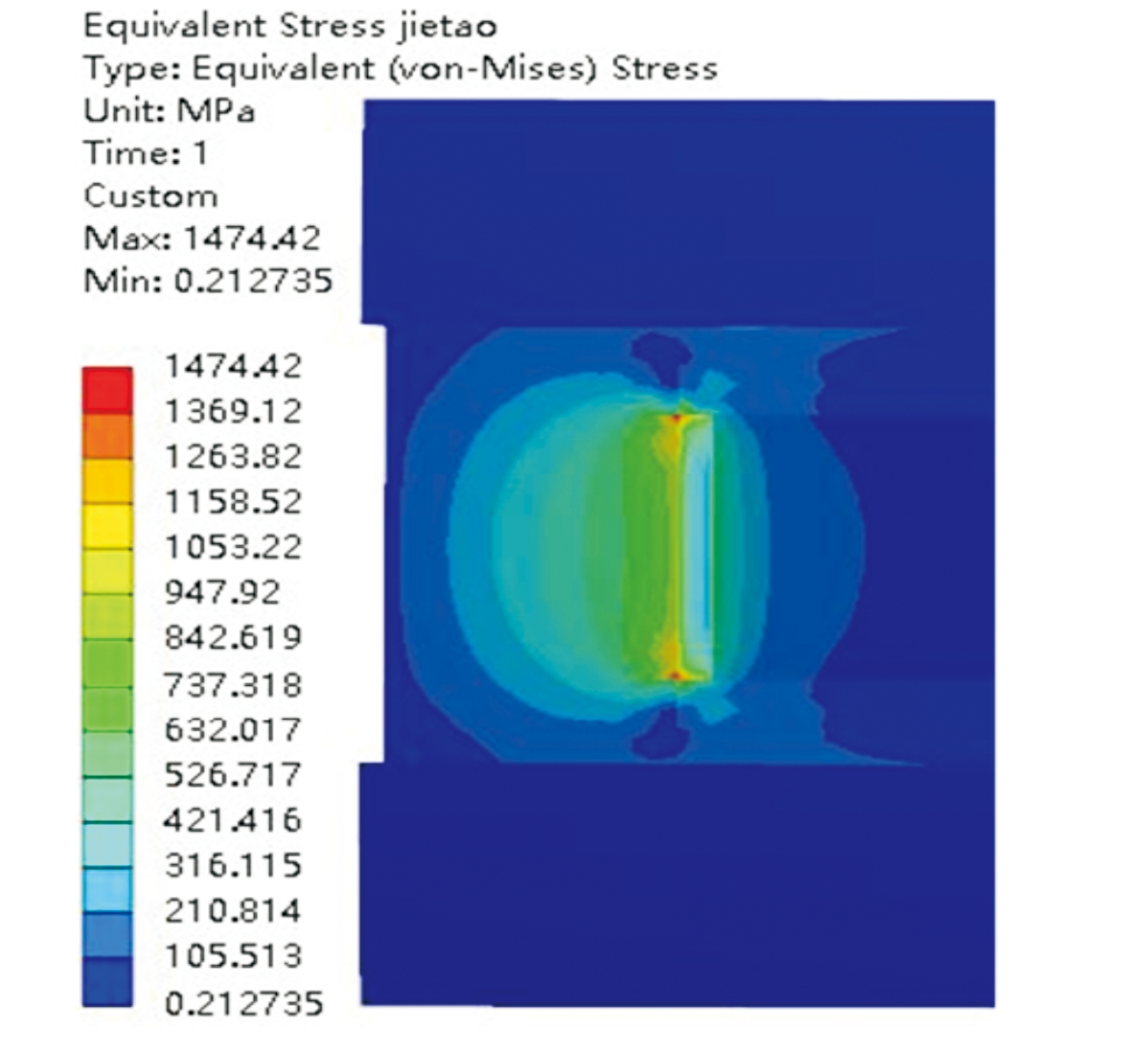
图5 节套应力云图
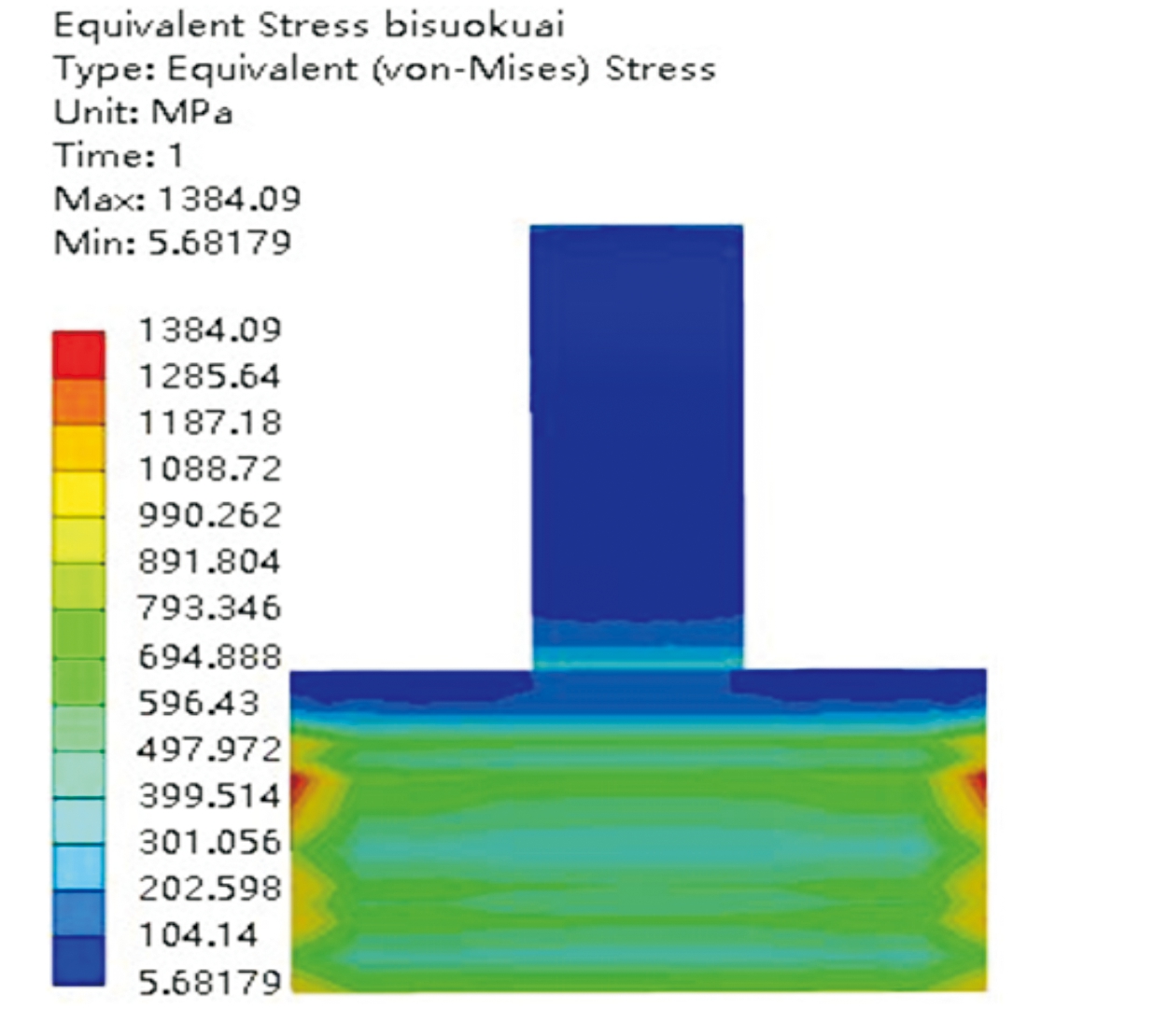
图6 闭锁块应力云图
2.3 结构改进及强度校核
对闭锁槽及闭锁块影响受力状态的部位进行倒圆角来减小应力集中程度。设闭锁槽受力面左右直角边圆角半径为r1，闭锁块受力面左右直角边圆角半径为r2，由机械结构分析知r1≤r2。本文根据相关结构的尺寸形状和制造加工的方式，采用15种倒圆角方案进行研究：
1) r1=r2=1 mm；2) r1=1 mm，r2=1.5 mm；3) r1=1 mm，r2=2 mm；4) r1=1 mm，r2=2.5 mm；5) r1=1 mm，r2=3 mm；6) r1=r2=1.5 mm；7) r1=1.5 mm，r2=2 mm；8) r1=1.5 mm，r2=2.5 mm；9) r1=1.5 mm，r2=3 mm；10) r1=r2=2 mm；11) r1=2 mm，r2=2.5 mm；12) r1=2 mm，r2=3 mm；13) r1=r2=2.5 mm；14) r1=2.5 mm，r2=3 mm；15) r1=r2=3 mm。在不改变其他条件的基础上，对结构进行15种方案的倒圆角，并分别进行静力学计算，计算结果中最大应力如表2所示。
由表2可知：① 当闭锁槽圆角半径不变时，最大应力随着闭锁块圆角半径的增大呈现先减小后增大再减小的趋势，这是由两不同半径圆角之间的间隙变化造成的；② 两圆角半径相同时，两圆角之间的间隙较小，最大应力较大；③ 整体来看，最大应力随着圆角半径的增大和两圆角之间间隙的增大而减小；④ 当闭锁槽圆角半径为2.5 mm且闭锁块圆角半径为3 mm时最大应力最小，应力集中程度最小。
表2 不同圆角情况的最大应力
(r1,r2)/mm(0.0,0.0)(1.0,1.0)(1.0,1.5)(1.0,2.0)(1.0,2.5)(1.0,3.0)(1.5,1.5)(1.5,2.0)Pmax/MPa1474.22 187.71 618.71 440.01 520.61 504.41 739.61 326.8(r1,r2)/mm (1.5,2.5)(1.5,3.0)(2.0,2.0)(2.0,2.5)(2.0,3.0)(2.5,2.5)(2.5,3.0)(3.0,3.0)Pmax/MPa1 478.01 526.61 564.51 225.41 279.01 463.71 214.61 736.1
闭锁槽圆角半径为2.5 mm且闭锁块圆角半径为3 mm时，部件应力云图如图7所示。从图7(a)、图7(b)可以看出，节套的最大应力出现在闭锁槽受力面的一条边上，闭锁块的最大应力出现在闭锁面上，均没有超过材料的屈服极限，且节套和闭锁块的受力状况均有明显改善，应力集中程度大幅减小。从图7(c)可以看出，最大应力小于材料的屈服极限，出现在机体上与闭锁块接触的圆弧面，表明炮膛合力通过圆弧接触面从机体传递到闭锁块。从图7(d)可以看出，最大应力远小于材料屈服极限，靠近机头的侧滚轮和侧滚轮轴受力较大，符合实际情况。
图7 部件应力云图
2个结构方案有限元分析结果对比如表3所示，对闭锁槽和闭锁块倒圆角后，节套闭锁槽最大应力减小17.62%，闭锁块最大应力减小16.61%。因此，对于严重影响受力状况的部位，根据结构的尺寸和形状进行合理的改进(倒圆角、倒斜角等)可以有效改善受力状况和应力集中程度。
表3 2个结构方案有限元分析结果对比
r1=0 mmr2=0 mmr1=2.5 mmr2=3.0mm改进前后对比/%节套最大应力/MPa1 474.42 1214.60减小17.62闭锁块最大应力/MPa1 384.091 154.22减小16.61
3 疲劳寿命分析
在某点或者某些点承受扰动应力，并且在多次循环扰动充分作用以后产生裂纹或者完全断裂的材料中所发生的局部的、永久结构变化的发展过程，称为疲劳[6]。材料在疲劳破坏前所经历的应力循环数称为疲劳寿命[7]。在结构满足强度指标要求的同时，有必要对节套和机心的疲劳寿命进行分析和预估。
在本文所使用的有限元分析软件中，疲劳模块拓展程序基于应力疲劳理论，适用于高周疲劳，进行疲劳分析是基于线性静力分析，在线性静力分析之后通过设计仿真后自动执行[8]，该模块采用Miner累积疲劳准则，为解决疲劳寿命问题提供了有效途径[9]。由于机心工作状态为高周疲劳状态，故用名义应力法(S-N法)进行疲劳寿命分析。
3.1 材料的S-N曲线
概率Miner准则认为小于疲劳极限的应力引起的损伤为零，但实际中低于疲劳极限的应力也会引起损伤，本文采用MM法则修正低于疲劳极限应力造成的损伤[10]。
由文献[11]可得：
lgNp=ap+bplgσ
式中：ap和bp为可靠度p下的材料疲劳参数；Np表示疲劳应力σ作用下可靠度为p时的疲劳寿命。本文分析45CrNiMoVA在95%存活率下的疲劳寿命，此时a95=25.925，b95=-7.450。
图8为45CrNiMoVA在双对数坐标下的lgσ-lgNp曲线。其中线段“1”的斜率为k1，表示在该可靠度下的有限寿命部分，线段“2”的斜率为k2，是应用MM法则在无限寿命范围内对S-N曲线的修正结果，线段“1”和线段“2”交点处对应的疲劳寿命为N95=106[3]。
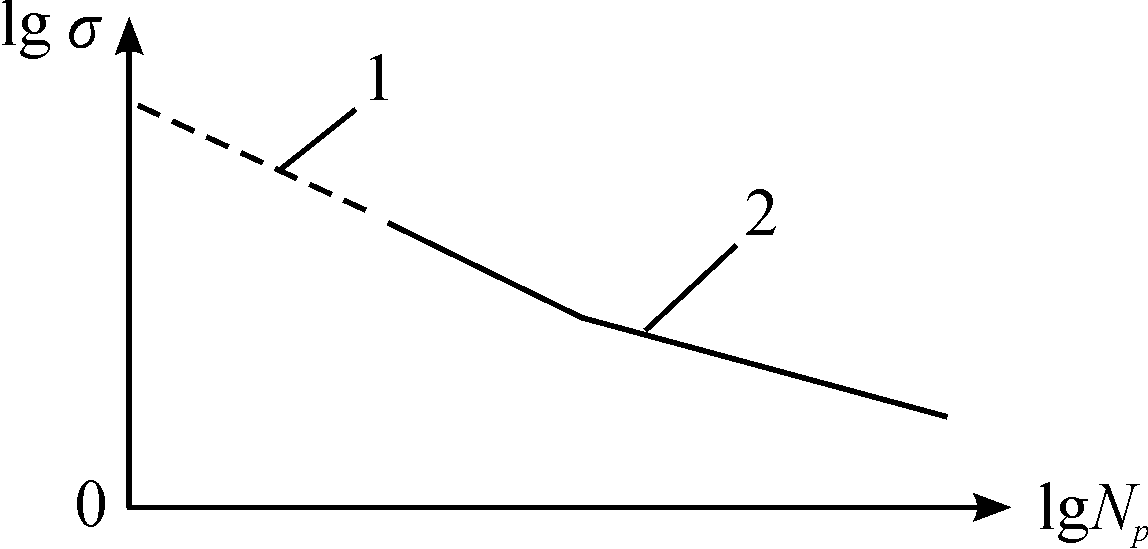
图8 材料的lgσ-lgNp曲线(应用MM法则)
lgN95=a95+b95lgσ
lgN95=0即N95=1时，
即线段“1”的起点坐标为(0，3.479 9)，可得σ=3 019.256 4 MPa，则应力幅为2σ=6 038.512 9 MPa，直角坐标为(1，6 038.512 9)，
由Miner准则得
由Miner修正的MM法则得
即N95=106时，
即线段“2”的起点坐标为(6，2.674 5)，可得σ=472.606 8 MPa，则应力幅为2σ=945.213 7 MPa，直角坐标为(106，945.213 7)，lgN95=10即N95=1010时，再由k2=-0.071 9和坐标(6，2.271 8)得线段“2”的终点坐标为(10，2.386 9)，可得σ=243.725 0 MPa，则应力幅为2σ=487.449 9 MPa，直角坐标为(1010，487.449 9)。
由计算结果得到S-N疲劳寿命曲线，如图9所示。
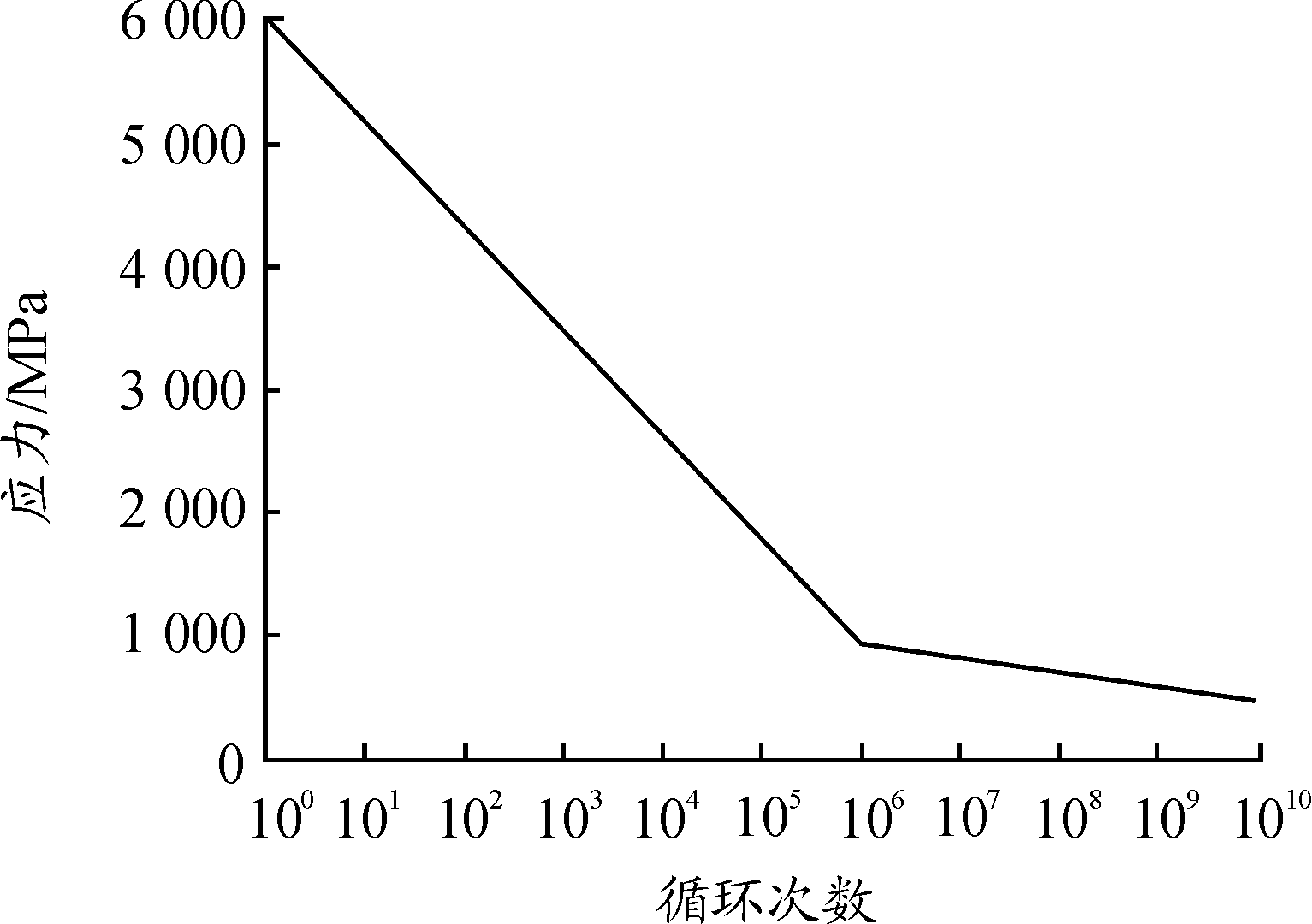
图9 95%存活率下的S-N曲线
3.2 疲劳寿命预测
火炮射击时炮闩受到近似脉动交变的载荷作用，其交变载荷的循环特性r=0[2]。脉动循环载荷，是指当施加载荷后又撤除该载荷，发生的脉动循环载荷现象[8]。
平均应力对构件的疲劳寿命影响很大，常用的平均应力修正理论有Goodman、Soderberg和Gerber[12]。对45CrNiMoVA材料，采用较为适合的Gerber修正理论[10]。应力集中对疲劳强度有显著影响[13]，疲劳强度因子用来修正实际构件的疲劳强度和理论之间的误差，本文取0.8。
利用疲劳寿命模块进行计算，结果如图10所示。由图10(a)可以看出，节套最小寿命为1.562 7×106次，危险部位出现在闭锁槽受力面的一条边上。由图10(b)可以看出，闭锁块最小寿命为4.180 6×106次，危险部位出现在闭锁块受力面上。在最大炮膛合力的脉冲作用下，节套和机心最小寿命均达到了106次量级，节套和机心寿命较小的部位也是静力学分析中应力集中程度较大的部位。由图10(c)可以看出，其他部件最小寿命超过了7×107次。由此可见，疲劳寿命对应力的大小是敏感的。
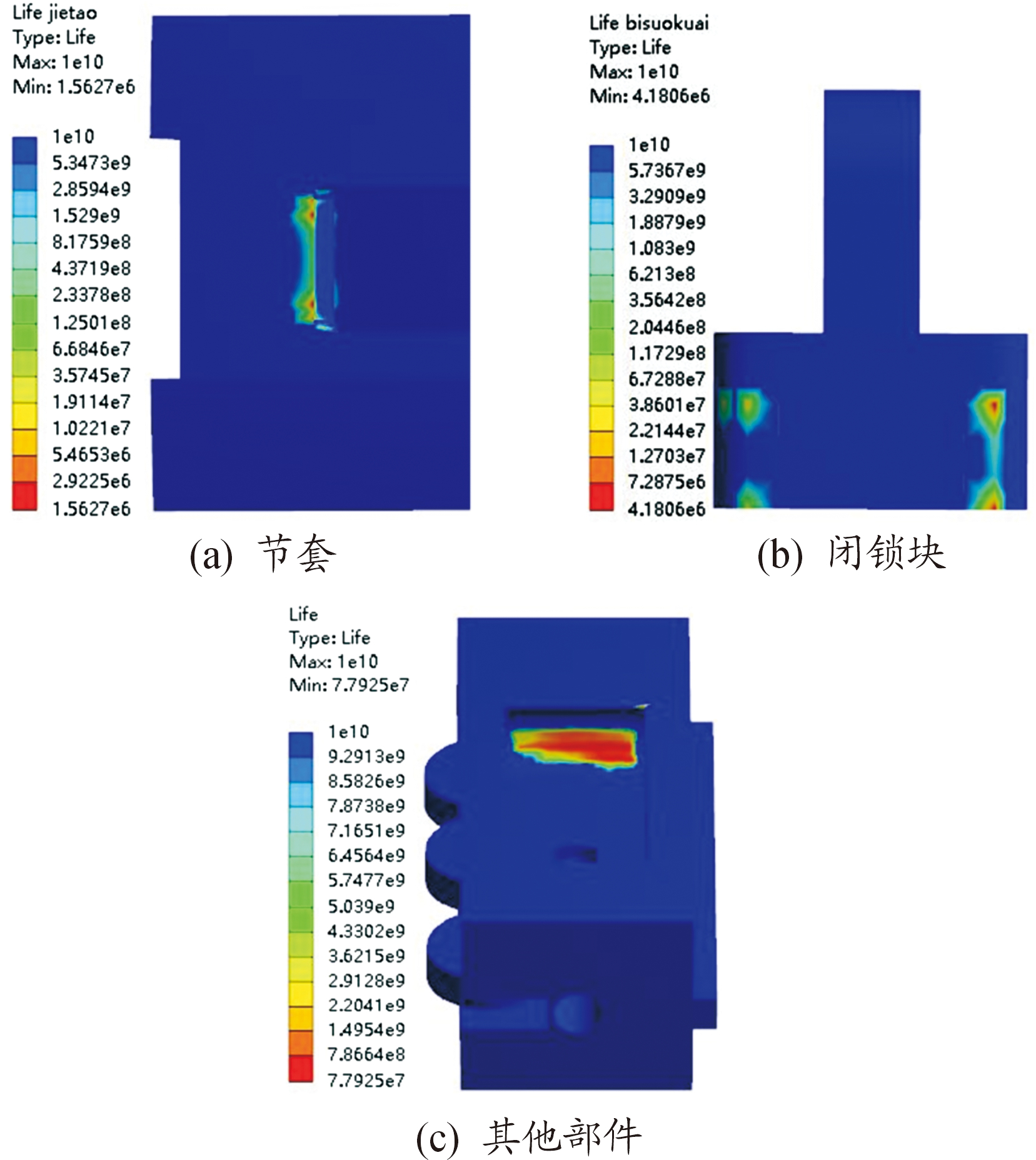
图10 95%存活率下部件寿命云图
4 结论
1) 对于应力集中部位，根据结构的尺寸和形状进行合理的改进可以有效改善受力状况和应力集中程度。
2) 部件最大应力随着闭锁槽、闭锁块圆角半径的增大和两圆角之间间隙的增大而减小。当闭锁槽圆角半径为 2.5 mm 且闭锁块圆角半径为3 mm时，部件应力集中程度最小且最大应力没有超过材料的屈服极限，相比无倒圆角的结构，节套闭锁槽最大应力减小17.62%，闭锁块最大应力减小16.61%。
3) 在最大炮膛合力的脉冲作用下，节套和机心最小寿命均超过了106次量级，节套和机心寿命较小的部位也是静力学分析中应力集中程度较大的部位，部件最小疲劳寿命大于实际使用寿命，满足寿命指标。
[1] 郝秀平，薄玉成，徐建.某转管武器机芯应力有限元分析[J].中北大学学报(自然科学版)，2010，31(02):113-116.
[2] 李魁武，宁变芳，曾志银，等.基于裂纹形成及扩展的火炮闩体寿命研究[J].兵工学报，2013，34(3):289-293.
[3] 胡慧斌，候晓锋，曹立军，等.冲击载荷作用下抽筒子疲劳寿命预测与试验验证[J]火炮发射与控制学报，2014，35(3)：68-73.
[4] 李涌，吴宝双.协同仿真技术某转管武器炮闩小闭锁齿疲劳寿命预测[J].火力与指挥控制，2015，40(12):141-144.
[5] YANG X，JIA Z，ZHANG Y.Dynamic stress Analysis of Automatic Weapons Breech Mechanism[C]//International Conference on Mechatronic Science，Electric Engineering and Computer.IEEE，2011:1267-1269.
[6] 方海涛,周云波,王显会,等.某型抗冲击波车身结构响应分析及疲劳强度校核[J].兵器装备工程学报,2018,39(09):144-150.
[7] 武彦杰，覃寿同，赵冰清，等.盾构机T形焊接结构的纯弯曲疲劳寿命研究[J].机械设计与制造，2012(08):124-125.
[8] 赵森森,方峻.某自动步枪闭锁机构强度寿命分析[J].兵工自动化,2019,38(01):6-10.
[9] 李云飞，史筱红.基于Workbench的含半穿孔油气管道疲劳寿命数值模拟[J].管道技术与设备，2017(05):1-3,47.
[10] 吴宝双.转管自动机炮闩运动仿真与疲劳寿命分析[D].太原:中北大学，2015.
[11] 《机械工程材料性能数据手册》编委会.机械工程材料性能数据手册[M].北京：机械工业出版社，1994:285-288.
[12] 刘明涛，孔祥浩，李彦启.基于Workbench的双啮合分度机构的疲劳分析[J].天津科技大学学报，2017，32(03):62-67.
[13] 姚卫星.结构疲劳分析[M].北京：国防工业出版社，2003.