任务分解是把上级意图转化为部队行动的关键操作,是实现部队协同作战,达成总目标的桥梁,也是辅助指挥员经济、合理使用作战资源(兵力和兵器)的重要手段[1]。作战任务分解作为任务规划中一项重要步骤,其合理性直接影响作战力量的分配,进而影响作战部队的行动和对资源的使用调度。
层次任务网络(Hierarchical Task Network,HTN)规划作为20世纪70年代末发展起来的一种基于知识的规划技术[2],可以利用任务树和对任务的形式化描述表述任务之间的相关关系[3],从而适用于大型复杂任务的分层分解。王涛[2]、肖海[3]等将HTN规划引入军事领域,并对规划粒度问题进行了扩展研究,但由于该研究中只专注了某一待分解的复合任务调用一种可行方法生成其子任务,而没有考虑可能存在多种分解、执行方案。宋泾舸等[4]实现了快速生成多个计划,但是缺少对分解结果间相互关系的统计,无法实现横向比较分析优化分解结果。
结合以上文献可知,尽管目前HTN规划方法与传统数学建模方法相比较,在任务规划方面具有很好的适用性,但也存在HTN规划分解时选择方法单一的问题,同时,如果增加多种方法的分解步骤,会大幅度增大任务分解、任务优化的规模。本文对HTN规划方法进行了扩展,将任务建模语言TAEMS与HTN规划结合,详细介绍了任务规划模型,进而提出多方法分解的HTN规划方法,并用TAEMS建模语言分析并剪枝,最后以边境反击作战为例进行验证,来说明方法的科学性和有效性。
1 引入TAEMS框架的HTN规划方法
HTN规划方法是应用最宽泛的智能规划方法之一。其基本思想是不断地将高层复合任务分解为简单的子任务。当所有的任务都是可以直接执行的原子任务时,分解过程停止,行动方案生成[9]。HTN规划中任务规划P定义为一个三元组P={I,W,D}。其中I表示战场态势的初始状态;W表示任务网络;D表示规划域知识。下面将从这几个方面对作战任务分解问题进行描述:
1.1 任务网络
HTN规划将任务分为两类:原子任务和复合任务,原子任务为不可分解的任务,即底层基本可执行任务;复合任务为一组子任务的父任务。任务分解树中根节点和内部节点表示复合任务;分解树中叶节点为原子任务。任务网络W是任务的集合和对这些任务的约束,令W={T,R},T为任务集合;R为任务相互关系集合。
1.1.1 任务集合T
令任务集合T中子任务为Tij:
T={Tij|i=1,2,…,x, j=1,2,…,y}
(1)
式中:i表示任务层级,层级中包含的任务数量记为N,依据约束条件对任务层级中N个任务进行排序; j表示排序后的任务序号,即Tij为第i层的第j个任务,任务结构示意图如图1所示。单个子任务定义为一个四元组:
Tij={name,ID,plist,dtime}。其中name表示任务名称;ID表示任务编号;plist为任务的属性特征参数列表,plist={function,significance,probability},function表示任务性能指标,significance表示任务重要性,probability表示任务成功完成的概率。本文仅列举参数列表其中几项,除此之外还可能包含任务难度、任务是否可以独立、任务执行和终止输入输出参数等;dtime为子任务的时间集,包括开始时间S(t),结束时间F(t)和任务截止时间DL(t)。
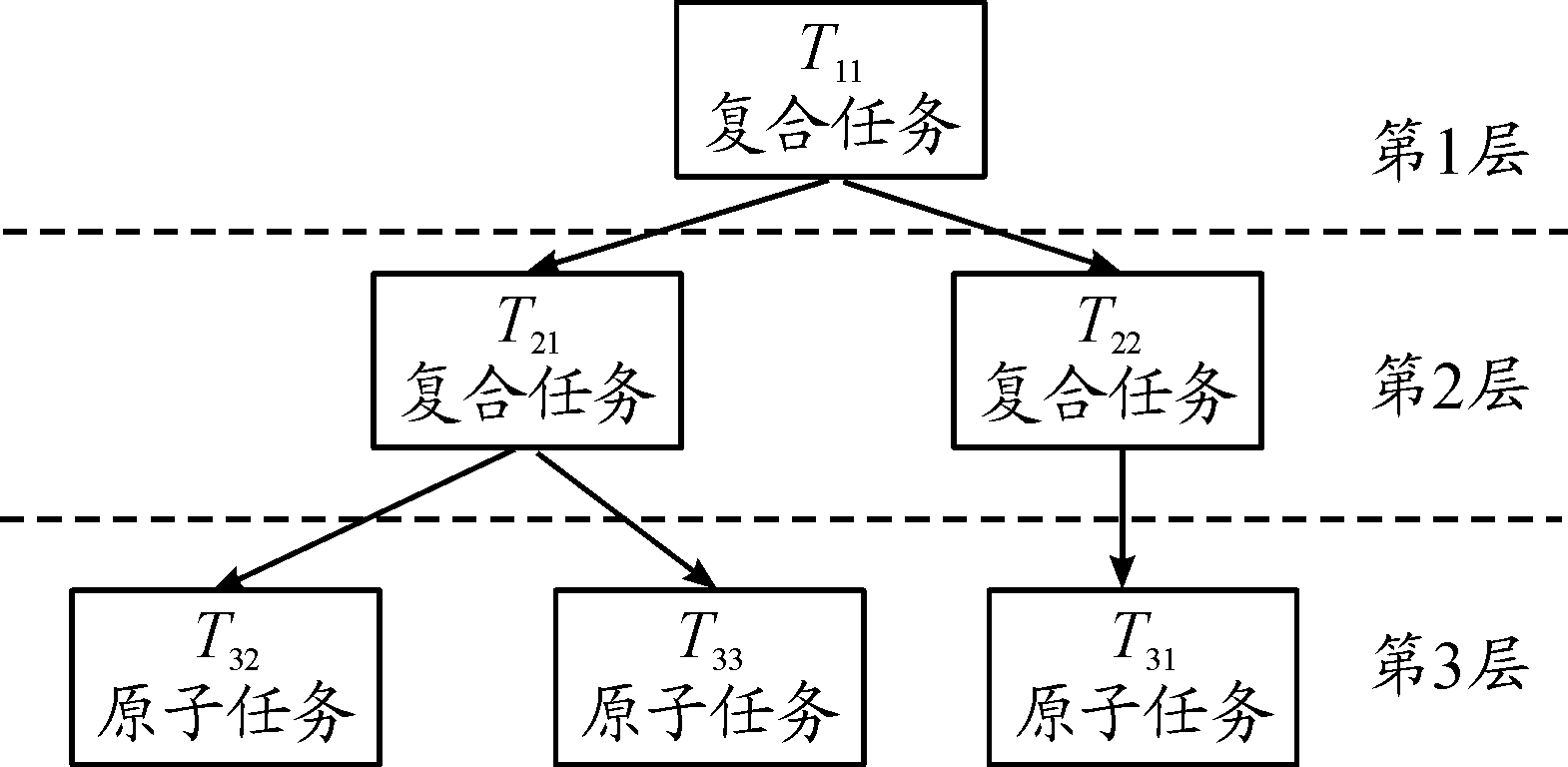
图1 任务结构示意图
1.1.2 任务关系集合R
R为任务分解问题中复杂相互关系集合,令R={Rset, φ}。其中Rset为逻辑关系集合,φ为约束关系集合。
1) 逻辑关系集合Rset
任务建模语言TAEMS在传统HTN模型基础上,应用非局部影响定义了任务间的依赖关系,同时与联合作战任务关系结合,综合得出任务逻辑关系集合。令Tia→Tib表示源任务Tia与目标任务Tib之间的关系。取任务Tia的关系集为Rsetia∈Rset:
Rsetia=f(Ractia)
(2)
Ractia![]() {from Tia to Tib Rintib Active|b=1,2,…a,…,z}
{from Tia to Tib Rintib Active|b=1,2,…a,…,z}
(3)
Rsetia储存Tia任务与Tib任务之间的逻辑关系;Active表示任务间逻辑关系有效。(3)式表示从Tia→Tib存在逻辑关系Rintib有效,Ractia储存了任务Tia所有逻辑关系。任务间的逻辑关系如下所述:
① 并发促进关系(Facilitate(Tia,Tib)):Tia任务的执行结果对Tib任务存在有利促进影响。
② 并发阻碍关系(Hinder(Tia,Tib)):Tia任务的执行结果对Tib任务存在不利阻碍影响。
③ 顺序与关系(EnableAnd(Tia,Tib)):只有在Tia被执行后,Tib才允许被执行,且Tia任务和Tib任务都需成功执行,其父任务才可成功执行。
④ 顺序选择关系(EnableSelect(Tia,Tib)):只有在Tia被执行后,Tib才允许被执行,且Tia任务和Tib任务仅需成功执行一个,其父任务即可成功执行。
⑤ 异或关系(Disable(Tia,Tib)):只有在Tia不被执行后,Tib才允许被执行,且Tib任务执行的成功与否决定了父任务的成败。
⑥ 相同关系(Equal(Tia,Tib)):任务Tia,Tib相同,为重复任务,只需成功执行一项任务即可。
⑦ 矛盾关系(Conflict(Tia)):任务Tib自我矛盾,不符合任务背景不可被执行。
并发促进关系和并发阻碍关系为“软”关系,源任务只会对目标任务产生影响,不会决定目标任务的执行;顺序与关系、顺序选择关系和异或关系为“硬”关系,直接决定目标任务是否可以被执行。
2) 约束关系集合φ
约束关系集合φ是对分解方法的选择以及分解过程的约束。令φ={φt,φc},φt为时间约束,φt={cdeadline,cRset},cdeadline为任务的时长约束,即每个任务必须在截止时间之前完成;cRset为任务间时序关系约束,即对任务之间的执行顺序进行约束,cRset与逻辑关系集合Rset关联,cRset是建立Rset的判断条件,Rset是cRset中约束的扩充与改进。φc为成本约束,φc={φnum, φinterrelation}, φnum为资源、人员数量约束,即执行任务时需要拥有大于等于执行条件的武器资源和战斗兵力;φinterrelation为资源、人员之间的相互干涉约束,即约束在不同空间、同一时间调用同一种资源或人员的情况。
1.2 规划域知识D
取任务Tij,令D={M,OP}。M为任务分解方法集,有m(k)∈Mactij∈M。Mactij为任务Tij的子分解方法集。m(k)为子方法集Mactij中一个分解方法,k为方法序号。m(k)={name′,Wm(k)},name′为复合任务的任务名称,Wm(k)为方法m(k)对应的任务网络。
OP为一组操作集合,OP={instantiation,rank,screen},instantiation表示作战任务实例化操作,rank表示对i层任务排序操作,screen表示从方法集M中筛选出任务Tij子方法集Mactij的操作。HTN规划中,选择方法集M中的方法作用于初始任务网络W,需要在不违背约束条件φ的情况下,完成分解任务网络W中的所有任务,分解完毕后得到完整任务分解网络存储在初始任务网络W0中。
2 扩展HTN规划
2.1 多方法分解扩展HTN
传统HTN分解流程中只调用一种适用于计算机识别、匹配作战任务的分解方法进行分解,然而方法集M中可能存在待分解任务的多个分解方法,因此需要对分解方法进行扩展。
设定分类标准g,若g=1,任务Tij为复合任务;若g=0,任务Tij为原子任务。依据时间约束φt对第一层待分解任务排序,并分配任务序号j,依据任务序号j顺序选择任务执行分解流程。
依据任务序号取任务Tij判断类型为复合任务后,将任务Tij的参数列表plist={function}作用于任务分解方法集M,得到任务Tij的子方法集Mactij。令子方法集Mactij中子方法 m(k) 个数为Q,依次调用子方法集Mactij中Q个方法分解任务Tij。并通过判断是否可以将任务Tij替换为对应方法 m(k) 的任务网络来完成,判定所选方法m(k)是否为有效方法。若替换成功,保留有效方法m(k),同时将Tij及分解后的子任务集存放于任务网络W0中;若替换失败则分解失败,从子方法集Mactij中移除无效方法m(k)。其中多方法分解示意图如图2所示。
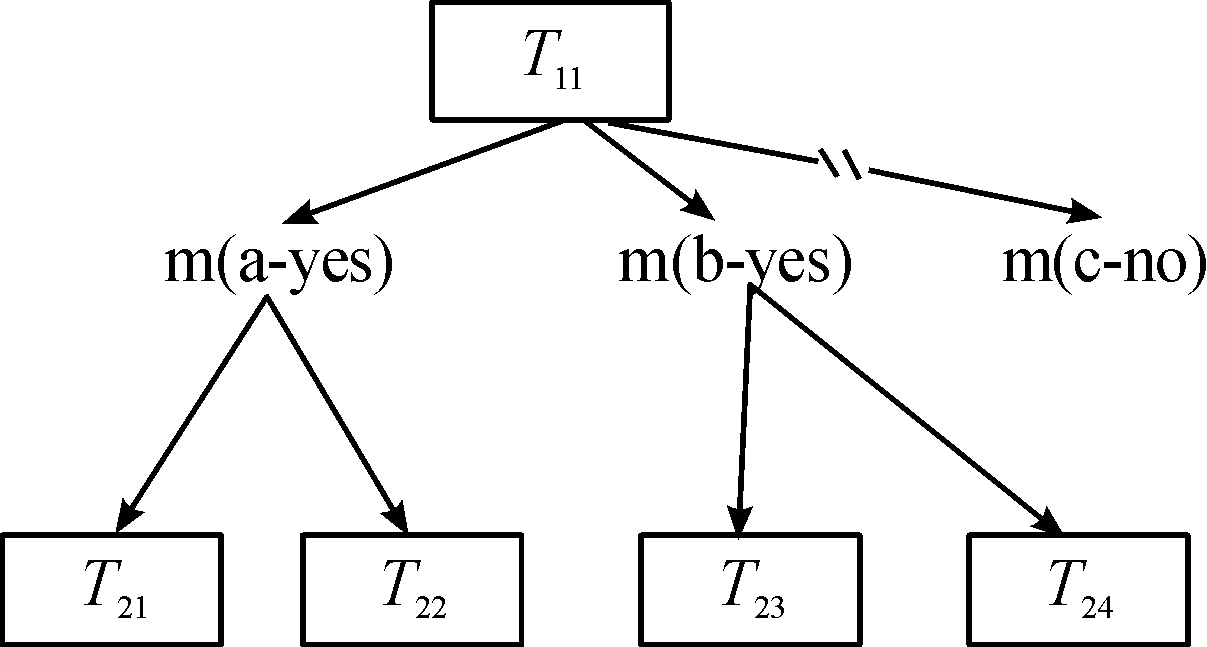
图2 多方法分解示意图(a,b,c∈k)
2.2 TAEMS分析
TAEMS分析应用于每层任务分解完毕后,将多方法分解后得到的多个子任务进行剪枝筛选,择优保留;并为子任务重新分配任务序号j。通过TAEMS分析进行筛选时经过两次判断。
首先每个子任务Tnm需遵守以下三方面特征:
① 质量:目标希望最大化,目标希望包含执行任务的精准性、可行度和完整性等,设质量函数为Q(Tnm,tnm)。
② 成本:目标试图最小化,即执行任务Tnm所需要的成本。
③ 持续时间:执行时间合理化。
Q(Tnm,tnm)∶[Tnm*tnm]→[quality_mn]
(4)
由式(4)可返回tnm时刻与任务Tnm相关的质量quality_mn。TAEMS任务网络中的节点由于S(t)、F(t)和LS(t)而受到约束,时间约束呈递归趋势,在分解树中自上而下应用。子任务继承其本身以及父任务时的约束最严格,任务违背时间约束将产生零质量,即任务无法被执行。
其次调用关系集Rset,判断任务间关系是否为异或关系Disable(Tia,Tib),若为Disable关系,将矛盾结果筛除;若不为Disable关系,判断子任务间关系是否为并发阻碍关系Hinder(Tia,Tib);若为Hinder关系,调用2个任务的参数列表plist,确定筛除或保留的任务;若不为Hinder关系,则对剩余已分配任务关系的任务进行遍历,判断是否存在重复结果、矛盾结果等情况,择优保留。此处举例了两种情况,以后研究中可以进行扩展。TAEMS分析图如图3所示
2.3 扩展HTN作战任务分解方法流程图
上述分析给出了多方法分解并用TAEMS分析剪枝的方法与步骤,扩展了HTN规划方法,优化了分解结果。上述扩展HTN作战任务分解方法流程如图4所示。图4中:i为任务层级; j为任务序号;k为方法序号;N为第i层任务数量;g为分类标准;Mactij为待分解任务的方法集;Q∶Mactij为中子方法个数;OP为操作;Rset为关系函数。
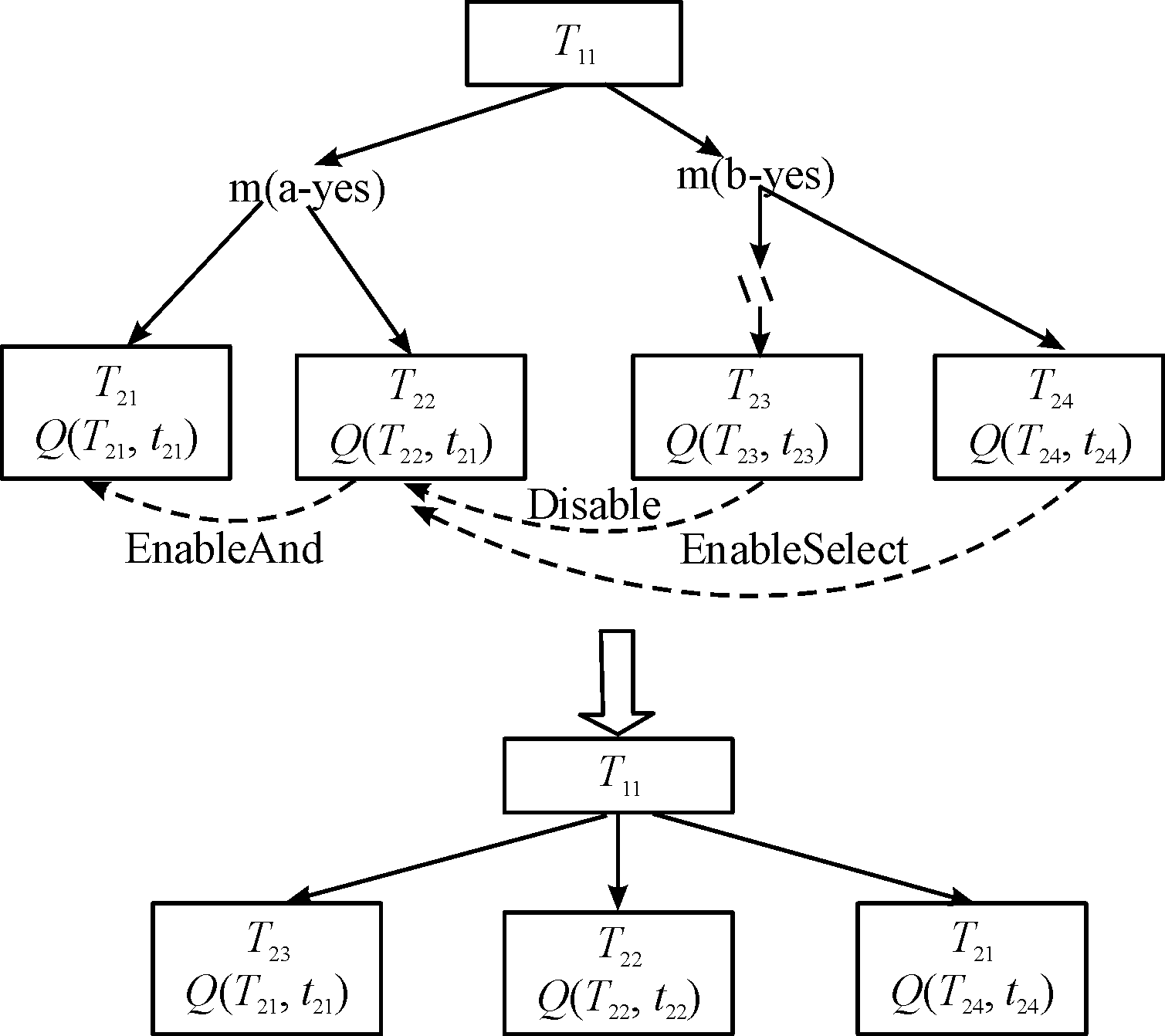
图3 TAEMS分析框图
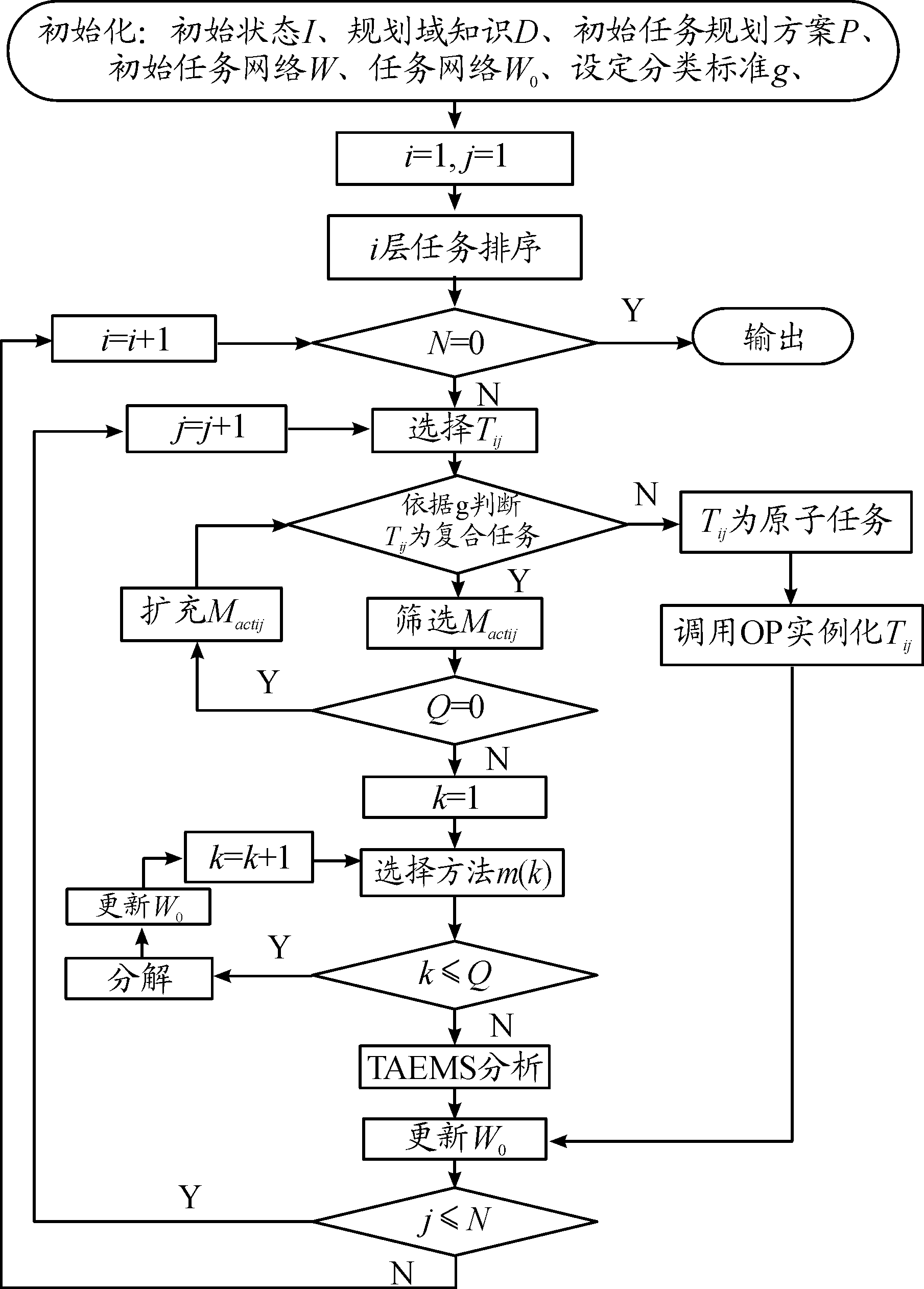
图4 作战任务分解流程框图
3 应用实例
面对边境地区局部快速入侵之敌,我们需要快速实施边境反击作战。已知敌目标已进入我方区域并设有临时阵地,同时临近我方地区附近设有敌方机场,为敌提供空中火力支援。我方指挥所接收命令后,设定2个目标占领敌方阵地,夺回我方区域;摧毁敌方机场。
图5为作战任务分解框图,分解框图中将2个任务间斜杠所在枝干右侧一枝任务剪去。图5中虚线表示2个任务之间的联系,箭头由源任务指向目标任务;虚线上的文字表示任务之间的关系类型。图6通过图5中任务关系类型,判断任务之间的先后顺序进行整体布局,从而可以明晰整个作战任务的执行规划。
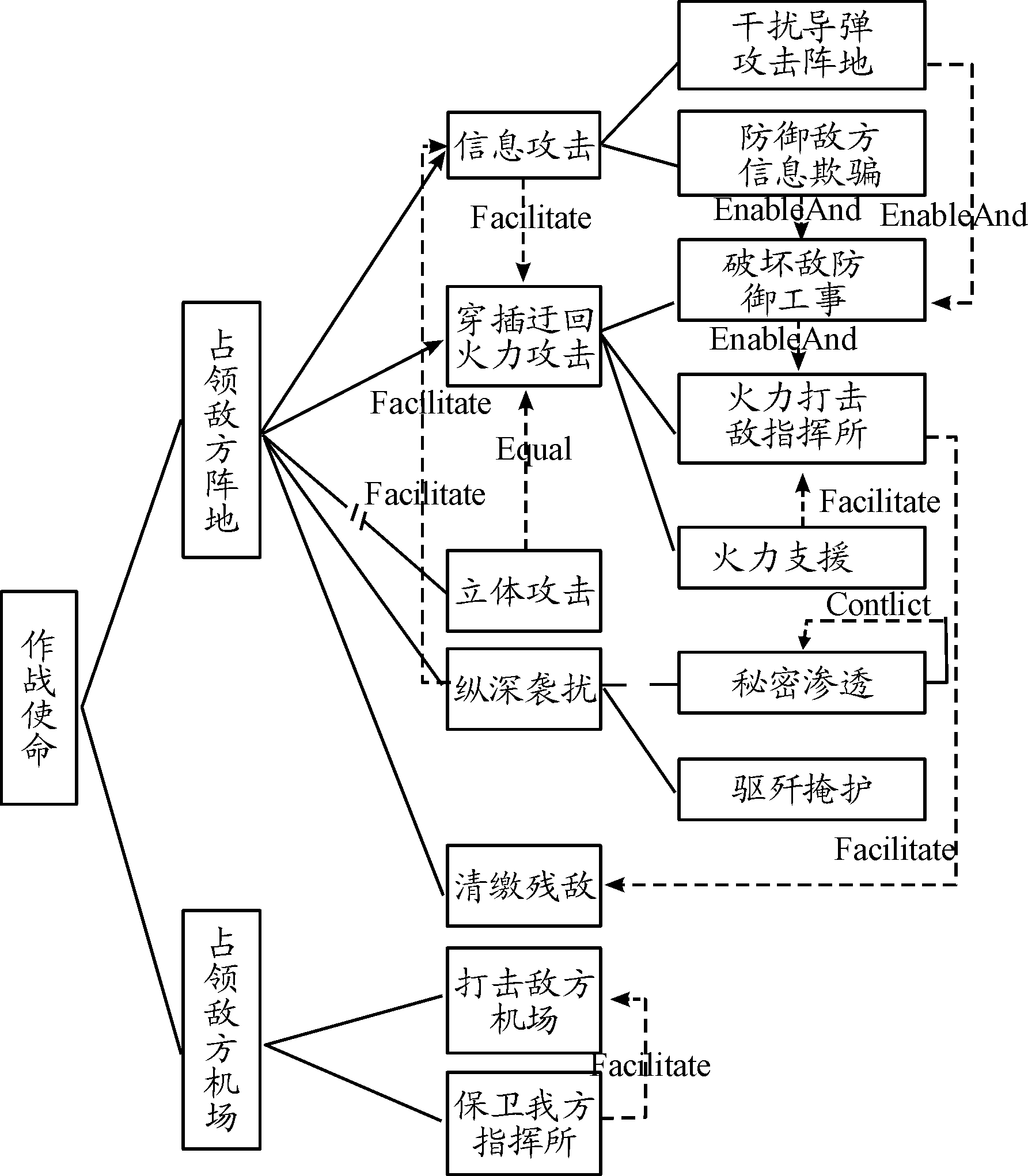
图5 边境快速反击作战任务分解框图
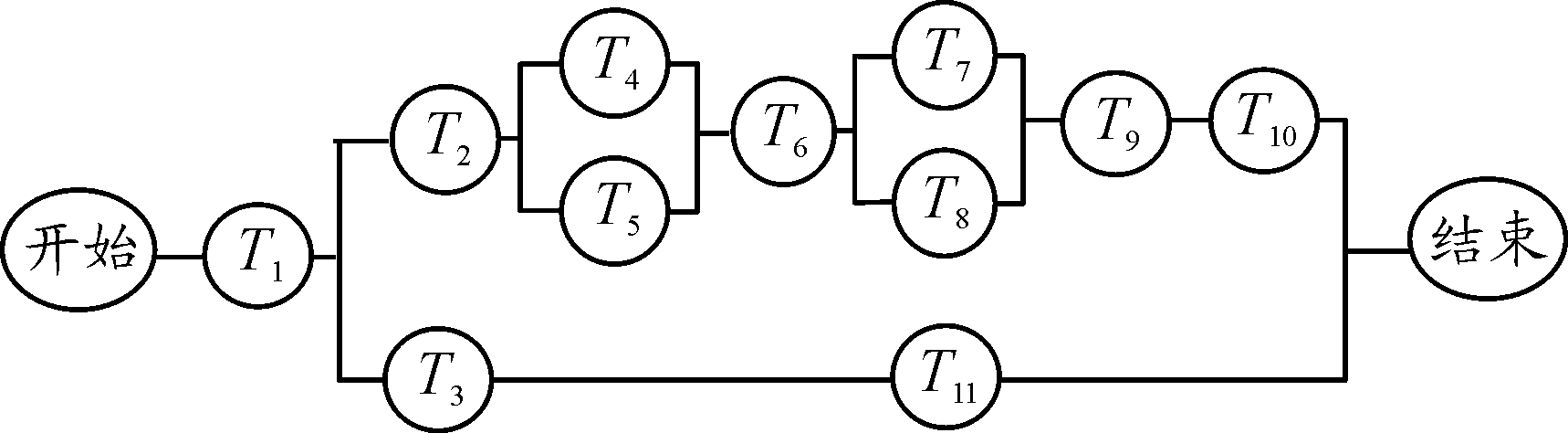
图6 边境快速反击作战任务网络框图
在此任务网络图中,对应的各个子任务分别为:T1保卫我方指挥所;T2驱歼掩护;T3打击敌方机场;T4干扰导弹攻击阵地;T5防御敌方信息欺骗;T6破坏敌防御工事;T7火力打击敌指挥所;T8火力支援;T9清缴残敌;T10占领敌方阵地;T11摧毁敌方机场。
4 结论
本文扩展了HTN规划中单一分解方法,引入TAEMS分析,明确任务执行的先后顺序并优化任务分解结果。最后以边境快速反击作战的任务分解图和任务网络图为例,验证了本文方法的科学性和有效性。本文方法可以运用于任务规划中任务分解步骤,为下一步作战部署提供先决条件。后期可在此基础上,对TAEMS分析中任务关系集进行扩充,完善任务筛选条件。
[1] 曹裕华,冯书兴,徐雪峰.作战任务分解的概念表示方法研究[J].计算机仿真,2007,24(8):1-4.
[2] 王涛,施展,赵玉林.基于HTN的变粒度作战计划快速生成框架[J].指挥控制与仿真,2015,37(1):19-23.
[3] 肖海,刘新学,舒健生,等.基于扩展HTN规划的作战任务分析方法[J].火力与指挥控制,2016,41(9):108-117.
[4] 宋泾舸,查建中,陆一平.HTN规划中面向多计划生成的顺序任务分解算法[J].北京交通大学学报,2009,33(4):46-49.
[5] 薛波,徐培德.基于HTN的卫星应用任务分解[J].科学技术与工程,2009,9(1):146-151.
[6] 罗文达.航母甲板任务规划方法研究[D].武汉:华中科技大学,2015.
[7] 廖沫,陈宗基.基于DTC的UCAV任务规划方法研究[J].系统仿真学报,2009,21(6):1565-1569.
[8] 萧毅鸿,周献中,张铁.扩展层级任务网络规划的变粒度作战任务分解策略[J].火力与指挥控制,2011,36(7):119-122.
[9] 王红卫,祁超.基于层次任务网络规划的应急响应决策理论与方法[M].北京:科学出版社,2014.
[10] 赵振宇,卢广山,廖沫,等.基于DTC和GPGP的多UCAV任务规划方法[J].北京航空航天大学学报,2011,37(3):305-310.
[11] 徐文星,梁菁菁,边卫斌,等.基于决策树剪枝法的危险品运输实时路径规划[J].化工学报,2018,69(S2):324-329.
[12] DECKER K S.TAEMS:A Framework for Environment Centered Analysis & Design of Coordination Mechanisms[C]//Foundations of Distributed Artificial Intelligence,Chapter.1996.
[13] WU J,DURFEE E H.Solving large TAEMS problems efficiently by selective exploration and decomposition[C]//International Joint Conference on Autonomous Agents & Multiagent Systems.DBLP,2007.
[14] ALFORD R,BERCHER P,AHA D W.Tight bounds for HTN planning with task insertion[C]//International Conference on Artificial Intelligence.AAAI Press,2015:291-298.
[15] VINCENT R,HORLING B,LESSER V.Experiences in simulating multi-agent systems using TAEMS[C]//International Conference on Multiagent Systems.IEEE,2002.