随着基于无线通信的CBTC(Communication Based Train Control System)系统在城市轨道交通列车上的应用，促进了列车控制技术的发展，在很大程度上缩短了列车的追踪间隔。但是，列车在实际运行过程中容易受到随机干扰因素的影响，使得列车偏离计划运行图。由于列车运行间隔短，若前行列车晚点时间过长时，可能导致列车运行的大面积紊乱，导致列车群连带晚点。因此，列车运行自动控制系统需要采取一定的调整措施，对偏离计划运行图的列车进行实时、高效地调整，使列车尽快恢复按图定计划运行，达到保障城市轨道交通运营效率和服务水平的目的。
目前，针对城市轨道交通列车运行调整已经取得了丰富的研究成果，国内外学者大多从构建模型的角度出发，将列车调整问题抽象为具体的数学模型[1-4]，并采用粒子群算法[5-7]、遗传算法[8-11]、萤火虫算法[12]等智能优化算法对模型进行求解。本研究从综合考虑乘客出行体验和企业运营服务考核指标的角度出发，以列车的总晚点时间和乘客延误等待总时间最少为优化目标，建立城市轨道交通列车运行均衡调整模型，并提出一种改进人工鱼群算法对模型进行求解。
1 列车运行均衡调整模型构建
城市轨道交通列车L={l1,l2,…,lM}通常按照列车计划运行图的到发时分在各车站S={s1,s2,…,sN}进行有序地运行和停靠。在实际运行过程中，受到各种随机干扰因素的影响，列车li在站点sj的实际到达时分
或者实际发车时分
不等于列车运行图的到达时分
或者发车时分
此时列车运行图偏离列车计划运行图，需要对列车计划运行图重新铺画。
在构建城市轨道交通列车运行均衡调整模型时，本研究给出以下假设：
1) 列车晚点时间在ATR(Automatic Train Regulation，ATR)阈值内，无需人工介入调整；
2) 列车晚点不包括改变列车运行次序、增加/取消列车车次以及发生设备故障的情况；
3) 延误只对发生初始延误的后续列车有影响。
1.1 约束条件
城市轨道交通列车调整的约束条件是复杂且相对固定的，主要包括停站时间约束、区间运行时间约束、追踪间隔时间约束和到发车时间约束等四项约束[13-14]。
1) 停站时间约束
停站约束时间可以表示成：
(1)
其中，Ts min和Ts max分别表示列车li在车站sj的最小停站时间和最大停站时间。
2) 区间运行时间约束
为了保障乘客出行的安全性和舒适性，列车的运行时间约束不仅对最小区间运行时间进行约束，也对最大区间运行时间也进行了约束，具体表示如下：
(2)
其中，Tr min和Tr max分别表示列车的最小区间运行时间和最大区间运行时间。
3) 追踪间隔时间约束
为了保障安全性，防止相邻列车发生追尾事件，规定列车追踪间隔时间约束如下：
(3)
其中: Tg min表示列车间的最小追踪间隔； Tfd min表示相邻列车到发最小间隔。
4) 到发车时间约束
为防止发生延误的列车对前面的列车产生影响，尽快实现“按图行车”，提高调整效率，对列车到发车时间进行约束，保证不会出现早于计划时间到发车的情况：
(4)
1.2 优化目标
列车的总晚点时间可以表示为各列车到达各车站的晚点时分和各列车从各车站出发的晚点时间之和受晚点影响的列车数Nl和到发时间线数Ns的改进公式：
(5)
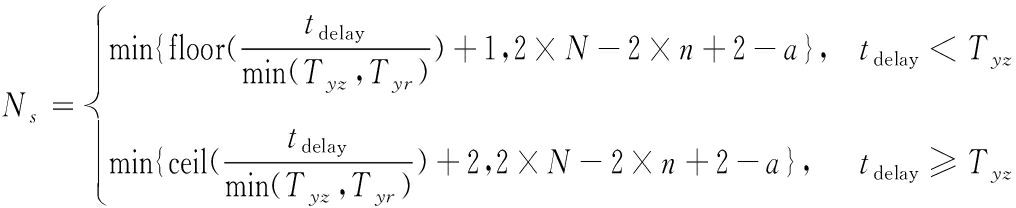
(6)
其中：tdelay为列车晚点时间； Tyz为列车追踪间隔冗余时间； Tyr为区间运行冗余时间；N和M分别车站总数和列车总数；n和m表示发生延误的车站和列车；a为延误类型标志，a=0表示列车到达延误，a=1表示列车发车延误；ceil(x)和floor(x) 函数分别表示x趋近于正无穷的整数和趋近于负无穷大的整数。列车总晚点时间最小函数可以表示成：
(7)
由于存在列车到发车约束条件，所以上述公式可以简化为：
(8)
晚点时域内乘客等待总时间最小函数表示如下：
(9)
其中：δn+j表示乘客在站点sn+j的进站速率；
表示列车lm+i-1在站点sn+j的滞留乘客人数，公式如下：
(10)
其中，
表示列车lm+i-1在站点sn+j的最大容纳量，但为了简化运算，着重强调目标函数的制定思想，本文均取固定值。
城市轨道交通列车运行均衡调整优化目标函数用列车总晚点时间最小函数和晚点时域内乘客等待总时间最小函数的加权和表示如下：
F=α1×F1+α2×F2=
(11)
其中，α1和α2分别为总晚点时间最小函数和晚点时域内乘客等待总时间最小函数的权重值，满足α1+α2=1。
2 人工鱼群优化算法
2003年，李晓磊博士提出了人工鱼群算法[15]，它是一种模拟自然鱼群行为的智能优化算法，是一种自上而下的寻优结构，其基本行为包括觅食、聚群、追尾和随机，逐步聚集在食物浓度最大的地方，通过模仿自然鱼的行为更快地找到全局最优值。为了兼顾列车自动调整优化效果与求解时间，本研究采用改进的人工鱼群算法对上述模型进行求解。
2.1 行为描述
假设有fishnum条鱼，每条鱼的状态Xi={x1,x2,…,xm},(i=1,2,…,fishnum)为待寻优变量，食物浓度f(Xi)为适应度函数，人工鱼之间距离dij=||Xi-Xj||, visual为人工鱼的视野，step为人工鱼的步长，δ为人工鱼拥挤度因子，try_number为尝试次数。
在城市轨道交通列车运行调整模型中，目标函数F>0恒成立，因此可以得到人工鱼群的食物浓度函数：
1) 觅食行为：假设人工鱼在t时刻的位置为Xi，在视野内随机选择状态Xj,如果f(Xi)<f(Xj)，则Xi向Xj方向前进一步得到Xnew，判断Xnew是否满足约束条件，满足则结束觅食行为；否则，重新选择Xj，判断是否满足前进条件，重复try_number次后，若不满足约束条件则转为随机行为。
在城市轨道交通列车运行调整模型中，对前进条件的要求较为严格，本研究提出改进的觅食行为Matlab伪代码如下：
function y=AF_prey(Xi)
for i=1∶trynumber
Xj=Xi+Rand*visual;
if f(Xi)<f(Xj)
if judge(Xnew)==1
y=Xnew
break;
else
continue;
end
else
continue;
end
end
end
其中：judge(Xnew)为判断Xnew是否满足约束条件的函数，如果满足约束条件，置1；反之，置0。
2) 聚群行为：假设人工鱼在t时刻的位置为Xi，计算视野内满足dij<visual的人工鱼数目nf及中心位置Xc，如果f(Xc)/nf>δf(Xi)，则Xi向Xc方向按式(12)得到Xnew，判断Xnew是否满足要求，如果满足则Xnew为下一个状态；否则执行觅食行为。
(12)
3) 追尾行为：假设人工鱼在t时刻的位置为Xi，搜索视野内满足dij<visual的人工鱼中食物浓度最大的伙伴，其位置记为Xj，如果f(Xj)/nf>δf(Xi),则按式(13)得到Xnew，判断Xnew是否满足要求，如果满足则Xnew为下一个状态；否则执行觅食行为。
(13)
4) 随机行为：假设人工鱼在t时刻的位置为Xi，当觅食行为重复try_number次后，仍不满足约束条件则执行随机行为：
Xnew=Xi+Rand*step
if judge(Xnew)==1
y=Xnew;
else
y=Xi;
2.2 求解流程
本研究应用改进的人工鱼群算法，对列车运行的出发时间和到达时间进行调整，求解目标函数值最优下的各列列车在各个站台的合理到发时问，具体求解流程如下：
步骤1 参数初始化。初始化列车运行图XR、列车总数M、车站总数N、列车追踪间隔冗余时间Tyz、区间运行冗余时间Tyr和列车各约束条件Ts min、Ts max、Tr min、Tr max、Tg min和Tfd min，输入列车晚点时间tdelay；
其中:
步骤2 人工鱼群参数初始化。初始化人工鱼群种群数目fishnum、人工鱼视野visual、人工鱼步长step、人工鱼拥挤度因子δ、尝试次数try_number和最大迭代次数Maxgen；
步骤3 根据式(5)和式(6)计算晚点时域参数；
步骤4 根据晚点时域参数，初始化人工鱼的状态Xi(i=1,2,…,fishnum)，并计算对应的食物浓度f(Xi);
其中
由于城市轨道交通列车运行调整模型约束条件复杂，因此为了保证初始化的人工鱼的状态Xi有足够可行解，提出以下初始化规则：
行规则：
Xi(ii, jj+1)=Xi(ii, jj)+Tg min+k*rand
列规则：
Xi(ii+1, jj)=Xi(ii, jj)+Ts min+k*rand
Xi(ii, jj)为到达线
Xi(ii+1, jj)=Xi(ii, jj)+Tr min+k*rand
Xi(ii, jj)为出发线
其中，k是初始化参数，根据列车晚点时间tdelay不同而调整。在进行初始化时，先初始化人工鱼的状态的第一行和第一列，然后按照行规则和列规则分别计算下一行的各个数据，对比选择既满足行规则和列规则的计算结果，判断结果是否满足到发车约束，如果满足则初始化成功；否则，选择相应的原到发车时间代替不满足约束的数据。
步骤5 对人工鱼的状态Xi按食物浓度f(Xi)降序排列，并设定全局最优pbest(X1)=f(X1)；
步骤6 按照人工鱼的4种行为对人工鱼的状态Xi进行更新，并选择食物浓度最大的行为更新结果作为人工鱼的状态Xi；
步骤7 判断是否满足结束条件，如果满足，进行步骤8；否则，转到步骤5继续执行；
步骤8 对人工鱼的状态Xi按食物浓度f(Xi)降序排列，并输出调整的列车运行时刻以及对应的全局最优解pbest(X1)；
步骤9 算法结束。
算法流程如图1所示。
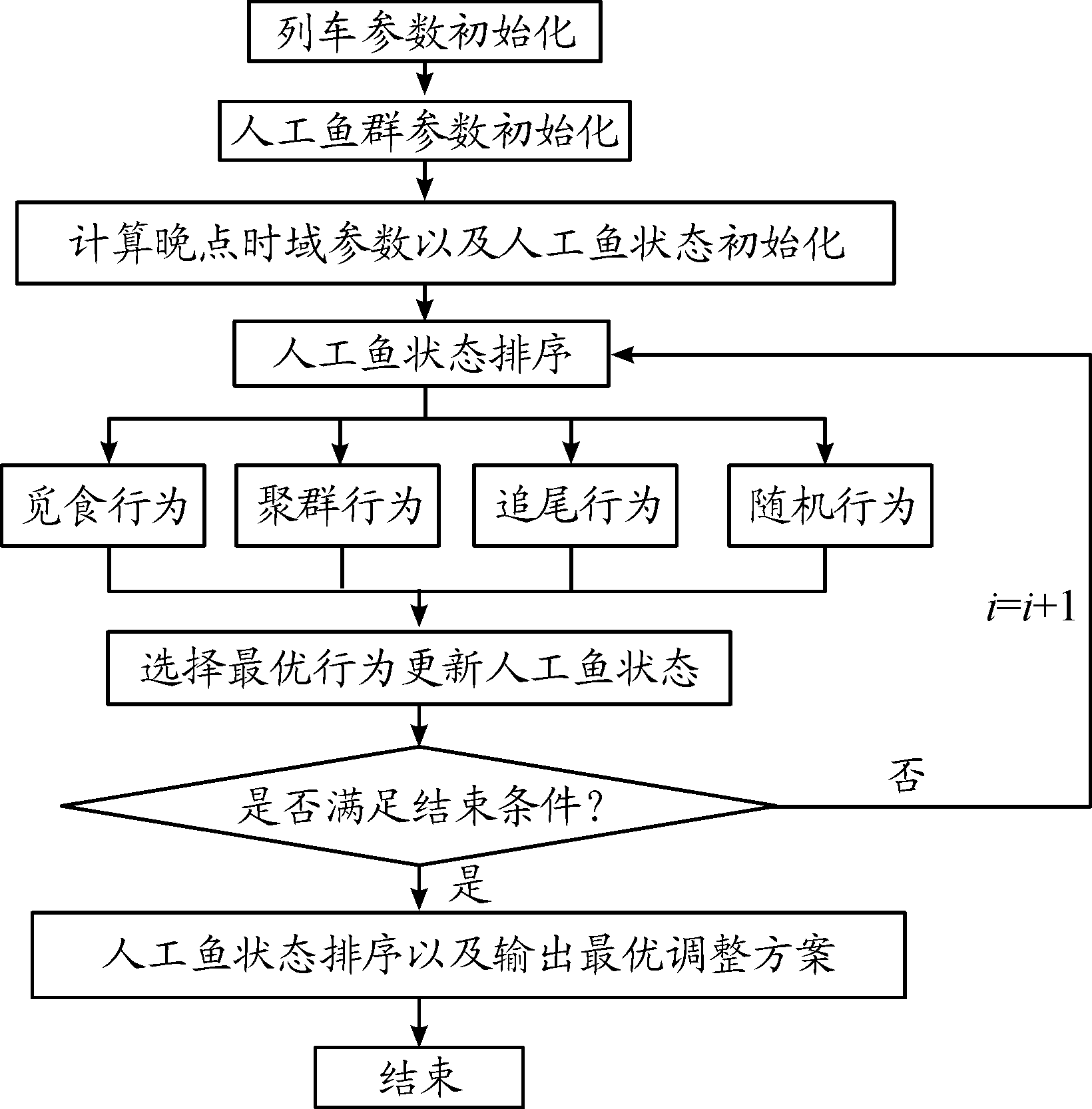
图1 人工鱼群算法求解流程框图
3 实例仿真
3.1 基本参数
南京地铁3号线全长44.9 km，其中地下段42.5 km、高架段2.4 km，共有林场站到秣周东路29座站台，本研究算法选择三号线胜太西路站到新庄站路段早高峰(7∶15∶48—8∶24∶07)期间运行的8列车，构造列车计划时刻表。列车区间运行参数以及鱼群算法相关参数如表1所示。
表1 列车区间运行参数以及鱼群算法参数
参数类别参数名称参数符号参数取值列 车 运 行 参 数最小停站时间Ts min25 s最大停站时间Ts max50 s最小追踪间隔Tg min280 s最小区间运行时间Tr min80 s最大区间运行时间Tr max140 s追踪间隔冗余时间Tyz60 s区间运行冗余时间Tyr10 s相邻列车到发最小间隔Tfd min200 s鱼 群 算 法 参 数鱼群个体数fishnum50最大迭代次数Maxgen300人工鱼视野visual140人工鱼步长step60人工鱼拥挤度因子δ0.05尝试次数try_number100目标函数参数F1权值α10.6F2权值α20.4
3.2 鱼群算法仿真
为了验证算法的适用性和有效性，假设第4辆车在经过南京南站时由于随机因素发生晚点，根据式(5)和式(6)，受晚点影响列车数Nl和到发时间线数Ns与追踪间隔冗余时间Tyz有关系，故分别选取小于追踪间隔冗余时间的晚点时间、大于1倍追踪间隔冗余时间的晚点时间和大于2倍追踪间隔冗余时间的晚点时间。
1) 当晚点时间小于追踪间隔冗余时间Tyz时，假设tdelay=40 s，根据式(5)和式(6)可以确定晚点时域受影响列车Nl=1和受影响到发时间线数Ns=5，根据鱼群算法得到的适应度收敛图和列车最优调整方案如图2和图3所示。
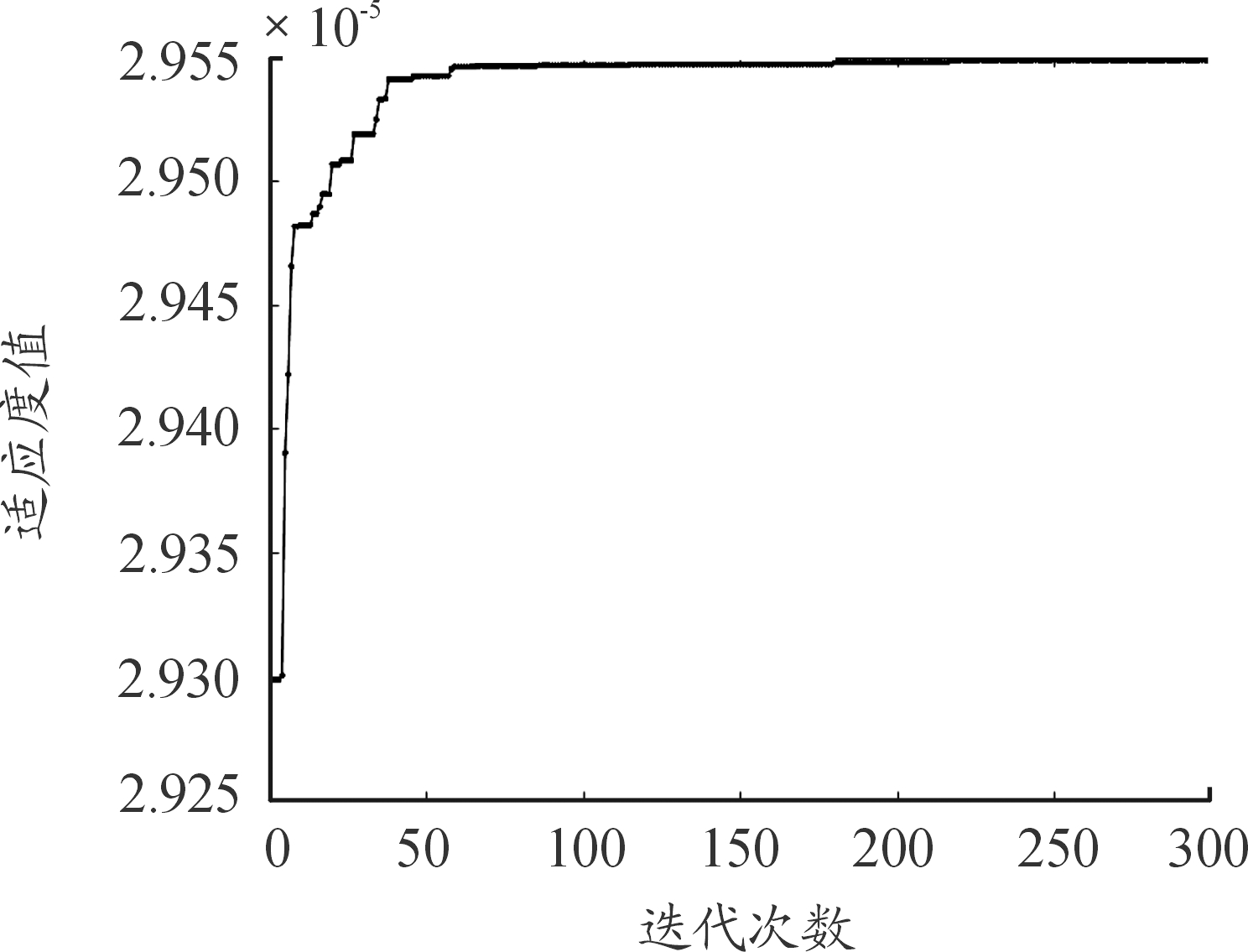
图2 tdelay=40 s时鱼群收敛曲线
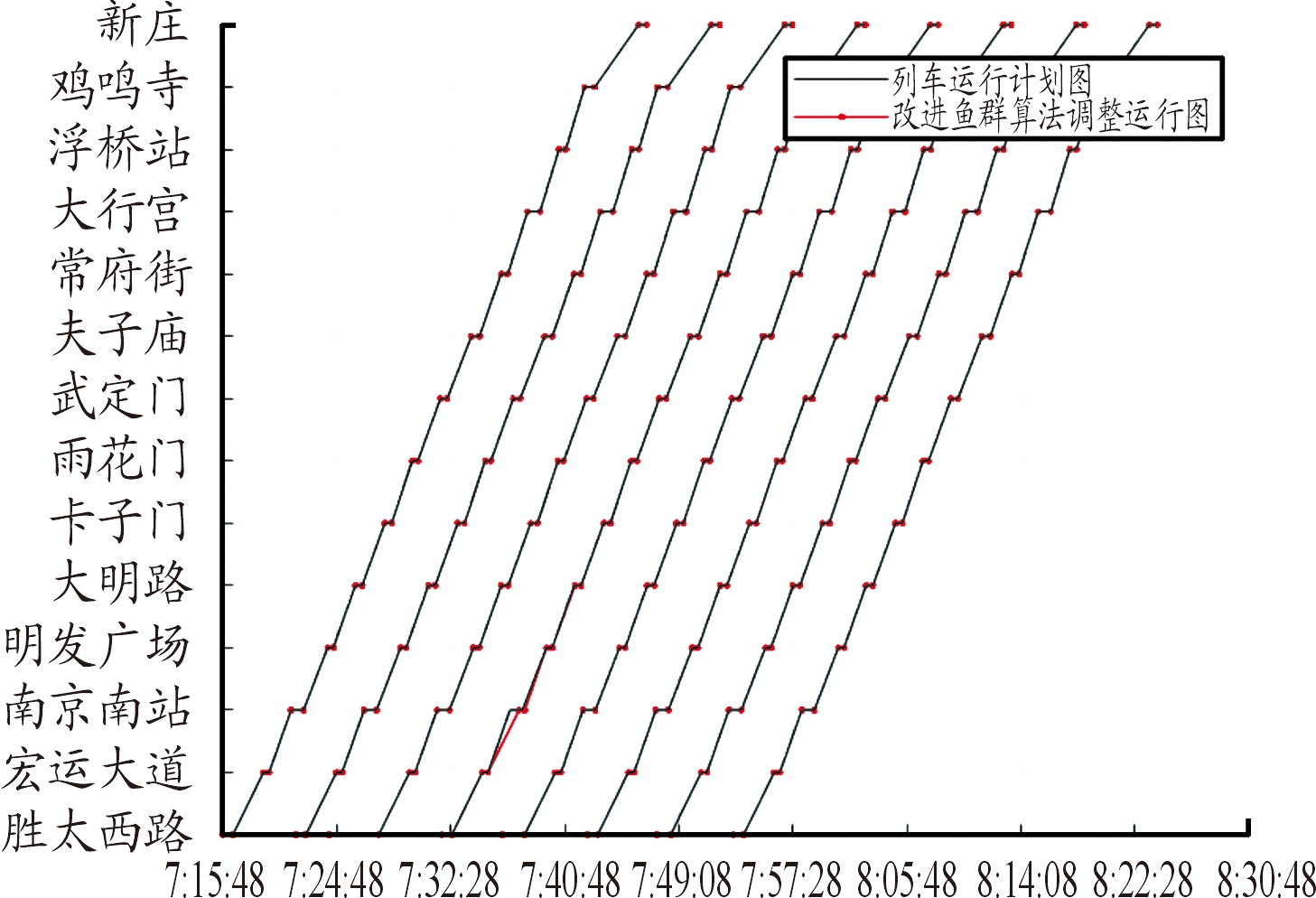
图3 tdelay=40 s时列车最优调整方案曲线
从图2可以看出，改进鱼群算法的收敛曲线在前50代收敛速度较快，当经过60代之后收敛曲线接近水平，算法优化结果为列车总晚点时间F1=53.055 6 s、列车晚点时域内乘客总等待时间F2=84 526 s；从图3可以看出，列车在南京南站到站晚点40 s时，经过本站发车时间调整，在明发广场站就调整回列车计划运行图，调整效率较高。
2) 当晚点时间大于追踪间隔冗余时间Tyz时，假设tdelay=80 s，根据式(5)和式(6)可以确定晚点时域受影响列车Nl=2和受影响到发时间线数Ns=10，应用改进鱼群算法得到的适应度收敛图和列车最优调整方案如图4和图5所示。
图4 tdelay=80 s时鱼群收敛曲线
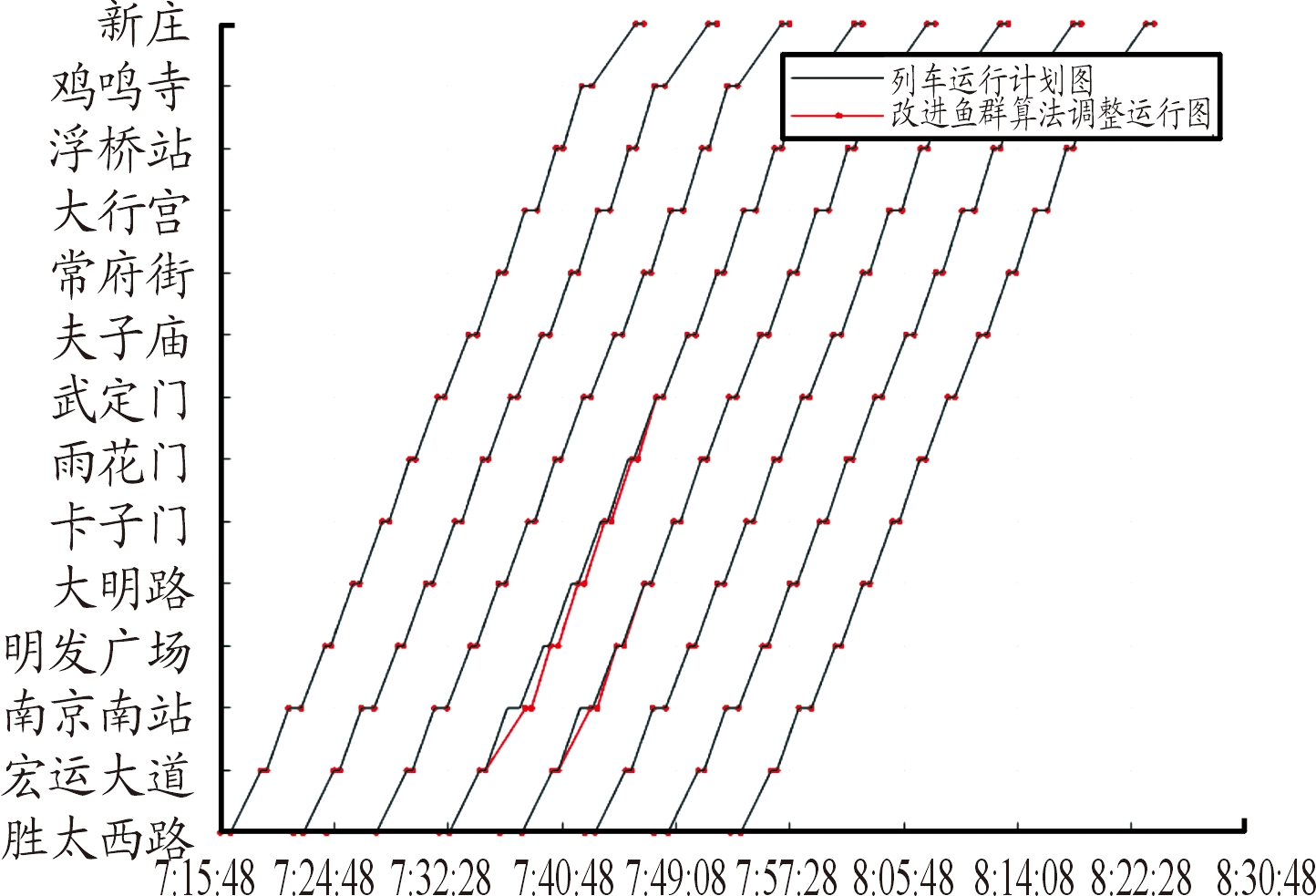
图5 tdelay=80 s时列车最优调整方案曲线
从图4可以看出，改进鱼群收敛曲线在前20代收敛速度较快，当经过30代之后收敛曲线接近水平，算法优化结果为列车总晚点时间F1=389.849 6 s、列车晚点时域内乘客总等待时间F2=168 180 s；从图5可以看出，由于列车在南京南站到站晚点80s大于间隔冗余时间Tyz，所以后续列车也受到影响，相继偏离计划运行图，在经过改进鱼群算法调整后，延误的车辆均较快调整到列车计划运行图。
3) 为了验证改进鱼群算法对列车发生程度较大的晚点的调整能力，假设tdelay=130 s，同理计算得到晚点时域受影响列车Nl=3和受影响到发时间线数Ns=15，根据鱼群算法得到的适应度收敛图和列车最优调整方案如图6和图7所示。
图6 tdelay=130 s时鱼群收敛曲线
图7 tdelay=130 s时列车最优调整方案曲线
从图6可以看出，改进鱼群算法的收敛曲线在前60代收敛速度较快，当经过60代之后收敛曲线接近水平，算法优化结果为列车总晚点时间F1=1 344.8 s、列车晚点时域内乘客总等待时间F2=8.884 4×105 s；从图7可以看出，在经过改进鱼群算法调整后，发生较大程度晚点的列车也能较快地调整到列车计划运行图，减少了列车间的延误传播。
4 结论
针对城市轨道交通列车运行调整问题，本研究建立了列车运行均衡调整模型；将列车运行调整的多约束条件作为人工鱼群的前进条件，提出了改进人工鱼群算法；选取南京地铁三号线的列车运行数据，分别对晚点时间40 s、80 s和 130 s 进行仿真，形成最优调整方案。仿真结果表明，改进的人工鱼群算法可以满足城市轨道交通列车运行调整的实时调整要求，具有优良的适应性和高效性，减少了列车间的延误传播，保障了列车运行效率和客运服务质量。
[1] BART KERSBERGEN,TON VAN DEN BOOM,BART DE SCHUTTER.Reducing the time needed to solve the global rescheduling problem for railway networks[C]//The 16th International IEEE Annual Conference on Intelligent Transportation System.The Hague,Netherlands,2013.
[2] LI Wang,ZHU Tao,XU Jie,et al.Bi-level programming model on passenger train operation in emergency[J].Journal of Southeast University (Natural Science Edition),2015,45(5):996-1001.
[3] 刘峰博,徐瑞华,江志彬.满足客流需求的地铁列车延误协同调整方法[J].同济大学学报(自然科学版),2018,46(02):215-221.
[4] KANG Liujiang,WU Jianjun,SUN Huijun,et al.A practical model for last train rescheduling with train delay in urban railway transit networks[J].Omega-International Journal of Management Science,2015,50:29-42.
[5] LIU K,WANG X,QU Z.Train Operation Strategy Optimization Based on a Double-Population Genetic Particle Swarm Optimization Algorithm[J].Energies,2019,12(13):2518.
[6] CHEN Shiming,LAI Yiping,JIANG Jihai.Research on particle swarm optimization algorithm for train operation adjustment[J].Application Research of Computers,2010,27(12):4460-4462.
[7] MENG X,JIA L,QIN Y,et al.Study on Train Operation Adjustment Based on Hybrid Convergent Particle Swarm Optimization[J].Journal of Shandong University,2009,41(11):58-66.
[8] 宁正,牛宏侠,张肇鑫.基于排队论的地铁列车运行自动调整优化模型[J].铁道科学与工程学报,2019,16(07):1826-1832.
SAHIN.Train re-scheduling with genetic algorithms and artificial neural networks for single-track railways[J].Transportation Research Part C,2012(27):1-15.
[10] 陈东,彭其渊,张燕,等.基于改进遗传算法的赶流列车运行调整研究[J].计算机工程与科学,2016,38(03):507-513.
[11] 柏赟,陈垚,陈玥,等.考虑列车总晚点和到发均衡性的地铁列车运行调整方法研究[J].交通运输系统工程与信息,2014,14(03):104-110.
[12] 段少楠,戴胜华.离散萤火虫算法在高速列车运行调整中的应用[J].计算机工程与应用,2018,54(15):209-213.
[13] WANG Jingjing.Ant Colony Optimization Algorithm applied to train operation adjustment of Urban Transit[J].Railway Computer Application,2016,25(7):1-3,17.
[14] 宁正,牛宏侠,张肇鑫.基于排队论的地铁列车运行自动调整优化模型[J].铁道科学与工程学报,2019,16(07):1826-1832.
[15] LI Xiaolei.A New Intelligent Optimization Method—Artificial Fish Swarm Algorithm[D].Hangzhou:Zhejiang University,2003.