中小口径自动武器承担着抗击敌低空、超低、超低空空袭兵器的任务,要求其火炮系统反应时间短、射速高、毁伤概率高、可靠性高等[1-2]。自动机作为中小口径火炮的核心机构要求具备射速高、后坐力小、射击精度高、可靠性要求高等特点,在射击过程中自动机关重件承受高冲击、强振动、高膛压等复杂冲击载荷循环环境。
闭锁机构是自动机实现开、闭锁的重要部件,在闭锁阶段,闩体转过一定的闭锁角,使得闩体与炮尾形成刚性闭锁。而在发射阶段,闩体头部的弹底窝处直接承受从药筒传递来的内腔火药气体的作用,使闭锁面承受巨大的冲击载荷,从而在闭锁面处产生较大的接触应力,属于高压高速撞击的非线性动力学问题[3]。
间隙在自动武器连接构件的运动副中是普遍存在的。一般来源于:① 设计过程中时,配合公差的选取会带来设计误差;② 制造与装配过程中,存在着加工误差;③ 使用过程中,对于自动武器而言,构件之间会发生高速碰撞,会产生磨损。间隙的存在会破坏理想机构的平稳性随着闩体与炮尾之间的闭锁面间隙不断加大,炮尾与闩体的实际机构模型会越来越偏离理想的机构模型,而闭锁面的应力波动、闭锁机构的裂纹萌生位置以及使用寿命也会发生变化[4-7]。本文重点分析在不同间隙存在时,冲击应力的波动对炮尾闭锁面上的疲劳寿命变化规律,以期能够得到一个合理的间隙取值范围为闭锁机构的抗疲劳设计以及强度设计提供参考依据。
1 炮尾闭锁面的冲击应力计算
建立尾闭锁面冲击应力计算模型的假设:
① 将可能存在于闭锁面之间的间隙从0~0.1 mm等分为11组;
② 以闩体与炮尾闭锁支撑机构为研究对象,在发射时,自动机刚性固定,不考虑药筒的影响;
③ 各闭锁面的间隙状态相同,表面质量均一致。
根据实际的闭锁关系,将闩体与炮尾之间定义面面接触关系,接触类型为摩擦系数为0.15的有摩擦的接触。并将在不考虑缓冲器的前提下,约束炮尾端面的全部方向的位移,闩体由于与炮尾形成了刚性闭锁,闩体只释放头部弹底窝面法线方向的位移(即膛压作用方向)。考虑到闩体的结构属于空间曲面、曲线结构,采用高阶二次单元,同时对各闭锁面以及闭锁面圆角处网格做加密处理,如图1所示。通过内弹道计算出闩体所受到的膛压曲线,如图2所示。

图1 有限元计算网格示意图

图2 膛压曲线
将膛压施加到闩体头部的弹底窝处。
采用瞬态动力学的方法对闭锁机构进行冲击强度的分析。炮尾与闩体的材料模型选用双线性随动硬化(Billnear Kinematic)材料模型,闩体与炮尾采用同种炮钢材料45CrNiMoVA,其材料参数如表1所示。
表1 45CrNiMoVA的材料参数

密度/(kg·m-3)弹性模量/GPa泊松比屈服强度/MPa切线模量/MPa78302140.2913252140
2 瞬态动力学分析
以其中一个炮尾闭锁面为研究对象,图3(a)~(e)分别对应间隙在0.02 mm、0.04 mm、0.06 mm、0.08 mm以及0.1 mm的工况下与理想模型之间炮尾闭锁面的冲击应力波动情况。无间隙时,闭锁面上的最大冲击应力的趋势与膛压曲线相同,在1.15ms时刻,闭锁面下方0.8 mm处出现值为1 497 MPa的最大冲击应力;在间隙为0.02 mm时,应力波动幅度与间隙为0的趋势相同。在炮尾闭锁面下方0.8 mm出现1 379.4 MPa的最大冲击应力;当间隙在0.04~0.08 mm时,闭锁面的应力在较长的一段时间内发生波动。最大冲击应力在1 534.7~1 651.3 MPa范围内变化,同时波动幅值较小时,其最大冲击应力出现在闭锁面上,膛压达到最值时,最大冲击应力出现同0~0.02 mm工况下的相同的位置;当间隙达到0.1 mm时,从0.72 ms直到1.67 ms,闭锁面上产生持续性的应力波动。

图3 不同间隙的冲击应力曲线
不同间隙时的炮尾闭锁面上最大冲击应力以及出现时刻,如表2所示。随着间隙的增大,最大冲击应力呈现递增的趋势,由于材料已经进入了塑性变形阶段,所以最大冲击应力的增幅较小。同时,炮尾闭锁面上的最大冲击应力出现的时刻也随着间隙量的增加而提前。
表2 不同间隙最大冲击应力数值及时刻
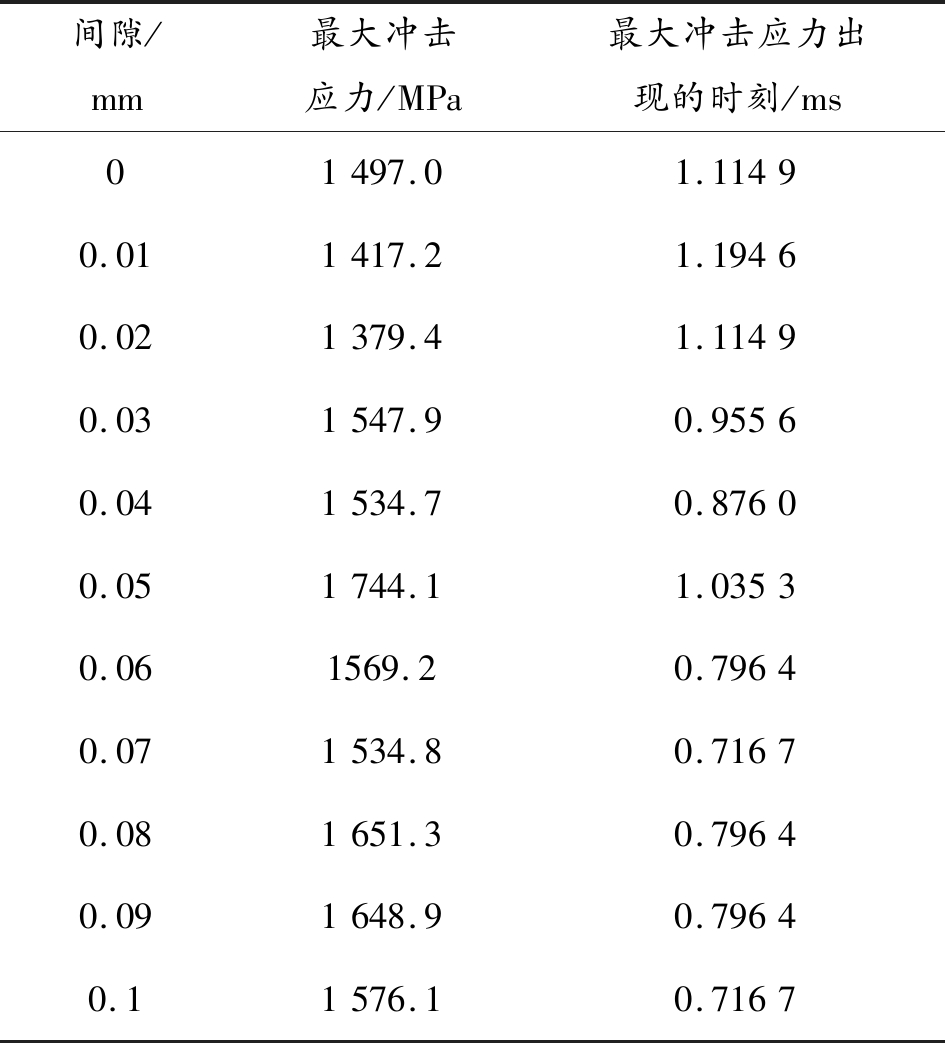
间隙/mm最大冲击应力/MPa最大冲击应力出现的时刻/ms01497.01.11490.011417.21.19460.021379.41.11490.031547.90.95560.041534.70.87600.051744.11.03530.061569.20.79640.071534.80.71670.081651.30.79640.091648.90.79640.11576.10.7167
结合上述曲线可以分析出,在膛压加载的初期,闩体与炮尾闭锁面之间的间隙会由于结构的变形以及闩体的轴向运动,而快速消隙;当膛压接近最大膛压时,由于加载速率很高,材料的应力应变的不均匀性要比非冲击载荷的大,随着间隙的增大,冲击应力逐渐增加,同时高应力的波动时间也越来越长。当膛压减小时,冲击应力随之下降。同时分析曲线以及表中数据,可以得到当炮尾在冲击载荷作用下,由于冲击应力在材料内部是以应力波的方式传递,炮尾闭锁支撑处的不规则结构,使得应力波发生反射与透射的叠加,使得应力波的传递方向发生变化,可能导致小应力变大,在结构的内部形成复杂应力。从而导致了最大等效应力位置出现了局部的随机性。但最大冲击应力位置范围在闭锁面下方的表面节点。
3 炮尾闭锁面的疲劳寿命
结构的疲劳寿命计算方法主要有:名义应力法、局部应力-应变法、能量法、场强法等。对自动机的闭锁机构而言,其所受到的载荷多为冲击载荷。
目前冲击疲劳的研究大体有两种观点和研究方法:第一是以能量载荷与破坏循环次数表征的A-N曲线法,即能量法,其局限性在于以A-N曲线法表征的材料冲击疲劳性能,无法直接用作材料的疲劳性能指标,对疲劳寿命不能采用定量的计算[8];第二是以应力或应变与破坏循环次数表征的S-N 曲线法,冲击应力疲劳法。在低载荷水平作用下,应力与应变呈线性关系,采用名义应力法与局部应力—应变法计算疲劳寿命是等效;在高载荷水平作用下,应变的变化要比应力变化程度大,采用局部应力—应变法计算疲劳寿命,计算结果更加精确。
通过分析炮尾闭锁面的冲击应力,可以看出材料已经进入了塑性阶段。因此,采用局部应力—应变法计算炮尾闭锁面的疲劳寿命。其基本思想在于,首先确定结构疲劳危险部位并计算出名义应力谱,通过有限元法计算局部应力应变谱,然后参考材料的力学性能参数,结合损伤累积理论,得到结构的疲劳寿命[9]。
3.1 材料的ε-N曲线
自动武器的寿命一般在3×104发以内[14],当寿命在101~105范围内,ε-N曲线采用Manson-Coffin公式精度较高。炮尾闭锁面的疲劳载荷属于非对称应变循环,故采用Morrow弹性应力线性修正。45CrNiMoVA的力学性能参数,如表3所示[10]。修正的Manson-Coffin公式如下:
表3 45CrNiMoVA的力学性能参数

名称45CrNiMoVA真实断裂强度σf/MPa1882真实断裂延性εf0.43断面收缩率ψ/%35弹性模量E/MPa214000强度极限σb/MPa1470
式中:Δε/2为总应变幅值;![]() 为疲劳强度系数;
为疲劳强度系数;![]() 为疲劳延性系数; σm为平均应力;E为材料的弹性模量;b为疲劳强度指数;c为疲劳延性指数;N为裂纹萌生寿命。
为疲劳延性系数; σm为平均应力;E为材料的弹性模量;b为疲劳强度指数;c为疲劳延性指数;N为裂纹萌生寿命。
3.2 诺伯近似解法
Neuber法是基于受纯剪棱柱体在特殊的材料应力应变关系得到的Neuber公式:
式中:S为名义应力;σm为理论应力集中系数;σ为缺口根部的局部应力;为缺口根部的局部应变。
为了使其适应一般情况,同时提高计算疲劳寿命的精度,将式中的理论应力集中系数KT用疲劳缺口系数Kf代替,在循环加载过程中,修正后的Neuber公式为:
式中:ΔS为名义应力幅值;Δσ为局部应力幅值;Δε为局部应变幅值。
在循环载荷作用下的迟滞回线方程为:
式中:K′为循环强度系数;n′为循环应变硬化指数。
根据表中的材料力学性能参数,通过四联点法估算公式[11],得到材料的疲劳性能参数,如表4所示。
表4 45CrNiMoVA的疲劳性能参数值

参数名称参数值疲劳强度系数/MPa1992疲劳延性系数0.24疲劳强度指数b-0.096疲劳延性指数c-0.56循环应变硬化指数0.17循环强度系数2550
其中疲劳缺口系数参考文献[12],取为1.53。
3.3 疲劳累积损伤准则
目前的工程应用中,大多数采用线性累积损伤理论进行计算疲劳寿命。其中应用范围最广的是线性Miner疲劳累积损伤法则。
该法则认为每次循环的损伤是线性叠加的。在每次变幅载荷作用下,循环的次数为Ni,那么每次循环的损伤值为1/Ni。n次循环下,造成的总损伤为
当总损伤值与循环次数的乘积为1时,结构达到循环次数。
3.4 疲劳寿命计算结果
结构在外载荷的作用下,外表面的应力水平通常情况下是最高的。所以,结构发生疲劳断裂现象大多数是从结构的表面产生裂纹源,随之裂纹扩展直至断裂。而零件的表面状态也是影响疲劳裂纹萌生的主要原因之一。表面状态的优劣从微观上来讲,相当于表面有侵入,在结构表面存在着沟壑,对表面的应力集中产生影响。这种大小尺寸不同的应力集中处与结构几何形状发生突变的效果是相同。对于高强度材料,其延性一般比较差,对结构的缺陷也就更敏感。在交变载荷的作用下,结构表面的应力集中会增加疲劳裂纹萌生的概率[13]。
根据2.1节的炮尾闭锁面的冲击应力计算结果及第3节修正后材料的ε-N曲线,表面粗糙度分别取为0.4 μm、1.6 μm、3.2 μm,分别对应常用抛光、精车以及粗车零件加工方法。对其疲劳裂纹萌生寿命进行计算。
不同间隙下的炮尾闭锁面疲劳裂纹萌生寿命曲线,如图4。分析粗糙度为0.4 μm的工况,在理想机构模型中,其炮尾闭锁面的疲劳裂纹萌生寿命为3 635发,随着间隙量的不断增大,在0.01~0.03 mm间隙下,其寿命在5 472~6 600 发,当间隙由0.03 mm增加到0.1 mm时,闭锁面的寿命由 5 472 发下降到1 368发。受间隙量的影响,导致闭锁面的疲劳裂纹萌生寿命由最高的6 600发下降到1 368发,其寿命下降79%;而在理想机构模型中,当粗糙度由0.4 μm增加到3.2 μm,炮尾闭锁面的寿命会随之由3 635发降低到3 083发。表面质量的不同会使得闭锁面寿命下降15.2%。
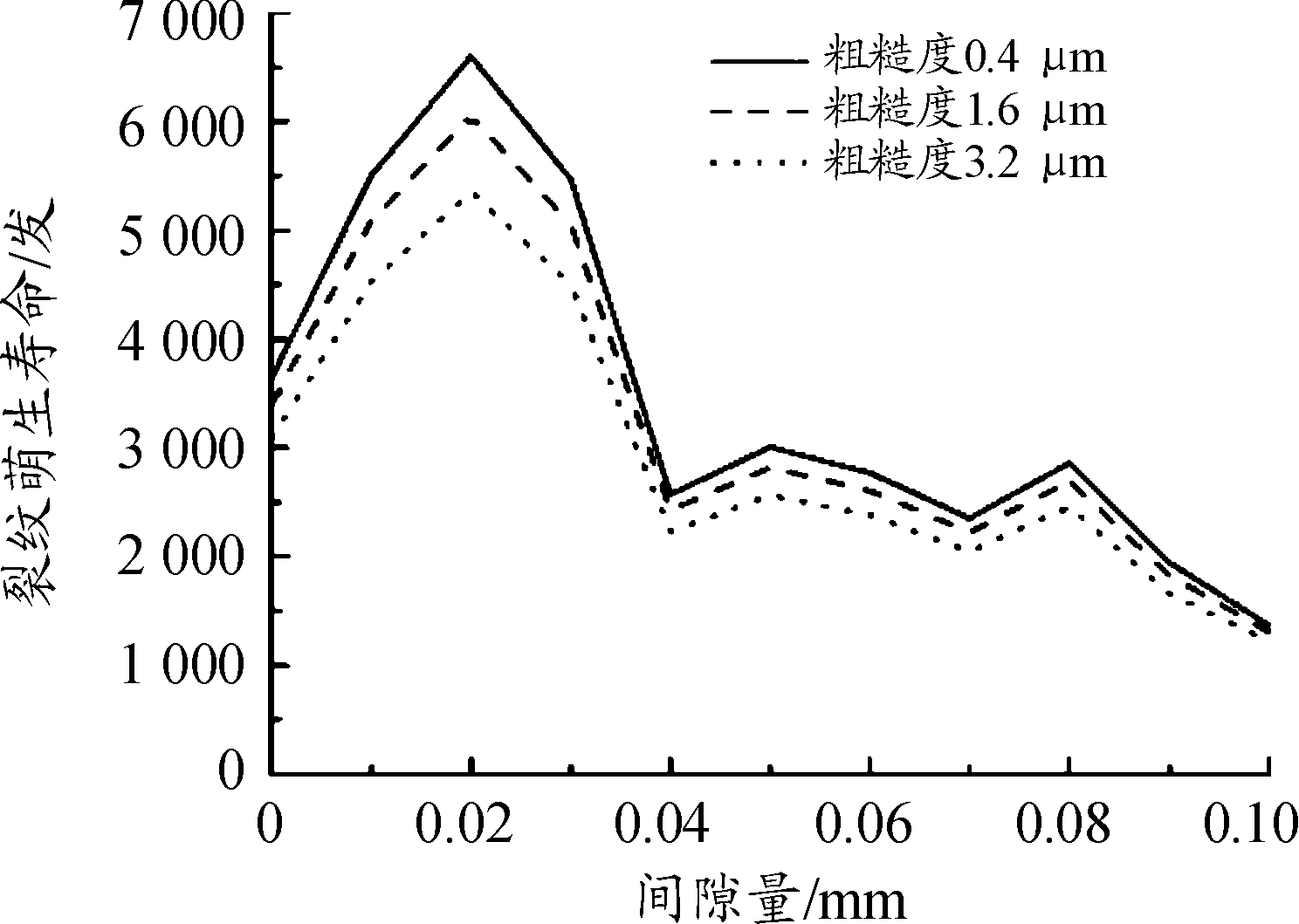
图4 疲劳裂纹萌生寿命曲线
在间隙量与表面质量两个因素的影响,闭锁面的疲劳裂纹寿命计算结果,如表5所示。分析表中数据,只考虑表面加工质量这一单一影响因素,在表面加工质量最好,即粗糙度为0.4 μm,闭锁面的裂纹萌生寿命最大下降率为79.3%;只考虑闭锁面的间隙量时,间隙量最佳,即间隙量在0.02 mm工况下,裂纹萌生寿命最大下降率为18.9%。而最优工况与最恶劣的工况相比,寿命下降率为81.5%。对比两个影响因素,间隙量的变化对疲劳寿命影响为主要因素。
表5 45CrNiMoVA炮尾疲劳裂纹萌生寿命

间隙/mm粗糙度Ra0.4μm1.6μm3.2μm寿命最大下降率/%036353400308315.20.0155045083452717.80.0266006059535118.90.0354725055450317.70.0425712427222913.30.0530072819256414.70.0627722608238514.00.0723532224204613.10.0828622691245814.10.0919481831166114.70.113681308122410.5寿命最大下降率/%79.378.477.1
炮尾闭锁面的疲劳裂纹寿命在不同间隙下会出现先增长到下降的趋势,是由于间隙量在0.01 mm到0.03 mm的范围下,循环冲击载荷与一般载荷相比,冲击载荷的加载的速率快,每次循环载荷的作用时间短,闭锁面上的冲击应力的波动幅度不大,其次闭锁面的冲击应力的波动频率较低,导致裂纹的萌生在冲击疲劳下是相对困难的;而间隙在[0.04,0.1](mm),由于冲击应力的波动频率较高,每次循环时,与[0,0.03](mm)相比,会造成次数更多的小范围的高应力的冲击,在高冲击应力的作用下,导致疲劳损伤值增加,最终导致炮尾闭锁面的裂纹萌生寿命大大降低。
4 结论
1) 在理想机构模型下,闭锁面的冲击应力的变化规律与膛压曲线相近,闭锁面上最大等效应力出现在膛压达到峰值的时刻附近;
2) 随着间隙量的增大,最大等效应力增大,最大等效应力出现的时刻也会提前,闭锁面上的高冲击应力的波动频率更高;同时,受到冲击应力的影响,疲劳寿命出现先增大后下降的趋势;
3) 闭锁面的疲劳寿命对间隙量变化相比表面质量变比更加敏感,合理的间隙量以及良好的表面质量不仅会降低结构在运动中的磨损量,同时可以大大提高结构的疲劳寿命。
[1] 杨雕,刘源远,黄少保,等.冲击载荷下身管延伸体改进设计及疲劳寿命研究[J].火炮发射与控制学报,2020,41(01):84-88.
[2] 李涌,吴宝双.协同仿真技术某转管武器炮闩小闭锁齿疲劳寿命预测[J].火力与指挥控制,2015,40(12):141-144.
[3] 葛藤,赵军,周克栋.某新型自动步枪闭锁机构动应力分析[J].弹道学报,2006(02):36-39.
[4] 徐家凡,何玲,王永娟.闭锁间隙对回转闭锁接触应力影响数值仿真分析[J].火炮发射与控制学报,2012(01):34-38.
[5] 刘伟,魏志芳,苑大威,等.回转式闭锁机构参数化设计与动力学仿真[J].火炮发射与控制学报,2018,39(02):75-80.
[6] 余芳,李屹,李家春,等.一种闭锁机构的闭锁力影响因素的研究[J].机电工程,2020,37(05):496-501.
[7] 昝博勋,薛百文,杨臻,等.某新型步枪的枪机寿命分析[J].兵器装备工程学报,2019,40(11):55-59.
[8] 张遥辉.钢铁材料冲击疲劳行为综述[J].中国设备工程,2020(06):211-216.
[9] 姚卫星.结构疲劳寿命分析[M].北京:国防工业出版 社,2003:1-2.
[10] 郑肖建.速射武器身管的疲劳寿命可靠性研究及退化分析[D].南京:南京理工大学,2014.
[11] 闫建伟,方峻.身管疲劳损伤与可靠寿命分析[J].机械设计与制造,2016(09):7-11.
[12] 贾长治,李亚东,郑坚,等.自行火炮扭力轴局部应力应变随机性分析及应用研究[J].机械强度,2012,34(05):744-750.
[13] 李魁武,宁变芳,曾志银,等.基于裂纹形成及扩展的火炮闩体寿命研究[J].兵工学报,2013,34(03):289-293.
[14] 赵森森.考虑多失效机理的枪械闭锁机构寿命与可靠性分析[D].南京:南京理工大学,2018.