随着我国军事及航空航天领域的迅猛发展,特装车辆扮演着越来越重要的角色,变速箱是车辆动力传动系统中的关键部件,对其进行健康监测和故障诊断显得十分重要。基于振动信号的故障诊断对故障较为敏感,且操作简单,无需拆解变速箱,得到广泛的应用。然而从变速箱等实际机械结构采集到的振动信号往往含有大量的噪声,如何降低噪声带来的影响,提取真实有效的振动信号,是目前面临的主要困难[1]。小波变换具有较好的刻画局部时频特征及多分辨率分析的能力[2],是目前信号降噪处理中较为广泛的一种方法[3]。常用小波降噪方法有小波分解与重构、阈值降噪、模极大值降噪、平移不变量降噪以及相关性降噪等[4]。小波阈值降噪法适应性广,降噪效果较好,且较为完好地保留了原始信号特征,因此是应用最广泛一种降噪方法。但小波降噪质量易受小波函数、分解层数等多参数的影响,目前尚无确定的小波函数与分解层数等参数选择的最优方法。
蔡铁等[5]提出一种对小波分解细节系数进行奇异谱分析来确定最佳分解层数的方法。王维等[6]提出一种去相关白化检验的小波阈值降噪最优分解层数确定自适应算法。李宗春等[7]将均方根差变化量、互相关系数、信噪比及平滑度归一化后求和,最大值对应小波分解最佳尺度。陶珂[8]运用信息熵的方法将归一化的均方根误差变化量、信噪比变化量以及平滑度变化量进行融合,通过识别拐点来确定最佳参数。朱建军等[9]将均方根误差与平滑度归一化后利用变异系数定权的方法将两种指标线性组合,得到新的复合评价指标,当指标最小时降噪效果最好。邓敏等[10]将归一化后的均方根误差、信噪比和平滑度进行变异系数赋权求和,得到一个综合评价指标,通过最小值判断最优参数。高山等[11]将均方根误差和平滑度进行均值化处理后,采用熵值定权法将两者线性组合,最小值时即为最佳分解尺度。以上方法存在未考虑细节收敛特征、分辨率低、需识别拐点等不同程度的不足,因此本文综合考虑以上不足,提出一种基于多元融合的小波降噪质量综合评估指标。通过某变速箱振动信号分析验证,表明该方法可以很好地评估小波降噪质量,为装备维修诊断过程中振动信号的小波降噪参数选取提供指导作用,具有一定的实际意义。
1 小波阈值降噪原理及传统评估指标
1.1 小波阈值降噪原理
设一维含噪信号的简单模型为
f(i)=s(i)+n(i)
其中:s(i)为真实信号;n(i)为噪声信号; f(i)为含有噪声的信号。
通常认为n(i)是服从分布为N(0,σ2)的高频白噪声,而实际结构中采集的真实信号s(i)一般是一些较为平稳的信号或是低频信号。小波阈值降噪通过对含噪信号进行小波分解,得到相应低频逼近系数和高频细节系数,然后采用合适的阈值函数对各高频细节系数进行阈值量化处理,最后将信号重构即可得到降噪后的信号。具体步骤如下:
1) 含噪信号的小波分解:选取小波函数及分解层数M,将含噪信号进行M层小波分解;
2) 高频细节系数的阈值处理:选择合理阈值对M层小波分解的高频细节系数进行阈值量化处理;
3) 信号重构过程:将阈值处理后的小波系数进行小波逆变换从而得到重构后的信号。
影响小波阈值降噪效果的因素有小波函数的选择,阈值的选择以及分解层数的选择等,目前主要是通过传统评估指标对小波降噪效果进行评价。
1.2 传统评估指标
传统小波降噪效果评估指标主要有均方根误差(RMSE)、信噪比(SNR)、平滑度(r)、相关系数(R)[11]。均方根误差指的是原始信号与降噪信号之间方差的平方根,描述了信号的高频细节特征,其值与分解层数呈正相关,越小代表降噪效果越好;信噪比指的是信号功率与噪声功率的比值,其值与分解层数呈负相关,越大代表降噪效果越好; 平滑度指的是降噪信号一阶差分方差根与原始信号一阶差分方差根的比值,描述了信号低频逼近特征,其值与分解层数呈负相关,越小代表降噪效果越好; 相关系数表示原始信号与降噪信号之间的接近程度,其值与分解层数呈负相关,越大代表降噪效果越好[10]。
上述指标均存在不足,单独某一指标仅能描述某方面降噪效果,存在较大的局限性。被测信号的真实值通常是未知的,如果未消除任何噪声时,均方根误差几乎接近0,信噪比亦很大,相关系数则接近1,这将导致评估指标严重失真,即使平滑度没有不一致性,但由于没有极值,因此,无法判断最优降噪效果[9]。
2 综合评估指标的建立
为了充分反映信号的总体特征趋势,本文选取了均方根误差变化量、信噪比变化量、平滑度和相关系数四个指标。信噪比变化量和均方根误差变化量代表信号降噪过程的细节收敛特征,经本文数据多次试验,其变化趋势随分解层数的增加先逐渐上升,当降噪效果达到一定程度后逐渐下降,符合降噪初期噪声消除较快,降噪后期效果提升不明显的实际情况。平滑度和相关系数代表降噪后信号与原始信号的相关程度,均与分解层数呈负相关,但平滑度越小越好,偏向于过度分解,而相关系数越大越好,偏向于欠分解。因此,该四个指标进行融合必然存在某一极大值,可以平衡各指标的影响,取得最佳降噪效果。运用变异系数对归一化后的指标进行权值分配[12],越难实现的指标权值越重,并线性组合形成一种新的小波降噪质量综合评估指标,其极大值表示该降噪方法降噪效果最佳。
均方根误差变化量、信噪比变化量、平滑度、相关系数,相关表达式如下:
varm(m)=RMSE(m+1)-RMSE(m)
其中:varm(m)代表两相邻分解层数之间的均方根误差变化量。RMSE(m)代表信号m层分解降噪后的均方根误差,其式为
其中: f(i)代表原始信号;![]() 代表m层分解后的降噪信号;n代表被测信号的长度。
代表m层分解后的降噪信号;n代表被测信号的长度。
vasnr(m)=|SNR(m+1)-SNR(m)|
其中:vasnr(m)代表两相邻分解层数之间的信噪比变化量;SNR(m)代表信号m层分解降噪后的信噪比,其式为
SNR=10×lg(Ps/Pn)
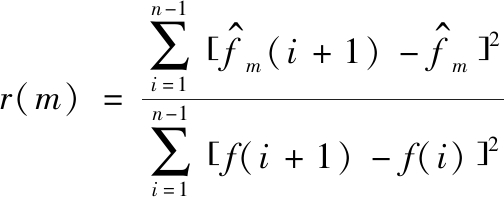
r(m)代表信号m层分解降噪后的平滑度。
R(m)代表信号m层分解降噪后的相关系数; σf(i)和![]() 则分别代表原始信号与m层分解降噪后信号的方差。
则分别代表原始信号与m层分解降噪后信号的方差。
各指标之间量纲和变化范围均不相同,不具有可比性,因此首先进行归一化处理,使其相互具备可比性,然后进行变异系数权值分配,最后线性组合形成一种新的小波降噪质量评估指标。具体计算流程如下:
1) 首先对各指标进行归一化操作,公式如下:
其中: N表示各状态下均方根误差变化量、信噪比变化量、平滑度以及相关系数; PN表示各指标的归一化值; max()和min()为取某指标最大值和最小值。
2) 然后计算各指标变异系数。变异系数相对客观地反映了整体的分散性程度,变异系数越高,就越难实现,分配的权值也就越高。
其中:CVPN表示各指标归一化后的变异系数; σPN和μPN表示各指标归一化后的标准差和均值。
3) 根据变异系数进行权值分配。
其中WPN表示各指标经变异系数进行赋权后的权值。
4) 最后通过各指标权值与归一化值线性组合形成新的综合评估指标T,寻找极大值即可得到对应的最优参数。
3 实例验证
采集某变速箱动力传动综合试验时的振动加速度信号(图1),由图1看出由于变速箱内部工作环境复杂,不同部件之间互相影响,因此该信号受到各种噪声的污染,是真实信号与噪声信号的混合信号,其波形十分不平稳且信噪比极低,仅从信号时域图或频谱图无法对变速箱状态进行判断,需对信号进行降噪处理,以便可以有效提取反映真实信号的特征信息,进行下一步状态评估和故障诊断。运用本文小波降噪质量综合评估指标选取小波函数及分解层数进行降噪,进而验证本文方法的准确性。
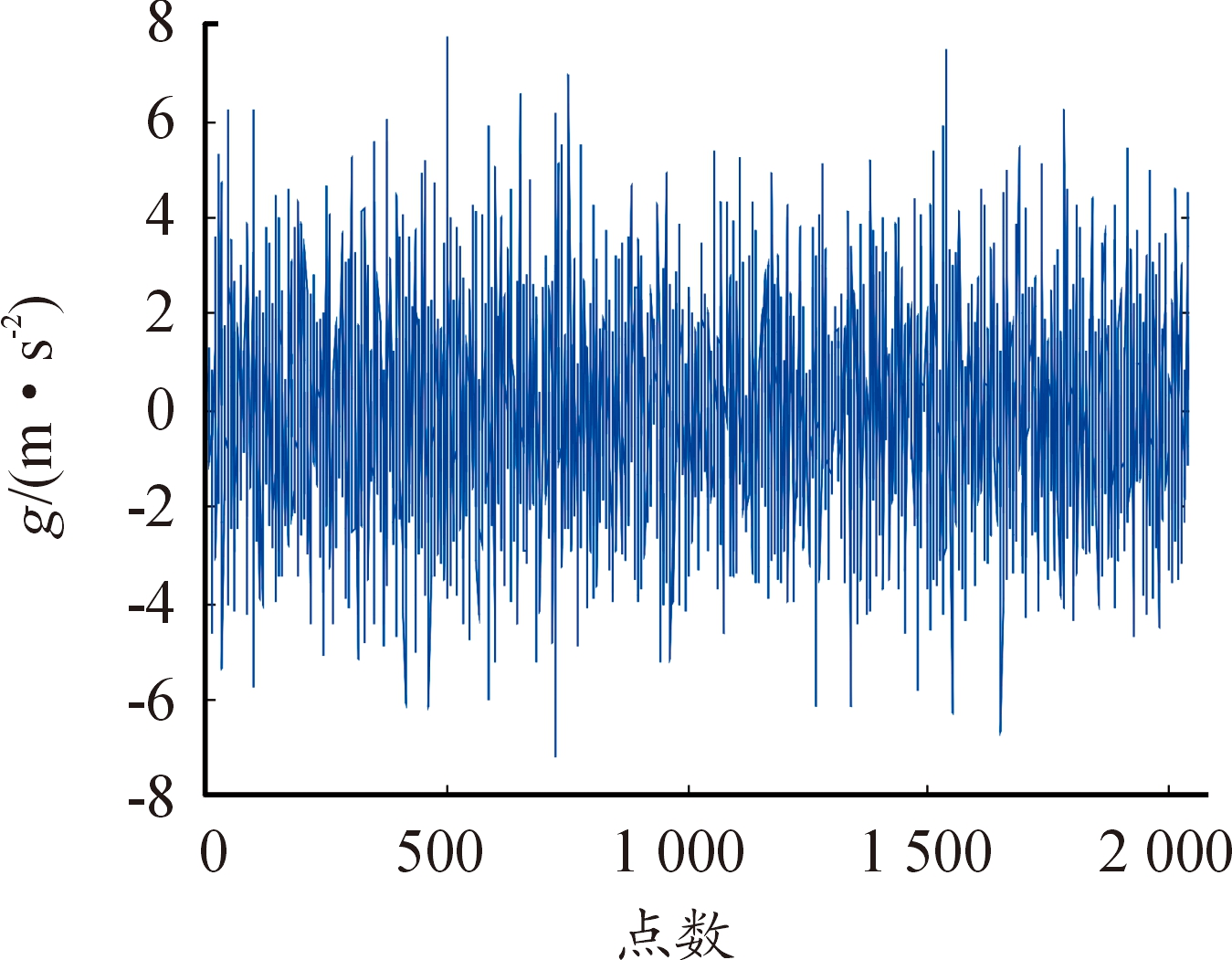
图1 变速箱原始振动信号曲线
该变速箱为单中间轴结构,输入轴齿轮齿数为35,中间轴与输入轴啮合齿轮齿数为32,中间轴齿轮与主轴1挡啮合处齿轮齿数为17,1挡齿轮齿数为47,试验时挡位为1挡,转速为1 450 r/min,扭矩为1 300 N·m,其余特征参数见表1。数据采集频率为10 kHz,截取试验稳定部分的前2 048个采样点作为数据,进行实例验证。
表1 变速箱试验相关特征参数

参数名称频率/Hz输入轴转频(f1)24.16输入轴与中间轴啮合频率(f2)845.83中间轴转频(f3)26.43中间轴与1挡齿轮啮合频率(f4)396.45
本文采用小波阈值降噪,以小波函数、分解层数作为备选参数。小波函数选择与机械振动信号波形特征类似且正交性与紧支性较好的db小波系(db4、db5、db6)和sym小波系(sym4、sym6、sym8)[4]。分解层数选择2~5层,防止层数过多导致滤除噪声的同时滤除真实信号,影响降噪效果。阈值选取采用基于史坦(Stein)的“rigrsure”无偏风险估计准则,阈值处理函数为软阈值函数。分别计算降噪后各参数组合下本文评估指标(varm,vasnr,r,R)以及文献[9]评估指标(r*,rmse*),结果见表2。将其归一化后采用变异系数进行权值分配,结果见表3。本文综合评估指标T以及根据文献[9]方法计算所得的复合指标T1,结果见表4。
表2 各参数组合下本文评估指标值与文献[9]评估指标值
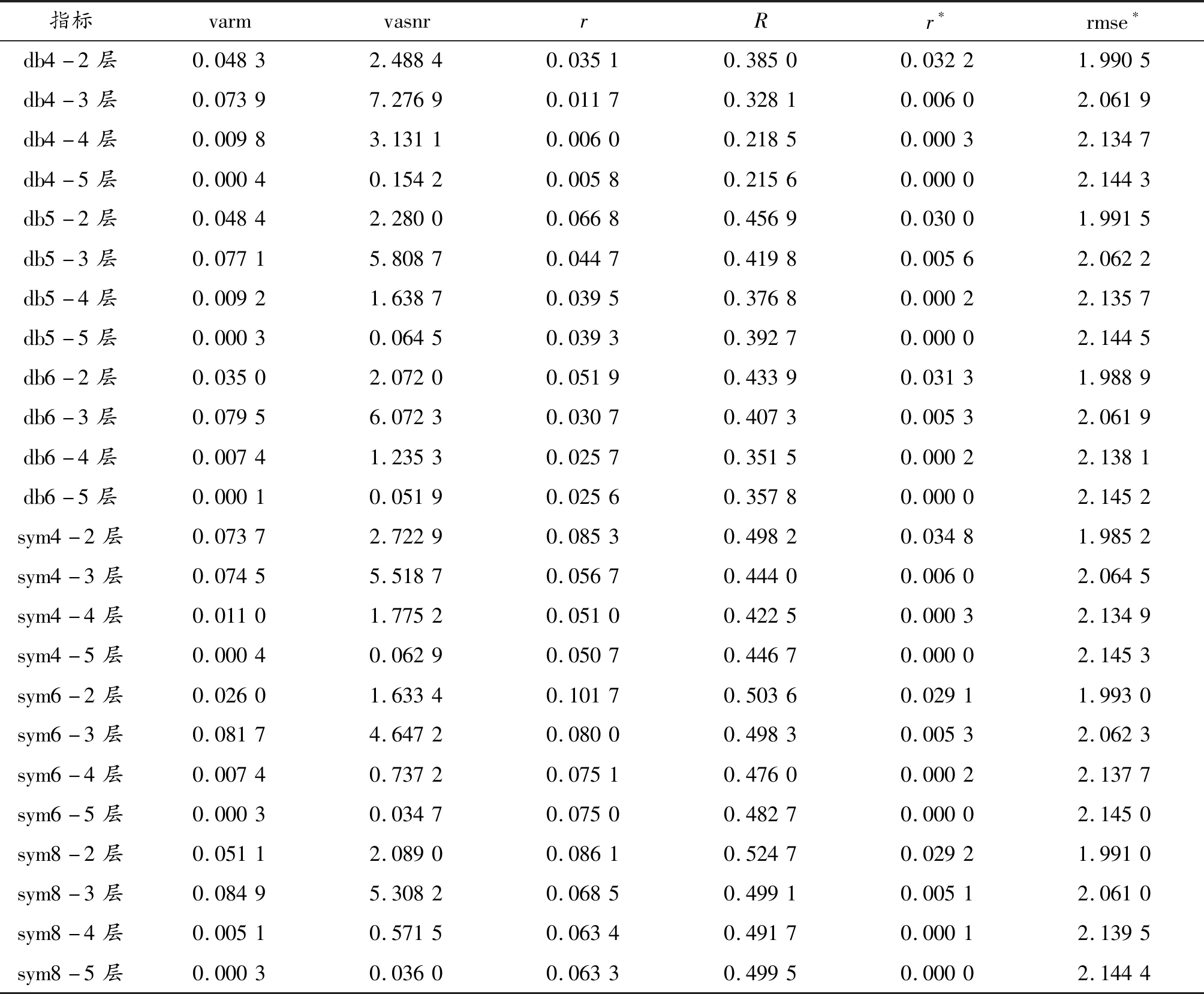
指标varmvasnrrRr∗rmse∗db4-2层0.04832.48840.03510.38500.03221.9905db4-3层0.07397.27690.01170.32810.00602.0619db4-4层0.00983.13110.00600.21850.00032.1347db4-5层0.00040.15420.00580.21560.00002.1443db5-2层0.04842.28000.06680.45690.03001.9915db5-3层0.07715.80870.04470.41980.00562.0622db5-4层0.00921.63870.03950.37680.00022.1357db5-5层0.00030.06450.03930.39270.00002.1445db6-2层0.03502.07200.05190.43390.03131.9889db6-3层0.07956.07230.03070.40730.00532.0619db6-4层0.00741.23530.02570.35150.00022.1381db6-5层0.00010.05190.02560.35780.00002.1452sym4-2层0.07372.72290.08530.49820.03481.9852sym4-3层0.07455.51870.05670.44400.00602.0645sym4-4层0.01101.77520.05100.42250.00032.1349sym4-5层0.00040.06290.05070.44670.00002.1453sym6-2层0.02601.63340.10170.50360.02911.9930sym6-3层0.08174.64720.08000.49830.00532.0623sym6-4层0.00740.73720.07510.47600.00022.1377sym6-5层0.00030.03470.07500.48270.00002.1450sym8-2层0.05112.08900.08610.52470.02921.9910sym8-3层0.08495.30820.06850.49910.00512.0610sym8-4层0.00510.57150.06340.49170.00012.1395sym8-5层0.00030.03600.06330.49950.00002.1444
表3 本文方法权值分配及文献[9]方法权值分配

权值varmvasnrrRr∗rmse∗本文0.34170.31970.19950.1431--文献[10]----0.59970.4003
表4 各参数组合下本文综合评估指标T值与文献[9]复合指标T1值

T2层3层4层5层T12层3层4层5层db40.43900.68330.17940.00630.59870.35870.37680.4043db50.52770.73890.24980.15030.56800.34450.39400.4054db60.42380.72630.18490.10520.55650.32600.38810.4044sym40.70510.75090.30730.19820.59970.35580.37500.4003sym60.4690.78930.29560.23850.54940.32550.38150.3993sym80.63180.85570.30990.27000.53800.31520.38770.4001
作T值及T1值变化趋势曲线(图2(a)与图2(b))。分析图2可知各小波函数下T值随分解层数的增加先递增后递减,具有极大值,且当小波函数为sym8小波,分解层数为3层时T值最大,因此认为sym8小波函数3层分解降噪效果最佳。各降噪方法下传统指标变化趋势曲线如图3所示,观察图3可知sym8小波函数2层和3层分解降噪的均方根误差均较小,信噪比及相关系数均较大,但该3个参数均偏向于欠分解,综合考虑平滑度的影响,作该两种降噪方法降噪信号时域曲线及频谱曲线,分别如图4和图5所示。从图4可以看出2层分解降噪信号仍然存在部分噪声,毛刺较多,而3层分解降噪信号消除噪声更加彻底,信号更加平滑,但细节部分仍然保存比较完整,整体趋势与原始信号也比较接近。观察图5可以发现3层分解降噪后的信号与2层分解降噪信号相比,更加有效地滤除了噪声信号,信噪比得到较大的提高,同时保留了输入轴转频(f1)、输入轴与中间轴啮合频率(f2)、中间轴与1挡齿轮啮合频率(f4)以及这些频率的倍频等有用特征频率。实测频率与变速箱原始频率的对比如表5所示,从表5中可以看出运用3层分解降噪后提取到的特征频率与原始频率平均误差率仅为0.47%,验证了通过该指标选取的sym8小波函数3层分解降噪在此状态下降噪效果最优,体现了综合评估指标的合理性。

图2 T值与T1值变化趋势曲线
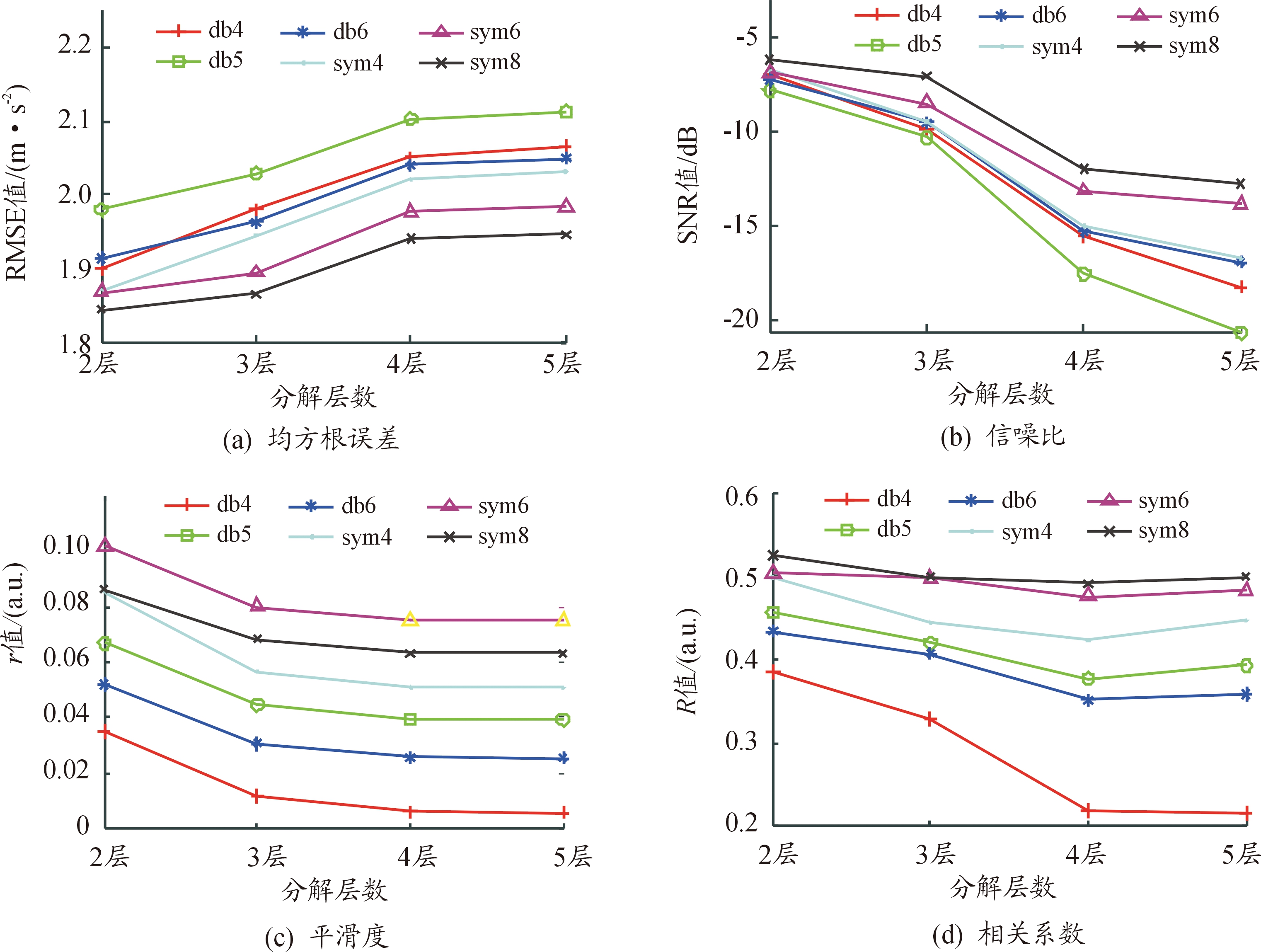
图3 各传统指标变化趋势曲线

图4 原始信号与降噪后信号曲线
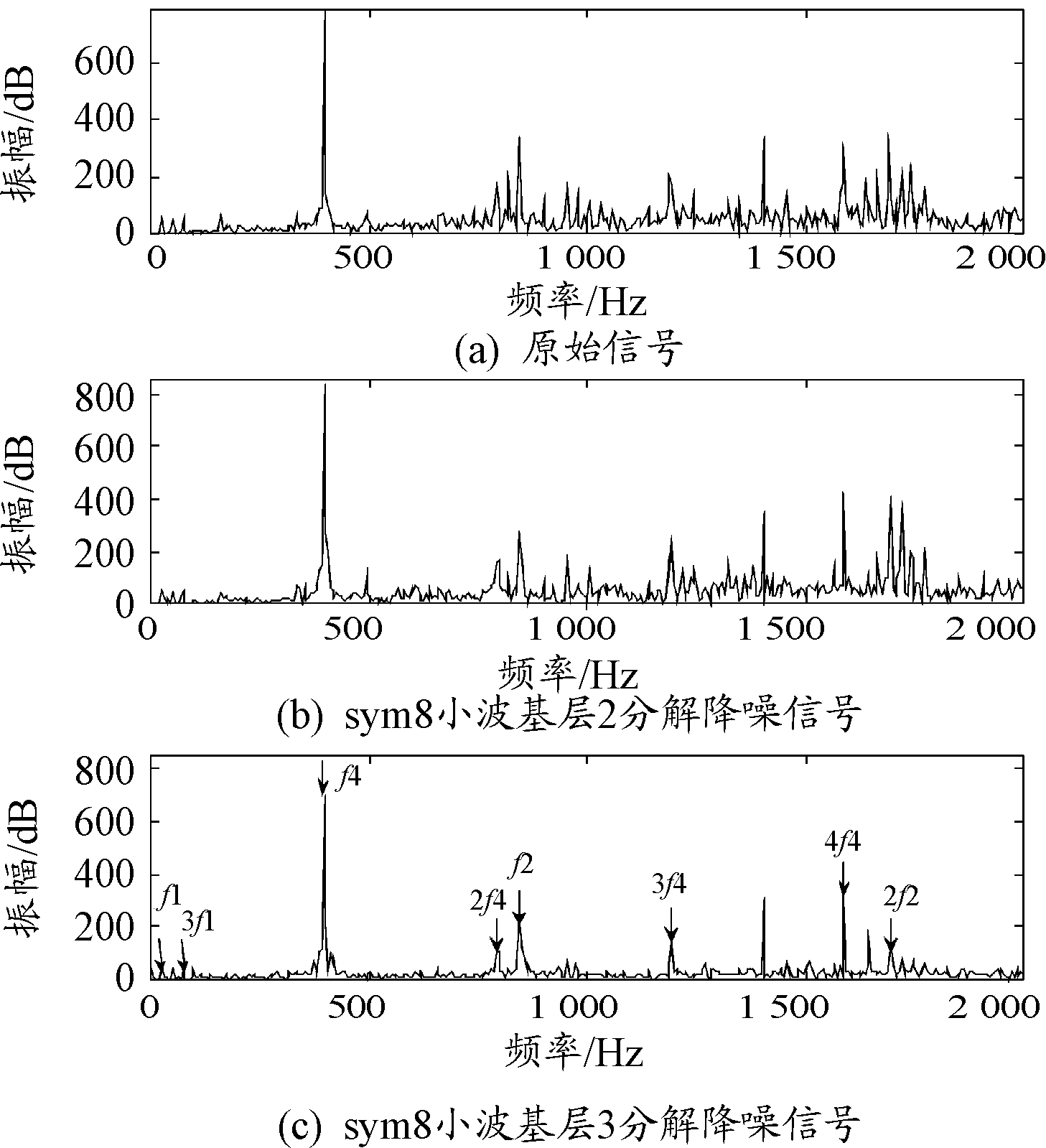
图5 原始信号与降噪后信号频谱曲线
表5 实测频率与原始频率误差
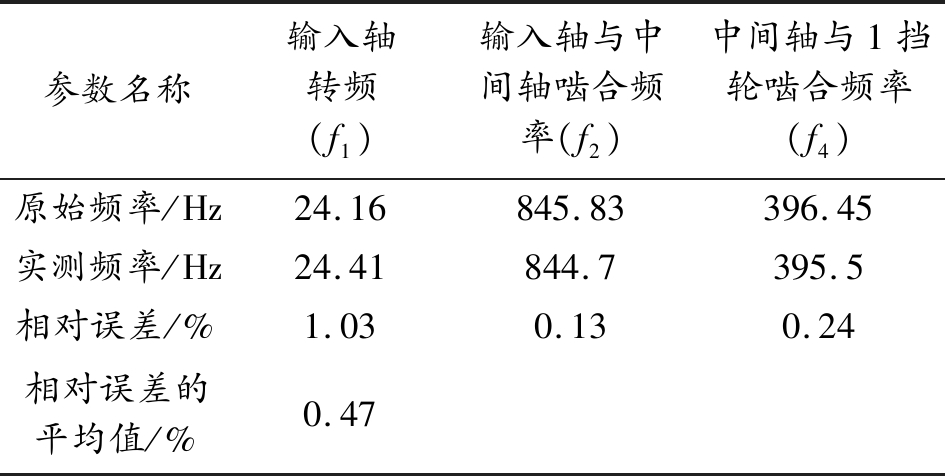
参数名称输入轴转频(f1)输入轴与中间轴啮合频率(f2)中间轴与1挡轮啮合频率(f4)原始频率/Hz24.16845.83396.45实测频率/Hz24.41844.7395.5相对误差/%1.030.130.24相对误差的平均值/%0.47
该参数组合与文献[9]方法计算所得复合指标T1最小值对应的最优参数组合一致(图2(b)),进一步证明综合指标的正确性。本文综合评估指标与文献[9]复合指标相比,综合考虑了均方根误差变化量和信噪比变化量,定量分析了信号降噪过程中的细节收敛特征,防止某项指标异常导致权值分配出现极端情况,抗干扰性更强,且平衡了平滑度以及相关系数的影响,防止降噪过程中出现欠分解或过度分解现象。除此之外,分析图2(b)可知,文献[9]复合指标存在一定的混叠现象,不利于降噪效果的分析,而本文综合评估指标则分辨率更高,误差更小。因此,本文方法较文献[9]方法相比存在一定的优势。同理可运用本文方法进行其他参数的降噪质量评估,如小波阈值函数等。
4 结论
本文选取了均方根误差变化量、信噪比变化量、平滑度以及相关系数等指标进行归一化,通过引入变异系数的方法进行权值分配并线性组合形成一种新的小波降噪质量评估指标。该方法综合考虑了降噪信号与原始信号的相关程度及信号降噪过程的细节收敛特征,并平衡了欠分解与过度分解的影响,具有较好的适应性和可靠性。经过实例验证,该指标可以很好地进行小波降噪质量评估,指导小波降噪参数选择,使得采集的信号在进行小波降噪处理后,提取到的特征频率与原始频率平均误差率仅为0.47%,效果显著,为小波降噪提供了一种新的质量评估指标,具有工程应用价值。
[1] 李浩,董辛旻,陈宏,等.基于小波变换的齿轮箱振动信号降噪处理[J].机械设计与制造,2013(03):81-83.
[2] 翁浩,高金吉.旋转机械振动信号压缩小波基优化选取方法[J].振动.测试与诊断,2013,33(03):437-444.
[3] 郜立焕,张利娜,朱建国,等.基于小波分析的齿轮箱振动信号消噪处理[J].机械传动,2010,34(03):50-52.
[4] 熊施园.基于小波分析的齿轮箱故障诊断技术研究[D].长沙:中南大学,2013.
[5] 蔡铁,朱杰.小波阈值降噪算法中最优分解层数的自适应选择[J].控制与决策,2006(02):217-220.
[6] 王维,张英堂,任国全.小波阈值降噪算法中最优分解层数的自适应确定及仿真[J].仪器仪表学报,2009,30(03):526-530.
[7] 李宗春,邓勇,张冠宇,等.变形测量异常数据处理中小波变换最佳级数的确定[J].武汉大学学报(信息科学版),2011,36(03):285-288.
[8] 陶珂.小波去噪质量评价方法研究[D].长沙:中南大学,2012.
[9] 朱建军,章浙涛,匡翠林,等.一种可靠的小波去噪质量评价指标[J].武汉大学学报(信息科学版),2015,40(05):688-694.
[10] 邓敏,吴光强.基于变异系数的小波降噪综合评价法[J].机电一体化,2016,22(03):30-35.
[11] 高山,李沁声.基于熵权的小波去噪评价指标[J].测绘与空间地理信息,2019,42(08):1-4.
[12] DELLWO V.Rhythm and Speech Rate:A Variation Coefficient for DeltaC[J].Language and language-processing,2006(1):231-241.