源定位技术一直是阵列信号处理的重要应用[1-3]。该研究课题广泛应用于FF源，麦克风接受到的是平面波,只需要估计DOA参数[4-6]。然而，对于NF源，平面波假设不再有效，因此需要同时提供DOA和距离参数[7-8]。针对这种问题，许多学者提出了种种算法来对FF源和NF源定位。上述所有算法都集中在纯FF或NF源场景中，但在许多实际应用中FF和NF源是共存的[9]，例如使用麦克风阵列的扬声器定位和地震勘探。在FF或NF混合源场景中，大多数纯FF或NF源的算法可能无法区分和定位混合源。
为了实现FF和NF混合源定位，近几年国内外很多学者都钻研于此，并研究出了大量解决此类问题方法。Liang等[10]利用四阶累积量和谱搜索，首次提出了一种有效的二阶MUSIC(Multiple Signal Classification多信号分类)定位算法(TSMUSIC)，但其计算复杂度较高，孔径损失相对严重。为了减小计算量，文献[11]提出了一种只使用二阶统计量的斜投影MUSIC算法(OPMUSIC)，但该算法的参数估计存在严重的孔径损失和一维谱搜索的问题，会产生额外的估计误差。Xie等人在文献[12]提出了一种基于时域四阶统计量的MUSIC MVDR算法，并且不需要知道信号源数目。Liu和Sun在文献[13-14]提出了协方差差分算法(TSMDA)来减小阵列孔径，为信号类型的分类提供了一种更合理的方法。我们了解到随着阵列的孔径增大，DOA参数的估计精度也越高[16]。为避免DOA模糊，现有方法的阵元间距都在四分之一波长之内[17]。最近，Wang等[15]提出了一种稀疏线阵来扩展阵列孔径，提高了估计精度。
本文提出了一种新的混合源定位算法。由于巧妙地使用了高阶累积量，ESPRIT算法和奇异值分解方法，该算法不仅对DOA和距离参数由有较好的估计性能，而且计算量也比现有算法低。
1 建立信号模型
考虑K个波长为λ的窄带独立混合源撞击到N= 2L+1个传感器稀疏线性阵列(SLA)上，该阵列由a、b、c三个麦克风子阵组成，每个子阵都有均匀排布的2M+1个阵元，N，L和M均为正整数。
在图1中，阵元间距为d，将d作为长度单位，子阵列的间距为dx=d·Δ，其中dx>>d，Δ为正整数。传感器位置向量P具有以下形式。
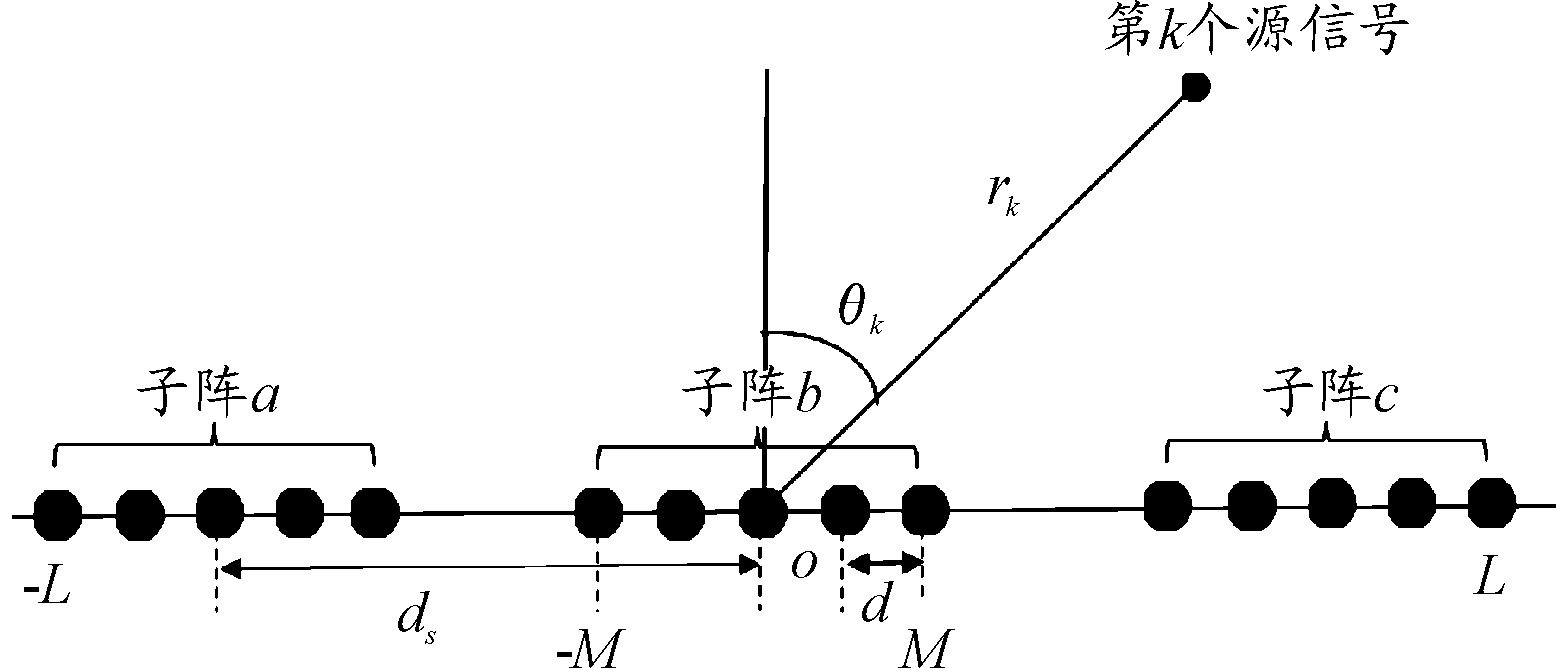
图1 稀疏线阵示意图
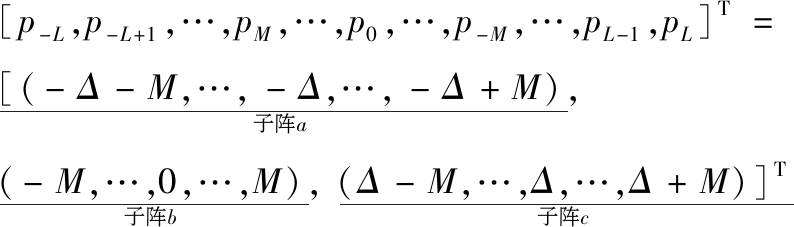
(1)
假设阵列中心为相位参考点。则阵列的输出可表示为
(2)
其中: xm(t)为第k个源信号； nm (t)为附加传感器噪声； τtm为第k个信号源传播到俩个麦克风时间的相对延迟。当第k个信号源是NF源时，即信号源位于菲涅尔区域，到中心麦克风的距离符合 0.62(D3/λ)1/2>rm>2 D2/λ这一条件，阵列孔径D=(N-1)d,
(3)
其中 γk和φk分别为
(4)
(5)
其中，λ是信号波长，θk∈[-π/2,π/2]和rk分别为第k个混合源的DOA和到麦克风阵列中心的距离。目的是得到第k个混合源的一个参数对(θk,rk)，然后辨别混合源中的FF源和NF源。
反之，如果第k个混合源是FF源，则τtm的形式为
(6)
将FF源和NF源的转向矢量统一为 (θ k,rk)，因为FF源的转向矢量可以看成类似近场信号的形式，即(θ k,+∞)。根据式(2)，由于FN源远大于菲涅尔区域的上界，而NF源处于菲涅尔区域[18]。因此，我们可以根据距离估计值的大小将混合源中FF源和NF源区别开来。
在混合场中，式(2)可以写为矩阵形式
x(t)=AFsF(t)+ANsN(t)+n(t)=AS+N
(7)
x(t)和n(t)是(2L+1)×1维复向量，
(8)
A=
(9)
n(t)=
(10)
(11)
2 混合源定位算法
2.1 混合源DOA估计
首先估计FF和NF混合源的波达方向，定义一个四阶累积量
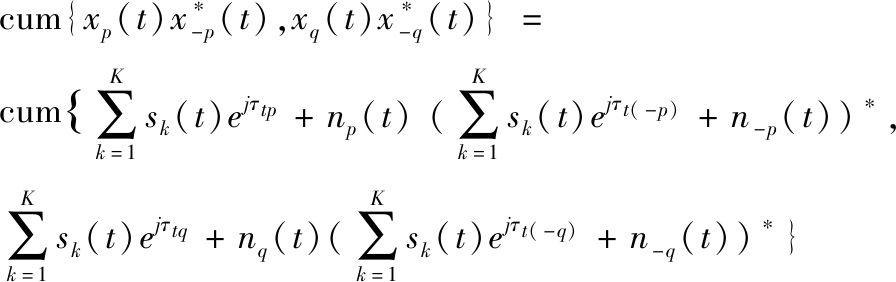
(12)
高阶累积量可以有效地抵抗高斯白噪声和有色噪声，当统计阶数不小于3时，高斯噪声的累积量应为零[19]，所以有
(13)
现在，令
结合等式(3)和(13)就可以得到一个不含距离参数的四阶累积量:
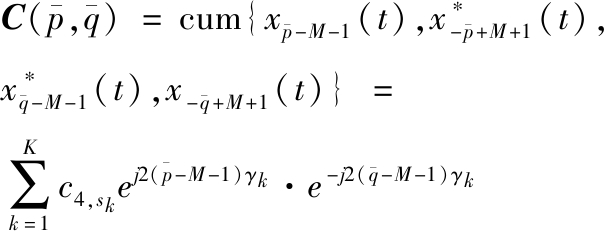
(14)
其中，c4,sk是信号源sk的四阶累积量。
写成矩阵形式：
(15)
向量
对角矩阵CS=diag(⎣cs1,…,csk」)为CN×N的K个最大特征值构成的对角矩阵，“( )H”则为矩阵的共轭转置。矩阵
为，
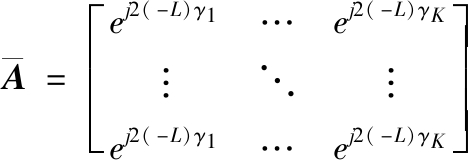
为了进一步减少运算量，并削弱噪声的影响，对四阶累积量矩阵C进行奇异值分解，写成厄米矩阵的形式
(16)
其中，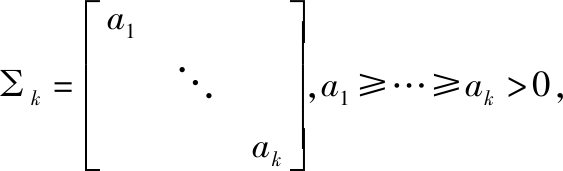
酉矩阵U∈UN×N=[u1,…,uk]和V∈VK×K=[v1,…,vk]。由于除了对角线上是奇异值其他位置都是零，有
CV=U∑VTV⟹CV=U∑⟹Cvi=uiai⟹
ai=Cvi/ui, i=1,…,K
(17)
如图2所示，四阶累积量C可分成俩个重叠子阵
和
并且
的秩为N。按照子空间旋转不变定理，所构造的不包含NF源距离参数的四阶累积量可表示为
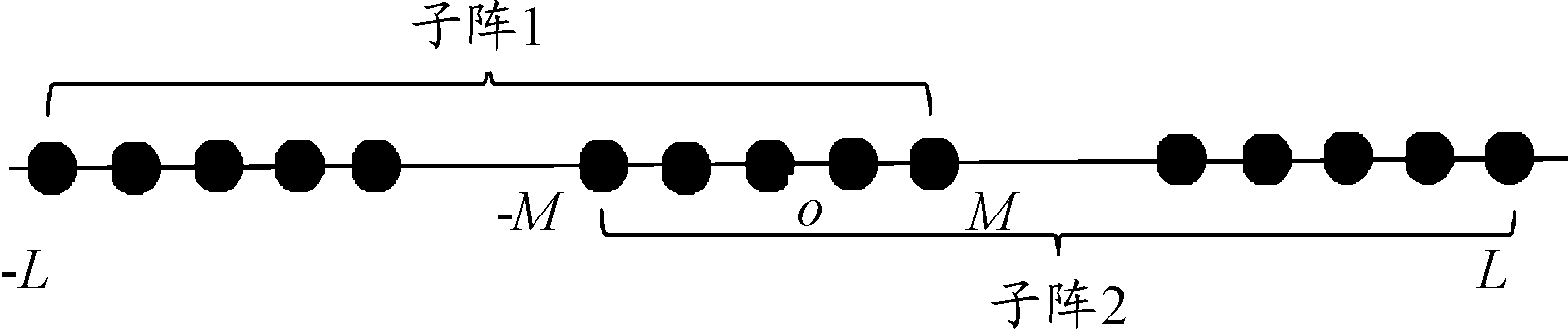
图2 用于DOA估计的2个重叠子阵示意图
Cθ=C1ΙC2
(18)
将Cθ进行特征值分解有
Cθ=TΦT-1
(19)
其中Φ为对角矩阵，其特征值为φi=e-2jγi，i=1,K,N。N阶矩阵A是其对应的特征向量组成，而且跨越了N×N的信号子空间。因而可以得到混合源信号的DOAs
(20)
2.2 近场源距离估计
为了获得更加精确的距离估计，根据不同入射角决定了阵列传感器之间的相位差的原理，区分远近场信号。当信号实际距离参数r远大于d时，SLA所接收到混合源信号的Δθ很小，则相邻传感器的相位差可表示为
Δφ=(4πd/λ)sinθk
(21)
定义一个垂直方向型函数
(22)
δt为振幅加权系数，当θ =θk时，函数值最大，此时取得的角度为混合源的波达方向。将式(22)表达为归一化函数
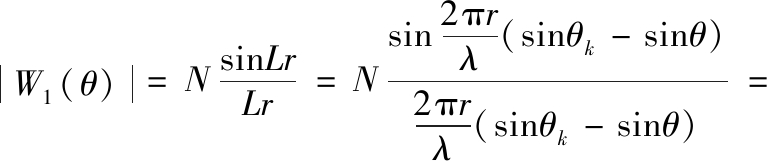
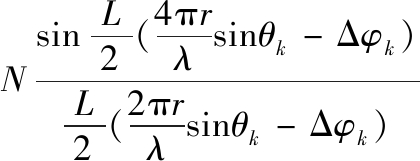
(23)
水平方向型函数表示为
(24)
将上式简化为
|W(θ,φ)|=|W2(θ,φ)|·|W1(θ)|
(25)
我们可以理解为俩个一维线阵方向函数的组合。通过多次改变阵列的相位，并结合式(5)，就可得到近场源的距离参数
(26)
求得的
跟DOA自动生成参数对(θk,rk )。可以按照参数r来辨别NF源和FF源。当r趋于无穷大时，表示对应的是FF源，否则是NF源。最终对混合源信号实现了分类和识别。
2.3 算法步骤总结
本文所提算法可总结为五步：
1) 构造并计算麦克风阵列接收混合源信号的累积量矩阵C，即式(12)；
2) 分析只含DOA的累积量矩阵C，并对C进行奇异值分解；
3) 通过构造的俩个重叠子阵重新表达累积量矩阵C为Cθ；
4) 利用酉ESPRIT算法实现DOA参数估计；
5) 利用相位差将信号强度通过曲线关系转化为距离参数，判断混合源类型；
3 讨论
3.1 阵列孔径
本文算法可以构造(2L+1)×(2L+1)维矩阵，然后将该矩阵分解为俩个2(2M+1)×2(2M+1)维矩阵，分别对应第一子阵和第二子阵。因此，该算法可以利用阵元为2L+1的SLA同时估计4M+1个信号源的DOA。OP MUSIC[11]算法可以定位2L个信源，而MUSIC MVDR[12]算法只能利用2L+1 个麦克风来定位L个信源。因此在阵列孔径上，该算法与OP MUSIC[11]算法接近，比OP MUSIC[11]有更好的性能。由此可以看出，相比MUSIC MVDR[12]算法，本文所提出的方法更好地防止了阵列孔径的损失。
3.2 计算复杂性分析
定义了混合源DOA的范围θ∈[-π/2,π/2]和NF源参数r处于菲涅尔区域.将本文所提算法与MUSIC MVDR[12]算法的复杂度进行对比。本文的计算负荷主要包括构造一个(2L+1)×(2L+1)维四阶累积量矩阵和一个2(2M+1)×2(2M+1)维四阶累积量矩阵、奇异值分解实现、ESPRIT算法和行列式实现与求解。计算复杂度为O{9(2L+1)2N+9(4M+2)2 N+4/3 (2L+1)3+4/3 (4M+1)3 }。而MUSIC MVDR[12]一共执行了三次一维MUSIC搜索，其计算复杂度O{9(2L+1)2N+9(L+2)2N+4/3(2L+1)3+4/3(L+2)3+2·π/Δθ(2L+1)2+K1(2L+1)2 }，K1为FF源个数。可见本文所提出方法的计算量要比MUSIC MVDR[12]算法小。
4 实验仿真
进行Matlab仿真来检验所提算法的有效性和精确性。选取多个等功率撞击信号，且在统计上是相关的，对于所有实验考虑d=λ/4的9元素SLA。选取OP MUSIC[11] 、MUSIC MVDR[12]、TSMDA[14] 这几种方法进行比较，OP MUSIC[11]、TSMDA[14]需要知道信号源个数，同时，OP MUSIC[11]要求知道FF源个数。s(t)=ejφk 具有非高斯形式，假定传感器噪声为高斯白噪声，相位φk∈[0,2π]。信噪比SNR以及均方根误差RMSE的公式可写为
(27)
(28)
K为混合源个数，M为蒙特卡罗实验次数，
是混合源DOA的估计值，θk为假定的值。为了更好地进行比较，采用文献[11]的计算方法，与计算估计值的克拉美罗界(Cramer-Rao)下界作对比。
4.1 验证算法有效性
假定空间中两个处于{20°,1.5λ}和{60°,1λ}的NF源对SLA产生冲击。设SNR=15 dB，快拍数为1 000， d=λ/2。假设采样频率为8 000 Hz，定位结果图形如图3所示。我们做另一个实验，设置d1=λ， d2=λ/2，d3=λ/3，d4=λ/4，其他一切都不变动，图4展示了信号源在20°和60°的波形。
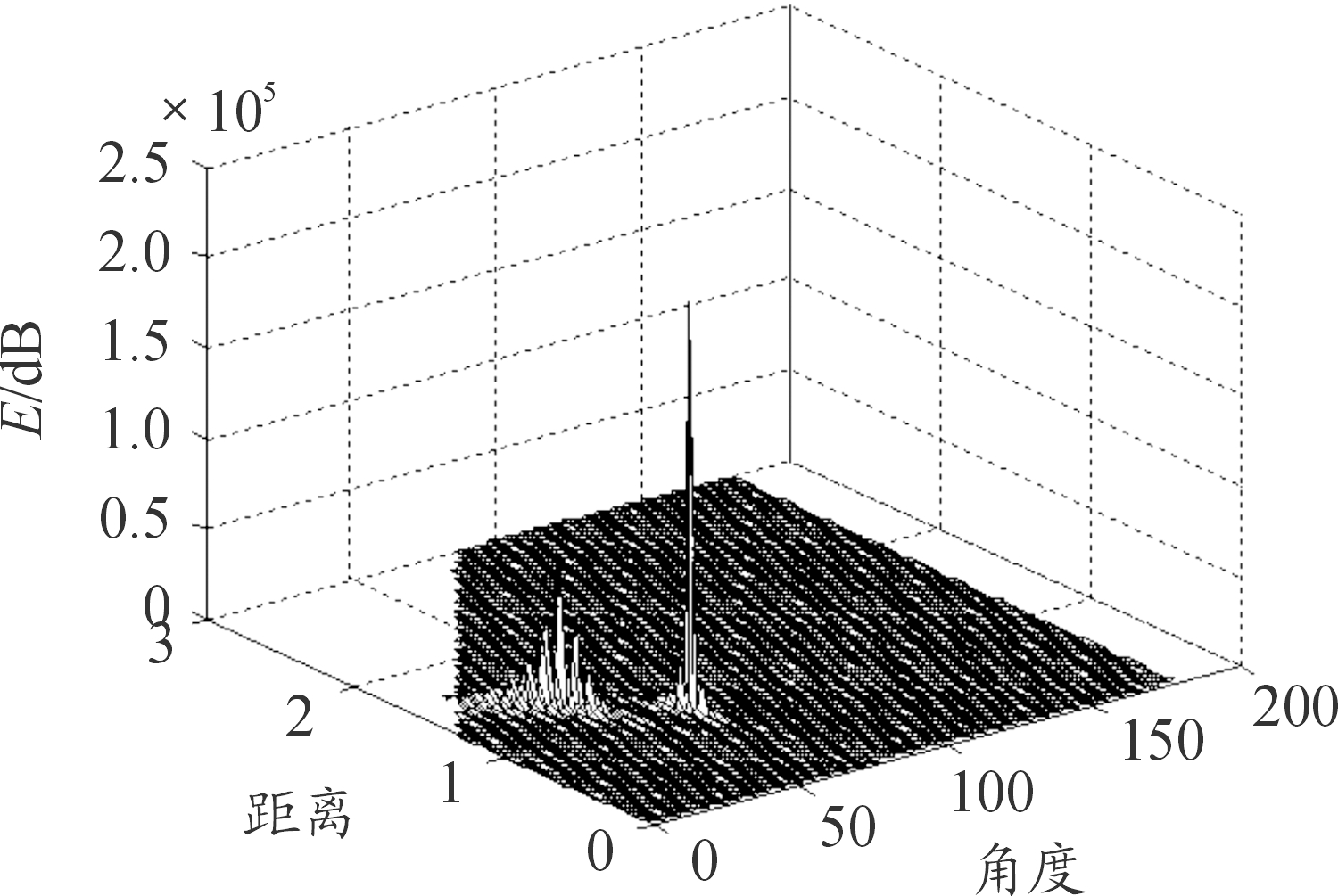
图3 信噪比为15 dB的定位结果图形
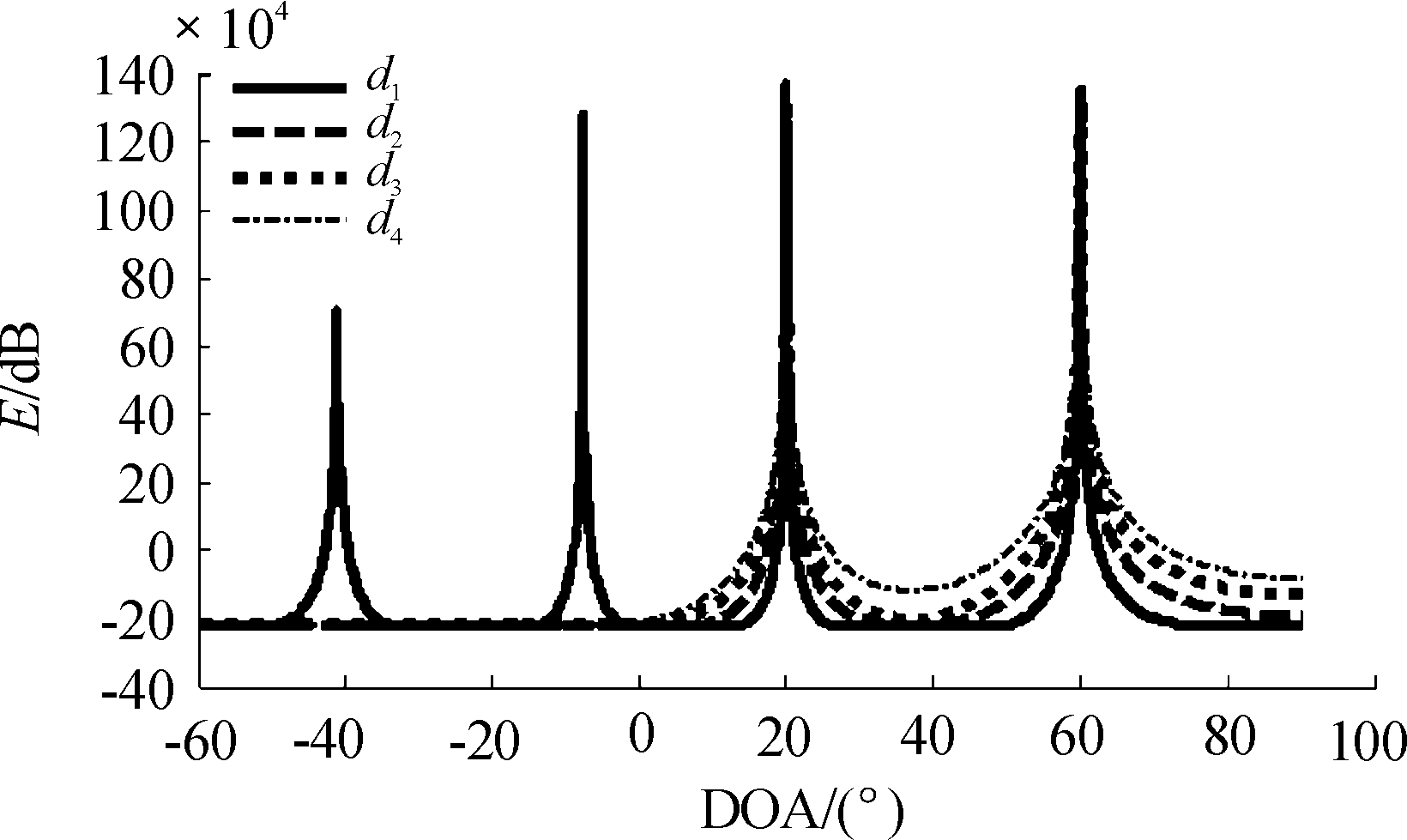
图4 不同阵元间距下对DOA的估计波形
在图3中可以看出，所提算法在SLA场景下成功定位了这两个信号源。从图中可以清楚的了解到信号源(r,θ)和信号强度E，具有良好地估计性能。图4中，在不同的阵元间距下(除了d1=λ的波形呈现4个波峰外)都得到了有效的DOA估计结果。
4.2 定位性能分析
假定两个窄带源信号(由一个来自(10°,+∞)的FF源和一个来自(30°,2λ)的NF源组成的)撞击到SLA上。将估计值的RMSE与从-20 dB到5 dB的SNR进行比较，并在图中显示了基于500个独立试验的结果。快照数设置为200。所提算法与其他算法分别对DOA和距离参数RMSE进行仿真，RMSE和CRB仿真曲线如图5，图6和图7所示。
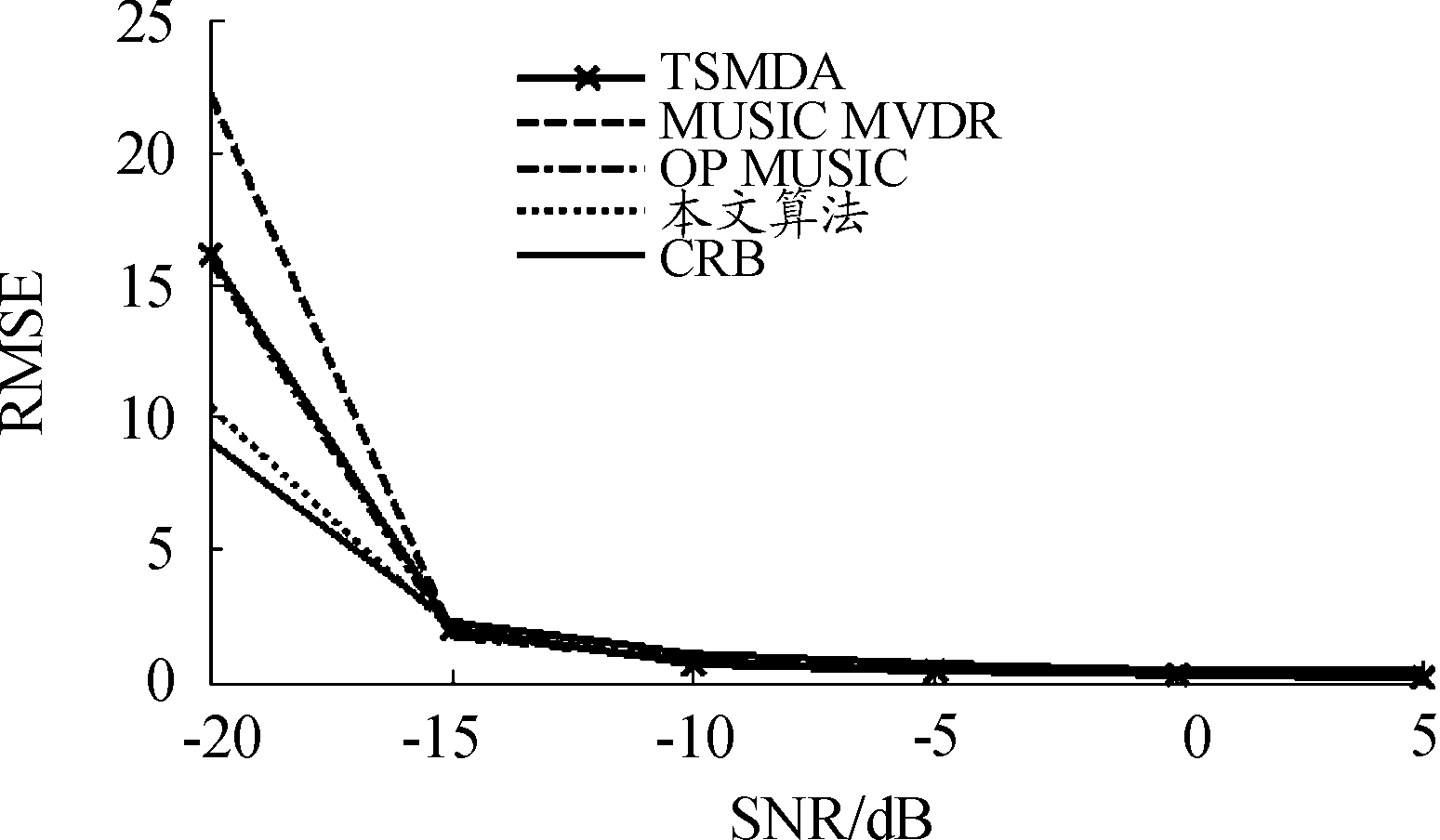
图5 FF源距离RMSE随SNR变化曲线
从图5可以看出，本文算法与MUSIC MVDR[12]、TSMDA[14]的估计精度接近，随着信噪比的增大，OP MUSIC[11] 、MUSIC MVDR[12]、TSMDA[14] 和本文算法能够接近并与CRB曲线重合，从中也可以看出不同信号源的DOA基本相同。但MUSIC MVDR[12]和TSMDA[14 在信噪比比较大时估计效果不佳。在图6中，FF源DOA波形基本与CRB重合，其他算法的波形与CRB相离较远。在图7中，虽然在信噪比低的时候，OP MUSIC[11]较为接近CRB，但当信噪比数值大的时候，NF源波形则偏离了CRB，其RMSE下降缓慢，所以偏离CRB曲线。从结果上看，本文算法对于FF源和NF源波达方向估计精度更接近CRB曲线。需要指出的是，本文算法不需要知道混合源个数K和NF源个数。
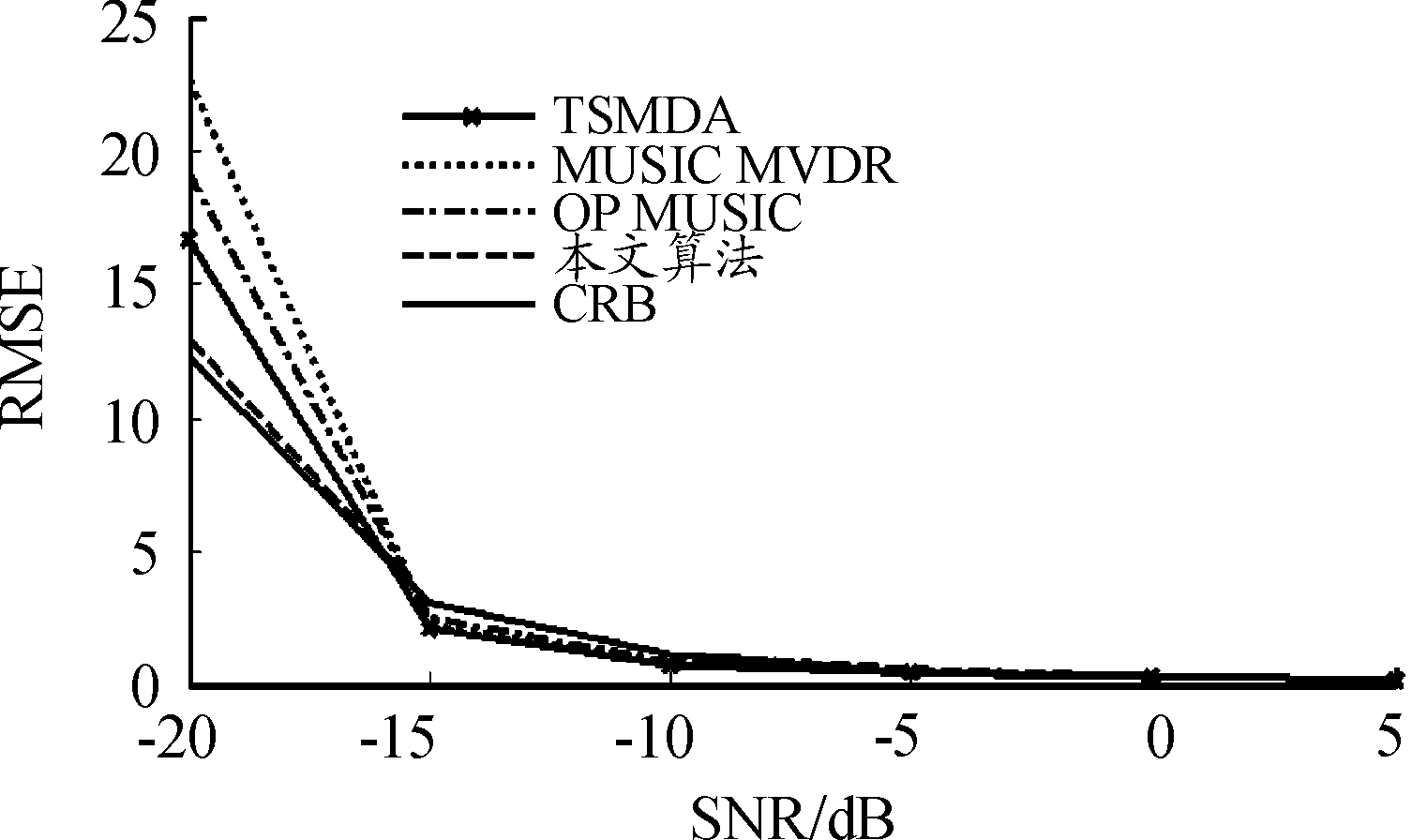
图6 NF源波达方向RMSE随SNR变化曲线
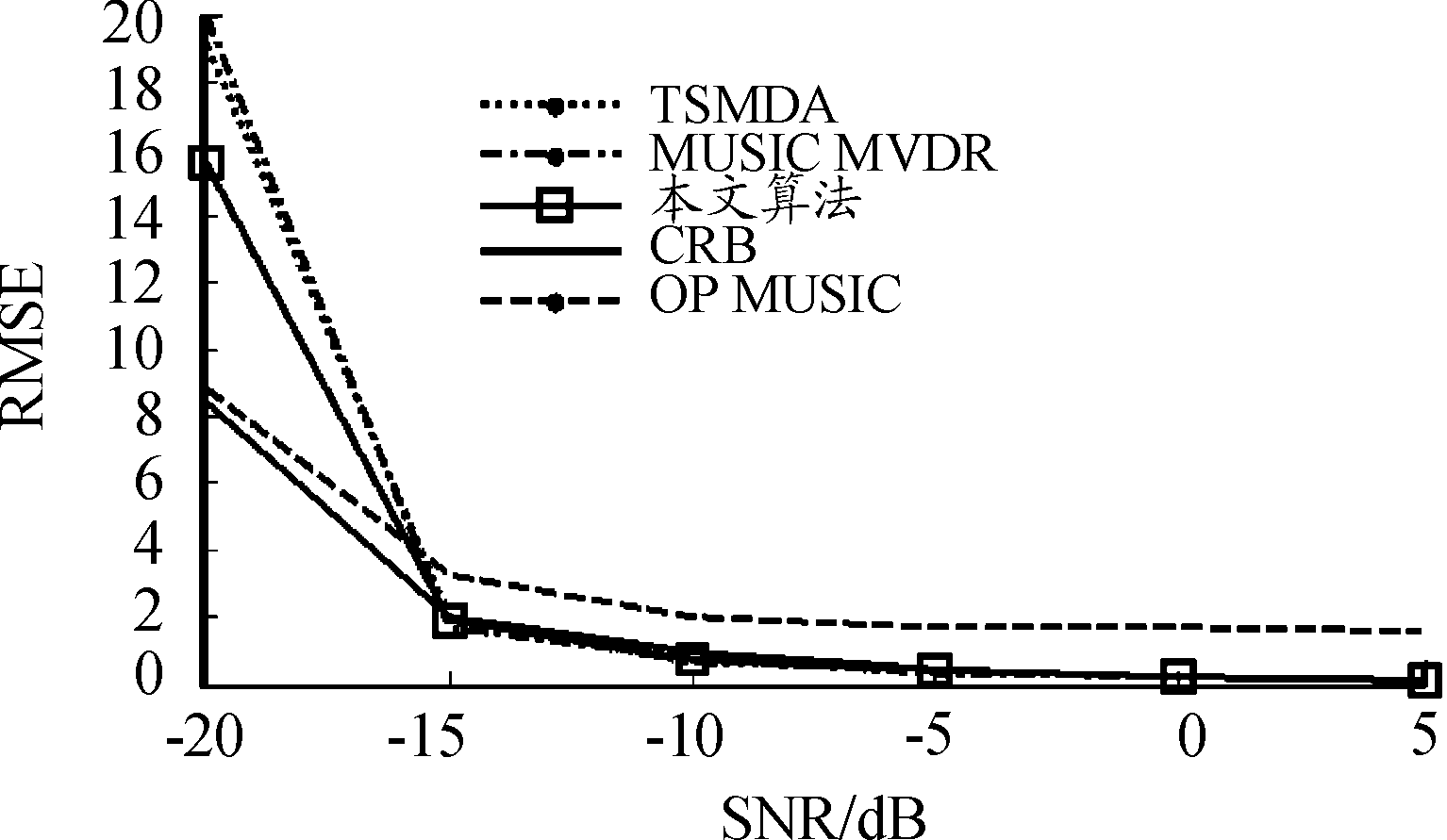
图7 NF源距离RMSE随SNR变化曲线
5 结论
提出了能直接辨别并定位NF和FF源低复杂度混合源定位算法。利用类ESPRIT算法实现更合理的信号定位，并用信号强度与相位差求NF源距离和确定这些源的类型。比现有的一些混合源定位算法，如MUSIC MVDR和OP MUSIC算法扩展了阵列孔径，减小了计算复杂度，提高了NF源距离参数的精度。
[1] HASSAN T U,GAO F,JALAL B,et al.Direction of Arrival Estimation Using Augmentation of Coprime Arrays[J].Information,2018(9):277.
[2] YAN F,LIU S,WANG J,et al.Fast DOA estimation using co-prime array[J].Electron Lett,2018,54:409-410.
[3] KRIM H.Two decades of array signal processing research:the parametric approach[J].IEEE Signal Process.Mag.1996,13:67-94.
[4] ROY R,KAILATH T.ESPRIT-estimation of signal parameters via rotational invariance technique[J].IEEE Trans.Acoust,Speech,Signal Process,1989，37(7)： 984-995.
[5] GAO F,GERSHMAN A B.A generalized ESPRIT approach to direction-of-arrival estimation[J].IEEE Signal Process.Lett,2005，12(3)：254-257.
[6] HE J,SWAMY M N S,AHMAD M O.Efficient application of MUSIC algorithm under the coexistence of far-field and near-field sources[J].IEEE Trans.Signal Process,2012，60(4)：2066-2070.
[7] JOHNSON R C.Antenna Engineering Handbook[M].3rd ed.New York,USA:McGraw-Hill,1993：9-12.
[8] ZHI W,CHIA M Y W.Near-field source localization via symmetric subarrays[J].IEEE Signal Process.Lett,2007，14(6)：409-412.
[9] HE J,SWAMY M N S,AHMAD M O.Efficient application of MUSIC algorithm under the coexistence of far-field and near-field sources[J].IEEE T rans.Signal Process,2012,60:2066-2070.
[10] LIANG J,LIU D.Passive localization of mixed near-field and far-field sources using two-stage music algorithm,IEEE Trans.Sig.Process.2010(58) 108-120.
[11] HE J,SWAMY M,AHMAD M O,Efficient application of MUSIC algorithm under the coexistence of far-field and near-field sources[J].IEEE Trans.Sig.Process,2012(60):2066-2070.
[12] XIE J,TAO H,RAO X,et al.Passive localization of mixed far-field and near-field sources without estimating the number of sources[J].Sensors，2015(15)：3834-3853.
[13] LIU G,SUN X.Spatial differencing method for mixed far-field and near-field sources localization[J].IEEE Sig.Process.Lett,2014(21)：1331-1335.
[14] LIU G,SUN X.Two-stage matrix differencing algorithm for mixed far-field and near-field sources classification and localization[J].IEEE Sens.J,2014(14):1957-1965.
[15] WANG B,ZHAO Y,LIU J.Mixed-order MUSIC algorithm for localization of far-field and near-field sources[J].IEEE Signal Processing Letters,2013(4)：311-314.
[16] 林波.阵列测向的稀疏超分辨方法研究[D].长沙：国防科学技术大学,2016.
[17] 刘亮,陶建武,黄家才.基于稀疏对称阵列的近场源定位[J].电子学报,2009,37(6):1307-1312.
[18] 朱灿萍.利用菲涅尔区的快速PO算法研究[D].上海：上海交通大学,2015.
[19] 魏平，肖先赐．基于四阶累积量的阵列扩展[J]．电子科学学刊,1997,19(6):745-750.