多层钢筋混凝土靶是钻地弹丸的重要目标之一。大量试验表明,钻地弹丸在斜侵彻多层靶过程中很容易发生如图1所示的弹道偏转,使弹体着靶姿态变差、侵彻阻力和弯矩陡增,给弹体的结构强度和装药安定性带来了极大的风险。因此,如何预测和控制弹丸斜侵彻多层靶的弹道是近年来钻地弹药领域的研究重点和热点之一。
目前关于弹丸斜侵彻混凝土靶弹道预测的外文资料并不多见,而国内则开展了大量研究,但主要集中于对斜侵彻整体靶的数值模拟和理论分析,较少涉及斜侵彻多层靶的弹道问题。闪雨等[1-3]针对弹体非正侵彻混凝土问题开展了质量侵蚀和运动轨迹研究;朱光辉[4]针对动能弹斜侵彻混凝土靶的跳弹问题,进行了理论和数值模拟分析,提出了头部形状、着角、着速对动能弹跳弹有重要影响的观点;王松川[5]针对弹体斜侵彻半无限介质的问题,采用弹靶分离思想建立了弹道预测模型,开发了快速计算程序;周燕[6]利用ANSYS/LS-DYNA软件分析了钻地弹头部形状、着角、着速、攻角对土壤中弹道的影响特性,获得了钻地弹在侵彻土壤过程中的运动轨迹;吴广[7]理论分析了不同头部结构对钻地弹侵彻半无限厚混凝土的弹道影响特性,但上述研究均未涉及侵彻多层靶的弹道稳定性问题。代廷静[8]通过对不同弹形弹丸侵彻多层靶的弹道进行数值模拟,提出了一种可提高弹道稳定性的扩尾形弹体结构,并进行了试验验证;程伟[9]采用数值模拟方法研究了偏航角速度对弹丸侵彻多层靶弹道影响,但采用数值模拟方法进行弹道预测所需的周期较长、效率较低。为实现弹丸斜侵彻多层靶弹道的快速预测,本文提出了一种弹丸斜侵彻多层靶弹道的工程分析方法。
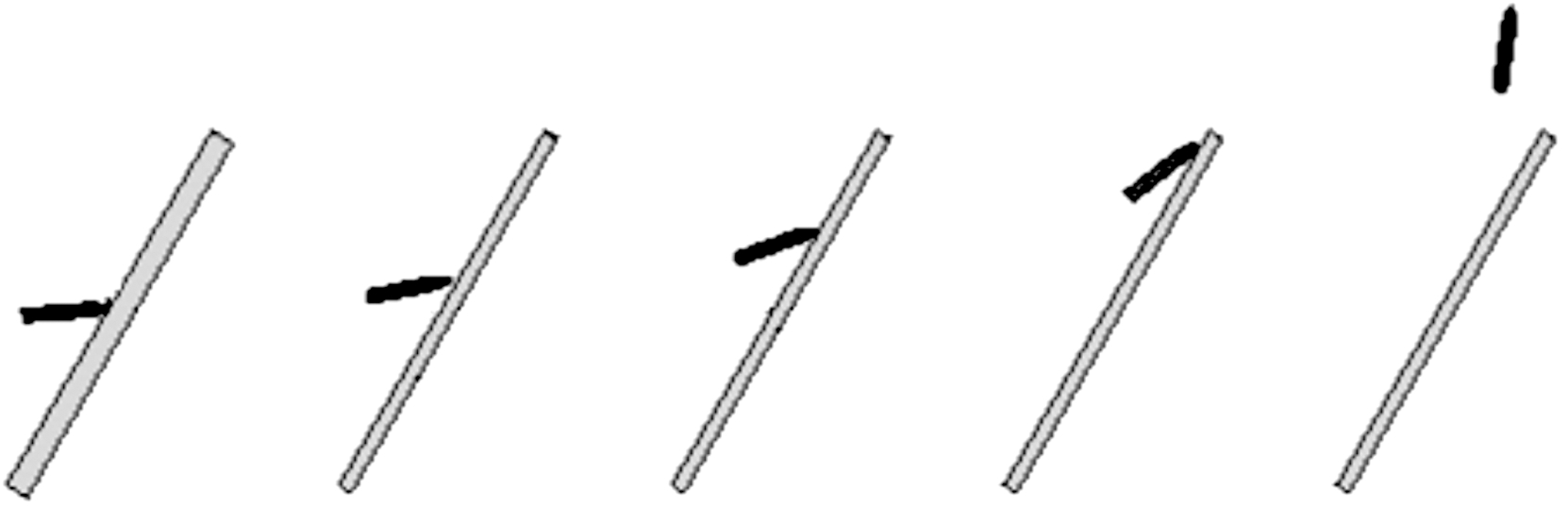
图1 侵彻多层靶过程中的弹道偏转示意图
1 斜侵彻多层靶弹道计算模型
1.1 坐标系建立
弹丸斜侵彻多层靶涉及弹体坐标系、靶体坐标系和地面坐标系等3个坐标系,为便于计算,可建立如图2所示的弹体坐标系xdydzd、靶体坐标系xbybzb和地面坐标系xgygzg。

图2 弹道计算所需的坐标系
弹体坐标系以弹尖为原点,弹轴指向尾部为xd轴正向,垂直于弹轴的地面上方为yd轴正向,根据右手定则确定zd轴正向。
靶体坐标系以弹着点为原点,指向内部的靶面法向为xb轴正向,平行靶面的地面上方为yb轴,根据右手定则确定zb轴正向。
地面坐标系以弹着点为原点,指向靶体内部的水平线为xg轴正向,垂直地面向上为yg轴,根据右手定则确定zg轴正向。
假设弹丸是刚性弹丸,不考虑其在变形过程中有任何弹性变形。
假定侵彻过程中弹轴始终位于弹体坐标系、靶体坐标系、地面坐标系z=0的坐标平面内,且假定弹体着靶瞬间,弹体的速度方向与地面坐标系xg轴保持一致、3个坐标系的原点重合。从而,随着侵深的增加,弹体坐标系原点将位于地面坐标系的某点P(px,py,0);若任意时刻弹轴负向与地面坐标系xg轴的夹角为βd,则地面坐标系到弹体坐标系的变换可看成先绕X轴旋转180°,再绕Z轴旋转180°+βd,即变换阵为
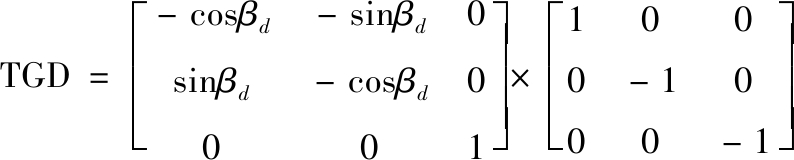
(1)
弹体坐标系到地面坐标系的变换矩阵可述为
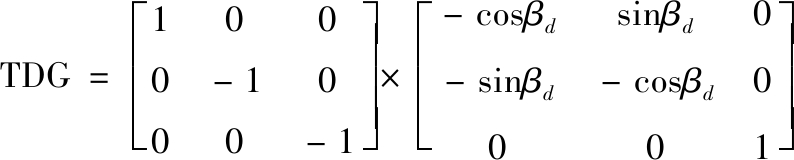
(2)
类似地,着角α不为零时,靶体坐标系xb轴将与地面坐标系xg轴形成夹角α。从而,地面坐标系到靶体坐标系的变换可看成绕Z轴旋转-α°,即变换矩阵为

(3)
1.2 弹体微元与靶标的接触判断
弹丸在斜侵彻多层靶过程中,与靶标的接触状态有多种,有时部分弹体微元与某层靶标发生接触碰撞,有时弹体与某几层靶标发生接触碰撞,有时弹体不与靶标发生接触而处于自由旋转状态,弹体微元只有与某层和某几层靶标发生接触时才会产生阻力,因此须判断弹体微元与靶标的接触碰撞关系。
对任一弹体微元(xd,yd,zd),其转换到地面坐标系的坐标为

(4)
再利用地面坐标系到靶体坐标系的转换关系,可得到弹体微元在靶体坐标系内的坐标值
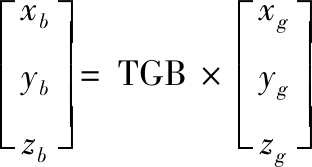
(5)
对比该坐标值与多层靶的位置参数,即可判断弹体微元是位于某层靶标内部或外部,若弹体微元位于某层靶标内部,则有可能产生侵彻阻力;若全部弹体微元均位于各层靶标外部,则表示弹体处于自由飞行状态。
1.3 弹体微元的法向速度计算
在斜侵彻条件下,速度矢量可能不与弹轴重合(如图3所示),从而导致弹体微元上的法向速度存在一定差异,进而导致弹体表面微元的法向阻力不符合轴对称关系。弹体表面微元的法向速度矢量可通过以下方法计算得到。
对任一弹体表面微元,其在弹体坐标系中的坐标为(xd,yd,zd),其切向角为θ,则该微元所处的圆锥曲面方程(弹体坐标系)可表述为
(6)
由此可得到该点归一化的法向量为![]() 其中
其中
(7)
若弹丸的速度矢量形式![]() 通过向量的点积计算,可得到微元的法向速度为
通过向量的点积计算,可得到微元的法向速度为![]() 若vn小于0,则表示微元法向速度与微元法向反向,该微元将不会与目标发生碰撞;若vn大于0,则表示微元将会与靶标发生碰撞。
若vn小于0,则表示微元法向速度与微元法向反向,该微元将不会与目标发生碰撞;若vn大于0,则表示微元将会与靶标发生碰撞。
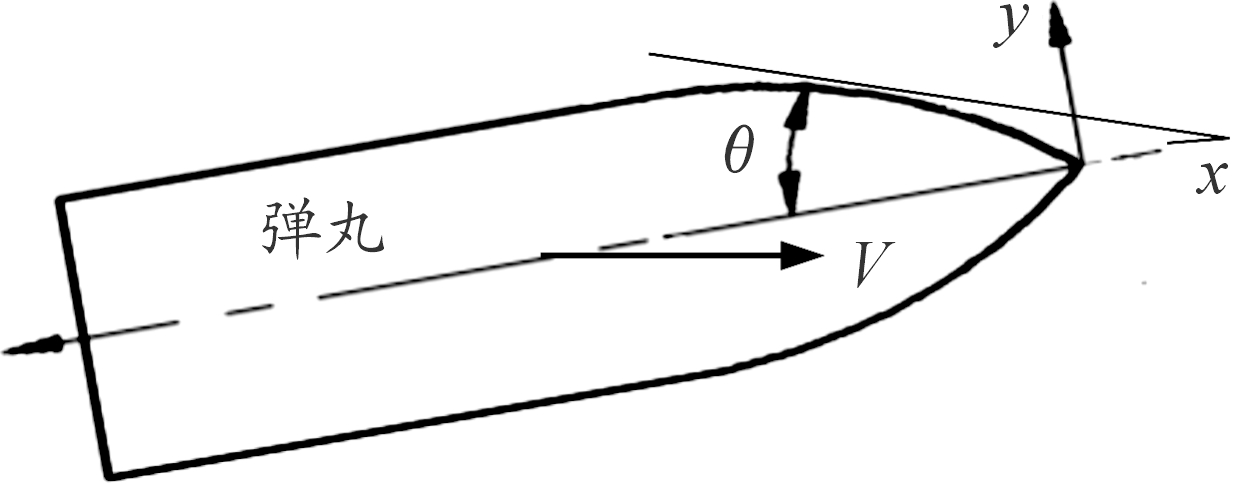
图3 速度矢量与弹轴的关系示意图
1.4 弹道轨迹计算
假定弹体微元与混凝土靶标的碰撞力符合动态空腔膨胀理论,则微元的法向应力可表述为[10-15]
(8)
式中,σn为弹体表面微元的法向阻力;A和B为与混凝土介质材料、靶标厚度、侵彻速度有关的常数;Y为混凝土材料的屈服强度;ρ为混凝土材料的密度;vn为弹体表面微元的法向速度。
根据图4,对弹体表面微元的法向阻力σn和摩擦阻力σt进行分解,可得到弹体表面微元受力对弹体轴向阻力fax和横向阻力f⊥的贡献:
![]()
(9)
式中,θ为弹体表面微元的切向角;dS为弹体表面微元的面积。
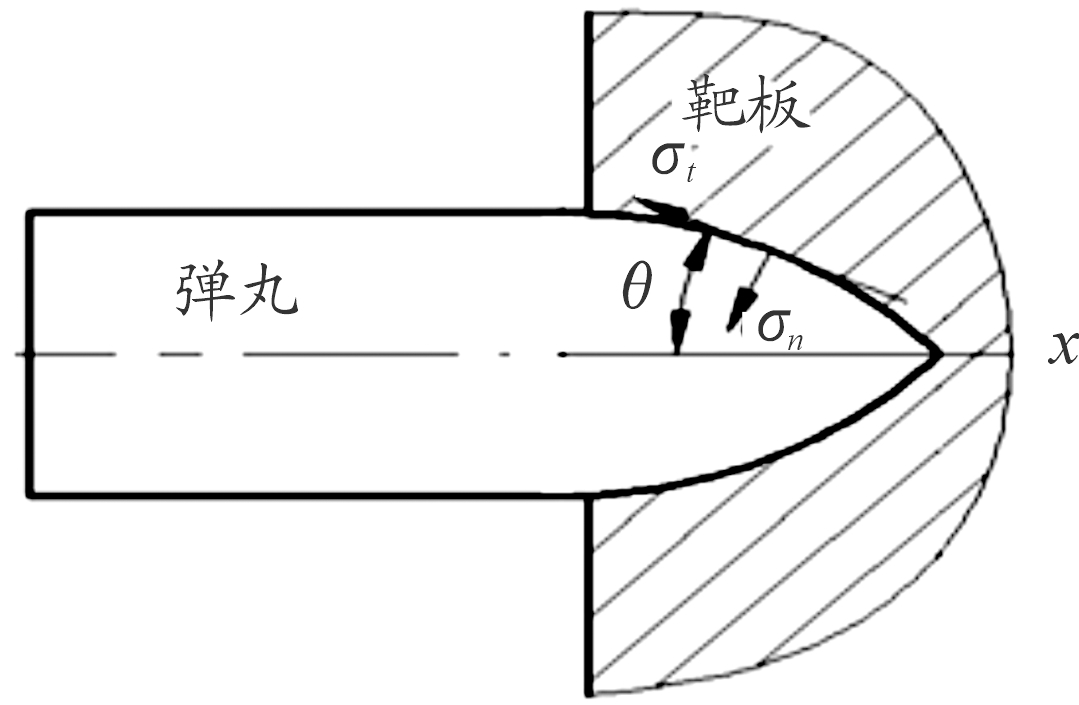
图4 弹体微元的受力示意图
假定弹丸侵彻多层靶过程中不发生变形和侵蚀,则弹体的弹轴、质心、外形均保持不变。一方面,对fax和f⊥进行积分,可求得弹体的轴向阻力Fax和横向阻力F⊥,即
(10)
(11)
若弹体的质量为m,则弹体轴向过载Aax和横向过载A⊥可分别为
Aax=Fax/m
(12)
A⊥=F⊥/m
(13)
另一方面,弹体微元轴向阻力fax和横向阻力f⊥会使弹体发生旋转。设微元与质心的轴向距离为l,微元与弹轴的径向距离为r,则微元横向阻力f⊥对质心位置的转动力矩为
m⊥=f⊥·l
(14)
弹体表面微元轴向阻力fax对质心位置的转动力矩为
max=fax·r
(15)
对弹体表面轴向、周向全部微元的力矩进行积分并叠加,即可得到钻地弹的合成转动惯量Md。若弹体绕对称轴的转动惯量为Iz,则旋转角加速度可表述为
η=Md/Iz
(16)
将上述参数转换至地面坐标系,就可确定任意时刻地面坐标系中弹体质心的位置、弹体的速度及弹轴方向等参数,从而可获得侵彻弹道数据。
2 斜侵彻多层靶弹道计算模型
根据前述计算模型可知,弹体斜侵彻多层靶是一个与时间有关的连续运动状态变化过程,无法通过解析方式直接表达。弹体斜侵彻多层靶的弹道计算流程如图5所示,并编制了Matlab程序。
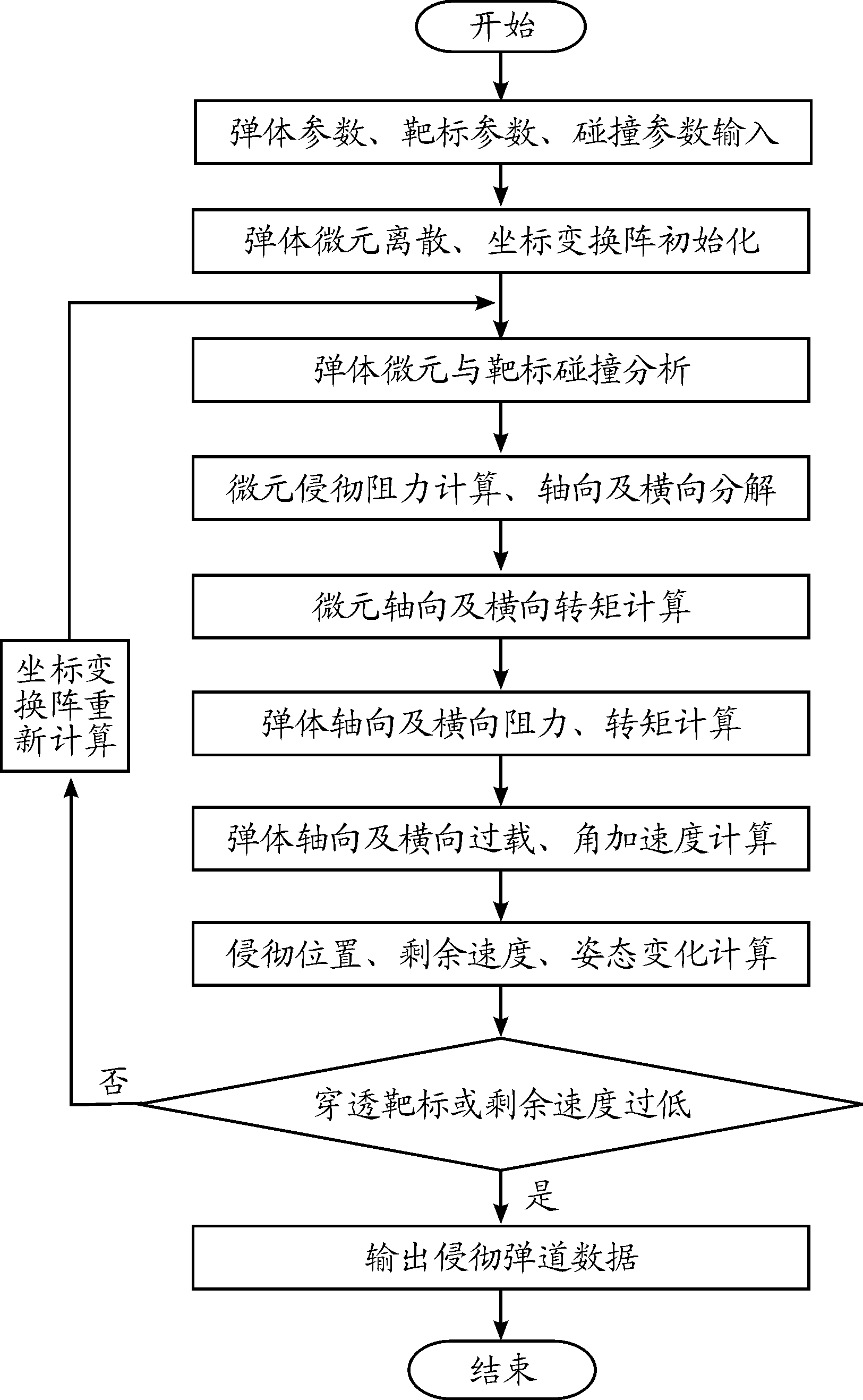
图5 斜侵彻多层靶弹道计算流程框图
首先,对弹体侵彻外形进行轴向和周向离散,获得弹体表面微元的形状和矢量参数,并根据碰撞条件确定弹体坐标系、地面坐标系、靶体坐标系之间的变换矩阵和逆矩阵:
for i=1:NN+1;
Xd(i)=(i-1)*Len D/NN; %母线横坐标
Yd(i)=double(subs(f1,ttd)); %母线纵坐标
end
for i=1:NN;
Yd1(i)=(Yd(i+1)-Yd(i))/(Len D/NN);
%微元斜率
end
bt=-AgBt*pi/180; %弹轴负向与地面X轴夹角
TZDG=[-cos(bt) sin(bt) 0; -sin(bt) -cos(bt) 0; 0 0 1];
TXDG=[1 0 0; 0 -1 0; 0 0 -1];
TDG=TXDG*TZDG; %弹体到地面的转换
……
其次,根据空腔膨胀理论计算弹体表面微元的法向阻力及轴向阻力分量、横向阻力分量,并分别计算轴向阻力分量、横向阻力分量贡献的转动力矩:
sn=AA+BB*vn*vn; %微元法向应力
Fax=Fax+sn*tf1*(-1)*dS; %弹体轴向阻力累加
Fhx=Fhx+sn*tf2*(-1)*dS; %弹体横向阻力累加
Mrot=Mrot+sn*tf2*(-1)*dS*(CenterD-Xd(i));
……
再次,计算弹体在离散时间区间内的加速度、速度、侵彻位置、侵彻姿态的变化情况;最后,根据弹体对靶体的出靶状态或剩余速度情况,确定是否进行下一次循环计算。
YY(tNLp)=YY(tNLp-1)+(XX(tNLp)-XX(tNLp-1))*tan(-tBt);
tPenY=YY(tNLp); %弹尖坐标修正
TT(tNLp)=(XX(tNLp)-XX(tNLp-1))/(-Vax(tNLp-1));
Vax(tNLp)=Vax(tNLp-1)+Fax/MassD*TT(tNLp);
Vhx(tNLp)=Vhx(tNLp-1)+Fhx/MassD*TT(tNLp);
if tbInOne==0%未与靶标碰撞
AngV(tNLp)=AngV(tNLp-1);
tBt=tBt-AngV(tNLp)*TT(tNLp);
else if tbNtRot==1 %弹体受靶标约束
AngV(tNLp)=0;
tBt=tBt-0.5*AngV(tNLp)*TT(tNLp);
else %弹体受转矩作用
AngV(tNLp)=AngV(tNLp-1)+Mrot/Id*TT(tNLp);
tBt=tBt-0.5*AngV(tNLp)*TT(tNLp);
end
3 实例计算
利用上述斜侵彻多层靶弹道计算模型和计算程序,对重量19.2 kg、直径φ100 mm、CRH=2、过质心横截面对称轴转动惯量为1.79 kg.m2的尖卵圆柱形弹丸以3°攻角、20°着角、900 m/s速度侵彻8层素混凝土靶(压缩强度40 MPa、层间距3 m、第1层厚度300 mm、其余层厚度180 mm,质量配筋率为2.2%)的弹道进行了计算,得到了如图6所示的计算曲线,与相近条件炮击试验(试验靶板为质量配筋率1%的钢筋混凝土,实例计算为素混凝土靶板;试验攻角通过高速摄影判读约为3度)的结果(弹道轨迹通过实测各层靶板侵孔中心位置获得,弹轴偏转角通过高速摄影判读弹丸侵彻各层靶板前的姿态获得)进行了对比。从图6可以看出,实例计算结果与试验结果基本相符,存在一定差异的可能原因是本文算法未考虑钢筋的影响。
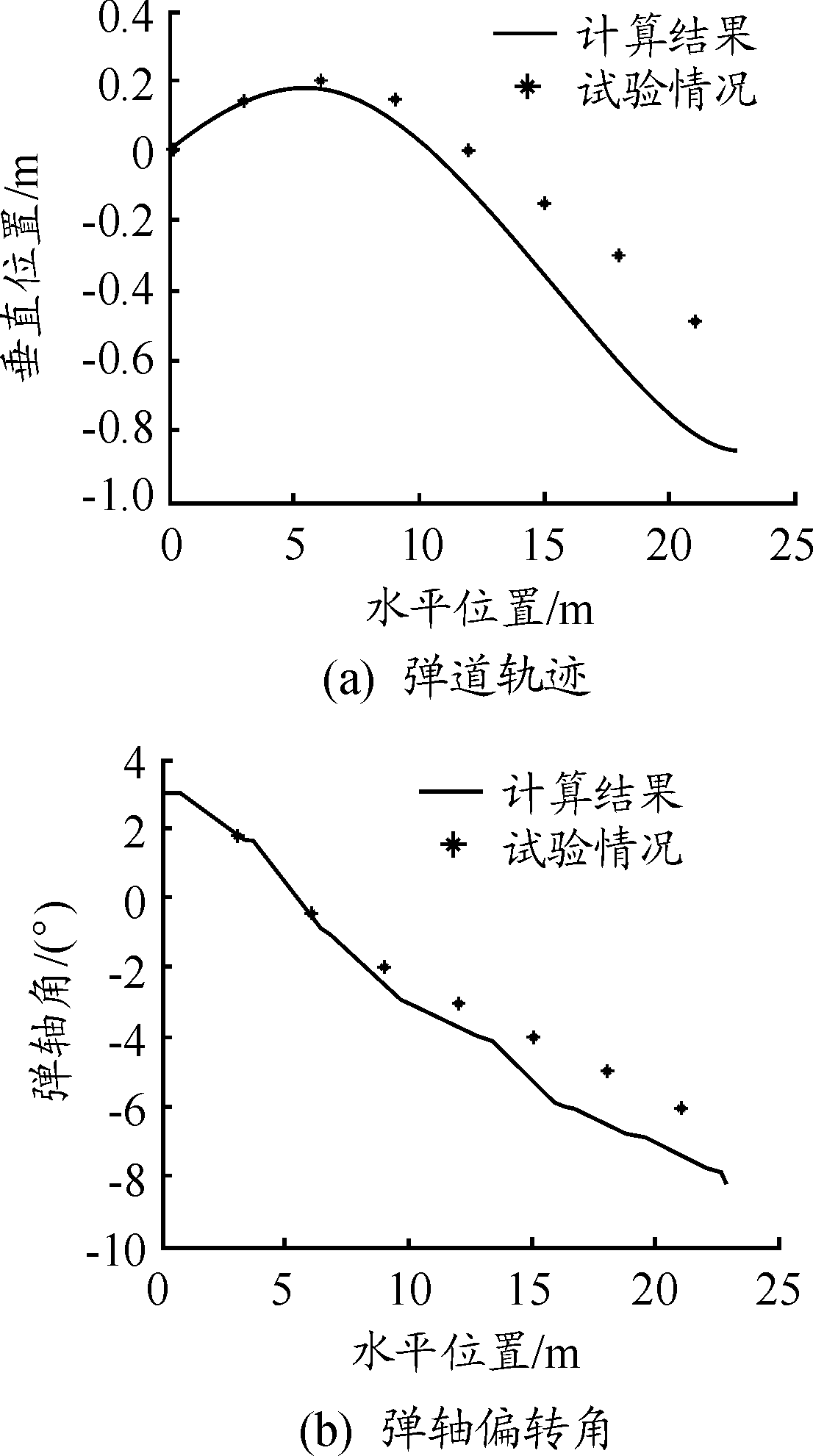
图6 算例1弹道计算曲线
重量19.2 kg、直径φ100 mm、CRH=3.3、过质心横截面对称轴转动惯量为1.79 kg·m2的尖卵圆柱形弹丸以2°攻角、20°着角、900 m/s速度侵彻8层混凝土靶(压缩强度40 MPa、层间距3 m、第1层厚度300 mm、其余层厚度180 mm)的弹道计算曲线如图7所示,与相近条件炮击试验(试验靶板为质量配筋率1%的钢筋混凝土,实例计算为素混凝土靶板;试验攻角通过高速摄影判读约为2°)的结果(弹道轨迹通过实测各层靶板侵孔中心位置获得,弹轴偏转角通过高速摄影判读弹丸侵彻各层靶板前的姿态获得)进行了对比。从图7可以看出,实例计算结果与试验结果基本相符,存在一定差异的可能原因是本文算法未考虑钢筋的影响。
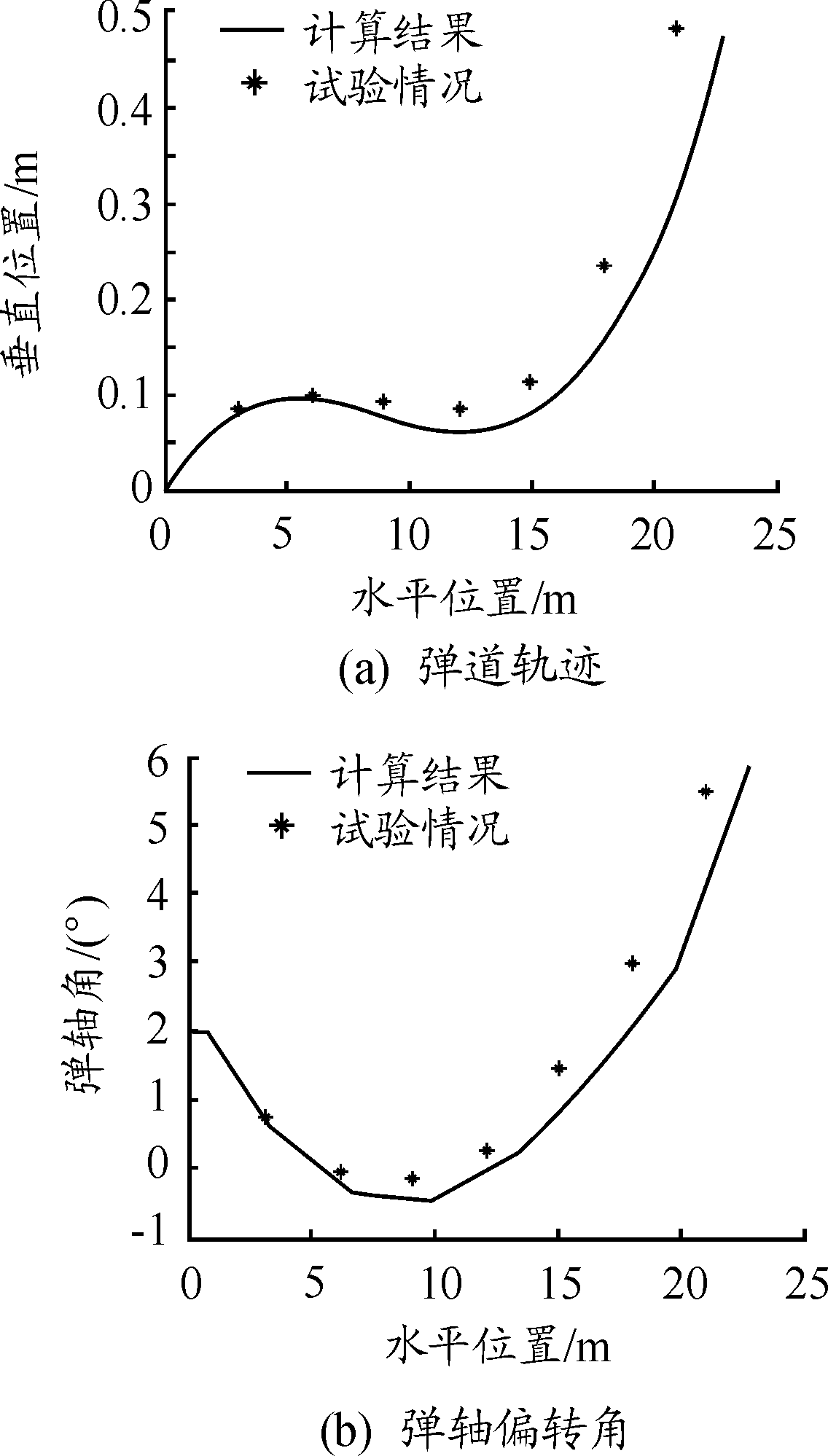
图7 算例2弹道计算曲线
4 结论
1) 应用空腔膨胀理论、刚体动力学理论初步实现了弹丸斜侵彻多层靶的快速弹道预测,计算结果与相近着靶条件的试验结果基本一致;
2) 本文建立的斜侵彻多层靶弹道预测方法和计算程序为弹道稳定性影响因素及特性分析、弹丸的优化设计提供了重要手段。
[1] 闪雨.弹体非正侵彻混凝土质量侵蚀与运动轨迹研究[D].北京:北京理工大学,2015.
[2] 畅博,李继东,敬怡东,等.辅助药型罩材料对超聚能射流成型和侵彻能力影响的仿真研究[J].兵器装备工程学报,2019,40(12):35-39.
[3] 闪雨,黄风雷.动能弹非正侵彻混凝土弹道稳定性研究[J].爆炸与冲击,2014.
[4] 朱光辉.动能弹斜侵彻混凝土靶跳弹规律分析[D].南京: 南京理工大学,2007.
[5] 王松川.弹体斜侵彻弹道快速预测方法研究[D].长沙:国防科技大学,2011.
[6] 周燕.钻地弹土中弹道影响因素的数值模拟研究[D].南京:南京理工大学,2009.
[7] 吴广.头部形状对弹丸半侵彻弹道的影响研究[C]//第十四届全国战斗部与毁伤技术学术交流会论文集.重庆: 2015.
[8] 代廷静.一种提高弹道稳定性的弹体结构[C]//第十四届全国战斗部与毁伤技术学术交流会论文集.重庆:2015.
[9] 程伟.偏航角速度对弹丸侵彻多层靶弹道影响[C].第十四届全国战斗部与毁伤技术学术交流会论文集.重庆:2015.
[10] LUK V K,FORRESTAL M J.Penetration into semi-infinite reinforced-concrete targets with spherical and ogival nose projectiles[J].Int.J Impact Engng,1987,6(4):291-301.
[11] CHEN X W,LI Q M.Deep penetration of a non-deformable projectile with different geometrical characteristics[J].Int J Impact Eng,2002,27:619-637.
[12] 康海峰,代廷静.弹体形状对侵彻弹道的影响分析[J].弹箭与制导学报,2012.4(32):73-76.
[13] 康海峰;动能弹非正侵彻弹道性能研究[D].南京:南京理工大学,2012.
[14] 张攀军;动能弹高速侵彻混凝土靶的规律研究[D].南京:南京理工大学,2011.
[15] 张雪岩,武海军,李金柱,等.弹体高速侵彻两种强度混凝土靶的对比研究[J].兵工学报,2019,40(02):276-283.