身管弹线膛一体化锻造技术在专用的四锤头精锻机上将毛坯一次锻打出弹膛和线膛。精锻后,身管内膛无需进行后续机加工[1],是一种净成形技术[2]。其特点有:锻造效率高,成品件寿命长、力学性能好等优点。目前身管内膛加工是采用线膛精锻加上后续弹膛机加工方法成形,导致弹线膛同轴度低、弹膛及线膛过渡部位尺寸精度差,造成自动武器射击精度不高,身管使用寿命低。而身管弹线膛一体化径向精锻技术作为当前兵器制造领域的先进制造技术之一,不仅可以解决上述问题,还可以减少加工流程、降低生产成本。
在身管精锻成形过程中,锻件的塑性变形远远大于弹性变形,因此以往的研究忽略了锻件变形后的回弹问题。但锻件在巨大的锻造压力下,在锤头卸载阶段和锻件卸下后会产生不可恢复的弹性变形,它将使身管的内外径尺寸出现误差,并长期保留下来,影响身管尺寸精度。
在身管精锻成形方面,樊黎霞等[3]对身管径向精密锻造的塑性应变与锻造比进行了研究,提出了局部锻造比的概念,并通过局部锻造比给出了单次锻打所产生的塑性应变增量。张鹤词[4]研究了阳线锻不到、膛线锻不透以及膛线过锻的特点和表现形式,并建立了3种缺陷的判断准则以及身管内膛成形极限图。张雪[5]建立了以径向和周向塑性应变为表征的身管内膛膛线锻透的判断准则,得到了以锻造比及毛坯内外径比为表征的身管锻透极限图。毕梦凡[6]分析了锻造工艺参数对锻后身管力学性能的影响,提出并优化了基于多参数响应面的身管力学性能预测模型。徐宝池[7]采用压缩实验、织构分析和有限元技术等分析测试方法研究了锻造比对5.8 mm口径精锻身管力学性能各向异性的影响。
在管件回弹研究方面,杨杰章[8]通过拉伸实验获得高温下弹性模量E与温度T的函数关系,进而推导出回弹计算公式,但未对理论推导出的回弹公式作进一步的误差分析。Hideaki Abe等[9]研究了工艺参数对皮尔格冷轧管尺寸精度的影响,认为冷轧过程中的不均匀回弹现象导致了冷轧管的椭圆度以及壁厚偏差。楚志兵等[10]以皮尔格冷轧不锈钢管为例,提出了皮尔格冷轧不锈钢管的回弹预测模型。王环珠等[11]采用有限元仿真软件模拟不同工艺参数下的皮尔格冷轧过程,对比分析了工艺参数对管材的尺寸精度以及回弹量的影响规律。Hui Long[12] 运用数值模拟技术分析工件与模具接触面之间的摩擦力、接触力、温度分布情况等因素对精锻件弹性变形产生的影响。
为了得出回弹与身管内、外表面径向尺寸的关系,本文以5.8 mm口径弹线膛同锻身管为研究对象,使用ABAQUS仿真软件分析研究过程参数对身管线膛部位内、外表面径向尺寸和回弹的影响规律。以便在设计芯棒和选择过程参数时考虑锻件径向尺寸变化的补偿。
1 身管精锻模型建立
身管由线膛和弹膛两部分组成。如图1所示,在锻造过程中,可将毛坯分为下沉段、锻造段和整形段三个阶段。在下沉段,毛坯内表面未与芯棒接触,毛坯内外径同时减小,壁厚基本不变,视为减径阶段;在锻造段,毛坯内表面与芯棒接触,壁厚减小,视为减壁厚阶段,几乎所有的毛坯塑性变形都发生在此阶段;在整形段,毛坯内外径基本不变,不发生进一步的塑性变形。
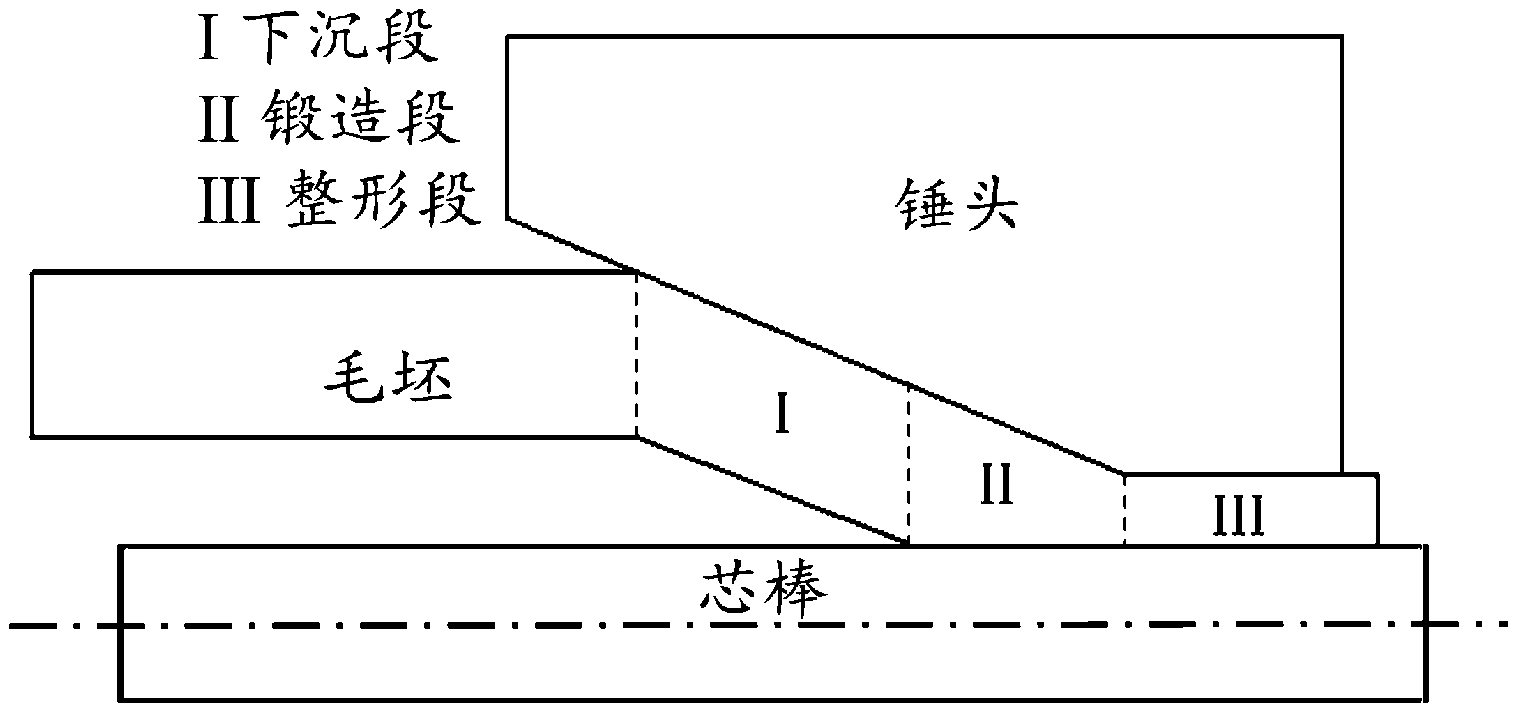
图1 身管精锻过程示意图
身管弹线膛锻打过程主要包括线膛锻打和弹膛锻打两个过程。线膛锻打过程中,芯棒相对锤头固定不动,毛坯在尾端夹头(夹持力)和前端挡块的作用下做旋转和进给运动,锤头作周期性的径向下压运动,使毛坯内壁贴合芯棒线膛,成形出膛线。
1.1 身管精锻有限元模型建立
根据身管精锻流程,使用有限元软件ABAQUS模拟身管线膛精锻过程。为降低计算量,对精锻过程作如下简化:考虑到四个锤头围绕毛坯对称分布,使用二维轴对称有限元模型代替三维模型;忽略锻打过程中芯棒、毛坯的旋转运动。简化后的有限元模型主要包括4个部件,分别是锤头、挡块、芯棒和毛坯。
锤头、芯棒的材料为硬质合金,其硬度、强度均高于毛坯材料,在锻打过程中产生的弹性变形很小,视为刚体。该径向锻造过程属于冷锻过程,因此忽略材料的温升对流变应力的影响,使用下式表述简化的材料本构模型:
σ=Bεn
(1)
式中,σ是等效应力; ε是等效塑性应变;n是加工硬化指数;B是常数。材料性能参数由拉伸试验获得,见表1。
表1 材料力学性能参数

杨氏模量/GPa泊松比屈服强度/MPaBn2070.392712250.065
使用罚函数接触法定义各部件之间的摩擦接触,滑移公式选取有限滑移公式。毛坯与锤头间的摩擦因数为0.25,毛坯与挡块间的摩擦因数为0.15,毛坯与芯棒间的摩擦因数为0.05。划分网格时,使用四节点轴对称减缩积分单元,单元尺寸为0.3 mm。
锤头锻打频率为1 200锤/min,使用如式(2)所示的正弦脉冲函数来描述锤头运动。此外,进给速度、夹持压力、锤头压下量等可变过程参数均由相应的载荷、边界条件控制。按上述方法建立的身管精锻有限元模型如图2所示。
a=A·sin(125.66t)
(2)
式中,A为锤头压下量(mm); t为锻打时间(s)。
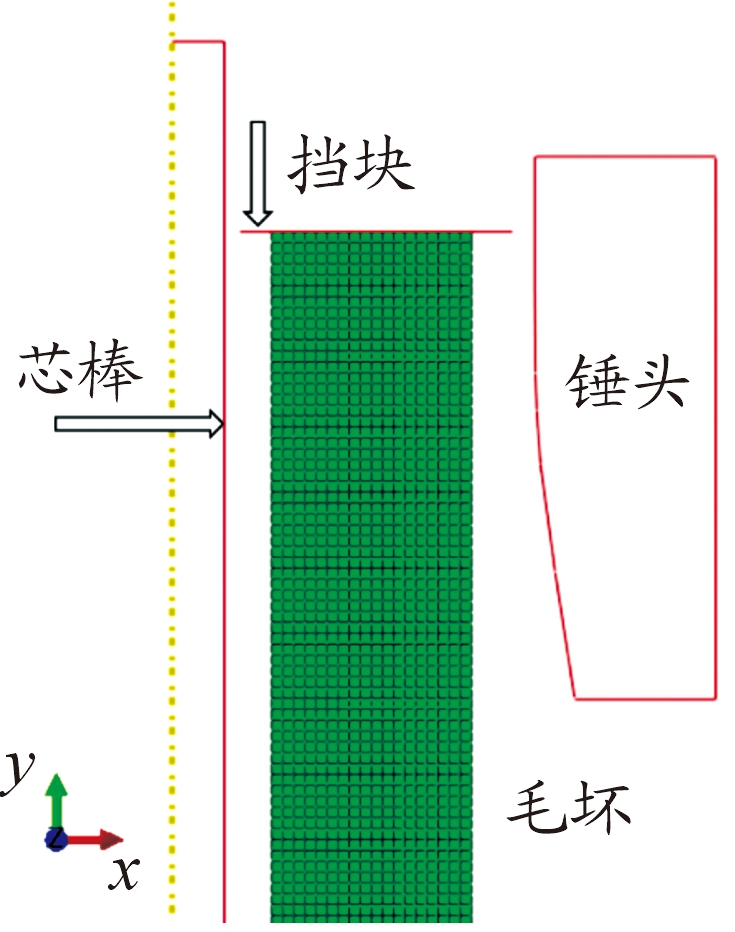
图2 身管精锻有限元模型示意图
1.2 身管精锻有限元模型验证
为了验证二维轴对称有限元模型的可靠性,将有限元模型计算出的锻打力与张鹤词[5]、FAN[13]等人试验测得的锻打力相比对。有限元模型中的尺寸、材料、过程参数均与试验保持一致。有限元计算出的锻打力与试验测得的锻打力如表2所示。
表2 锻打力有限元模拟值与实测值
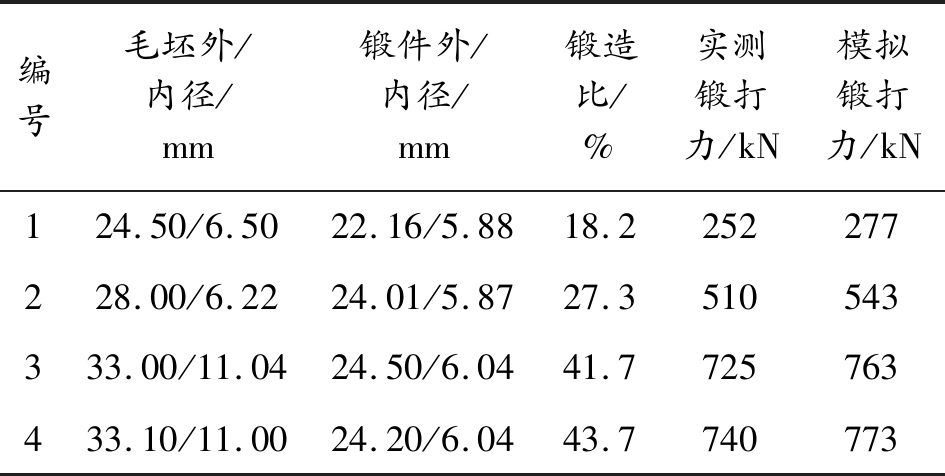
编号毛坯外/内径/mm锻件外/内径/mm锻造比/%实测锻打力/kN模拟锻打力/kN124.50/6.5022.16/5.8818.2252277228.00/6.2224.01/5.8727.3510543333.00/11.0424.50/6.0441.7725763433.10/11.0024.20/6.0443.7740773
从表2可以看出,有限元计算的锻打力与试验所测的锻打力较为接近,有限元计算的锻打力略大于试验测得结果,但是最大偏差只有9.9%。考虑到二维轴对称有限元模型默认锤头与毛坯完全接触,而在实际锻打时,4个锤头沿周向存在间隙,且锤头内表面由两条夹角为155°的轮廓线组成,锤头内表面与毛坯外轮廓并非完全接触。导致有限元模型中锤头与毛坯的接触面积大于实际情况。所以有限元计算结果略微偏大于试验结果。通过上述分析,认为此二维轴对称有限元模型的计算结果是可靠的。
2 身管线膛径向尺寸与回弹分析
采用前述有限元模型模拟进给速度、夹持力、锻造比、毛坯外径和内径之比(以下简称径比)对身管线膛径向尺寸的影响。过程参数取值参考实际加工经验,如表3所示。毛坯内径为11 mm,芯棒直径为5.762 mm保持不变。毛坯外径分别为29、31、33、35 mm,径比分别为2.6、2.8、3.0、3.2;进给速度分别为100、200、300、400 mm/min;夹持力分别为25、30、35、40 kN;总锻造比为23.8%、42.4%、45.0%、47.8%,对应的锻造段锻造比为5.7%、24.4%、27.7%、31.5%。控制变量法的基准值分别为30 kN夹持力,200 mm/min进给速度,42.4%总锻造比和3.0径比。
表3 模拟过程参数值
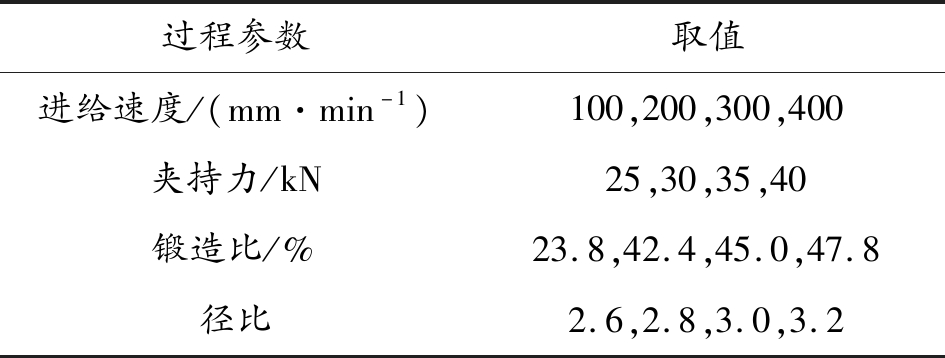
过程参数取值进给速度/(mm·min-1)100,200,300,400夹持力/kN25,30,35,40锻造比/%23.8,42.4,45.0,47.8径比2.6,2.8,3.0,3.2
总锻造比φ与锻造段锻造比φ1的计算公式如下。
(3)
(4)
式中,A0为毛坯横截面积;AM为锻造段入口处横截面积;AN为整形段入口处横截面积;R0为毛坯外半径;R1为锻造段入口处半径;R2为锻后身管外径;Ri为毛坯内径;Rm为芯棒半径。
2.1 过程参数与身管径向尺寸偏差的关系
在身管精锻成形过程中,锤头与毛坯为非连续性接触,在锤头提升时,毛坯因受力而产生的塑性应变将永久保留,弹性应变会恢复,但在下一次锻打时,又使上次的回弹消失。于是,只有最后一次锻打所产生的弹性应变才是应当考虑的,因为这最后一次锻打的弹性应变是在锤头卸载后立刻回复的残存回弹,不会再有下一次的锻打去消除它,它将使身管的内外径尺寸出现误差,并长期保留下来。
根据产生回弹原因的不同,将身管的径向弹性回弹量分为μ1和μ2。μ1为由于锤头卸载所产生的径向弹性回弹量,μ2为工件卸下时,夹持力卸载后所产生的径向弹性回弹量。根据有限元分析结果,锤头压下时,毛坯径向受压,所以当锤头卸载后,材料回弹方向为身管扩径方向,设为正向。在夹持力卸载阶段,卸载了身管尾端的夹持压和前端的挡块,身管两端不再受到挤压约束,因此材料回弹方向为身管缩径方向。为了研究过程参数对锻打工件最终成形尺寸的影响,把径向尺寸的变化分成两步来考虑:第一步是锤头抬起时实际径向尺寸和理想径向尺寸的差别,规定为径向尺寸偏差μ1;第二步是工件卸下后径向尺寸的变化值,规定为μ2。
2.1.1 过程参数对径向尺寸偏差μ1的影响
为提高径向尺寸数据的可靠性,锻打一定时间,待锤头远离挡块且身管已成形区域的应力应变趋于稳定时,提取锤头整形段结束点的内外表面结点径向尺寸,得出过程参数对身管径向尺寸偏差μ1的影响规律,分别如表4,表5,表6和表7所示。不同锻造比下的锤头位置分别为27.76、24.30、23.80、23.20 mm,不同径比下的锤头位置分别为21.16、22.74、24.30、25.86 mm,其余各表的锤头位置均为24.30 mm。
表4 不同进给速度的径向尺寸偏差
μ1有限元预测 mm
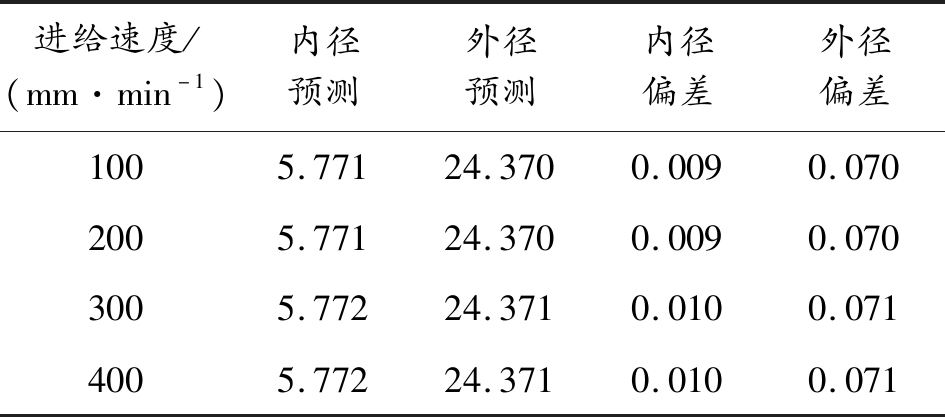
进给速度/(mm·min-1)内径预测外径预测内径偏差外径偏差1005.77124.3700.0090.0702005.77124.3700.0090.0703005.77224.3710.0100.0714005.77224.3710.0100.071
表5 不同夹持力的径向尺寸偏差
μ1有限元预测 mm
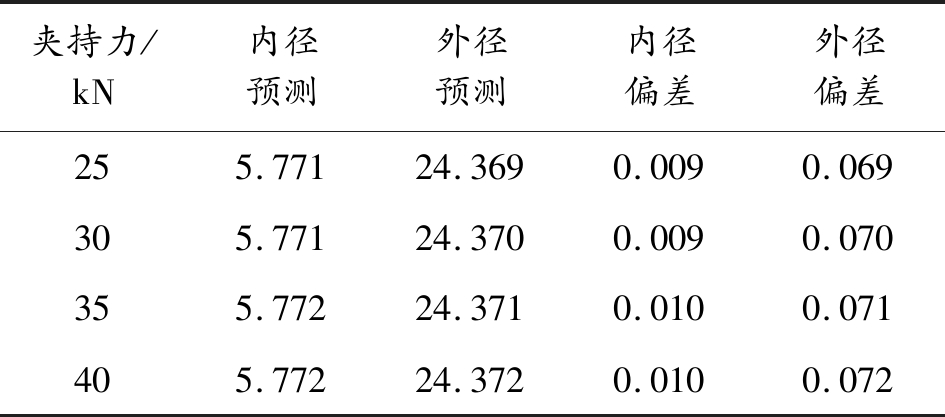
夹持力/kN内径预测外径预测内径偏差外径偏差255.77124.3690.0090.069305.77124.3700.0090.070355.77224.3710.0100.071405.77224.3720.0100.072
表6 不同锻造比的径向尺寸偏差
μ1有限元预测 mm
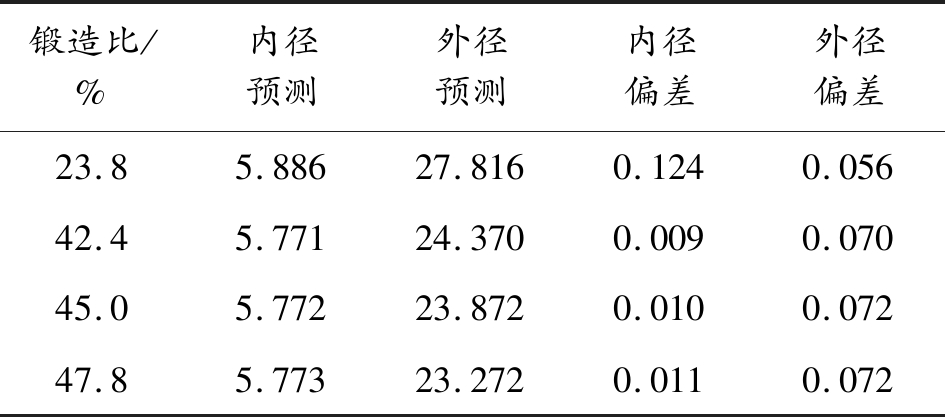
锻造比/%内径预测外径预测内径偏差外径偏差23.85.88627.8160.1240.05642.45.77124.3700.0090.07045.05.77223.8720.0100.07247.85.77323.2720.0110.072
表7 不同径比的径向尺寸偏差
μ1有限元预测 mm
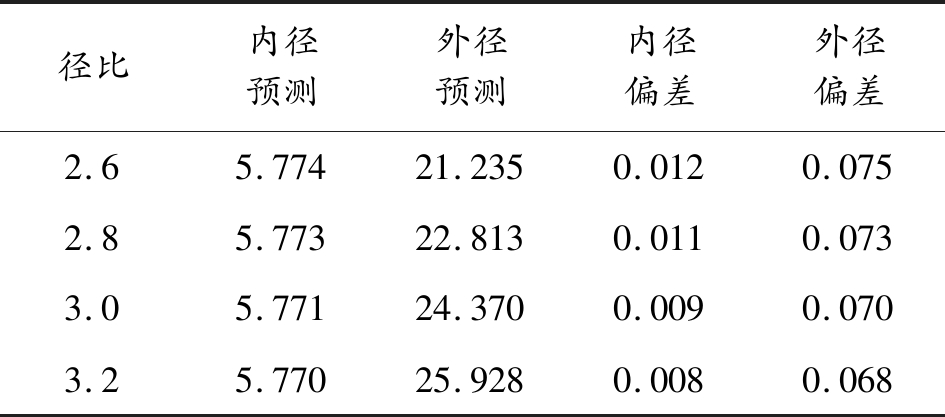
径比内径预测外径预测内径偏差外径偏差2.65.77421.2350.0120.0752.85.77322.8130.0110.0733.05.77124.3700.0090.0703.25.77025.9280.0080.068
将内径偏差和外径偏差作图,得到过程参数对内径和外径的偏差的影响曲线,如图3。
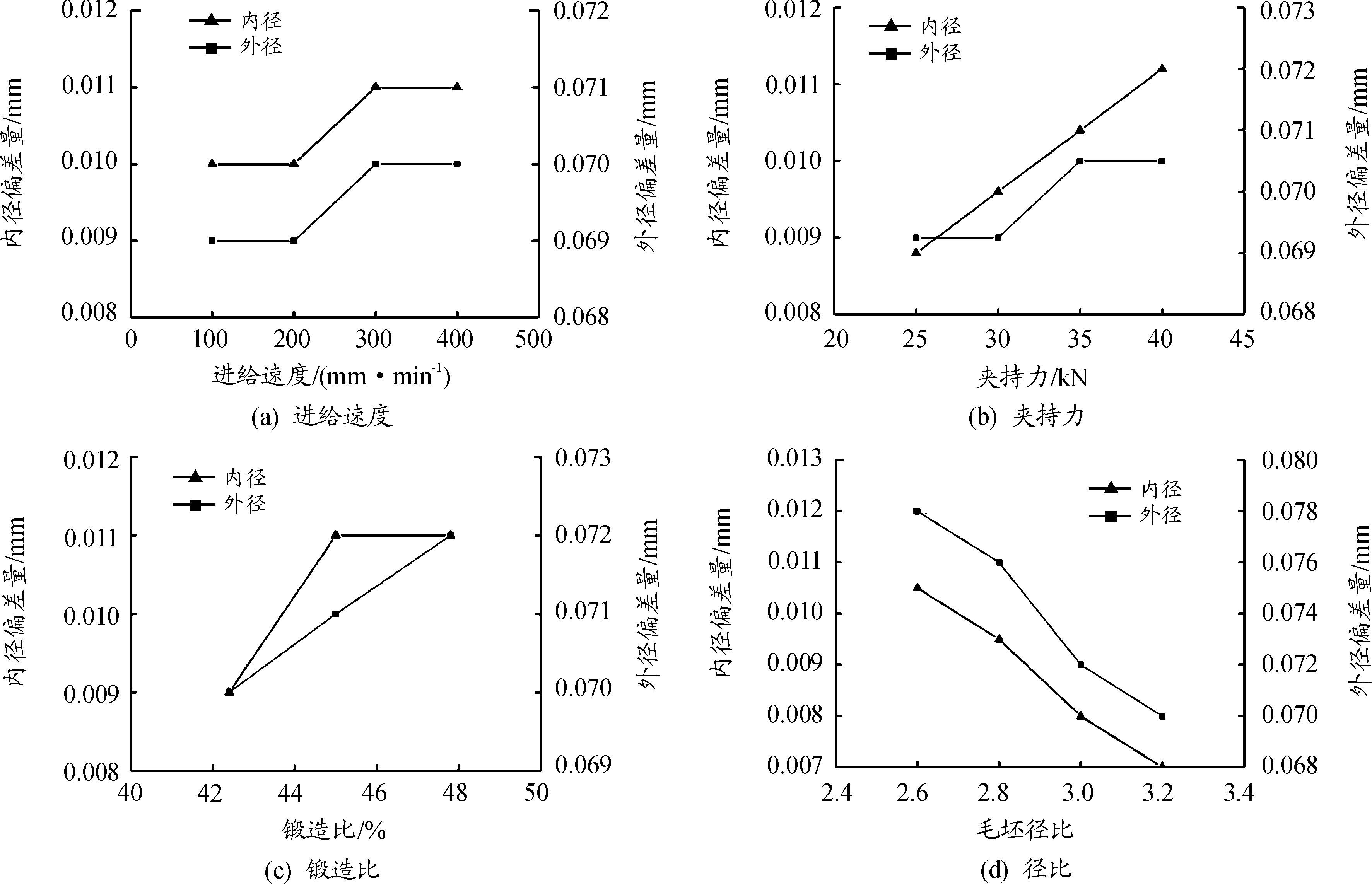
图3 过程参数与径向尺寸偏差量μ1的影响曲线
从图3(a)可以看出,身管内、外径均随着进给速度的增大而增大。在100 mm/min到400 mm/min的范围内,内径尺寸最大变化1 μm,外径尺寸最大变化1 μm。因此,当进给速度增加,身管内外径尺寸误差增加,每增加100 mm/min,内表面径向尺寸平均增加约0.25 μm,超出了内表面粗糙度小于0.2 μm的要求。因此,从粗糙度和加工效率角度出发,推荐进给速度小于200 mm/min。
从图3(b)可以看出,身管内、外径均随着夹持力的升高而增大,外径尺寸偏差量增大的速率为1 μm/(5 kN)夹持力。在25 kN到40 kN的变化范围内,内径尺寸最大变化1 μm,外径尺寸最大变化3 μm。因此,在工件能夹紧的前提下,夹持力越小越好。
从表6和图3(c)可以看出,当锻造比为23.8%时,身管内径尺寸偏大124 μm。根据张雪[5]的研究结果,锻造段锻造比的大小决定了身管内膛的锻透性,对于径比为3的毛坯管,可以保证锻透的理论锻造段锻造比为24%,对应的总锻造比为42%,23.8%的总锻造比显然不满足身管内膛的锻透性要求。当身管发生未锻透缺陷时,身管内膛填充不饱满,从而导致身管内径尺寸偏大。而当锻造比满足锻透性要求时,随着锻造比的增大,线膛内外径尺寸均增大,内径尺寸偏差量增大的速率为0.37 μm/(1%锻造比)。在42.4%到47.8%的锻造比范围内,内径尺寸最大变化2 μm,外径尺寸最大变化2 μm,因此对锻造比,首先要锻透,才能使尺寸精度稳定,在锻透的前提下,锻造比越小尺寸精度越好。
从图3(d)可见,身管线膛内、外径均随着径比的增加而降低。即当内径不变,毛坯厚度增加时,内、外径的偏差值减小,内径尺寸偏差量减小速率为1.4 μm/(0.2径比),外径尺寸偏差量减小速率为2.4 μm/(0.2径比)。当外径从29 mm增加到35 mm时,内径尺寸最大变化值为4 μm,外径尺寸最大变化7 μm。通常在锻打步枪枪管时,毛坯壁厚较薄,而锻造机枪枪管时,毛坯壁厚较厚,锻造步枪枪管时内径回弹偏差较大。
由上述分析可知,身管内膛锻透是保证尺寸精度的必要前提,在锻透的前提下,身管内、外径尺寸偏差随进给速度、锻造比和夹持力的增加而增加,因为随着上述过程参数的增加,锻造力增大,径向锻造应力也增大,回弹也随之增大。当径比增加时,径向刚度增大,于是径向回弹减少。图4为身管径向尺寸偏差随常用过程参数变化而产生的变化幅值K,可以看出,在现有的过程参数变化范围内,径比的影响程度最大。也就是说,锻打壁厚小的毛坯所产生径向尺寸偏差比锻打壁厚大的毛坯大,设计芯棒时补偿量要大一些。在同一壁厚范围内,当过程参数变化时,内径的变化幅值K不超过2 μm,即调整过程参数时,引起的径向尺寸偏差通常在公差范围内。
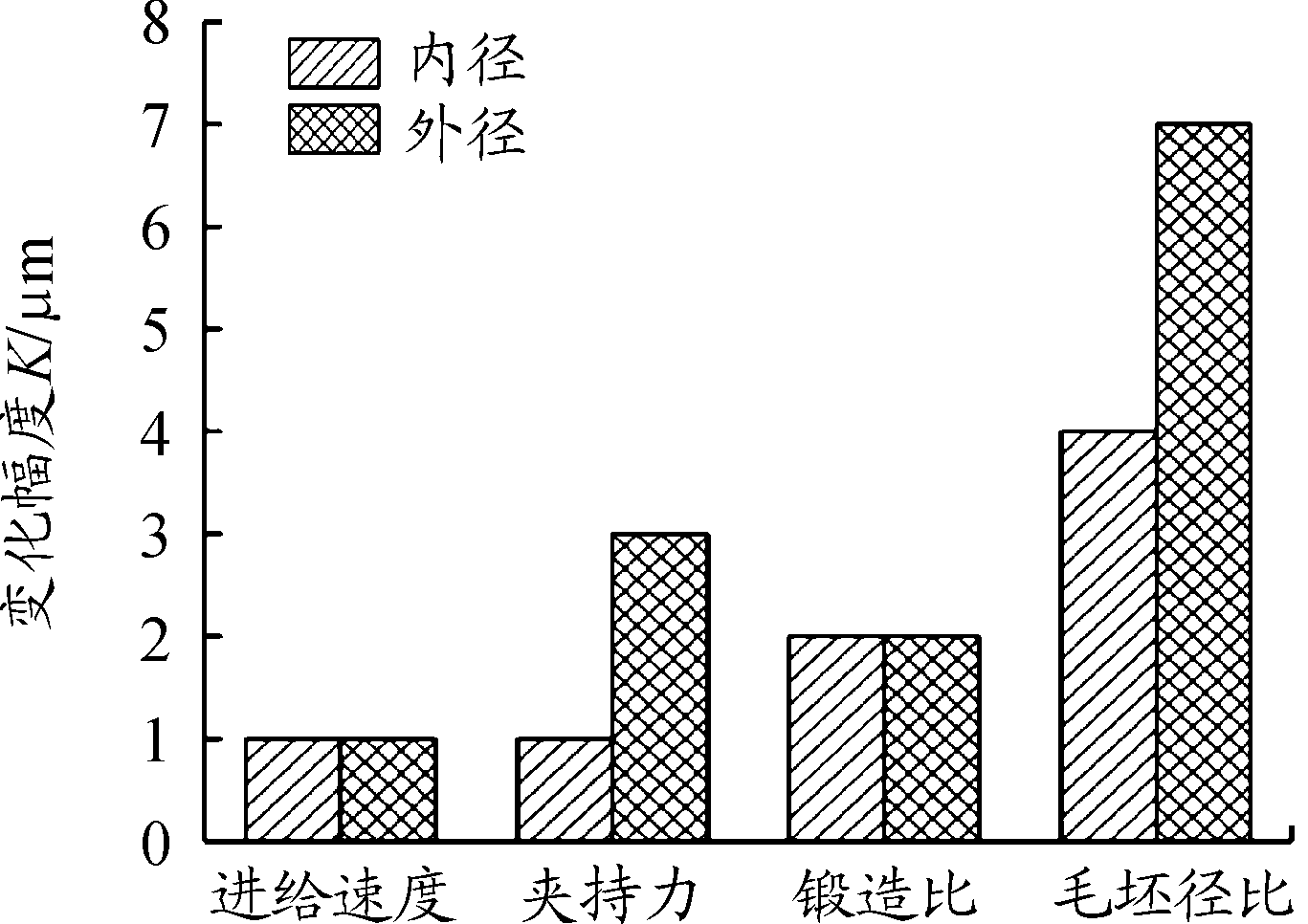
图4 不同过程参数对线膛径向尺寸的影响程度直方图
2.1.2 过程参数对径向尺寸偏差μ2的影响
前文分析了因锤头卸载所产生的径向弹性回弹量μ1,现继续分析当工件卸下时所产生的径向弹性回弹量μ2。毛坯在锻造过程中存在一段较长的稳定成形段,应力沿轴向分布较为均匀,因此在稳定成形段内等间隔取五个截面的回弹量均值为μ2。其值与夹持力大小和夹持力卸载前的应力状态有关,但分析发现,影响μ2的主要因素为夹持力大小,在不考虑夹持力卸载前的应力状态时,夹持力大小对μ2的影响规律也是成立的。可以得出:
1) 在基准算例下(30 kN夹持力,200 mm/min进给速度,42.4%总锻造比和3.0径比),夹持力对应的夹持压力为39 MPa,此时内表面μ2为-0.000 3 mm,外表面μ2为 -0.001 2 mm。当进给速度或锻造比变化时,只要夹持力不变,夹持力卸载阶段产生的回弹量μ2对线膛径向尺寸的影响很小。
2) 当夹持力变化,夹持应力随之发生变化,μ2改变,变化值随应力值增加而增加,但由于夹持力变化范围较小,μ2变化值不大,见表8。
表8 不同夹持力的径向尺寸偏差μ2

夹持力/kN25303540夹持压力/MPa33394653内径/mm-0.0003-0.0003-0.0003-0.0004外径/mm-0.0010-0.0012-0.0014-0.0016
3) 当夹持力不变,但径比发生变化,即外径发生变化时,由于受力面积不同,相应的应力值也不同,回弹量μ2发生变化,变化量与夹持应力值成正比,见表9。
表9 不同径比的径向尺寸偏差μ2

径比2.62.83.03.2夹持压力/MPa53453935内径/mm-0.0004-0.0003-0.0003-0.0003外径/mm-0.0014-0.0013-0.0012-0.0012
比较μ1和μ2,发现由锤头抬起引起的回弹量比卸下夹持力引起的回弹量大一个数量级,μ2对径向尺寸的影响很小。
2.2 考虑回弹的身管径向尺寸与补偿
通过上述分析可知,材料回弹导致了身管径向尺寸的变化。分析表中数据,发现身管的内径尺寸DI和外径尺寸DO与身管内外表面径向回弹量μ1、μ2关系为:
DI=Dm+2(μi1+μi2)
(5)
DO=Dn+2(μo1+μo2)
(6)
式中,Dm为芯棒直径;Dn为锻件设定外径;由锤头轨迹决定; μi1、μi2分别对应锻件内表面的μ1和μ2; μo1、μo2分别对应锻件外表面的μ1和μ2。
将2.1节中预测的偏差μ1和μ2加起来,得出了几种不同锻打条件下身管成形后的径向尺寸总偏差如表10所示。可以看出,在满足锻透性条件下,过程参数的变化对身管径向尺寸偏差影响较小。因此在实际生产中,通过调整过程参数来满足成形要求的方法并不十分有效,需要根据回弹量修改模具的公称尺寸。针对锻件内径尺寸偏大的现象,可以通过减小芯棒外径的方法使锻件内径满足要求;针对锻件外径尺寸偏大的现象,可以通过增大锤头压下量的方法控制锻件外径尺寸。分析表10数据可以发现,在此过程参数范围内,身管内外表面的预测偏差最大值分别约为0.01 mm、0.07 mm,(过程参数为200 mm/min进给速度,30 kN夹持力,42.4%锻造比,2.6径比),最小值为0.007 mm、0.066 mm(过程参数为200 mm/min进给速度,30 kN夹持力,42.4%锻造比,3.2径比)。据此,将芯棒的设计直径减小0.01 mm,锤头压下量增大0.035 mm,以补偿工件回弹对尺寸精度的影响。
使用前述有限元模型,使用相同的毛坯模拟仿真锻件成形尺寸,将芯棒的设计直径减小0.01 mm,锤头压下量增大0.035 mm。取进给速度200 mm/min,夹持力30 kN,锻件外径24.3 mm。模拟结果显示,锻件内径为5.762 mm,锻件外径为24.306 mm,与标准尺寸分别相差0 mm,0.006 mm。由此可见,通过此回弹补偿方法可以使锻件尺寸满足锻件要求。
表10 过程参数设置及成形后偏差值预测
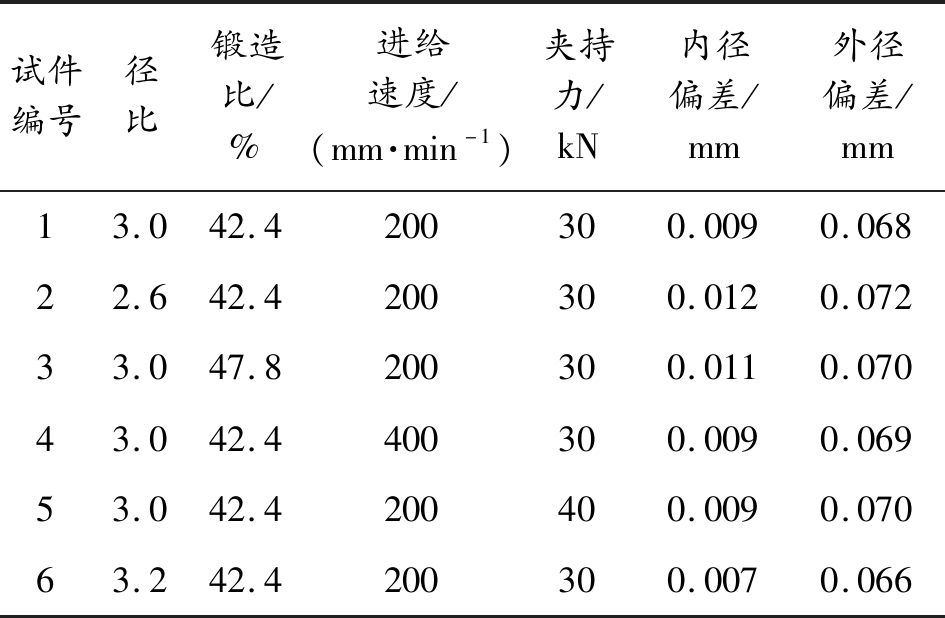
试件编号径比锻造比/%进给速度/(mm·min-1)夹持力/kN内径偏差/mm外径偏差/mm13.042.4200300.0090.06822.642.4200300.0120.07233.047.8200300.0110.07043.042.4400300.0090.06953.042.4200400.0090.07063.242.4200300.0070.066
3 验证
为了验证有限元分析的结果,使用SKK-10型精锻机进行实际锻打试验。由于改变过程参数对身管内径尺寸的影响幅度很小,不足0.01 mm,而检测内膛所用的标准通规、止规只能精确到0.01mm,不满足检测精度要求,无法验证过程参数对身管内径的影响规律,因此仅验证锻后身管内外表面的预测回弹量以及锻透性对身管内径的影响。锻打过程参数如表11所示。
试件1使用的芯棒直径为5.87 mm,使用标准通规止规检测试件1,发现其阳线直径为5.88 mm,大于标准值0.01 mm,可以认为试件1的内表面单边径向回弹量为0.005 mm。对试件1进行有限元模拟,得出其内径预测回弹量偏差为0.006 mm,与试验结果相差0.001 mm,可以证明有限元模型的准确性。
使用游标卡尺检测试件2,沿着身管线膛部分等间隔量取3次外径取均值为24.34 mm,大于设定值0.04 mm。在锻打试件2时,操作人员根据前一批锻打结果,在原有的设定基础上将锤头多压下0.01 mm,因此,实际的外表面单边回弹量为0.03 mm,与与有限元预测的身管外表面回弹量结果相差9%。误差来源与过程参数变化和锻后身管外径不均匀有关。
使用工业内窥镜观察试件3和4的内膛成形情况,如图5所示。试件3未锻透,其内膛阳线部分比较粗糙,未填充好,试件4满足锻透性要求,阳线部分成形良好。使用标准通规止规检测,试件3的阳线直径为5.85 mm,大于标准值0.08 mm。试件4的阳线直径为5.77 mm,与标准值相同。据此可以证明锻透性对尺寸精度的影响。
表11 试件编号及过程参数设置值

试件编号毛坯外径/mm毛坯内径/mm锻造比/%进给速度/(mm·min-1)夹持力/kN124.506.5047.4613026232.9211.0841.8018037330.2011.6430.7012035430.2011.6441.2012035

图5 身管内膛成形情况
4 结论
1) 随着进给速度、夹持力的增加,身管内外径偏差μ1均增大。当锻不透时,身管径向尺寸超差严重。在锻透的条件下,随着锻造比的增加,偏差μ1增大。锻透是保证尺寸满足要求的基本条件。
2) 随着毛坯径比的增加,偏差μ1减小。毛坯径比对偏差μ1影响程度最大,其次是锻造比、夹持力和进给速度。在实际生产中,在锻透前提下,应尽量使用较低的进给速度、夹持压力和锻造比。步枪枪管毛坯壁厚薄,径比小,内径偏差大,更需要补偿。
3) 在锻透前提下,身管内外径偏差μ2与夹持力大小和夹持力卸载前的应力状态有关,并随着夹持应力增加而增大。且μ2比μ1小一个数量级,所以身管径向尺寸回弹偏差主要来源于μ1。
4) 提出了在5.8口径常用过程参数范围内,减小芯棒外径0.01 mm,增大锤头压下量0.035 mm作为回弹补偿,有助于提高身管内表面径向尺寸的精度。
5) 验证了锻透性对身管内径的影响以及身管内外表面的预测径向回弹量。
[1] 田文松,罗荣,代安源.枪管径向冷精锻成形技术的应用研究[J].精密成形工程,2009(03):58-62.
[2] 赵震,白雪娇,胡成亮.精密锻造技术的现状与发展趋势[J].锻压技术,2018,43(07):90-95.
[3] FAN Lixia,WANG Zhigang,WANG He.3D Finite Element Modeling and Analysis of Radial Forging Processes[J].Journal of Manufacturing Processes,2014,16:329-334.
[4] 张鹤词.身管线膛精锻成形极限研究[D].南京:南京理工大学,2018.
[5] 张雪,樊黎霞,张鹤词.身管线膛精密径向锻造的锻透性分析[J].兵工学报,2019,40(03):28-34.
[6] 毕梦凡,方峻,樊黎霞,等.精锻成形身管力学性能预测分析与工艺优化[J].兵器装备工程学报,2020,41(05):161-165.
[7] 徐宝池,杨晨,樊黎霞,等.变形量对冷径向锻造身管力学性能各向异性的影响[J].兵器装备工程学报,2020,41(05):81-85.
[8] 杨杰章.钢在温锻时的回弹[J].华东化工学院学报,1986(01):107-113.
[9] ABE H,IWAMOTO T,YAMAMOTO Y,et al.Dimensional Accuracy of Tubes in Cold Pilgering[J].Journal of Materials Processing Technology.2016,231:277-287.
[10] 楚志兵,吕阳阳,黄庆学,等.皮尔格轧机冷轧不锈钢管回弹预测模型的建立与验证[J].四川大学学报,2015,47(02):165-171.
[11] 王环珠,楚志兵,李伟,等.皮尔格冷轧无缝钢管成形工艺参数及力学研究[J].热加工工艺,2019,48(15):88-93.
[12] LONG Hui.Dimensional Errors of Cold Formed Components using FE Simulation[J].Journal of Materials Processing Tech,2004,151(1).
[13] FAN Lixia,WANG Zhigang,WANG He.3D Finite Element Modeling and Analysis of Radial Forging Processes[J].Journal of Manufacturing Processes,2014,16:329-334.