爆轰产物状态方程是描述炸药爆轰CJ状态之后的爆轰产物系统中各物理量的关系式,是研究计算爆炸力学问题的基础。其中JWL状态方程由于能够比较精确地描述炸药爆轰产物的膨胀驱动过程,目前在武器设计、工程爆破、爆炸加工等领域得到了广泛应用的很多大型有限元软件,如LS-DYNA、ABAQUS、MSC.Dytran、AUTODYN等都在炸药材料模型中包含了JWL状态方程。
JWL状态方程是由Lee于1965年在Jones和Wilkins工作的基础上提出的,该方程的未知参数需要通过炸药的圆筒试验及二维流体动力学程序来确定。圆筒试验是使炸药在铜管中爆炸,利用高速扫描相机记录下管壁在爆轰产物驱动下的膨胀过程,得出圆筒半径变化曲线,然后采用含有JWL状态方程的二维流体动力学程序来对圆筒试验进行数值模拟,不断修改JWL状态方程参数,直至数值模拟结果与圆筒试验结果相符合,从而确定最终的JWL状态方程参数。
由于确定JWL状态方程参数过程中的圆筒试验所用药柱尺寸小、形状规则,而实际战斗部装药尺寸较大、外形复杂,战斗部实际装药密度一般要低于圆筒试验的装药密度,因此圆筒试验通常给出的是炸药在一种较高装药密度下的JWL状态方程参数。在破片战斗部威力数值仿真中,需要用到同种炸药在其他密度下的JWL状态方程参数时,一般认为JWL状态方程的A、B、R1、R2、ω和E0这6个参数是不随装药密度变化的。但通过对文献中PETN和HNS两种炸药在不同密度下的JWL状态方程研究发现,JWL状态方程的参数明显与装药密度有关,装药密度对炸药的驱动能力影响较大。因此,研究炸药在不同密度下的JWL状态方程参数,对提高破片战斗部威力数值仿真的准确度具有重要意义。
本研究通过理论分析及与两种炸药JWL状态方程参数的对比,建立了不同装药密度下的JWL状态方程参数计算方法,可快速准确地确定出炸药在任意密度下的JWL状态方程参数。
1 目前的研究现状
目前国内关于装药密度对JWL状态方程参数的影响研究很少,炸药在不同密度下的JWL状态方程参数仅极少数炸药可在公开文献中查到,这大大影响了JWL状态方程在实际应用中的精度。国内也有人通过基于理论模型建立的BKW[1]、γ率状态方程[2]、VLW[3-4]、KHT[5]等状态方程的计算结果拟合得到炸药的JWL状态方程的参数,但均需要知道炸药的详细配方及相关参数才可得出较为可信的结果,而工程上很多新炸药的配方和一些参数都是未知的,因此很难通过此方法获得炸药的JWL状态方程参数。下面对炸药在不同装药密度下的JWL状态方程参数进行理论分析和研究。
2 不同装药密度下的炸药JWL状态方程
炸药爆轰产物的JWL状态方程形式如下:
![]()
(1)
式中:A、B、R1、R2、ω为炸药的JWL状态方程参数。
在CJ点处,JWL状态方程形式如下:
(2)
式中: PCJ为炸药的爆压; VCJ为炸药的爆容; E0为炸药的初始比内能。
从式(2)可以看出,JWL状态方程的A、B、R1、R2、ω 5个参数需要知道炸药的爆压、爆容和初始比内能才能确定,而这3个参数均与炸药的装药密度有关。
1968年,康姆莱特(kamlet)等提出了计算CHNO型炸药爆压和爆速的半经验半理论计算公式,称为康姆莱特公式[6],它适用于装药密度大于1 g/cm3的情况。其形式简单,计算精度较高,具体形式如下:
(3)
PCJ=1.558φρ2
(4)
(5)
式中: φ为与炸药的组分有关的参数; ρ为炸药的装药密度。
若已知某装药密度ρ0时的爆速D和爆压PCJ,则由式(4)可推导出炸药在任意密度下的爆压如下:
(6)
由式(5)可推导出炸药在任意密度下的爆速如下:
(7)
将式(2)代入式(6)可得:

(8)
将式(8)与式(2)对比,可以得到炸药在任意装药密度下的爆轰产物JWL状态方程参数如下:
(9)
其余3个参数R1、R2、ω保持不变。
3 结果分析与对比
采用上述模型计算了PETN和HNS两种炸药在不同密度下的JWL状态方程参数,并根据文献[7]和文献[8]中两种炸药在不同密度下JWL状态方程参数,制作了对爆轰产物膨胀的压力-体积曲线。PETN炸药JWL状态方程参数的文献值与计算值对应的爆轰产物膨胀压力-体积曲线对比如图1所示。HNS炸药JWL状态方程参数的文献值与计算值对应的爆轰产物膨胀压力-体积曲线如图2所示。

图1 PETN文献值与计算值的P-V曲线
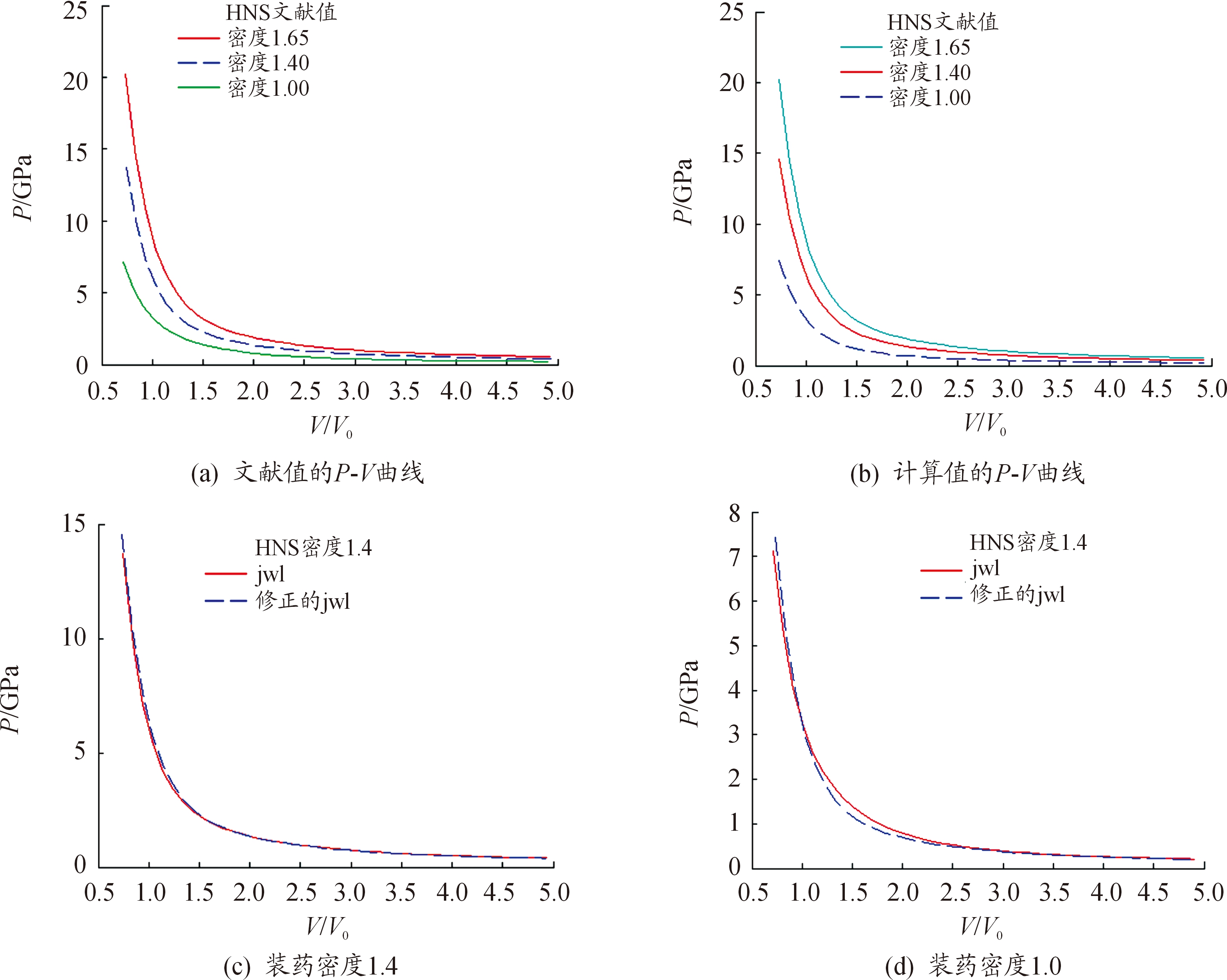
图2 HNS文献值与计算值的P-V曲线
从图1(a)~1(b)和图2(a)~2(b)可以看出,当装药密度降低时,爆轰产物在高压段的压力曲线明显下降,若在数值仿真时对低密度装药采用高密度下测得的JWL状态方程参数,将给仿真结果带来较大的计算误差,尤其是当圆筒试验的装药密度与实际装药密度相差较大时,应当对JWL状态方程参数进行相应的修正。
从图1(c)~1(d)和图2(c)~2(d)可以看出,PETN和HNS两种炸药在装药密度大于1 g/cm3时,爆轰产物膨胀 P-V 曲线计算值与文献值在高压段和低压段均吻合较好,比较准确地反映了炸药在不同密度下爆轰产物膨胀规律,因此将来可以在战斗部威力数值仿真中应用该模型对某些炸药的JWL状态方程的参数进行修正,以提高数值仿真结果的精度。
PETN和HNS在不同密度下的JWL状态方程参数计算值与文献值如表1与表2所示。
表1 PETN炸药不同密度下的JWL状态方程参数

ρ/(g·cm-3)D/(m·s-1)PCJ/GPaE0/GPaA/GPaB/GPaR1R2ω1.77[7]830033.510.10617.0516.9264.401.200.251.5[7]745022.08.56625.3023.2905.251.600.281.26[7]654014.07.19573.1020.1606.001.800.280.88[7]51706.25.025348.6211.2887.002.000.241.5741724.067.25443.1612.164.401.200.251.26663316.985.12312.698.584.401.200.250.8853918.282.50152.524.184.401.200.25
表2 HNS炸药不同密度下的JWL状态方程参数

ρ/(g·cm-3)D/(m·s-1)PCJ/GPaE0/GPaA/GPaB/GPaR1R2ω1.65[8]703021.507.45463.108.8734.551.350.351.4[8]634014.506.00366.506.7504.801.400.321.0[8]51007.504.10162.7010.8205.401.800.251.4630415.485.36333.406.394.551.350.351.051417.902.74170.103.264.551.350.35
注:上表中带上标行的数据为文献值。
由表1和表2可以看出,2种炸药不同密度下的JWL状态方程参数计算值与文献值差异较大,但两种炸药不同密度下的爆轰产物膨胀P-V曲线计算值与文献值吻合较好,这说明JWL状态方程的参数在数学上存在不唯一解。
例如某破片战斗部装填DNTF基炸药,通过圆筒试验结果拟合得到DNTF基炸药的JWL状态方程,并测得装药密度为1.875 g/cm3,爆速为8 649 m/s,但实际由于装药条件限制,战斗部的装药密度仅为1.77 g/cm3。根据该炸药圆筒试验的JWL状态方程参数及参数,由式(6)和式(7)可计算出实际装药密度下的参数,分别用两套参数采用LS-DYNA进行战斗部爆炸过程的数值仿真,破片初速仿真结果如下:
从图3可以看出,原始参数和修正后参数的破片最大速度分别为2 390.3 m/s和2 174.4 m/s,而试验测得破片的最大初速为2 120 m/s。由此可见,修正后的参数仿真得到的战斗部破片速度均与试验结果吻合更好。
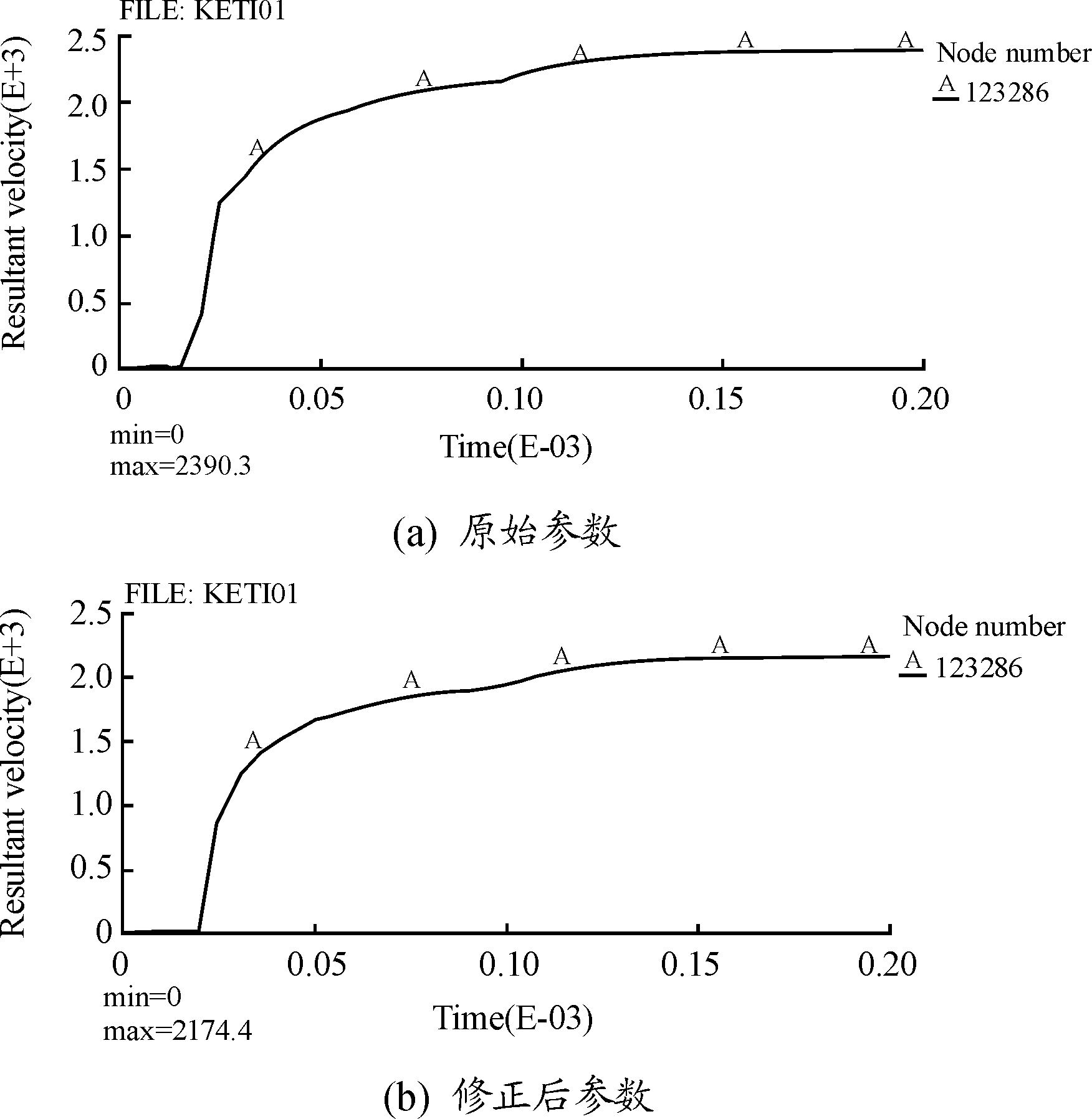
图3 战斗部中心位置破片速度的仿真曲线
4 结论
1) 当装药密度降低时,爆轰产物在高压段的压力会明显下降,若在数值仿真时对低密度装药采用高密度下测得的JWL状态方程参数将给仿真结果带来较大的计算误差,尤其是当圆筒试验的装药密度与实际装药密度相差较大时,应当对JWL状态方程参数进行修正。
2) PETN和HNS两种炸药在装药密度大于1 g/cm3时,爆轰产物膨胀P-V曲线计算值与文献值在高压段和低压段均吻合较好,比较准确地反映了炸药在不同密度下爆轰产物膨胀规律,因此将来可以在战斗部威力数值仿真中应用该模型对某些炸药的JWL状态方程的参数进行修正,以提高数值仿真结果的精度。
3) 两种炸药不同密度下的JWL状态方程参数计算值与文献值差异较大,但两种炸药不同密度下的爆轰产物膨胀 P-V 曲线计算值与文献值吻合较好,这说明JWL状态方程的参数在数学上存在不唯一解。
4) 通过用圆筒试验得到的DNTF基炸药JWL状态方程参数及本模型修正后的参数,分别进行数值仿真并与试验对比,修正后的参数仿真得到的战斗部破片速度与试验结果吻合更好。
因此,本研究的计算模型可以较为准确地预测炸药在不同装药密度下的JWL状态方程参数和爆轰产物膨胀规律,能够用于破片战斗部威力数值仿真中提高仿真结果的准确度,为未来的精密战斗部设计提供理论支撑。限于公开文献中关于炸药在不同装药密度下的JWL状态方程参数较少,该模型的准确性还有待更多的试验数据验证和完善。
[1] MADER C L.Numerical modeling of explosives and propellants[M].New York:CRC Press,1998.
[2] 刘文祥,李捷,钟方平.组合y状态方程在数值计算上的应用及分析[J].爆炸与冲击,2009,29(2):209-212.
[3] 韩勇,龙新平.用VLW状态方程计算水的冲击Hugoniot曲线[J].爆炸与冲击,2010,30(1):17-20.
[4] 肖成良,刘清杰,卢校军,等.改性B炸药的做功能力[J].四川兵工学报,2014,35(10):128-132.
[5] 项大林,荣吉利.基于KHT程序的RDX基含铝炸药JWL状态方程参数预测研究[J].北京理工大学学报,2013,33(3):239-243.
[6] 赵铮,陶钢,杜长星.爆轰产物JWL状态方程应用研究[J].高压物理学报,2000,23(4):277-282.
[7] DOBRATZ B M,CRAWFORD P C.LLNL Explosives Handbook[M].[S.l.]:[s.n.],1985.
[8] FINGER,LEE.High Explosives Equations Of State[M].LLLL memorandum,1972.