导弹在水下发射、出水航行过程中的结构动力学环境极其复杂。目前有限元分析技术以及边界元流固耦合分析技术不断发展,能够得到一定精度的模态参数,但水下导弹运载器结构复杂,且发射过程中对各项参数要求极其精密。工程应用中,需要根据具体工况,通过改变设计使物体的固有频率避开某些特定频率来提高安全系数。由于仿真计算过程中,仿真参数的设置与实际工程应用存在一定偏差,导致仿真结果与试验得到的模态特性仍然存在一定差异,因此,需要进行模态试验来得到相关模态参数。焦安超等[1]通过“天宫一号”飞行器的模态试验,得到的实验数据与仿真数据相差不大,并能够根据仿真数据来选择模态试验的激励点位置等参数。孙海文等[2]在探空火箭上的模态试验同样印证了这一结论。但水下发射状态与陆上有很大不同,结构在水下运动时,附连水的质量会影响结构的动力学特性,同时水的阻尼效应与空气也有较大差别。结构在水中运动时液体对结构产生两种效应,一是附加在结构表面的附加水质量,二是粘性阻滞效应。前者增大了结构的运动质量,使得水中结构的固有频率降低;后者阻碍结构运动,增大了阻尼系数[3]。附加质量能够进行估算,而干、湿模态阻尼有较强的非线性,只有依靠试验才能掌握阻尼特性[4-7]。要研究水的附加阻尼,需对结构进行干、湿两种模态试验。通过试验能够比较分析干、湿模态阻尼特性的差别,便于进行载荷分析。王在铎等[8]使用圆筒缩比模型,进行水下湿模态试验,研究刚体在水下平动和转动的阻尼比,并得到了一阶弯曲的附加质量系数,具有一定的参考意义,但试验未考虑到水深的影响,且试验获取的数据信噪比较低,这可能是因为加速度传感器的性能参数以及水下密封手段所致。导弹发射过程中的动态响应数据十分重要,但目前国内外针对水下发射整个出水过程的模态研究大多处于仿真阶段,缺少试验数据与其相互补充和验证。文章搭建了模态试验系统,分别做了空气和浅水中的模态试验,得到了大量试验数据,研究了不同水深对模态试验结果的影响,为后续研究水下发射的动力学特性提供了有效参考。
1 试验原理
本试验采用了耐压壳体结构来模拟运载器,作为模态试验件。该运载器主要由头部、中段、尾部组成,如图1所示。

图1 试验件安装环境
空气中,运载器采用吊挂方式,在节点位置使用弹性绳将两端吊起,使其处于水平自由状态。此种安装方式可以补偿重力对其基频特性的影响,使试验结果更加趋近于真实状态[9]。水下模态试验中,由于浮力大于运载器的重力,使用弹性绳将运载器与配重块连接起来,使配重块沉于水底,运载器悬浮水中。空气中模态试验采用力锤和激振器两种激振方式。力锤试验时,使用力锤敲击运载器表面特定位置使其产生振动,粘贴于运载器表面的加速度传感器实时测得结构相应信号,并传入LMS数据采集系统。同时,粘贴于力锤上的力传感器实时将力锤的冲击信号传入数据采集系统。激振器试验时,信号发生器发出一个特定的激振源信号给功率放大器,将此信号放大之后给激振器,激振器将此信号加载到运载器的激励点上,粘贴于运载器表面的加速度传感器实时测得结构相应信号并将其传入采集系统。通过Test.lab模态分析软件确定运载器的传递特性,选择合适的算法得到模态相关参数。试验原理如图2所示。

图2 模态试验原理框图
2 试验系统建模
2.1 建立运载器试验模型
定义从运载器头部看,最低点为第Ⅰ象限,逆时针每隔90°依次定义为第Ⅱ、第Ⅲ和第Ⅳ象限如图3(a)所示。选择运载器头部顶点为坐标原点,X轴沿耐压结构轴线指向尾部,第Ⅲ象限为Y轴,第Ⅱ象限为Z轴,X轴、Y轴和Z轴满足右手法则。根据测试点选择原则,结合模态数值仿真结果,在运载器壳体结构表面布置5圈和头部顶点,每圈沿圆周均布4个测点(依次为Ⅰ、Ⅱ、Ⅲ、Ⅳ象限),共计21个测点,如图3(b)所示。各站位距离运载器头部的距离见表1,站位编号规则为:第0圈站位为头部顶点,测量点编号为G0001;第一圈站位从底部Ⅰ象限开始逆时针分别为G0101~G0104;第二圈站位从底部Ⅰ象限开始逆时针分别为G0201~G0204;…;第五圈站位从底部Ⅰ象限开始逆时针分别为G0501~G0504。
2.2 建立激振模型
试验中,G0001测点位于头部顶点,使用2个加速度传感器,分别测量y向和z向的加速度。其他测点的方向为:第一象限为-y,第二象限为+z,第三象限为+y,第四象限为-z。
按照测点布置方案布置好测点之后,使用力锤分别取G0001测点x方向,G0202测点,G0203测点,G0302测点,G0303测点敲击,对比其频响函数,最终确定当敲击点为第2圈时,其效果最好。

图3 测点建模位置图
表1 不同圈的位置分布
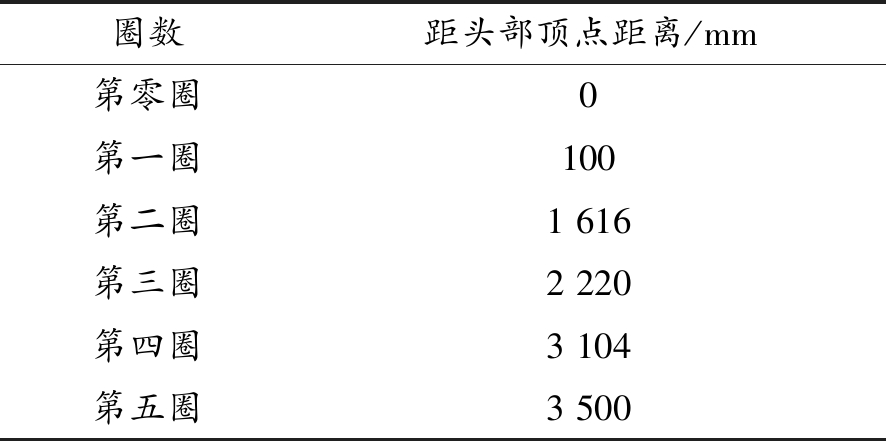
圈数距头部顶点距离/mm第零圈0第一圈100第二圈1616第三圈2220第四圈3104第五圈3500
空气中模态试验时,激振器垂直放置于地面,从下往上垂直抵于耐压结构第二圈表面,故激振点为G0201,+Y方向。水下模态试验时,由于激振器不能放置于水下,将激振器倒置悬挂,垂直于水面,从上往下抵于耐压结构表面第二圈,激振点为G0203,-Y方向。
3 试验数据分析
本试验分别做了空气中模态试验和水下模态试验,并将试验数据与仿真数据作了对比。
3.1 模态参数识别方法
运载器受到激振源的激振信号产生多点振动加速度,通过LMS系统建立起输入激振与多点振动加速度响应的对应关系,从而得到多组频响函数,使用正交多项式曲线拟合法对所测频响函数进行曲线拟合,并用抗干扰能力强的PolyMax 算法,识别出各阶模态频率对应的模态参数[10-13]。对于识别出的频率中,若有两个频率非常接近,首先观察振型动画,若其振型相似,则计算这两阶模态之间的MAC值;若MAC值大于0.85,则认为这两阶模态是同一阶模态。此时,再通过拟合的频响函数虚部图和相干函数,确定虚部图中峰值较大且对应的相干函数值为1或者接近1的频率点为真实模态,剔除另外一个虚假模态,最终确定合理的模态参数值。
3.2 空气中模态试验力锤与激振器试验结果分析
空气中模态试验使用力锤激励和激振器激励2种激励方式,其试验结果见表2与图4所示。
表2 力锤激励与激振器激励结果比较

模态阶次力锤模态频率/Hz模态阻尼比/%模态振型激振器模态频率/Hz模态阻尼比/%模态振型1106.3180.76一阶弯曲(绕y轴)106.0951.14一阶弯曲(绕y轴)2109.3390.19一阶弯曲(绕z轴)109.1740.48一阶弯曲(绕z轴)3273.8820.32一阶扁涨(y向带弯曲)273.7570.37一阶扁涨(y向带弯曲)4290.4200.26一阶扁涨(z向带弯曲)290.7390.35一阶扁涨(z向带弯曲)

图4 空气中模态试验振型
根据表2与图4的结果可以看出,在空气中进行模态试验时,使用力锤和激振器进行激振,其低阶模态频率与阻尼比基本一致,振型差别不大。可以认为模态试验中,激振源选择合适的情况下,激振方式对模态参数影响不大。
3.3 水下模态试验结果分析
试验中,规定运载器壳体第三象限距离水面的高度为水深值。由于在水下试验,力锤敲击会带起周围水波振动,从而影响到运载器的自由状态,因此,使用激振器激励。
在测点G0203的-Y方向用激振器进行激励,分别进行了0、50 mm、80 mm、100 mm和150 mm水深试验。对这5组数据进行分析,识别出的模态参数见表3。
根据表3,将各阶模态频率和阻尼比数据随水深变化关系绘制关系图如图5所示。
表3 水下模态不同水深试验数据
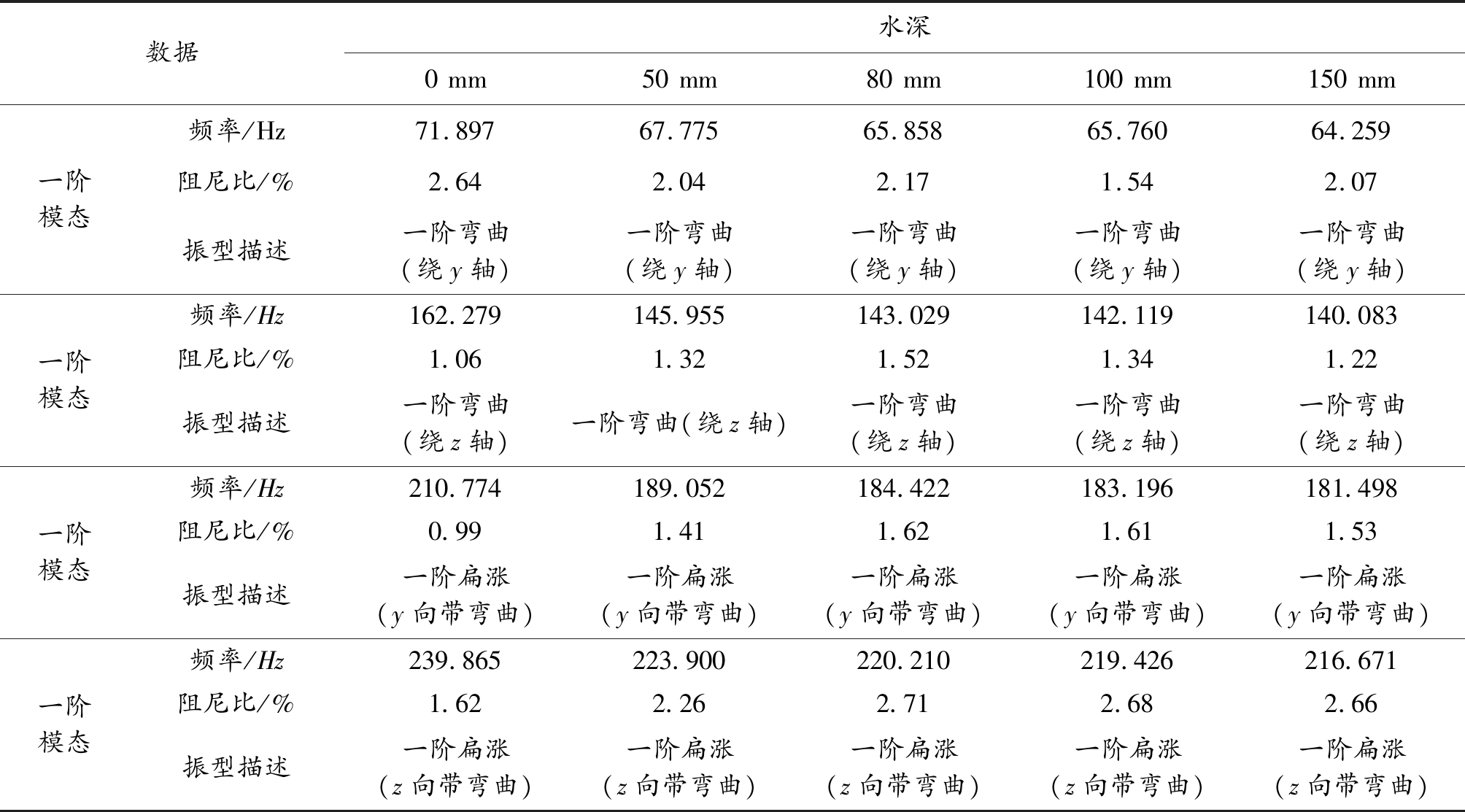
数据水深0mm50mm80mm100mm150mm一阶模态频率/Hz71.89767.77565.85865.76064.259阻尼比/%2.642.042.171.542.07振型描述一阶弯曲(绕y轴)一阶弯曲(绕y轴)一阶弯曲(绕y轴)一阶弯曲(绕y轴)一阶弯曲(绕y轴)一阶模态频率/Hz162.279145.955143.029142.119140.083阻尼比/%1.061.321.521.341.22振型描述一阶弯曲(绕z轴)一阶弯曲(绕z轴)一阶弯曲(绕z轴)一阶弯曲(绕z轴)一阶弯曲(绕z轴)一阶模态频率/Hz210.774189.052184.422183.196181.498阻尼比/%0.991.411.621.611.53振型描述一阶扁涨(y向带弯曲)一阶扁涨(y向带弯曲)一阶扁涨(y向带弯曲)一阶扁涨(y向带弯曲)一阶扁涨(y向带弯曲)一阶模态频率/Hz239.865223.900220.210219.426216.671阻尼比/%1.622.262.712.682.66振型描述一阶扁涨(z向带弯曲)一阶扁涨(z向带弯曲)一阶扁涨(z向带弯曲)一阶扁涨(z向带弯曲)一阶扁涨(z向带弯曲)

图5 模态数据随水深变化曲线
根据表3和图5可以看出,运载器的各阶模态频率随着水深增加而逐渐减小。从水深0 mm到50 mm时,模态频率衰减较快,水深从50 mm到150 mm时模态频率衰减较慢。而模态阻尼比随水深变化没有明显规律。模态振型随水深变化一致性较好。刘庆茂[14]认为,附连水的质量是导致物体在水中固有频率下降的主要因素,且附连水质量越大,固有频率下降越多。根据张成等[15]的附连水质量计算方法,水深会影响附连水的质量,弹体在深水域的附加质量比浅水域大得多。本试验中,随着水深增加,附连水的质量也在增加,模态频率随之减小。若水深增加到一定程度,则试验状态趋近于无限流域,附连水的质量趋近于定值,则模态频率趋近于稳定值。
3.4 模态试验数据与仿真数据对比
试验前对该运载器做了干湿模态仿真,数值仿真数据如表4所示。
由于空气对运载器的附加质量和阻尼比均很小,所以将空气中模态试验数据与干模态仿真数据作比较,可以看出,干模态仿真数据与实验数据的各阶模态频率相差不大,均在7%以内,各阶振型基本一致,阻尼比相差不大。此结论与目前国内外大量科研工作者通过不同试验件模态试验所得到的结果基本一致。
将水下模态试验数据与湿模态仿真数据做对比,可以看出仿真得到的各阶模态频率与水下模态试验得到的各阶模态频率相差比较大,这是因为试验时水深度有限,而仿真是在无限流域中进行的。根据上节得出的结论,水的深度会直接影响到模态频率,且水越深模态频率越小并最终趋于定值。可以认为,仿真中无限流域的湿模态频率即为水下模态试验随水深而最终趋近的定值。例如本试验件的湿模态仿真结果中,一阶模态频率为57.2 Hz,而水下模态试验中水深为150 mm时,一阶模态频率为64.259 Hz,若水深继续增加,试验数据将会趋近57.2 Hz。
表4 模态仿真频率与振型数据

模态阶次干模态频率/Hz振型物理描述湿模态频率/Hz振型物理描述1113.05一阶弯曲(绕y轴)57.2一阶弯曲(绕y轴)2116.96一阶弯曲(绕z轴)59.1一阶弯曲(绕z轴)3232.85一阶扁涨(y向带弯曲)106一阶扁涨(y向带弯曲)4239.43一阶扁涨(z向带弯曲)109.14一阶扁涨(z向带弯曲)
4 结论
通过多组不同状态下的模态试验,并将模态试验结果与仿真数据作对比分析,得出重要结论:① 使用力锤激振与激振器激振所得结果差别不大,即模态试验结果与激振方式关系不大;② 水下模态试验时,不同水深对于模态频率有重大影响。随水深增加,模态频率逐渐减小,且减小的速度变慢,并趋近于定值;③ 干模态仿真结果与试验结果偏差不大,湿模态偏差很大,仿真时需考虑自由面效应;④ 试验件在空气中和水中模态频率相差很大,不能用干模态数据代替湿模态试验结果。
[1] 焦安超,冯咬齐.“天宫一号”目标飞行器结构模态试验方法[J].航天器环境工程,2011,28(6):593-596.
[2] 孙海文,胥磊.某火箭模态分析与模态试验[J].兵器装备工程学报,2017,38(6)176-179.
[3] 李家盛.螺旋桨和水翼流固耦合机理与计算方法研究[D].上海:上海交通大学,2018.
[4] LI Yuanqi,WANG Lei,SHEN Zuyan.Added-mass estimation of flat membranes vibrating in still air[J].Journal of Wind Engineering and Industrial Aerodynamics,2011,99(8):815-824.
[5] 邱振宇,陈务军,赵兵,等.飞艇主气囊结构湿模态分析与试验研究[J].振动与冲击,2017,36(12):61-67.
[6] 刘瑞骏,郝志勇,郑旭,等.改进的湿模态法在流固耦合中的应用[J].振动与冲击,2017,36(22):199-204.
[7] 贾文成,王鹏辉,张永亮.新一代大型火箭全箭模态试验[J].强度与环境,2017,44(2):1-9.
[8] 王在铎,马斌捷,贾亮,等.水下附加质量及阻尼的试验研究[J].强度与环境,2018,45(3):15-19.
[9] 吴松,臧旭,龙新军,等.吊挂式模态试验系统动力学建模和分析[J].航空学报,2018,39(s1):722191.
[10] 郝丙飞,王红岩,芮强.坦克火炮身管模态分析及试验验证[J].兵器装备工程学报,2017(10):74-78.
[11] PEETERS B,GUILLAUME P,AUWERAER HV,et al.Automotive and aerospace applications of the PolyMAX modal parameter estimation method[C]//Proceedings of IMA 22. Dearbom,MI,USA,2004.
[12] PEETERS B,AUWERAER H V,GUILLAUME P,et al.The PloyMAX frequency domain method:a new standard for modal parameter estimation[J].Shock and Vibration,2004(11):395-409.
[13] 孙鑫晖,郝木明,王淮维.PolyMAX 模态参数识别算法的快速实现[J].振动与冲击,2011,30(10):6-8.
[14] 刘庆茂.复杂结构水下模态试验研究[J].导航与航天运载技术,1997(4):23-29.
[15] 张成,张大海,郭航航.弹体出水附加质量计算及对阻尼系数的影响分析[J].船海工程,2013,42(6):187-190.