电动缸是将伺服电机、减速机和丝杠集成于一体的模块化产品,它将伺服电机的旋转运动转化为丝杠推杆的直线运动,具有传动效率高、定位精度高、响应快、结构简单、占用空间小、维护方便、寿命长、环境适应性强等优点[1-2],近几年在航空航天、武器装备等领域获得了越来越多的关注和应用。为了合理利用炮塔空间,简化结构设计,某大口径火炮高低随动系统采用电动缸作为传动机构。
对于电动缸伺服系统的位置控制,目前已经开展了大量研究。张爱龙等[3]在电动缸位移和力伺服系统中采用带前馈的PID控制器,获得了较好的跟踪精度。徐永利等[4]将基于模糊PID参数整定的力/位混合控制方法应用于基于电动缸的重力补偿控制中,获得了稳定的重力补偿精度。秦幸妮等[5]将自抗扰控制技术应用在某舰炮电动缸伺服系统中,跟传统PID控制相比,提高了伺服系统的响应速度,减小了定位和跟踪误差。段学超等[6]在巨型射电天文望远镜的设计中,采用带前馈的数字伺服滤波器实现了电动缸的高精度轨迹跟踪控制。陈国迎等[7]在转向台架加载系统的研究中采用PID 力闭环控制和串联校正方法使电动伺服系统加载力能快速跟踪目标值,同时减小扰动下多余力的影响。曾从吉等[8]将智能分区PID算法应用于电动缸伺服系统中,减小了系统的稳态误差[8]。史成城等[9]在电动缸控制系统中采用遗传算法对PID参数进行整定,获得了较好的控制效果。李木国等[10]采用模糊PID和超前补偿控制策略,减小了电动缸推杆在往复运动过程中由于电机频繁正反转带来的相位延迟和幅值误差。
本文针对采用电动缸作为传动机构的某大口径火炮高低随动系统的位置控制器进行研究,建立了火炮身管的运动学模型和动力学模型,提出了一种变系数误差平方根和带前馈的PID分段控制策略,应用于火炮高低随动系统的位置控制器设计,有效解决了由于电动缸带来的速比非线性导致随动系统快速性和精度之间难以匹配的问题,具有较好的工程适用性。
1 高低随动系统建模
某大口径火炮高低随动系统采用电动缸作为传动机构,电动缸的一端与火炮摇架铰接,另一端与火炮座圈铰接,其简化的结构示意图如图1。
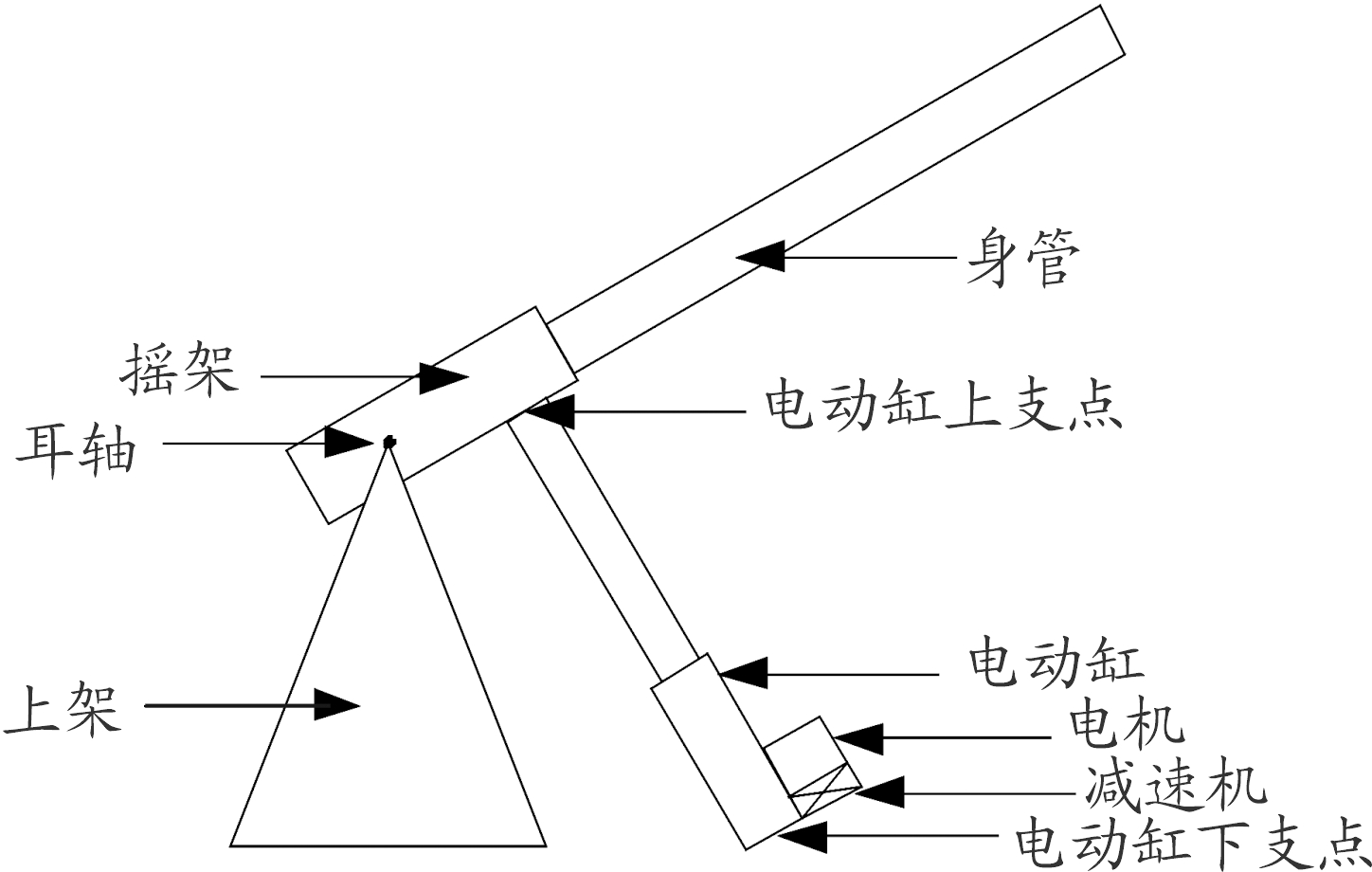
图1 高低随动系统结构示意图
1.1 高低随动系统运动学建模
根据图1建立火炮身管的运动学简图,如图2。图2中,o为过耳轴(火炮身管俯仰运动的回转中心)的铅垂线与过电动缸下支点的水平线的交点,l1为耳轴到电动缸下支点的距离(m),l2为耳轴到电动缸上支点的距离(m),l3为电动缸伸出后的总长度(m),l0为电动缸伸出前的最小长度(m),θ为耳轴与电动缸下支点连线跟火炮身管之间的夹角(rad)。
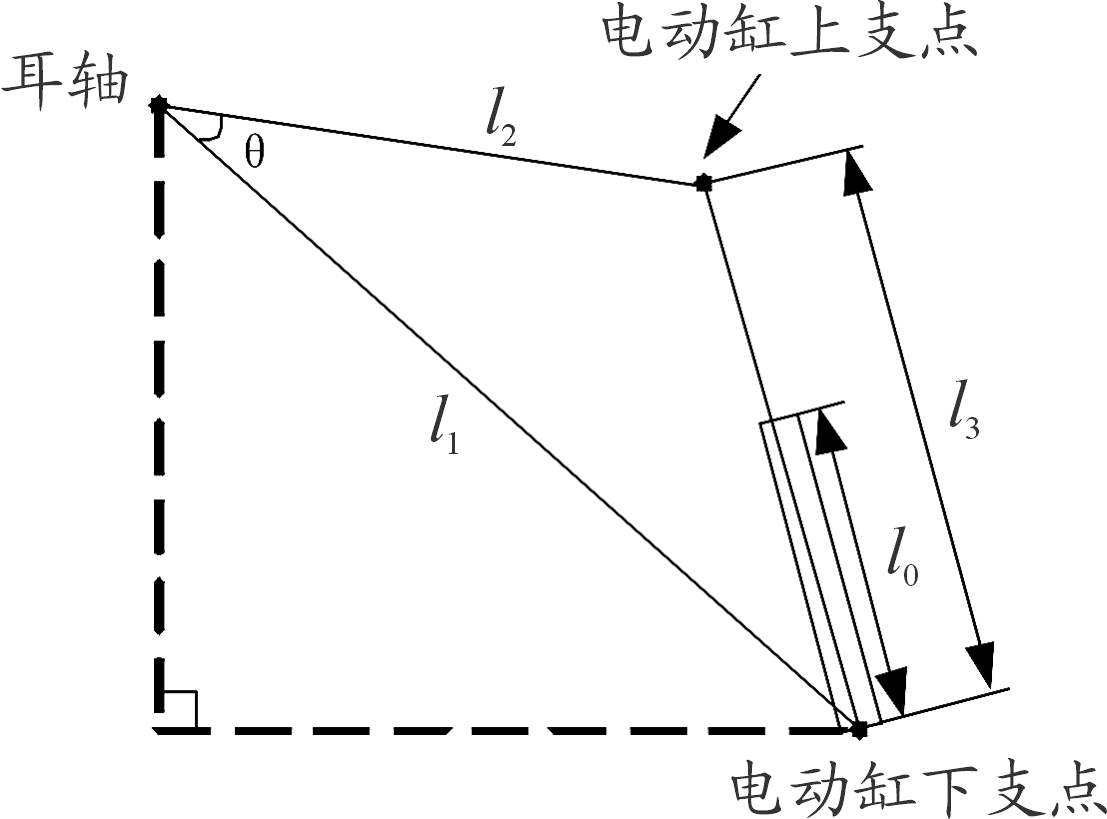
图2 火炮身管运动学简图
假设电动缸中丝杠伸出的线速度为v(m/s),丝杠的导程为s(m),电动缸中减速机的减速比为i1,电机转速为n(r/min),电机角速度为ωm(rad/s),则有:
(1)
l3=l0+vt
(2)
根据图2对火炮身管进行运动学分析,得到:
(3)
(4)
将式(4)两边对t求导,得到:
![]()
(5)
将式(1)代入式(5),得到:
(6)
式(6)中:![]() 根据式(6)可知:电机角速度与火炮身管角速度之间的速比i2不为定值,随火炮身管所处角度变化。
根据式(6)可知:电机角速度与火炮身管角速度之间的速比i2不为定值,随火炮身管所处角度变化。
1.2 高低随动系统动力学建模
根据图1建立火炮身管的动力学简图,如图3。图3中,Fg为电动缸丝杠伸出的力(N),F1为电动缸丝杠伸出的力在垂直于耳轴到电动缸上支点连线上的分量(N),β为电动缸上支点与下支点连线跟火炮身管之间的夹角(rad),γ为Fg跟火炮身管之间的夹角(rad),TL为火炮身管的不平衡力矩(N·m)。
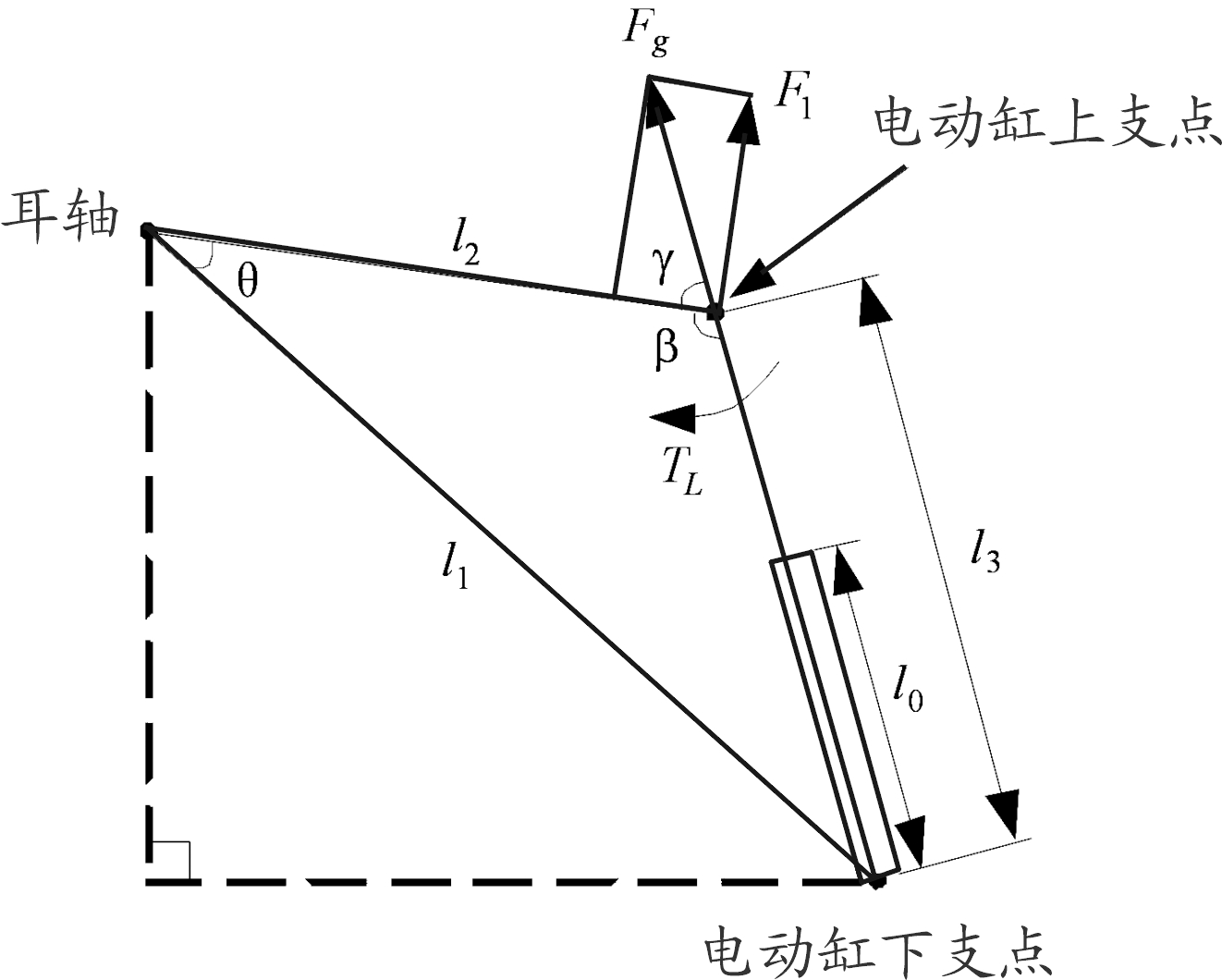
图3 火炮身管动力学简图
假设电机的力矩系数为Kt(N·m/A),电机的q轴电流为iq(A),电动缸中减速机的效率为η1,电动缸中丝杠的效率为η2,电机轴输出的扭矩为Tm(N·m),丝杠输出的扭矩为Tg(N·m),火炮身管的转动惯量为J1(kg·m2),电机转子的转动惯量为J2(kg·m2),电机转子的转动惯量折算到负载侧的等效转动惯量为J3(kg·m2),忽略电动缸中减速机和丝杠的转动惯量影响,则有:
Tg=Tmi1η1=Ktiqi1η1
(7)
Fg=Tg2πη2s=Ktiqi1η12πη2s
(8)
J3=J2i1
(9)
图3中,根据余弦定理有:
![]()
(10)
根据正弦定理有:
(11)
(12)
根据图3可知:
F1=Fgsinγ=Fgsin(π-β)=Kciq
(13)
式(13)中:
假设身管为刚体,根据刚体定轴转动定律可知:
(14)
(15)
其中:BM为粘滞摩擦因数(N·m/(rad/s))。根据式(15)可知,火炮身管角加速度与电机电流之间为非线性关系。
2 位置控制器设计
误差平方根和带前馈的PID分段控制策略既有效利用了系统的加减速能力,保证了随动系统的快速性,又具有良好的跟踪性能,因此在高炮随动系统的位置控制中获得了广泛的应用,其基本原理为:根据位置误差的大小将系统分为线性区和非线性区,在线性区采用带前馈的PID控制,保证系统具有良好的跟踪性能,在非线性区采用误差平方根控制,尽量减小系统的制动段长度,保证随动系统的快速性。在非线性区采用误差平方根控制的条件包括[11]:系统具有优良的速度跟踪性能,速度环滞后小;系统能提供恒定的角加速度。
本文研究的大口径火炮高低随动系统采用了永磁同步电机和全数字伺服驱动技术,具有良好的速度跟踪性能,满足采用误差平方根控制的条件一,但是由于其采用了电动缸作为传动机构,从式(15)可知,当电机电流iq为定值时,身管角加速度随身管所处角度变化,因此不满足条件二。本文对误差平方根和带前馈的PID分段控制策略进行改进,提出了变系数误差平方根和带前馈的PID分段控制策略,应用于随动系统的位置环控制器设计。位置控制器的输出n1(r/min)为
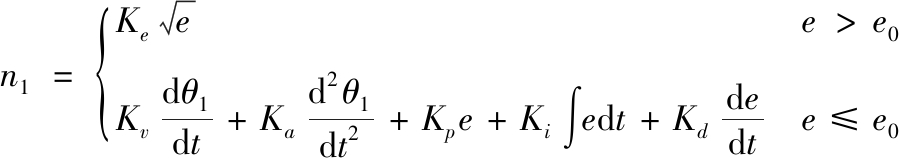
(16)
式中:Ke为误差平方根系数;e为角位置误差(rad);e0为线性区和非线性区的分界点(rad);Kv为速度前馈系数;Ka为加速度前馈系数;θ1为角位置主令(rad);Kp为比例系数;Ki为积分系数;Kd为微分系数。
在式(16)中,系数Kv、Ka、Kp、Ki、Kd通过系统调试确定。考虑到误差平方根控制的特点,即误差越小,位置控制器输出的变化率越大,越有利于利用系统的最大加速度制动,同时考虑到等速和正弦跟踪时,需要足够的线性区保证跟踪性能,因此将本系统的线性区和非线性区的分界点e0设置为0.05 rad。Ke的计算方法如下:
假设非线性区制动段任一时刻火炮身管的期望角速度为ω1(rad/s),制动结束时火炮身管的期望角速度为ω0(rad/s),期望系统提供的角加速度为![]() 根据角速度、角加速度和角位移之间的关系得到:
根据角速度、角加速度和角位移之间的关系得到:
(17)
通常期望制动结束时火炮身管的角速度为0,因此令ω0=0,得到:
![]()
(18)
由于n1的单位为r/min,ω1的单位为rad/s,两者的单位不统一,根据身管角速度与电机角速度之间的关系以及n1和ω1之间的单位换算关系可知:
(19)
式中: i2为电机角速度与火炮身管角速度之间的速比。对比式(16)和式(19),得到:
![]()
(20)
式中:电机角速度与火炮身管角速度之间的速比i2根据式(6)计算,即![]() 根据式(15)计算,即
根据式(15)计算,即![]()
3 验证
采用电动缸传动的某大口径火炮的部分参数如下:l1=2.308 m,l2=0.58 m,i1=2.15,s=0.003 8 m,Kt=1.83 N·m/A,η1=0.86,η2=0.84,J1=73 100 kg·m2,J2=0.6 kg·m2。在高低随动系统的位置控制器设计中,采用了本文提出的变系数误差平方根和带前馈的PID分段控制策略,程序采用C语言实现。将实际炮塔部分安装在调试台架上,测角器安装在火炮耳轴上,测量火炮身管的实际角度,作为位置反馈,进行了随动系统真实负载调炮实验。实验中,采用示波器测量角位置误差,设置角位置误差的最大限幅值为25 mrad。
图4为从0 mrad到1 570 mrad调转的位置误差曲线,从图4可以看出:到位误差为0.4 mrad,调转时间为2.2 s,超调量为3 mrad。图5为从1 570 mrad到0 mrad调转的位置误差曲线,从图5可以看出:到位误差为0.4 mrad,调转时间为2.1 s,超调量为2 mrad。从定位调转位置误差曲线看,调转过程速度快,超调量小。图6为负载在20 (°)/s 等速运动时的跟踪误差曲线,从图6可以看出:位置跟踪误差最大为1.86 mrad。图7为负载在幅值为25°,周期为6.28 s的正弦运动时的跟踪误差曲线,从图7可以看出:位置跟踪误差最大为3.2 mrad。从等速跟踪和正弦跟踪误差曲线看,跟踪误差小。
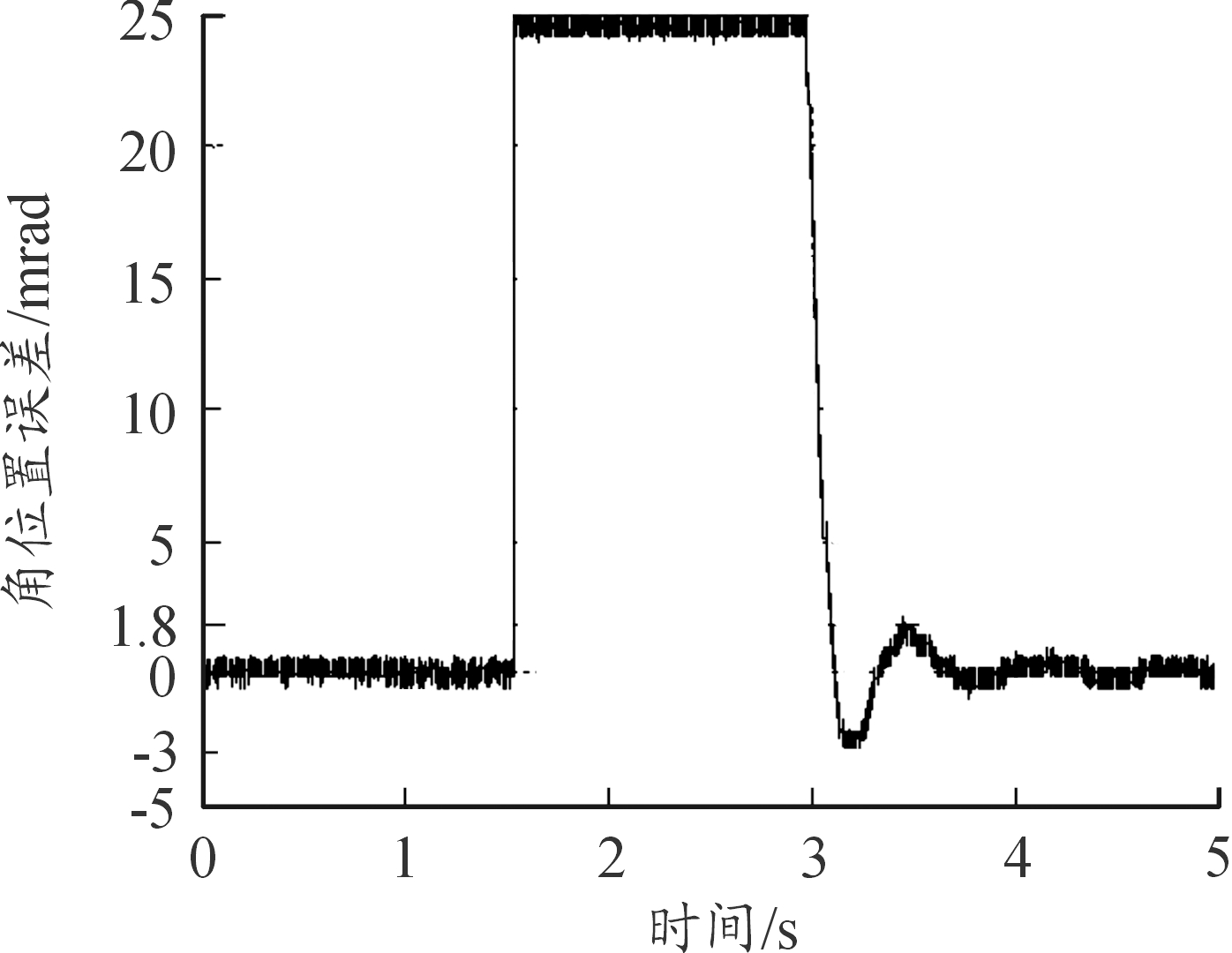
图4 0 mrad到1 570 mrad调转的位置误差曲线

图5 1 570 mrad到0 mrad调转的位置误差曲线

图6 负载在20(°)/s 等速运动时的跟踪误差曲线
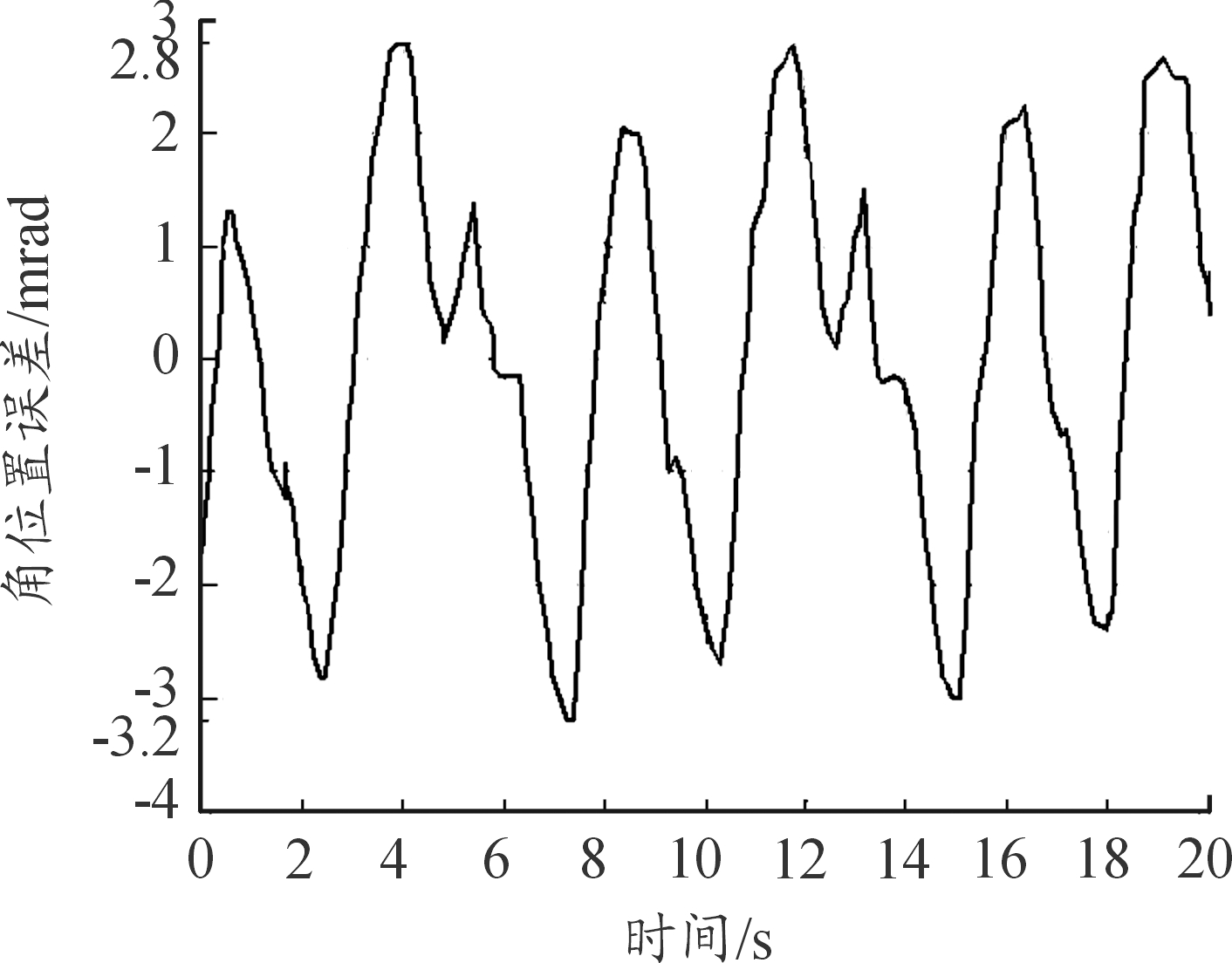
图7 负载在幅值为25°,周期为6.28 s的正弦运动时的跟踪误差曲线
4 结论
对采用电动缸作为传动机构的某大口径火炮高低随动系统进行分析,建立了火炮身管的运动学模型和动力学模型,提出了变系数误差平方根和带前馈的PID分段控制策略,利用火炮身管的运动学模型和动力学模型计算误差平方根的控制系数,将该控制方法应用于随动系统的位置控制器设计中。实验结果表明:变系数误差平方根和带前馈的PID分段控制策略对于采用电动缸作为传动机构的火炮随动系统,能够获得较高的定位精度和跟踪精度,系统快速性好,超调量小,具有工程实用性。
[1] 陈超,赵升吨,崔敏超,等.电动缸的研究现状和发展趋势[J].机械传动,2015,39(3):181-185.
[2] 吴静,赵洪.电动缸系统控制研究[J].西南科技大学学报,2015,30(4):60-64.
[3] 张爱龙,喻镇涛,伊斯武,等.基于cRIO平台的电动缸位移与力伺服控制系统设计[J].电气传动,2019,49(4):89-92.
[4] 徐永利,李潇男,刘勇,等.空间机械臂地面竖直方向重力补偿控制系统设计[J/OL].机器人.https://doi.org/10.13973/j.cnki.robot.190042.
[5] 秦幸妮,姜明,刘彦艳,等.自抗扰控制技术在电动缸伺服系统中的研究[J].火炮发射与控制学报,2019,40(1):49-52.
[6] 段学超.柔性支撑Stewart平台的分析、优化与控制研究[D].西安:西安电子科技大学,2008.
[7] 陈国迎,何磊,宗长富,等.基于电动伺服系统的转向试验台阻力加载策略的研究[J].汽车工程,2018,40(2):226-233.
[8] 曾从吉,单梁,陆建荣.智能分区PID控制算法在电动缸伺服系统中的研究[J].计算机测量与控制,2015,23(6):1967-1971.
[9] 史成城,张宏立.电动缸测控系统的仿真与通信[J].自动化仪表,2013,34(7):19-21.
[10] 李木国,刘于之,张群,等.电机伺服系统中的数字控制技术研究与实现[J].计算机测量与控制,2010,18(5):1082-1084.
[11] 陈明俊,李长红,杨燕.武器伺服系统工程实践[M].北京:国防工业出版社,2013:70-74.