在现代战争中,随着武器打击目标的能力越来越强,相应的防御体系也在迅速发展,对于具有重要战略价值的目标,其防护要求也大大提高。混凝土作为一种复合材料,通常由水泥、砂浆、碎石(骨料)及水等混合构成,具有良好的耐火性、可浇注性以及来源广泛的特点。混凝土作为桥梁、地下防护结构以及其他建筑物中,应用最为广泛的材料,在军事和民用方面都有极大的应用[1-2]。如何有效地打击混凝土这类目标,已经被各国军事部门所关注,并积极寻求有效的毁伤手段和方法。
研究高速弹丸对混凝土类目标的侵彻效应,对于有效打击敌方重要建筑以及加强自身防护能力,具有重要的现实意义。因此,我国学者进行了大量有关弹丸侵彻混凝土靶板的试验以及数值模拟研究。马天宝[3]等基于大口径发射平台进行了100 mm口径卵形弹体高速侵彻钢筋混凝土靶体的实验,获得了弹体的侵彻深度及钢筋混凝土靶体的破坏数据。王茂英[4]利用LS-DYNA对具有相同属性的弹体,以相同的入射速度,垂直侵彻和贯穿混凝土靶和钢筋混凝土靶的过程进行数值模拟,研究表明随着弹体入射速度的增大,钢筋混凝土靶与混凝土靶的厚度比值降低,钢筋混凝土抗侵彻能力比纯混凝土抗侵彻能力增强。张明润[5]等采用数值模拟的方法,利用LS-DYNA建立动力学模型,分析了弹丸在侵彻混凝土过程中加速度的变化,以及混凝土开坑的整个过程,为实际工程中混凝土结构抗侵彻设计提供指导依据。张雪岩[6]等进行了弹体高速侵彻C60高强度混凝土的试验,并与弹体高速侵彻C35普通强度混凝土试验结果进行对比。韦宁[7]根据Hamilton原理和有限元理论,通过LS-DYNA对高速弹体侵彻混凝土靶进行了数值模拟,结果表明弹体的速度及弹头长径比对混凝土靶的侵彻深度有较大影响。
进行混凝土靶板抗弹性能研究,在浇筑混凝土靶板过程中,为达到靶板预期的强度、刚度等要求,需要很长一段时间的准备与测试,影响其试验的时效性,因此建立混凝土靶板等效靶,等效替代混凝土靶板进行抗弹性能研究。考虑等效材料强度、价格以及通用性的要求,故使用45#钢作为等效材料,替代混凝土进行相关试验研究,从而大大提高试验的效率,并节约成本,便于保证研究进度。
1 等效原则的建立
关于靶板等效原则,大致可以分为以下4种,即材料强度等效原则、极限穿透速度等效原则、剩余穿深等效原则和靶体吸收动能等效原则[8]。靶体吸收动能等效原则,即以弹体在侵彻贯穿靶板过程中动能损失大小为等效指标及衡量标准,表示为:
(1)
其中: mp为弹丸质量; v0为弹丸的初速度; vr为弹丸剩余速度。
在数值模拟计算过程中,假设不考虑弹体磨蚀及变形带来的影响,侵彻过程弹体损失的动能,可以在已知弹丸质量、弹丸初速以及弹丸剩余速度的情况下,通过上述公式计算获得。
本文主要通过LS-DYNA进行垂直侵彻贯穿混凝土靶板及等效钢靶的数值模拟研究,在此选用靶体吸收动能等效原则进行等效靶研究,即以相同属性、相同速度弹丸垂直侵彻贯穿厚度为hs钢靶与厚度为hc混凝土靶板,当弹丸剩余速度相同时,即认为厚度hs钢靶为厚度hc混凝土靶板的等效靶。
2 有限元模型建立
高速弹丸侵彻混凝土时,会出现成坑、裂纹和崩落的现象,利用LS-DYNA软件,进行非线性动力学仿真。本文采用Lagrange动力学算法,利用材料失效、侵蚀接触和单独失效模型等完成高速弹丸侵彻贯穿混凝土靶板动力学仿真。其中弹丸及等效钢靶采用JOHNSON-COOK本构模型,混凝土由于结构和材料的特殊性,本文选用RHT本构模型。
2.1 JOHNSON-COOK本构模型
基于连续损伤力学及粘塑性力学的JOHNSON-COOK动态本构模型,在绝热条件下充分考虑金属材料的应变率效应与温度软化效应[9],能够很好地描述30CrMn钢和45#钢在侵彻载荷作用下产生的大变形以及高应变,将屈服应力表示为等效塑性应变、应变率和温度的函数:
(2)
(3)
式中: σeq为屈服应力; εeq为等效塑性应变;![]() 是无量纲等效应变率;Ar为准静态屈服应力;Tr为参考温度;Tm为材料熔点;Br为应变硬化系数;n为应变硬化指数; Cr为应变率相关系数;m为温度系数。
是无量纲等效应变率;Ar为准静态屈服应力;Tr为参考温度;Tm为材料熔点;Br为应变硬化系数;n为应变硬化指数; Cr为应变率相关系数;m为温度系数。
金属材料受到碰撞等载荷作用,在高应变率下会产生塑性变形过程,需要引入JOHNSON-COOK动态本构模型的断裂准则,有效断裂应变表示为:
(4)
式中:εf为失效塑性应变值;D1~D5为材料常数;σh为材料的静水压力。当损伤参量![]() 超过1时(Δεp为等效塑性应变增量),材料失效。
超过1时(Δεp为等效塑性应变增量),材料失效。
2.2 RHT本构模型
混凝土的RHT本构模型,综合考虑了应变硬化、失效面、压缩损伤和应变率效应等特点,全面反映混凝土的动态力学性能,在动能弹侵彻混凝土靶板的数值仿真中应用比较广泛。RHT本构模型引入了失效面、弹性极限面和残余强度面,分别对混凝土的失效强度,初始屈服强度及残余强度的变化规律进行描述[10-11]。
RHT模型对失效面的处理十分细致,定义失效面Yf为关于压力P,Lode角θ和应变率![]() 的函数:
的函数:
Yf=Ytxc*R3*Fr
(5)
式中:Ytxc表示压缩子午线; Fr表示应变率强化因子。
(6)
(7)
(8)
式中: fcs表示混凝土单轴抗压强度; fts表示混凝土单轴抗拉强度; P*为归一化压力; ![]() 表示失效面常数;N表示失效面指数;
表示失效面常数;N表示失效面指数;![]() 分别为等效应变率和参考应变率;D表示压缩应变率指数;a表示拉伸应变率指数;Q2是压力相关函数; θ为应力偏量第二、三不变量的函数。
分别为等效应变率和参考应变率;D表示压缩应变率指数;a表示拉伸应变率指数;Q2是压力相关函数; θ为应力偏量第二、三不变量的函数。
弹性极限面Ye与失效面Yf的比例关系表达式为:
Ye=Yf*Fe*Fcap
(9)
式中: Fe是弹性强度与失效面强度之比,一般取常数; Fcap是盖帽函数。
残余失效面Yr是压力的相关函数:
Yr=BP*M
(10)
式中:B为残余强度面常数;M为残余强度面指数。
2.3 材料模型及参数
由于靶板及弹丸具有对称性,为节省计算时间,故建立1/4模型进行仿真计算;为更好地表现侵彻效果,对弹丸头部以及混凝土靶中心区域网格进行加密,剩余部分网格适当稀疏。选用卵形实体弹丸进行仿真,弹丸直径为90 mm,长度250 mm,建模及网格划分如图1所示。

图1 弹体1/4模型及网格划分示意图
混凝土靶板横截面积为720 mm×720 mm,建模效果及网格划分如图2所示,在对称面上施加对称边界约束,设置计算时间步长为0.6 μs。

图2 混凝土靶板网格划分示意图
弹丸材料选用30CrMn钢,等效靶板材料选用45#钢,其力学性能参数如表1所示,混凝土材力学性能参数如表2所示[12-13]。
表1 30CrMn钢及45#钢力学性能参数

材料密度/(g·cm-3)弹性模量/GPa泊松比30CrMn钢7.832050.345#钢7.842100.3
表2 混凝土力学性能参数
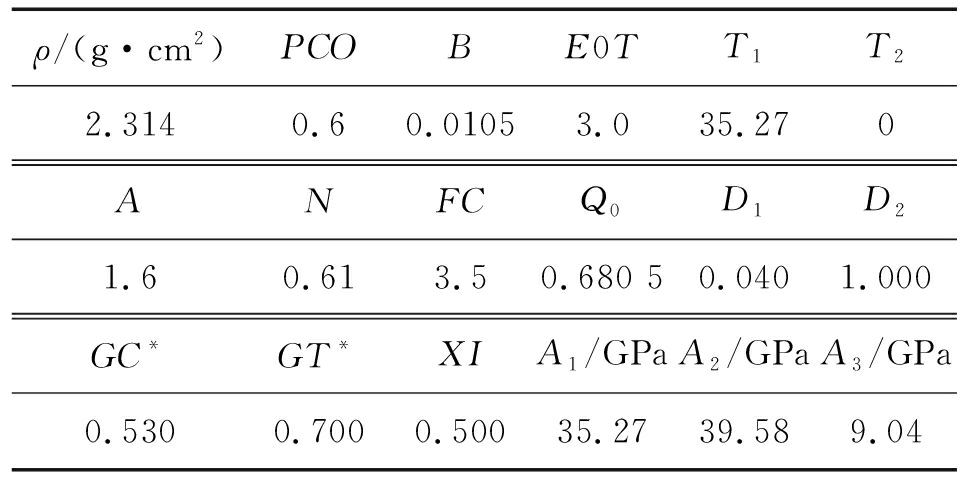
ρ/(g·cm2)PCOBE0TT1T22.3140.60.01053.035.270ANFCQ0D1D21.60.613.50.680 50.0401.000GC*GT*XIA1/GPaA2/GPaA3/GPa0.5300.7000.50035.2739.589.04
2.4 仿真验证
为验证本文采用数值模拟方法的合理性,利用LS-DYNA软件进行弹丸以130 m/s的速度侵彻混凝土靶板的数值模拟仿真,获得弹丸加速度峰值约为16 000g,侵彻靶板深度为20 cm;徐文峥实验中弹丸以130 m/s的速度侵彻混凝土靶板[14],获得弹丸加速度峰值约为16 000g,侵彻深度为17 cm。由于实验过程中侵彻过程会出现诸多影响因素,因此仿真结果中侵彻深度偏大,仿真加速度曲线与实验加速度曲线趋势基本一致,如图3所示,证明本文数值模拟仿真结果具有可靠性。
3 仿真结果分析
3.1 弹丸侵彻混凝土靶板
弹丸高速侵彻混凝土靶板,弹体加速度曲线大致分为4个阶段。当弹丸以1 200 m/s的速度侵彻50 cm混凝土靶板时,弹丸加速度曲线如图4:0~100 μs时间段内,弹丸以一定速度撞击混凝土,弹头与靶体的横截相交面不大,侵彻阻力较小,此时加速度较小;100~300 μs这一时间段内,由于弹头部分与靶体的横截相交面不断增大,弹体的直径与横截面的直径接近之时加速度接近达到最大值11万g;300~500 μs时间段内最大加速度对应于弹体的尾端面,与靶体表面处于同一表面深度时,随后的加速度维持在最大值附近;500~600 μs时间段内弹丸头部冲出靶板,所受阻力逐渐减小,加速度逐渐降低,当弹丸整体贯穿靶板时,弹丸所受加速度减为零[15]。
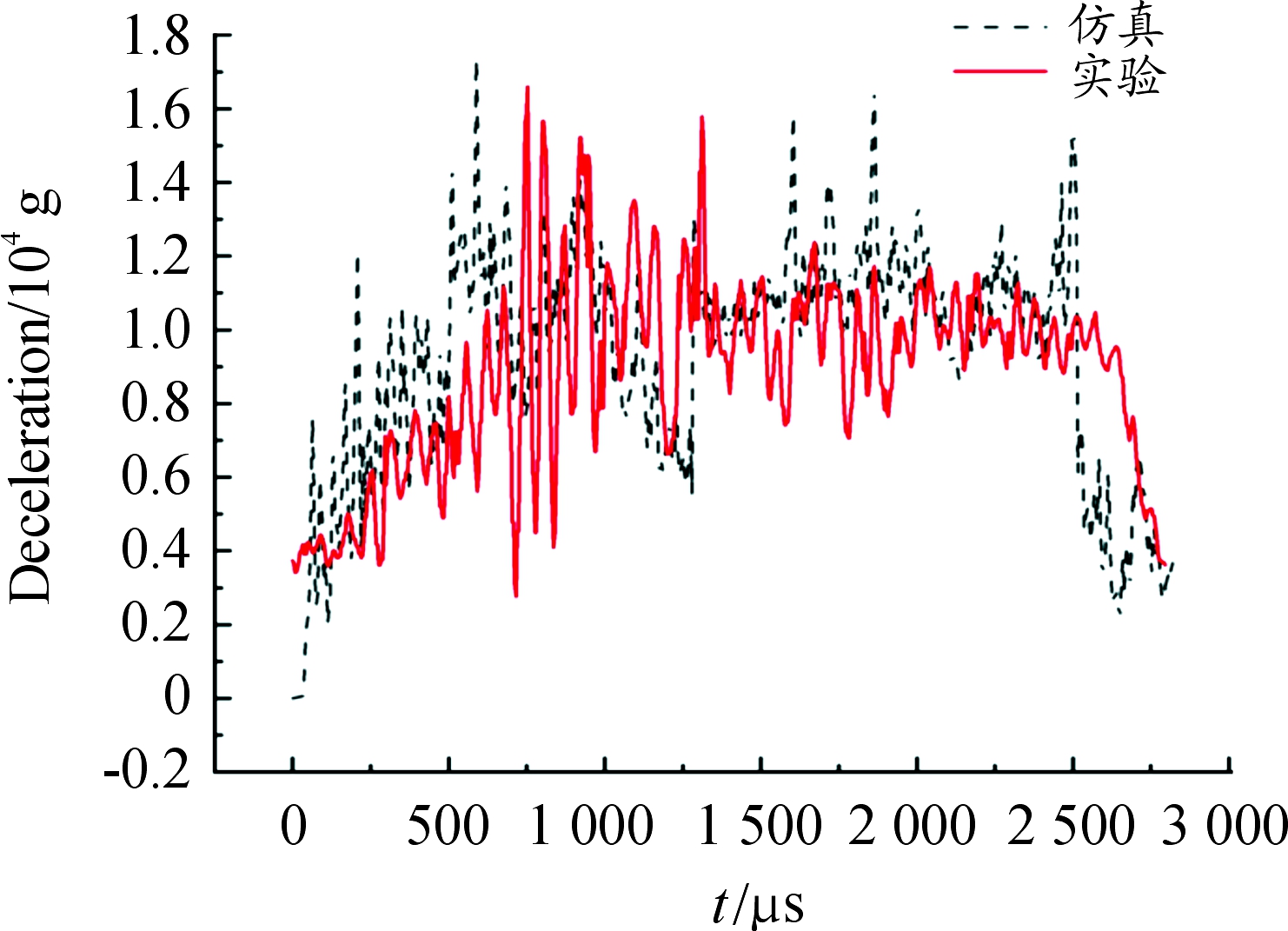
图3 实验与仿真加速度曲线

图4 1 200 m/s贯穿混凝土靶板加速度曲线
弹丸垂直侵彻贯穿混凝土时仿真过程如图5所示,首先会在靶板表面开坑,随着侵彻深度增加,靶板会逐渐产生大量裂纹。

图5 高速弹丸侵彻贯穿混凝土靶板仿真过程
利用LS-DYNA有限元软件进行动力学仿真,弹丸以 1 200、1 000、800 m/s的速度垂直侵彻贯穿厚度为20、30、50、80、100 cm的混凝土靶板,获得3组弹丸加速度曲线如图6所示。
由3组不同速度下弹丸侵彻混凝土加速度曲线对比可知,以1 200 m/s的速度侵彻5种厚度的混凝土靶板,弹丸加速度峰值由低到高分别为7万g、10万g、11万g、13万g、14万g,即以相同速度侵彻混凝土靶板,靶板厚度越大弹体损失能量越大,加速度峰值越大;以3种速度侵彻相同厚度混凝土靶板,1 200 m/s时弹丸加速度峰值最大,1 000 m/s时弹丸加速度峰值次之,800 m/s时弹丸加速度峰值速度最小,即以不同速度侵彻混凝土靶板,弹丸撞击靶板时速度越大,弹丸所受阻力越大,弹丸加速度峰值越大。
3.2 弹丸侵彻等效钢靶
弹丸垂直侵彻贯穿钢靶时,与混凝土靶板相比较,不会有开坑、裂纹及崩落的现象出现,弹丸完全贯穿钢靶时,钢靶中心会出现一个较圆滑的孔洞,弹丸垂直侵彻贯穿钢靶效果过程如图7所示,弹丸加速度曲线如图8所示。
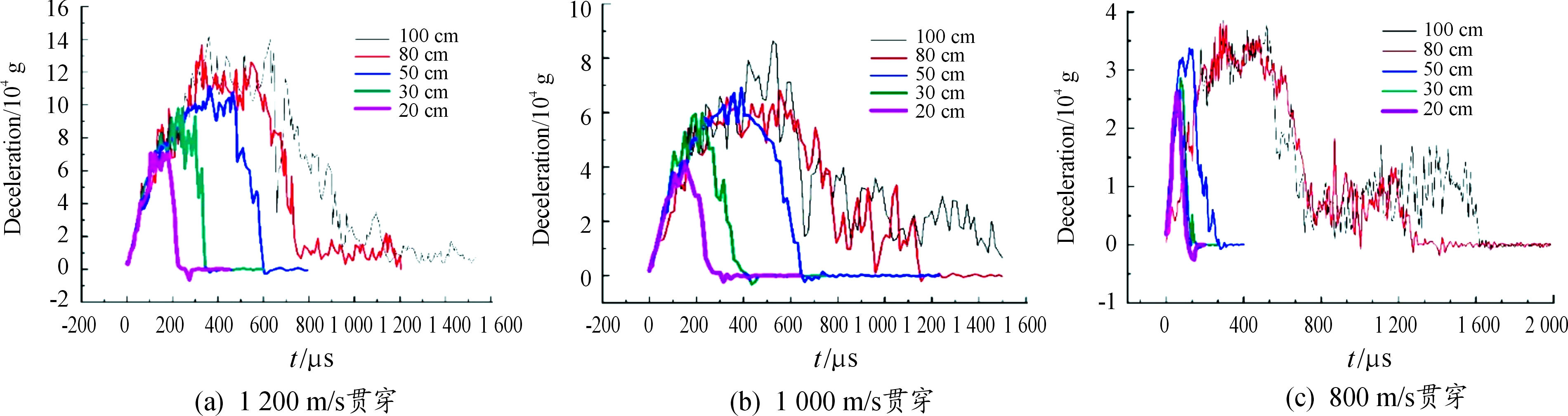
图6 3组弹丸侵彻混凝土靶板加速度曲线

图7 高速弹丸侵彻等效钢靶仿真过程

图8 3组弹丸侵彻等效钢靶加速度曲线
由图6与图8对比可知,弹丸以1 200、1 000、800 m/s的速度垂直侵彻贯穿钢靶,与弹丸侵彻混凝土靶板相比较,当弹丸剩余速度相同时,贯穿的钢靶厚度更薄,弹体所受阻力更大,加速度最大值更大。
3.3 混凝土靶板与钢靶厚度等效关系
根据靶体吸收动能等效原则,以相同速度相同角度贯穿侵彻不同材料靶板,当弹丸损失能量相同时,即弹丸的剩余速度相同时,认为两种靶板具有相同的防护能力,即两靶板等效。获得3种速度下、五组不同厚度混凝土靶板对应等效钢靶的厚度,如表3、表4、表5所示。
表3 1 200 m/s状态下靶板剩余速度
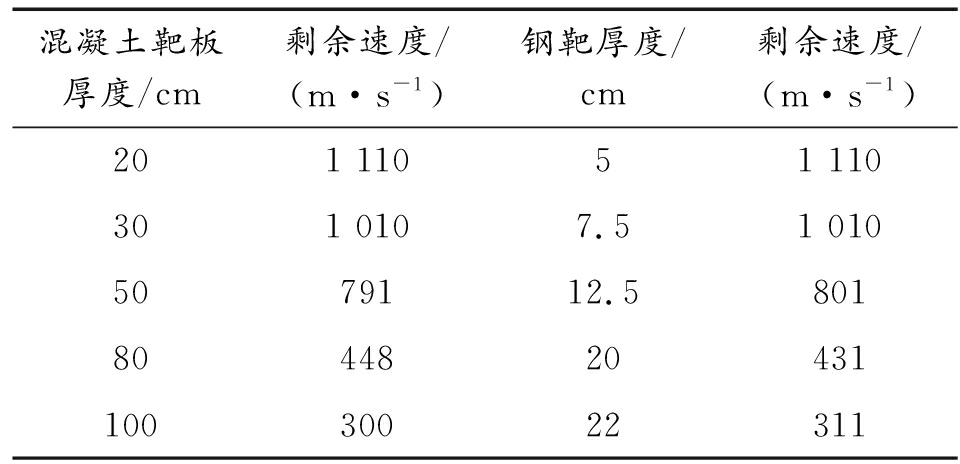
混凝土靶板厚度/cm剩余速度/(m·s-1)钢靶厚度/cm剩余速度/(m·s-1)201 11051 110301 0107.51 0105079112.5801804482043110030022311
表4 1 000 m/s状态下靶板剩余速度
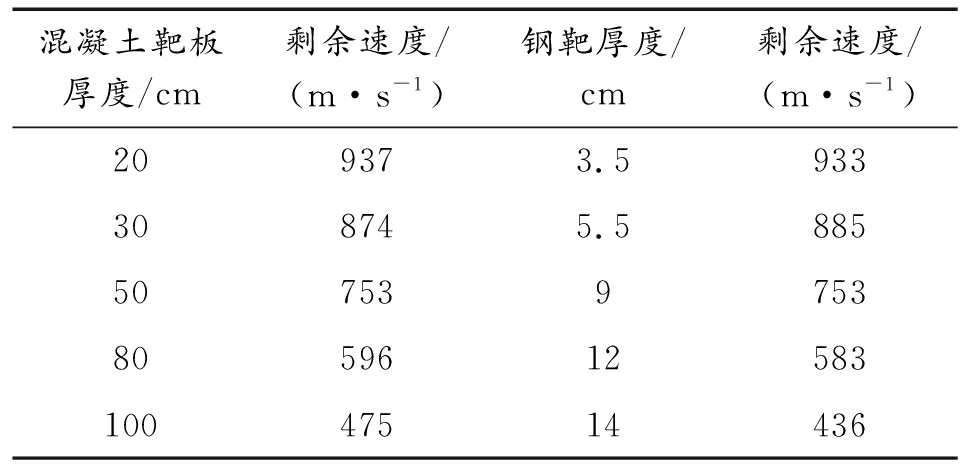
混凝土靶板厚度/cm剩余速度/(m·s-1)钢靶厚度/cm剩余速度/(m·s-1)209373.5933308745.5885507539753805961258310047514436
表5 800 m/s状态下靶板剩余速度

混凝土靶板厚度/cm剩余速度/(m·s-1)钢靶厚度/cm剩余速度/(m·s-1)2075627623073837395065756538058175931005568549
根据上述所获得厚度的离散数据,利用MATLAB拟合混凝土靶板与等效钢靶厚度转换关系曲线,并显示转换方程。
3种速度下等效方程近似为三次方程,获得三组转换关系:
速度为1 200 m/s时,等效方程为:
0.24hs+0.009
(11)
速度为1 000 m/s时,等效方程为:
+0.21hs-0.19
(12)
速度为800 m/s时,等效方程为:
0.1hs-0.022
(13)
其中: hs为等效钢靶厚度; hc为混凝土靶板厚度。
分别对40、60 cm混凝土靶板与等效钢靶的厚度转换关系进行验证,将钢靶计算厚度与钢靶仿真厚度进行比较,验证结果如表6所示,验证结果可得,转换厚度误差不大于10%。
表6 等效靶厚度转化关系验证

速度/(m·s-1)混凝土靶板厚度/cm钢靶计算厚度/cm钢靶仿真厚度/cm误差/%1 2004010.23102.36014.99166.31 000407.3188.66010.26102.6800403.8344.3605.4669.0
4 结论
1) 以相同速度侵彻靶板时,靶板厚度越大弹体损失能量越大,加速度峰值越大;以不同速度侵彻相同厚度靶板时,弹丸撞击靶板时速度越大,弹丸所受阻力越大,弹丸加速度峰值越大。
2) 根据靶体吸收动能等效原则,建立混凝土靶板等效钢靶,创建混凝土靶板与等效钢靶的厚度转换关系式。根据几组离散的仿真数据,拟合出三种速度下混凝土靶板与等效钢靶之间的厚度转换关系,并利用数值模拟再次进行验证,计算结果与仿真结果误差不大于10%,为日后混凝土抗弹试验以及等效靶研究打下基础。
5 结束语
混凝土强度等级众多,本文只对C35强度的混凝土靶板进行相关研究,对其他强度混凝土是否具有相同等效性还有待验证;同时,由于混凝土属于脆性材料,抗拉性能较小,而45#钢属于弹塑性材料,具有较大的抗拉性,采用靶体吸收动能等效原则的可靠性也需进一步展开研究。
[1] 薛建锋.弹体侵彻与贯穿混凝土靶的效应研究[D].南京:南京理工大学,2016.
[2] 庞洪鑫.高速侵彻钢筋混凝土靶板的数值模拟研究[D].北京:北京理工大学,2015.
[3] 马天宝,武珺,宁建国.弹体高速侵彻钢筋混凝土的实验与数值模拟研究[J].爆炸与冲击,2019(5):1-14.
[4] 王茂英,赵革,贾小志,等.弹体侵彻贯穿混凝土与钢筋混凝土等效关系数值分析[J].北京理工大学学报,2011,31(06):631-633,651.
[5] 张明润,张咏侠,张彤,等.高速弹丸侵彻混凝土靶板数值模拟研究[J].山西建筑,2014,40(04):49-51.
[6] 张雪岩,武海军,李金柱,等.弹体高速侵彻两种强度混凝土靶的对比研究[J].兵工学报,2019,40(02):276-283.
[7] 韦宁.高速弹体冲击侵彻混凝土靶数值模拟分析[J].黑龙江交通科技,2018,41(06):11-12,15.
[8] 于蓝.基于后效损伤的陶瓷复合装甲等效靶研究[D].北京:北京理工大学,2016.
[9] 徐云,胡玉梅,赵为民,等.7003铝合金本构模型参数和力学性能研究[J].机械强度,2019,41(06):1321-1326.
[10] 王喆.弹体高速侵彻混凝土靶的数值模拟研究[D].北京:北京理工大学,2015:25-28.
[11] 杨铮.混凝土动态随机损伤本构模型研究[D].长沙:国防科学技术大学,2008:12-13.
[12] CHRISTIAN H,JURGEN S.Comparison of the RHT Concrete Material Model in LS-DYNA and ANSYS AUTODYN[C]//11th European LS-DYNA Conference.Salzburg,Austria,2017.
[13] THOMAS B,WERNER R.The RHT concrete model in LS-DYNA[C]//8th European LS-DYNA Users Conference.Strasbourg,French2011.
[14] 徐文峥,王晶禹,陆震,等.弹性弹体侵彻混凝土靶板的过载特性研究[J].振动与冲击,2010,29(5):91-96.
[15] 杨榕,徐文峥.弹药侵彻混凝土过载性能的数值模拟[J].弹箭与制导学报,2009,29(4):129-132.