传统航天器对接装置主要包括:抓手-碰锁式、电磁式、三爪式、机械臂式、类锥-杆式等,其中电磁式对接装置具有对接冲击小、没有羽流污染以及质量轻等诸多优点[1-5]。空间电磁对接通过安装在相邻两个航天器上的电磁线圈所产生的电磁力来控制它们之间的相对运动实现对接。空间电磁对接的作用距离较短,在卫星电磁对接之前卫星的姿态控制系统会将对接卫星与目标卫星和初步调整一致,但姿态控制系统的误差(俯仰角约≤0.15°,滚转角约≤3°)通常不容忽视[6]。空间电磁柔性对接技术针对姿态控制系统作用完成后(对接卫星与目标卫星距离≤0.5 m)对接卫星与目标卫星之间的姿态误差进行高精度控制,提高对接时卫星姿态的一致性,降低对接时的相对速度减小碰撞,实现柔性对接。
本文首先建立Maxwell三维电磁有限元模型,计算出卫星空间电磁柔性对接加速靠近阶段与柔性对接阶段带有姿态角度误差的电磁力/力矩,然后通过MATLAB建立牛顿-欧拉方程解析出卫星对接过程中时间相对加速度、对接距离、相对速度、角度以及角速度等关系为动力学的仿真提供输入和参考,将电磁有限元的计算结果导入到ADAMS的模型中进行仿真,最后通过对比分析刚体动力学模型与MATLAB的计算结果,验证空间电磁柔性对接过程中的姿态调整能力以及卫星对接过程中的动力学特性。
1 工作原理
电磁柔性对接系统采用三组电磁铁直列式布局,如图1所示,主电磁铁位于中间,副电磁铁伴随两侧。通过改变电磁铁中电流大小及方向控制主被/动卫星间的电磁力/力矩,从而在较短距离内调整主/被动卫星的相对速度并修正姿态误差。
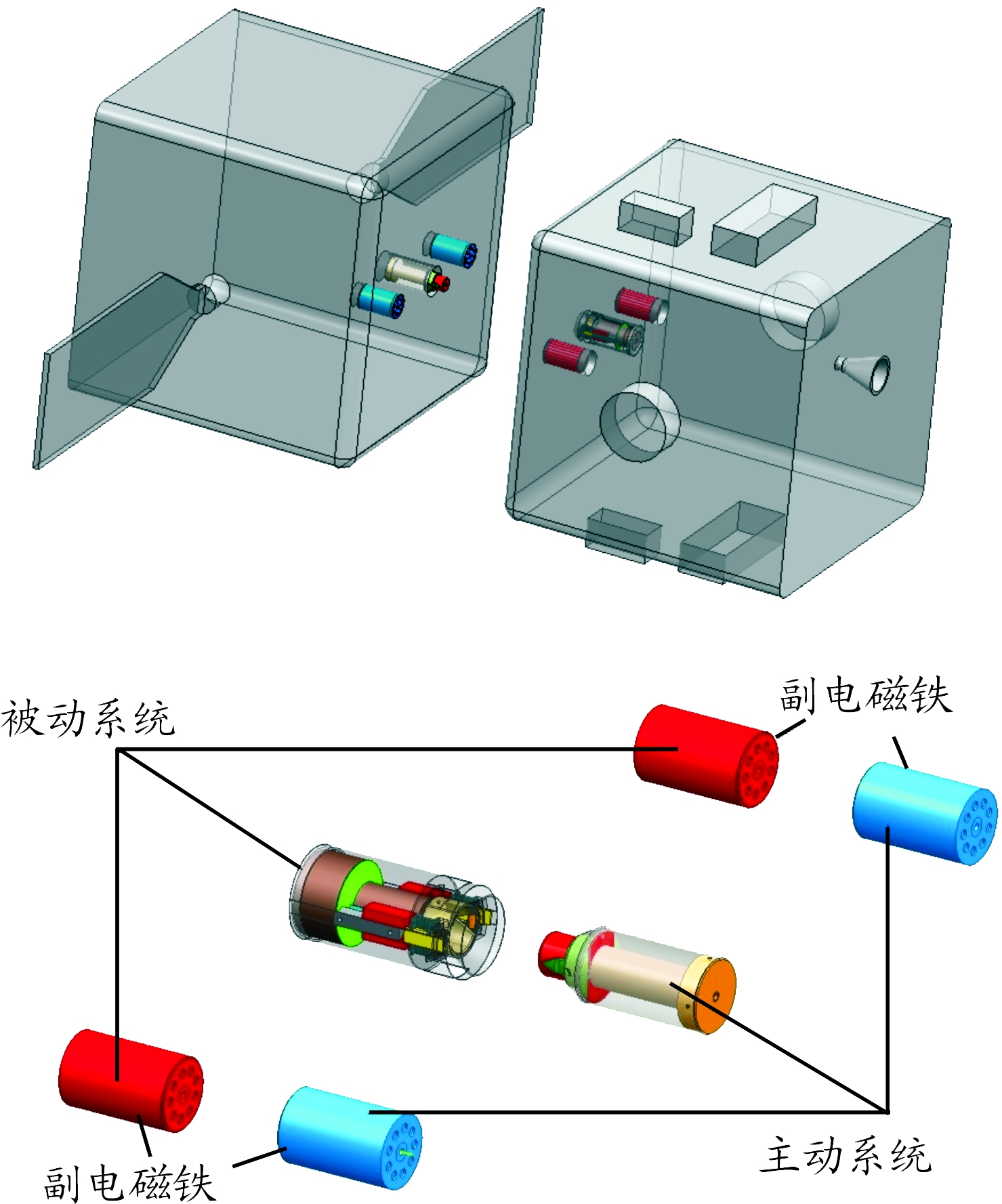
图1 卫星及电磁铁模型示意图
两卫星在110~500 mm范围内为加速靠近阶段,如图2所示,此阶段主动卫星与被动卫星对应的电磁线圈接通相同方向的电流,产生电磁引力。利用副电磁铁产生的基于卫星质心的电磁力矩对卫星的俯仰/滚转角度差进行修正,实现加速靠近和对接姿态调整。0~110 mm范围内为柔性对接段,如图3所示,此阶段主动卫星与被动卫星内的主电磁线圈接通反向电流,产生电磁斥力,副电磁铁减小电流,保持较小电磁引力用于维持姿态稳定。在该阶段调整卫星的滚转角,并在主被动卫星在发生对接接触之前,使主动卫星与被动卫星相对速度接近0 m/s。滚转角和俯仰角的调整方式如图4和图5所示。

图2 加速靠近段示意图
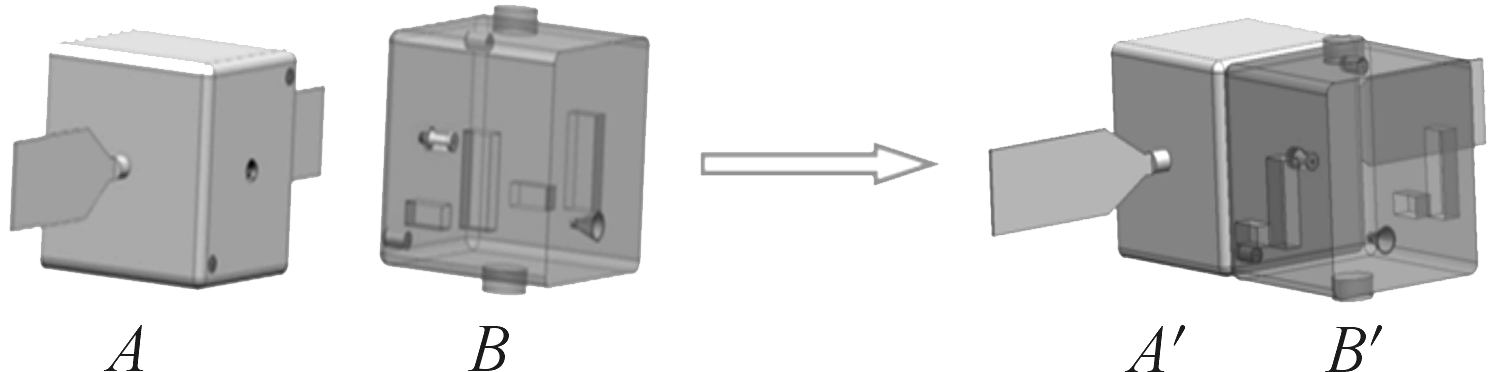
图3 柔性对接段示意图
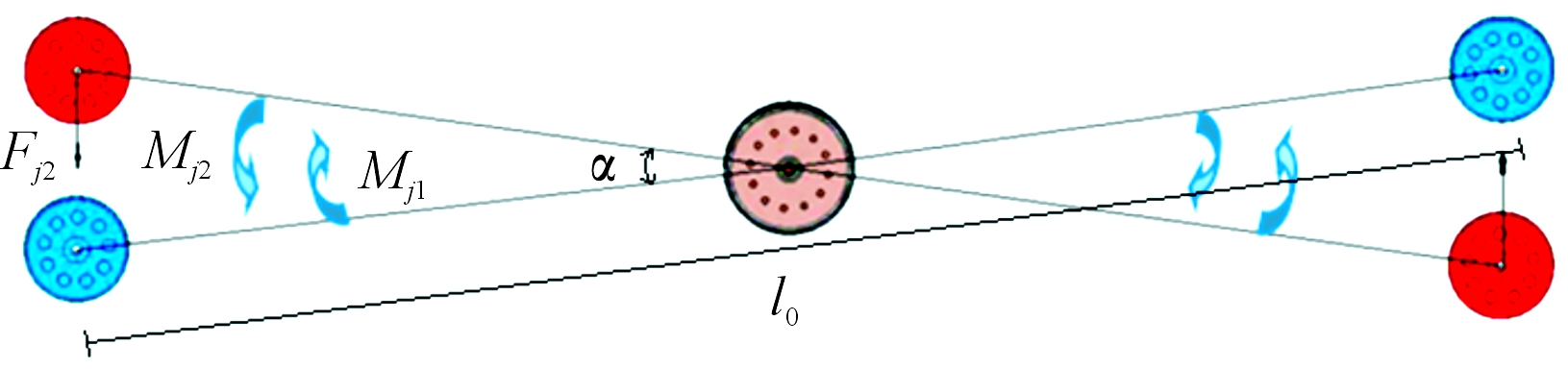
图4 滚转角调整示意图
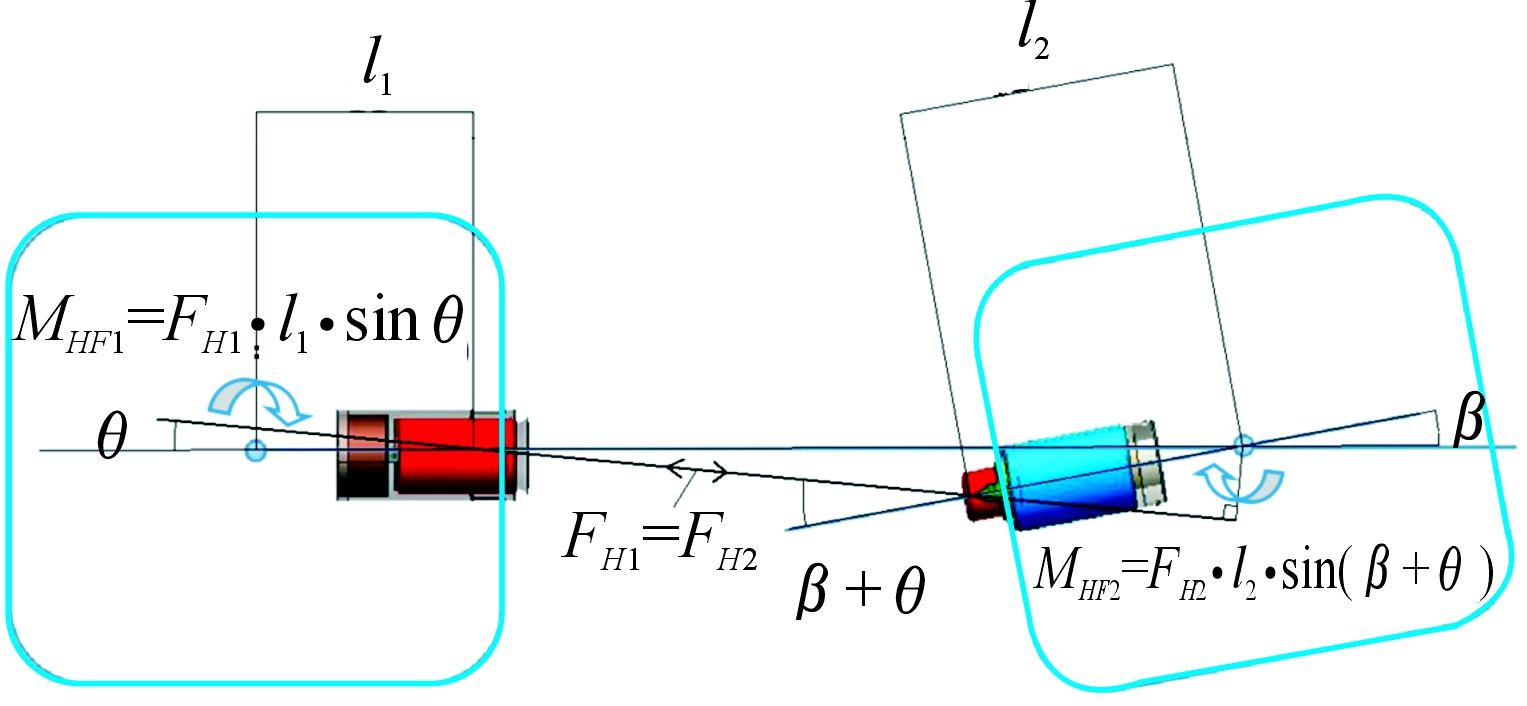
图5 俯仰角调整示意图
2 电磁有限元模型的建立及仿真分析
2.1 电磁铁模型建立
在空间电磁对接过程中,要求对接过程和电流变化缓慢进行,近似将卫星间的磁场简化为三维静磁场。电磁铁的磁场强度主要受到卫星的体积、功耗以及发热平衡约束[7]。电磁铁的尺寸参数如表1所示。
电磁铁是由螺线管和铁芯组成的,铁芯为实心圆柱体,指定铁芯材料属性为Steel_1008;假设螺线管的几何模型为空心圆柱体,指定线圈材料属性为copper;在线圈截面施加电流激励源,电流激励源source =电源电流×线圈匝数。选择自适应网格划分,用包裹全部模型的立方体真空域做边界域。
表1 电磁铁参数

主动主电磁铁被动主电磁铁副电磁铁长度/mm1457584外半径/mm2224.521.4内半径/mm996
1) 加速靠近段。设置俯仰角度范围:0° ~0.15°,滚转角度范围:1°~3°,设置相对距离:500 mm~110 mm,步长:5 mm。输入参数设置见表2,电磁有限元模型如图6所示。
表2 加速靠近段电磁铁输入参数及电磁铁间力属性

主动主电磁铁被动主电磁铁副电磁铁 线圈安匝数/A3 7002 3002 600电磁铁间力属性引力引力
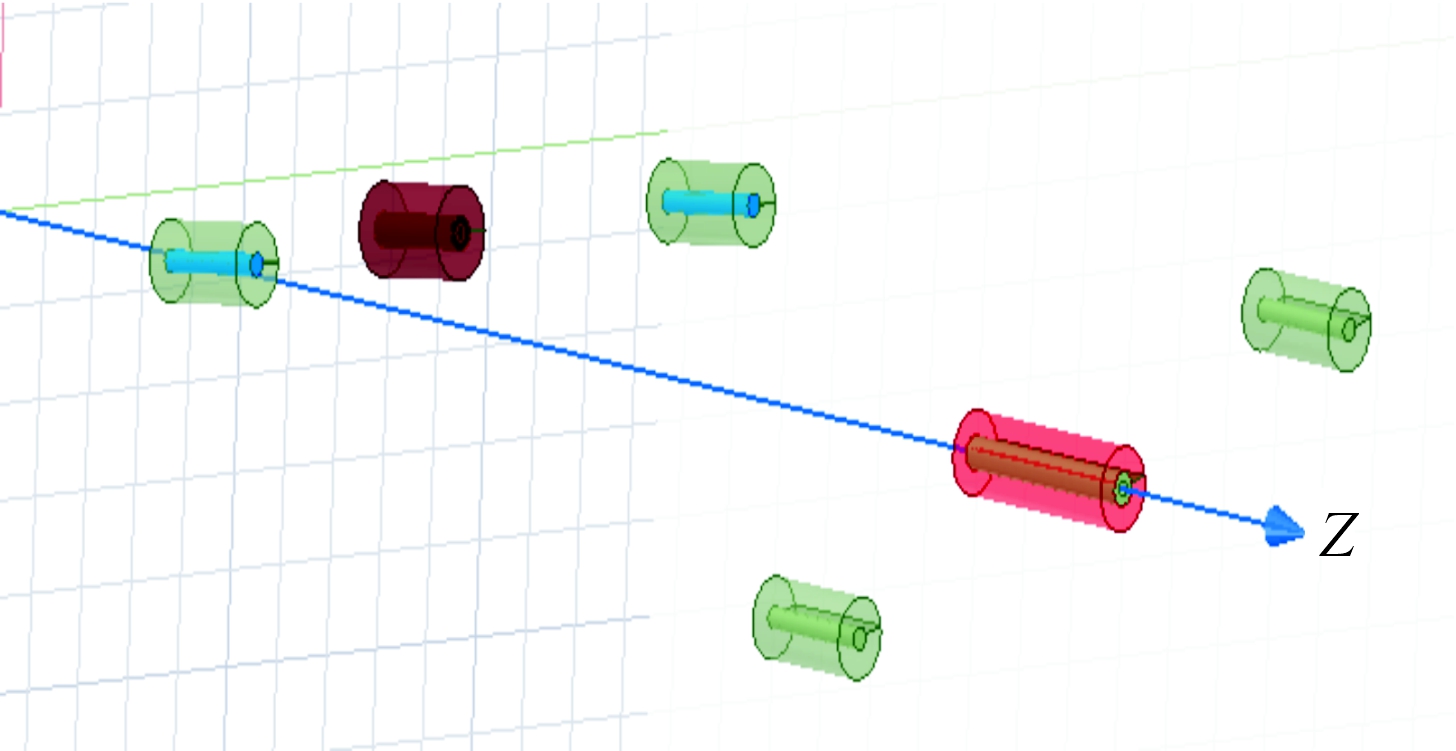
图6 加速靠近段电磁铁模型示意图
2) 柔性对阶段。设置滚转角度范围:1°~3°,设置相对距离:110 mm~0 mm,步长:5 mm,输入参数设置见表3,电磁有限元模型如图7所示。
表3 柔性对接段电磁铁输入参数及电磁铁间力属性

主动主电磁铁被动主电磁铁副电磁铁 线圈安匝数/A3 7002 300650电磁铁间力属性斥力引力
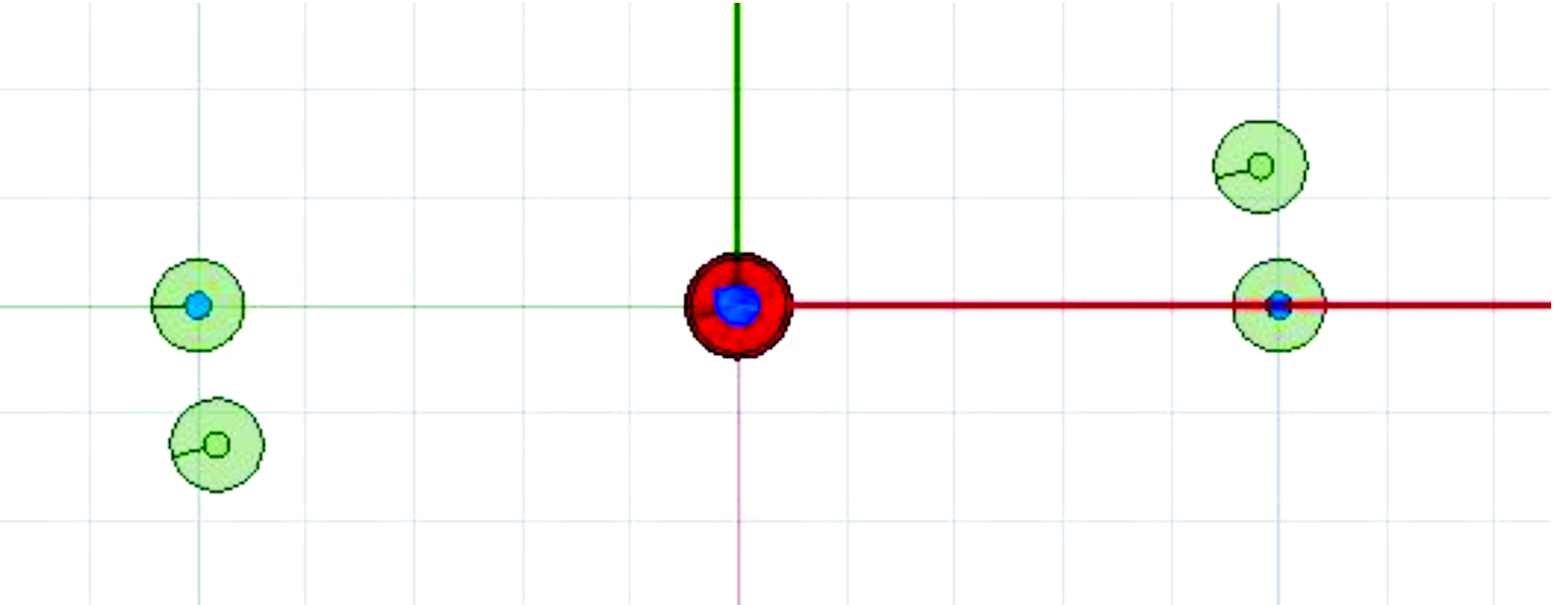
图7 柔性对接段电磁铁模型示意图
2.2 仿真结果
假设主动卫星与被动卫星对接平面之间相对距离(即电磁装置间的相对距离)L0为自变量。主动系统电磁装置Z轴方向受力大小为Force10_z,被动系统电磁装置Z轴方向受力大小为Force11_z,输出不同距离时电磁装置之间产生的Z轴方向电磁引力如图8所示。
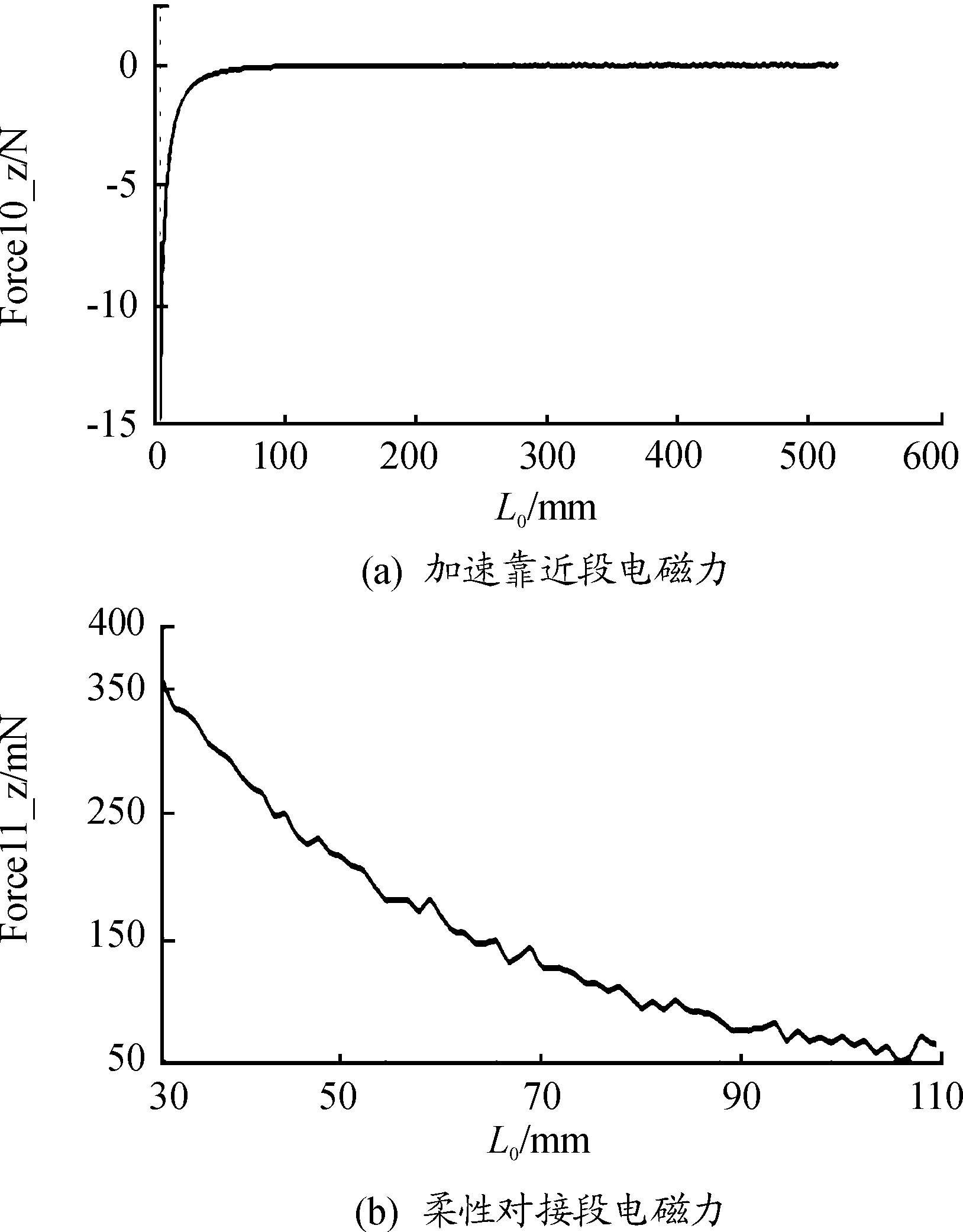
图8 电磁装置间电磁力与距离关系曲线
假设两模块化卫星为质量和惯性矩均相同的实心正方体,卫星的初始速度与初始的角速度均为零,根据牛顿-欧拉方程及有限元积分法计算出时间-相对速度、时间-滚转角、时间-俯仰角关系,结果如图9所示。
根据计算结果得出柔性对接过程和姿态调整过程如下:
1) 加速靠近段,主动卫星与被动卫星由相对距离500 mm加速靠近至距离110 mm处,相对速度由0 m/s加速至0.016 m/s,调整俯仰角度0.384 7°,调整滚转角度0.275 9°,该阶段用时96 s;
2) 柔性对接段,主动卫星与被动卫星由相对距离110 mm处开始减速靠近至距离46.5 mm处,相对速度由0.016 m/s减速至0.000 67 m/s,调整滚转角度0.1180 5°,该阶段用时9.6 s;
3) 主动卫星与被动卫星由相对距离46.5 mm处开始加速靠近至接触,接触时相对速度为0.005 4 m/s。
电磁柔性对接过程共调整俯仰角0.384 66°,滚转角 0.393 95°。
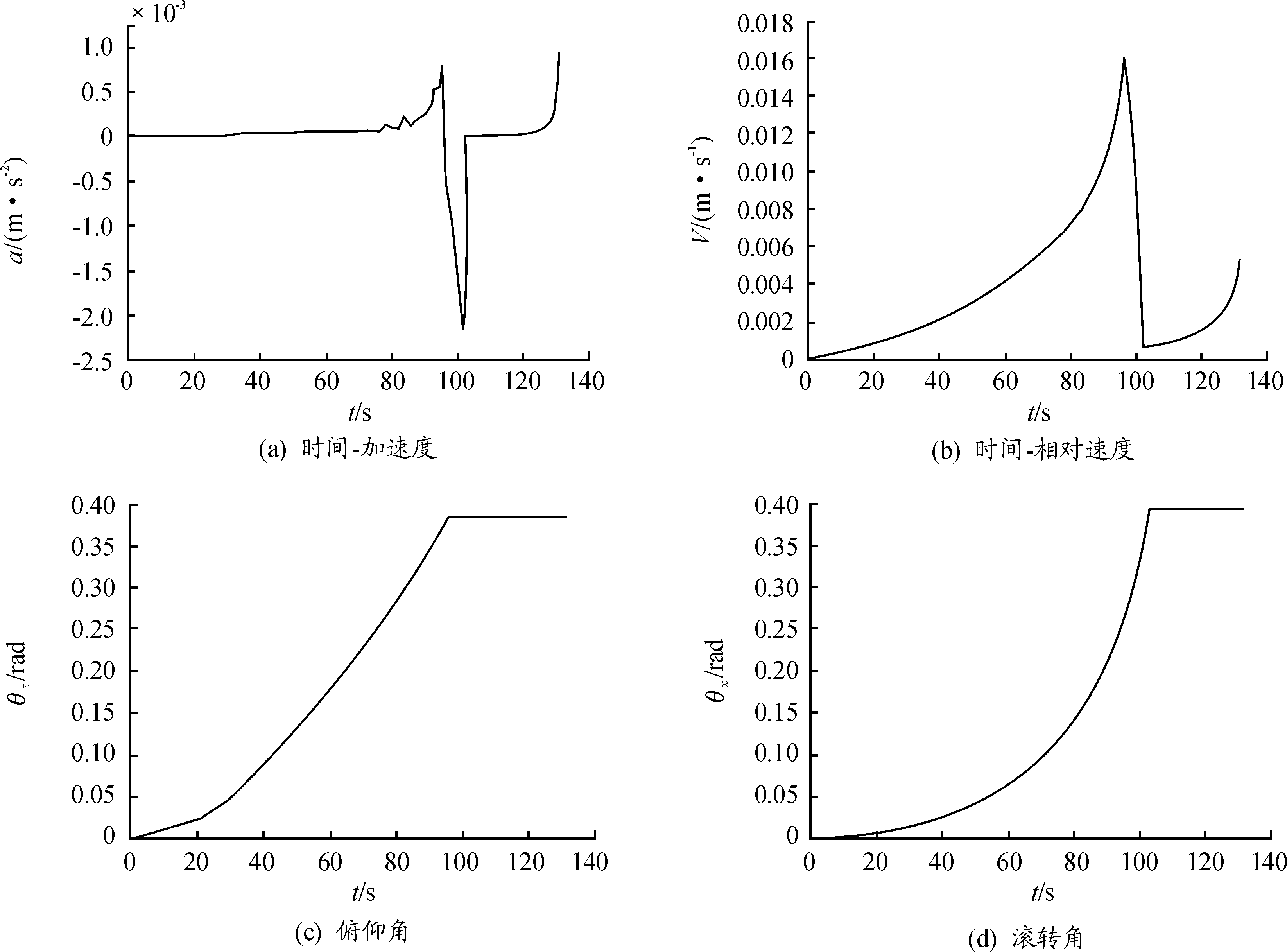
图9 卫星电磁柔性对接过程计算曲线
3 动力学模型
3.1 模型定义与假设
模型定义以主动卫星与被动卫星以Z轴为对接轴,主动卫星与被动卫星相对距离500 mm。以主动卫星为基准定义两卫星之间滚转角度差为3°,俯仰角度差为4°。空间电磁柔性对接系统ADAMS模型如图10所示。电磁铁线圈指定为铜材料,铁芯指定为钢材料,将其余所有零部件均指定为铝材料。
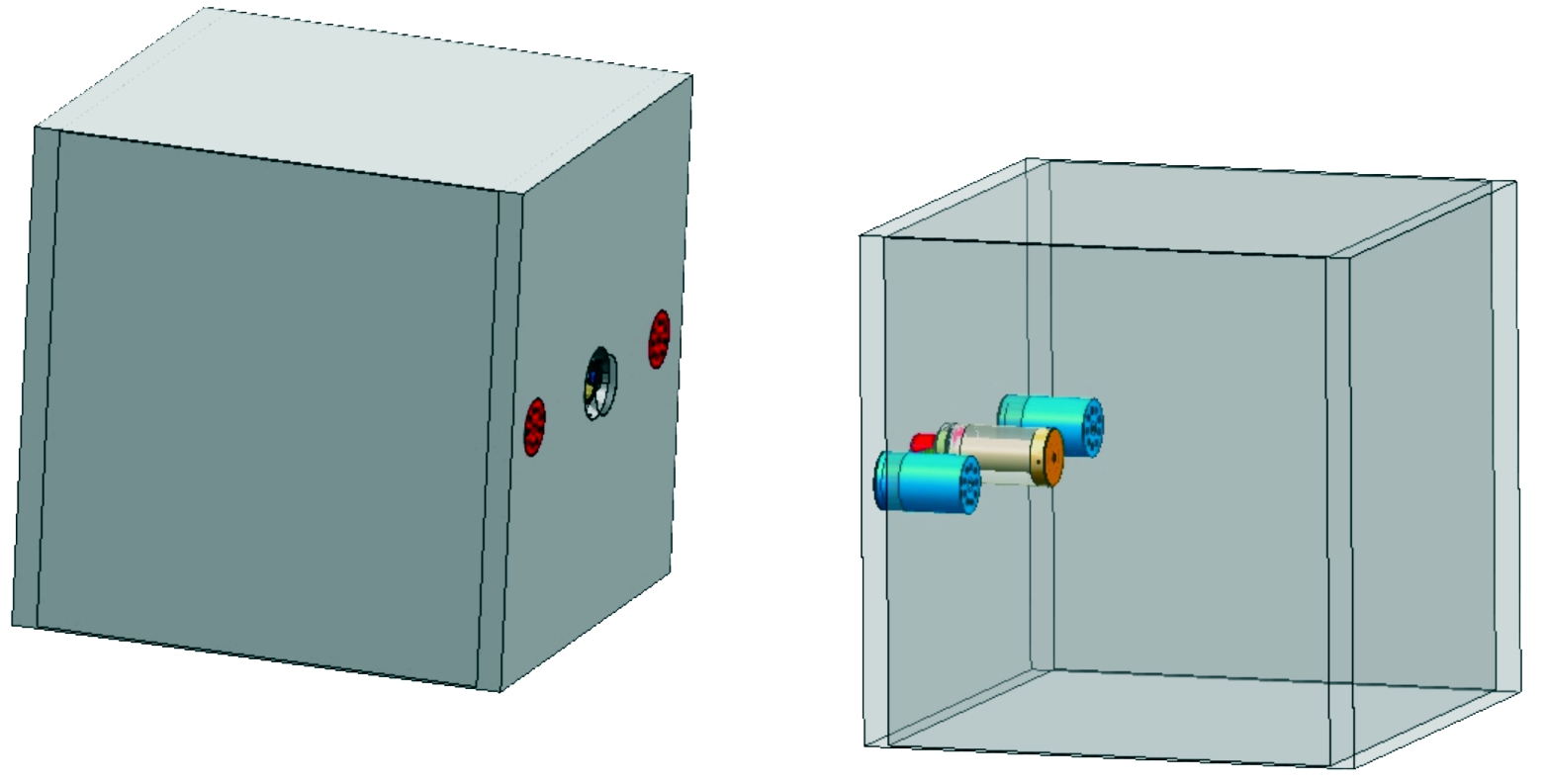
图10 ADAMS动力学模型示意图
空间电磁对接的动力学建模过程中,模型零部件较多,系统较为复杂,为减小计算量和缩短计算时间,对模型进行以下简化和假设[5]:
1) 相互接触且不参与运动的零部件之间进行布尔加和操作,作为一个零件处理;
2) 如无具体要求或特殊说明时,模型的零部件均看作刚体;
3) 模型按照实际的运动规律添加约束,不考虑模型的尺寸公差和误差;
4) 动力学仿真按照在空间环境下进行,重力加速度为零。
3.2 仿真结果
将本文第2节中通过有限元分析与数值计算得到的两卫星之间的电磁力与距离的关系,导入到ADAMS进行SPLINE插值,将电磁力的SPLINE函数用于驱动仿真MOTION,仿真结果如图11所示。
根据全对阶段动力学仿真结果可以看出:
1) 加速靠近段,主被/动卫星相对速度由0 mm/s加速至5.4 mm/s,调整俯仰角度0.051 7°,调整滚转角度0.086 7°,该阶段用时100 s;
2) 柔性对接段,主/被动卫星由相对距离110 mm处开始减速靠近,调整俯仰角0.257 4°,调整滚转角度0.398 5°,该阶段用时30 s;
3) 主动卫星与被动卫星接触时的相对速度为0.004 59 m/s,柔性对接过程用时130.071 s,共调整俯仰角0.309 1°,滚转角度0.485 2°。
4) 主被动卫星130 s时开始接触,主动卫星与被动卫星之间发生碰撞,速度曲线产生震荡。通过卫星内部装置继续调整滚转角,至t=155 s对接结束时,共调整滚转角差3.5°。
通过柔性对接的动力学仿真可以看出,电磁柔性对接技术的动力学仿真结果基本符合基于电磁有限元模型对接过程的计算结果。
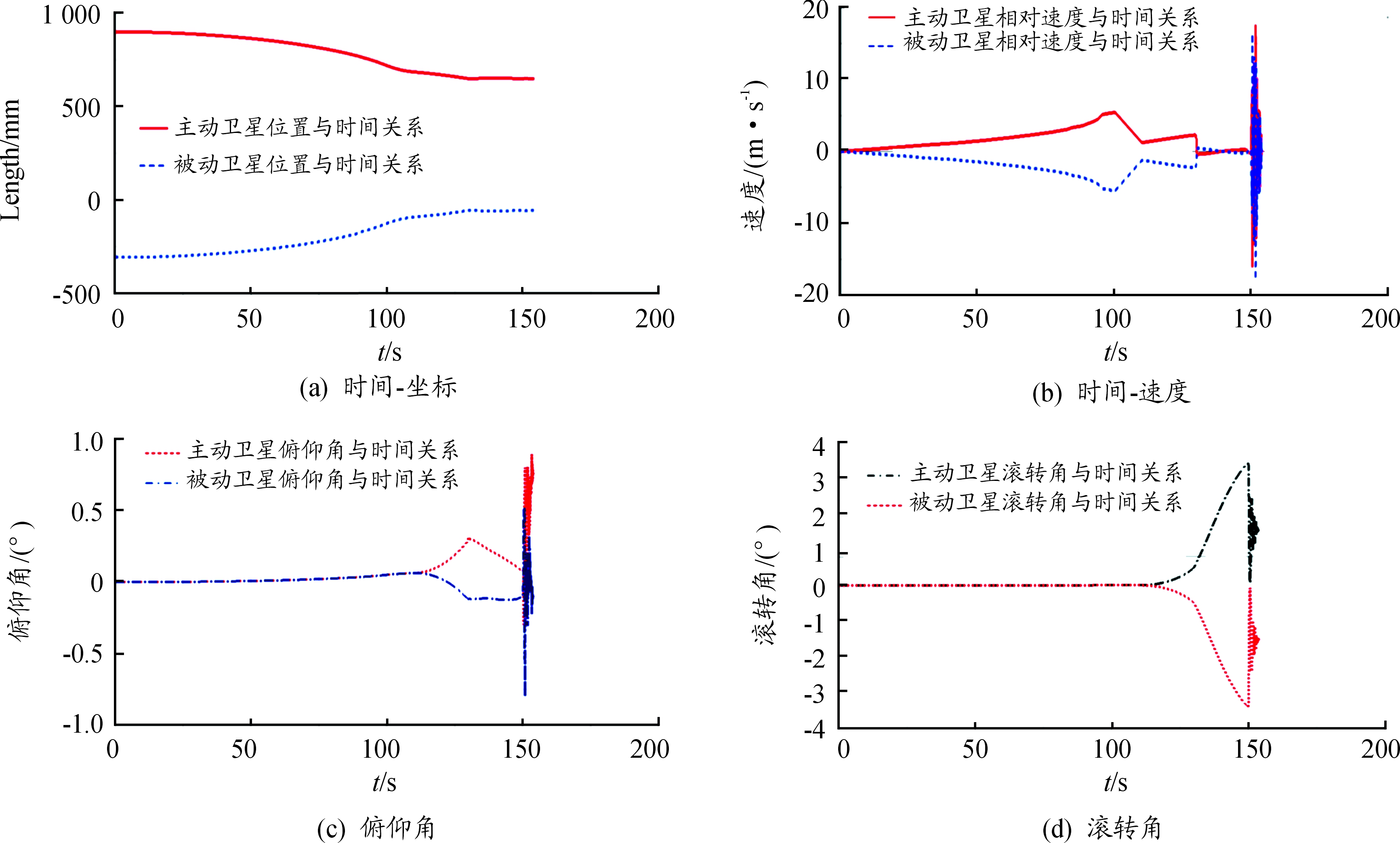
图11 全对接段动力学仿真结果曲线
4 结论
1) 空间电磁柔性对接技术具有作用范围≥0.5 m、俯仰角姿态调整范围≤±0.38°和滚转角姿态调整范围≤±0.39°条件下实现对接速度≤0.005 5 m/s的能力。
2) 采用Maxwell 3D、MATLAB、ADAMS解决电磁学与动力学耦合计算方法,可用于实时仿真卫星在电磁力作用下的运动学与动力学过程。
[1] SHI K,LIU C,BIGGS J D,et al.Observer-based control for spacecraft electromagnetic docking[J].Aerospace Science and Technology,2020,99(07):105759.
[2] MILLER D W,AHSUN U,RAMIREZ-RIBEROS J L.Control of electromagnetic satellite formations in near-earth orbits[J].Journal of Guidance Control and Dynamics,2010,33(6):1883-1891.
[3] ZHANG Y,YANG L,ZHU Y,et al.Angular-Momentum Management of Spacecraft Electromagnetic Docking Considering the Earth’s Magnetic Field[J].Journal of Guidance,Control and Dynamics,2013,36(3):860-869.
[4] 王龙,杨乐平,许军校.电磁编队飞行与电磁交会对接关键技术及进展[J].装备指挥技术学院学报,2009(01):78-82.
[5] 原永亮,杨臻,张秀华.基于ADAMS某新型电磁对接机构结合过程分析[J].机械设计,2016(33):51-54.
[6] 王大鹏,刘育强,陈绍龙,等.基于线性协方差方法的交会对接误差分析[J].中国空间科学技术,2011,31(01):48-55.
[7] 慕忠成,叶东,吴树范.纳卫星电磁对接机构技术[J].北京航空航天大学学报,2018,44(12):2644-2650.