散热器是装甲车辆冷却系统中的重要部件,其性能对装甲车辆的动力性、经济性和可靠性有至关重要的作用[1]。因此,散热器的优化设计是冷却系统设计中的重要环节[2]。对于车用散热器的优化设计,国内外很多学者进行了相关研究。闫玉英等在对散热器流动特性分析的基础上,建立了数学模型,利用罚函数法进行了设计[3]。李晓光利用FLUENT建立了某型商用汽车散热器的数值计算模型,并利用风洞试验测试了相关数据,讨论了翅片结构对散热器性能的影响[4]。王任远利用Laminar法针对散热器建立了流固耦合模型,研究了不同结构参数对传热系数的影响,最后得到了一组最优解[5]。向高利用风洞试验数据拟合得到了数学模型,在此基础上利用FLUENT软件分析了各结构因素对散热性能的影响,最后得到了综合性能较佳的散热器结构参数[6]。景陶敬等针对当前汽车散热器散热性能不佳的情况,利用试验与仿真结合的方法,讨论了流速散热性能的影响[7]。目前,针对车辆散热器优化时考虑的因素较少,多将优化简化为线性问题来解决,随着高功率密度柴油机和机电混合传动的采用,热负荷大幅度增加,因此装甲车辆的冷却系统热负荷较大,考虑的因素较多,需要进行多目标优化。
本文利用解析法和基于CFX的流体力学仿真模型分别对某型散热器进行了计算,验证了CFD仿真模型的精度;选取了目标函数和设计变量,利用最优拉丁超立方设计法构建了设计空间,建立了基于径向基神经网络的替代模型,利用对照组数据检验了模型的精度;利用萤火虫算法对替代模型进行了多目标优化,得到了最优解集;最后利用蒙特卡洛法对影响因素进行了统计学分析。
1 散热器建模及计算
1.1 几何模型及边界条件设置
1.1.1 计算模型的建立
该型散热器的芯体主要由水管和散热片等组成。在散热片上,按水管的截面形状和尺寸冲孔,再将它串套在水管上,然后在一定温度下进行焊接构成芯体。散热器的几何实体模型如图1所示。散热器芯体几何结构的局部示意图如图2。

图1 散热器几何模型示意图
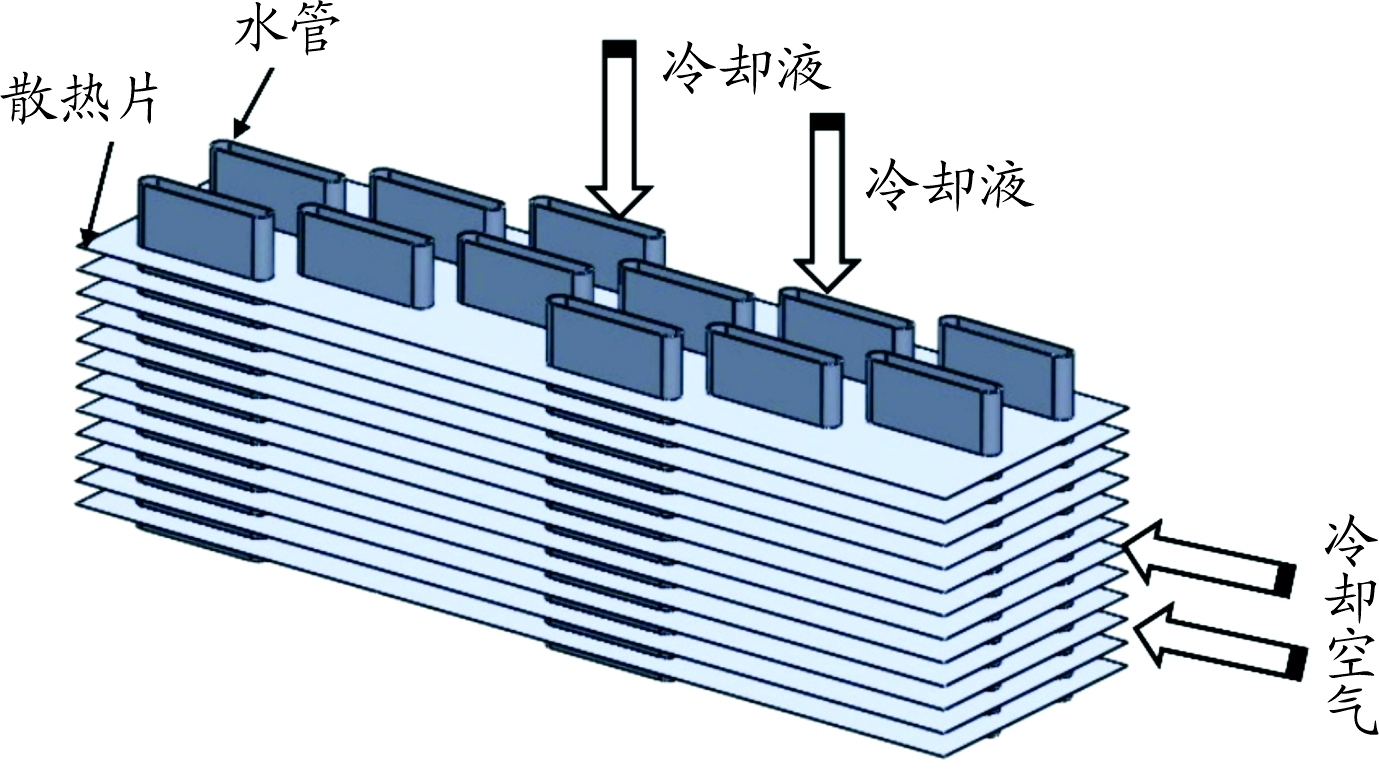
图2 散热器几何结构局部示意图
散热器中流体的流动与传热分析是散热器设计和冷却系统匹配设计的重要环节[8]。要进行数值计算,必须首先获得待求解空间区域的几何模型,由于车辆散热器中,流体在散热器内外流道中流动,内外流道之间通过对流、导热完成热量的交换,在利用CFX建立模型时利用完整的几何模型会造成网格数量大,收敛慢等问题,因此对散热器整体进行研究时,必须对散热器模型进行简化处理[9]。为了提高计算效率,根据散热器的结构特点,对计算区域确定如下:计算区域的长度定为芯体的长度,高度定为两个散热片之间的距离,宽度设定为恰好能涵盖水管错列位置为一个周期的距离,选取的区域计算模型如图3所示。

图3 区域计算模型示意图
1.1.2 网格无关性检验
由于冷却空气和冷却液之间的水管厚度很薄且面积较大,因此,这里将其作为壁面进行处理,以减少网格数量。为了保证仿真精度,减少网格数量对计算的影响,因此需要进行网格无关性检验[10]。在进行网格划分时,网格相关度共取5组,范围由0~100之间。在入口速度为11 m/s情况下进行计算。图4为空气流过散热器内部的压力损失随网格相关度的变化情况。从计算结果可以看出,随着网格相关度的增加,压力损失出现下降趋势,网格相关度由60~100的变化中,相对误差为1.83%,均值为602.643,标准差为8.264,变异系数为0.013,大致趋于稳定,从提高计算效率角度可以看作网格的变化对计算结果不再产生影响,因此网格无关度取为60,网格数量为298 112。
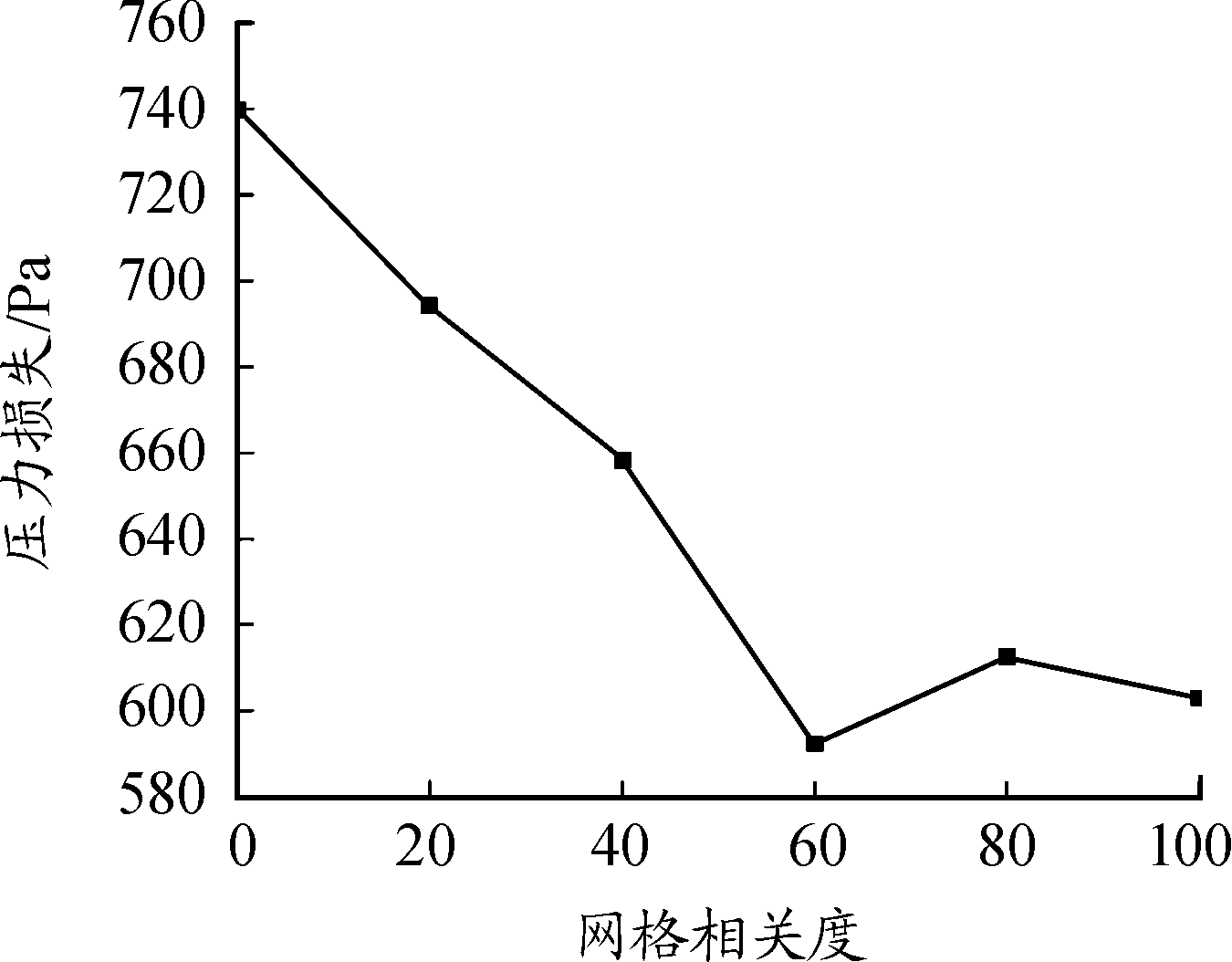
图4 散热器压力损失随网格相关度的变化
1.1.3 边界条件设置
已知空气的流量为0.81 kg/s,压力为24.5×104 Pa,温度为160 ℃,冷却水的流量为14.4×103 kg/h,冷却水进口温度为25 ℃。
根据散热器芯体结构以及分析的目的,确定了管片式散热器芯体空气侧CFD分析区域及边界条件设置如图5所示,在入口处设置流量入口边界,出口处设置自由出口边界,水管处设置热边界条件,管片设置为壁面条件,横向壁面设置为周期性边界条件[11]。边界条件设置如图5所示。
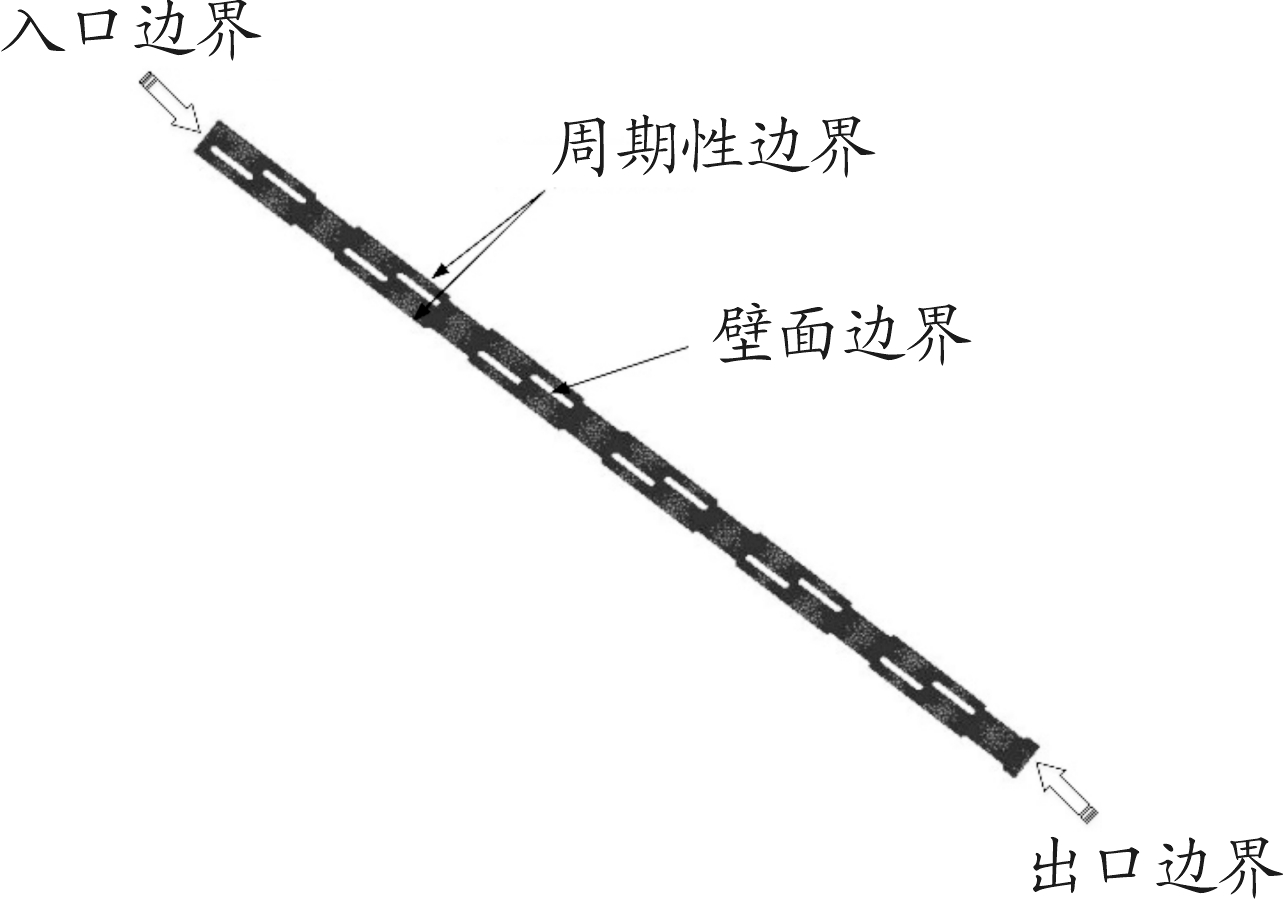
图5 边界条件设置示意图
1.2 解析法
装甲车辆上使用的散热器一般为紧凑式散热器,冷却空气流经紧凑式散热器时的压力损失可表示为
Δp=Δpi+Δpcf-Δp0
(1)
式中:Δpi为散热器芯体进口处的压力损失;Δp0为芯体出口处的压力回升;Δpcf为芯体内的压力损失。
由理论分析得出,流体流经散热器芯体入口和出口处的压力损失为
(2)
(3)
式中:vm为质量流速;v1为芯体进口截面处的比体积;v2为芯体出口截面处的比体积;σ为散热器的流通面积与迎风面积之比;Kc为入口压力损失系数;Ke为出口压力损失系数。
散热器芯体内的压力损失计算公式为
(4)
式中: f 为空气侧摩擦因子; L为流道长度;vL为流体平均比容;De为流道当量直径。
当在散热器中流动时,由于流体流经每一管排时都有一次收缩和膨胀,芯体的第一管排和最后一个管排与中间各管排的阻力情况并无显著差别,因此,进出口处的压力损失实际上已经包括芯体内的黏性摩擦损失中,因此压力损失的计算公式可化简为
(5)
由于散热器芯体的流体流动加速所引起的压力损失较小一般可以忽略,上式可以简化为
(6)
1.3 结果对比及分析
计算采用CFX进行计算,设定参考压力为101 325 Pa,为了方便与解析解进行对比,在散热器的质量流量分别设为0.41 kg/s、0.55 kg/s、0.69 kg/s、0.77 kg/s、0.81 kg/s,其中根据文献[5],该型散热器在流量为0.81 kg/s时的试验值为685.2 Pa,通过计算得到了散热器在不同的入口质量流量下CFD仿真和解析解以及试验值(见图6)。
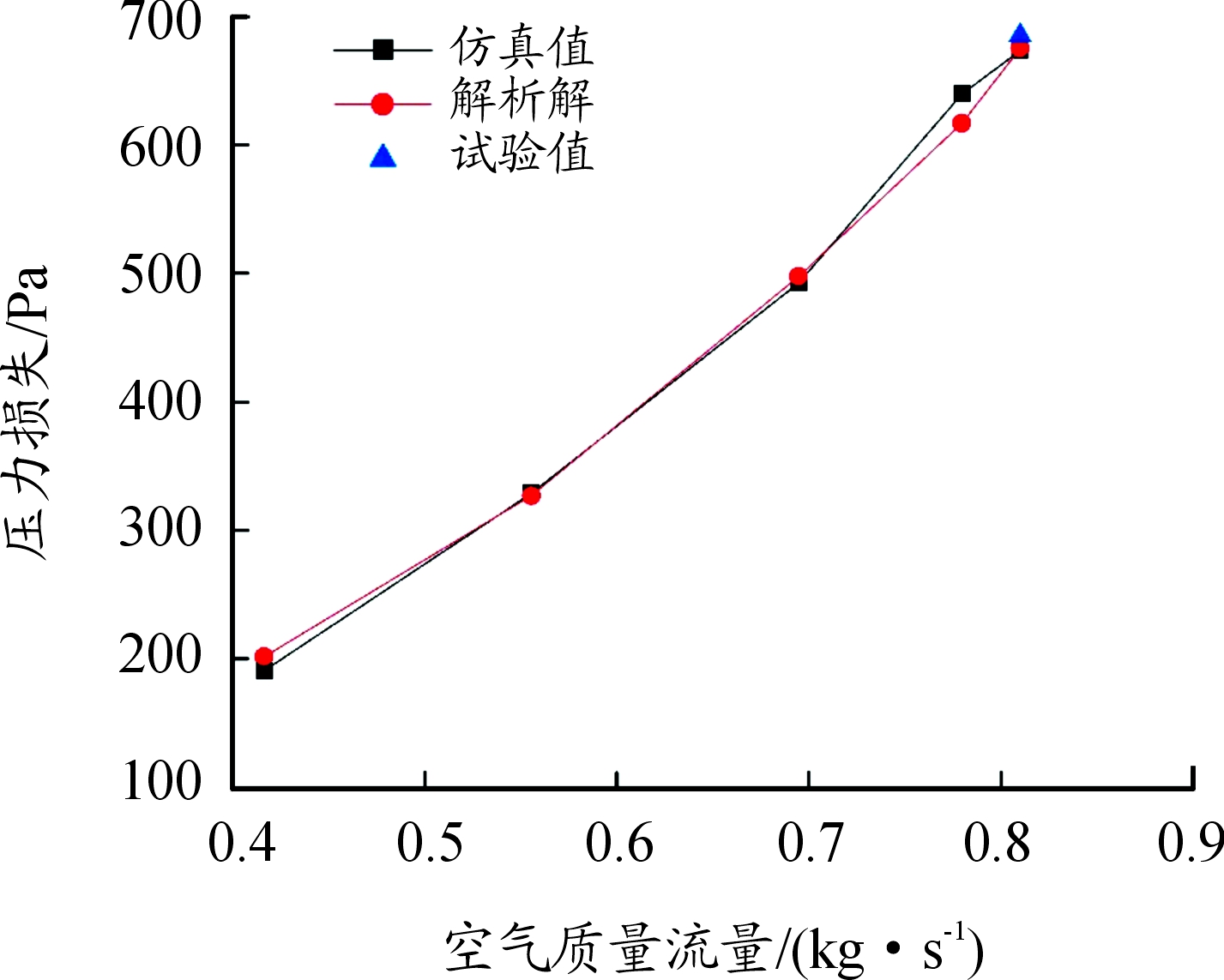
图6 仿真值与解析解曲线
通过对比,在空气质量流量为0.81 kg/s处,仿真值和解析解分别为673.167 Pa和675 Pa,残差为1.833 Pa,试验值比二者较高,较仿真值,其相对误差为1.76%。仿真值与解析解之间的最大相对误差为3.9%,均方误差为0.000 52,决定系数为0.999 137 951,相关系数为0.999 324 7,从统计学角度看,两组解较为接近,通过以上分析,可以看出仿真值的结果比较可靠。图7为局部散热片速度流线图,可以看出,最大速度达到12.29 m/s,且沿空气流线方向,速度大小分布也不均匀,大致呈阶梯状分布。图8为局部散热器片压力分布图,从图8中可以看出出口处压力较小,最大值位于速度入口处,达到了223.26 Pa。
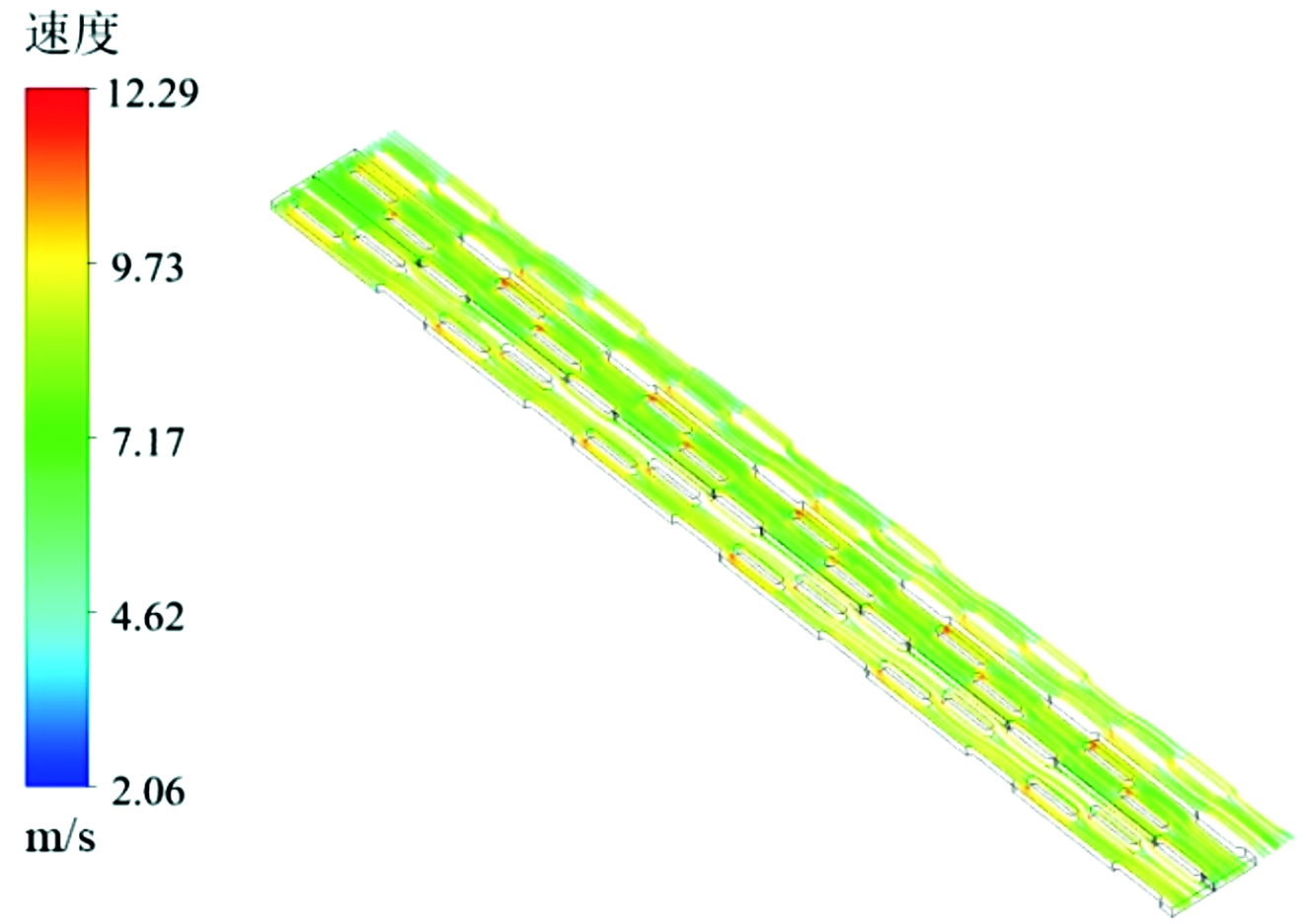
图7 局部散热器片速度流线图

图8 局部散热器片压力分布图
2 基于径向基神经网络的替代模型建立
2.1 设计变量的确立
本研究的优化对象为某型装甲车辆管带式散热器,该散热器的几何模型如图9所示。该种散热器的散热片为百叶窗形翅片,冷却空气从散热片中流过,冷却液从扁平管内流过。冷却液的热量经过管壁表面的对流换热和翅片的导热,最后由冷却空气将热量带走,由于该型散热器的结构较大,特征重复较多,因此本文的计算区域取两根水管之间的宽度,高度选为能够涵盖散热片变化恰好为一个周期的距离[12]。

图9 散热器几何模型示意图
CFD计算得到了当迎风速度为4 m/s、8 m/s、12 m/s情况下的速度云图如图10、图11和图12所示。从图10~图12中可以看出,随着迎面风速的增加,管带式散热器内部流动特性变化明显;空气从入口百叶窗进入,沿着百叶窗流动,在百叶窗中部变向,最后从出口百叶窗流出。气流由一个百叶窗流入到另一个百叶窗相当于一个收缩管道,气流加速运动,因此百叶窗翅片间流动速度比较大;流速最大的地方出现在模型中部偏后位置,也就是流动改变方向的第一个翅片通道,主要原因是气流在流经该区域之前有一个气流加速,经过该处气流换向时通流截面突然减小所致。迎面速度为 4 m/s 时,空气以轴向流动为主,而迎面速度为8 m/s和 12 m/s 时,空气以穿越百叶窗区域为主,主要原因是雷诺数较低时,在翅片近壁面处,空气形成很厚的边界层,阻碍空气向窗翅区流动,随着雷诺数的增加,空气流动边界层变薄,窗翅区空气流动阻力降低,空气的流动方向也逐渐向窗翅区过渡。

图10 迎面风速为4 m/s时速度云图

图11 迎面风速为8 m/s时速度云图

图12 迎面风速为12 m/s时速度云图
图13为风速为12 m/s时百叶窗散热器流动方向的压力变化曲线,压力随着流动方向长度的增加而降低。在流动单元中部附近变化曲率较小,而在其他地方基本呈线性变化。流动单元前半部分压降略小于后半部分压降,这也是由于后半部分流速变大,雷诺数增加,流体穿越百叶窗也越多,流速增加导致摩擦阻力损失增大,从而使得压力损失也变大。
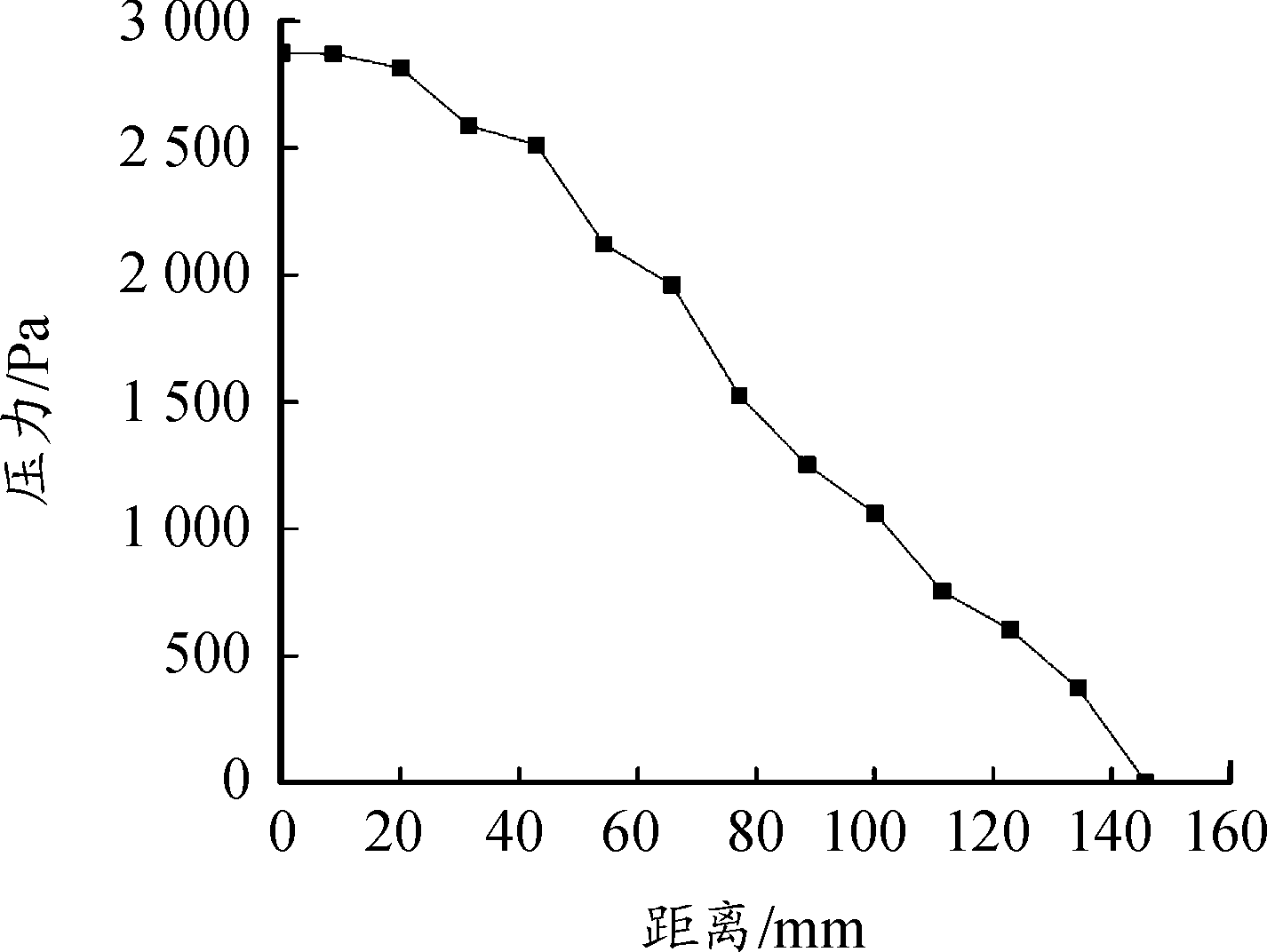
图13 管带式散热器流动方向压力分布曲线
2.2 设计变量和目标函数
车辆散热器在设计时,应根据车辆冷却系统的要求来设计散热器的结构及其参数[13],车辆冷却系统对其系统内散热器的要求,可以是在给定的空间容积和允许的压力损失条件下,使得散热器具有尽可能大的散热能力,散热器热力设计优化模型应该包括目标函数、设计变量和约束方程。该散热器的翅片结构为百叶窗形翅片,散热器几何结构参数如图14所示,其中l、a、Fh、Fp和δf为百叶窗间距、百叶窗开度、翅片高、翅片间距和翅片厚度,本研究选取这5个参数作为设计变量。目标函数为散热量Φ和空气侧压力损失Δp。设计变量的约束条件为

(7)
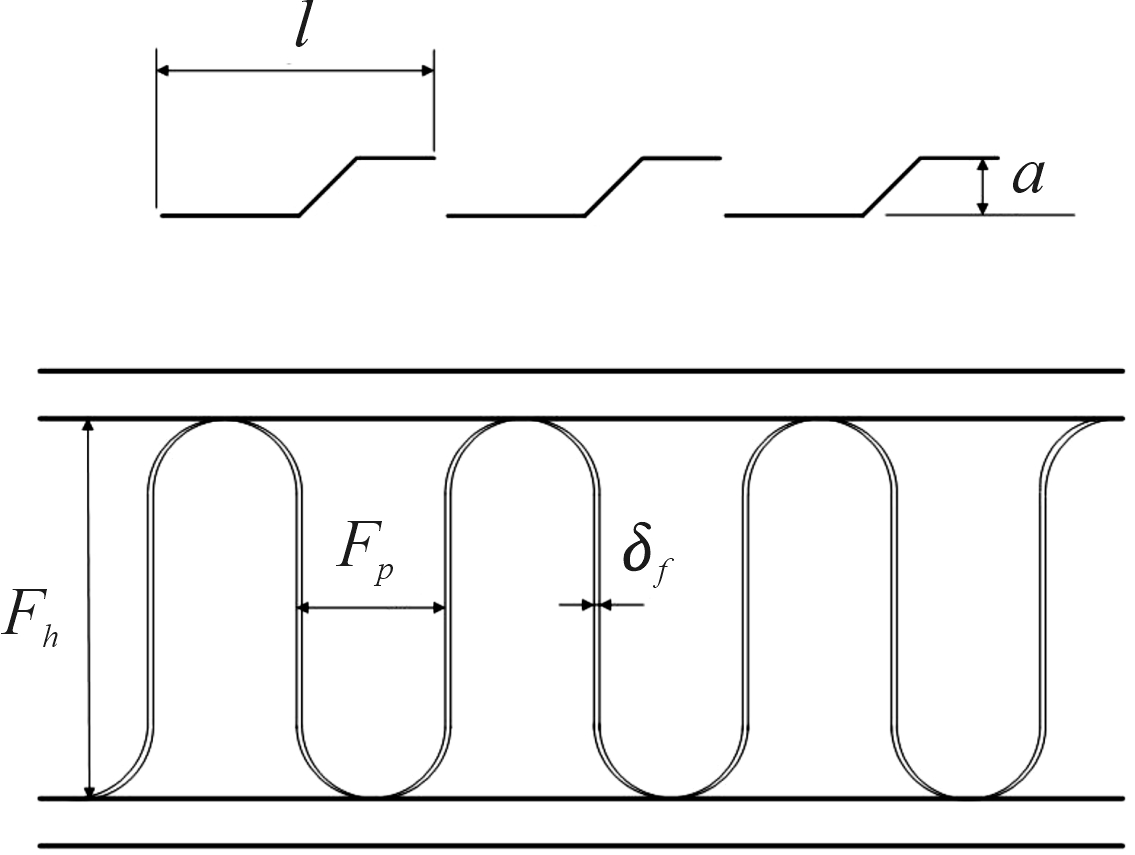
图14 散热器几何结构参数示意图
2.3 样本点抽取
最优拉丁超立方设计改进了随机拉丁超立方设计的均匀性,使因子和响应的拟合更加精确真实,具有非常好的空间填充性和均衡性[14]。本次共抽取了15组样本点,最后抽取样本点如表1所示。
不同种类的车辆,由于其发动机经常所处的工况不相同,故其散热器的设计工况点和校核工况点也不相同。本文为装甲车辆用的水散热器,发动机较多地处于最大扭矩工况点附近工作,风扇和水泵的工作转速都比较低,使得散热器处在比较恶劣的条件下工作[15]。所以,应该把最大扭矩点工况作为散热器的设计工况,而把发动机的额定工况作为校核工况。
表1 样本点数据

laFhFpδf9.070.988.182.650.128.071.447.163.060.159.851.468.823.250.179.971.227.034.540.149.410.908.504.210.189.251.056.894.020.128.631.107.322.850.139.651.388.324.440.108.710.849.143.380.148.370.876.682.800.179.580.999.454.990.168.891.299.034.710.198.491.347.963.580.169.011.267.673.920.118.201.157.763.680.19
2.4 替代模型的建立
以最大扭矩工况点为例,利用CFD模型对抽取的15个样本点进行了计算,利用径向基神经网络建立替代模型。根据实验设计点的值及其响应,得到了这5个参数的部分替代模型,如图15所示。
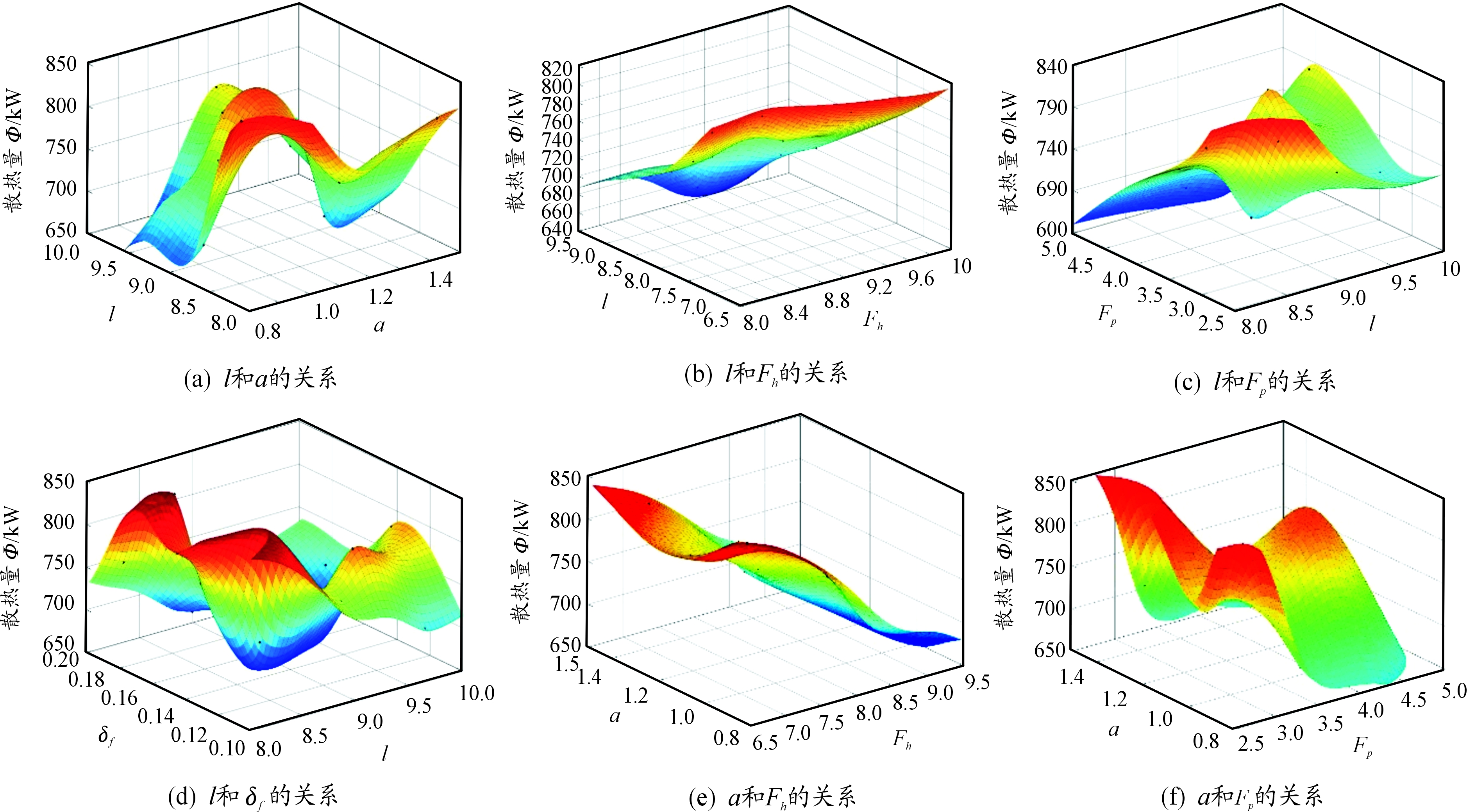
图15 部分替代模型示意图
为了验证替代模型的精度,选用决定系数来评价拟合效果,决定系数R2的计算公式为

式中:i为样本点的个数;yi为样本点的实际值;fi为样本点的预测值;![]() 为样本点的平均值。目标函数为散热量Φ和压力损失Δp的决定系数计算结果为0989 7和0.964 28,如图16(a)和16(b)所示。这表明所建立基于RBF径向基神经网络的模型精度较高,可以满足计算的需要[16]。
为样本点的平均值。目标函数为散热量Φ和压力损失Δp的决定系数计算结果为0989 7和0.964 28,如图16(a)和16(b)所示。这表明所建立基于RBF径向基神经网络的模型精度较高,可以满足计算的需要[16]。
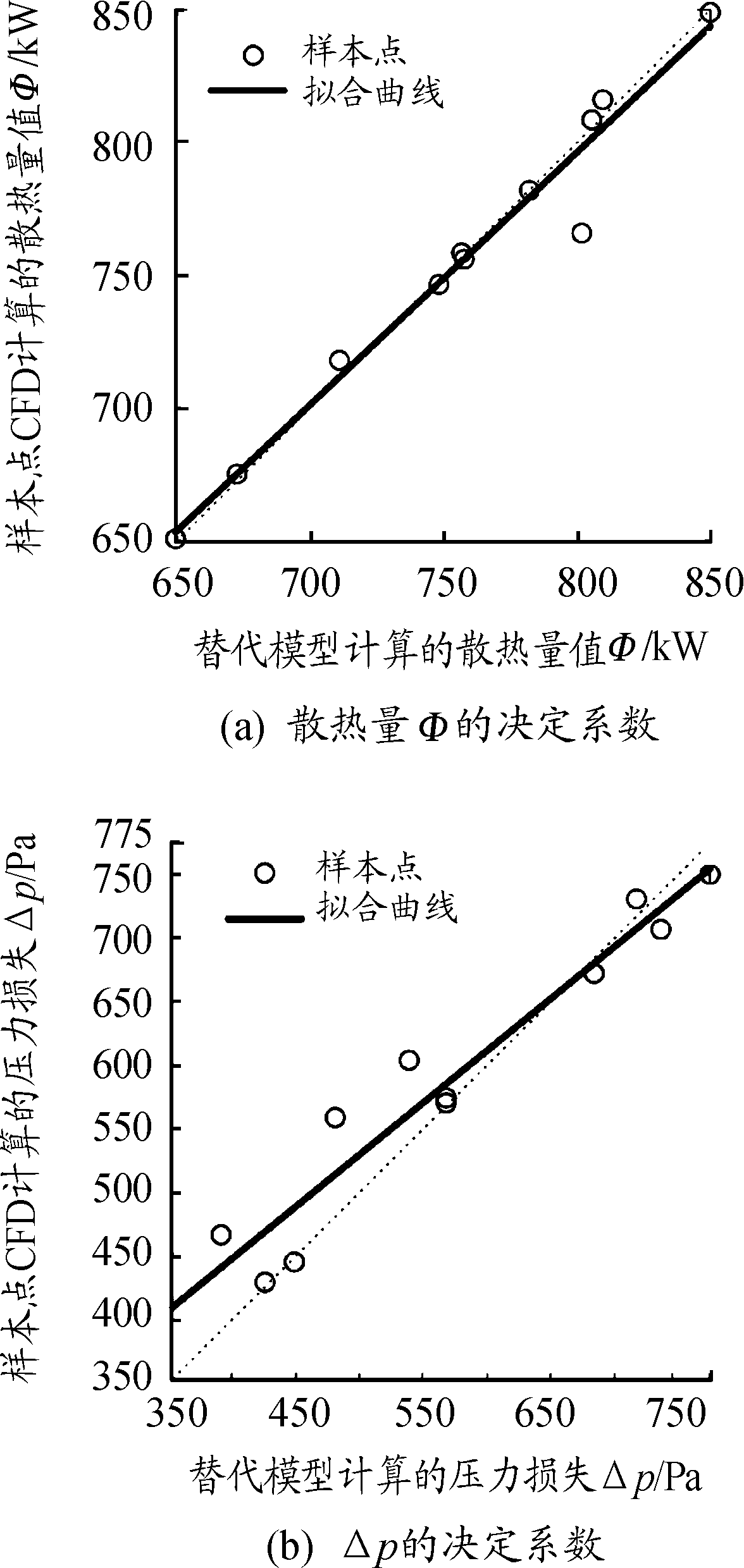
图16 决定系数计算曲线
2.5 计算结果分析
图17(a)和图17(b)为百叶窗间距l按照正态分布进行1 000次蒙特卡洛抽样计算得到的散热量Φ和空气侧压力损失Δp的关系曲线,另外4个设计变量均取取值范围的中间值。从图17中可以看出:散热量随着百叶窗间距的增加而变大,压力损失随着百叶窗间距的增加先增大后减小。图18(a)和图18(b)为百叶窗开度a按照正态分布进行1 000次蒙特卡洛抽样计算得到的散热量Φ和空气侧压力损失Δp的关系曲线。从图18中可以看出:散热量随着百叶窗开度的增加而变大,压力损失随着百叶窗开度的增加先增大后减小。图19(a)和图19(b)为翅片高Fh按照正态分布进行 1 000 次蒙特卡洛抽样计算得到的散热量Φ和空气侧压力损失Δp的关系曲线。从图19中可以看出:散热量随着百叶窗开度的增加而降低,压力损失随着百叶窗开度的增加而减小。

图17 百叶窗间距与散热量和压力损失的关系曲线

图18 百叶窗开与散热量和压力损失的关系曲线

图19 翅片高与散热量和压力损失的关系曲线
图20(a)和图20(b)为翅片间距Fp按照正态分布进行1 000次蒙特卡洛抽样计算得到的散热量Φ和空气侧压力损失Δp的关系曲线。从图20中可以看出:散热量随着百叶窗开度的增加而降低,压力损失随着百叶窗开度的增加先变小后增大。图21(a)和图21(b)为翅片厚度δf按照正态分布进行1 000次蒙特卡洛抽样计算得到的散热量Φ和空气侧压力损失Δp的关系曲线。
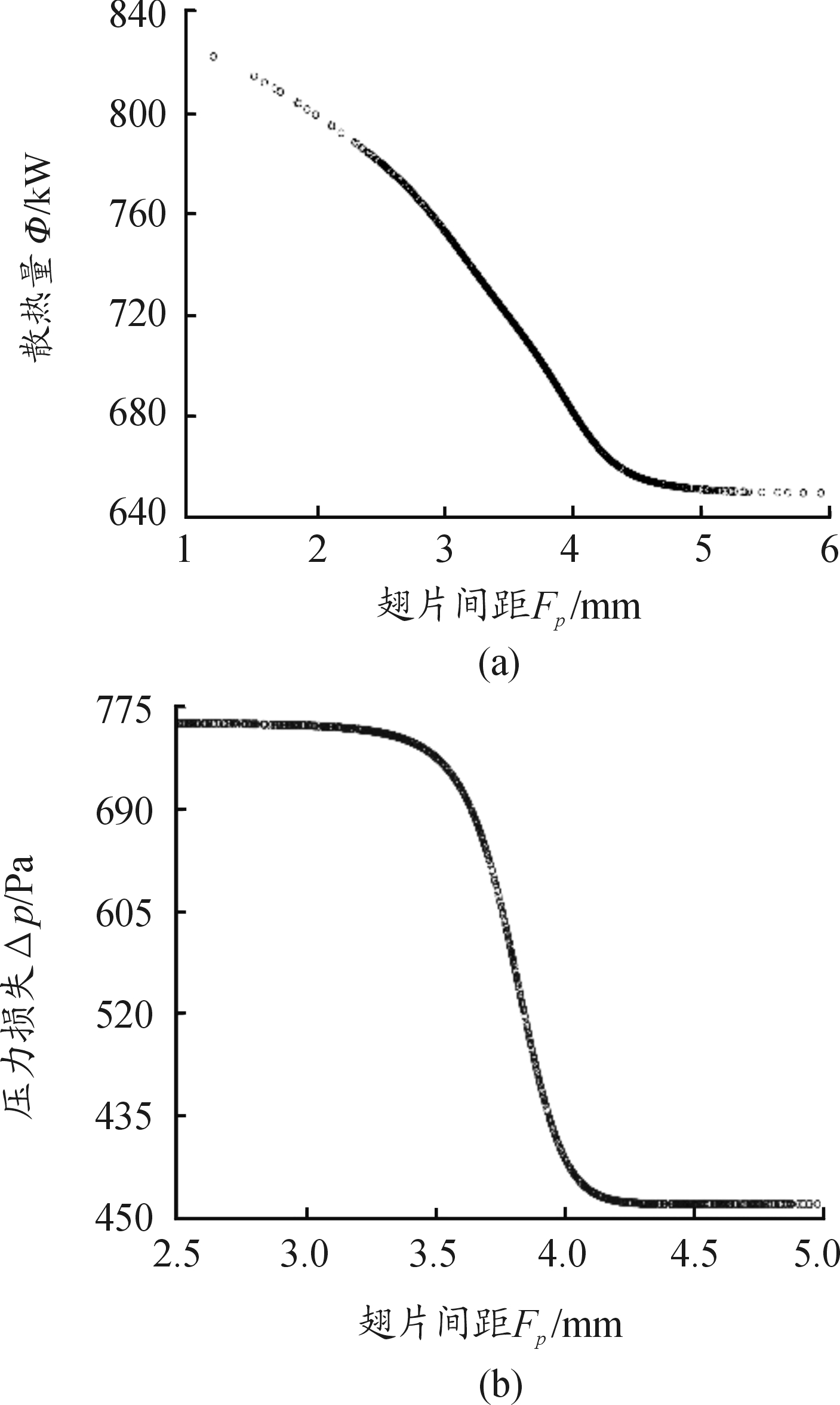
图20 对翅片间距抽样得到的分布
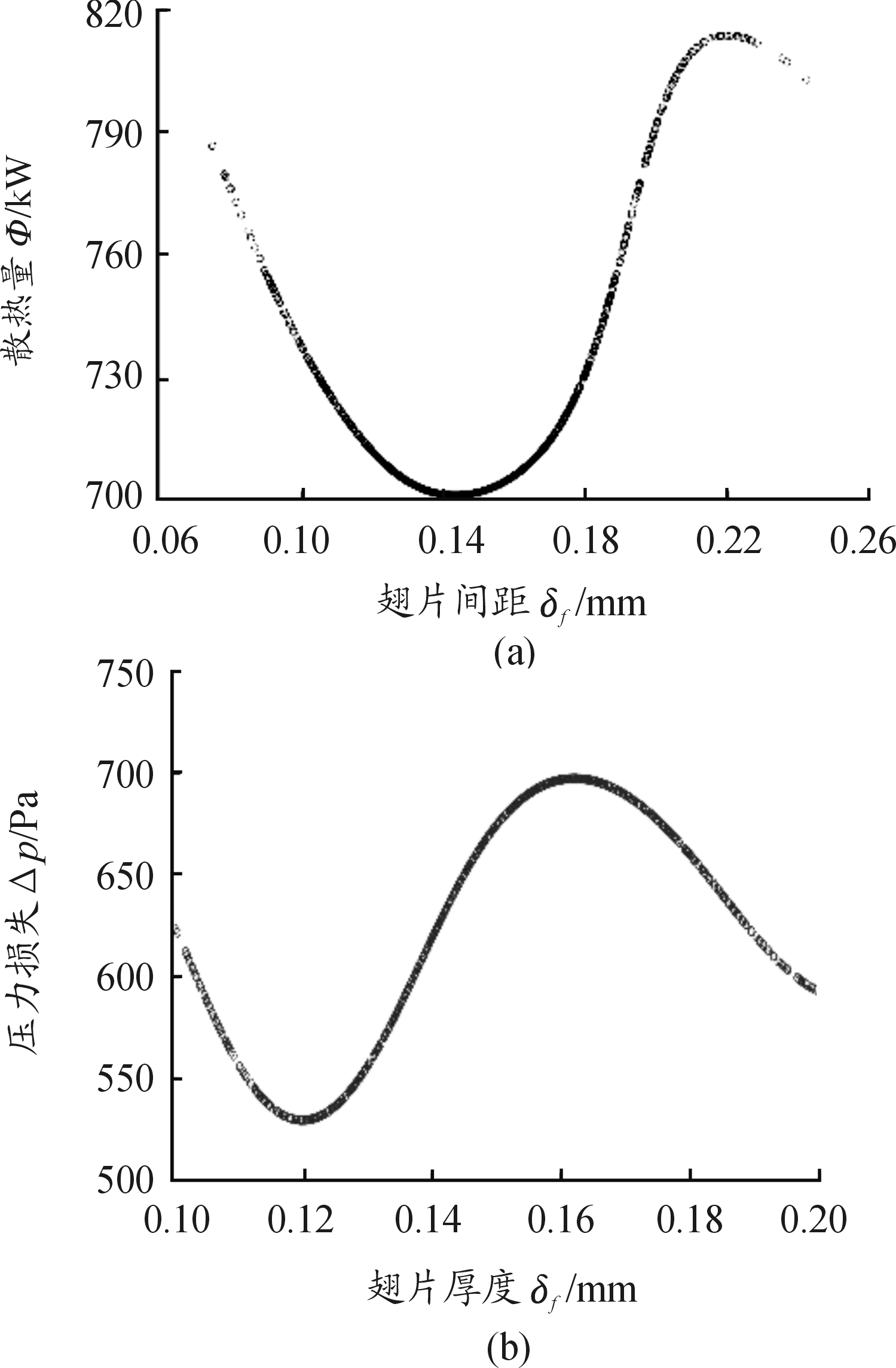
图21 对翅片厚度抽样得到的分布
从图21中可以看出:散热量随着百叶窗开度的增加先减小后增加,压力损失随着百叶窗开度的增加先变小后增大。从上述这些规律中可以看出,每个设计变量相对于目标函数的变化趋势是不同甚至是矛盾的,因此不可能通过调整设计变量让两个目标函数同时达到最优,只能在各个目标之间进行协调和权衡,尽可能使每个目标尽可能均达到最优,而这种优化解也不可能是单一解,而是一个解集,一般称为帕累托前沿。
3 基于萤火虫算法的多目标优化
自然界中的群居昆虫,它们虽然个体结构简单,但是通过个体间的合作却能够表现极其复杂的行为能力。萤火虫算法是一种模拟萤火虫行为的群集只能优化算法,由于它具有控制参数少且易于实现等特点,为解决存在于科学领域的多目标优化问题提供了一种新的方法。基于萤火虫算法的多目标优化流程如图22所示。
利用萤火虫算法进行计算时,需要设置相关参数。萤火虫算法参数设置如表2所示。
利用萤火虫算法求得的帕累托前沿如图23所示。从图23中可以看出,散热量的取值范围为797~807 kW,压力损失的取值范围为400~460 Pa,从散点的分布情况来看,不可能使二者同时达到最优,如果决策者追求散热量尽可能地大,应该往右上角取值,如果对压力损失比较重视,则应该往左下角取值。本文对压力损失和散热量综合考虑,选择了一组使各个目标尽可能最优的折衷方案,该组的位置如图23所示,设计变量的尺寸分别为l=8.22,a=1.43,Fh=6.5,Fp=5,δf=0.12,将优化后的尺寸利用CFD仿真可以得到散热量为803.5 kW,压力损失为417.559 Pa,与优化前相比,散热量增加了6%,压力损失降低了13.8%。
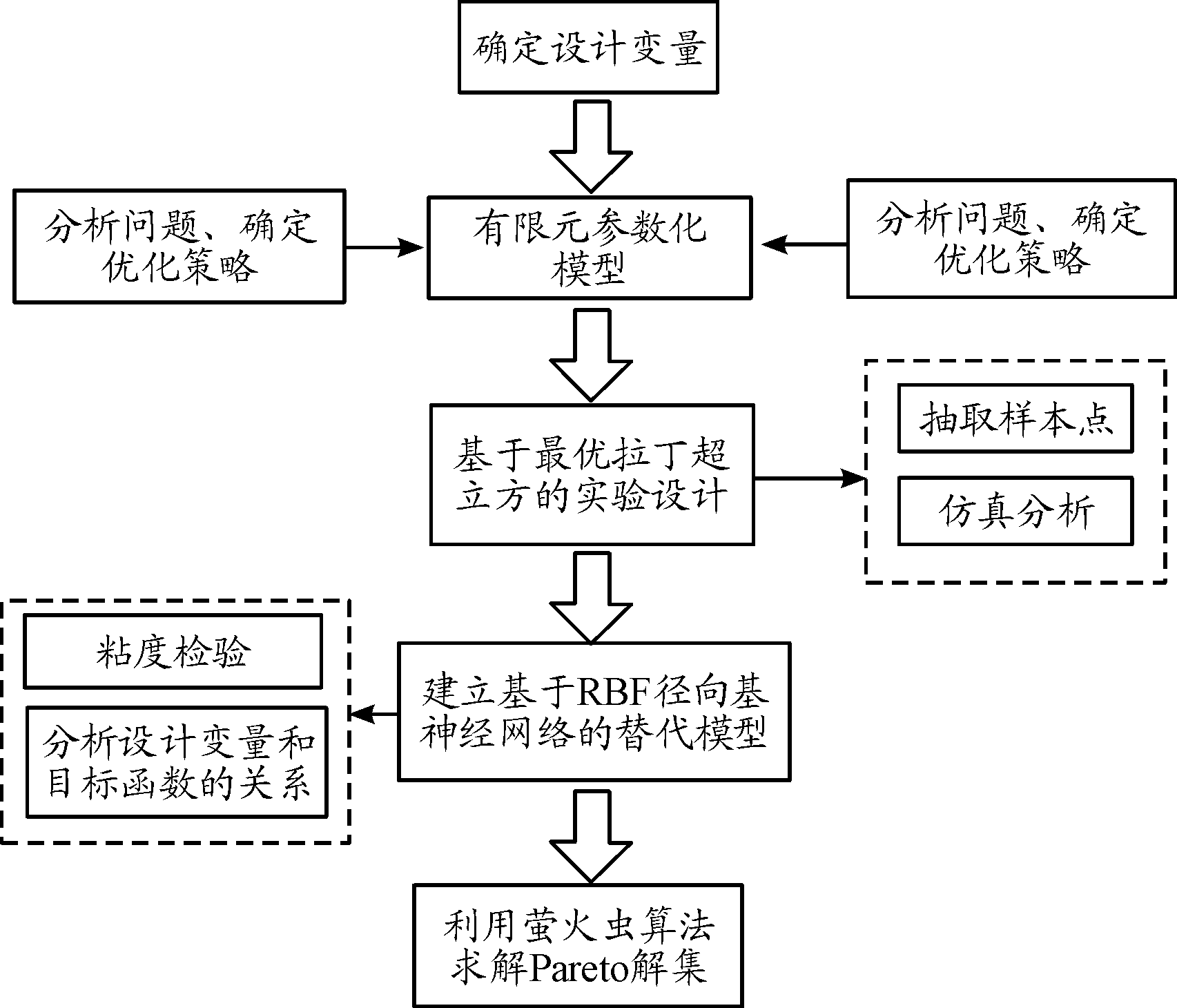
图22 基于萤火虫算法的多目标优化流程框图
表2 萤火虫算法参数设置

类别参数设置最大迭代次数10 000萤火虫数目25惯性权重初始值0.8亮度0.2吸引力0.1步长因子0.4高斯变异系数0.5
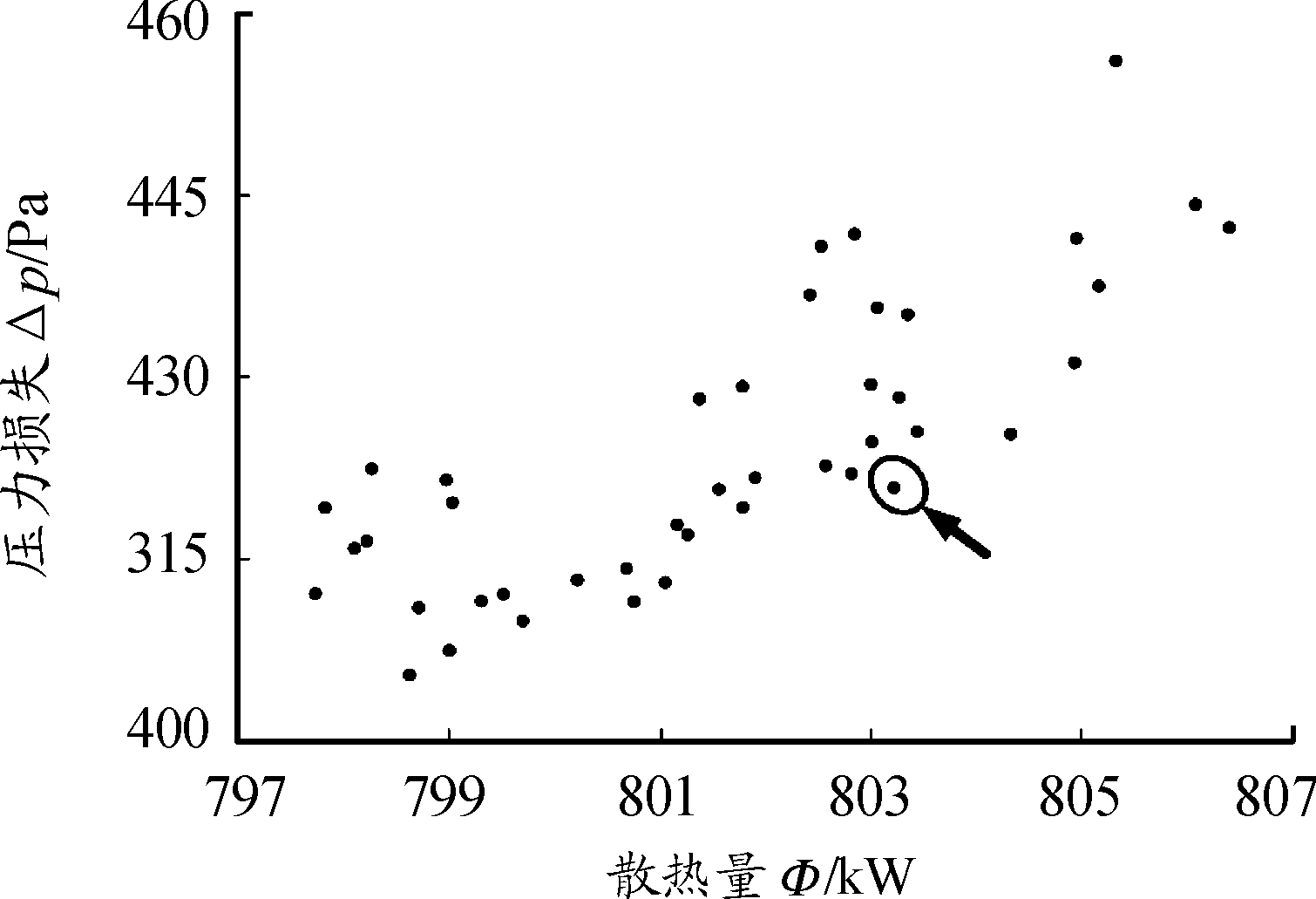
图23 帕累托前沿示意图
4 结论
1) 本文所建立的基于CFX的装甲车辆散热器模型的精度较高,与解析解之间的最大相对误差仅为3.9%。
2) 通过对散热器的仿真计算可以散热片中的空气流速分布不均匀,大致呈阶梯状分布。散热器片出口处压力较小,最大值位于速度入口处。
3) 所建立的基于RBF神经网络的替代模型精度较高,目标函数为散热量Φ和压力损失Δp的决定系数计算结果为0.989 7和0.964 28,完全满足计算精度。
4) 利用萤火虫算法所得到的优化后的结构散热量增加6%,压力损失降低13.8%。
[1] 王志军.管带式散热器的设计及其参数化设计系统的研究[D].济南:山东大学,2011:12-19.
[2] 姚仲鹏,王新国.车辆冷却传热[M].北京:北京理工大学出版社,2001:222-256.
[3] 闫玉英,玄哲浩.带百叶窗的管带式散热器传热分析与结构参数优化[J].内燃机学报,1992(4):371-376.
[4] 李晓光.汽车百叶窗翅片式散热器性能数值模拟与风洞实验研究[D].天津:天津大学2012:14-28.
[5] 王任远,李建雄,吴金星.散热器空气侧百叶窗翅片结构参数优化[J].流体机械,2013(06):82-86.
[6] 向高.百叶窗翅片散热器性能试验与数值模拟研究[D].武汉:华中科技大学,2016:35-39.
[7] 景陶敬,沈辉,单金良,等.管带式散热器传热性能数值模拟与风洞实验研究[J].中国农机化学报,2019,40(01):128-131.
[8] 袁志群,许建民.汽车散热器空气流动阻力特性的数值计算研究[J].厦门理工学院学报,2009(04):44-48.
[9] 李世伟,吴国荣,袁聿震,等.百叶窗结构参数对管带式散热器流动传热特性影响的研究[J].内燃机与动力装置,2012(01):28-31.
[10] 张毅.车辆散热器模块流动与传热问题的数值分析与试验研究[D].杭州:浙江大学,2006:36-47.
[11] 孙红运.车用内燃机散热器的标定与匹配[D].沈阳:沈阳理工大学,2017:23-40.
[12] 傅达,崔毅,阎心怡,等.活塞换热边界自动标定方法研究[J].内燃机工程,2018,39(05):66-72.
[13] 何振鹏,谢海超,仲崇高,等.基于宏观空穴理论的主轴承多目标优化设计[J].润滑与密封,2018,43(11):93-101.
[14] 乔鑫,夏天,刘莹.基于组合优化策略的白车身轻量化设计[J].汽车实用技术,2018,273(18):120-123.
[15] 曾志新,李鑫.汽车发动机冷却系统散热器建模仿真与设计[J].汽车工程师,2019(9):18-21.
[16] 邵兴杨.基于FLUENT的汽车管带式散热器整体模拟[J].现代机械,2019(4):25-28.