车轮型装药,又称“轮孔药”。它可以看作是星孔药的延伸,通常作为火箭发动机推进剂燃料或是底排药剂使用。文献[1-5]对国内外火药和推进剂的发展现状进行了综述,指出了火药和推进剂的发展方向。文献[6]对星型药柱的固化降温过程进行了研究,分析了固化降温过程中推进剂的温度场变化的分布情况及应力应变危险区域,为推进剂固化降温提供参考。文献[7]对星孔型药柱进行了研究,推导出星孔型药柱的余药燃烧面积公式。文献[8]设计了星孔装药的燃面退移仿真的可视化系统。文献[9]研究了星孔型药柱和车轮型药柱的减面燃烧规律,研究结果表明减面性较大时,优先选用星孔型药柱。文献[10]基于参数化建模,建立车轮型药柱的参数化有限元分析模型,得到了装填分数不小于初始设计且最大应变比初始设计小了30%的药柱形状。文献[11]把车轮型装药用于底排弹,推导出了底排装置内车轮装药燃烧规律的数值计算模型,计算结果符合底排装置内的燃气压力变化规律,并与地面实验结果数据吻合良好。
目前,有关车轮型药柱燃烧规律的研究文献公开发表很少,因此本文建立了车轮型药柱燃烧面积公式,划分车轮型药柱的燃烧阶段以及对影响燃烧规律的因素进行了分析研究。
1 车轮型药柱
车轮型药柱作为星孔装药的延伸,可以通过改变药形尺寸,获得不同燃烧特性。如图1所示,其结构主要的几何参数有:外径D、长度L、轮臂数n、1/2轮臂厚e1、最大有效肉厚e2、特征长度l、轮臂高h、角分数ε、轮臂角θ、轮顶角圆弧半径r、轮底角圆弧半径r1、轮臂过渡半径r2。
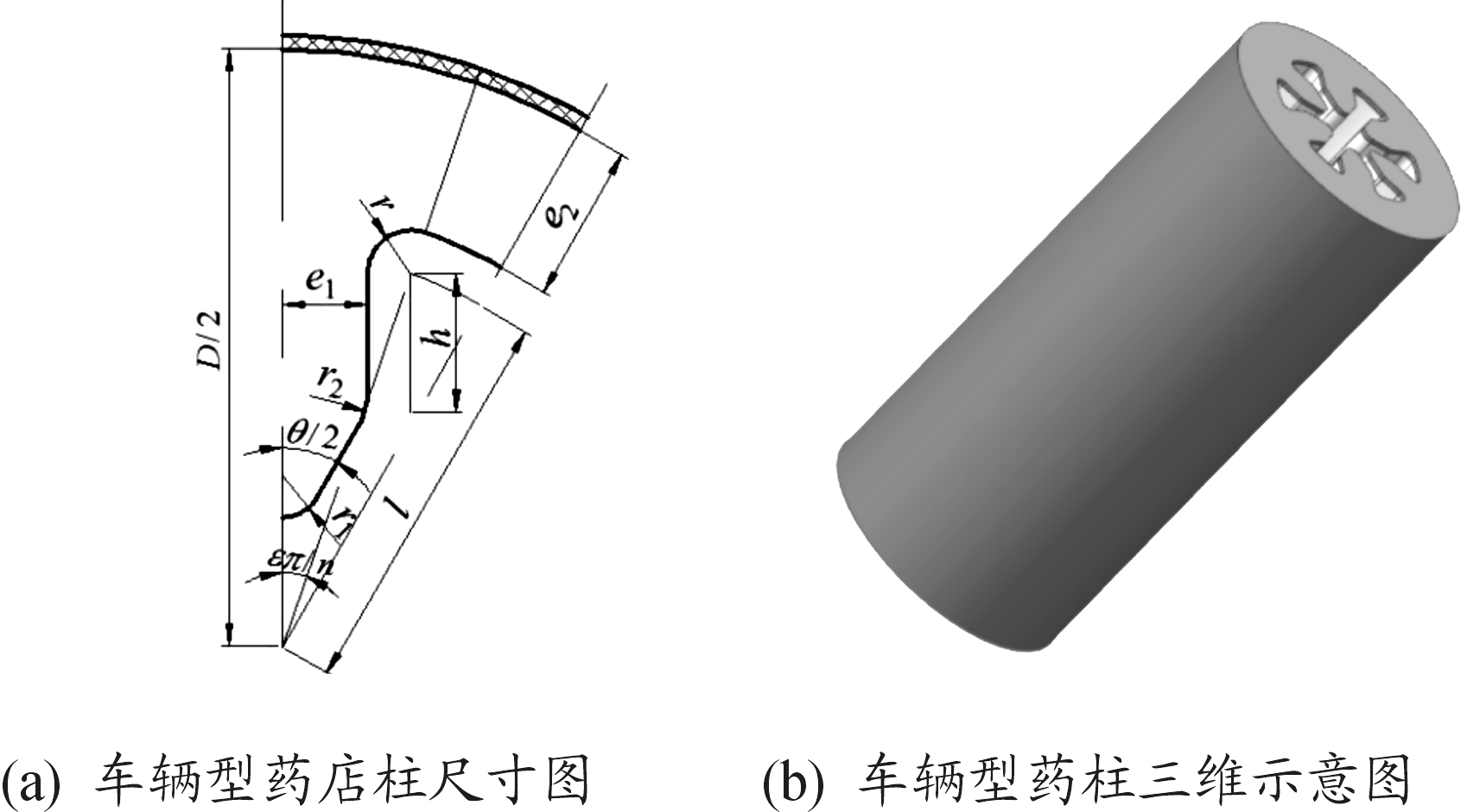
图1 车轮型药柱示意图
2 理论基础
本文采用几何燃烧定律[12]。
本文研究的车轮型药柱外侧表面和两端面有包覆层,仅内侧表面燃烧。按照几何燃烧规律和装药形状特征分析,可将其分为3个燃烧阶段。
第1阶段:从原始轮孔燃烧开始,到轮臂消失结束,此时药柱为单孔花形药柱。
第2阶段:燃烧从单孔花形药柱开始,燃去肉厚推进到药柱的最大有效肉厚值结束。燃烧结束时分裂为多个小三角棱柱。
第3阶段:也是余药阶段,燃烧从多个小棱柱开始,到全部装药燃烧完为止,剩下包覆层。
车轮型药柱内孔尺寸参数较多,为简化起见,假设装药外围及两端包覆,轮孔为等截面,且所有轮臂的形状相同,即厚度和高度相等,则半个轮角的周长变化规律就可以代替整个轮形装药燃烧面积的变化规律。
车轮型药柱分为两种不同的形状,如图2所示。

图2 两种不同轮形装药示意图
当e1<e2时,药柱燃烧分为3个阶段,即轮臂消失前、轮臂消失后和余药燃烧。
当e1=e2时,药柱燃烧没有第2阶段,只有轮臂消失前和余药燃烧。
因为在燃烧过程中轮臂数n和药柱长度L是不变的,所以燃烧面积可以直接用半个轮形的周长来代替计算。
为了推导方便,先假设r1=r2=0,则轮孔半角β=π/n。
车轮型药柱燃烧面的变化如图3所示,从图3中可以看出:半个轮形的周长是由两个不断增长的圆弧AB、BC和两条不断缩短的直线CD、DE、组成,初始燃烧周长为c0:
(1)
当燃烧面积推进到H点时,轮臂消失,即直线段消失。这时一般情况下燃烧面积突然下降,然后进入下一燃烧阶段[13-15]。
轮臂消失的条件如式(1)所示:
(2)
3 燃烧面积公式推导
根据划分的燃烧阶段,推导各个阶段的燃烧面积公式,其中各个阶段的燃烧面积的位置如图3所示。

图3 车轮型药柱燃烧变化示意图
3.1 第1阶段(轮臂消失前)燃烧面积
该阶段燃去肉厚e的变化范围是e=0到e=e1=lsin(εβ)-r,由图3可以看出,半个轮形的周长为
(3)
根据几何关系整理可得
(4)
以上推导的是r1=r2=0时的轮形装药第1阶段燃烧面积,实际用的轮形装药其轮臂是有圆弧过渡的,这些圆弧可以减小应力集中,也可以在加工药柱时容易脱模,不损害尖角。
对于轮臂有过渡圆弧的轮孔药柱,其第1阶段的总周长为
c1=![]()
(5)
总的燃烧面积为
Ab1 =![]()
![]()
(6)
3.2 第2阶段(轮臂消失后)燃烧面积
对于e1=e2情况的车轮型药柱,轮臂消失时,直接进入余药燃烧阶段。
对于e1<e2情况的车轮型药柱,轮臂消失时,燃烧进入第2阶段,该阶段燃去的肉厚是从e=e1=lsin(εβ)-r到e=e2=D/2-l-r。
由图3可以看出
(7)
经整理可得:
c2=l(l-ε)β+(r+e)β+
![]()
(8)
第2阶段总的燃烧面积为
Ab 2 = 2nL · l(l-ε)β + 2nL(r + e)β+
(9)
3.3 第3阶段(余药)燃烧面积
车轮型药柱余药阶段的燃烧面积变化如图4所示。由该图可知,当燃面烧到时![]() 此时燃去的肉厚等于e2,燃面迅速减小,
此时燃去的肉厚等于e2,燃面迅速减小,![]() 由变为
由变为![]() 此时开始的燃烧即为余药燃烧。为了准确地计算内弹道曲线,必须考虑余药燃烧面的变化。
此时开始的燃烧即为余药燃烧。为了准确地计算内弹道曲线,必须考虑余药燃烧面的变化。

图4 余药阶段燃烧周长变化示意图
由图4可知,余药燃烧的肉厚从e=e1开始到![]() 结束,
结束,![]() 的表达式为
的表达式为
(10)
所以余药燃烧结束时的肉厚为
(11)
则余药阶段的周长为
c3=2n(e+r)∠GO′F=
2n(e+r)(∠O′OG+∠OO′F)
经整理得:
c3=![]()
(12)
总的余药燃烧面积为
Ab 3 =![]()
2nL(r + e)(π-εβ)+
(13)
3.4 计算结果与分析
通过使用MATLAB软件对药柱燃烧面积3个阶段的表达式进行编程,得到车轮型药柱e1<e2和e1=e2时燃烧表面积与燃去肉厚关系的曲线,如图5所示。
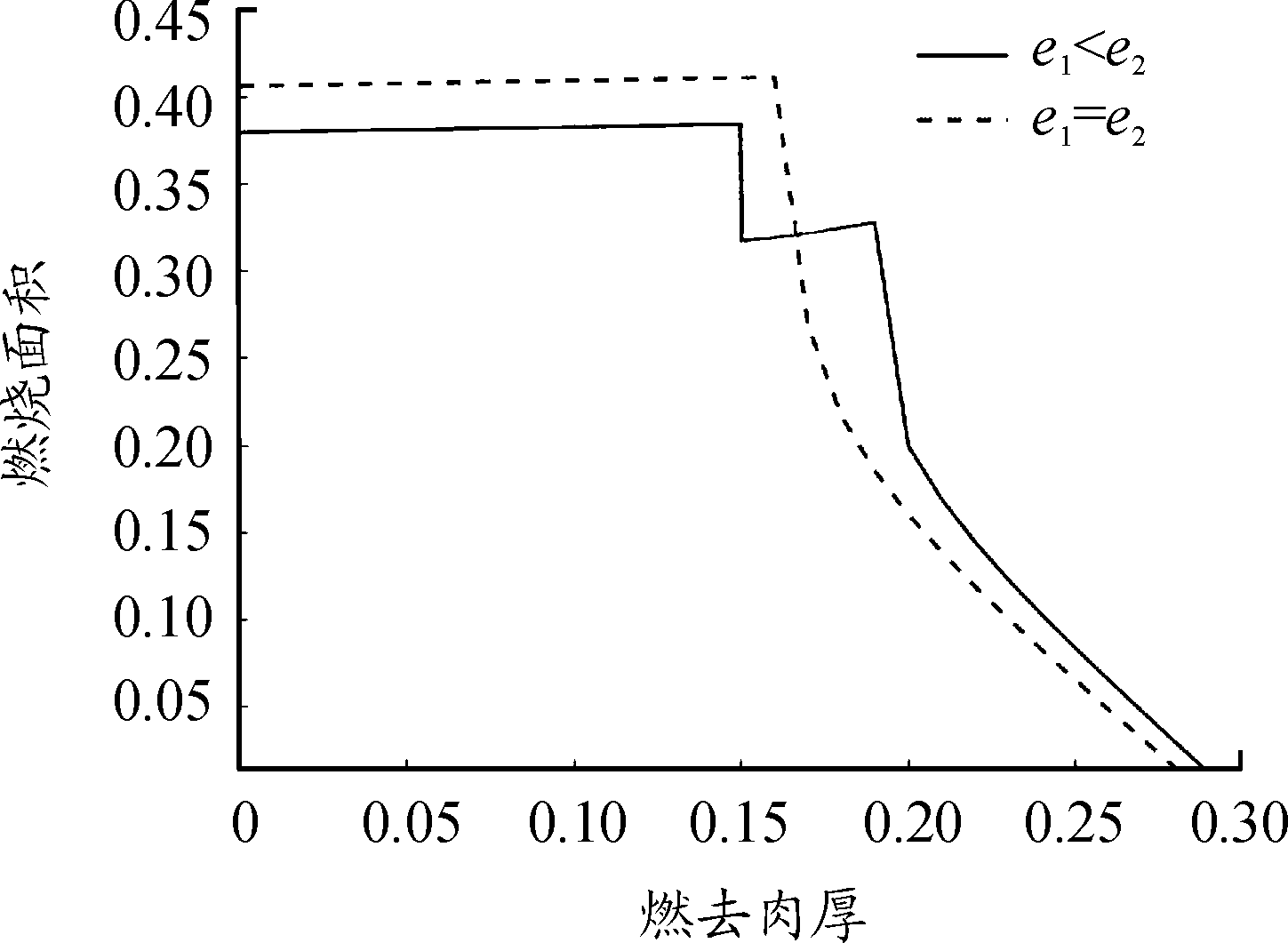
图5 两种肉厚形式的燃烧面积与燃去肉厚关系曲线
从图5中可以看出:当e1<e2时,药柱燃烧呈3个阶段。当e1=e2时,药柱燃烧成两个阶段。当e1<e2时,燃烧情况较复杂,更具有代表性。所以本文重点讨论车轮型药柱e1<e2时的燃烧规律。
4 恒面燃烧规律研究
对车轮型药柱燃烧规律进一步研究。根据车轮型药柱燃烧面积的计算公式,设第1阶段燃烧面积Ab1为f1(e),第2阶段燃烧面积Ab2为f2(e)。将燃烧面积f1(e)、 f2(e)对燃去肉厚e求导,可得:

(14)
整理式(13)可得:

(15)
根据式(15)所示,对第1阶段燃烧面积变化规律产生影响的结构参数为n,l,L,θ。对第2阶段燃烧面积变化规律产生影响的结构参数为n、l、ε、r。
4.1 恒面燃烧判断条件与分析
要探究车轮型药柱的恒面燃烧条件,则需df(e)/de恒为0,即式(15)恒为0,求解:第1阶段n≈4.078,第2阶段n≈-0.367。若按照恒面燃烧的条件,轮臂数须为正整数,则计算得到的第一阶段和第二阶段的n值均不满足要求,因此,车轮型药柱燃烧过程不具有恒面性。
4.2 轮臂数的选择
燃烧面积变化率df1(e)/de、df2(e)/de与轮臂数n的关系如图6所示。图6中网格平面为df(e)/de=0。
通过图6(a)可以看出:当n=4.1时,df1(e)/de=0,但轮角数必须为正整数,所以,以n取4为分界点,进行讨论。当轮臂数n≤4时,车轮型药柱燃烧第一阶段呈增面燃烧规律,当轮臂数n≥5时,车轮型药柱燃烧第一阶段呈减面燃烧规律。图6(b)可以看出:燃烧第二阶段,当轮臂数较小时,燃烧面积变化率逐渐减小,当轮臂数较大时,燃烧面积变化率趋于平稳,但df2(e)/de恒大于0,车轮型药柱呈增面燃烧规律。
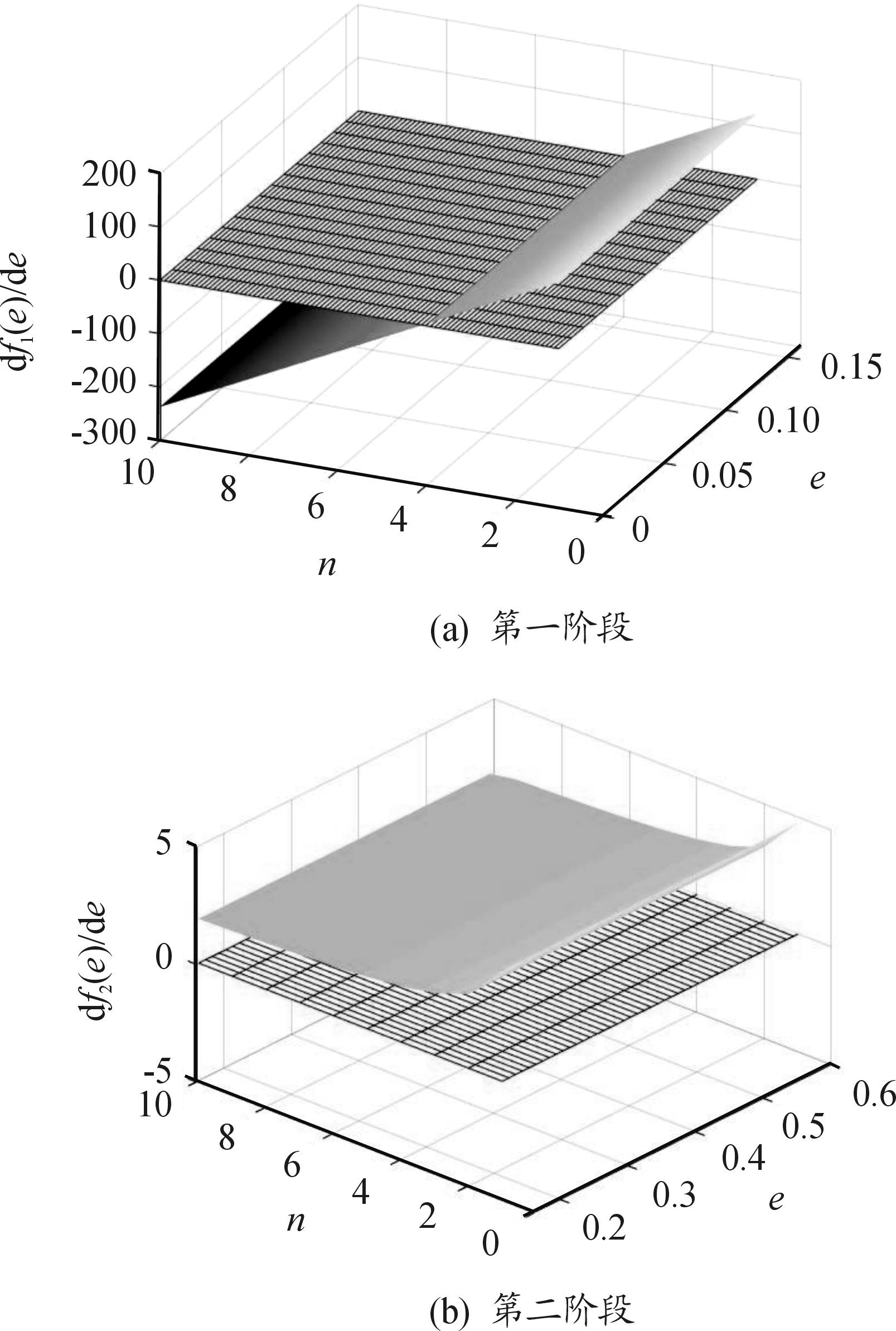
图6 df(e)/de与n的关系曲线
图7给出了轮臂数在3~6时,车轮型药柱的面积曲线。从图7中可以看出:当n=3,燃烧只有2个阶段,除此之外的3条曲线都存在3个燃烧阶段,n=4时,第1阶段呈增面燃烧,且增面变化率较小。n=5,6时,第1阶段呈减面燃烧,第2阶段呈增面燃烧,第3阶段呈减面燃烧。当n=4时,燃烧第1阶段更接近恒面。因此,取n=4进行下一步研究。
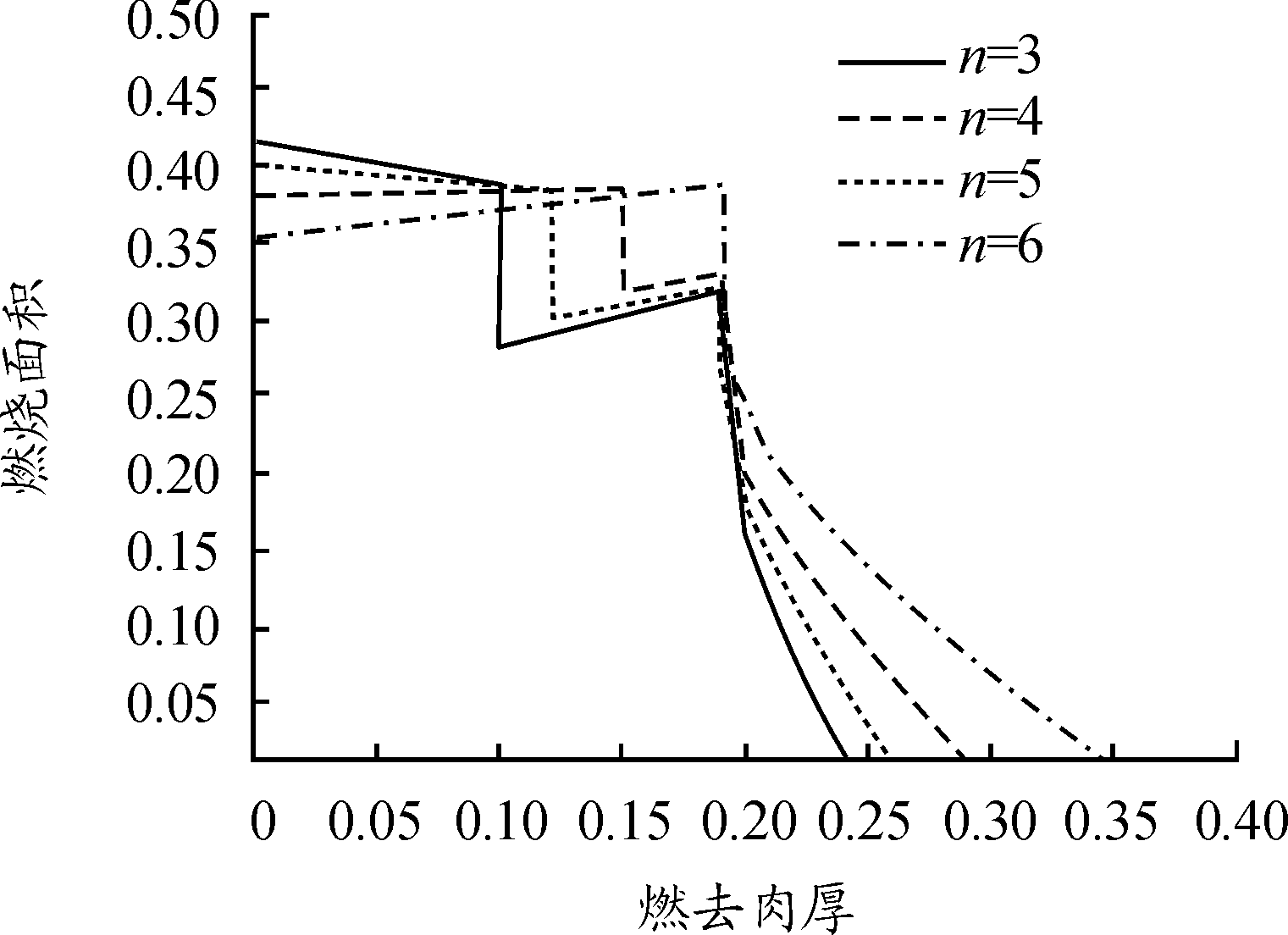
图7 轮臂数对燃烧面积的影响曲线
4.3 轮臂角对第一阶段燃烧面积的影响
燃烧面积变化率df1(e)/de与轮臂角θ的关系如图8所示。图8中网格面代表df1(e)/de=0。
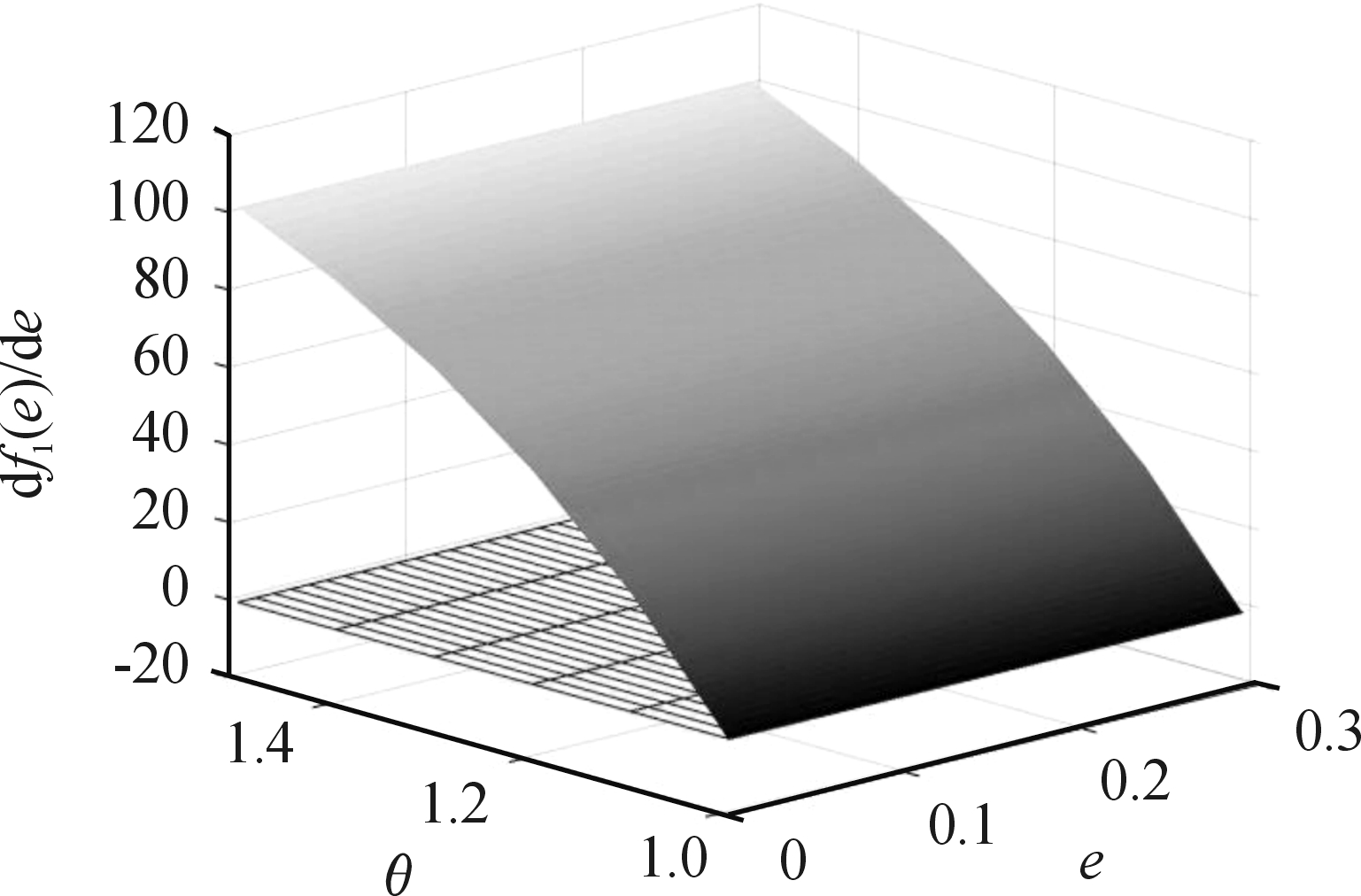
图8 df1(e)/de与θ的关系曲线
从图8中可以看出:当θ∈(π/3,π/2)时,随着θ的减小,药柱燃烧面积变化率逐渐趋于平稳,且恒大于0,车轮型药柱呈增面燃烧规律。根据恒面燃烧的需求,选取θ=π/3进行下一步研究。
4.4 角分数对第二阶段燃烧面积的影响
燃烧面积变化率df2(e)/de与角分数ε的关系如图9所示。图9中网格面代表df2(e)/de=0。

图9 df2(e)/de与ε的关系曲线
从图9中可以看出:燃烧面积变化率曲面变化趋势平稳,且恒大于0,由此可见,角分数ε的变化对第2阶段燃烧规律无明显影响。
4.5 敏感度分析
当取轮臂数n=4,轮臂角θ=π/3,角分数ε=0.8时,分析结构参数l、L、h、r、r1和r2对燃面变化率df1(e)/de和df2(e)/de 的影响。
由图10(a)可知,对第1阶段燃烧面积变化率df1(e)/de最敏感的结构参数为l和L,图10(b)可知,对第2阶段燃面变化率df2(e)/de最敏感的结构参数为l。下一步将重点研究df1(e)/de、df2(e)/de与l、L及l的关系。
4.6 药柱长度对第一阶段燃烧面积的影响
以药柱直径D为基准对L做无量纲处理,得到燃烧面积变化率df1(e)/e与药柱长度L/D的关系如图11所示。网格面代表df1(e)/de=0。
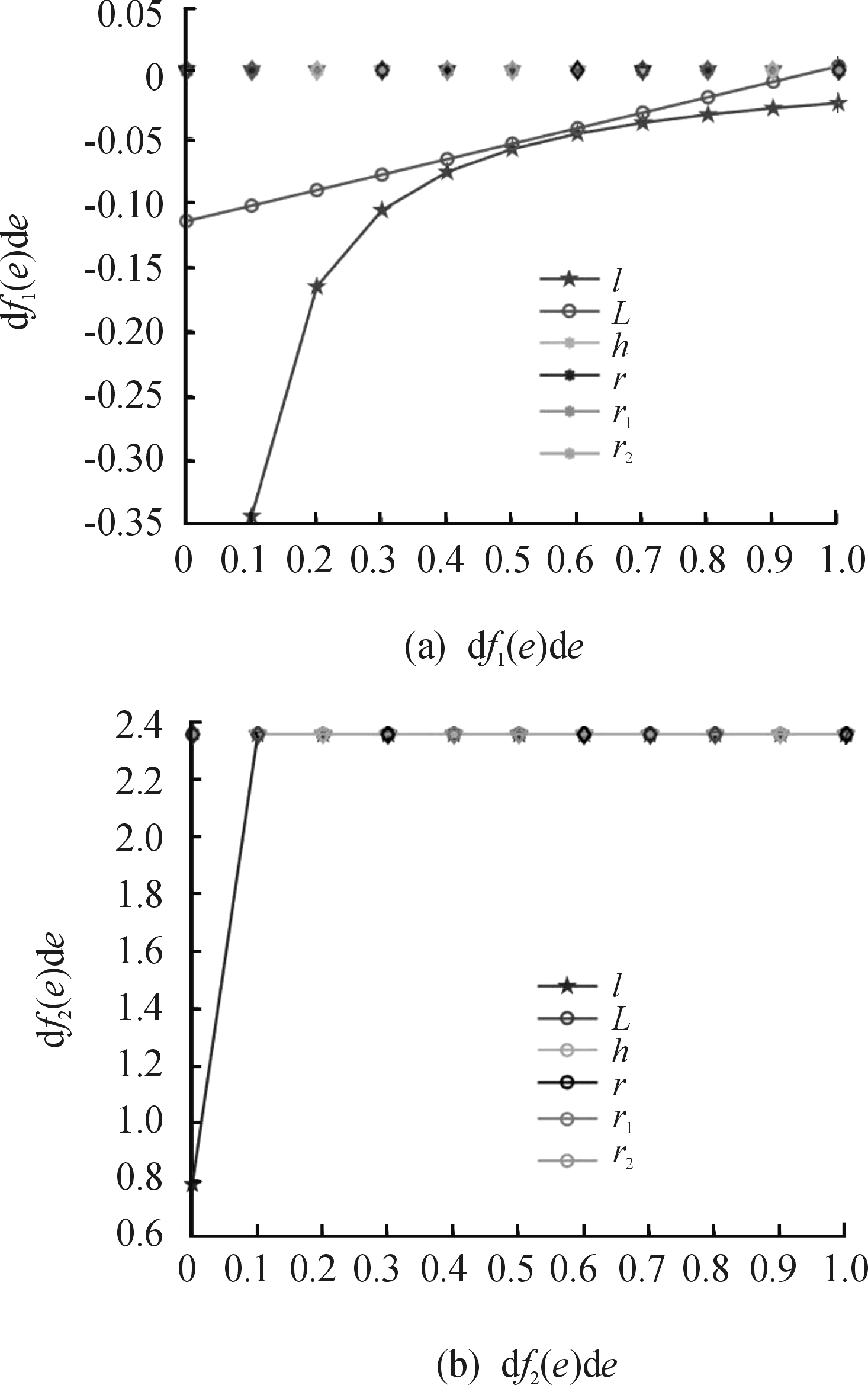
图10 燃面变化率与结构参数的关系曲线

图11 df(e)/de与长径比的关系曲线
由图11可以看出:当L/D∈(0.1,0.3)时,燃烧面积变化率趋势逐渐增大,且恒大于0,车轮型药柱呈增面燃烧规律。根据恒面燃烧的需求,选取L/D=0.1的药柱进一步研究其燃烧规律。
4.7 特征长度对燃烧面积的影响
燃烧面积变化率df(e)/de与特征长度l的关系如图12示,网格面代表df(e)/e=0。
由图12(a)可以看出:当l<0.3时,燃烧面变化率逐渐增大,当l>0.3时,燃烧面积变化率趋于平稳。但df1(e)/de恒大于0,车轮型药柱始终呈增面燃烧规律。由图12(b)可以看出:当l<0.3时,燃烧面变化率趋势平稳,随着l增大逐渐减小,df2(e)/de大于0,车轮型药柱呈单增面燃烧。当l>0.3时,燃烧面变化率趋势下降较快,df2(e)/de小于0,车轮型药柱呈单减面燃烧。

图12 df(e)/de与l的关系曲线
4.8 算例
根据对车轮型药柱燃烧规律的分析结果,选取一组车轮型药柱结构参数进行计算验证,参数见表1。
表1 车轮型药柱参数

参数数值参数数值药柱长度L/mm11药柱直径D/mm110轮臂数n4角分数ε0.8特征长度l/mm34轮臂高h/mm10轮顶角圆弧半径r/mm2轮底角圆弧半径r1/mm5轮臂过渡半径r2/mm2轮臂角θ/radπ/3
以药柱直径D为基准,进行无量纲处理,得到L=0.1,D=1,n=4,ε=0.8,l=0.3,h=0.07,r=0.02, r1=0.04,r2=0.02,θ=π/3。将无量纲处理的参数代入e1、e2计算公式得e1=0.1635,e2=0.172 7,e1<e2,根据第3节研究结果,药柱燃烧存在3个阶段。药柱的轮角数为4,轮臂角为π/3,根据4.2~4.3的研究结果,药柱第1阶段接近恒面燃烧,第2阶段为增面燃烧,第3阶段为减面燃烧。
将上述参数代入燃烧面积计算式(3)、式(5)和式(8)中。计算结果如图13所示。燃烧存在3个阶段,且第1阶段接近恒面燃烧,第2阶段药柱呈增面燃烧,第3阶段为减面燃烧,算例结果与理论研究结果相吻合。
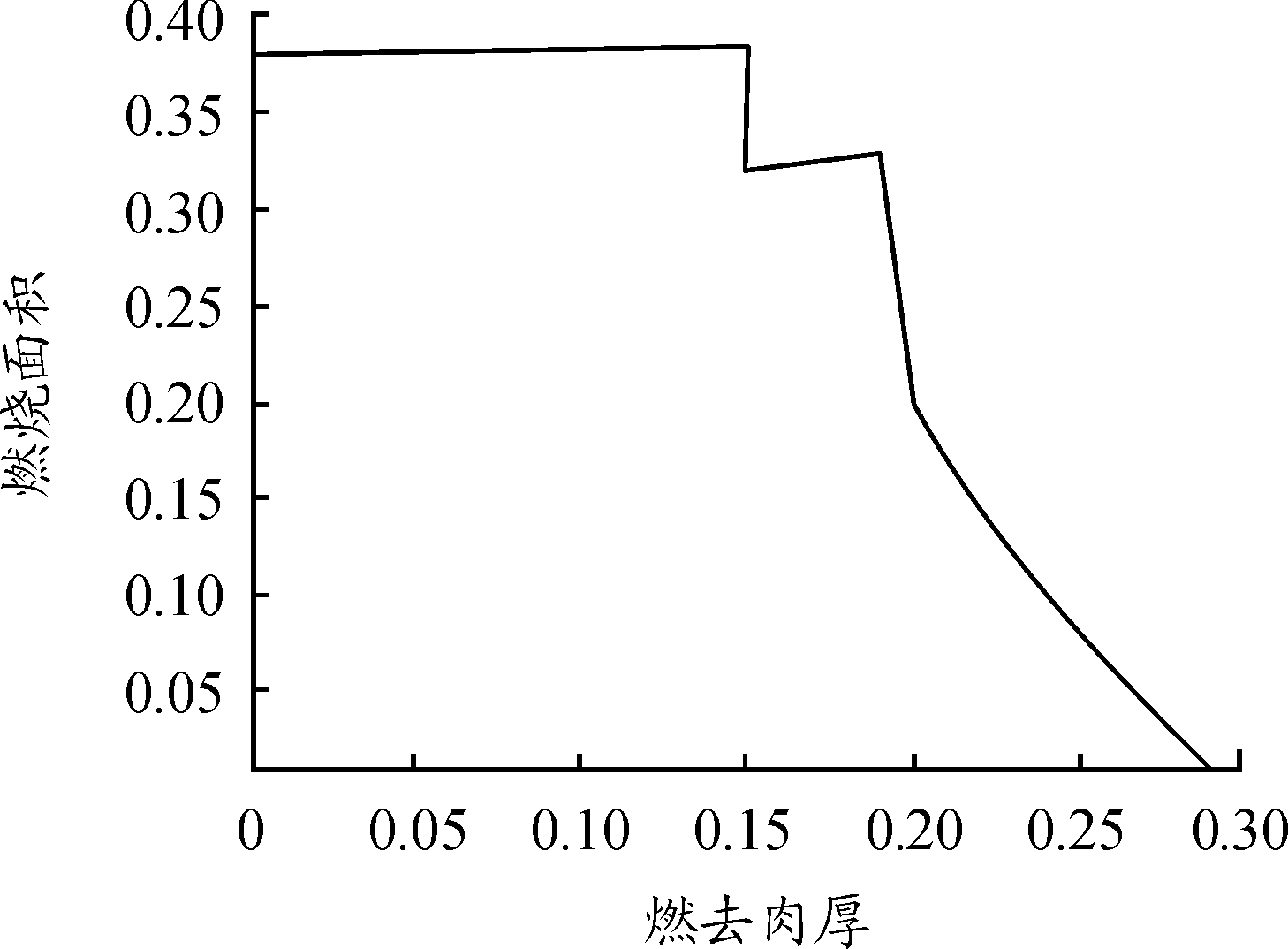
图13 燃烧面积变化曲线
5 结论
当e1<e2时,车轮型药柱的燃烧过程分为3个阶段。当e1=e2时,车轮型药柱燃烧划分为2个阶段。
当轮臂数n为4时,药柱燃烧第1阶段呈增面性。燃烧第2阶段呈单增面性,且增面变化率变化较大。当n大于等于5时,药柱燃烧第1阶段呈减面性,燃烧第2阶段呈单增面性,且增面变化率变化平稳。其他结构参数对车轮型药柱的燃烧规律影响很小。
算例证明,当轮臂数n=4,轮臂角θ=π/3,药柱长径比为0.1时,燃烧过程中出现近似的恒面燃烧,且出现在燃烧的第1阶段。
[1] CHOUDHRI M K,ASTHANA S N,et al.Studies on High Energy LOVA Composition[C]//24th International Annul Conference of ICT,1993.
[2] SIMMONS R L.Designing advanced gun propellants with improved energy release[C]//32th International Annul Conference of ICT,2001.
[3] SIMMONS R L.Guidelines to higher energy gun propellants[C]//27th International Annul Conference of ICT,1996.
[4] 王泽山.有关发射药和推进剂发展问题的一些观点[J].中国工程科学,2002,4(01):92-93.
[5] LAVERITT C S.Relative erosivity of nitramine gun propellants with thermoplastic/elastomer binder systems[R].MD:Army Research Lab,Aberdeen Proving Ground,2001.
[6] 肖志平,张泽远,邢国强.星型药柱固化降温瞬态热力耦合分析[J].航空兵器,2014(01):40-43.
[7] 张为华.星孔药柱设计研究[J].推进技术,1993(01):41-45.
[8] 陈步学,王凌燕,吴心平.星孔装药燃面退移图形显示研究[J].推进技术,1996,17(06):33-38.
[9] 詹君彪,相升海,李世鹏,等.减面燃烧规律的药柱选用准则[J].弹箭与控制学报,2015,35(05):85-91.
[10] 李磊,唐国金,段静波,等.基于参数化建模的车轮型药柱形状优化[J].国防科技大学学报,2011(01):11-16.
[11] 易文俊,汤瑞峰,孟仁宾.车轮型装药底排装置内弹道计算[J].弹道学报,1996(03):31-34.
[12] 杨月诚.火箭发动机理论基础[M].西安:西北工业大学出版社,2010.
[13] 周长省,韩珺礼,陈雄,等.野战火箭发动机设计[M].北京:国防工业出版社,2015.
[14] 王泽山,何卫东,徐复铭.火药装药设计原理与技术[[M].北京:北京理工大学出版社,2006.
[15] 郭梦飞,郭颜红,尚永腾.基于MDF方法的装药燃面推移算法研究[J].航空兵器,2016(01):60-63.