粗大误差是在测量中,因反常因素造成测量值超出正常测量值范围的误差。常用的基于统计方法的粗大误差判断准则有3σ,Grubbs,Chauvent,Dixon准则[1],非统计判别法有信息熵与灰色理论判别法[2]。目前冲击波测试中超压值的粗大误差判别还没有统一的规定要求。根据GJB 6390.3—2008面杀伤导弹战斗部静爆威力实验方法8.3节建议,实测值可采用3σ准则进行粗大误差计算。在实际工程中受到测试样本数量的制约,一般情况下会选用Grubbs准则对超压值进行剔除粗差处理。
在实际测试中,由于壳体破裂非均匀、装药位置、现场风速、近地冲击波场不规则反射叠加等问题,爆炸冲击波场具有非均匀的特点[3]。这也导致相同比例距离下捕获数据的超压值不完全服从正态分布,存在取值范围较为极端的‘好值’,因此在采用基于统计的3σ、Grubbs准则剔除粗差时会出现一定的误判情况。同时3σ和Grubbs准则都对最小样本数量有一定的要求,受测试环境恶劣的影响很有可能出现只有极少数测点捕获到数据无法进行粗差判别的情况。因此,本文提出归一化相似度判别法作为3σ,Grubbs粗大误差判别准则的一个补充以解决上述问题。
1 冲击波数据粗大误差来源
冲击波测试时超压数据的粗大误差主要来源于两个方面,一方面是测试环境发生剧烈变化导致的粗大误差,例如爆炸产生的热冲击[4]、强光、机械振动[5]导致的传感器寄生效应[6]。爆炸产生的地震波与传感器安装钢板上的应力波共同作用在传感器上,会导致传感器因为振动产生寄生输出,在波形中表现为高频的毛刺。硅片裸漏的压阻传感器受爆炸光影响较大,闪光响应可能会在超压峰值区域叠加正负随机的电压输出,在波形中表现为出现跳变的极端值[7]。测试环境剧烈变化也包括爆炸产生的强电磁场[8-9]对采集系统的干扰;战斗部的破片、场地内的碎屑、石子等击中传感器或传感器的安装钢板导致强冲击振动,被打到的测点在击中时刻后的波形会淹没在杂乱信号中无法辨别。
另一方面是人为因素导致的粗大误差。在静爆场地布设时传感器至爆心的距离、传感器安装钢板的水平角度都会对测点超压值产生大小的影响;同时数据读取错误、灵敏度表对应错误等人工操作也会导致测试数据出现粗大误差。
2 超压值的粗差判别方法
在对冲击波超压值进行数据处理时,应结合测试记录与数据波形剔除由于环境突变等物理因素或操作不规范等人为因素导致的粗大误差,但使用人工方式确定‘好值’挑拣剔除粗大误差在效率上无法满足数据的处理要求,同时缺乏量化标准,在工程中需引入一定的准则、算法对粗大误差值进行剔除。
2.1 基于统计的误差判别准则
Grubbs准则以样本x呈正态分布为前提,首先确定显著性水平α,得到置信概率P,根据Grubbs检验表得到当前样本数量对应的临界值Gp,计算样本的标准差σ(x)找到样本剩余误差绝对值的最大值,如果该值大于等于标准差与临界值的乘积,可判定该值为粗大误差,剔除后对剩余样本重新进行上述检验直到剩余样本不含粗大误差为止。
标准差(贝塞尔)公式:
(2)
Grubbs检验法公式:
(3)
式中: n为样本个数;为第i个样本值;为样本算数平均值;vi为第i个样本的剩余误差;Gp为格拉布斯临界值。当样本数小于25个时,显著性水平α的值选为0.01[10],对应的置信概率为99%。Grubbs检验对样本数量最低要求为3个。
2.2 归一化相似度判别法
由于冲击波场的非均匀性,实测得到的超压峰值通常分散度较大。存在采用统计方法的粗差判别准则时将部分超压峰值过于极端,但数据波形正常的测点值剔除的情况。同时也存在因为环境因素过于恶劣,导致捕获数据低于3个时,Grubbs准则无法对波形进行粗差剔除的情况。基于以上情况,本研究提出了一种归一化相似度判别法,该方法将归一化的理论超压曲线与实测波形在超压峰值到达时刻后一段时间内的波形相似度作为该测点超压值是否为粗大误差的标准。
欧几里得平均距离(MEM)公式:
(4)
归一化后实测波形序列与理论超压曲线的相似度采用欧几里得平均距离(MEM)作为评价指标,见式(4)。式中n为序列取点的个数; PTi为理论超压序列i点对应的值; Pi为实测超压数据i点对应的值。归一化相似度判别法的取值范围在[0,1]之间,越接近0波形相似度越高,越接近1波形相似度越低,经过对多组样本的实验将0.3作为粗大误差判别的阈值,当计算结果大于0.3时,可以认为该波形的超压峰值属于粗大误差。
理论超压曲线计算需要首先根据Kinney-Grahame公式计算测点对应比例距离下的超压峰值,根据TNT爆炸冲击波正压时间修正公式[11]计算正压时间,将超压峰值ΔP正压时间τ+与对应的衰减系数代入Friedlander经验拟合公式中得到理论超压值-时间曲线。
Kinney-Grahame公式
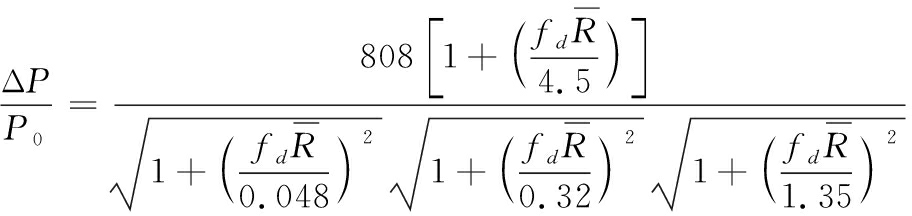
(5)
(6)
TNT正压时间修正公式
(7)
Friedlander修正公式
(8)
式(5)~式(8)中:ΔP为超压峰值![]() 为比例距离;p0为测试环境气压;pair为标准大气压,取0.101 3 MPa; T0为测试环境温度; Tair为标准温度288.16 K; τ+为正压作用时间(ms); m为装药量(kg); b为衰减系数由超压峰值ΔP决定。
为比例距离;p0为测试环境气压;pair为标准大气压,取0.101 3 MPa; T0为测试环境温度; Tair为标准温度288.16 K; τ+为正压作用时间(ms); m为装药量(kg); b为衰减系数由超压峰值ΔP决定。
考虑到爆炸场存在的高温、破片与振动冲击等因素,在冲量动态加载至准静态加载区域[12]即超压波形部分指数衰减区会含有大量的环境噪声。这些噪声与超压波形叠加对测试数据与理论曲线的相似度造成一定的影响,因此本方法选取超压峰值后50 μs~1 ms之间受影响相对较小的区域进行相似度研究。归一化相似度判别法考察实测波形是否贴合理论曲线的衰减规律,可以针对单一数据进行处理,剔除毛刺过大、振荡剧烈、压力过程不以指数形式衰减等与理论曲线似度较低的数据。
3 实测数据分析与处理
3.1 样本分析
某次实验在比例距离3.065 m/kg1/3处测得的超压值如表1所示,并使用Kinney-Grahame经验公式计算出了比例距离在2.810~3.831 m/kg1/3间的部分理论超压值,如表2。
表1 比例距离3.065 m/kg1/3处超压值
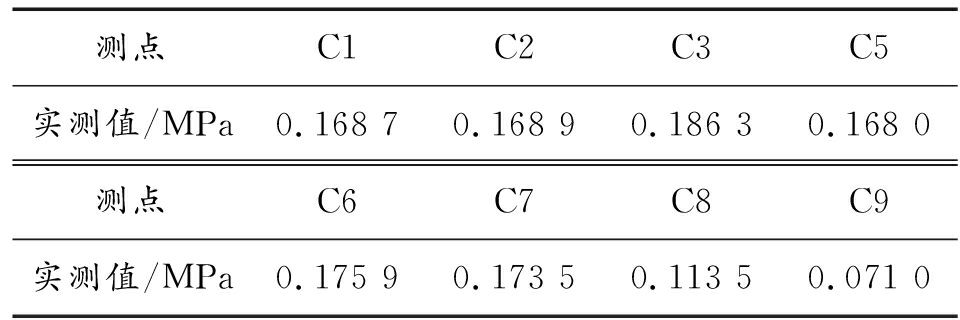
测点C1C2C3C5实测值/MPa0.168 70.168 90.186 30.168 0测点C6C7C8C9实测值/MPa0.175 90.173 50.113 50.071 0
表2 不同比例距离下超压理论计算值
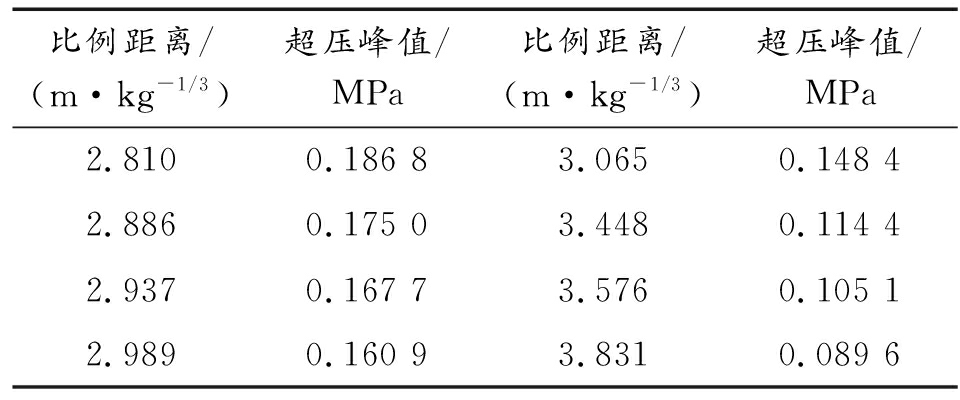
比例距离/(m·kg-1/3)超压峰值/MPa比例距离/(m·kg-1/3)超压峰值/MPa2.8100.186 83.0650.148 42.8860.175 0 3.4480.114 4 2.9370.167 7 3.5760.105 12.9890.160 93.8310.089 6
结合表1与表2数据可以发现,C组样本的均值为 0.145 2;标准差为0.039 8;极差为1.179 3 MPa;该组样本的离散程度较大,是爆炸冲击波不均匀性的典型表现。C1-C7样本普遍高于均值,其中C1、C2、C5测点峰值接近2.937 m/kg1/3处理论值,C6、C7测点接近2.886 m/kg1/3处理论值,C3为该组样本的最大值,对应比例距离2.810 m/kg1/3处理论值。C8、C9样本峰值偏小,其中C9样本作为最小值比样本均值低51.1%,接近3.831 m/kg1/3处理论值。与C测点的理论值(3.065 m/kg1/3处)相比,C3测点值高25.5%,C8测点值低23.5%,C9测点值低52.16%,从统计的角度看这3个测点值与理论值的偏差较大,是可能的疑似粗大误差值。
为更好地分析测点数据,根据式(5)~式(8)计算了3.065 m/kg1/3处理论超压值,图1中P-t为理论超压曲线。可以看出C测点的实测超压C1至C7波形与理论曲线较为贴近,符合冲击波信号上升沿陡峭、超压峰值高、压力衰减过程呈指数衰减的特征。虽然C1在超压峰值后出现短暂尖峰,C6与C7在正压区间动态加载区域有较大振荡,但没有影响整体波形的衰减趋势。C4测点被破片击中,没有捕获到波形数据。
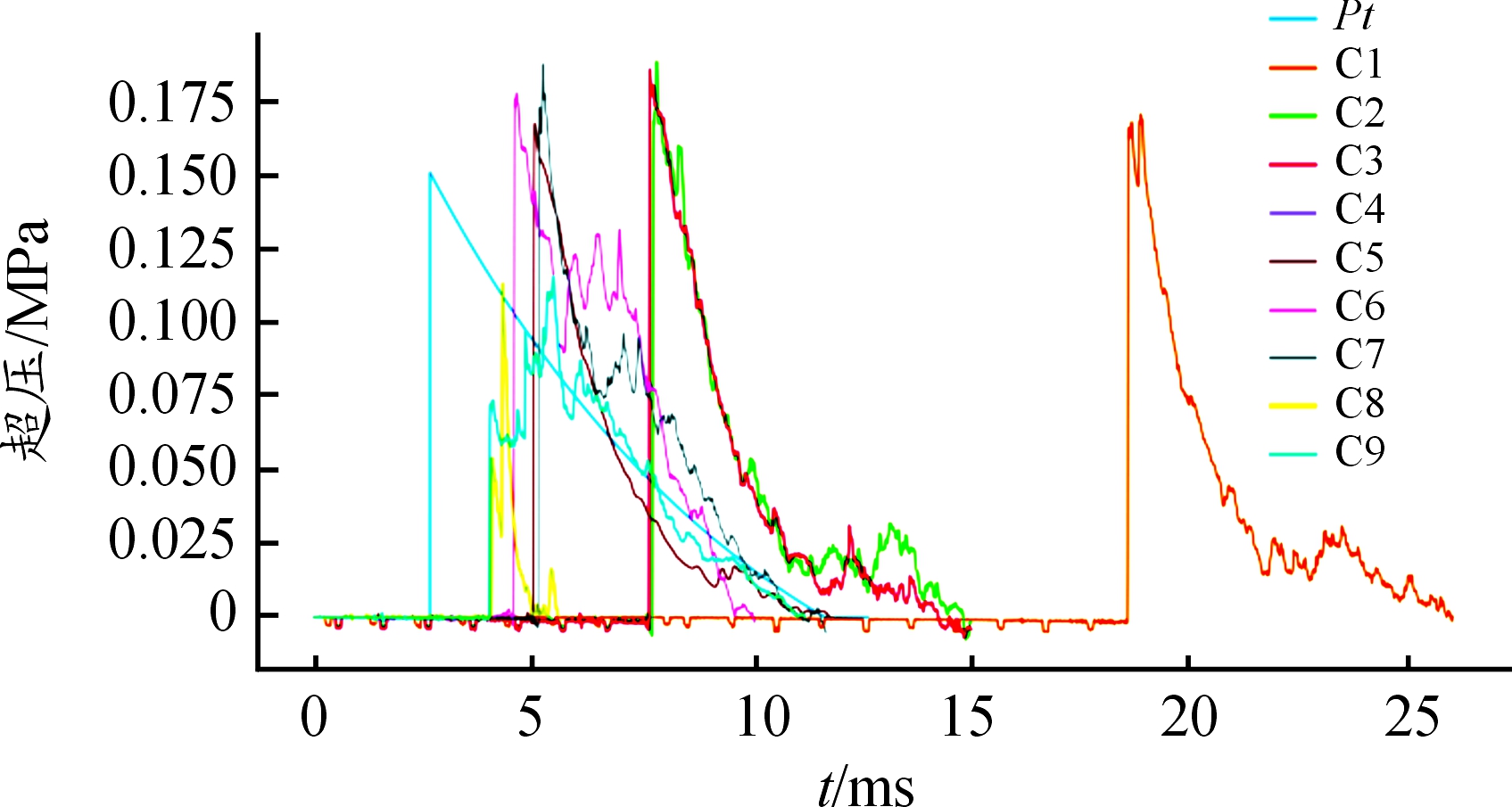
图1 理论超压曲线与实测超压波形
C8测点波形虽然也具有衰减形式,但是峰值后大部分区段衰减率极快且不符合指数衰减形式。与理论曲线Pt正压时间长达9.013 ms相比该测点正压时间仅为1.249 ms,且幅值较低,可以确认该波形并不符合冲击波特征。C9测点在波形上升沿到来19 μs后出现第一个峰值,波形在振荡上升中于上升沿1 469 μs后出现最大值,随后呈指数形式衰减。理论上冲击波上升沿在1~2 ns之间[13],受传感器响应时间限制[14],一般超压峰值取冲击波上升沿到达后100 μs内的最大值作为超压峰值[15]。从波形的超压峰值时刻到正压结束时刻来看,C9测点捕获的是一段受损的冲击波波形,其中超压峰值部分很有可能受到环境因子影响未能完整捕获。
结合表1表2数据以及图1之波形分析,可以初步确定C3测点值是冲击波场非均匀性的一种体现,C8、C9测点值是粗大误差测量值。
3.2 样本粗差判别
对C组的数据分别采用Grubbs准则与归一化相似度判别法进行样本数据的粗大误差剔除处理。首先采用Grubbs判定准则,显著性水平α取0.01,对超压值数据进行循环剔除,判定结果统计在表3中。
表3 Grubbs准则剔除表
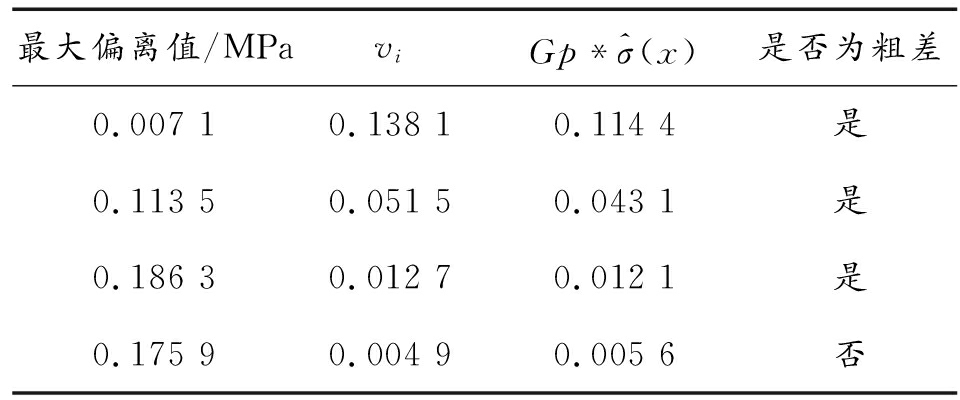
最大偏离值/MPaviGp*^σ(x)是否为粗差0.007 10.138 10.114 4是0.113 50.051 50.043 1是0.186 30.012 70.012 1是0.175 90.004 90.005 6否
Grubbs准则剔除了3个偏离值最大的数据,分别为C9、C8、C3。采用Grubbs准则,虽然可以剔除C8、C9测点,但同时也剔除了波形正常、数据有效的C3测点。
采用归一化相似度判别法对超压数据进行处理,考虑到C测点距离爆心较远,波形衰减区叠加环境噪音较小,因此取超压峰值后400 μs内的波形研究实测波形与理论波形的相似度。数据的采样频率是1 MHz,400 μs对应在超压序列中取点个数n=400。
截取段实测值与理论值归一化波形对比如图2所示,归一化处理实现了超压波形的无量纲化,避免了取值范围比较极端的冲击波被剔除,同时保留了波形的衰减特征用于辨别与冲击波相似度较低的超压波形。将归一化相似度法计算结果统计在表4,可以看出经过处理的C组数据中C1~C7波形的与理论曲线Pt的贴合度较好,经归一化相似度判别法计算后的取值较小,可以认为C1~C7波形的超压峰值不是粗大误差值。C8、C9归一化波形与理论曲线Pt的相似度较低,归一化相似度计算值大于阈值0.3,因此判别C8、C9测点的超压峰值属于粗大误差。
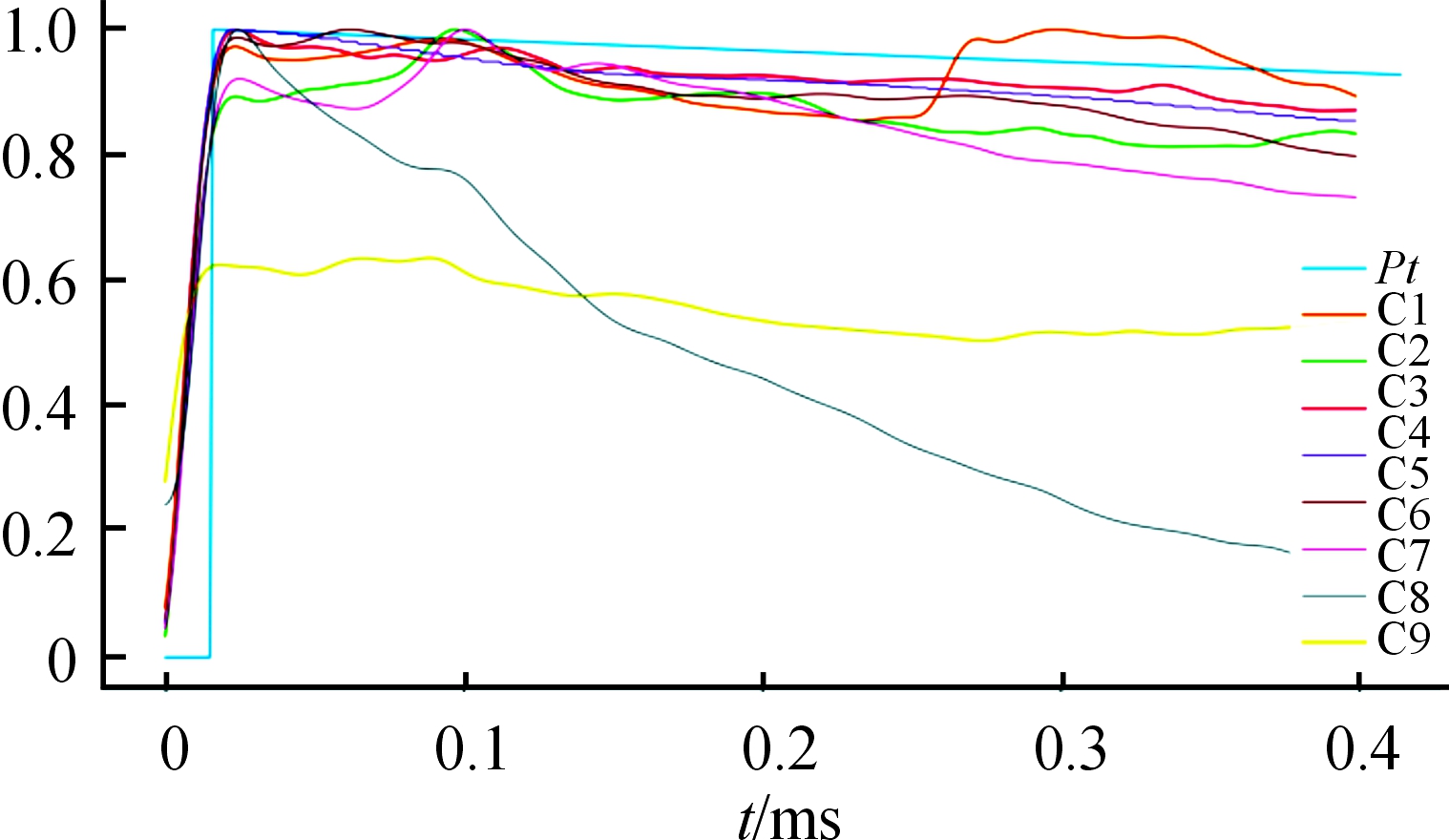
图2 理论值与实测值归一化波形
表4 归一化相似度欧氏距离
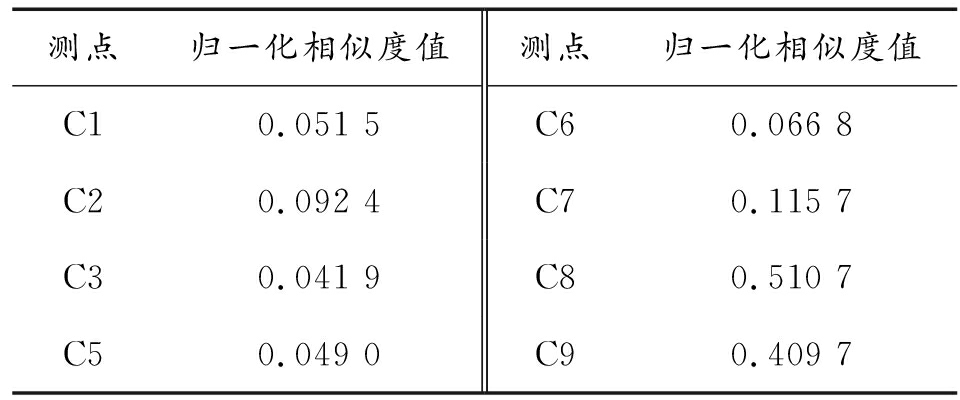
测点归一化相似度值测点归一化相似度值C10.051 5C60.066 8C20.092 4C70.115 7C30.041 9C80.510 7C50.049 0C90.409 7
4 结论
本文提出了一种归一化相似度粗大误差判别法。采用归一化相似度判别法与Grubbs准则对实测数据进行剔除粗差处理,能够较好地剔除与冲击波相似度低的粗大误差值,保留符合冲击波特征的值。归一化相似度判别法可以针对单一样本进行粗差剔除,在实际工程应用中,可以达到较好的处理效果。
[1] 刘艳,于露.粗大误差判定准则在靶场试验数据预处理中的应用[J].长春理工大学学报(自然科学版),2018,41(03):139-142.
[2] 张晓光.冲击波超压场重建技术研究[D].太原:中北大学,2018.
[3] 姬建荣,苏健军,张玉磊,等.不同量级TNT爆炸冲击波正压时间的试验研究[J].科学技术与工程,2018,18(05):202-206.
[4] SELESOVSKY J,KRUPKA M.The using of LS-DYNA for the simulation of heat transfer in explosives[J].Journal Of Computer-Aided-Materials Design,2007,14(02):317-325.
[5] MURARI P R,ARVIND K M,HEMANT A.Blast vibration dependence on total explosives weight in open-pit blasting[J].Arabian Journal of Geosciences,2020,13(13).
[6] 李琛.冲击波压力传感器寄生效应抑制方法研究[D].南京:南京理工大学,2017.
[7] 杜红棉,祖静,张志杰.压阻传感器8530B闪光响应规律研究[J].测试技术学报,2011,25(01):78-81.
[8] LI Jianqiao,HAO Li,LI jian.Theoretical modeling and numerical simulations of plasmas generated by shock waves[J].Science China Technological Sciences,2019,62(12):2204-2212.
[9] MKRTCHYAN A H,SH L,GRIGORY.Shock wave generated megahertz radiation of atmosphere[J].IEEE Transactions on Plasma Science,2019,47(1):118-120.
[10] 熊艳艳,吴先球.粗大误差四种判别准则的比较和应用[J].大学物理实验,2010,23(01):66-68.
[11] 王芳,冯顺山,俞为民.“超压—冲量”毁伤准则及其等毁伤曲线研究[J].弹箭与制导学报,2003(S2):126-130.
[12] 朱坚民,宾鸿赞,王中宇,等.测量数据粗大误差的非统计判别[J].华中理工大学学报,2000(04):17-19.
[13] Л.П.奥尔连科.爆炸物理学[M].北京:科学出版社,2011:51-69.
[14] 杜红棉,祖静.常用冲击波压力传感器动态特性实验研究[J].弹箭与制导学报,2011,32(2):214-216.
[15] 祖静,马铁华,裴东兴.新概念动态测试[M].北京:国防工业出版社,2016:291-297.