整车悬架系统振动控制特性的时域和频域仿真分析,均需要以一定的路面激励为输入,才能得到悬架系统各状态量的响应特性。随机路面激励可以反映出悬架系统各条件下的综合性能,运用最为广泛。如对车辆悬架系统施加随机路面激励(等级路面激励),通过时域分析可以得到车辆悬架系统性能评价指标的统计特性[1],通过频域分析可以计算出车辆悬架系统各响应量的功率谱密度[2]。由此可知,建立合理准确的路面激励模型,对车辆悬架系统动力学特性分析有着重大的影响。目前国内外学者已经设计出了多种随机路面激励模型的建模方法,如谐波叠加法[3]、滤波白噪声法[4]、ARMA模型法[5]、傅里叶逆变换法[6]等。考虑上述各建模方法的原理和特点,在此选取容易计算并实用性强的滤波白噪声法建立随机路面激励模型。
1 单轮时域路面激励模型
作为车辆悬架系统外部输入的随机路面激励,主要采用路面功率谱密度来描述其统计特性[7],其拟合表达式为[8-9]:
(1)
对于车辆悬架系统动力学特性分析而言,车辆行驶速度也是需要考虑的一个因素,将空间频率功率谱密度Gxr(n)转换为时间频率功率谱密度Gxr(f),可以引入车速这一变量。当车辆以一定速度v行驶于空间频率为n的路面上时,其等效的时间频率f可表示为:
f = vn
(2)
由此可推导出空间频率功率谱密度和时间频率功率谱密度的转换公式为:
(3)
当w = 2时,有时间频率功率谱密度表达式为:
![]()
(4)
在式(1)中,当n→0时,Gxr(n) →∞;在式(3)、式(4)中,当f→0时,Gxr(f) →∞,这不符合工程实际情况[10]。因此,在此考虑空间下限截止频率nmin和时间下限截止频率fmin = vnmin,则有:
![]()
(5)
(6)
滤波白噪声法生成的路面激励模型是通过一阶滤波白噪声系统来描述的。一阶滤波白噪声系统属于单自由度线性系统,仅有一个激励量W(t)和一个响应量xr(t),则依据随机振动理论,响应量和激励量在频域内的关系和其功率谱密度之间的关系为:
xr(f)=Hxr~W(f)W(f)
(7)
Gxr(f)=![]() GW(f)
GW(f)
(8)
一阶滤波白噪声系统的时域一般表示为:
(9)
对式(9)变换可得:
(10)
对式(10)进行傅里叶变换可得:
xr(f)(2πf·j+a)=bW(f)
(11)
由式(7)可以得到一阶滤波白噪声系统的频响函数为:
(12)
![]()
(13)
由式(8)可以得到一阶滤波白噪声系统响应量的功率谱密度为:
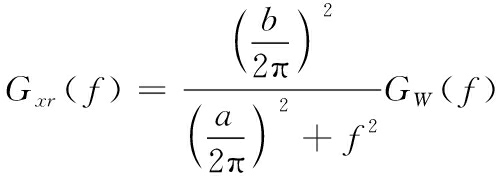
(14)
由文献[10]可知,标准高斯白噪声的功率谱密度为1,即:
GW(f)=1
(15)
于是有一阶滤波白噪声系统响应量的功率谱密度为:

(16)
对比式(6)和式(16),可以得到一阶滤波白噪声系统参数为:
(17)
至此,可推导出基于滤波白噪声法生成的路面激励模型为:
(18)
2 左半车时域路面激励模型
若由式(18)确定出的由单位白噪声Wrlf(t)生成的左前轮时域路面激励为xrlf(t),则同侧左后轮的时域路面激励xrlr(t) 可表示为:
xrlr(t)=xrlf(t-τ)
(19)
(20)
式(20)中,Lfr为车辆前后轮轮距。
由傅里叶变换可将式(19)转化为:
xrlr(ω)=xrlf(ω)e-jωτ
(21)
则车辆左前轮路面激励到左后轮路面激励的传递函数可表示为:
(22)
采用2阶Pada近似计算,可得到传递函数为:
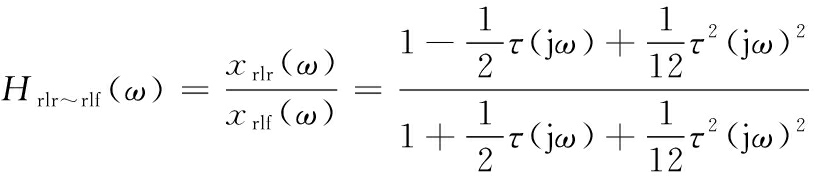
(23)
将其转化为车辆左前轮路面激励和左后轮路面激励相关性的状态方程和输出方程为:
(24)
Yfr=CfrZrq+DfrUx
(25)
基于式(18),可以得到以滤波白噪声作为输入、左前轮激励和左后轮激励作为输出的左半车辆路面的过渡方程、状态方程和输出方程为:
(26)
(27)
Yfr=CfrXfr
(28)
3 前半车时域路面激励模型
若有由单位白噪声Wrlf(t)生成的左前轮时域路面激励xrlf(t),则其(自)功率谱密度可表示为Gxrlf(ω),w = 2πf。假设有由单位白噪声Wrrf(t)生成的右前轮时域路面激励及其(自)功率谱密度分别为xrrf(t)和Gxrrf(ω),由于在同一道路上两条不同车轮轨迹的路面不平度统计特性相同,即左前轮路面激励与右前轮路面激励的自功率谱密度是相同的,则有:
Gxrrf(ω)=Gxrlf(ω)
(29)
由式(15)可知,单位白噪声Wrlf(t)与Wrrf(t)具有相同的功率谱密度,即:
GWrlf(ω)=GWrrf(ω)=1
(30)
则由式(7)和式(8)可知,左前轮激励量Wrlf(t)和响应量xrlf(t)在频域内的关系和其功率谱密度之间的关系可表示为:
xrlf(ω)=Hxrlf~Wrlf(ω)Wrlf(ω)
(31)
![]()
(32)
同理右前轮激励量Wrrf(t)和响应量xrrf(t)在频域内的关系和其功率谱密度之间的关系可表示为:
xrrf(ω)=Hxrrf~Wrrf(ω)Wrrf(ω)
(33)
(34)
对比式(29)和式(30)可以得到左前轮和右前轮频率响应函数之间的关系为:
Hxrlf~Wrlf(ω)=Hxrrf~Wrrf(ω)
(35)
上述2条不同车轮轨迹的路面不平度的随机过程存在互谱,即左前轮路面激励与右前轮路面激励是相干的,在通过左前轮建立右前轮时域路面模型时需要考虑其相干性。假设有左前轮时域路面激励到右前轮时域路面激励的互功率谱密度为Gxrlfxrrf(ω),令左前轮时域路面激励xrlf(t)为系统的输入,右前轮时域路面激励xrrf(t)为系统的输出,则根据随机振动理论可知,系统输入与系统输出之间的互功率谱密度与系统输入的自功率谱密度之间的关系为:
Gxrlfxrrf(ω)=Hxrrf~xrlf(ω)Gxrlf(ω)
(36)
车辆左前轮时域路面激励与右前轮时域路面激励的相干函数可以定义为:
(37)
考虑式(29)可得:
Gxrlfxrrf(ω)=cohxrlfxrrf(ω)Gxrlf(ω)
(38)
对比式(36)和式(38)可得:
|Hxrrf~xrlf(ω)|=cohxrlfxrrf(ω)
(39)
目前国内外学者已经根据实际测量的路面不平度数据拟合建立了多种相干函数的数学模型。在此设计考虑路面激励频率、车辆轮距和车辆行驶速度的相干性函数的数学模型,该模型与测量曲线相当接近,并且结构形式简单便于计算,可表示为:
(40)
式(40)中: ρ为拟合系数; Llr为车辆左右轮轮距。
由式(40)可知,该模型可以表征路面激励频率、车辆轮距和车辆行驶速度对相干性的影响,与上述实测分析结果趋势一致。
考虑车辆左前轮时域路面激励与右前轮时域路面激励的相干性,可将Wrrf(t)定义为Wrlf(t)和另一不相干的单位白噪声Wrri(t)的双输入系统的响应量,可知其功率谱密度为:
GWrri(ω)=1
(41)
假设有系统输出Wrrf(t)与两个输入Wrlf(t)、Wrri(t)之间的频率响应函数分别为HWrrf~Wrlf (ω)、HWrrf~Wrri (ω),则有激励量与响应量在频域内的关系和其功率谱密度之间的关系可表示为:
Wrrf(ω)=HWrrf~Wrlf(ω)Wrlf(ω)+HWrrf~Wrri(ω)Wrri(ω)
(42)
(43)
将式(42)代入式(33),可得:
xrrf(ω)=Hxrrf~Wrrf(ω)Wrrf(ω)=
Hxrrf~Wrrf(ω)HWrrf~Wrlf(ω)Wrlf(ω)+
Hxrrf~Wrrf(ω)HWrrf~Wrri(ω)Wrri(ω)
(44)
考虑式(35)有:
xrrf(ω)=Hxrlf~Wrlf(ω)HWrrf~Wrlf(ω)Wrlf(ω)+
Hxrrf~Wrrf(ω)HWrrf~Wrri(ω)Wrri(ω)=
HWrrf~Wrlf(ω)xrlf(ω)+
HWrrf~Wrri(ω)Hxrrf~Wrrf(ω)Wrri(ω)
(45)
考虑由左前轮时域路面激励xrlf(t)到右前轮时域路面激励xrrf(t)的频率响应函数为Hxrrf~xrlf (ω),则有:
HWrrf~Wrlf(ω)=Hxrrf~xrlf(ω)
(46)
由式(39)可知:
|HWrrf~Wrlf(ω)|=cohxrlfxrrf(ω)
(47)
考虑式(30)和式(41),可将式(43)改写为:
![]()
(48)
可将频率响应函数HWrrf~Wrlf (ω)和HWrrf~Wrri (ω)表示为:
![]()
(49)
![]()
(50)
式(49)、(50)中,n为系统阶数。为了简化计算,可以将其近似为2阶系统,则有:
![]()
(51)
(52)
由此,可将式(51)和式(52)转化为计算车辆右前轮路面激励单位白噪声Wrrf(t)的状态方程和输出方程,有:
(53)
Yrw=CrwZrw+DrwUw
(54)
基于式(18),可以得到以滤波白噪声作为输入、左前轮激励和右前轮激励作为输出的前半车辆路面的过渡方程、状态方程和输出方程为:
(55)
(56)
Ylr=ClrXlr
(57)
4 整车时域路面激励模型
综合上述前3节的分析,可基于滤波白噪声法建立车辆4轮时域路面激励模型。由式(18)、式(26)、式(27)、式(28)、式(55)、式(56)和式(57)可得,以滤波白噪声作为输入,左前轮激励、右前轮激励、左后轮激励和右后轮激励作为输出的整车路面的过渡方程、状态方程和输出方程分别为:
(58)
![]()
(59)
Yr=CrXr
(60)
考虑将过渡向量与状态向量扩展为增广状态向量,有:
(61)
则可以得到由增广状态向量建立的四轮时域路面激励模型的状态方程和输出方程分别为:
![]()
(62)
(63)
5 路面激励模型仿真
对第4节所构建的四轮时域路面数学模型进行仿真分析验证,得到4个车轮路面激励输入的时域信号如图1所示。

图1 路面激励输入时域信号曲线
左前轮与左后轮路面激励输入的时域信号如图2所示。由图2可以看出,2个路面激励输入幅值相同,有一定的相位差,仿真结果与实际路面激励输入相符。
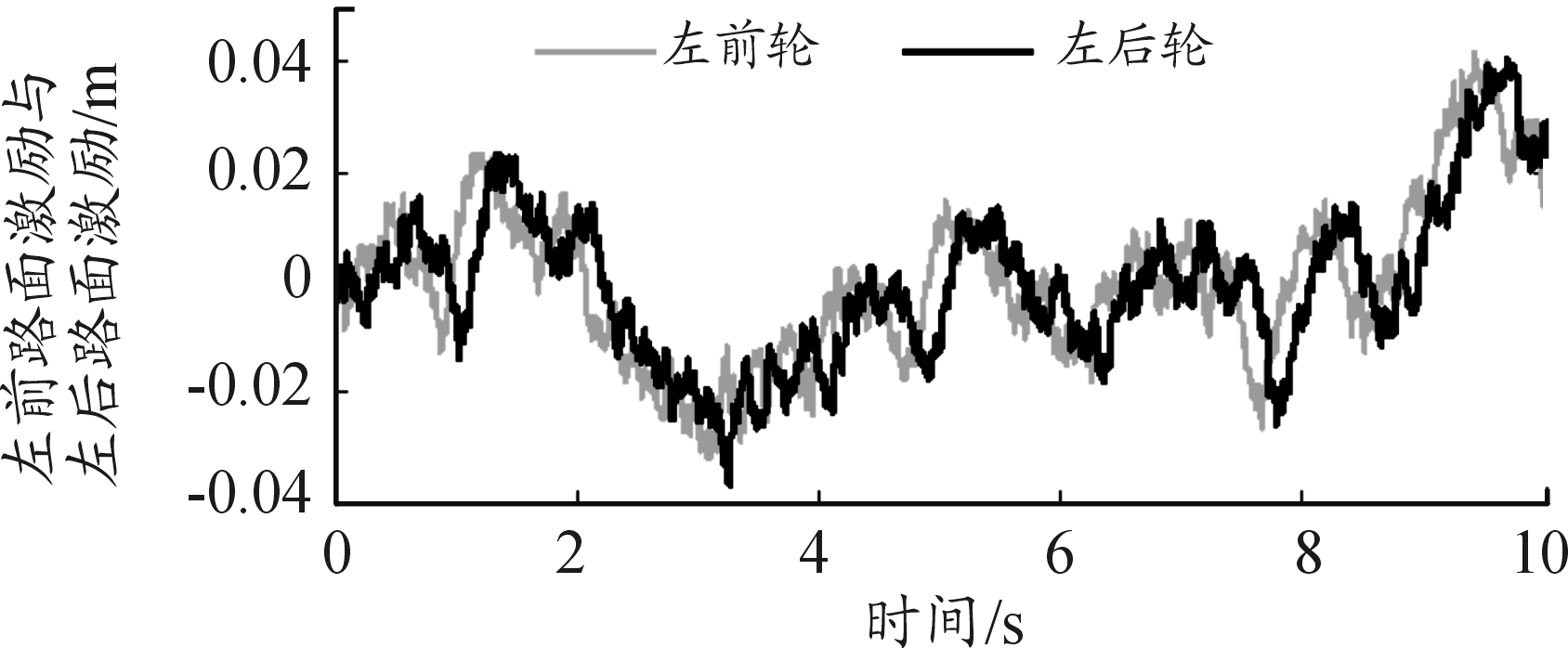
图2 左前轮与左后轮路面激励输入时域信号对比
左前轮与右前轮路面激励输入的时域信号对比如图3所示。由图3可以看出,两个路面激励输入相近。在低频时的路面激励有几乎相同的幅值和相位,而高频时的相关性较差,仿真结果与实际路面激励输入相符。

图3 左前轮与右前轮路面激励输入时域信号对比
左前轮与右前轮路面激励输入的相干性如图4所示。由图4可以看出,仿真得到的车辆左前轮与右前轮路面激励输入的相干性与式(40)理论模型和式(49)近似模型相一致,符合实际路面激励低频相干性强、高频相干性弱的特点,并与图3的时域分析结果一致。
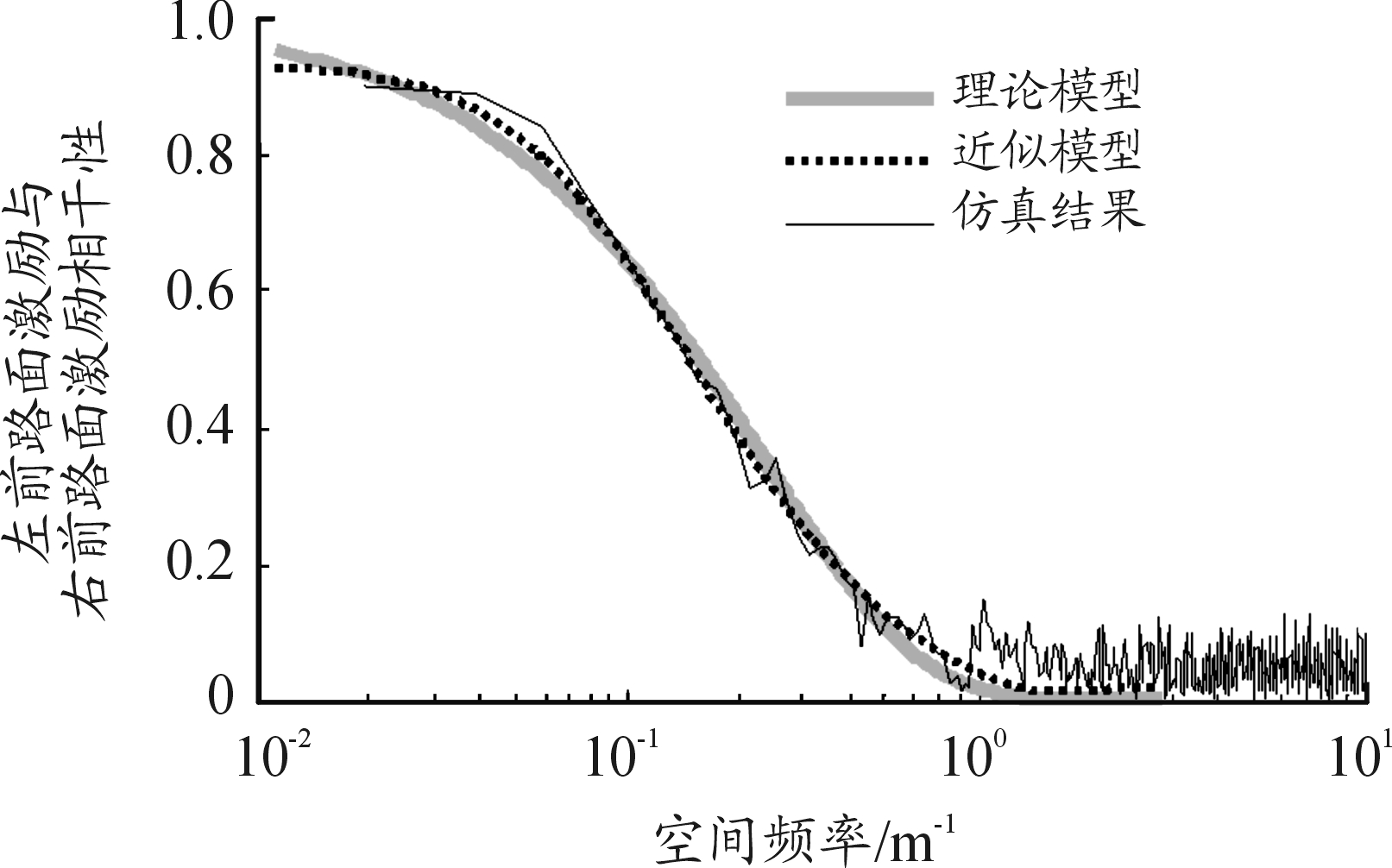
图4 左前轮与右前轮路面激励输入的相干性
6 结论
基于滤波白噪声法建立了单轮时域路面激励模型;在此基础上,考虑延时特性建立了后轮时域路面激励模型,以此给出左半车时域路面激励模型;考虑相干性建立了右轮时域路面激励模型,以此给出前半车时域路面激励模型;综合构建出车辆四轮时域随机路面激励模型,通过时域和频域的仿真分析验证了该整车四轮时域路面激励模型的有效性,说明了该路面激励模型可以用于整车悬架系统振动控制特性仿真分析。
[1] GHASEMALIZADEH O,TAHERI S,SINGH A,et al.Semi-active suspension control using modern methodology:a comprehensive comparison study[C]//Proceedings of the 2014 Ground Vehicle Systems Engineering and Technology Symposium (GVSETS),2014.
[2] 郭孔辉,隋记魁,宋晓琳,等.高速车辆横向减振器模糊天棚半主动控制研究[J].工程设计学报,2012,19(03):174-181.
[3] PARAFOROS D S,GRIEPENTROG H W,VOUGIOUKAS S G.Country road and field surface profiles acquisition,modeling and synthetic realisation for evaluating fatigue life of agricultural machinery[J].Journal of Terramechanics,2016(63):1-12.
[4] JIN Y F,LUO X.Stochastic optimal active control of a half-car nonlinear suspension under random road excitation[J].Nonlinear Dynamics,2013,72(01):185-195.
[5] 谢伟东,王磊,佘翊妮,等.随机信号在路面不平度仿真中的应用[J].振动、测试与诊断,2005,25(02):126-130.
[6] 任宏斌.阻尼连续可调油气悬架及其控制技术研究[D].北京:北京理工大学,2016.
[7] 余志生.汽车理论[M].5版.北京:机械工业出版社,2014.
[8] 任宏斌,陈思忠,吴志成,等.车辆左右车轮路面不平度的时域再现研究[J].北京理工大学学报,2013,33(03):257-259.
[9] 陈杰平,陈无畏,祝辉,等.基于Matlab/Simulink的随机路面建模与不平度仿真[J].农业机械学报,2010,41(03):11-15.
[10] 陈绍维.微型客车平顺性建模、仿真及参数匹配研究[D].长春:吉林大学,2011.