大数据时代,网络上的数据呈现了爆炸性的增长,推荐算法能够帮助用户在海量数据中快速、有效、准确地获取感兴趣及有用的信息。用户的个性化需求不断增长,各种个性化推荐系统借助大数据得以实现,各个公司也致力于开发各种推荐算法系统,这样可以让用户对产品着迷,有效提升用户对产品的粘性,增加用户的忠诚度。
传统的推荐算法主要可以分为3种:基于内容的推荐算法(content-based recommendation)、协同过滤推荐算法(collaborative filtering recommendation)和基于知识的推荐算法(knowledge-base recommendation)[1]。近些年来,深度学习在计算机视觉、人脸识别、自动语音识别、自然语言处理、自动驾驶等领域取得了突破性的进展。基于深度学习的推荐算法可以在各个领域中都被采用,比如在电子商务中推荐用户可能喜爱的商品;在最近极其火爆的短视频中推荐用户喜爱的视频;在线上着装购物中为用户推荐穿着搭配方案等[2]。基于深度学习的推荐算法本质是图片分类,通过不同图片的标签,对深度学习的神经网络进行训练,根据标签对图片进行分类[3]。
本文提出了一种基于深度学习的细粒度图像推荐算法。细粒度图像算法能够较好地感知图片的细节,如形状、材质、纹理等特性。因此,细粒度相对于对粗粒度的大类别,可以进行更加细致的子类推荐。本算法首先使用数据集分类模型对杂乱无章的数据集进行分类,然后使用改进KNN聚类算法对数据集进行初选,再通过深度学习VGG-16网络进行训练,并在经典数据集中对算法进行了验证。实验结果表明,和其他经典推荐算法相比,该算法的正确率有明显提高。
1 图像推荐方法原理
本文所提出的图像推荐算法包括3个步骤:数据集分类、数据集初选和数据集训练,其中数据集训练是推荐算法的核心。
数据集分类采用三元组模型实现,作用是将训练集的图片生成三元组为单位的训练集。如何有效地生成三元组训练集,会很大程度影响最终结果。此外,可以通过不同的组合形成不同的三元组,变相增加了整个数据集的大小,使得数据量相对较小的数据集也能用深度学习网络训练出不错的效果。在生成三元组过程中使用了随机选取图片的方法,不可避免地会出现损失特别小、很难处理的三元组,从而阻碍了网络的训练,因此需要对三元组数据集进行初选。
数据集初选采用改进KNN算法实现,能够在数据集中选取更加有效的图像。KNN算法(k-nearest neighbors,KNN)又称K最近邻算法,是一种基于机器学习的分类算法,工作原理是利用训练数据对特征向量空间进行划分,并将划分结果作为最终算法模型[4-6]。本文采用一种新的数据预处理机制来改进算法,即将特征参数类相关度概念引入KNN分类,能够提高算法的准确性和效率。
数据集采用深度学习进行训练。这部分作用是将图片映射成特征向量,即通过大量数据集训练优化参数得到,是本文推荐算法的核心。深度学习(deep learning)是基于学习数据特征内容的算法,使用多层非线性处理单元进行特征提取和转换[7-8],每个连续层使用前一层的输出作为输入。深度学习选用VGG网络,它是较为优秀的图像分类方法,在各种场合都有使用[9-10]。VGG有2个版本VGG-16和VGG-19分别是16层网络和19层网络,本文选用的是VGG-16,与VGG-19相比有几乎完全相同的准确度,但是由于VGG-16网络结构层数少,运算速度更快一些[11]。
2 基于深度学习的图像推荐算法
2.1 三元组模型分类
在分类之前,引入一个概念,即如何定义2张图片的相似度。这里用到了欧几里得距离,是在m维空间中2个点之间的真实距离。在此模型中的公式为:
D(f(p1), f(p2))=![]()
(1)
式(1)中: p1、p2是图片; f 是映射函数,将图片映射成特征向量。当D(f(p1),(p2))值越小时,2张图片越相似。
数据集分类采用经典三元组模型,该模型训练学习的基本单元,包含3个图像:查询图像(anchor image),正面图像(positive image)和负面图像(negative image)。其中正面图像是与查询图像相近的图像,或者可以说是通过查询图像要推荐的图片;负面图像是与查询图像不相近的图片,或者是不希望通过查询图像推荐的图像。三元组模型的目标如图1所示,扩大查询图像与负面图像之间的距离,并减少与正面图像之间的距离。

图1 三元组模型的学习目标示意图
2.2 KNN改进算法
KNN改进算法是对三元组模型分类后的数据集进行初选,即在KNN中引入特征参数类相关度差异优化距离机制。
2.2.1 特征参数类相关度差异优化距离机制
特征参数ti相关度Corr(ti)的定义:设是训练样本集,它包含了n个不同类别的样本,这些类别分别用C1,C2,…,Cr,…,Cn表示,样本记为Xi(i=1,2,…,m)[12-14]。设Xi具有q个特征属性Ap(p=1,2,…,q),Ap具有v个特征参数ti(i=1,2,…,v),|ti|记为具有特征参数ti样本的个数,|tir|记为特征参数ti在Cr类样本中出现的次数,则特征参数ti的类相关度(期望信息)为:
(2)
式(2)中:![]() 为具有特征参数ti样本的概率;
为具有特征参数ti样本的概率;![]() 为特征参数ti在Cr中出现的概率; Diff(ti)熵值体现了特征参数ti对样本隶属的期望值,是特征参数ti对分类作用的不确定性的度量;e(ti)越小,ti对分类的作用越大。当|ti|=|tir|时,e(ti)→0,ti对样本隶属类r完全确定。以e(ti)为主体,当e(ti)=0时,
为特征参数ti在Cr中出现的概率; Diff(ti)熵值体现了特征参数ti对样本隶属的期望值,是特征参数ti对分类作用的不确定性的度量;e(ti)越小,ti对分类的作用越大。当|ti|=|tir|时,e(ti)→0,ti对样本隶属类r完全确定。以e(ti)为主体,当e(ti)=0时,![]() 值无意义,即特征参数ti对样本隶属类r明确,与样本的分布无关联。
值无意义,即特征参数ti对样本隶属类r明确,与样本的分布无关联。
样本间的距离d(X,Y)的定义为:
![]()
(3)
式(3)中:![]() 是样本Xi特征参数相关性的转化;
是样本Xi特征参数相关性的转化;![]() 是样本Xj特征参数相关性的转化。将特征参数类相关度值替代马氏距离机制中原数据的特征,并赋予相应的权重值以计算样本间的相似程度。由于特征参数相似性是分类训练器中潜在的关联关系,它的存在可以减少样本间距离的计算误差。因而,类相关度能有效地度量样本间特征的相似程度,进而最大程度地提取与待分样本相似的近邻样本,从而得到正确的分类结果。
是样本Xj特征参数相关性的转化。将特征参数类相关度值替代马氏距离机制中原数据的特征,并赋予相应的权重值以计算样本间的相似程度。由于特征参数相似性是分类训练器中潜在的关联关系,它的存在可以减少样本间距离的计算误差。因而,类相关度能有效地度量样本间特征的相似程度,进而最大程度地提取与待分样本相似的近邻样本,从而得到正确的分类结果。
2.2.2 特征参数类相关度优化距离的KNN改进算法
针对经典KNN算法,采用新的数据预处理机制改进算法,将特征参数类相关度概念引入KNN分类。大量的研究表明,训练数据的类别如果不再细分的话,类别数不是很多,特征参数的重复率也较高,尤其对于一些常用的数据更是如此。如果使用降维方法对数据进行相似度计算,会因为数据向量维数偏低或维数不适中而丢失过多、甚至重要的特征信息,从而影响分类效果。基于此因素考量,改进算法仍采用传统KNN算法中将训练集样本与待分样本的所有特征属性值均作为相似度计算参数的模式,主要通过优化距离机制,从根本上保证KNN分类的准确性及效率。
采用类相关度优化距离的KNN改进算法的实现:
输入:训练集与测试集合表示为(X1,Y1),(X2,Y2),…,(Xm,Ym),Xi∈Rm, Yi∈Zm。输出:测试集的类别标签 class(T)。
1) 根据式(2)计算训练集中每个样本及待分样本的所有特征参数对分类的相关度Diff,由Diff值向量化数据特征集,对样本参数进行相关度计算预处理,实现基于类相关度的样本特征提取,其中X=[X1,X2,…,Xm]2, Y=[Diff(t1),Diff(t2),…,Diff(tq)]T。
2) 使用式(3)计算待分样本与训练集各样本的距离。
3) 判断样本的类别归属。
按照x和xi的距离远近排序,得到最近的k个样本,根据这k个样本的类别得到x的类别。
2.3 VGG-16网络
数据集采用深度学习VGG-16网络进行训练,将图片映射成特征向量,通过大量数据集训练优化参数得到。VGG-16的深度学习网络原理如图2所示。
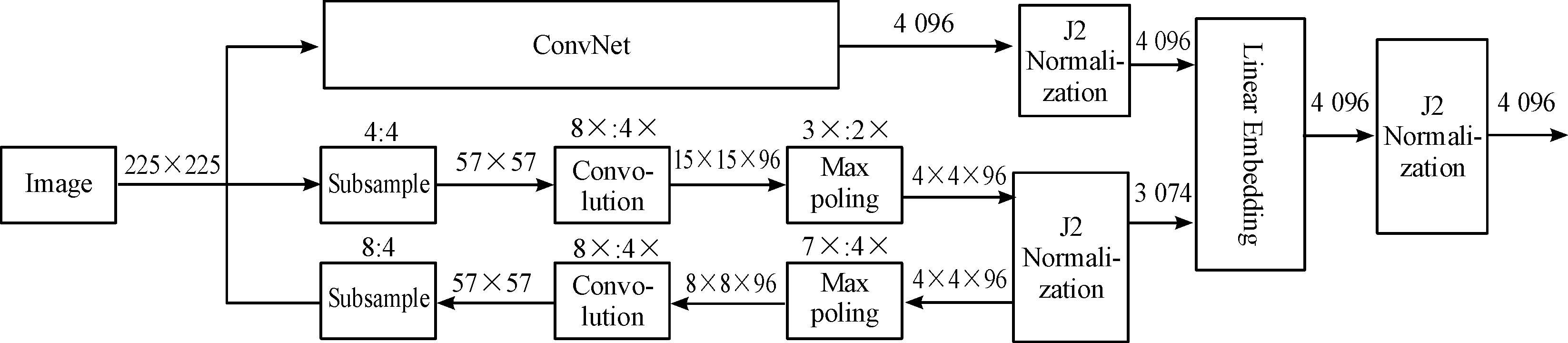
图2 VGG-16原理框图
VGG-16网络主要由图2中的ConvNet和2个较浅的卷积网络组成,这三者为平行结构[15-16]。ConvNet有多层卷积网络,其作用是捕获图片语义,而其他2个网络架构是捕获图片的视觉信息,最后将这三部分结果线性合,然后进行归一化,最终得到结果为4 096维的向量。其中Normalization是一种提高神经网络性能和稳定性的技术,这个想法是以一种方式来标准化输入,使得它们的平均输出激活为零,标准偏差为1,创建统计学的移位和缩放版本。这个操作可以使得网络训练速度更快,使权重更容易初始化,可以允许更高的学习率,使更多激活函数可行,使得训练更深的网络成为可能,防止过拟合[17-18]。
在这网络结构中,卷积层起到了局部特征检测器的作用,最大池化层则是增加神经网络的鲁棒性,归一化增加了网络的鲁棒性以及加快了模型的收敛。
在本文中使用的VGG-16网络,其结构如图3所示,共13个卷积层(convolution+ReLU)、3个全连接层(fully conneted+ReLU)、5个池化层(max pooling)。
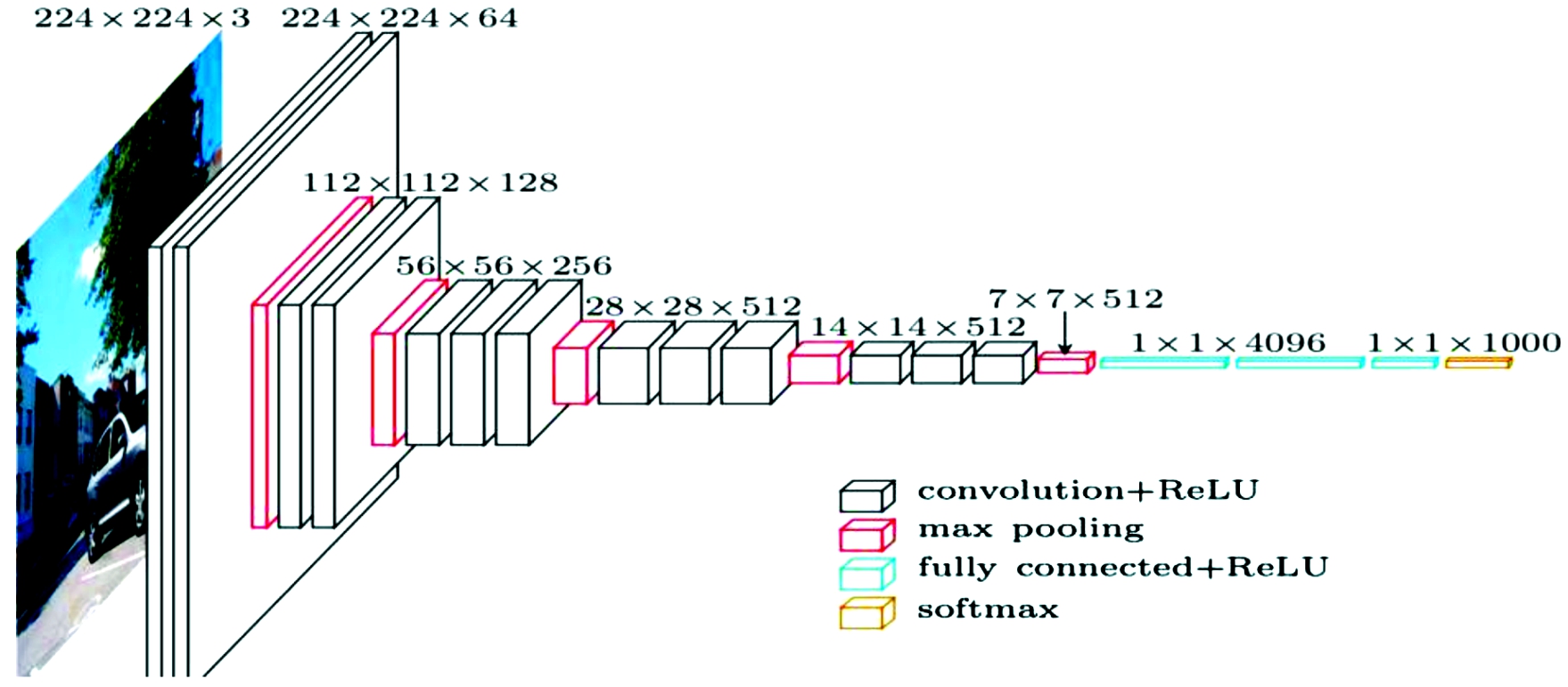
图3 VGG-16结构示意图
模型中除了归一化处理,还采用Dropout防止过拟合。Dropout是指在每一步训练过程中,按一定概率随机忽略某些神经元[19]。这里“忽略”是指这些神经元在向前传播和反向传播中不被考虑。在每个训练阶段,单个节点或者以概率1-p从网络中被抛弃,或者以概率p保持,从而留下减少的网络。其步骤可分为:① 按概率随机删除网络层中的一些隐藏的人工神经元,但保持输入输出神经元数量不变;② 将输入经过修改后的网络进行前向传播,然后将误差通过修改后的网络进行反向传播;③ 对于另外一批的训练样本,重复上述操作①。由于计算的神经元减少,可以在一定程度上加速学习,Dropout工作示意图如图4所示。

图4 Dropout工作示意图
3 实验
3.1 训练集
本实验使用了MSTAR官方数据集,该数据集是经典的公开军事目标训练集,来自美国国防高级研究计划署,包括 60 000 个样本,测试数据集有10 000个样本。每个MSTAR官方数据集的图片是28*28像素的灰度军事图片,记录了前苏联的T72坦克、A64坦克等武器装备的雷达图像。MSTAR官方数据集截图如图5所示。

图5 MSTAR官方数据数据集截图
3.2 模型训练
训练时候使用了4 200组分类模型做训练,525组分类模型做验证集,考虑到该数据集图片种类繁多、训练数据太少,可能会导致收敛速度慢、验证集损失居高不下的结果,因此把推荐算法的目标范围缩小,目的是用少量数据即可得到较好的推荐结果。这样可以有效地规避上述问题,也不会导致欠拟合现象发生。
3.3 实验结果
由于计算能力的限制,GPU显存为4G,批大小(batch size)最多只能设为7组分类模型,即21张图,epoch为5。在实验中分别训练了T72坦克和A64坦克两种型号的图片,推荐图片分别见图6和图7所示。

图6 假想的T72坦克推荐图片

图7 假想的A64坦克推荐图片
从图6、图7推荐结果可见,该算法能够较好地提取两种坦克细致的特征,根据细粒度的内容进行T72和A64坦克推荐。
该算法在测试集上的正确率如表1所示,正确率计算方法是:给定一组三元组<q,p,n>,若D(q,p)<D(p,n),则算正确,否则错误。由表1可见,相比传统的目标检测及推荐算法,该算法具有较好的效果,可以在细粒度的情况下进行目标的推荐,而且不需要细粒度的标签。
各种网络结构算法在公开数据集ILSVRC上的表现如表2所示,具体为验证集和测试集的错误率统计。其中最后一行为本文算法在数据集中的性能表现:top-1 val错误率为23.2%,top-5 val错误率为6.2%,top-5 test错误率为6.5%。可见,和其他经典推荐算法相比,错误率有所下降,性能得到有效提高。
表1 测试集正确率

One-stage methodsBackboneAPAP50AP75APsAPMAPLSSD513ResNet-101-SSD31.250.433.310.234.549.8DSSD513ResNet-101-DSSD33.253.335.213.035.451.1VGG-16无34.550.034.019.037.249.3VGG-16KNN36.252.140.120.038.651.2
表2 验证集和测试集的错误率
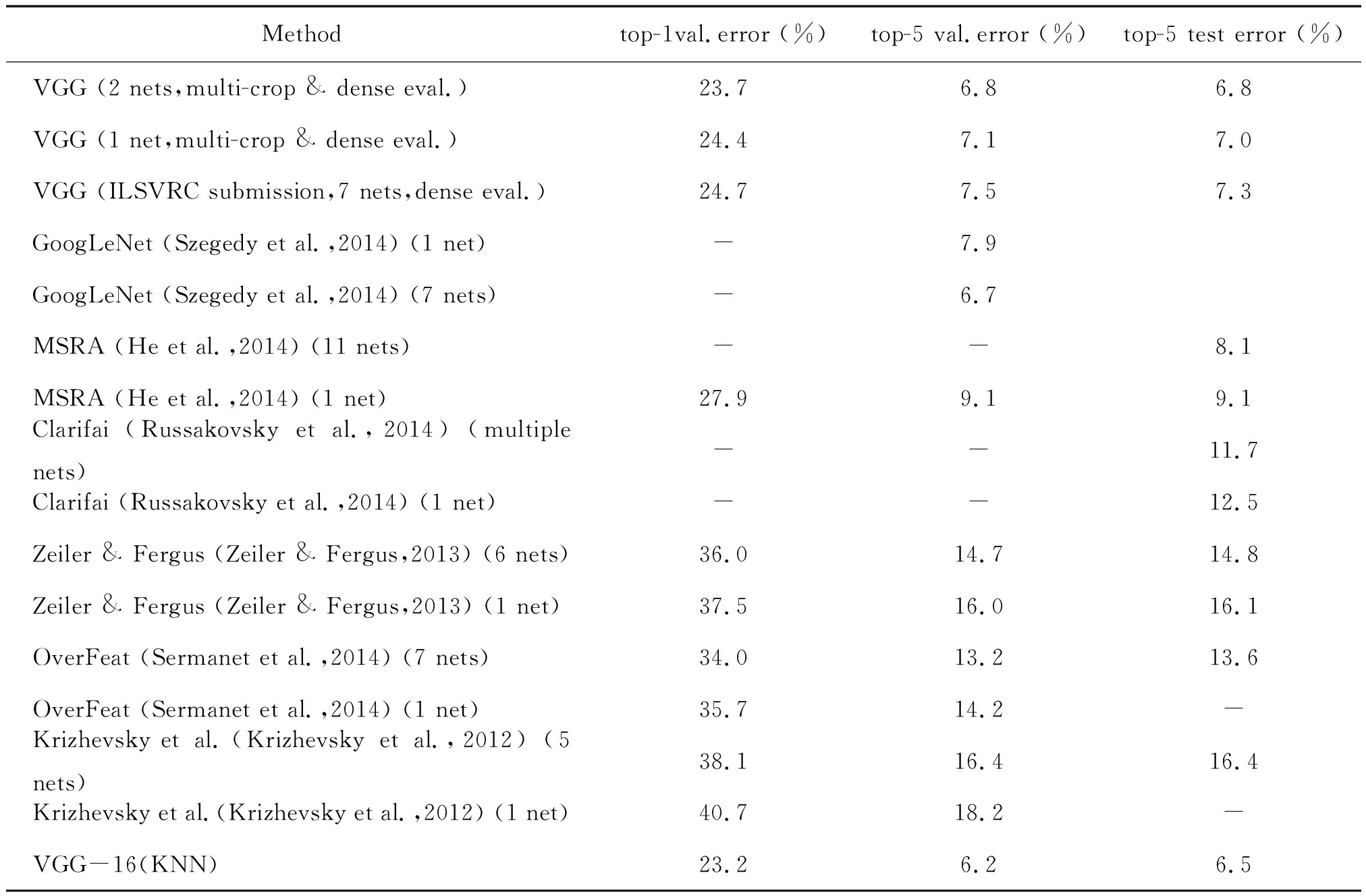
Methodtop-1val.error (%)top-5 val.error (%)top-5 test error (%)VGG (2 nets,multi-crop & dense eval.)23.76.86.8VGG (1 net,multi-crop & dense eval.)24.47.17.0VGG (ILSVRC submission,7 nets,dense eval.)24.77.57.3GoogLeNet (Szegedy et al.,2014) (1 net)-7.9GoogLeNet (Szegedy et al.,2014) (7 nets)-6.7MSRA (He et al.,2014) (11 nets)--8.1MSRA (He et al.,2014) (1 net)27.99.19.1Clarifai (Russakovsky et al.,2014) (multiple nets)--11.7Clarifai (Russakovsky et al.,2014) (1 net)--12.5Zeiler & Fergus (Zeiler & Fergus,2013) (6 nets)36.014.714.8Zeiler & Fergus (Zeiler & Fergus,2013) (1 net)37.516.016.1OverFeat (Sermanet et al.,2014) (7 nets)34.013.213.6OverFeat (Sermanet et al.,2014) (1 net)35.714.2-Krizhevsky et al.(Krizhevsky et al.,2012) (5 nets)38.116.416.4Krizhevsky et al.(Krizhevsky et al.,2012) (1 net)40.718.2-VGG-16(KNN)23.26.26.5
4 结论
本文提出了一种基于深度学习的细粒度图像推荐算法,使用分类模型对杂乱无章的数据集进行分类,然后采用改进KNN聚类算法实施初选,再通过VGG-16网络进行训练,并在经典军事目标训练集数据集MSTAR对所提算法进行验证。该算法淡化了标签的作用,使得网络具有较好的扩展性,可以对没有训练过的类别进行预测;能对更细节的图像进行推荐;可以将图片映射的向量存储,有效节约计算资源,提升算法的运行速度。和其他经典推荐算法相比,提出的算法在公开数据集ILSVRC中的错误率下降,性能得到有效提高。
[1] 黄震华,张佳雯,张波,等.语义推荐算法研究综述[J].电子学报,2016,44(09):2262-2275.
[2] 黄立威,江碧涛,吕守业,等.基于深度学习的推荐系统研究综述[J].计算机学报,2018,41(07):1619-1647.
[3] 吕刚,张伟.基于深度学习的推荐系统应用综述[J].软件工程,2020,23(02):5-8.
[4] WU X H,ZHU J,WU B,et al.Classification of Chinese vinegar varieties using electronic nose and fuzzy Foley-Sammon transformation[J].Pubmed,2020,57(04):146-148.
[5] SEBASTI N F,BENJAMIN B,NORA R.An efficient algorithm for approximated self-similarity joins in metric spaces[J].Elsevier,2020,91:47-52.
N F,BENJAMIN B,NORA R.An efficient algorithm for approximated self-similarity joins in metric spaces[J].Elsevier,2020,91:47-52.
[6] QIAO L,LI G,TAO H,et al.Full characterization for material constants of a promising KNN-based lead-free piezoelectric ceramic[J].Elsevier,2020,46(05):167-171.
[7] 赵学彤,杨亚东,渠鸿竹,等.组学时代下机器学习方法在临床决策支持中的应用[J].遗传,2018,40(09):693-703.
[8] 奚雪峰,周国栋.面向自然语言处理的深度学习研究[J].自动化学报,2016,42(10):1445-1465.
[9] 王艳,李昂,王晟全.训练集对遥感图像超分辨率下自动目标识别影响的研究[J/OL].重庆理工大学学报(自然学):1-8[2020-09-15].http://kns.cnki.net/kcms/detail/50.1205.T.20200915.1054.004.html.
[10] WU Q,YAN F F,CHAI Z L,et al.Crowd counting by the dual-branch scale-aware network with ranking loss constraints[J].IET Computer Vision,2020,14(03):121-126.
[11] LIU Y J,XU Y F,MENG X Z,et al.A Study on the Auxiliary Diagnosis of Thyroid Disease Images Based on Multiple Dimensional Deep Learning Algorithms[J].Current medical imaging,2020,16(03):184-189.
[12] 尹剑,邱远宏,欧照凡.长江流域实际蒸散发的遥感估算及时空分布研究[J].北京师范大学学报(自然科学版),2020,56(01):86-95.
[13] 许璐,张红,王超,等.简缩极化SAR数据处理与应用研究进展[J].雷达学报,2020,9(01):55-72.
[14] 朱铮宇,邱华愉,杨春玲,等.基于特定韵母发音事件分析的语音唇动一致性判决方法[J].华南理工大学学报(自然科学版),2020,48(01):139-146.
[15] NASIRI A,OMID M,TAHERI-GARAVAND A.An automatic sorting system for unwashed eggs using deep learning[J].Journal of Food Engineering,2020,283:67-72.
[16] BANAN A,NASIRI A,TAHERI-GARAVAND A.Deep learning-based appearance features extraction for automated carp species identification[J].Aquacultural Engineering,2020,89:134-139.
[17] 李宗凌,汪路元,禹霁阳,等.遥感舰船目标检测识别方法[J].遥感信息,2020,35(01):64-72.
[18] DING L,ZHANG H Y,XIAO J S,et al.A Lane Detection Method Based on Semantic Segmentation[J].Computer Modeling in Engineering & Sciences,2020,122(03):132-136.
[19] 黄亦其,刘琪,赵建晔,等.基于深度卷积神经网络的红树林物种无人机监测研究[J].中国农机化学报,2020,41(02):141-146,189.