轨迹测量是通过雷达、光电设备、GPS设备等试验测试系统对目标运动过程中的位置、速度和轨迹等信息进行获取的过程。是航空、航天、汽车、船舶试验测量过程中的重要技术[1-2]。目前在采用雷达、光电经纬仪、激光测距机等设备对飞行器轨迹测量过程时，必须通过滤波方法的方法对结果数据进行预测和修正，使航迹测量结果更加精确。研究表明，在跟踪或测量机动目标时，交互多模型(Interacting Multiple Model，IMM)算法是一种有效提升目标跟踪的方法[3-6]。其通过运用多个模型分别来匹配目标不同的运动状态，并认为不同运动模型间的转移概率是一个马尔可夫过程，然后完成然对机动目标开展自适应模型匹配，从而提升了机动目标的测量精度。中外学者将IMM算法分别与非线性卡尔曼滤波[7-11]、粒子滤波[12-13]等算法相结合，通过滤波器的改进提升状态观测的精度。本研究结合飞行器机动的特点，利用不匹配模型误差压缩率的更新信息调整马尔可夫状态转移矩阵，实现快速切换模型的目的；并结合自适应无迹卡尔曼滤波(AdaptiveUnscented Kalman Fliter AUKF)算法，进一步改善飞行器轨迹测量滤波效果，提高了机动飞行器轨迹测量精度。
1 IMM算法
IMM算法包含多个模型和与之对应的滤波器，各模型之间按照马尔可夫转移概率进行切换[14-15]。图1为交互模型算法原理框图，根据目标运动特性，建立一个具有有限个数的模型集，对于目标跟踪而言，可以是匀加速运动模型(CA)、匀速运动模型CV、不同机动概率的Singer模型和当前统计模型[16-17]等。
图1 交互模型算法原理框图
根据交互系数，计算出每一种滤波器的上一步估计值；根据上面模型集的特点创建对应个数的滤波器，主要由各种卡尔曼滤波器构成，进行一步滤波；根据每个滤波器的估计残差计算模型概率；最后根据模型概率加权计算状态的联合估计，估计值出输和其协方差阵。
1.1 模型混合与滤波器预测估计
首先要给出先验的模型转移概率π，表征各模型间相互转换的概率，这个模型转移概率集合是根据目标的运动特性估计的，其有效生成也是IMM算法的难点：
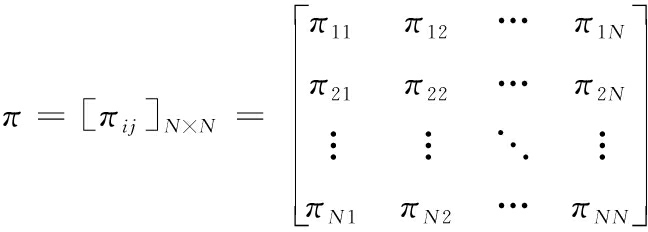
(1)
如果
为k-1时刻滤波器j的状态估计值， Pj(k-1/k-1)为相应的状态协方差阵，
为k-1时刻模型j的概率，则交互后第j个滤波器在k-1时刻的输入应为各个滤波器的滤波值按照概率进行混合，表示如下：
(2)
其中，
为滤波器模型i在k-1时刻的估计值，
计算如下：
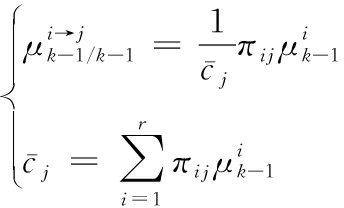
(3)
另外还要估计k-1时刻各个滤波器的协方差输入矩阵Poj(k-1/k-1)，其中Pi(k-1/k-1)为各个模型在k-1时刻的状态估计协方差矩阵：
(4)
(5)
将上述估计的
与协方差矩阵Poj(k-1/k-1)作为各个滤波器的输入，代入各个滤波器当中，根据观测值z(k)计算出当前各个滤波器的估计值和估计协方差值
和Pj(k/k)。
1.2 模型概率更新与状态输出
设模型滤波器残差为
表示预测观测值与实际观测值的差，相应的协方差为
并假定服从高斯分布，则模型j的可能性
可以计算如下：
(6)
式中，残差
和协方差
分别为：
(7)
模型可能性是一个动态范围非常大的数值，为了更好地使用这个信息，将其进行归一化：
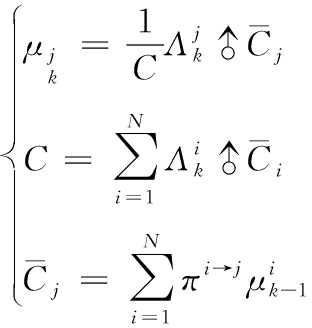
(8)
其中：
表示k-1时刻模型i的混合后概率；
为表示k时刻由所有N个模型转移到第j个模型后的全概率；
实质上就是归一化后的
用以表征k时刻模型j的修正概率。
最后，根据之前计算得到的概率、估值、协方差计算模型混合输出，对各个滤波器的输出值进行加权平均，得到混合状态滤波值
和混合状态方差P(k/k)：
(9)
(10)
2 飞行器轨迹测量滤波模型的建立
2.1 运动模型集
航空器在飞行过程中，其运动模型无法由一种准确的运动模型进行观测，因此本文通过建立匀加速模型(CA)、机动转弯模型(MCT)以及当前统计模型(CS)3种系统模型来描述航空器在空中的运动。
当目标在二维平面内做运动时，k时刻目标离散系统的状态方程为：
x(k+1)=Φ(k)x(k)+G(k)W(k)
(11)
Z(k)=H(k)X(k)+V(k)
(12)
其中：
为k时刻的系统状态矢量，其中，
和
分别为横轴和纵轴的位置分量、速度分量与加速度分量；Φ(k)为系统转移矩阵；G(k)是系统噪声转移矩阵；W(k)为系统噪声矩阵。噪声方差定义为Q(k)，H(k)为观测矩阵，V(k) 为观测系统噪声矩阵，噪声方差定义为R(k)。
CA模型[17]系统转移矩阵Φ(k)与噪声转移矩阵 G(k) 为：
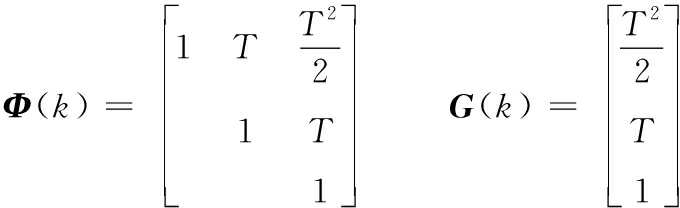
(13)
在MCT模型[18]中，转弯加速度为一个特定值，转弯角度为ω，当ω>0时为左转弯，当ω<0时为右转弯，ω=0为匀速直线运动，其系统转移矩阵Φ(k)为：
(14)
噪声转移矩阵G(k)为：
(15)
“当前”统计模型[5]是一种利用目标的先验知识来预测和修正后验知识的原理来设计目标模型的[19]。具体形式如下：
(16)
x(t)为目标的位置，
为目标的随机加速度，
为当前加速度，w(t)为零均值有色白噪声，α表示机动频率，w(t)是均值为零，方差为
的白噪声。加速度的“当前”概率密度是通过修正的瑞利分布来描述的，其系统模型的递推形式：
(17)
式中：
(18)
系统包含白噪声w(t)，且Q(k)为：
(19)
具体的Q(k)参数定义，可翻阅参考文献[20]。
2.2 带自适应因子的AUKF 算法
UFK滤波器的核心思想是通过选取一系列Sigma采样点，这些采样点能够完全表征出高斯密度的实际均值和协方差，使这些点经过非线性系统的传递得到后验的估计。主要分为Sigma点权值计算，时间更新，测量更新3个步骤，具计算过程，可翻阅参考文献[9]。
但工程中，测量噪声vk的统计特性rk与Rk无法先验得知，本研究利用改进型Sage-Husa噪声统计估值器，对测量噪声统计特性Rk进行估计，来改善滤波器的性能[9]。式子中bf为遗忘因子，本文取bf=0.98，在计算上述UKF时将
置换，即可形成AUKF滤波器。使用的时候需要选择测量噪声期望与协方差估计值
和
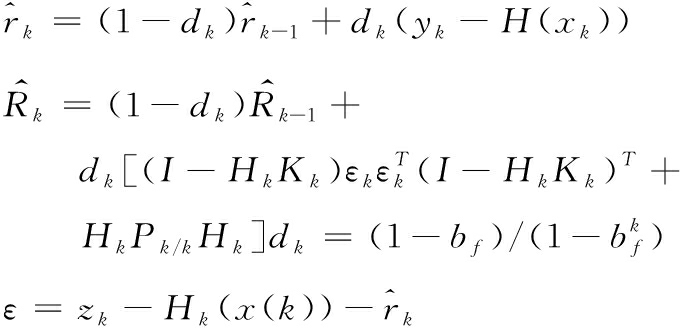
(20)
2.3 自适应改进的IMM更新模型
针对IMM算法中马尔可夫概率转移矩阵是通过先 验知识确定，本文通过构建当前时刻某个模型的滤波估计值与下一步交互输入作用后的输出值的偏差，与当前时刻该模型对应滤波器的输出值与融合输出值的偏差之比定义为误差压缩率：
(21)
在这里，λi(k)是通过范数的形式表达。将式(2)、式(3)和式(9)代入式(21)，可以计算出多模型的压缩率为：
(22)
通过模型误差压缩率修正后的概率转移矩阵为：
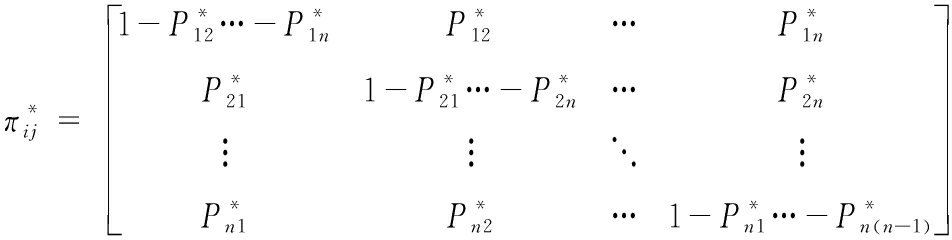
(23)
其中l为调节因子，当l=0时，概率转移矩阵没有得到修正，自适应程度最低；当l=1时，转移矩阵完全由压缩率决定，自适应程度越高，本文采用l=1，进行后续仿真。综上所述，通过向IMM算法增加自适应算子构成AIMM，并结合AUKF滤波器，一同构成了一种基于AIMM-AUKF的飞行器轨迹测量算法模型。
3 仿真与验证
为了验证本文提出的滤波算法的效果，将其和“当前”模型相结合的UKF滤波算法，以及传统IMM算法进行对比仿真实验。
仿真场景：假设带有光电与雷达吊舱的测量飞机与被探测飞行器目标在二维坐标下运动，并处于同一惯性坐标系下。测量飞机，在惯性系的位置为(-100 km，10 km)，并以(300 m/s，0)的速度匀速飞行；载机的定位标准误差(10 m，10 m)，雷达的探测精度为相对距离标准差150 m，光电测量角度误差标准差0.1°。被测飞行器在惯性系位置(100 km，20 km)以(-1 800 m/s，0)的速度飞行，并在10 s，16 s时分别产生了小机动和较大机动。其中状态变量选择为为目标在惯性系下2个轴方向的位置、速度和加速度状态变量选择为
为目标在惯性系下2个轴方向的位置、速度和加速度。滤波器初值为x0=[10.1 km，20.1 km，1 820 m/s，-20 m/s，0 m2/s，0 m2/s]，估计协方差矩阵P0=[3002，3002，1002，1002，402，402]，各模型的初始概率u0=[1/3，1/3，1/3]，转移矩阵初始值为：
仿真结果如图2～图7所示。从图2、图4、图6中可以发现在机动较小的目标运动时，AIMM-AUKF算法相比AUKF与IMM-AUKF能够适当提高位置、速度与加速度的估计精度，但误差的数量级与其他两种算法接近。从图3、图5、图7可以发现在目标产生较大机动时，AIMM-AUKF算法能够以较快的速度估计出目标的位置、速度与加速度，算法的收敛速度最快，进一步满足机动条件下飞行器航迹跟踪要求，取得了较为理想的结果
为了进一步验证算法的有效性，根据典型飞机的动态特性，进行了随机产生了20种飞行轨迹，并对不同算法在测量过程的标准差进行了统计。。
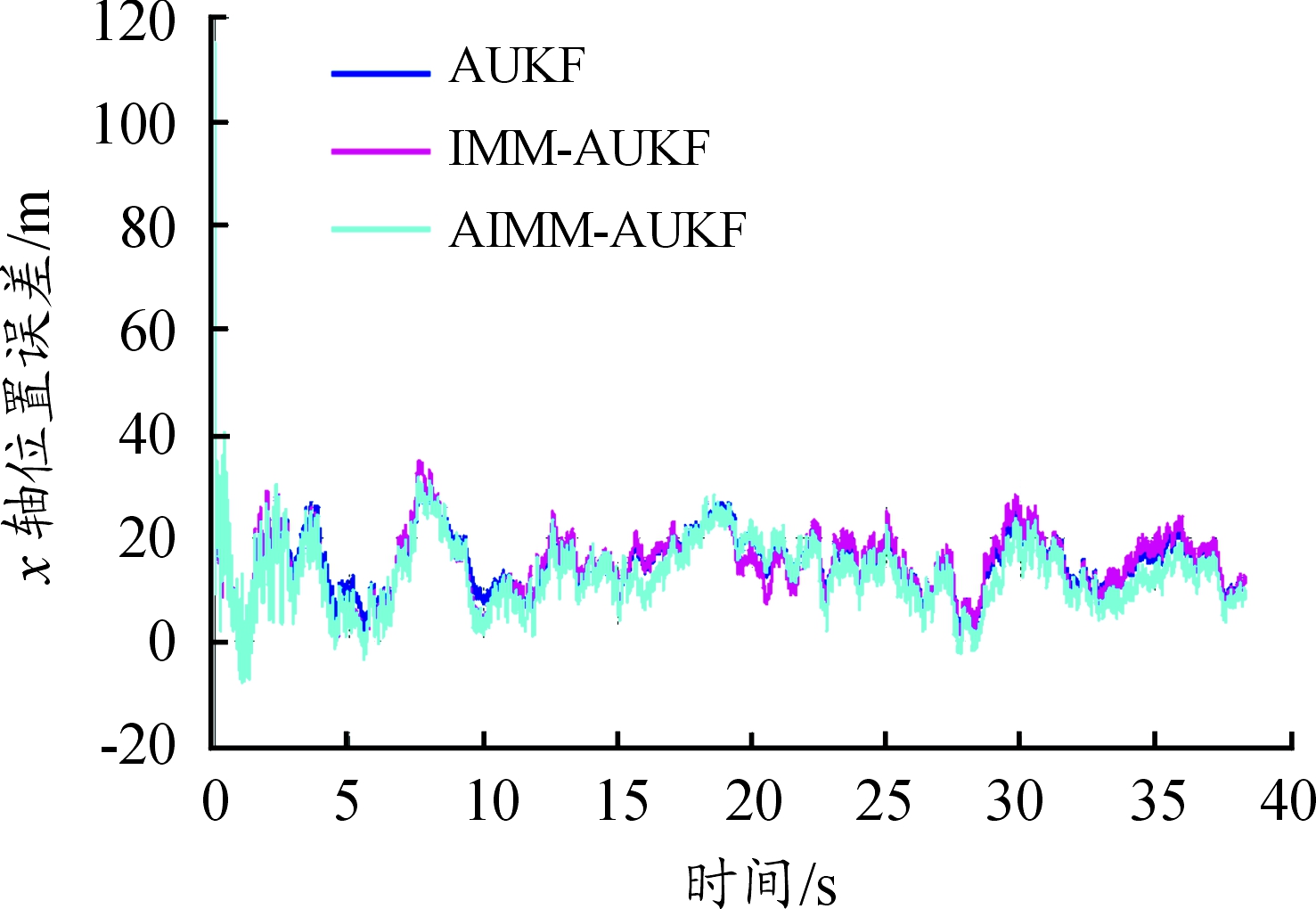
图2 x方向位置误差曲线
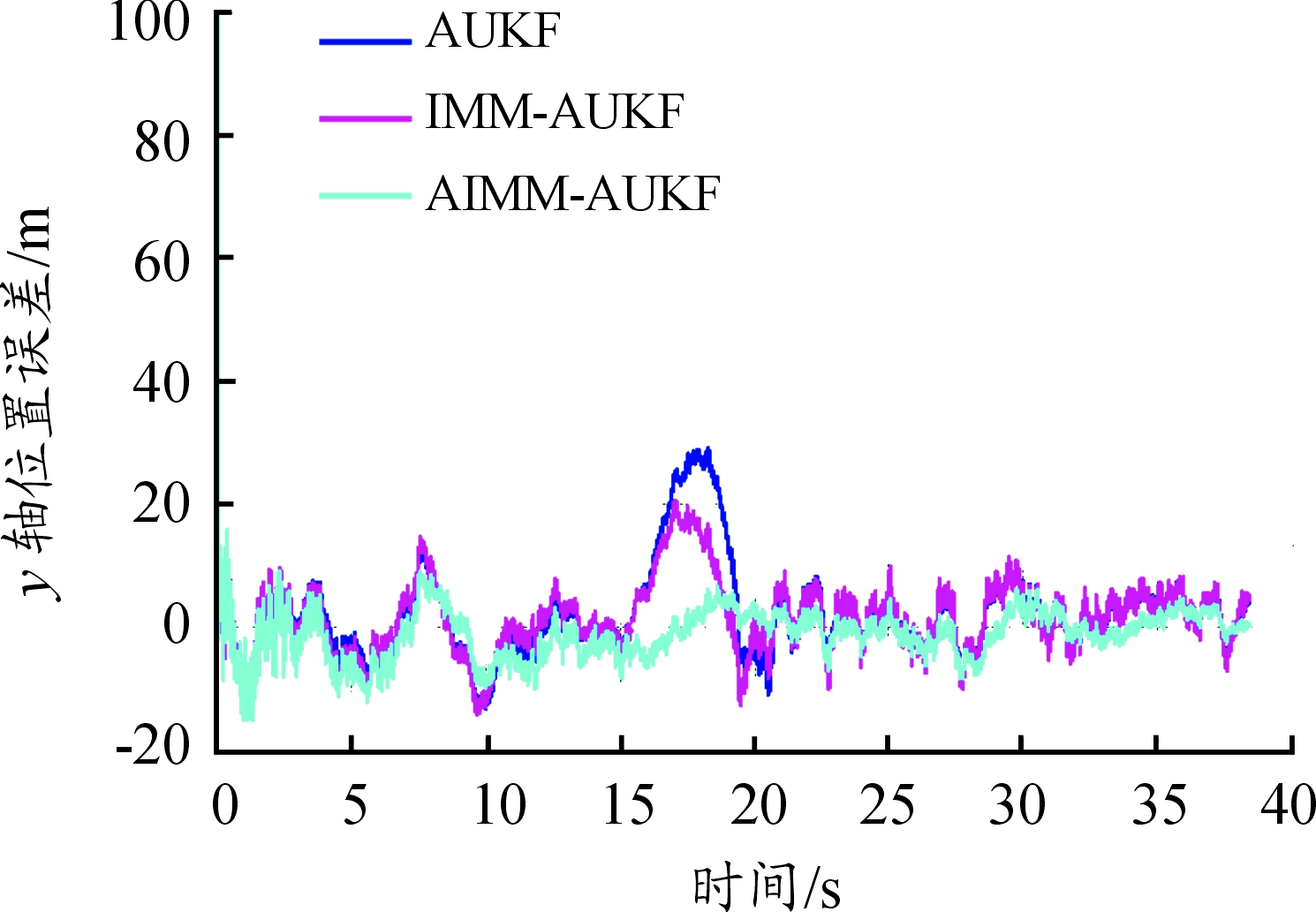
图3 y方向位置误差曲线
图4 x方向速度估计曲线
图5 y方向速度估计曲线
图6 x方向加速度估计曲线
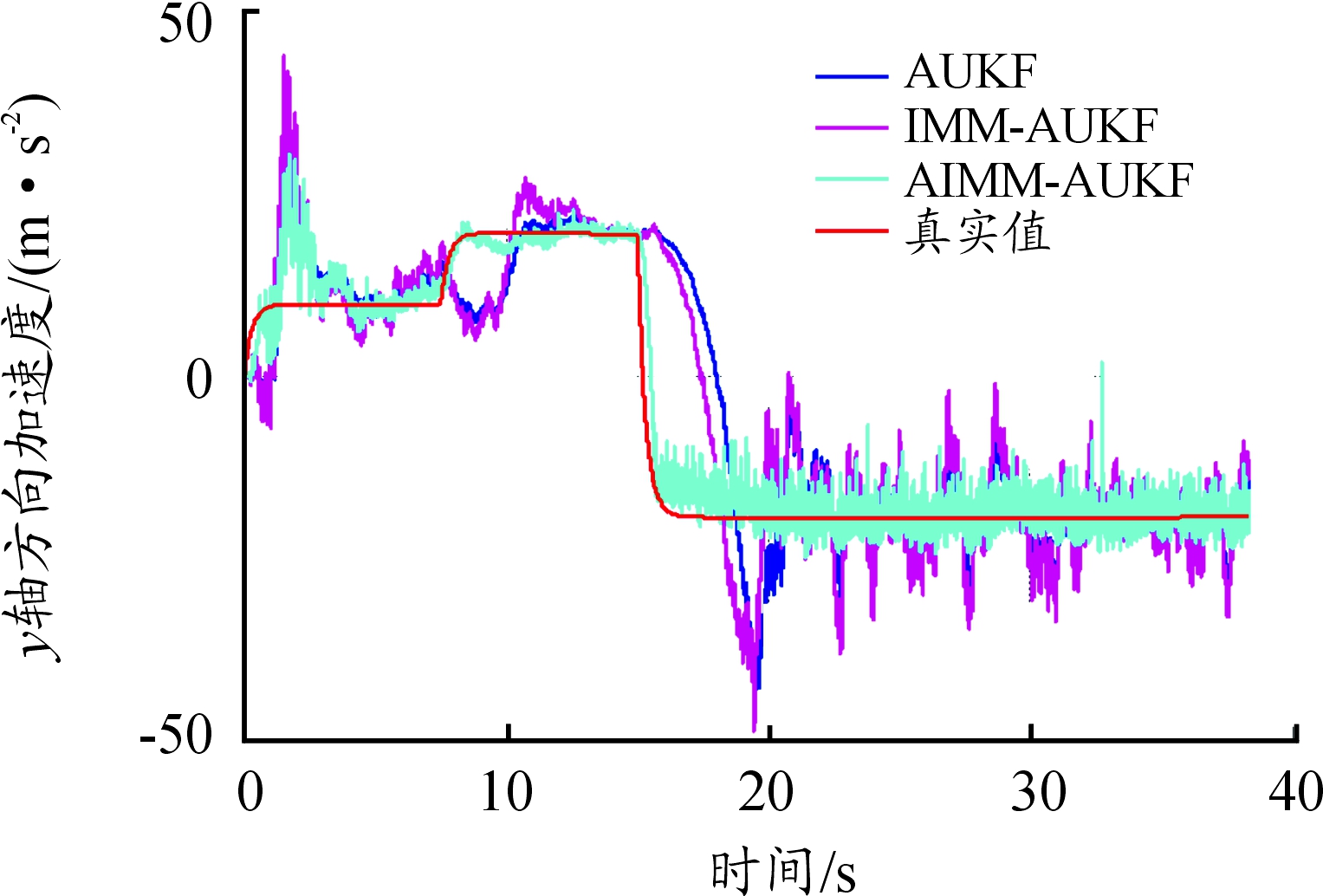
图7 y方向加速度估计曲线
表1为上述仿真初始化条件下x、y方向上测量飞行器位置、速度、加速度以及飞行方位等航迹细信息，估计误差标准差的统计结果。AIMM-AUKF的RMS范围值远小于AUKF和IMM-AUKF，说明在估计精度和稳定性方面AIMM-AUKF要显著优于AUKF和IMM-AUKF。
表1 滤波器误差标准差统计
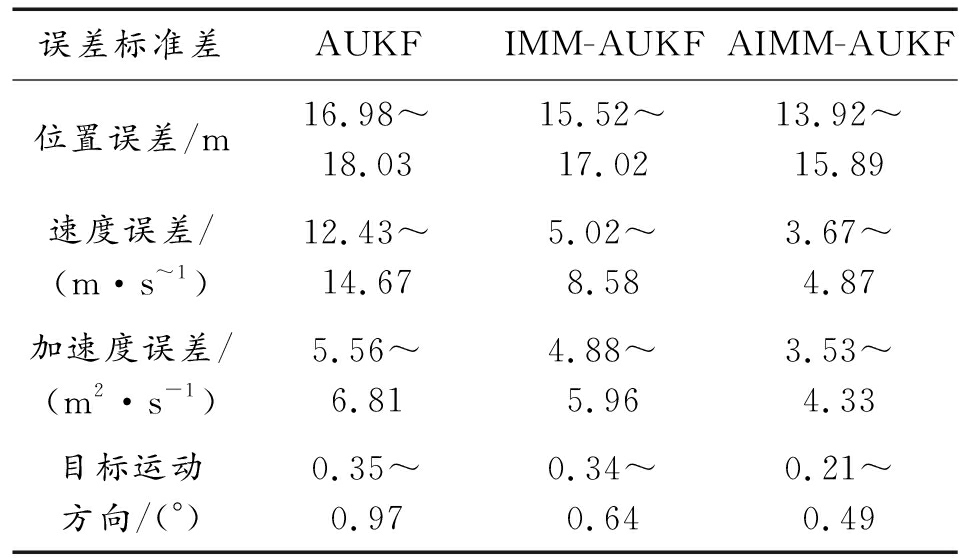
误差标准差AUKFIMM-AUKFAIMM-AUKF位置误差/m16.98～18.0315.52～17.0213.92～15.89速度误差/(m·s～1)12.43～14.675.02～8.583.67～4.87加速度误差/(m2·s-1)5.56～6.814.88～5.963.53～4.33目标运动方向/(°)0.35～0.970.34～0.640.21～0.49
4 结论
在飞行器运动模型集引入AUKF非线性滤波算法，并对传统IMM算法作自适应改进，形成了AIMM-AUKF的滤波算法。AIMM-AUKF相比传统算法，提高了对空中机动目标的轨迹测量精度和收敛速度。下一步将考虑将AIMM-AUKF算法引入到轨迹测量系统做工程测量验证。
[1] 张红玉.基于交互多模型的机动目标跟踪算法研究[D].大连：大连海事大学，2017.
[2] 张浩然，易文俊，管军，等.基于MEMS/北斗的火箭弹弹道参数测量方法[J].兵器装备工程学报，2017，38(09)：41-47.
[3] MAZOR E，VERBUCH A，BAR-SHALOM Y，et al.Interacting multiple model methods in target tracking：A survey[J].IEEE Trans on Aerospace and Electronic Systems，1998，34(1)：103-123.
[4] JOHNSTON L A，KRISHNAMURTHY V.An improvement to the interacting multiple model (IMM) algorithm[J].IEEE Transactions on Signal Processing，2001，49(12)：2909-2923.
[5] 姜仁华，谢洋，刘闯，等.基于改进“当前”统计模型的机动目标IMM跟踪算法[J].现代雷达，2019，41(02)：39-42.
[6] 孙再强，李银伢，戚国庆.道路网机动目标空地平台协同跟踪方法研究[J].兵器装备工程学报，2017，38(09)：95-101.
[7] 张云洲，付文艳，项姝，等.室内环境下基于IMM-EKF算法的移动目标定位[J].计算机研究与发展，2014，51(11)：2408-2415.
[8] 刘昌云.雷达机动目标运动模型与跟踪算法研究[D].西安：西安电子科技大学，2014.
[9] 刘伟，刘宁.一种基于UKF交互多模型算法[J].雷达科学与技术，2015(03)：302-304.
[10] THEUMA K，CHIRCOP K，GAUCI J，et al.Implementation and Evaluation of a Multimodel Filter for Aircraft Ground Operations[J].2019.
[11] YUN J，RYOO C K.Missile Guidance Law Estimation Using Modified Interactive Multiple Model Filter[J].Journal of Guidance Control and Dynamics，2014，37(2)：484-496.
[12] 闫文利，王建刚，柳毅.多模型粒子滤波在机动目标跟踪中的应用[J].电光与控制，2012(01)：22-25，77.
[13] 焦迎雪.改进的交互多模型粒子滤波算法在机动目标跟踪中的应用[D].太原：太原理工大学，2013.
[14] 徐林.基于交互多模型和平滑变结构滤波器的机动目标跟踪研究[D].合肥：合肥工业大学，2019.
[15] 司玉洁，宋申民.高超声速飞行器模型建立与交互多模型轨迹跟踪算法[J].黑龙江大学工程学报，2017，8(02)：58-68，75.
[16] 谭顺成，王国宏，王娜.IMM-Singer模型的机动目标跟踪算法[J].火力与指挥控制，2012，37(02)：32-34.
[17] 张浩为，谢军伟，葛佳昂，等.基于波形调度的机动目标跟踪算法[J].电子学报，2019，47(03)：560-567.
[18] 董宁，徐玉娇，刘向东.一种带自适应因子的IMM-UKF的GPS/BD-2导航方法[J].宇航学报，2015，36(6)：676-683.
[19] 王尔申，翟秋刚，徐嵩，等.基于改进交互式多模型算法的ADS-B航迹滤波方法研究[J].电光与控制，2019，26(04)：75-80.
[20] KUMAR K S P，ZHOU H.A \“current\” statistical model and adaptive algorithm for estimating maneuvering targets[J].Journal of Guidance Control & Dynamics，1984，7(5)：596-602.