常规兵器地面动态模拟试验中,火箭橇试验是最逼近真实环境、置信度最高的一种试验手段,弥补了空中飞行试验中试验数据获取难度大、获取试验数据不精确、参数获取数量少、代价高等不足,对武器系统改进设计、提高可靠性、缩短研制周期以及节省试验费用等具有重要意义。
火箭橇试验时以橇车为载体,以火箭发动机为动力,通过橇车在轨道上高速运动,模拟常规兵器以及民用高新产品在空中的飞行状态,同时通过光、电、遥等测试手段,测试被试品在运动状态下性能参数的试验方法。试验速度是火箭橇试验的主要指标,也是试验条件控制的关键环节,直接关系试验成败。火箭橇试验时,橇车质量、外形、火箭发动机推力、轨道表面粗糙度等因素都会对试验速度产生影响。
为了具体分析橇车速度影响因素,首先利用火箭橇动态试验时,外测得到的橇车全弹道速度、加速度、距离和橇车质量等参数,反向计算了2种不同类型橇车的气动阻力系数,并将气动阻力系数、火箭发动机推力和橇车质量等参数代入橇车弹道方程,对橇车速度、距离进行了拟合,拟合结果与实际动态试验结果吻合,验证了气动阻力系数推导方法和推导结论的正确性。并对某次动态试验时最高速度、最高速度达到时运行距离等进行了预测,预测结果与实际测试结果相同,进一步验证了橇车气动阻力系数计算方法和研究结果的正确性。然后对不同滑动摩擦系数、橇车质量、气动阻力系数和火箭发动机推力情况下的速度进行了计算,得出以下结论:气动阻力系数对橇车速度影响最大;发动机推力和橇车质量是影响橇车速度的次要因素;滑动摩擦力对速度影响最小。
1 橇车弹道方程
橇车全弹道分为以下3个部分[1]:
加速段:在火箭推力作用下,使橇车加速到所需的速度;
滑行段:橇车在空气阻力及摩擦阻力作用下减速滑行;
刹车段:橇车在水刹车作用下减速,直至停止。
加速段,橇车在运动方向上主要受3个力:火箭推力T、空气阻力Ra和轨道摩擦阻力Rf。加速段运动方程为[2~4]:
(1)
式中:CD为空气阻力系数;A为橇车迎风截面积(m2); ρ为空气密度(kg/m3); V为橇车运动速度(m/s); Rf为摩擦阻力(N),Rf=ufmg; uf为滑动摩擦系数,一般取值0.05~0.2;m为橇车总质量(包含橇车、火箭发动机、被试品和测试设备等),由于火箭发动机推进剂燃烧,因此橇车质量为变质量。
在动态试验前,对橇车摩擦力进行了测试:Ⅰ型橇车(测试时质量580 kg,见后文)静摩擦力882 N,滑动摩擦力304 N,因此在气动阻力系数计算时忽略摩擦力影响,定义气动阻力系数![]() 则式(1)变化为:
则式(1)变化为:
(2)
滑行段,橇车只受空气阻力和摩擦阻力,运动方程为[5-7]:
(3)
滑行段内T=0,则式(3)变换为与式(2)相同的方程,有:
(4)
2 气动阻力系数计算与验证
2.1 气动阻力系数计算
在Ⅰ型橇车和Ⅱ型橇车动态试验中,根据全弹道外测数据,得到橇车速度、加速度与时间的关系曲线,如图1和图2所示。从图1可以看出,Ⅰ型橇车有一段明显的滑行段,因此可以根据滑行段内橇车质量、速度、加速度等参数(见表1)计算橇车气动阻力系数。根据公式(4)得到Ⅰ型橇车每一时刻的气动阻力系数(CDAρ/2)为0.46(如图3所示)。
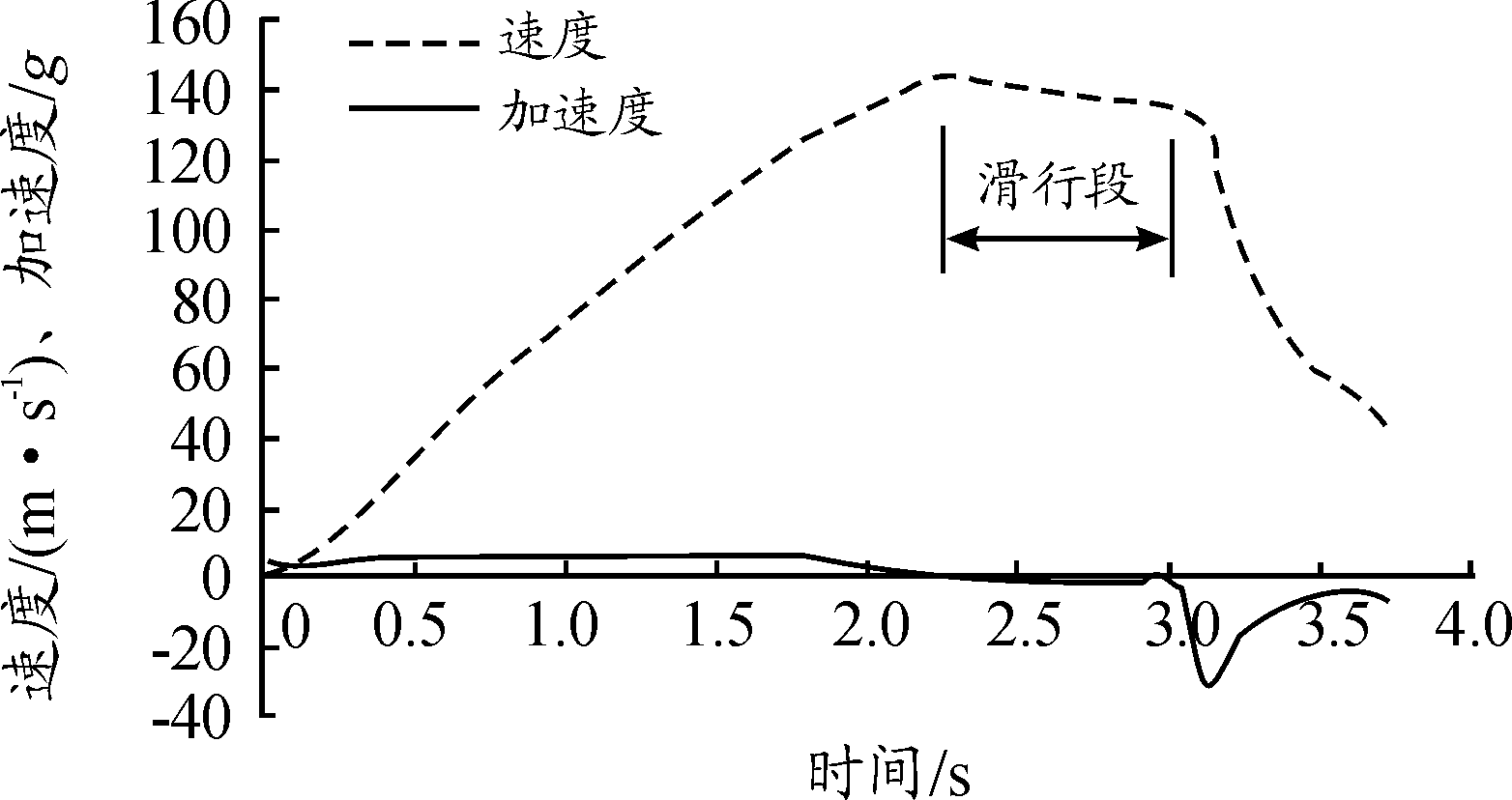
图1 Ⅰ型橇车速度、加速度曲线

图2 Ⅱ型橇车速度、加速度曲线

图3 Ⅰ型橇车气动阻力系数曲线
从图2可以看出,Ⅱ型橇车没有明显的滑行段,但从火箭发动机推力曲线(图4)可以看出,发动机推力基本稳定,发动机推进剂燃烧速度基本恒定,因此可以根据发动机推进剂燃烧时间[5],确定每一时刻橇车质量m′为:
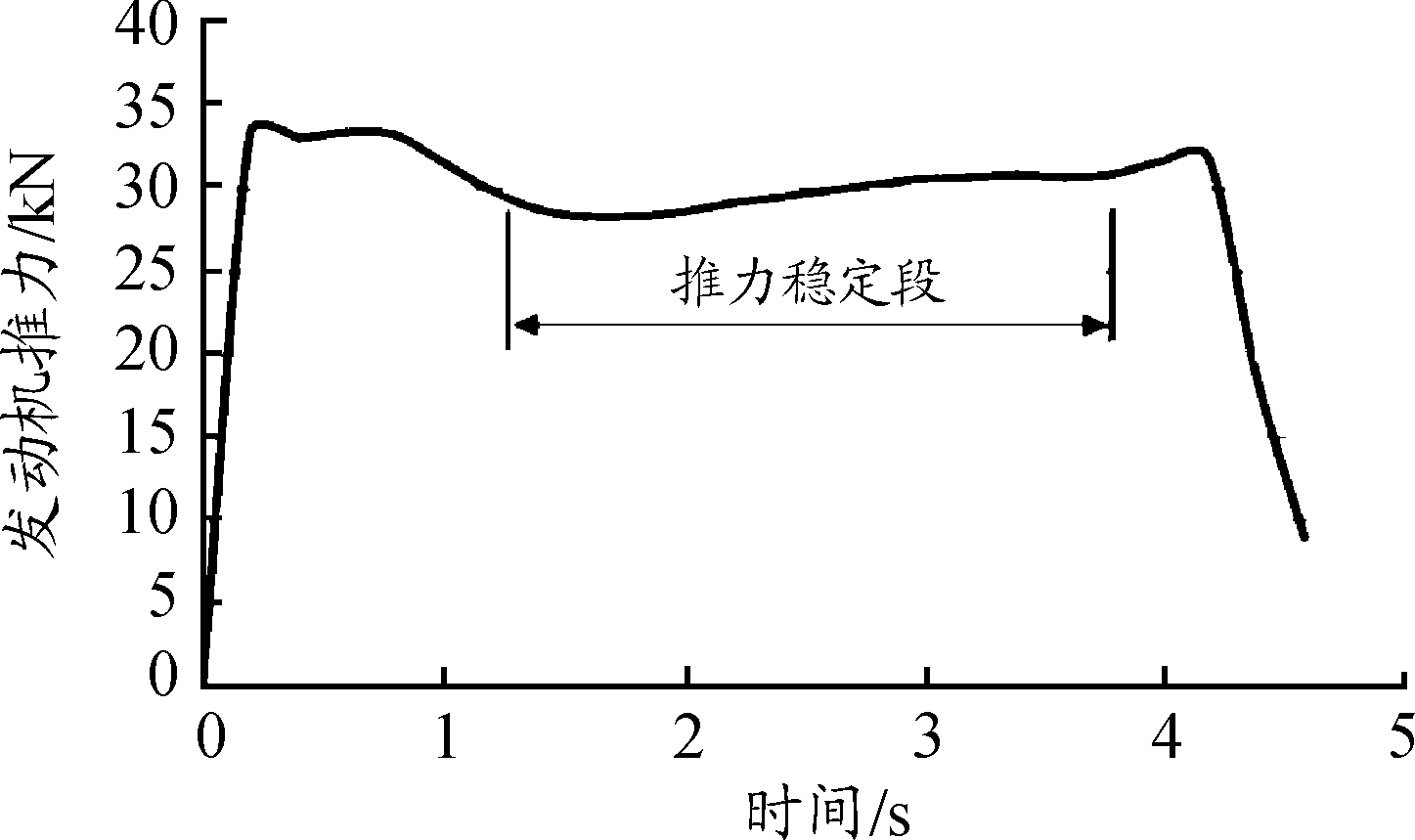
图4 发动机推力曲线
m′=m总-(t/t燃)×m推进剂
(5)
式中: m总为橇车 的总质量(kg);t为某一时间(s);t燃为火箭发动机的燃烧时间(s);m推进剂为火箭发动机推进剂质量(kg)。
因此,将推力稳定段内每一时刻火箭发动机推力、橇车质量和图2中外弹道测试参数代入式(2)中,即可得到Ⅱ型橇车每一时刻的气动阻力系数为0.45,如图5所示。
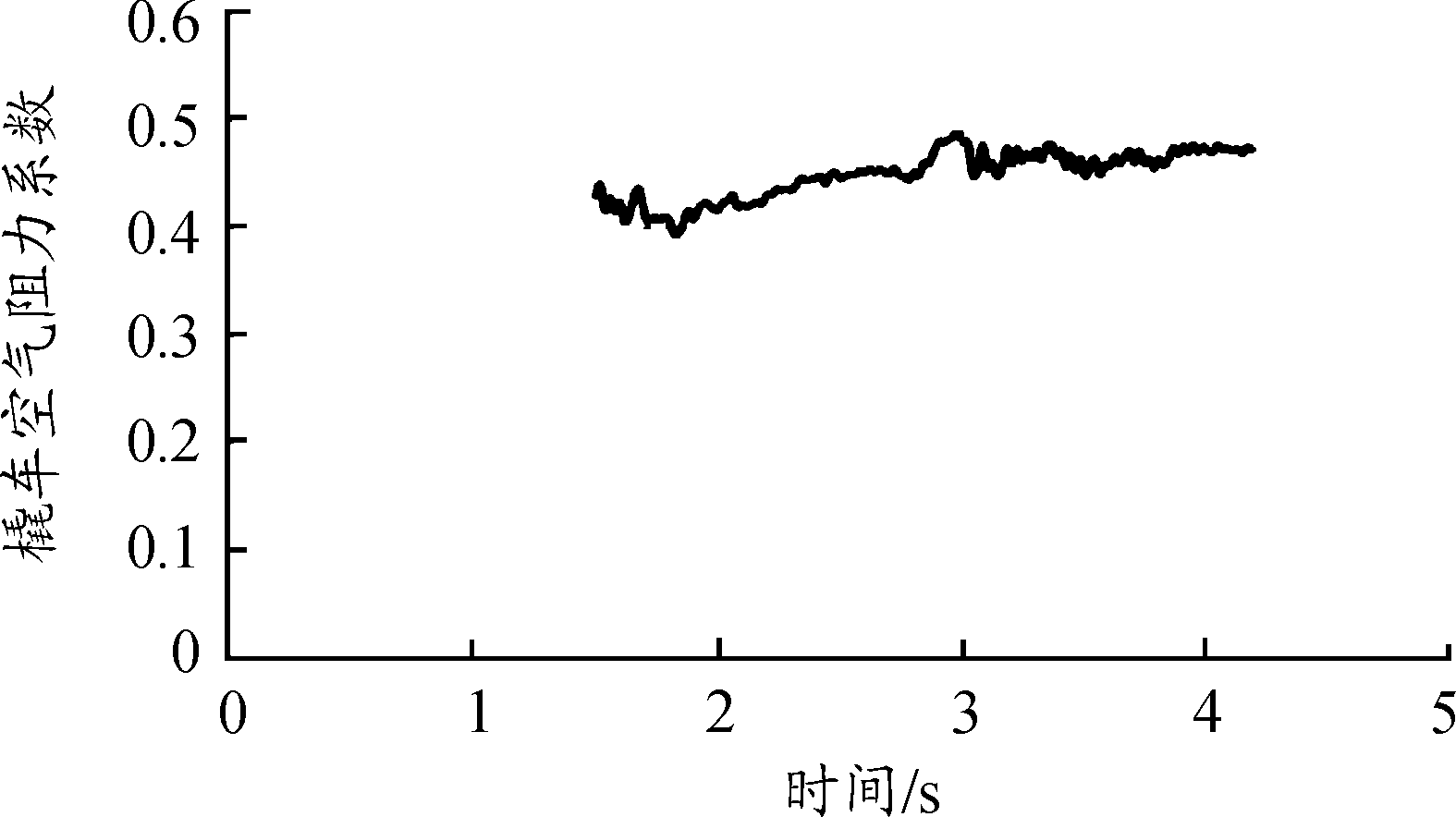
图5 Ⅱ型橇车气动阻力系数曲线
2.2 气动阻力系数验证
加速段内,在t1时刻,火箭发动机推力为T1,橇车质量为m1,橇车速度为V1,到达t2时刻后,火箭发动机推力变为T2,橇车质量为m2,橇车速度为V2,由于Δt=t2-t1极小(≤0.05 s),此时可以忽略火箭推力和橇车质量的变化对速度的影响,将橇车当作匀加/减速处理[8-11],则:
(6)
达到tn时刻时,达到的Vn速度为:
![]()
(7)
当计算出V1、V2、…、Vn以后,就得到橇车加速段速度。
滑行段内,将火箭推力T=0和橇车在这一段时间范围内的平均气动阻力系数(0.45),代入加速段内速度计算式(4),得到滑行段速度。
Ⅱ型橇车某次试验中,搭载试验载荷后,橇车质量和选用发动机推力均发生变化,但橇车外形基本无变化[6-9]。利用计算的气动阻力系数和已知的橇车质量、选用火箭发动机的推力数据等参数对试验过程中橇车速度进行了预测,得到Ⅱ型橇车推算速度、距离与外测速度、距离曲线,如图6所示。从图6可以看出,预测Ⅱ型橇车在2.0 s时,达到最高速度300 m/s;外测Ⅱ型橇车在2.0 s时达到最高速度302 m/s;全程外测速度与预测速度最大误差≤5%,验证了气动阻力系数推导的正确性。
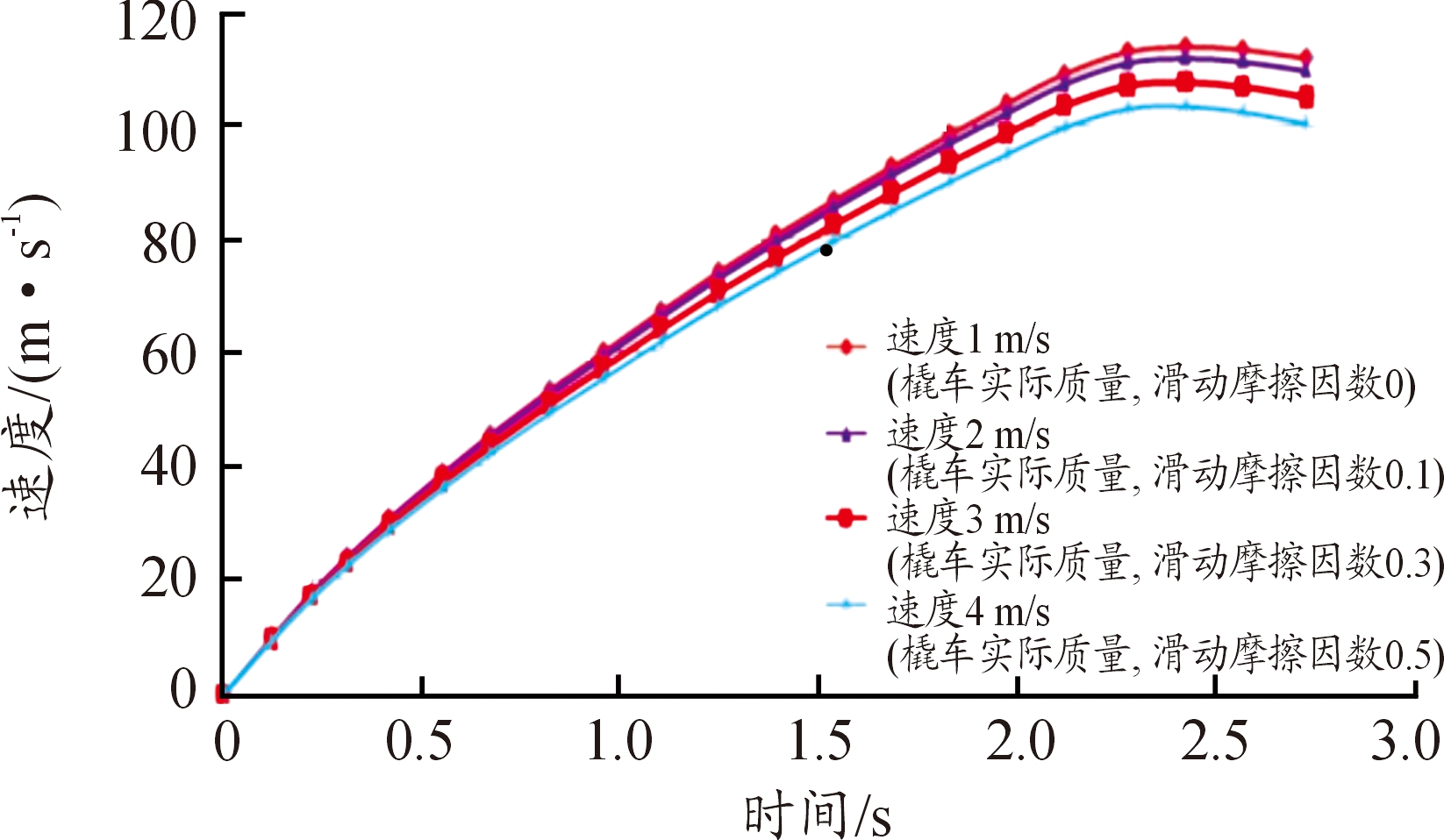
图6 Ⅱ型橇车试验速度曲线
3 原因分析
1) 滑动摩擦系数对速度的影响
图7是滑动摩擦因数分别为0,0.1,0.2和0.5时,橇车速度变化。从Ⅰ型橇车速度变化可以看出,u=0时,橇车速度114 m/s;u=0.5时,橇车速度103 m/s,橇车最大速度相差11 m/s。从Ⅱ型橇车速度变化可以看出,u=0时,橇车速度283 m/s;u=0.5时,橇车速度272 m/s,橇车最大速度相差11 m/s。滑动摩擦因数对速度影响较小。
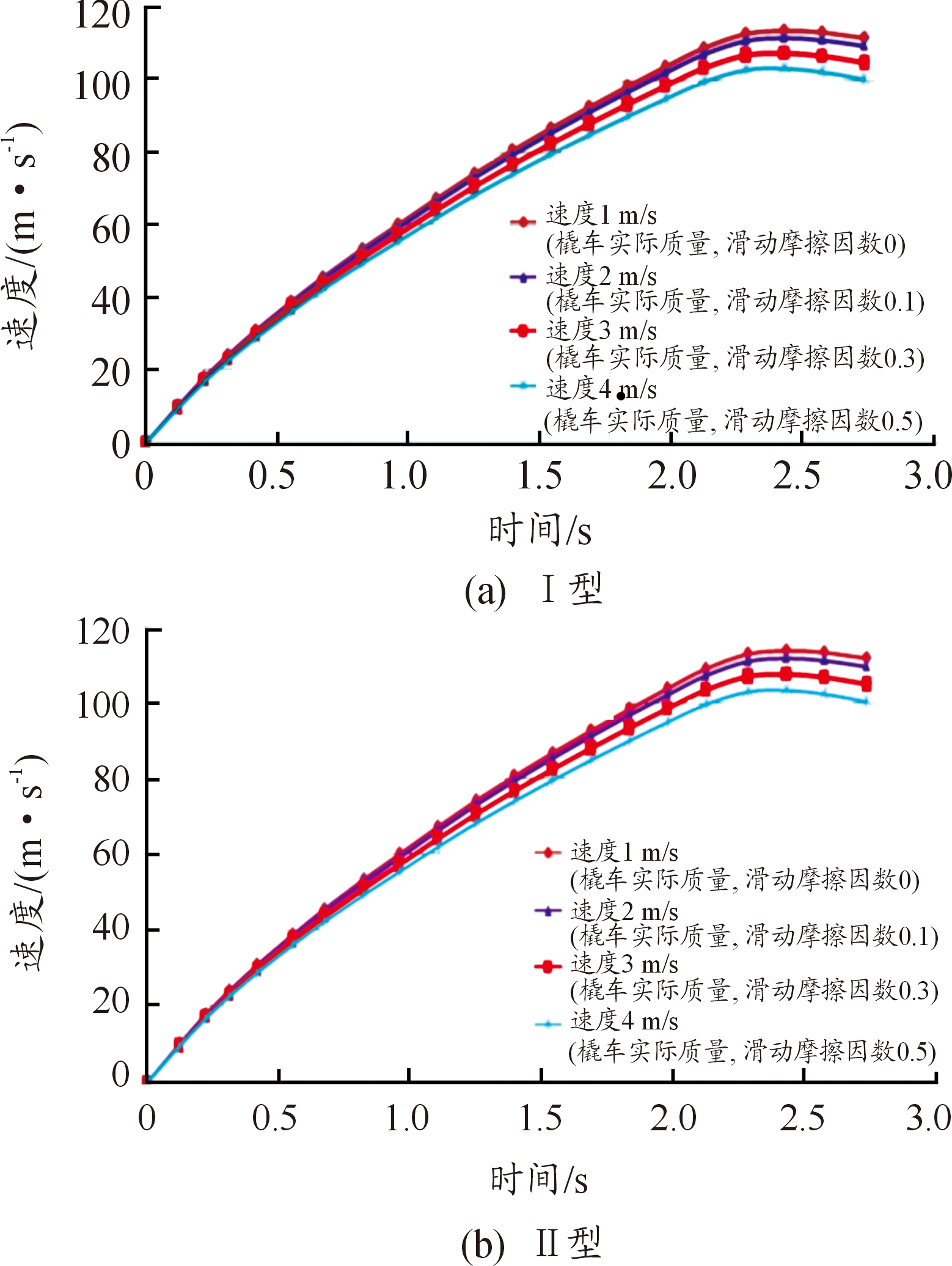
图7 在不同滑动摩擦因数下的橇车速度曲线
2) 橇车质量对速度的影响
在不同橇车质量下的速度变化如图8所示,从图8可以看出,橇车质量对橇车最高速度产生一定影响。橇车质量减少60 kg时,Ⅰ型橇车速度由114 m/s提升至125 m/s,速度提升11 m/s,Ⅱ型橇车速度由278 m/s提升至295 m/s,提升17 m/s。橇车质量对橇车运行速度产生一定影响。
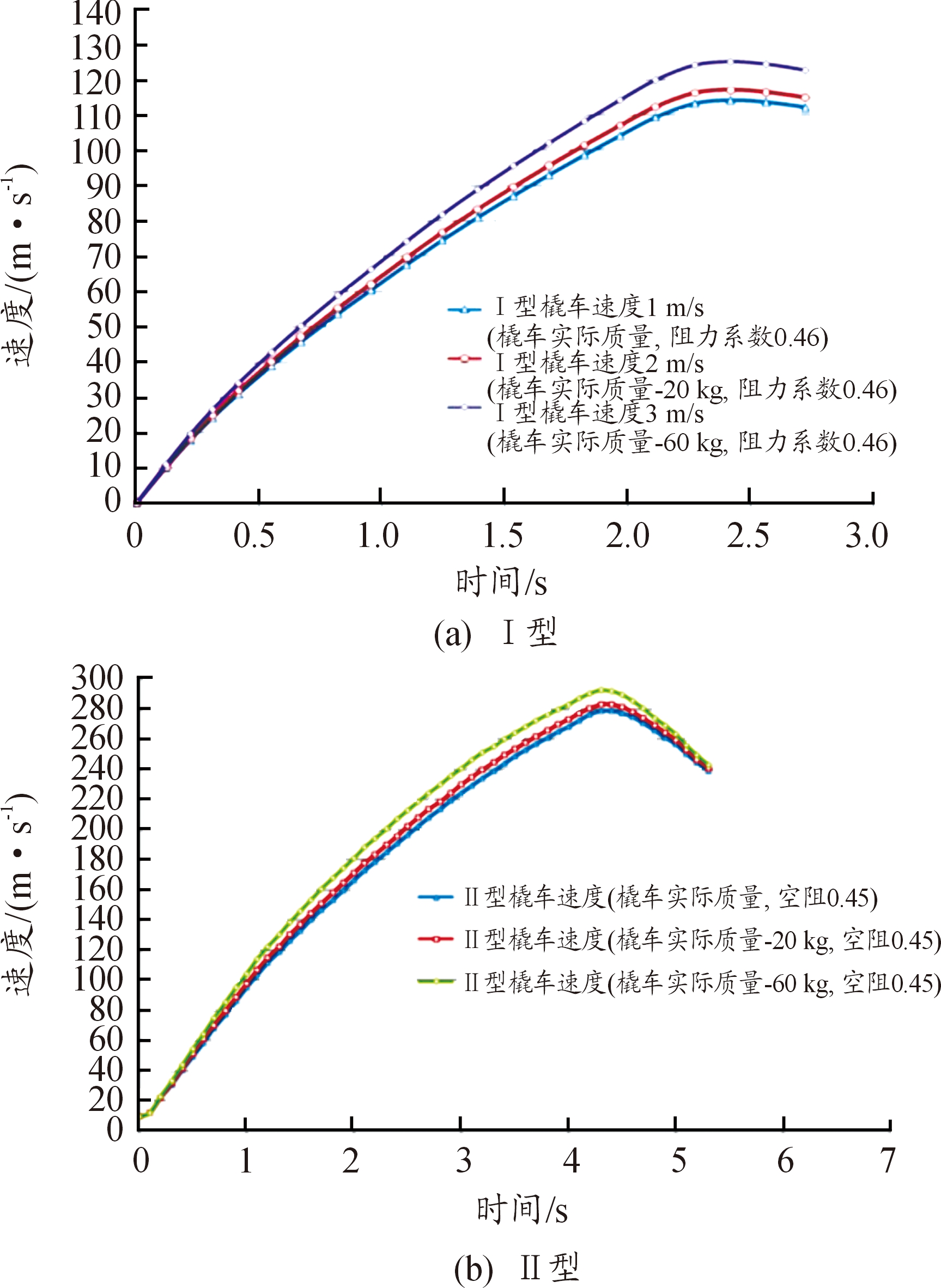
图8 在不同橇车质量下的速度变化曲线
3) 气动阻力系数对速度的影响
在不同气动阻力系数下的橇车速度变化如图9所示,从图9可以看出,对低速运动的Ⅰ型橇车,气动阻力系数对速度影响并不大,实际质量下,气动阻力系数为0.278和0.46时,速度分别为117 m/s和114 m/s(相差3m/s)。对高速运动的Ⅱ型橇车,气动阻力系数对速度影响很大,实际质量下,气动阻力系数为0.18和0.45时,速度分别为343 m/s和278 m/s(相差65 m/s)。对高速运动Ⅱ型橇车,气动阻力系数对橇车实际运行速度影响最大。
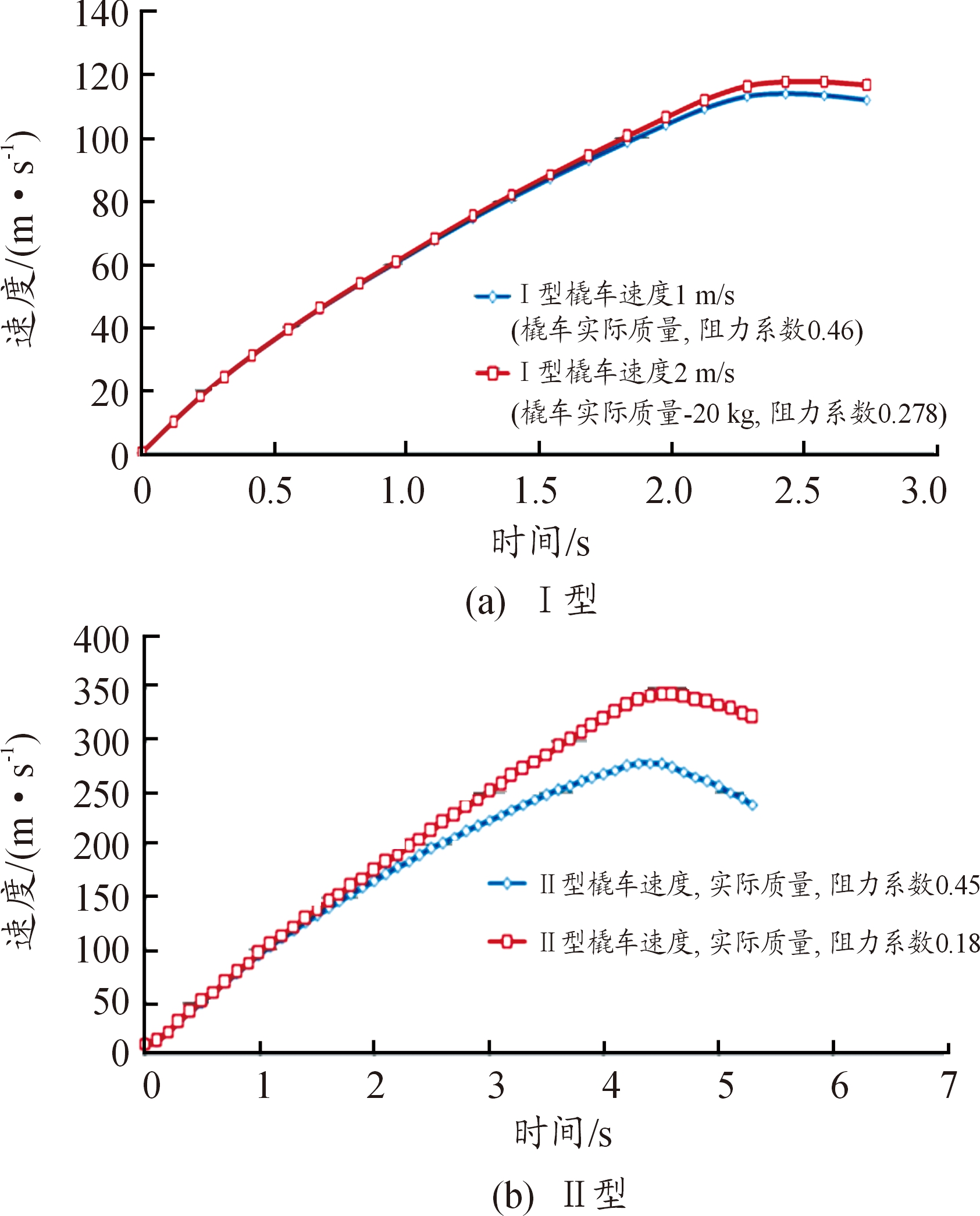
图9 在不同气动阻力系数下的橇车速度变化曲线
4) 火箭发动机推力对速度的影响
两型火箭发动机总冲基本相等,但实际推力和燃烧时间差别较大(具体见表1)。即使将B型火箭发动机更换为A型火箭发动机,Ⅱ型橇车最大速度也仅能从278 m/s提升至302 m/s(如图10所示),速度提升24 m/s,与橇车质量减少60 kg时,速度提升量(17 m/s)相差不大。但使用A型火箭发动机,并将气动阻力系数减小为0.18时,即使Ⅱ型橇车质量不减少,橇车速度也可以由278 m/s提升至360 m/s,速度提升82 m/s,速度提升量远高于橇车质量变化对速度的影响。
表1 常温下火箭发动机内弹道参数

参数名称A型火箭发动机B型火箭发动机最大推力/kN40.2132.21平衡推力/kN32.2327.89药柱燃烧时间/s3.614.25发动机工作时间/s3.825.12发动机总冲/(kN·s)115.30115.20

图10 在不同火箭发动机推力下的橇车速度变化曲线
通过上述分析,各影响因素对橇车速度影响所占的比例如表2所示。气动阻力系数过高是橇车运行速度偏低的决定性因素,由于气动阻力系数过高,导致橇车速度偏低所占的比例高到80%;火箭推力偏低(低于设计值),导致橇车速度偏低所占的比例达到16%;橇车速度较低时(≤120 m/s),由于橇车质量偏重,导致橇车速度偏低所占的比例达到80%;滑动摩擦因数过高对橇车速度的影响可以忽略。
表2 各影响因素所占比例
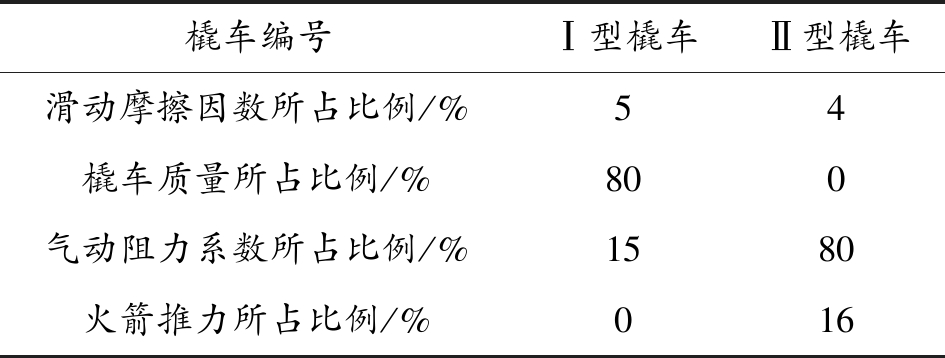
橇车编号Ⅰ型橇车Ⅱ型橇车滑动摩擦因数所占比例/%54橇车质量所占比例/%800气动阻力系数所占比例/%1580火箭推力所占比例/%016
4 结论
1) 高速运动时(对应表中Ⅱ型橇车),气动阻力系数对速度影响达到80%,是影响橇车速度决定性影响因素;火箭发动机推力对速度影响达到16%,是主要因素之一;滑动摩擦系数对速度影响为4%,是次要原因;橇车质量所产生的影响可以忽略。橇车设计时,要特别注意:气动阻力系数和发动机推力、燃烧时间是决定橇车运行速度的主要因素,橇车质量,对橇车速度也产生一定影响。
2) 根据外测速度、加速度、距离等参数,反向计算橇车气动阻力系数的方法简单可行,可用该方法指导常规兵器火箭橇试验时橇车设计工作。
3) 火箭橇橇车设计工作一旦完成,其最高速度已经固定,通过增加橇车质量和气动阻力系数的方法,可以向下调节橇车运行速度,拓展橇车速度适用范围;通过简单的更换火箭发动机型号、调整滑靴间隙和关键部位整流等方法可以小范围提升火箭橇运行速度。但如果需要大幅提升火箭橇运行速度,则需要重新设计橇车、选配火箭发动机。
[1] 邹伟红.火箭滑橇空气动力的数值模拟[D].南京:南京理工大学,2008.
[2] 钱翼稷.空气动力学[M].北京:北京航空航天大学出版社,2005.
[3] 刘军,李磊子.火箭橇气动阻力系数取值方法技术研究[C]//中国空气动力学会测控技术专委会第六届四次学术交流会.中国空气动力学会,襄阳:2013:15-18.
[4] 赵继波,赵峰,谭多望,等.火箭橇加载试验技术研究[J].爆炸与冲击,2007,27(06):572-576.
[5] 王元友.固体火箭发动机设计[M].北京:国防工业出版社,1984.
[6] 伍贻兆.跨声速空气动力学[M].北京:国防工业出版社,2004.
[7] 王铁城.空气动力学实验技术[M].北京:国防工业出版社,1986.
[8] XIAO J,LI X Y,ZHANG L R,et al.Brake force calculation for water-brake device in high speed of doub1etrack rocket sled test[C]//Proc.of the IOP Conference Series:Materials Science and Engineering,2019.
[9] XIAO J,XUE Q,ZHANG W W,et al.Design of Single Layer Vibration Dmping System for Rocket Sled[C]//Proc.of the 2018 Intermatational Conference on Physics,Mathematics,Statistics Modelling and Simulation,Wu Zhen,China,2018:16-18.
[10] ZHANG WW,XIAO J,ZHANG L R,et al.The Measurement Data Processing Method of Speed Sensor in Rocket Sled Whole Course Speed Measurement[C]//Proc.of the2019 IEEE 3rd international conference on electronic information technology and computer engineering,Xianmen 2019:18-20.
[11] 肖军,李新颖,张林锐,等.高速双轨橇车水刹车强度校核[J].兵器装备工程学报,2019(01):16-18.