大型地下工事,机库等重点目标均存在通风管道,通风管道包括直管道和弯曲管道,高空核电磁脉冲可以通过管道进入工事、机库内部,可能造成电子元器件失灵,逻辑电路翻转,电子系统崩溃的严重后果。因此针对管道核电磁脉冲耦合响应研究十分必要,研究结果可为管道抗核电磁脉冲加固提供参考。
通风直管道的高空核电磁脉冲耦合响应已有相关研究,但由于建筑形态各异,通风系统中广泛存在的管道网络,支路连接,拐弯情况不可避免出现,弯曲管道的高空核电磁脉冲耦合响应研究未见相关文献,故开展相关研究具有重要意义。
高空核电磁脉冲具有极高强度的能量,具有峰值场强高,频谱范围宽,前沿极陡峭的特点[1],对电子元器件具有极大威胁,可以通过传导耦合、辐射耦合的方式作用于天线、电力线、元件等物体,产生极高的场强、电压、电流,破坏系统或设备[2]。广大学者对高空核电磁脉冲进行了深入研究,谢彦召等[3]分析了核电磁脉冲波形标准及特性,张举丘等[4]通过数学公式推导,结合计算机编程技术计算研究了高空核电磁脉冲对埋地油气管道、架空油气管道的耦合问题。王晨东等[5]基于BLT方程分析了埋地管道的电磁脉冲响应规律,刘青等[6]研究分析了埋地管道核电磁脉冲的响应不确定度量化。从上述文献可知,核电磁脉冲及管道的研究比较丰富,但通风管道和油气管道不同,尤其是弯曲管道,涉及到脉冲的反射叠加问题,且管道功能不同,设计参数也各异,可能随工事、机库各异呈现多样化。通风直管道的核电磁脉冲响应已有研究,因此针对通风弯管道的响应分析很有必要。
1 高空核电磁脉冲
高空核电磁脉冲一般指距地面40 km以上的高空核爆炸产生的瞬发γ射线与周围空气介质相互作用产生的辐射瞬变电磁场,源区场强可达105 V/m量级[7]。由于产生的电磁脉冲能量强度大,覆盖范围广,爆心视界范围内皆能受到攻击,因此相比地面核爆与低空核爆更受关注。高空核爆炸发生后,地面可以测到3种波形,分别为早期E1波形,中期E2波形,晚期E3波形[8],E2和E3部分主要威胁较长电力线和中低频设备,E1部分蕴含能量占据整体能量的99%,对电子系统及设备干扰破坏最为明显[1],因此高空核电磁脉冲研究主要针对E1部分进行分析。国内外通常使用双指数形式来模拟高空核电磁脉冲波形。其表达式为
E(t)=E0k(e-βt-eαt)
其中E0=50 kV/m,为场强最大值,k=1.30(IEC标准),为修正系数,α=4.0×107/s,为脉冲前沿参数, β=6.0×108/s,为脉冲后沿参数。其时域波形如图1所示。
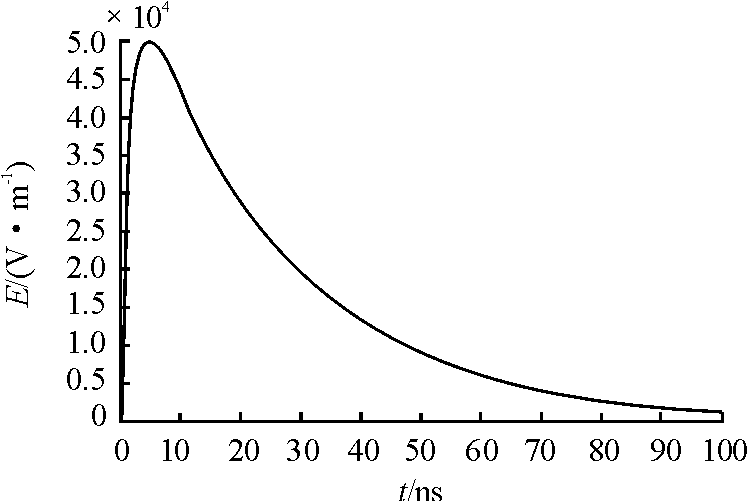
图1 高空核电磁脉冲时域波形
2 通风弯管道电磁环境研究
2.1 标准通风弯管道模型
通过控制单一变量的方法研究通风弯管道内电磁环境的影响因素。首先建立一个标准弯曲管道模型,在模型内部设置合理的测量点,高空核电磁脉冲从管道左侧垂直入射进入管道内部,通过有限积分法对管道内部电磁场分布进行仿真计算,得到管道内部电磁场分布情况,研究其他变量的影响时,在标准弯曲管道模型基础上保持单一变量,改变管道的弯曲位置和弯曲次数,设置相应的测量点,比较各个测量点的电场强度变化情况,分析弯曲管道内部影响电磁环境的主要因素。
设置标准模型为两次直角弯曲,管道半径为75 cm,管道厚度为1 cm,管道为金属铁材质,管道总长度约为7 700 cm,分为长管道3 000 cm,第1个拐弯471 cm(所有拐弯半径为300 cm),中间连接部分管道750 cm,第2个拐弯471cm,长管道3 000 cm。在标准模型入射端口,坐标为(-3 300,750,0),弯曲管道前端,坐标为(-300,750,0),弯曲管道中部连接处,坐标为(0,100,0),第2个弯道后部,坐标为(400,-600,0)4个地方设置测量点,标准模型及测量点位置如图2所示。
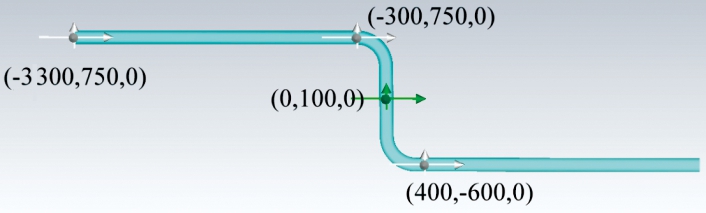
图2 标准弯曲管道模型示意图
仿真计算得到通风弯管道内部各测量点耦合场强,从图3可以看出:随着距离管道端口长度的增加,耦合响应得到的场强数值在减少,入射端口处初始场强为42 350 kV/m。259 ns有一个极高峰,峰值为72 449 kV/m,通过电磁波理论分析得出,这个极高峰是第一道入射波传入管道后,在弯道内壁面反射的回波和入射波叠加造成的。此时场强极高,大大高于入射波场强。
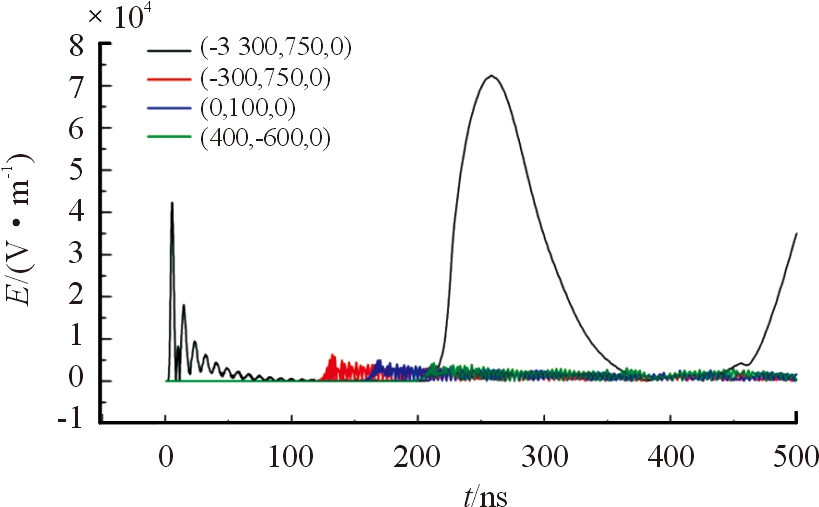
图3 测量点仿真计算结果曲线
管道横截面上场强分布不均匀,仿真计算出口处横截面上的耦合场强,通过计算结果分析横截面上场强分布的规律,并找出最大场强值。在半径为75 cm的横截面上,竖直向下的直径标号为1,每30°顺时针旋转步进一次,每30°步进时所处直径间隔15 cm设置测量点,测量点分布位置如图4所示,仿真计算结果如表1所示。
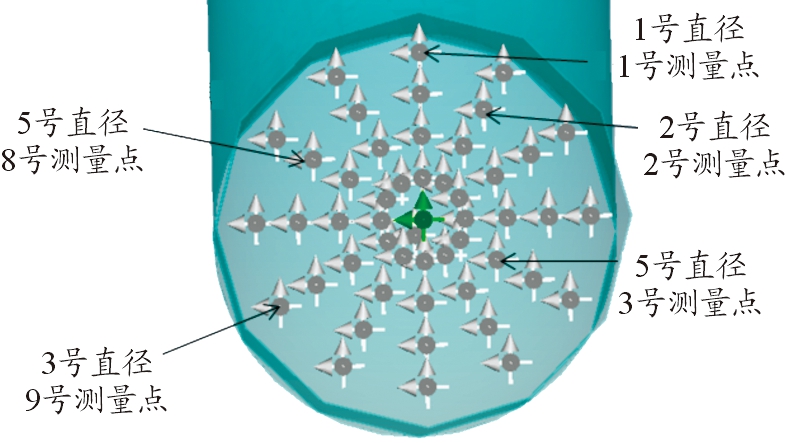
图4 横截面处测量点分布位置示意图
由表1可以看出:管道出口处横截面耦合场强最大值在1号直径最下面的测量点出现,即横截面中轴线最下面的点,场强值为165 613 V/m,是入射场强最大值50 000 V/m的3倍多。分析1号直径测量点,最大值为最下面的测量点,次大值为最上面的测量点,且由最大值降序排列时,测量点下面,上面对称位置交替排列,越靠近中点耦合场强数值越小,在中点达到最小值,且最小值为81 871 V/m,仍旧远大于入射最大场强50 000 V/m,但和横截面最大值相比小了一半以上。
表1 测量点最高耦合场强
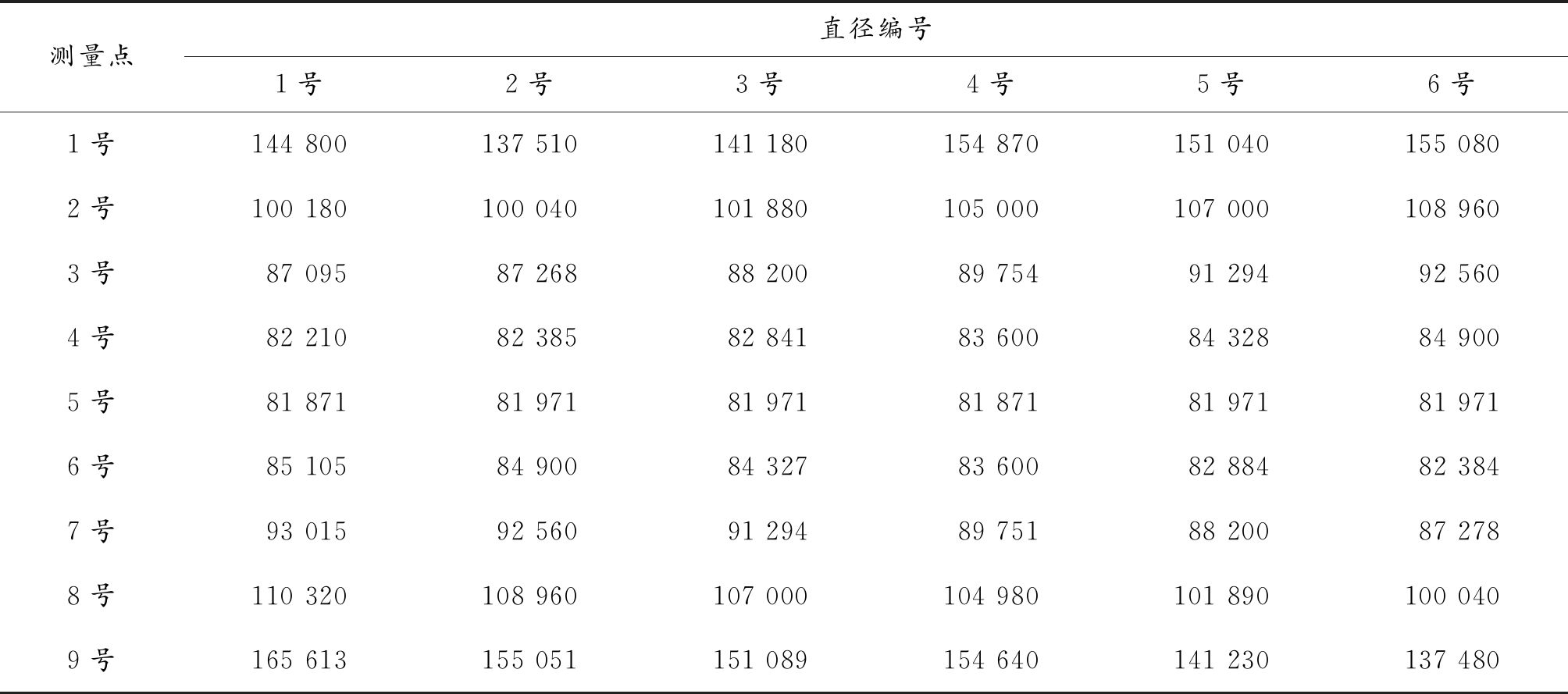
测量点直径编号1号2号3号4号5号6号1号144 800137 510141 180154 870151 040155 0802号100 180100 040101 880105 000107 000108 9603号87 09587 26888 20089 75491 29492 5604号82 21082 38582 84183 60084 32884 9005号81 87181 97181 97181 87181 97181 9716号85 10584 90084 32783 60082 88482 3847号93 01592 56091 29489 75188 20087 2788号110 320108 960107 000104 980101 890100 0409号165 613155 051151 089154 640141 230137 480
按照同样的方法在距出口18 m处研究横截面场强耦合规律,可以得到,在管道内部,横截面上场强大小比较接近,最大耦合场强为4 975 V/m,中心处耦合场强为4 047 V/m,和横截面最大值相比减少了18.7%。
管道出口处横截面上的耦合场强规律和管道内部耦合规律具有较大差别,总的来说,中心处耦合场强最弱,管道截面下部比上部对称位置处耦合场强要大,且最大场强耦合处接近管道底端。
2.2 通风管道弯曲位置影响
在标准通风弯管道模型基础上,改变通风管道弯曲位置,在距离管道入射端口10 m、30 m、50 m处弯曲管道,同时在距离管道入射端口5 m、25 m、45 m处对场强进行仿真计算,使得每个计算点距离弯曲位置5 m,同时针对每种工况对管道入口处,管道出口处进行计算仿真,针对仿真数据进行分析得到通风弯管道弯曲位置对电磁脉冲耦合响应的影响。图5~图7为弯曲位置示意图。

图5 弯曲位置示意图(距端口10 m处)
图6 弯曲位置示意图(距端口30 m处)

图7 弯曲位置示意图(距端口50 m处)
针对以上3种工况进行仿真计算,比较分析3种工况下,管道入口处,弯曲位置前5 m处,管道出口处的耦合场强。耦合场强如图8~图10所示。

图8 入射口、弯曲前5 m处及出口处耦合场强(10 m处弯曲)曲线

图9 入射口、弯曲前5 m处及出口处耦合场强(30 m处弯曲)曲线
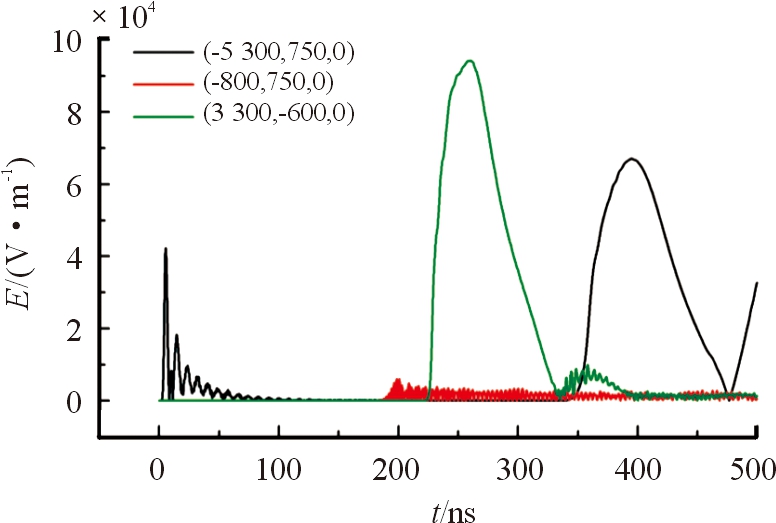
图10 入射口、弯曲前5 m处及出口处耦合场强(50 m处弯曲)曲线
由以上3种不同弯曲位置的耦合场强计算结果分析,管道入射端口处初始耦合场强分别为42 349 V/m、42 351 V/m、42 351 V/m,3个数值基本一致。分析入射端口出现的极高峰,管道弯曲位置距离入射端口越近,第1个反射回波和入射波叠加的极高峰出现时间越短,峰值越高。10 m、30 m、50 m 处弯曲情况第1个反射回波峰值依次为83 972 V/m、72 449 V/m、66 986 V/m,由于波的叠加,使得极高峰峰值场强超过入射波。峰值场强随着弯曲位置距离入射端口长度增加而减少,这也符合随着管道长度增加能量衰减的规律。
分析弯曲管道出口处的耦合场强,此时极高峰出现是因为电磁脉冲传播到管道出口处,管道出口处涉及到2种介质的阻抗匹配问题。此时阻抗匹配失衡,管道出口处出现的极高峰可能是反射回波和入射波叠加造成在。分析管道出口处峰值场强,分别为76 468 V/m、82 104 V/m、94 196 V/m,3个数值以此增加,管道出口处峰值场强极高,并随着管道弯曲位置距离入射端口长度增加而增加。在管道出口处应着重考虑电磁脉冲的相关防护问题。
2.3 通风管道弯曲次数影响
在标准通风弯管道模型基础上,改变通风管道中间弯曲长度,使上下两节长管道之间落差为18 m,以保证高度适应多次弯曲,设置弯曲次数为2次、4次、6次,对距离管道出口前12 m、15 m、17 m,进行仿真计算,保证计算点距弯曲管道入口处距离一致,空间相对位置一致,管道总长一致,通过数值仿真分析管道弯曲次数对管道内部耦合场强的影响。图11~图13为不同弯曲次数示意图。
图11 弯曲2次管道模型示意图

图12 弯曲4次管道模型示意图
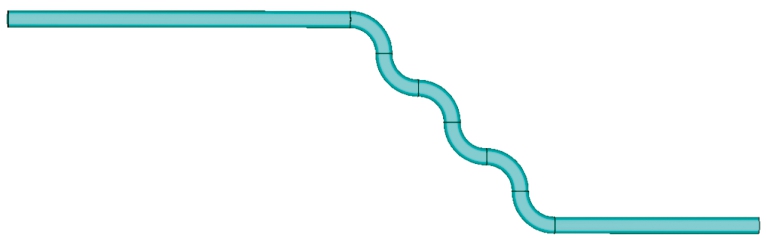
图13 弯曲6次管道模型示意图
针对3种管道模型,分别进行仿真计算分析,结果如图14~图16所示。
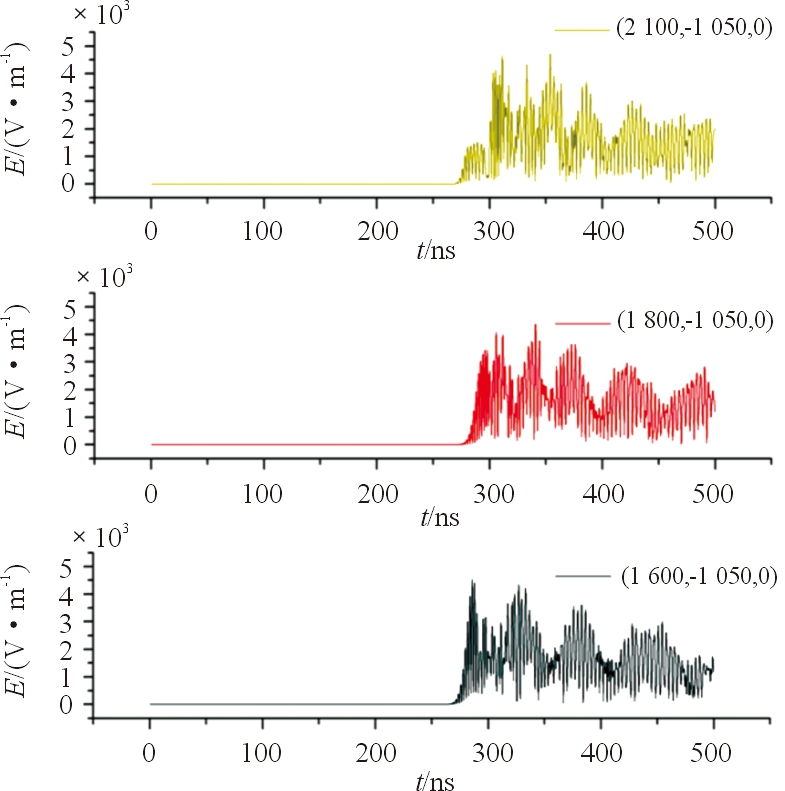
图14 弯曲2次耦合场强仿真曲线
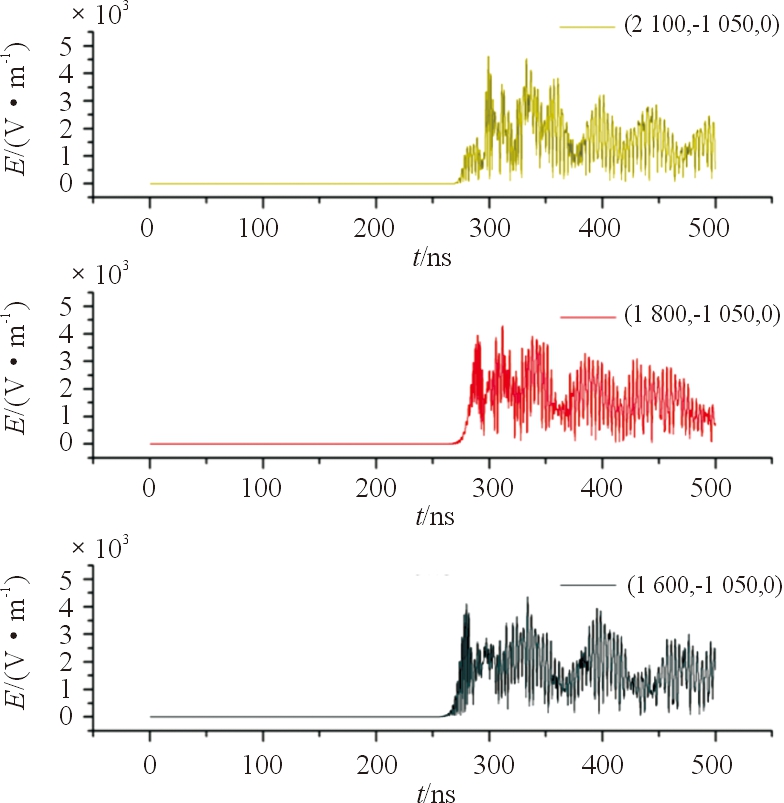
图15 弯曲4次耦合场强仿真曲线
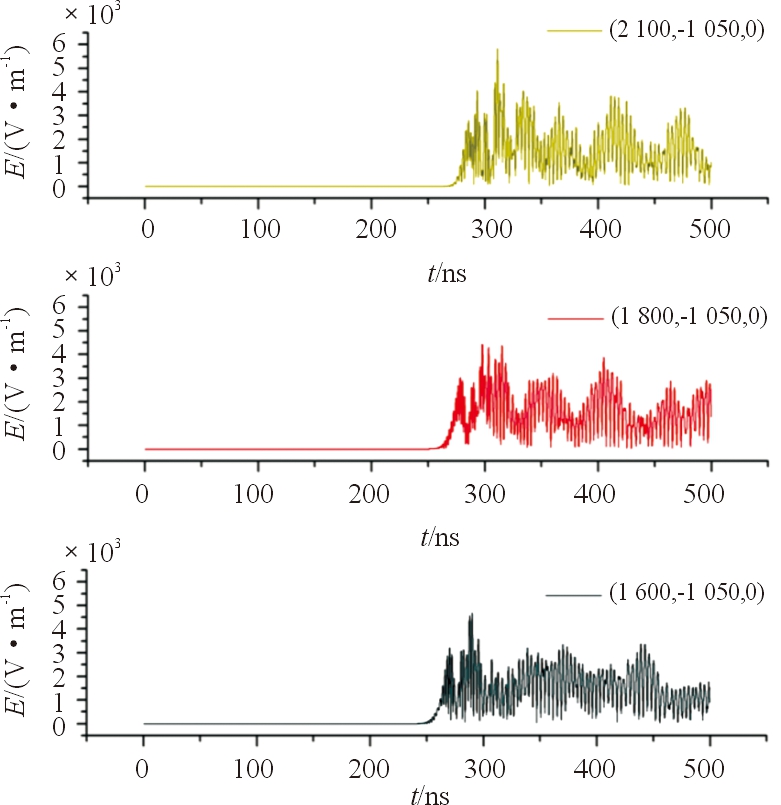
图16 弯曲6次耦合场强仿真曲线
3种管道弯曲次数工况下,在距出口12 m处耦合场强最大值分别为4 716 V/m、4 630 V/m、5 835 V/m,在距出口 15 m 处耦合场强最大值分别为4 374 V/m、4 308 V/m、4 430 V/m,在距出口17 m处耦合场强最大值分别为4 540 V/m、4 376 V/m、4 689 V/m,由以上数据可以分析得出,管道弯曲次数从2~4次,管道内部相同点耦合场强降低,但是从弯曲次数4~6次,耦合场强却增加,弯曲2次情况增加最为明显。增加管道弯曲次数可能增强管道内部最强耦合场强,也可能降低管道内部最强耦合场强。
值得注意的是,管道出口前管道内部耦合场强大体出现振荡趋势,这可能和管道出口与空气相接出现阻抗匹配失衡导致的回波与入射波叠加有关,分析管道弯曲次数和距管道出口处相同长度点的第1次极值耦合场强,在距出口15 m处第一次极值耦合场强分别为4 070 V/m、3 971 V/m、3 030 V/m,在距出口17 m处第1次极值耦合场强分别为4 540 V/m、4 120 V/m、3 200 V/m。以上2个点第1次出现极值的场强大小和弯曲次数有关,场强随着弯曲次数增加而降低,距出口17 m处弯曲4次相比弯曲2次降低了2.4%,弯曲6次相比弯曲4次降低了23.7%,距出口15 m处分别降低了9.3%、22.3%,故可以断定,增加弯曲次数可以降低管道内部初始耦合场强,但必须考虑管道出口阻抗匹配失衡造成的回波叠加。在现实情况中,弯曲次数和回波叠加须协调分析处理。
2.4 标准弯曲管道耦合场强数据分析
针对标准弯管道,仿真计算管道内部各个点耦合场强数值,通过数据分析得出电磁脉冲在管道内部传播的规律。
将表2数据绘制成图,横坐标为距管道入射口距离,纵坐标为耦合场强,由于入射处端口场强极大,故舍去入射处端口场强,将其余数据绘制成图,直观了解耦合场强随时间变化规律,如图17所示。
表2 标准弯管道第1部分横管道耦合场强数据
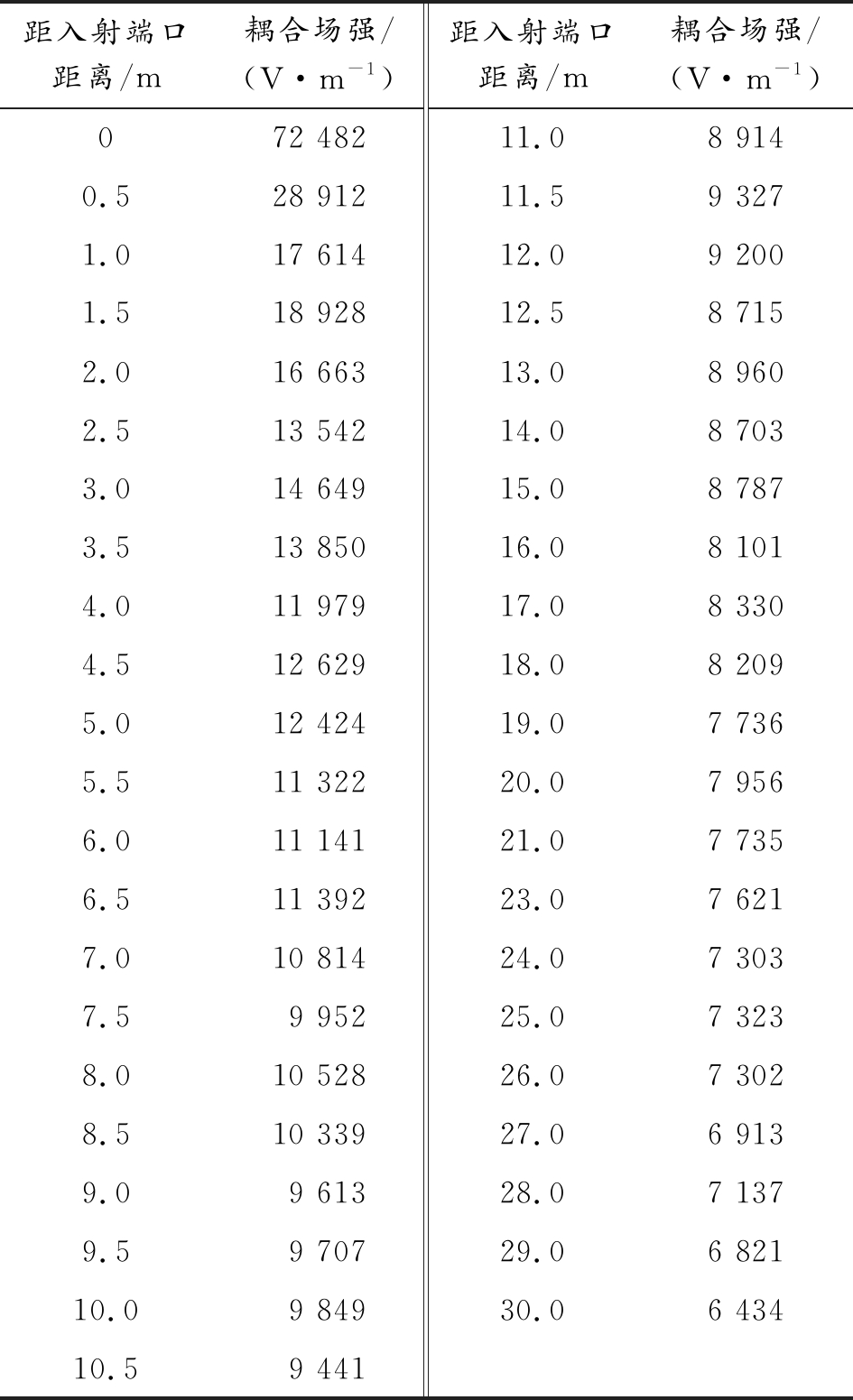
距入射端口距离/m耦合场强/(V·m-1)距入射端口距离/m耦合场强/(V·m-1)072 48211.08 9140.528 91211.59 3271.017 61412.09 2001.518 92812.58 7152.016 66313.08 9602.513 54214.08 7033.014 64915.08 7873.513 85016.08 1014.011 97917.08 3304.512 62918.08 2095.012 42419.07 7365.511 32220.07 9566.011 14121.07 7356.511 39223.07 6217.010 81424.07 3037.59 95225.07 3238.010 52826.07 3028.510 33927.06 9139.09 61328.07 1379.59 70729.06 82110.09 84930.06 43410.59 441
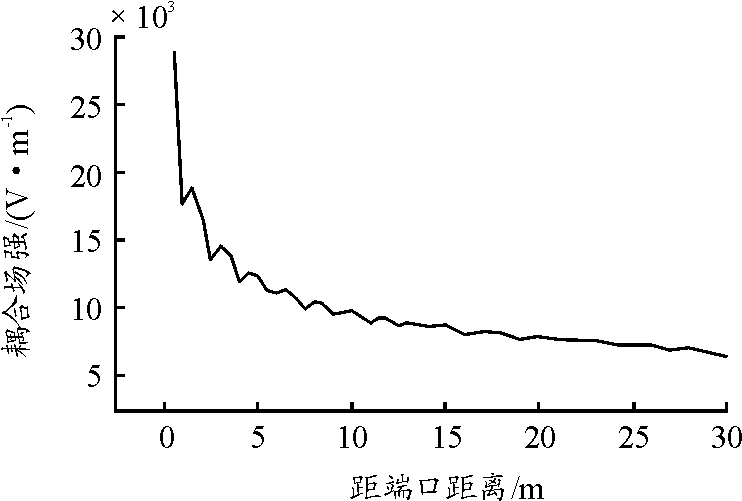
图17 第1部分横管道耦合场强随距入口处距离变化曲线
由图17可以看出:耦合场强大体随着入射距离增加而减少,在入射端口处减小的较为迅速,随着入射距离增加,减小的速度减缓。
将表3数据绘制成图,横坐标为距上管道中轴线垂直距离,纵坐标为耦合场强,如图18所示。
表3 标准弯管道第2部分竖直管道耦合场强数据
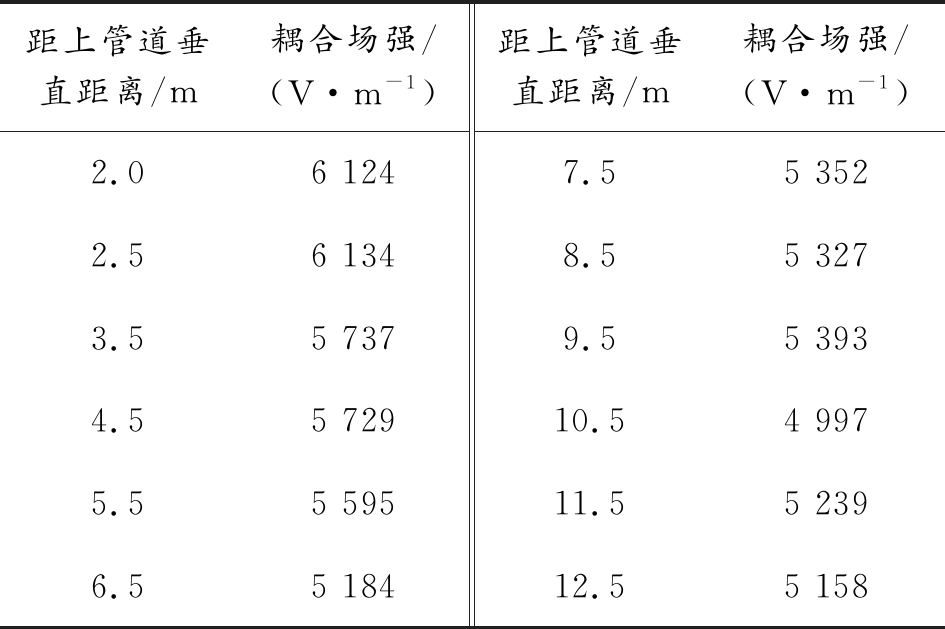
距上管道垂直距离/m耦合场强/(V·m-1)距上管道垂直距离/m耦合场强/(V·m-1)2.06 1247.55 3522.56 1348.55 3273.55 7379.55 3934.55 72910.54 9975.55 59511.55 2396.55 18412.55 158
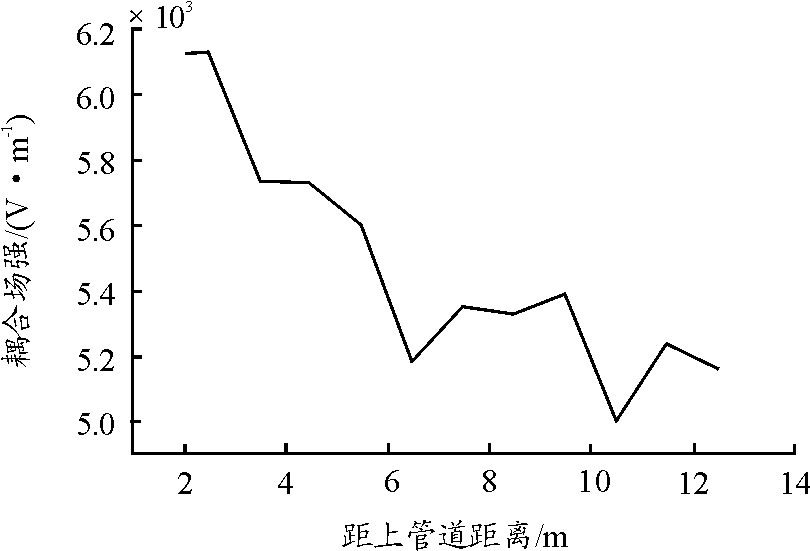
图18 中间竖直管道耦合场强随距上管道距离变化曲线
由图18可以看出:竖直管道耦合场强大体随着距上管道距离增加而减少,减少幅度较小,局部有异常波动,数值上升,这种情况可能和竖直管道出口处和横管道相连接,电磁脉冲在管道内部反射回波和入射波叠加有关。
将表4数据绘制成图,横坐标为距中间竖直管道中轴线距离,纵坐标为耦合场强,如图19所示。
表4 标准弯管道第3部分横管道耦合场强数据
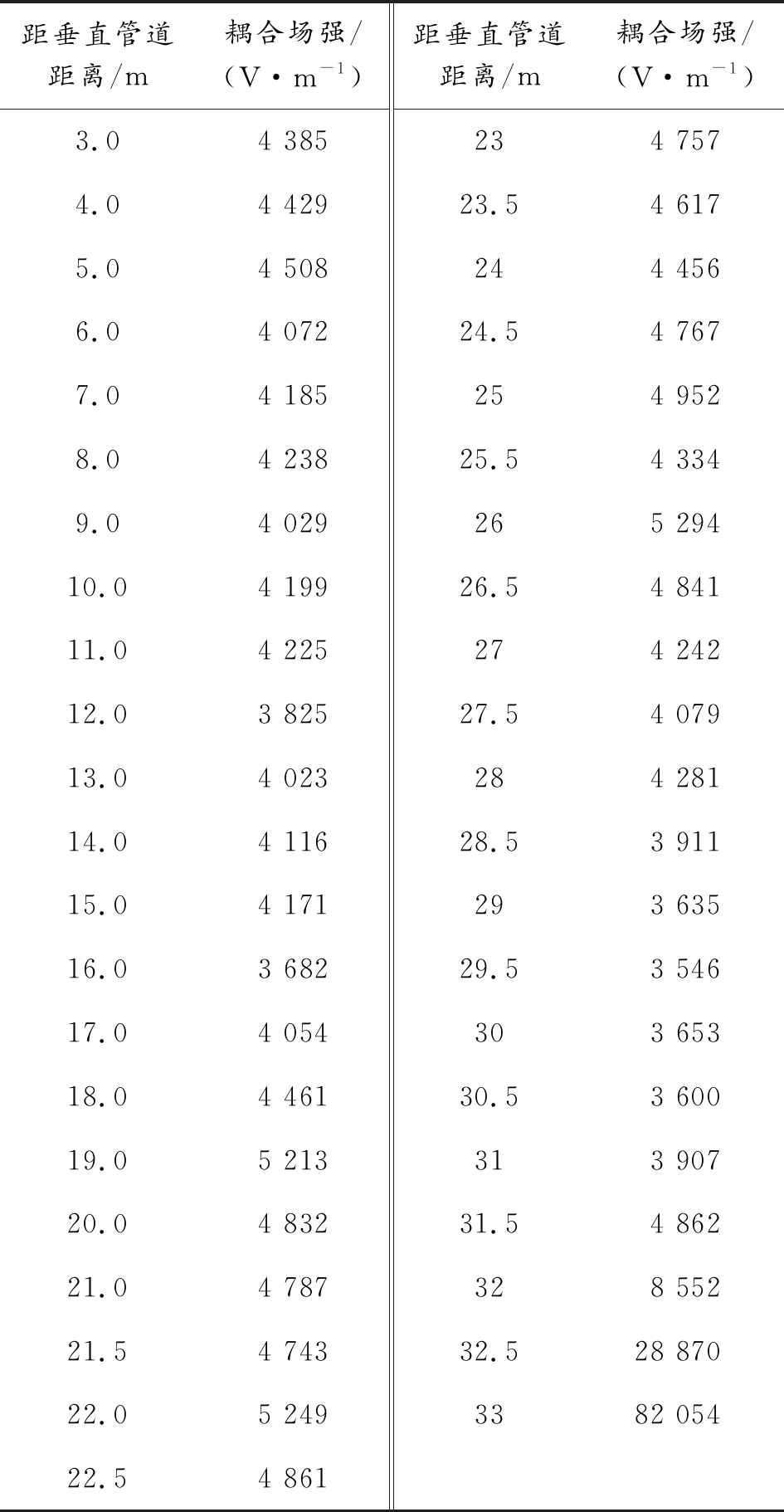
距垂直管道距离/m耦合场强/(V·m-1)距垂直管道距离/m耦合场强/(V·m-1)3.04 385234 7574.04 42923.54 6175.04 508244 4566.04 07224.54 7677.04 185254 9528.04 23825.54 3349.04 029265 29410.04 19926.54 84111.04 225274 24212.03 82527.54 07913.04 023284 28114.04 11628.53 91115.04 171293 63516.03 68229.53 54617.04 054303 65318.04 46130.53 60019.05 213313 90720.04 83231.54 86221.04 787328 55221.54 74332.528 87022.05 2493382 05422.54 861
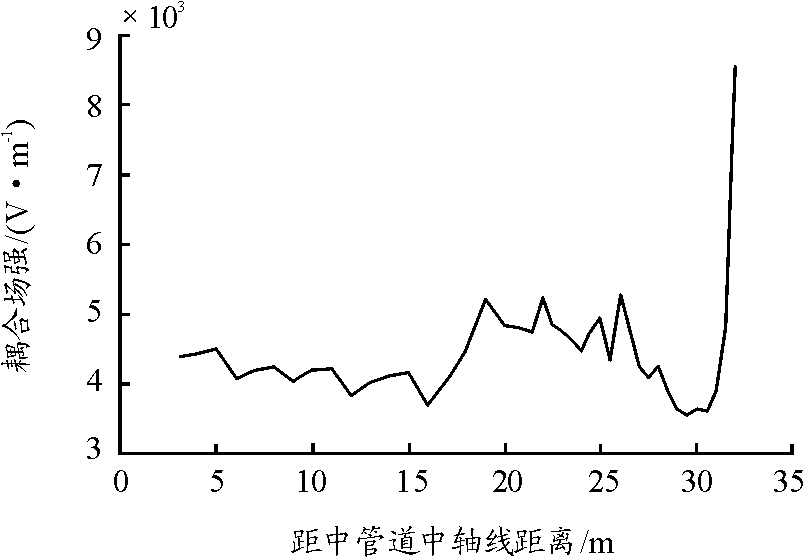
图19 第3部分横管道耦合场强随距竖直管道距离变化曲线
由图19可以看出:第3部分横管道耦合场强在刚开始波动下降,但下降幅度极小,紧接着有较大幅度上升,然后产生振荡,场强上下波动,在管道末端,场强较快下降又急剧上升,管道末端和空气相连接,涉及阻抗匹配问题,较为复杂,反射回波和入射波叠加造成管道内部耦合场强振荡及出口处场强异常急剧上升。
针对管道末端和空气相连接的的出口处场强急剧上升的现象,可以在管道入口处增加金属网,或者增加金属蜂窝波导结构[9],金属网和波导结构会吸收反射一定量电磁波,降低管道内部电磁脉冲能量,或者使管道接地[10],都能够有效减少管道内部耦合场强,进而减少管道出口处场强;在阻抗匹配方面,可以在端口处使用复合材料过渡,使电磁脉冲振荡叠加减少,进而降低管道出口处场强。
3 结论
高空核电磁脉冲在弯曲管道传播时,管道入口处由于反射波叠加造成耦合场强急剧升高,管道内部耦合场强随管道长度增加而减少,管道出口处由于阻抗匹配失衡导致反射波叠加,场强急剧升高。管道弯曲位置距管道入口处越近,管道出口处耦合场强越小。管道弯曲次数越多,初始耦合场强极值越小,但是最高耦合场强和管道弯曲次数没有明显关系。
[1] 谭志良,胡小锋,毕建军,等.电磁脉冲防护理论与技术[M].北京:国防工业出版社,2013.
[2] 刘培国,孙继斌,李高升,等.战场电磁环境效应对信息化战争的影响[J].军事运筹与系统工程,2006,20(03):43-47.
[3] 谢彦召,孙蓓云,周辉,等.地面附近的高空核爆电磁脉冲环境研究[J].强激光与离子束,2003(07):680-684.
[4] ZHANG J Q,LIANG Z S.Effects of high-ltitude electromagnetic pulse on buried pipeline[J].International Journal of Applied Electromagnetics and Mechanics,2017,55(04):5074-522.
[5] 王晨东,刘青,徐清秀.基于BLT 方程的埋地管道电磁脉冲响应规律[J].科学技术与工程,2018,18(28):93-98.
[6] 刘青,王晨东,李湛宇.埋地管道HEMP响应的不确定度量化[J].电工技术学报,2019,34(09) 1789-1797.
[7] 王坚,李路翔.核武器效应及防护[M].北京:北京理工大学出版社,1993.
[8] HOAD R,RADASKY W A.Progress in high-altitude electromagnetic pulse(HEMP) standardization-Ergin[J].IEEE Transactions on Electromagnetic Compatibility,2013,55(03):528-538.
[9] 王迪.HEMP环境下车辆电磁屏蔽技术防护效能研究[D].长春:吉林大学,2015.
[10] 周璧华,石立华,王建宝,等.电磁脉冲及其工程防护[M].2版.北京:国防工业出版社,2019.