机翼设计是现代飞行器设计过程中至关重要的环节,而其中机翼的质量对飞行器的综合性能表现有着显著影响[1-2]。因此在机翼设计过程中,不可避免的需要知晓机翼质量在不同设计参数条件下相对准确的估计值,从而更好的把握综合设计变量[3]。对于有相似布局的飞行器,在有足够多的相关质量统计数据的情况下,可以运用统计学方法得到质量估算的经验公式,Raymer[4]和Howe[5]等人系统发展了质量估算统计学方法,但该方法局限于相似的机翼结构布局、材料特性,且估算值一般存在10%左右的误差。而在科学工程领域有着广泛应用的有限元方法,因其计算精度高的优势,在飞行器结构质量计算过程中被逐渐采纳,欧阳星等[6-7]详细研究了该方法并取得了卓著的成效,但是该方法计算过程较为复杂,计算耗时较长,需要建立详细的有限元分析模型,所以往往存在着计算精度与计算成本之间的矛盾。
针对在方案初步设计阶段对小型巡航飞行器机翼质量快速准确预测的实际需求,本文在更为普遍应用的工程梁方法的基础上,把该方法进一步拓广,将机翼设计参数与结构尺寸、结构质量联系起来,构建一种参数-结构-质量计算框架,以实现便捷、准确的机翼质量估算。
1 机翼质量预测方法概述
众所周知,飞行器设计是一个涉及多重因素的复杂组织过程,各因素之间存在相互制约关系,也互相耦合影响[8],比如飞行器的结构质量会受到载荷分布、气动力、结构设计方案和几何外形等诸多因素的影响,而质量的变化又会导致翼载荷以及燃料质量的变化,进而对航程等其他参数产生影响。所以,准确预测结构质量对整体方案设计的可靠性与鲁棒性具有重要意义[9]。为了提高质量预测的精确性与可靠性,本文以有限元思想为指导,将各设计参数纳入考量范围,设计一种简易的梁式结构机翼质量计算方法:
由实际研究对象的设计参数初步确定机翼的平面形状与翼型;然后将机翼离散化为一系列翼段,把翼段内部结构等效简化为盒型梁、肋板、蒙皮面板等结构,由气动系数确定各种结构受载情况以及机翼各段的内部结构尺寸;最后结合具体的结构质量计算手段确定机翼各组成部件质量,将各段机翼结构质量叠加得到整体的机翼质量。计算流程如图1所示。
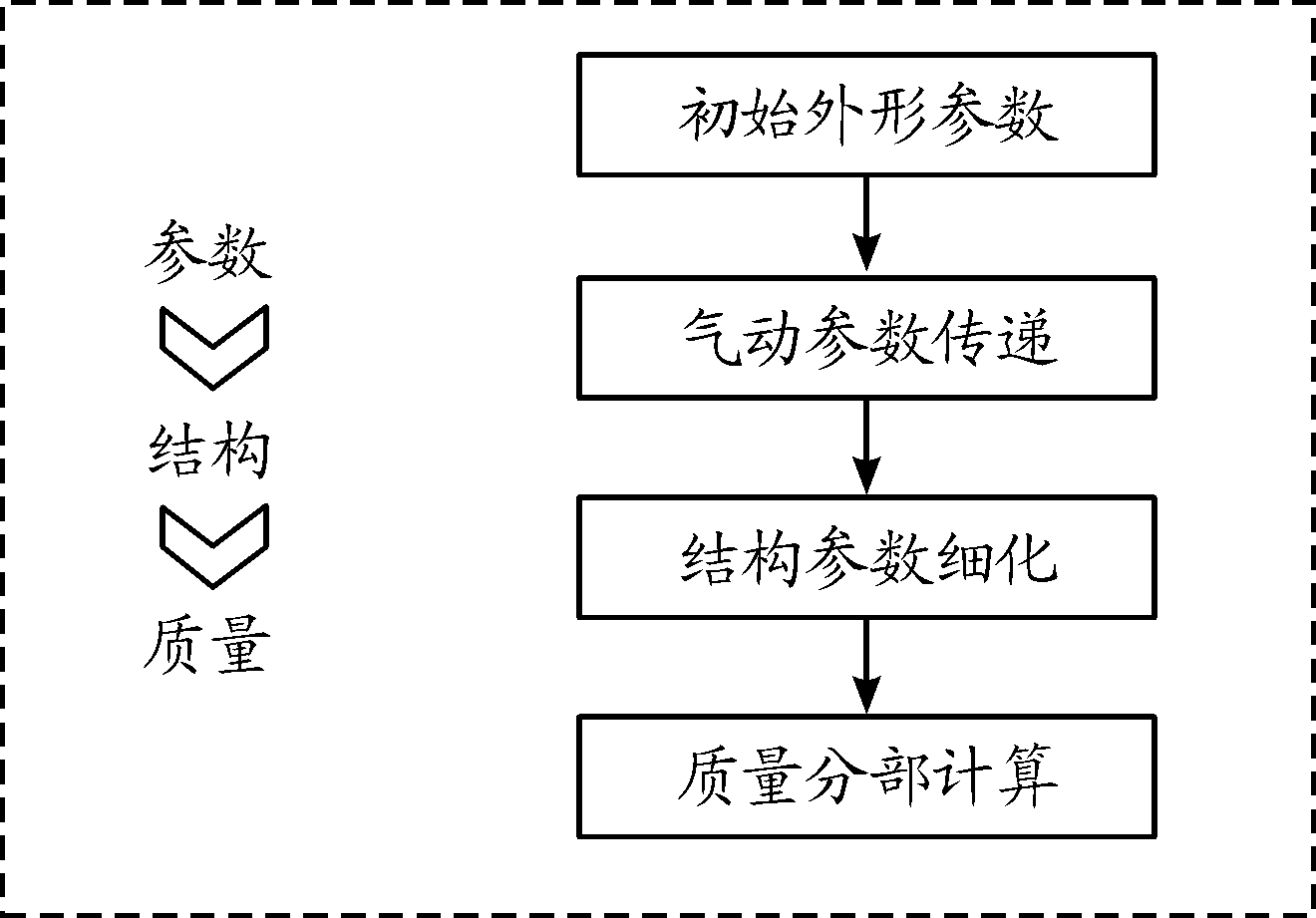
图1 机翼质量计算流程框图
2 具体计算方法
2.1 机翼外形参数化
要想明确机翼质量与结构参数之间的关系,首先得根据平面几何参数以及翼型相关数据,建立机翼初始模型,为气动参数及结构尺寸确定奠定基础。
本文取机翼的根弦长度CR、梢弦长度CT、前缘后琼角Λ、半展长b来确定机翼平面外形,如图2所示。翼型参数坐标点通过翼型数据库软件获取。
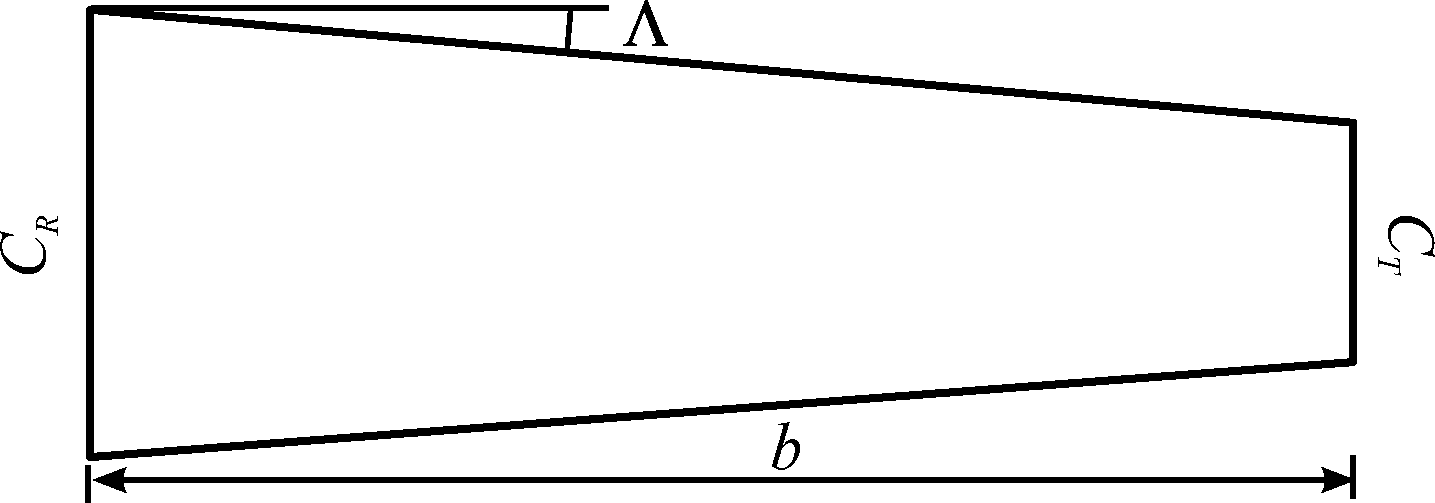
图2 机翼参数及外形简化示意图
2.2 气动载荷分析
机翼在飞行过程中具体的载荷分布对机翼的内部结构形式和结构质量均有重要影响,所以机翼质量估算一般从机翼的载荷分析入手,由飞行器实际飞行工况确定机翼所受各种载荷情况,再将受载情况分解到机翼各部分载荷结构中,进一步结合具体的材料特性参数确定该部件的结构质量[10-11]。
为了快捷的建立飞行器的参数化模型,并估计其气动参数。本文利用参数化飞行器设计工具OpenVSP[12]来快速创建由通用工程参数所定义的飞行器三维模型。然后根据实际的飞行马赫数、飞行高度、攻角等工况,应用OpenVSP中气动估算功能模块计算气动系数,图3所示为不同攻角条件下的升力系数随展向位置分布曲线。
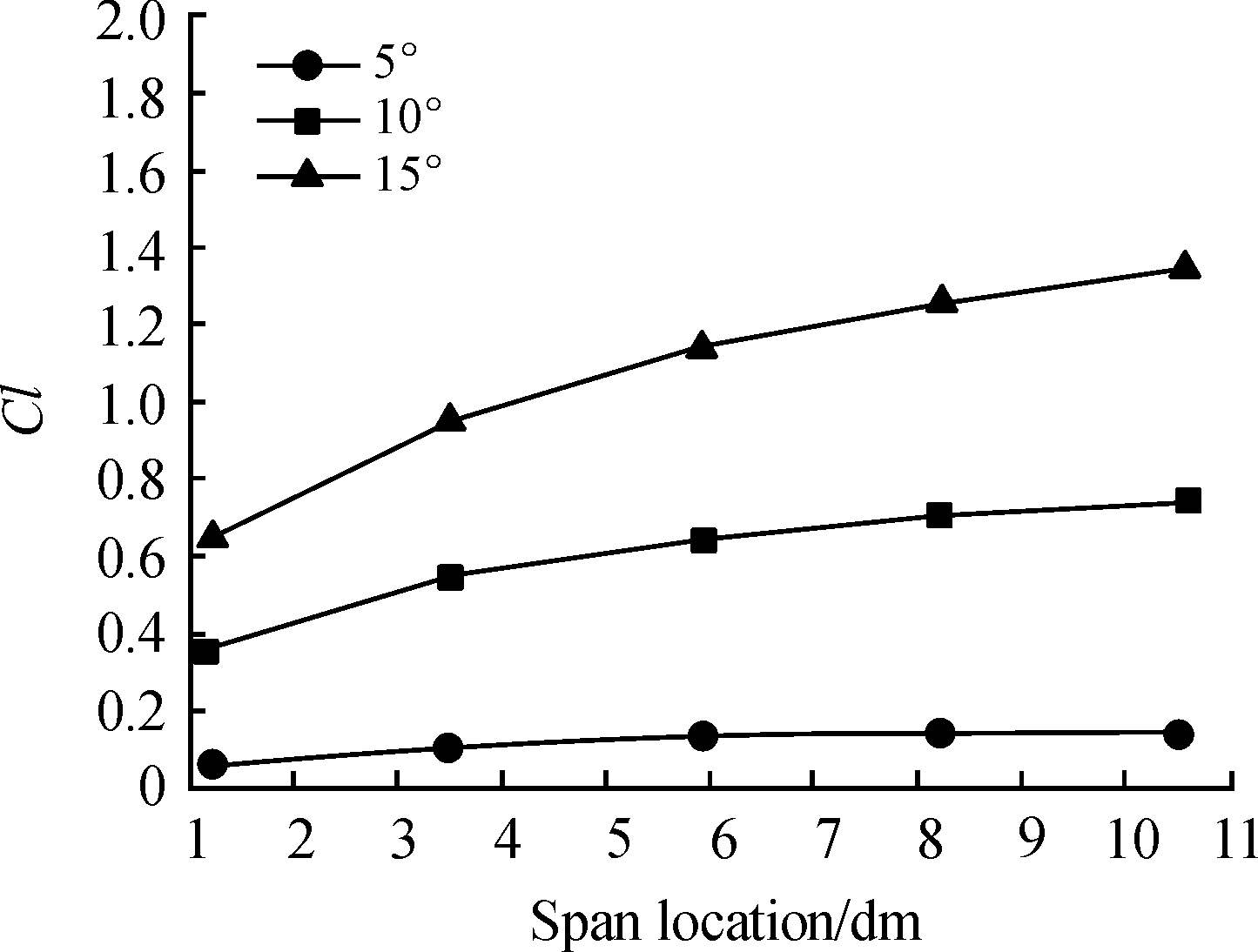
图3 升力系数展向分布曲线
根据文献[13],可将气动力系数转化为力载荷,再以展向载荷分布的形式加载到离散化的翼盒结构单元中。展向位置载荷分布w(y)按下式计算:
(1)
式中: CL为飞行器的整体设计升力系数;cav为机翼几何平均弦长;Cζ(y)为局部升力系数;y为机翼展向相对翼根位置;c(y)为展向任意位置弦长,计算方式为:
![]()
(2)
本文所研究的对象为小型巡航飞行器的近似梯形直翼,其局部升力系数可根据升力线理论通过机翼展向环量函数来表示[14]:
(3)
式中: S为机翼的有效面积,![]() 为升力系数的展向分布。
为升力系数的展向分布。
2.3 翼段质量估算参数化模型
由于在机翼展向的不同位置,翼梁与蒙皮等结构的承载情况与结构尺寸也不同。为了精确化分析结构质量,根据图2所示的参数化外形模型,将整体的机翼结构沿展向离散化为一系列连续的机翼段单元,分别计算各段的结构质量。为简化计算流程,将机翼的分段部位与翼肋分布位置等同,具体计算原则详述于后文翼肋质量计算部分,机翼单元化离散示意图如图4。

图4 机翼离散化示意图
2.3.1 翼梁单元结构尺寸与质量
翼梁主要承受由升力产生的弯曲力矩与剪切力。计算时往往将翼梁的结构质量分解为承弯质量与承剪质量。机翼任意截面段的所受剪力大小为:
(4)
式中: q为动压,计算式为![]() 为实际飞行工况下的大气密度;v为飞行速度。
为实际飞行工况下的大气密度;v为飞行速度。
则承剪质量为:
(5)
式中: τs为材料许用剪切应力; ρl为翼梁材料密度。
翼梁的承弯质量一般计算为:
Wbi=(ρlg![]() A(y)dy)
A(y)dy)
(6)
式中A(y)为翼梁的等效截面积:
(7)
式中![]() 为效率因子,一般取0.81~0.84。有效深度d(y)可以近似为:
为效率因子,一般取0.81~0.84。有效深度d(y)可以近似为:
d(y)=δhmax(y)
(8)
式中δ是弯曲效率系数,一般取0.87~0.89[15]。hmax是第i段单元机翼的平均最大厚度(根据翼型参数计算)。t(y)为当前位置翼梁的厚度:
(9)
式中: fs是安全系数,一般取1.5; σs为材料许用弯曲应力; L为机翼实际升力; ηcp为翼段的压心参考位置,计算公式如下:
(10)
Myi为每个翼段上的弯矩分布函数:
(11)
2.3.2 蒙皮尺寸与质量
机翼蒙皮上受到直接的气动力载荷,由机翼空气动力学分析可知,飞行时上翼表蒙皮处于压缩状态,下翼表蒙皮处于拉伸状态。
因此,翼段内上下蒙皮厚度分别可通过以下公式计算:
![]()
(12)
![]()
(13)
式中: M是第i段机翼上的弯矩分布; σb是允许拉伸应力; σs是允许挤压应力; Cpu和Cpl为上下蒙皮的弦向长度。
根据在不同展向位置蒙皮的承载情况确定等效的上下蒙皮的厚度。则第i段机翼的蒙皮质量可以估算为:
![]()
(14)
式中: ρm为蒙皮的材料质量密度; wu和wl为翼型上下曲线的数值积分长度; z为机翼蒙皮表面的结构跨度:
![]()
(15)
2.3.3 翼肋质量
翼肋主要起到维持机翼外形,将上下蒙皮气动载荷传递给翼梁的作用,要想较准确地估算翼肋的质量,需要知道翼肋的拓扑结构,肋截面积、材料特性,以及翼肋沿机翼展向的分布、数量情况。机翼截面单元如图5所示。
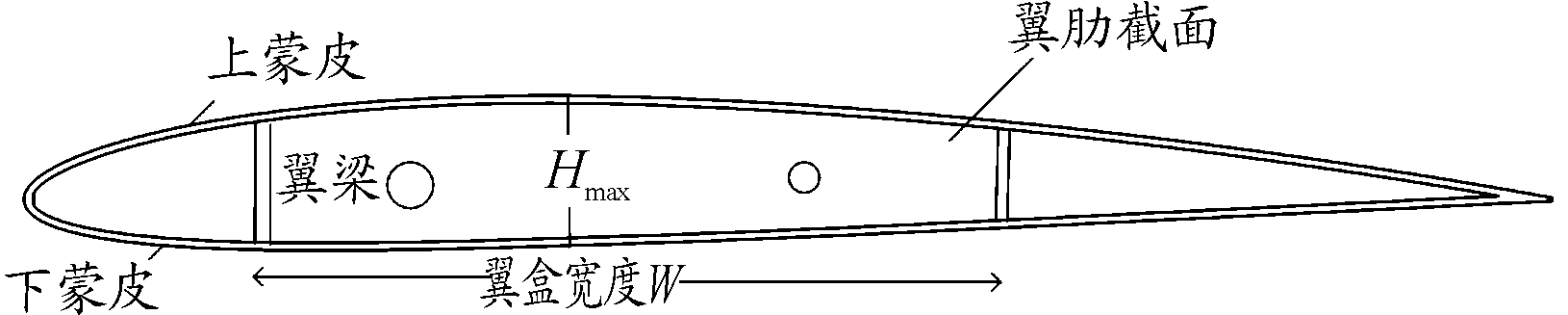
图5 翼肋截面单元示意图
采用Torenbeek的半经验方程式[16]的修正式来估算翼肋质量:
Wri=kexpkrρrSlidref
(16)
式中: kexp为经验校正因子; kr为经验常数,可以近似为5.5×10-4; ρr为翼肋的材料密度; Sli为第i个翼肋的截面参考面积。
计算方法如下:
Sli=c(yi)![]() (rui-rli)dx
(rui-rli)dx
(17)
式中: rui和rli分别为翼型上下曲线的归一化纵坐标值; dref为统计参考深度。
第i段翼盒的肋间距离l(i)可由机翼材料的极限抗压强度来间接确定[17]:
(18)
式中: F为材料的效率因子,一般取0.8~0.9; Et为材料切线模量; δucs为材料的极限抗压强度; P(i)为第i个单元的极限受压载荷强度。
由机翼总体参数及各单元肋间距的计算结果,进而可以确定翼肋的数量。
不同于客机和运输机等大型机翼的复杂结构,本文所研究对象没有发动机吊舱及油箱等结构,所以不考虑惯性卸载作用。
2.3.4 参数化整体质量计算模型
将各机翼段的质量相加,就得到机翼主要的结构质量,此外,还包括其他的机翼杂项质量包括胶漆、连接件、铆钉、局部开口加强部件、前后缘结构等次结构。其质量一般占机翼结构总质量的5%~10%左右。所以机翼的整体结构质量可以此来计算:
Wwing=∑(Wmpi+Wbi+Wri)+Wsec
(19)
3 算例验证与结果
根据上述计算方法,编程实现具体计算过程。计算中涉及的所有非参数系数,都由具体的机翼材料参数实际值确定。
3.1 计算框架
在建立好机翼质量估算模型后,开展不同参数组合下的机翼质量估算时,涉及到参数输入,气动参数获取,结构质量计算等重复性工作,人为计算效率低下且易出错。所以运用多学科联合优化软件Isight平台,搭建机翼结构质量计算框架,利用该平台可以方便的实现气动参数计算、结构受载分析与质量计算等组件调用及相关参数的传递,发挥其作为“软件机器人”的功能。如图6为计算流程框图。
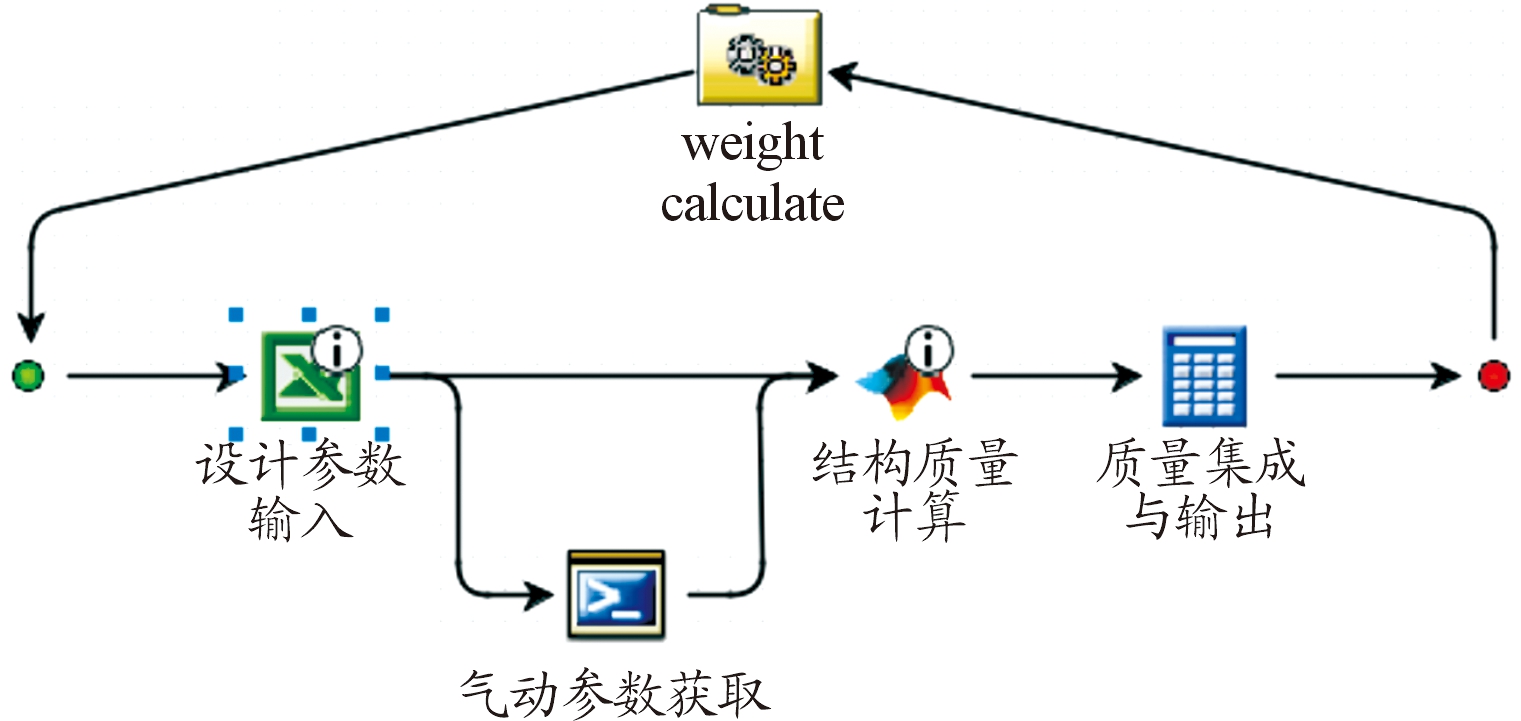
图6 Isight组件及计算框图
设计参数预先写入Excel工作表中,作为数据输入组件,将初始参数分别传递给质量计算程序和气动分析组件,然后质量计算组件结合气动数据进行质量计算,最后输出机翼结构质量。这样,可以在改变设计变量时通过软件自动调用组件,实现计算的高效性。
3.2 算例结果
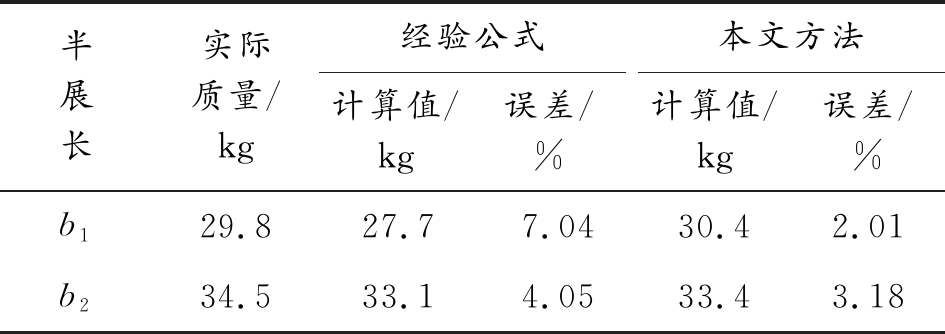
本文选取文献[18]中巡航飞行器模型的实际机翼设计参数作为算例验证数据。首先以半展长为变量,固定其他设计参数,分别运用本文计算方法与文献中经验公式方法计算机翼质量,结果如表1所示。
表1 机翼质量计算结果
半展长实际质量/kg经验公式计算值/kg误差/%本文方法计算值/kg误差/%b129.827.77.0430.42.01b234.533.14.0533.43.18
由表1计算结果可以看出本文方法的计算误差在4%以内,而且与传统经验公式相比,计算误差减少约1%~5%。
为了考量翼型参数对机翼整体质量的影响,固定半展长b2以及其他设计参数,分别选取3种不同的翼型(RAE2822、NACA2410、NACA64-110)计算机翼质量,得到如表2所示的结果。
表2 不同翼型机翼质量

翼型RAE2822 NACA2410NACA64-110机翼质量/kg37.333.435.9
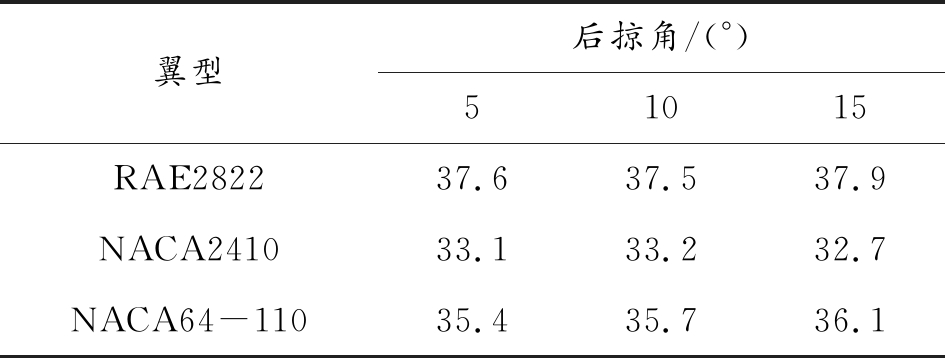
同样,上述3种不同翼型的计算基础上,以后掠角参数(分别取5°、10°、15°)为控制变量,计算得到机翼质量关于后掠角参数,如表3所示。
表3 不同后琼角机翼质量 kg
翼型后掠角/(°)51015RAE282237.637.537.9NACA241033.133.232.7NACA64-11035.435.736.1
由表2和表3的结果可以看出后掠角对机翼质量的影响相对翼型对质量的影响较小。
4 结论
本文在已知初始设计参数以及基本结构形式的情况下,将机翼设计参数、模块载荷分析、结构质量计算等环节联系起来,利用Isight平台集成分析模型的优势,便捷地实现了离散化机翼质量计算方法,并通过实例验证了该方法的准确性。
与经验公式法和有限元方法相比,这种离散单元方法将精度和计算复杂度进行了合理的折中,可以快速预测不同参数条件下的机翼质量,因此可以将该机翼质量预测框架集成到飞行器总体一体化设计中去,提供有效的质量学科支持。
本文的研究只针对简单机翼构型的质量估算,对于其他大型复杂构型机翼的质量计算还需详细研究;此外,还可以此模型为基础,以结构质量最小为设计目标开展机翼结构参数优化设计;也可以运用近似模型的数学原理,构建出机翼参数与质量之间的高精度响应面模型。
[1] 胡婕,王如华,王稳江,等.客机机翼气动结构多学科优化方法[J].南京航空航天大学学报,2012,44(4):458-463.
[2] WRIGHT J R,COOPER J E.Introduction to Aircraft Aeroelasticity and Loads[J].John Wiley & Sons,West Sussex,England,UK,2007,30(3):856-869.
[3] BINDOLINO G,GHIRINGHELLI G,RICCI S.and TARRANEO,M.Multilevel structural optimization for preliminary wing-box weight estimation[J].Aircraf,47(2):475-489.
[4] RAYMER D P .Enhancing Aircraft Conceptual Design Using Multidisciplinary Optimization[J].Royal Institute of Technology (KTH),Sweden,Report 2002-2 May 2002.
[5] DENIS H.Aircraft Loading and Structural Layout[J].American Institute of Aeronautics and Astronautics,2004.
[6] 余雄庆,欧阳星,邢宇,等.机翼结构重量预测的多学科分析优化方法[J].航空学报,2016,37(1):235-243.
[7] 陈华,邓扬晨.基于满应力优化与有限元分析的机翼结构质量估算法[J].航空计算技术,2006,36(3):85-90.
[8] TORENBEEK E.Synthesis of Subsonic Airplane Design[M].Delft University Press,Kluwer Academic Publishers,Appendix C.Prediction of Wing Structural Weight,1982.
[9] ROSKAM.Airplane Design Part V:Component Weight Estimation,Design,Analysis and Research Corporation[M].Kansas,USA,2003.
[10] OBERT E.Aerodynamic design of transport aircraft[M].Amsterdam,The Nethelands:IOS Press BV,2009.
[11] SMITH D D,IDIKVEREN A T.FRISWILL,et al.Multi-objective optimization for the multiphase design of active polymorphing wings[J].AIAA,2012,49(4):1153-1160.
[12] 吕凡熹,李正洲,邓经枢,等.面向飞行器概念设计的全速域气动分析工具[J].空气动力学学报,2017,35(5):625-632.
[13] KELM R,LAPPLE M.GRABIETZ M et al.Wing Primary Structure Weight Estimation of Transport Aircrafts in the Pre-Development Phase[C]//54th Annual Conference of SAWE,Huntsville,Alabama,USA,22-24.
[14] VIANA J R,BUTKEWITSCH S,LEAL M F.Optimization of aircraft structural components by using nature-inspired algorithms and multi-fidelity approximations[J].Global Optimization,2009,45(3):427-449.
[15] TORENBEEK E.Development and Application of a Comprehensive,Design-sensitive Weight Prediction Model for Wing Structures of Transport Category Aircraft.Delft Delft University of Technology[M].Delft University Press,1992.
[16] HOWE D.The prediction of aircraft wing mass,proceedings of the institution of mechanical engineering[J].Aerospace Engineering,1996,210:135- 145.
[17] 魏思.飞机总体设计中机翼重量评估方法研究[D].南京:南京航空航天大学,2010.
[18] 张嘉良,秦伟伟,秦庆强,等.考虑多重影响因素的巡航飞行器增程优化设计研究[J].航空兵器,2020,27(2):32-38.