1 引言
固体火箭发动机广泛应用于各种型号的装备中。目前研究表明:推进剂/衬层粘接界面的粘接破坏是固体发动机结构完整性破坏的关键形式之一[1]。陆上运输时所受振动载荷对其结构特别是衬层/推进剂粘接界面影响较大,在温度、振动2种因素同时作用下粘接界面的损伤情况将比单因素的情况更加复杂,构建温度、振动载荷作用下的损伤规律意义重大。
目前损伤研究主要从单因素进行[2-3],张波[4]、刘磊[5]利用自制的粘接试件开展了振动试验,研究了恒温振动载荷作用下粘接界面力学性能下降规律。Nikola Gligorijevic[6]和李高春[7]则通过不同温度下的拉伸试验,研究温度对推进剂模量的影响。基于推进剂热粘弹属性,不同温度下其模量会发生改变,考虑到实际运输过程中发动机受载的多样性,有必要开展温度和振动耦合作用下的损伤评估。目前应用在粘接界面上的多载荷分析较少,此处借鉴电子器件中的研究方法,美国马兰大学的Qi,Wilkinison等设计了在温度、振动同时作用下的加速试验[8]。张卫采用线性累积损伤方法和渐进损伤叠加方法对电子产品失效寿命进行预测[9]。
基于上述分析,本文针对车载运输过程中固体发动机受载情况,构建基于实测数据的振动载荷谱;利用有限元软件研究不同温度、振动环境下推进剂/衬层粘接界面的应力分布情况;基于Miner损伤理论构建粘接界面累积损伤模型,研究了实际运输过程中粘接界面损伤分布规律。
2 振动载荷谱构建
2.1 载荷预处理
通过采集2种路况下运输车振动传感器数据,得到符合笛卡尔坐标系的连续加速度数据,x轴表示车辆前进方向,y轴表示左右侧方向,z轴表示垂向方向。消除信号中的趋势项,处理后的两段加速度信号如图1和图2所示。
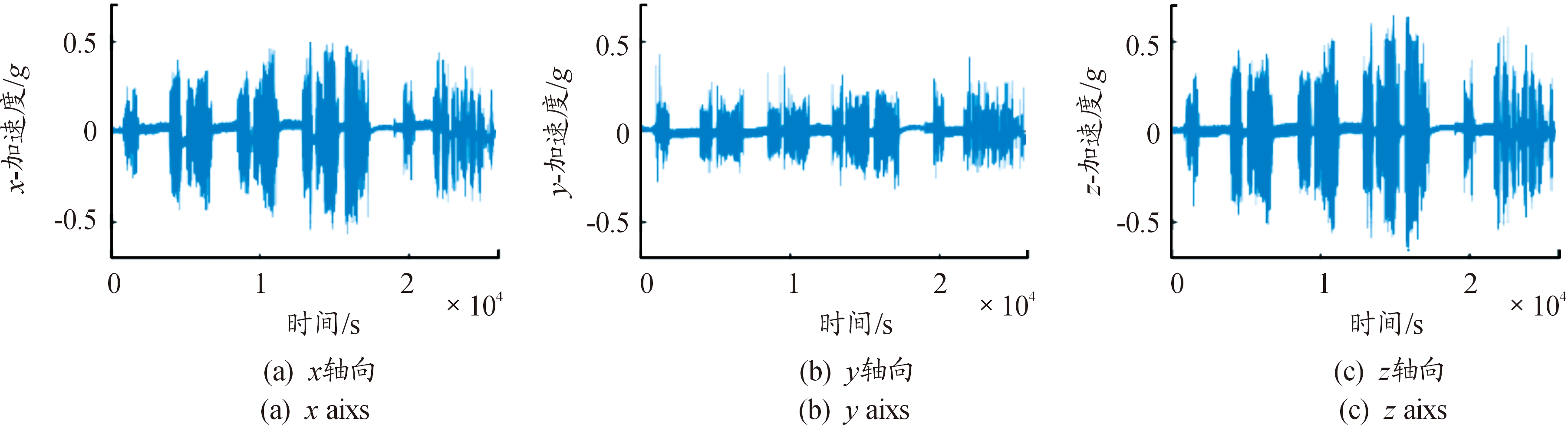
图1 第1种路况振动加速度信号曲线
Fig.1 Vibration acceleration history of the road condition 1

图2 第2种路况振动加速度信号曲线
Fig.2 Vibration acceleration history of the road condition 2
依据信号变化幅值可以将采集信号分成3种情况的信号段,分别对应-0.04~0.04 g,-0.5~0.5 g和-1~1 g 3个范围,为进一步研究能量分布情况,对信号功率谱密度(power spectral density,PSD)进行分析。
2.2 功率谱分析
由于竖直方向上所受载荷幅值最大,重点研究z轴向载荷,各信号段的PSD如图3所示。
从图3(a)可以看出,情况1下振动载荷能量主要集中在20 Hz以上的高频段上,能量峰值集中在几个频率点上,整体PSD低于0.002 g2/Hz。图 3(b)为情况2下的PSD,能量主要集中在1~10 Hz和60~80 Hz两个频段上,整体PSD介于0.001~0.03 g2/Hz之间。观察图 3(c),情况3下载荷能量主要集中在10~30 Hz上,PSD值大于0.001 g2/Hz,最高可达0.5 g2/Hz。在PSD上3种情况下载荷存在较大差别,为了后续试验设计,需要构建包含各种情况的载荷谱。

图3 各信号段PSD曲线
Fig.3 PSD of each signal segment
2.3 振动载荷谱构建
采用了基于PSD对运输条件进行分类的方法[10]。根据国际平整度指数(IRI)[11] 对道路状况进行分类[12]。表1显示了3个振动等级(A,B和C)及其PSD范围。假设采集过程中行驶速度不变,计算各振动等级下的里程与总里程的比值,A级占33%,B级占65%,C级占2%,以里程占比作为权重计算等效PSD,如图4所示。
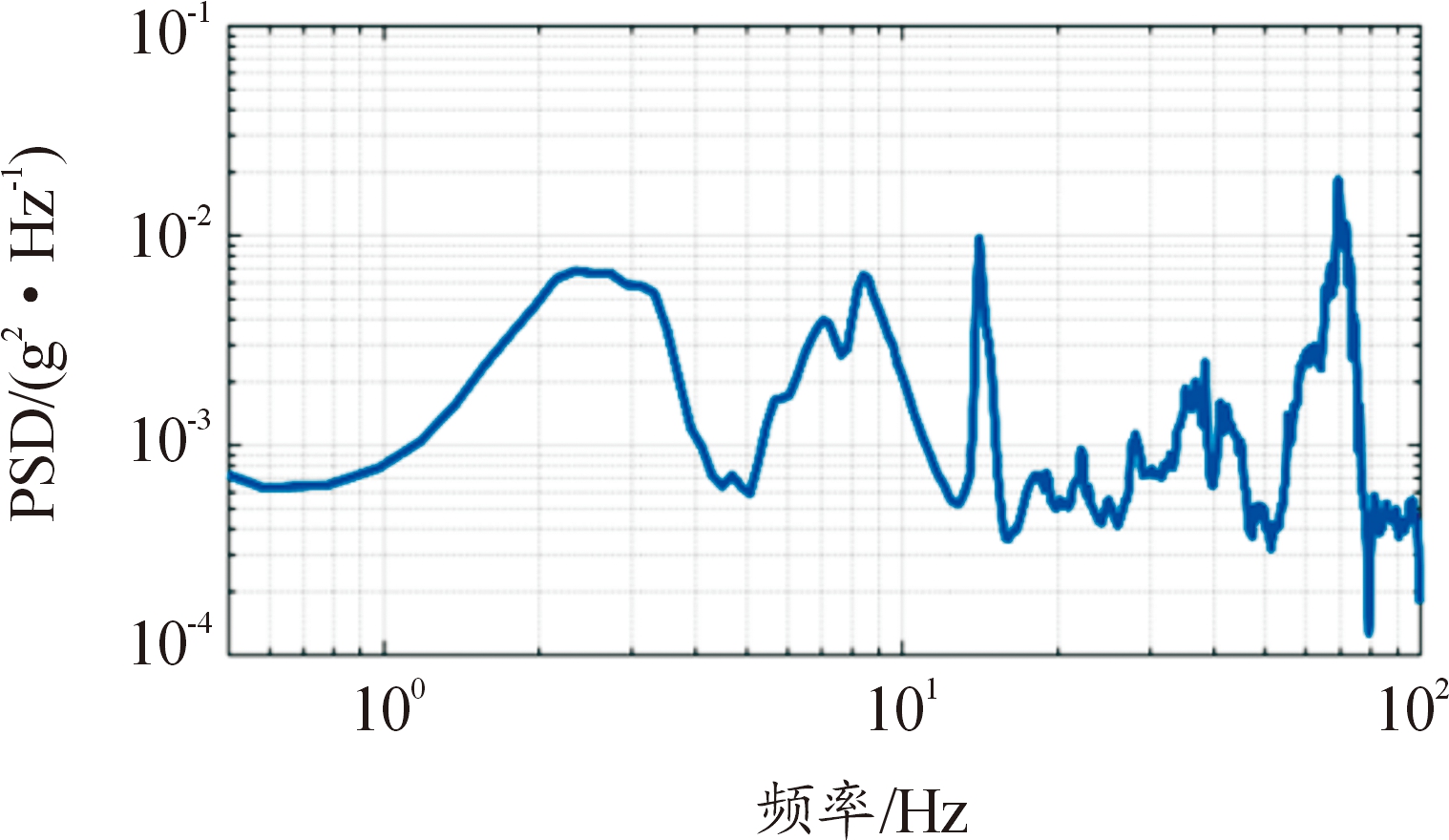
图4 等效PSD曲线
Fig.4 Equivalent PSD curve
表1 基于PSD的振动级别划分
Table 1 Classification of vibration levels based on PSD

等级PSD/(g2·Hz-1)AGood<0.002BNormal0.002-0.03CBad>0.03
可以看出等效PSD上载荷能量主要集中在5~15 Hz、30~45 Hz和60~80 Hz 3个频段上。
3 温振环境下固体发动机仿真分析
3.1 模型建立及参数设置
从图5可以看出,发动机模型从外到内依次为壳体,绝热层,推进剂药柱。其中在后封头位置,壳体与绝热层之间设置有人工脱粘层,起应力释放作用。

图5 发动机模型示意图
Fig.5 Schematic diagram of engine model
整个仿真过程包括固化降温和振动过程模拟,需要给定的材料参数包括密度、模量等参数,具体数值见表2。考虑到药柱的热粘弹特性,构建如式(1)[13]所示的热粘弹模型。
表2 各部件参数设置
Table 2 Parameter settings of various components

参数壳体绝热层/衬层人工脱粘层推进剂密度(kg·m-3)7 8001 0501 0501 800模量/MPa2.1×1055.73E(t)热导率/(W·kg-1·K-1)390.30.350.6热膨胀系数/K-11.1×10-59.2×10-59×10-51×10-4比热容/(J·kg-1·K-1)5.1×1022.2×1032.2×1031.1×103泊松比0.30.4990.4950.495
![]()
(1)
考虑到实际情况下壳体与衬层、衬层与推进剂界面粘接牢固,将边界条件简化为绑定约束,人工脱粘层和壳体间不设置约束。为模拟实际发动机在公路运输过程中受载情况,本文设置两个分析步进行:
分析步1:进行固化降温的模拟。设置初始零应力温度为58 ℃,考虑到壳体热膨胀系数相对推进剂而言较小,因此忽略壳体形变,对壳体外表面施加完全固定约束,整体施加重力载荷。壳体与外界表面传热系数为20 W·(m2·℃),通过改变环境温度,获得发动机内部不同应变状态,整个过程总时长设置为1.7×106 s(约20 d)。
分析步2:模拟实际振动过程。此过程是建立在分析步1中得到的不同温度下发动机内部应力应变状态的基础上进行的,假设振动开始时刻发动机受载为零。将载荷谱转化为加速度形式施加在装药上,同时在y轴向设置重力载荷。简化约束条件为模型外表面y轴向(即竖直方向)固定约束,考虑到工作站性能限制,该计算时长设置为300 s。
3.2 仿真结果
由于发动机卧式放置时竖直方向载荷较大,对应模型x0z平面垂直方向上的s22应力,为分析不同温度和不同位置上应力分布情况,本文在粘接界面上下端面各设置一条计算路径,分别记为路径A和B,如图6所示。
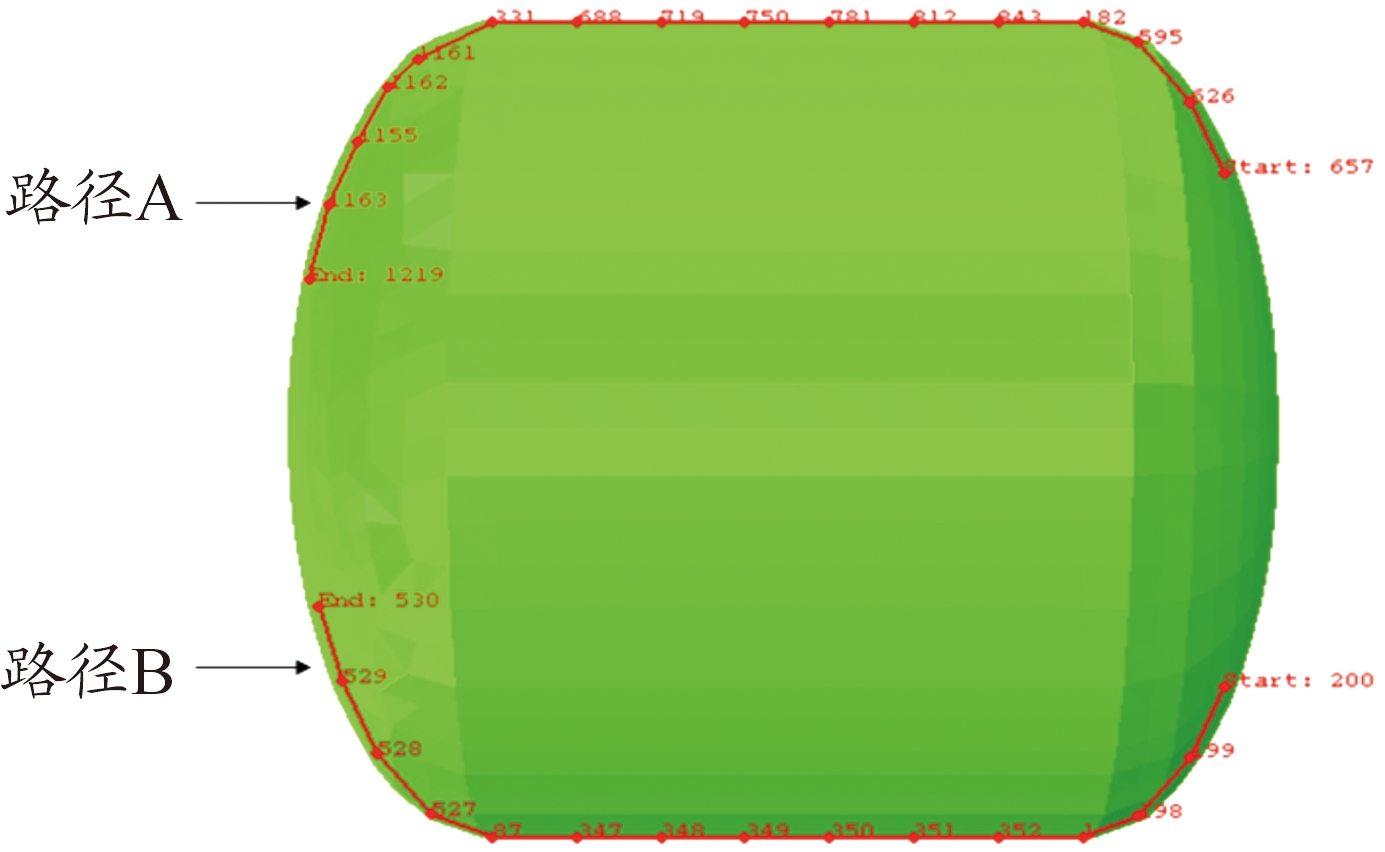
图6 设置计算路径示意图
Fig.6 Schematic diagram of setting the calculation path
设置的2条路径A和B都始于后封头人工脱粘层前沿处,依次向上、向下途经后封头、圆筒段和前封头。以振动137.4 s时路径上s22应力分布情况为例,如图7所示。

图7 137.4 s时刻路径上各节点s22应力曲线
Fig.7 The value of s22 at each node on the path at 137.4 s
以15 ℃时的路径上应力分布情况为例,见图 7(c),路径A、B上s22呈现出双峰值分布,在距离后封头端面132 mm处出现第1个应力极大值,对应后封头与圆筒段相接处;沿路径移动,应力先减小后增大,在距离后封头端面521 mm处出现第2个应力极大值,对应前封头与圆筒段相接处,其中路径A上应力值要高于路径B上。对比分析图 7(a)~(e)所示各温度下路径A、B的应力分布情况,可知2条路径上的s22应力都呈现出双峰值的形式,应力最大值出现在距离后封头端面521 mm处,随着温度升高两应力峰值的差距越来越小,路径上应力值也逐渐降低。以路径A为例,温度为-5 ℃时路径上应力最大值为65.1 kPa,35 ℃时路径上应力最大值为31.7 kPa。
4 温振载荷下粘接界面损伤计算
4.1 S-N曲线拟合
参考曲凯[14]设计的定应力变程往复拉伸试验,参照标准QJ 2038.1-91[15]制作方形粘结试件,设计定应力粘接界面往复拉伸试验拟合S-N曲线,试件如图8所示。
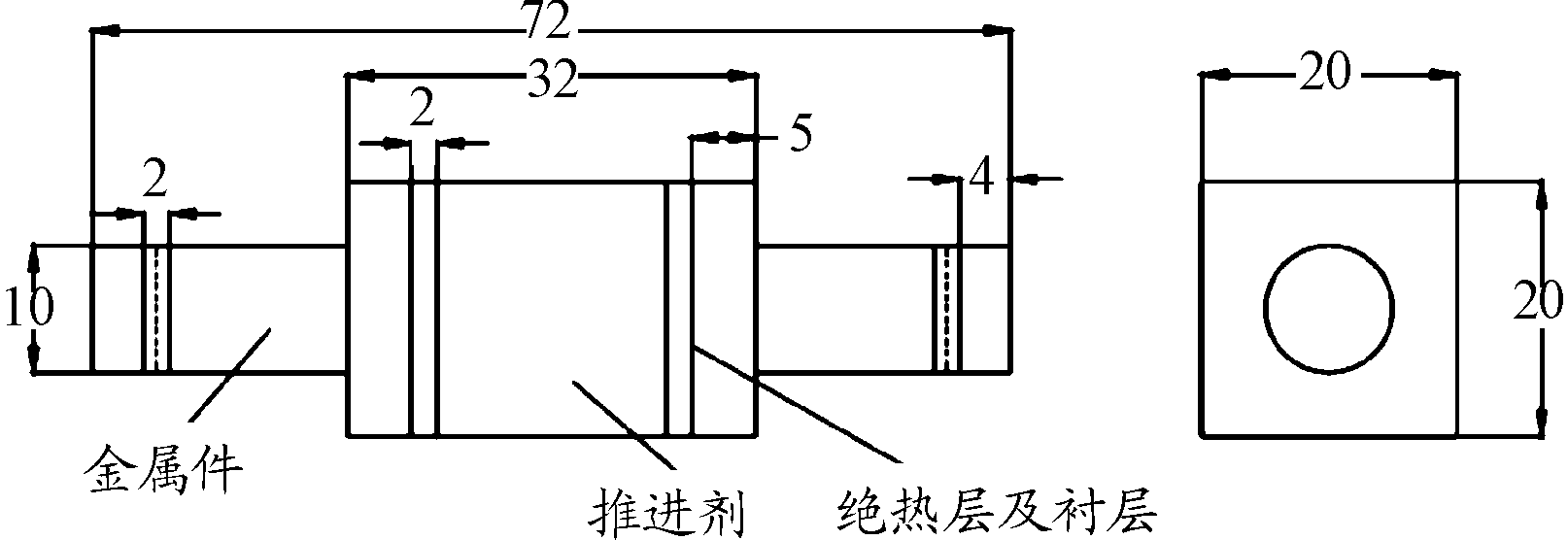
图8 方形粘结试件示意图
Fig.8 Schematic diagram of square bonded test piece
记录粘接试件发生破坏时的循环加载次数,如表3所示。基于幂函数形式[16]对试验数据进行拟合,拟合的S-N曲线如图9所示,拟合方程如式(2)所示,相关系数为0.985 39。
N·S4.231 6=3.712 (2)
表3 不同定位移下的循环加载次数
Table 3 Cyclic loading coefficients under different positioning shifts

S/MPaNln N0.55283.3320.50493.8920.45824.4070.401875.2310.353245.781

图9 拟合S-N曲线
Fig.9 Fitting S-N curve
4.2 损伤计算
提取仿真计算结果,利用雨流计数方法对应力变程统计计数,基于Miner准则和渐进损伤叠加方法[9],在累积损伤模型中增加温度修正项,如式(3)所示:

(3)
考虑到推进剂热粘弹属性影响,参考文献[13]给出的热应力作用下累积损伤计算方法,式中aT为温度转化因子。
(4)
基于Miner准则假设,忽略定应力和交变应力相互影响,将损伤累积叠加,得到实际运输条件下的损伤:
D=Dh+Ds
(5)
假设每年运输里程为500 km,时间为2个月,其余时间导弹贮存在弹库中,贮存温度为25 ℃。参考文献[16]得到如表4所示的日均温时间占比。取每个温度区间平均值,计算导弹服役10年的损伤情况,如图10所示。
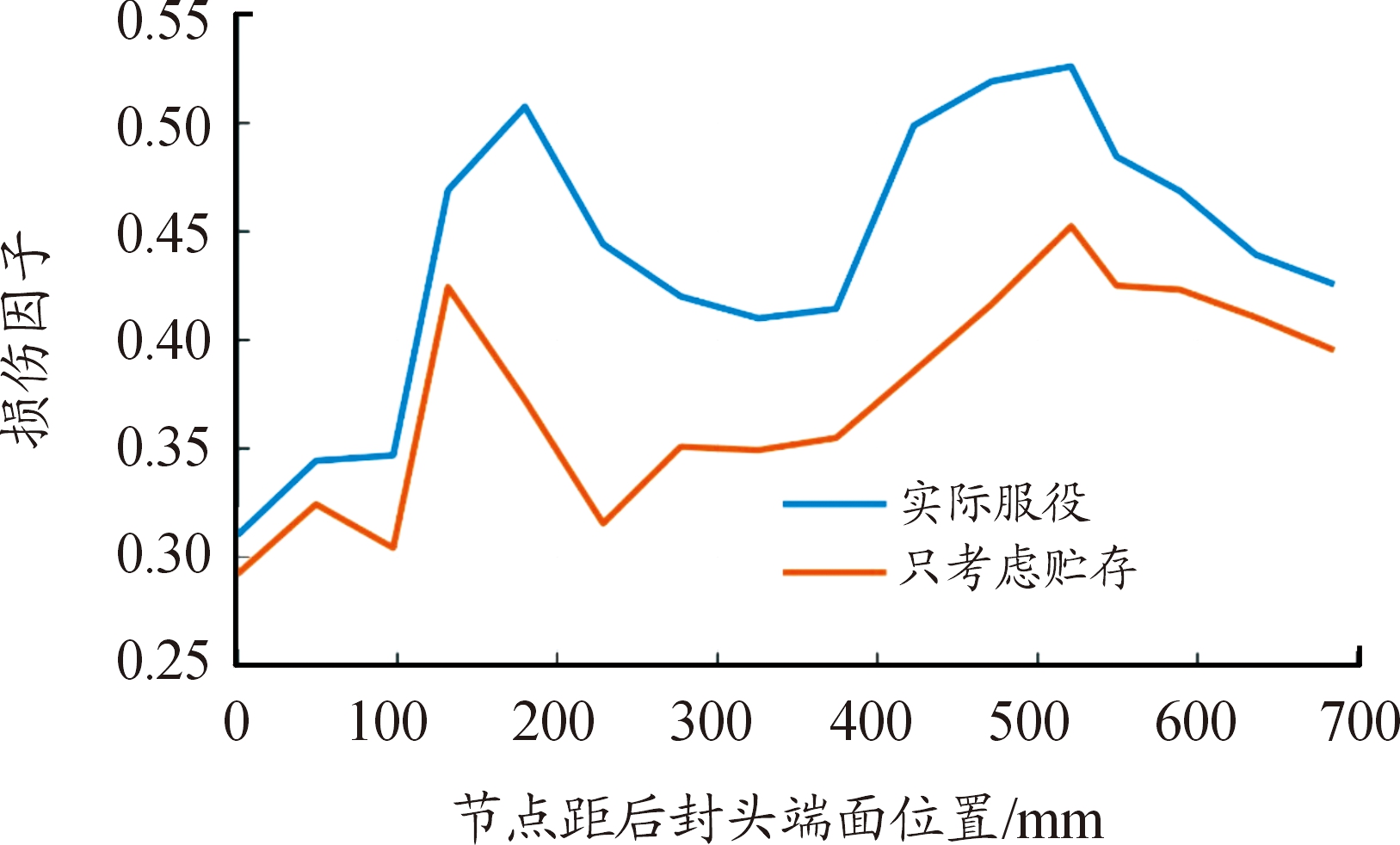
图10 实际运输环境下的振动损伤曲线
Fig.10 Damage curve under transportation environment
表4 运输过程日均温时间占比
Table 4 Percentage of daily average temperature

温度范围/℃时间占比/%(-10,0]3(0,10]24(10,20]33(20,30]38(30,40]2
可以看出实际服役的损伤计算结果与只考虑的情况相近,在距离后封头边缘180 mm和521 mm附近出现损伤极大值,确定实际服役下损伤的关键部位在距离后封头端面120~250 mm和400~600 mm两个区间范围内,其中距离后封头端面521 mm处的损伤因子最大,为0.526 3。在长时间服役后,应重点检查此部位的损伤情况。
5 结论
1) 基于推进剂热粘弹属性,通过有限元软件模拟运输过程中发动机受载情况,应力在计算路径上呈双峰值分布,在距离后封头端面521mm处应力值最大。
2) 综合温度、振动和重力的影响,在距离后封头端面120~250 mm和400~600 mm两个区域内损伤较大。
[1] 李鹏.基于工业CT的固体火箭发动机装药脱粘修复技术研究[D].烟台:海军航空工程学院,2015.
Li Peng.Research on Debonding Repair Technology of Solid Rocket Motor Charge Based on Industrial CT[D].Yantai:Naval Aeronautical Engineering Institute,2015.
[2] 李高春,韩永恒,黄卫东,等.装药累积损伤评估及参数敏感性分析[J].兵器装备工程学报,2018,39(03):11-14.
Li Gaochun,Han Yongheng,Huang Weidong,et al.Accumulated damage assessment and parameter sensitivity analysis of charges[J].Ordnance Equipment Engineering Journal,2018,39(03):11-14.
[3] 许彪,高山,李高春,等.某型导弹助推器潜入式喷管失效机理分析[J].兵器装备工程学报,2017,38(05):82-86.
Xu Biao,Gaoshan,Li Gaochun,et al.Failure mechanism analysis of a certain type of missile booster submersible nozzle[J].Ordnance Equipment Engineering Journal,2017,38(05):82-86.
[4] 张波,董可海,李金飞,等.振动载荷对立贮式发动机粘接界面损伤影响[J].推进技术,2018,39(05):137-143.
Zhang Bo,Dong Kehai,Li Jinfei,et al.The effect of vibration load on the damage of the bonding interface of vertical storage engine[J].Propulsion Technology,2018,39(05):137-143.
[5] 刘磊,李金飞,宋佳明.固体发动机推进剂/衬层粘接试件振动损伤分析[J].指挥控制与仿真,2020,42(03):136-140.
Liu Lei,Li Jinfei,Song Jiaming.Vibration damage analysis of solid motor propellant/liner bonding specimens[J].Command Control and Simulation,2020,42(03):136-140.
[6] Gligorijevic N,Rodic V,Zivkovic S,et al.Mechanical characterization of composite solid rocket propellant based on hydroxy-terminated polybutadiene[J].Hemijska Industrija,2015,70:67-67.
[7] 李高春,李树谦,郭宇,等.不同温度和拉伸速率下复合推进剂力学性能及破坏模式分析[J].固体火箭技术,2019(3).
Li Gaochun,Li Shuqian,Guo Yu,et al.Analysis of the mechanical properties and failure modes of composite propellants at different temperatures and extension rates[J].Solid Rocket Technology,2019(3).
[8] Qi,Wilkinison,Osterman,Pecht.Failure analysis and virtual qualification of PBGA under multiple environmental loadings[C].Electronic Components and Technology,2004.
[9] 张卫.考虑多失效机理耦合的电子产品寿命预测方法研究[D].长沙:国防科学技术大学,2014.
Zhang Wei.Research on the life prediction method of electronic products considering the coupling of multiple failure mechanisms[D].Changsha:National University of Defense Technology,2014.
[10] 椎名 武夫.Derivation of PSD for Random Vibration Test Based on the Field Data Obtained in Japan[J].包装技術,2015,53:158-163.
[11] Michael W Sayers,Thomas D.Gillespie,and William D.O.Paterson(1986),Guidelines for Conducting and Calibrating Road Roughness Measurements,World Bank Technical Paper Number 46.
[12] ISO(1982),Reporting vehicle road surface irregularities,TC 108/SC 2/WG 4,N57.
[13] 邱欣.某固体火箭发动机粘接系统损伤特性与使用寿命评估技术研究[D].烟台:海军航空工程学院,2015.
Qiu Xin.Research on the damage characteristics and service life evaluation technology of a solid rocket motor bonding system[D].Yantai:Naval Aeronautical Engineering Institute,2015.
[14] 曲凯.舰载固体火箭发动机装药疲劳损伤研究[D].烟台:海军航空工程学院,2011.
Qu Kai.Research on fatigue damage of shipborne solid rocket motor charge[D].Yantai:Naval Aeronautical Engineering Institute,2011.
[15] QJ2038.2—1991.固体火箭发动机燃烧室界面粘接强度 测定方法 剪切法[S].北京:中华人民共和国航空航天工业部,1991.
QJ2038.2—1991.Measuring method for bonding strength of solid rocket motor combustor interface shear method[S].Beijing:Ministry of Aeronautics and Space Industry of the People’s Republic of China,1991.
[16] 李高春,黄卫东,董可海.固体火箭发动机全寿命环境载荷分析[J].装备环境工程,2019(3):101-105.
Li Gaochun,Huang Weidong,Dong Kehai.Environmental load analysis for the whole life of a solid rocket motor[J].Equipment Environmental Engineering,2019(3):101-105.