1 引言
机载设备是指对飞机飞行中的各种信息、指令和操纵进行测量、处理、传递、显示和控制的设备。飞机在飞行过程中会把振动、冲击、过载等力学载荷传递给机载设备,因此,机载设备所处力学环境往往比较恶劣。与此同时,为确保飞机良好的机动性、经济性和作战半径,往往对机载设备的质量提出非常苛刻的要求。这样一来,有限的结构质量必须用到刀刃上,在确保机载设备在轻量化的前提下,需要更精细化的开展强度设计。
机载设备的结构骨架往往采用铸造、锻造或焊接一体的形式,其目的是保证结构应力传递的连续性,减少中间连接环节引起的应力集中。对于应力梯度变化较大的区域,通常采用变截面厚度或加强筋的形式,但这样会导致结构的拓扑形式复杂[1]。面对复杂的结构拓扑形式,对其进行动力学仿真或疲劳寿命预测[2],仿真过程中的网格数量庞大,划分难度急剧增加,难以全面顾及所有的应力关注区域,造成结构应力解偏离真实值,进而影响结构疲劳寿命预测结果的准确性[3]。
鉴于此背景,本研究基于递归思想,先用较为粗略的网格获取系统的位移与应力解,通过应力解判定结构危险区域,将危险区域作为局部分析对象对其进行网格细分。通过将整体模型的位移边界映射局部详细模型的边界,再次进行精细化仿真,从而得到准确的应力解,实现更为合理的疲劳寿命预测。
2 递归仿真流程介绍
机载设备中某些重要的零部件常常会因为局部的应力集中而失效。此时如果采用精确的整体模型仿真,仿真效率将非常低。甚至在某些复杂零部件的动力学仿真或疲劳寿命预测中会因为计算机硬件原因而导致计算过程终止。对于此类问题,可以用递归方法解决,具体步骤如下[4]:
1) 建立系统整体的较为粗略的有限元分析模型;
2) 进行系统整体模型的有限元分析;
3) 分析结果的后处理,获得整体模型的位移场;
4) 建立包含整体位移矢量场的有限元场;
5) 建立详细的局部分析模型;
6) 引入上述的位移有限元场作为局部分析模型的边界条件;
7) 进行局部模型的有限元分析,获得局部模型详细的应力场。
3 边界映射理论
在计算三维有限元场的插值时,使用了力学计算中常用的具有几何和力学意义的线性假设。三角网线性插值法在网格范围内均匀分配数据,对于二维情况,三角网线性插值法根据Delaunay三角剖分准则,连接数据点间的连线形成三角形,各个三角形都是采用原始数据点定义,因此这样就把三角形和原始数据紧密联系起来[5]。
对于三维情况,采用重心坐标进行线性插值。图1中点m所在的四面体的 4个顶点为A,B,C,D,直角坐标(xi,yi,zi)(i=1,2,3,4)。点m直角坐标(x,y,z),四面体的重心坐标为(a1,a2,a3,a4),ai(i=1,2,3,4)是以点m为顶点,以各底面为底的四面体体积与原四面体ABCD的体积之比:
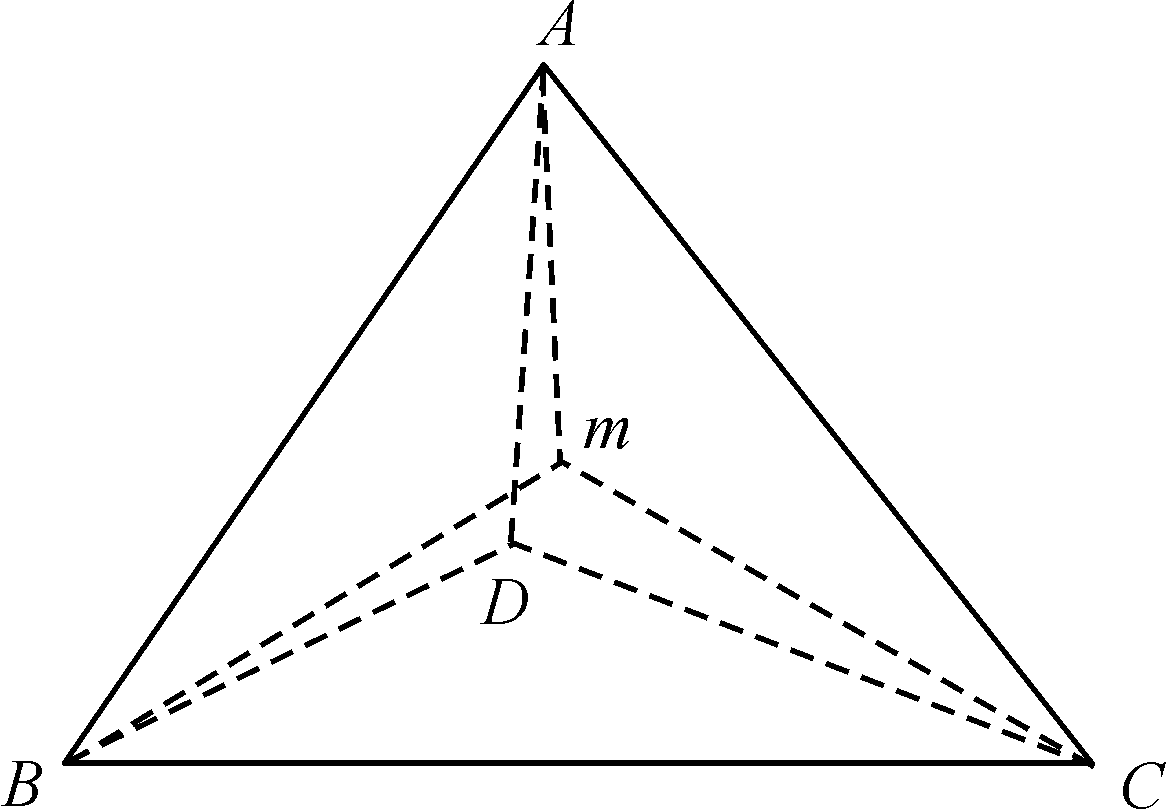
图1 四面体插值

(1)
点m的直角坐标与重心坐标之间,满足下列变换关系:
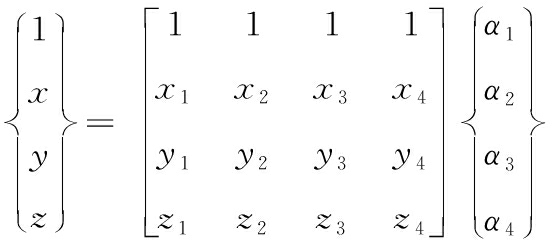
(2)
把点m的重心坐标分量ai(i=1,2,3,4)作为其所在四面体的4个顶点位移值的权重,则点m的位移值可由式(3)计算:
uM=α1uA+α2uB+α3uC+α4uD
(3)
4 仿真与验证
4.1 案例选择
以某机载雷达阵面过渡框为例,其结构外形如图2所示,为获得良好的整体刚度与力传递特性,过渡框采用ZTC4整体铸造成型。该过渡框安装在飞机框架上,用以支撑雷达天线阵面可靠工作,因此属于关键承载构件。平台要求该过渡框结构具备3 000飞行小时寿命。

图2 过渡框结构外形示意图
机载雷达过渡框承受的力学环境包括:冲击、振动与过载。其疲劳寿命与其长期承受的振动环境相关,本研究用随机振动寿命去校验过渡框的设计是否满足要求[6-7],其功能振动条件如图3所示,耐久振动量级按照功能振动的1.6倍执行。
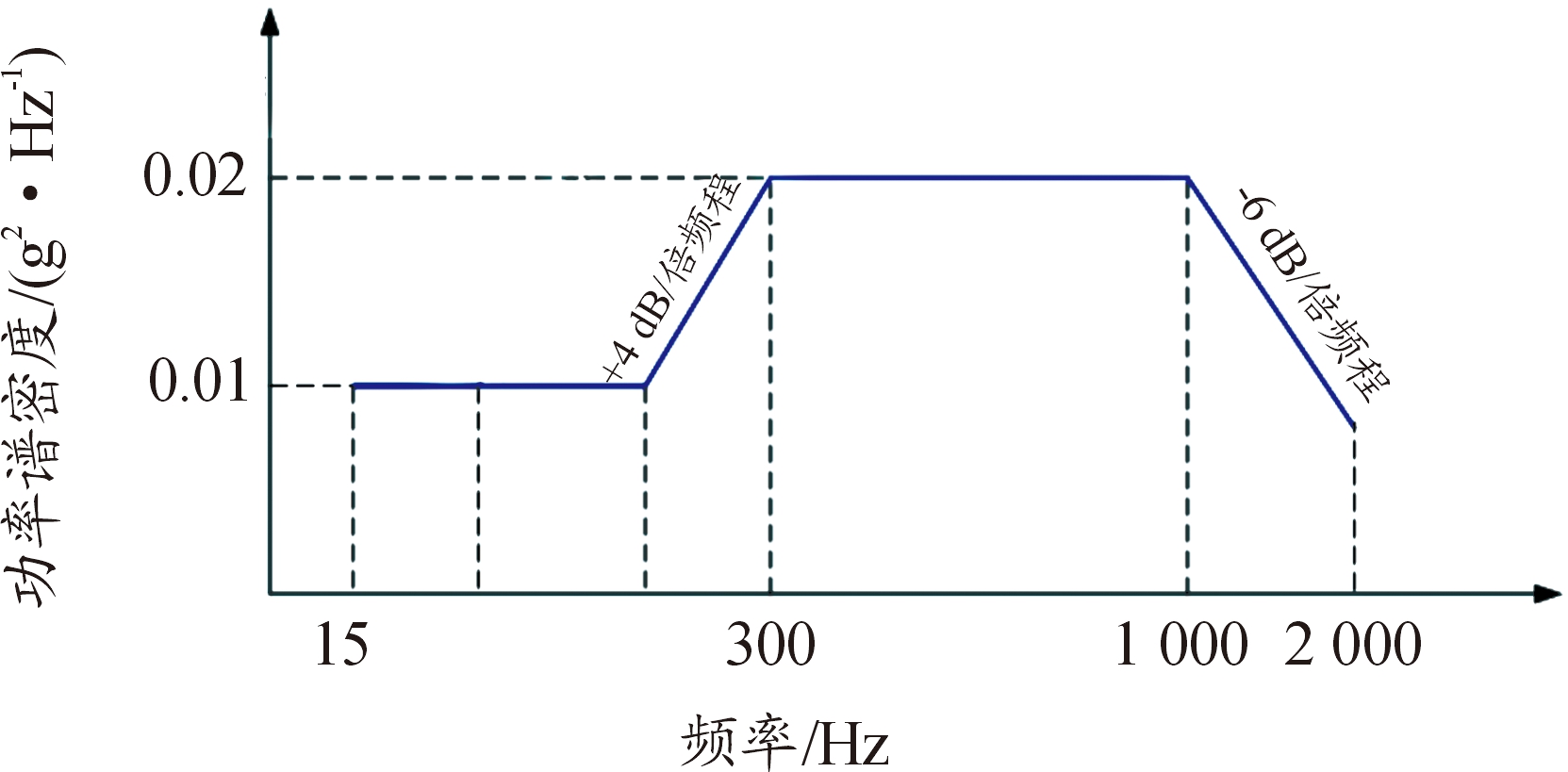
图3 振动功率谱
4.2 整体位移与应力解
首先,对案例对象开展完整的系统仿真,获得振动工况下的整体位移与应力解。根据应力水平与分布,初步确定系统的危险区域,得到后续必须包络的局部详细模型边界;根据整体位移解,可以按照上述第2节的相关理论,通过边界映射,获得详细局部模型的位移边界,便于后续开展局部模型的精细仿真。详细分析流程如图4所示[8]。
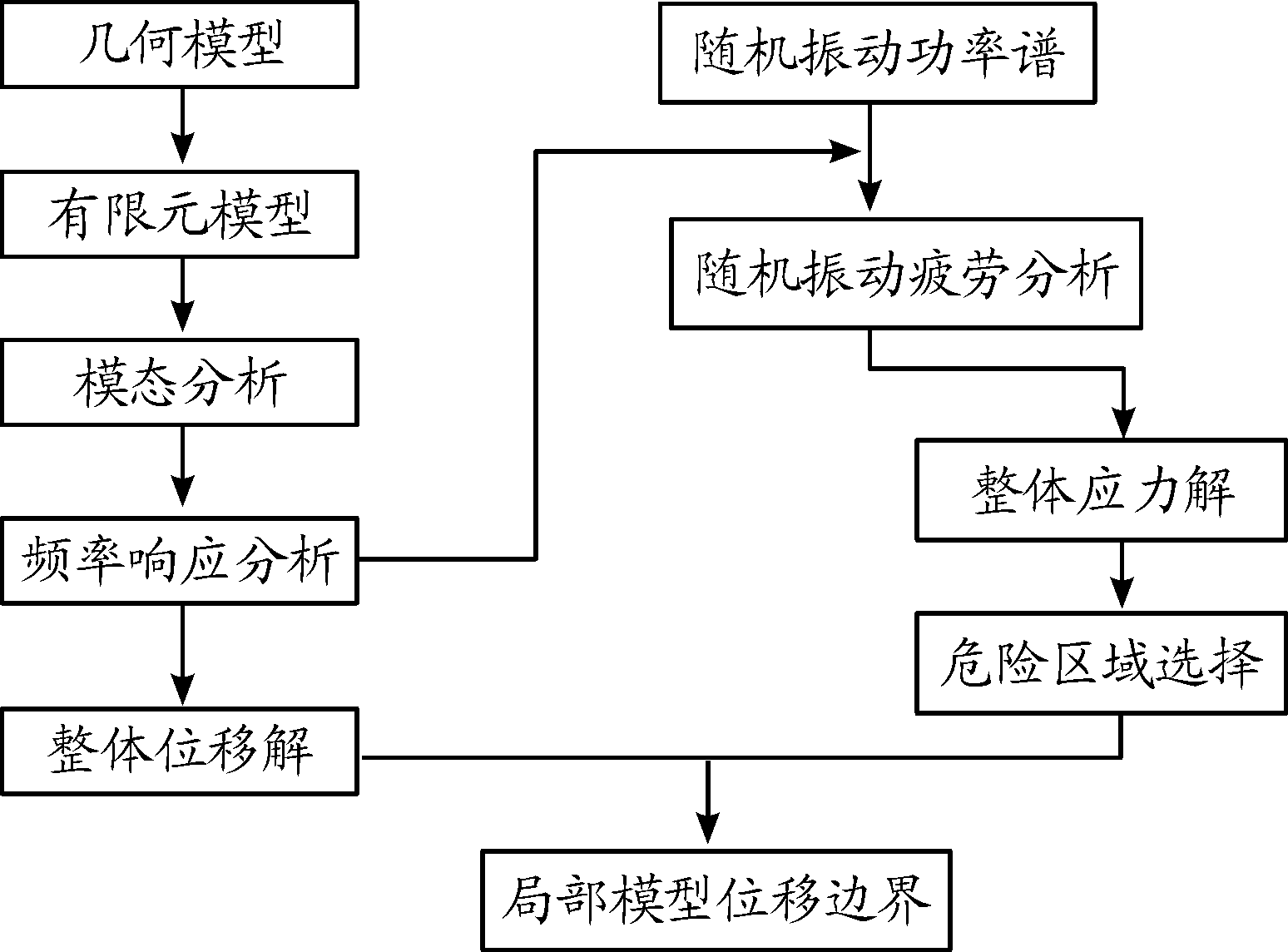
图4 详细分析流程框图
依据图4的流程,对图2的过渡框模型开展3个方向的随机振动系统仿真,其中X方向系统应力水平最高,系统的1σ应力云图如图5。整体来看,过渡框应力分布存在较大的不均衡性,图5中左上与右上连接点区域应力水平最高,呈左右对称分布,应力梯度较大。
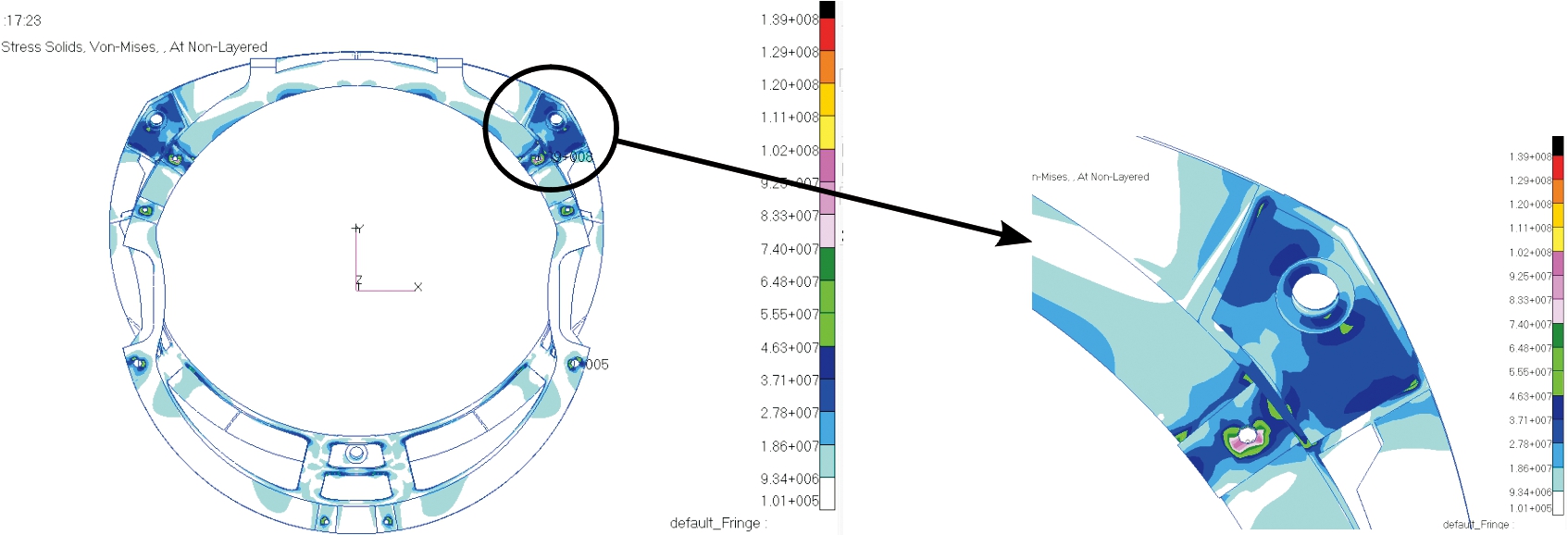
图5 过渡框随机振动下应力云图
根据应力分布,为提升位移边界准确度,适当将区域外推放大,平滑区域边界的位移梯度,鉴于应力水平左右对称,确定图6的红色区域为危险区域。因此,需要针对该区域的局部模型进行精细化仿真,进一步提升应力精度,确保结构强度满足要求。
分别取X、Y、Z三个方向频响位移结果,依据图6确定的边界区域,得到边界节点位移解如图7所示。其中图7(a)为80 Hz频点的整体位移解,图7(b)为某边界节点在全频段内的位移解,该节点位移将通过边界映射方法转化为局部详细模型的位移边界[9]。
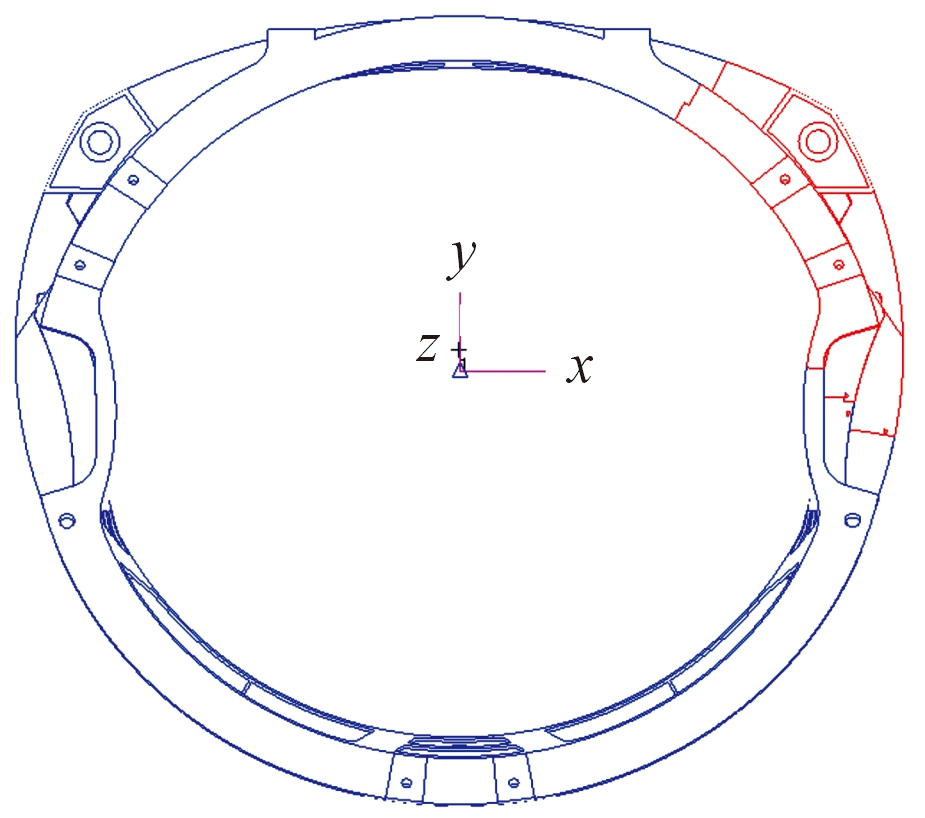
图6 危险区域(局部模型区域)示意图

图7 位移云图及典型边界点位移曲线
4.3 局部详细应力解
取危险区域模型,对其进行网格细化,确保应力梯度大的区域获得更为细致的网格密度,从而使其能够准确地反映应力梯度变化,得到图8所示的局部细化模型。

图8 局部细化模型示意图
按照细化后的局部模型,通过施加边界映射位移,得到细化后模型的频率响应结果如图9、图10、图11。
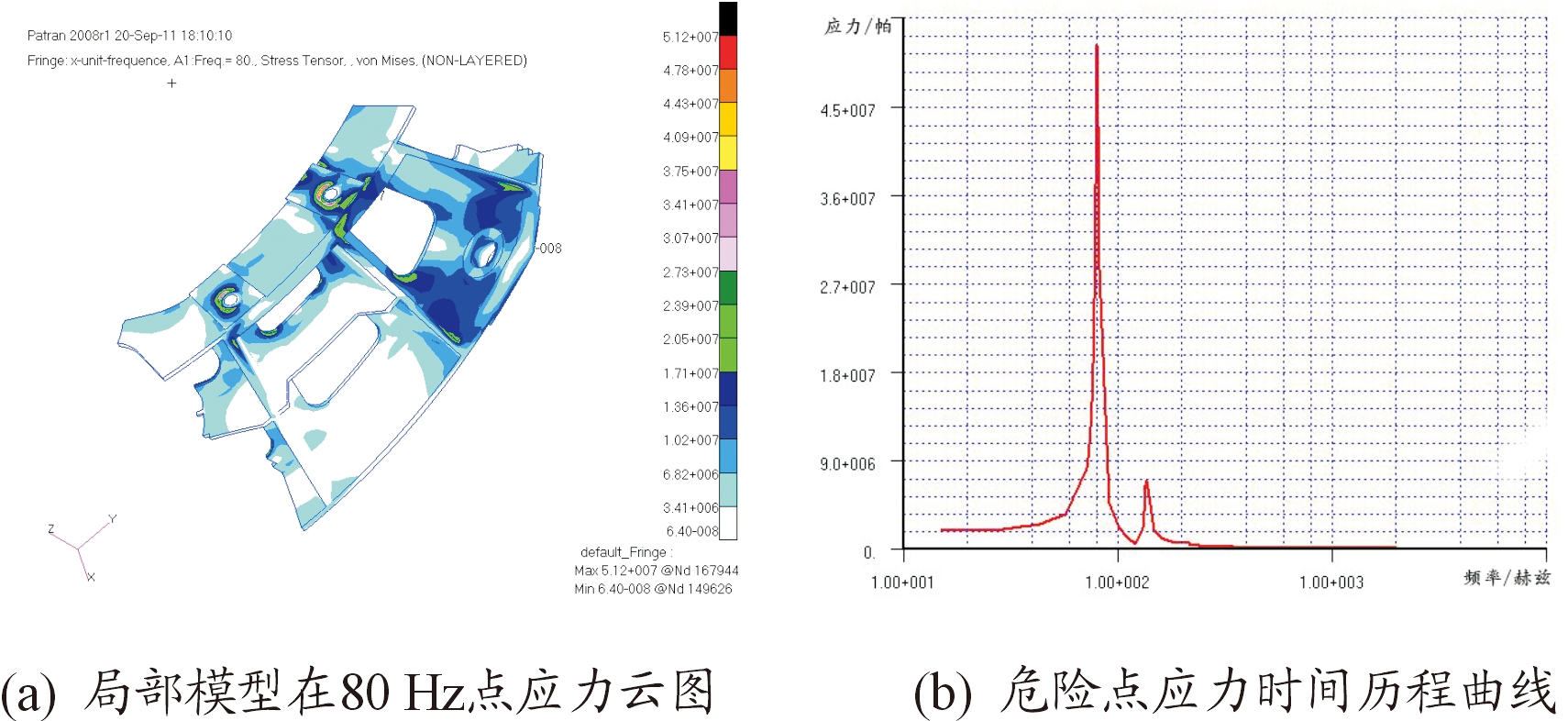
图9 X方向局部模型频率响应结果
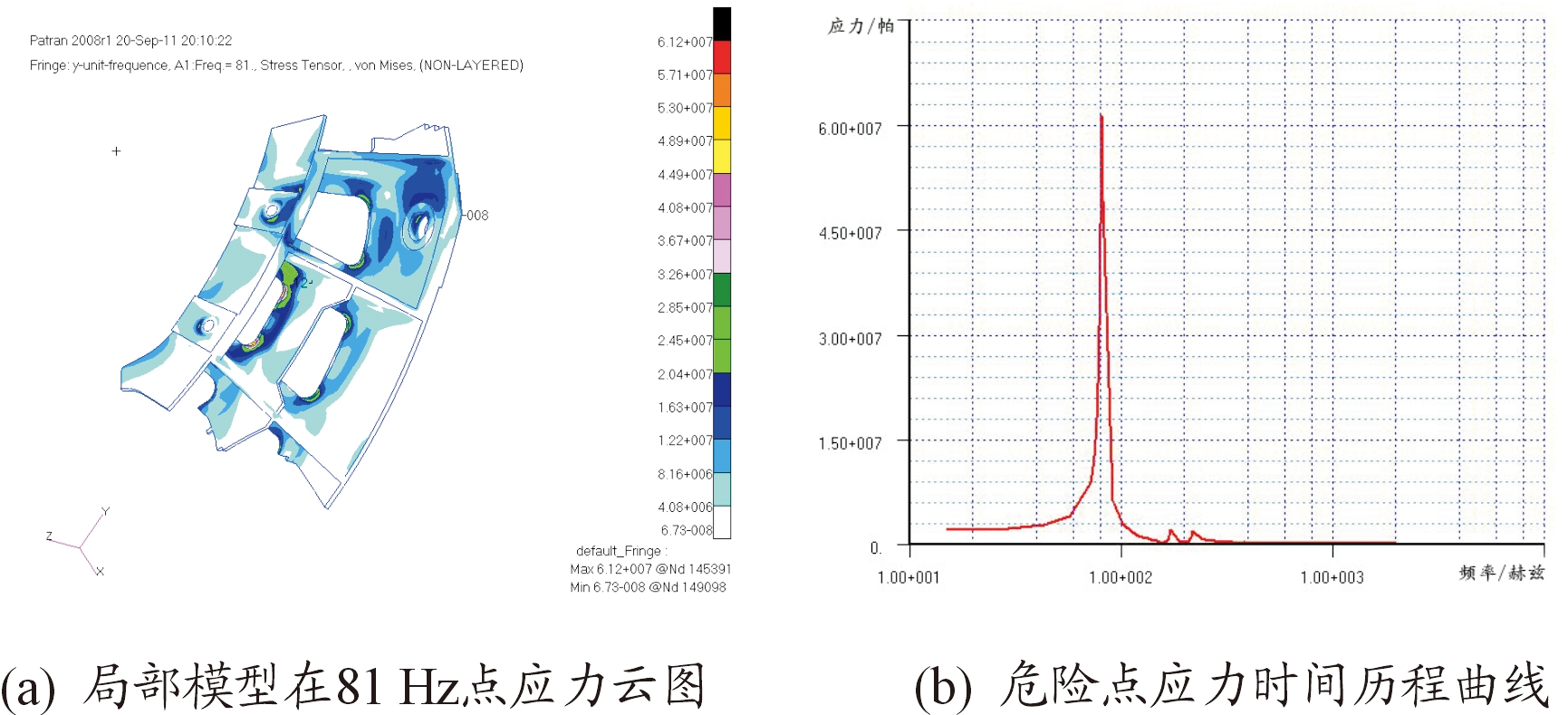
图10 Y方向局部模型频率响应结果
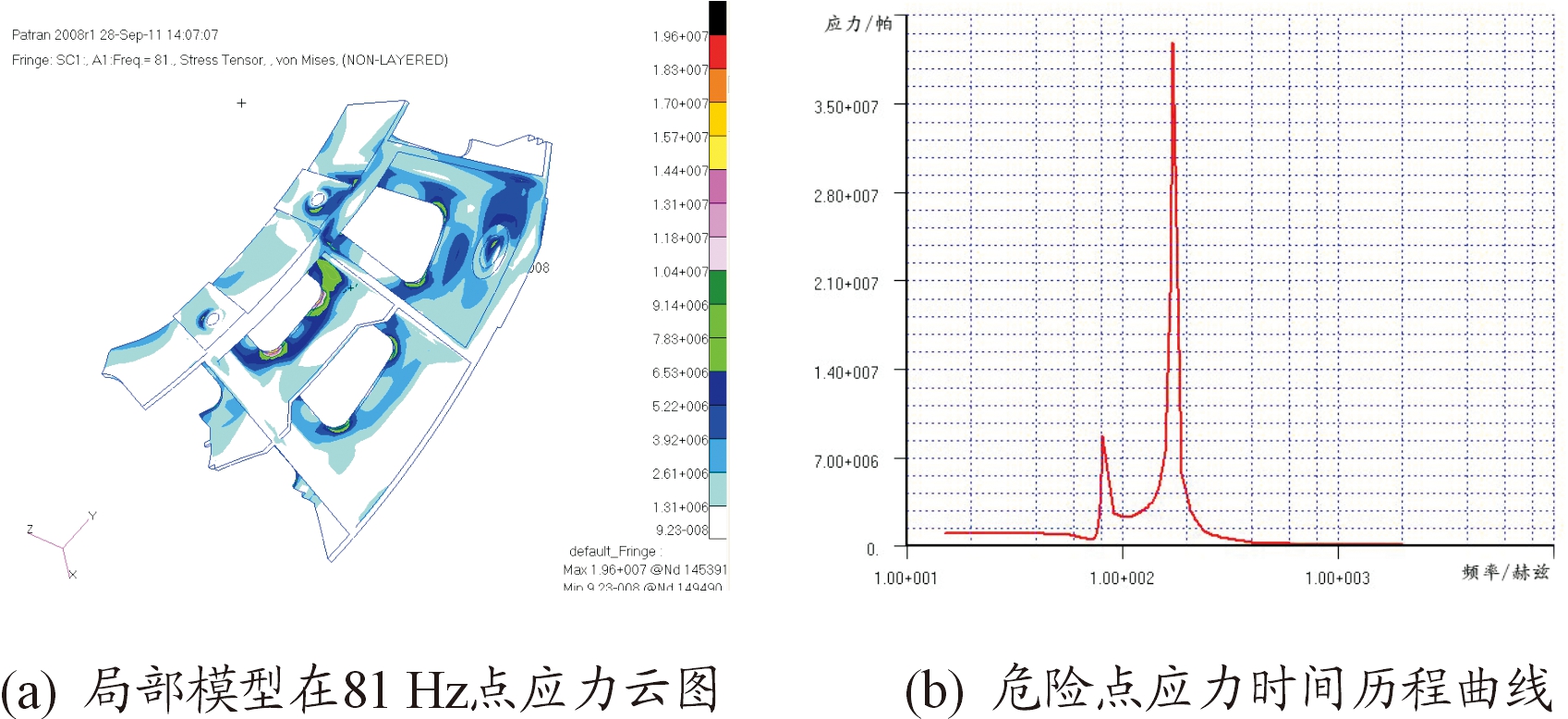
图11 Z方向局部模型频率响应结果
4.4 疲劳寿命预测
过渡框选用ZTC4铸造钛合金进行铸造成型。对于钛合金疲劳性能的研究已经证明在高应力或大应变幅下,裂纹萌生寿命与总的疲劳寿命相比非常小,在低周疲劳条件下,零件的寿命是由疲劳裂纹扩展抗力决定的。对于典型的无缺陷的钛合金而言,可以将高周疲劳强度作为判断抵抗疲劳裂纹萌生能力的标准。图12为ZTC4合金的S-N曲线[10]。
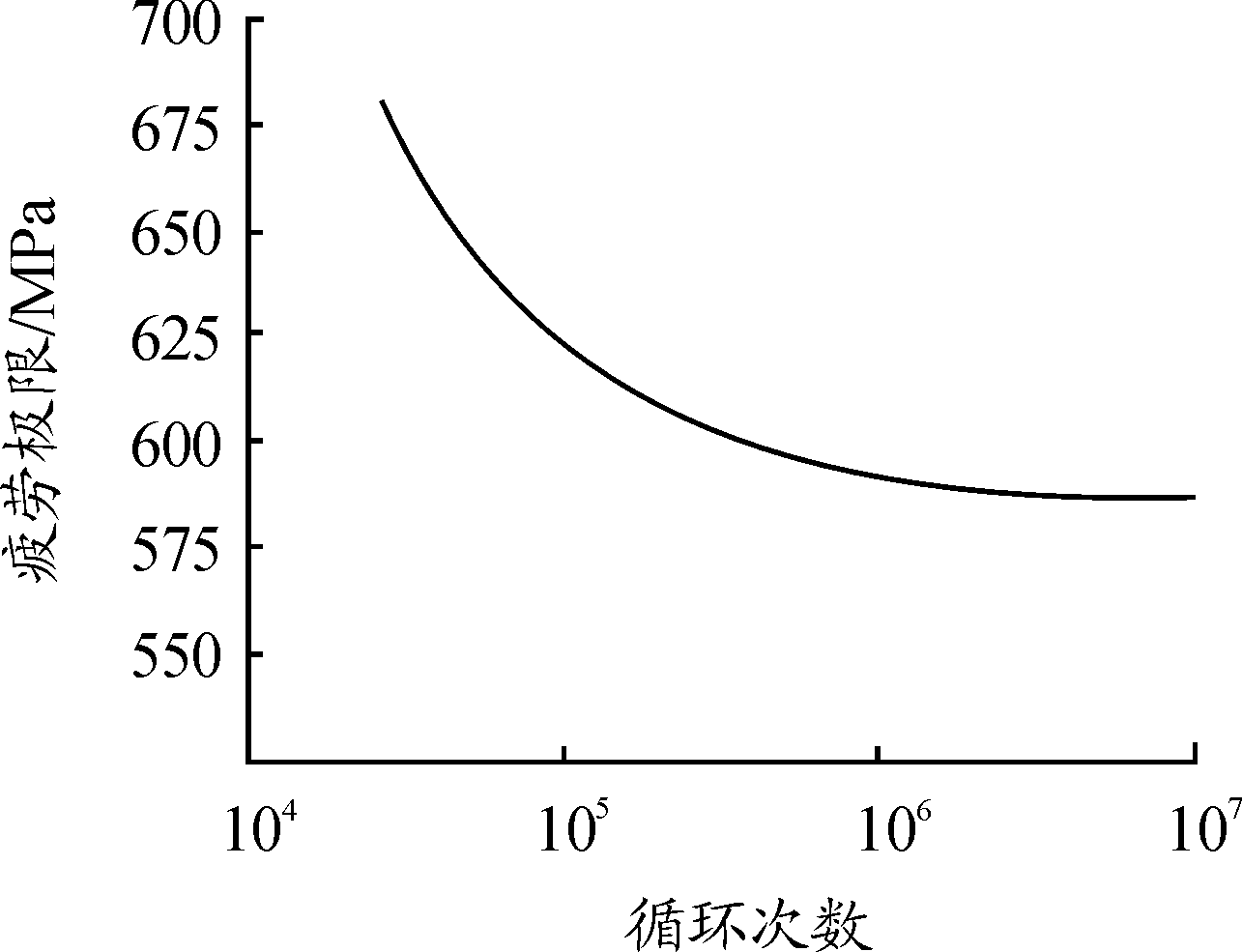
图12 ZTC4高周疲劳S-N曲线(R=-1)
以3.3节局部模型的单位频响应力结果作为输入,叠加振动耐久功率谱作为最终输入载荷,采用Palmgren-Miner线性累积损伤理论,将有限元模型导入MSC.Fatigue中开展疲劳寿命分析[11],得到如图13所示的三向疲劳寿命云图。其中图13中黑色圆框范围为最小寿命区域,且三向均为统一区域。

图13 过渡框局部模型疲劳寿命云图
过渡框在耐久振动工况下最小疲劳寿命情况如表1所示。
表1 过渡框最小疲劳寿命情况

振动方向仿真结果/s发生位置折算时间/hX向1.94×105连接孔53.89Y向1.40×105腹板圆角处38.89Z向9.63×104腹板圆角处26.75
当耐久试验量值为功能量值的1.6倍时,耐久试验持续每轴向2.5 h,对应的结构寿命500飞行小时当量。该过渡框要求与飞机同寿命设计,即渡框的设计寿命为3 000飞行小时,因此耐久振动试验时间可用下式计算得到[12-13]:
T1=T0(W0/W1)4
(4)
式中:T0=(2/60)×(成品预计飞行寿命时间)(h); T1为耐久试验持续时间(g); W0为功能试验振动量值(g2/Hz); W1为耐久试验振动量值(g2/Hz)。
按照已知条件,成品预计飞行寿命为3 000 h,耐久试验量级为功能试验量级的1.6倍,得到耐久振动的持续的时间为15 h。而根据耐久振动计算的疲劳寿命在Z向最小,为26.75 h,大于15 h的设计寿命时间,因此符合寿命设计要求。
4.5 验证
为验证3.4节仿真预测结果的可信度,结合产品力学试验考核进行了实物试验验证。试验采用加速寿命方式进行,选取图3振动谱量级的1.6倍作为试验输入,满足每轴向15 h即说明结构寿命符合设计要求[14]。
为了更为准确地反映结构三轴随机振动疲劳寿命,综合权衡试验工作量与试验结果颗粒度,试验按照图14的流程进行开展。

图14 试验流程框图
搭建如图15(a)的试验环境开展试验,试验进行到Z向22 h 34 min的时候,在腹板圆角处出现细微裂纹,具体位置如图15(b)所示,该位置与仿真结果所列最小寿命位置(图13黑色圆框位置)一致。试验停止,将裂纹区域取样送专业机构进行检测,裂纹形貌如图15(c)所示,裂纹为典型疲劳破坏特征。

图15 过渡框振动试验情况
从试验结果可以看出,结构发生疲劳破坏的位置与机理均与仿真分析结果完全一致。
试验裂纹出现时间稍短于仿真分析时间,一方面是因为仿真与实际不可避免存在一定偏差,仿真时设定的材料属性和连接条件较为理想,人为增大了结构刚强度。另一方面仿真时分别按照三轴独立进行核算,未考虑各轴向间的损伤累积。
5 结论
本研究论述了基于递归思想的复杂结构疲劳寿命预测流程。并以某机载雷过渡框为例,通过先行开展系统随机振动分析确定危险区域和位移边界,然后依照位移边界开展详细模型频响分析,得到精确的应力解,在应力解的基础上开展疲劳寿命评估。最后通过实物试验进行验证,试验结果与仿真结论吻合。研究结果表明,提出的复杂结构疲劳寿命预测方法为类似机载设备的疲劳寿命预测评估提供了一套行之有效的解决途径,具有一定的应用价值。可供同类结构疲劳寿命评估参考借鉴。
[1] 李雨,魏强.机机载电子装备轻量化设计初步研究[J].现代电子技术,2014,38(15):148-149.
[2] 吕军,王忠金,王仲仁.有限元六面体网格的典型生成方法及发展趋势[J].哈尔滨工业大学学报,2001,33(4):485-486.
[3] 张钊,张万玉,胡亚琪.飞机结构振动疲劳分析研究进展[J].航空计算技术,2012,42(2):60-63.
[4] 冯国全,周柏卓,王娟.基于递归技术的鼠笼式弹性支承疲劳强度分析[J].航空发动机,2007,33(3):23-26.
[5] 王德玲,李春光,葛修润.三维有限元位移场插值问题的研究和应用[J].岩土力学,2004,25(2):216-218.
[6] 郭小曦,张仁群.机载设备振动条件确定方法的研究[J].环境技术,2013,2013(5):6 -8.
[7] 李超.基于功率谱密度的疲劳寿命估算[J].机械设计与研究,2005,21(2):6-8.
[8] 王长武,张幼安.随机疲劳分析在机载设备疲劳寿命预测中的应用[J].中国机械工程,2004,15(21):1906-1908.
[9] 刘朋.基于界面位移控制的频响子结构法及试验研究[D].大连:大连理工大学,2018.
[10] 宋余九.金属材料的设计·选用·预测[M].北京:机械工业出版社,1998.
[11] 刘龙涛,李传日,程祺,等.某结构件的随机振动疲劳分析[J].振动与冲击,2013,32(21):97-101.
[12] 王冬梅,谢劲松.随机振动试验加速因子的计算方法[ J].环境技术,2010,28( 2):47-51.
[13] 李奇志,陈国平,王明旭,等.振动加速因子试验方法研究[J].振动、测试与诊断,2013,33(1):35-39.
[14] 蒋瑜,陶俊勇.结构振动疲劳加速试验技术研究[J].装备环境工程,2016,13(5):30-35.