1 引言
由于雷达工作环境的复杂性,雷达回波信号中包含大量的地物、气象、海洋等杂波和各种干扰。传统的信号处理技术,如动目标显示、动目标检测和恒虚警率等,对雷达回波信号进行检测后,不能完全滤除杂波,仍会存在大量的剩余杂波。这些剩余杂波不仅会形成虚假点迹,影响航迹的质量,还可能会导致数据处理系统饱和,影响雷达探测性能的发挥。因此,对信号处理后的剩余杂波进行有效抑制具有重要的研究意义。
目前,国内外对剩余杂波抑制方法的研究取得了一些成果。文献[1]提出了基于AdaBoost的雷达剩余杂波抑制方法,该方法运用自适应提升算法构造决策树分类器,通过组合多个基学习器的结果对目标和杂波进行分类,解决了弱学习器在特征不明显的杂波点迹上表现不佳的问题。文献[2]提出了一种基于径向基神经网络的海杂波抑制方法,通过改进的IGWO算法进行优化,解决了GWO算法收敛速度慢,易陷入局部优化的不足,对海杂波具有较好的抑制作用。文献[3]针对复杂天气条件下,气象雷达杂波抑制效果差的问题,提出了一种基于模糊神经网络的杂波抑制方法,利用神经网络训练得到地杂波各极化参数的隶属函数,该方法的识别结果更符合地杂波宽分布和非均匀分布的特性,对地杂波抑制起到了较好的效果。文献[4]综合考虑了目标与杂波在幅度、相位、距离等特征的差异,利用综合特征因子评估过滤杂波,降低了虚假航迹率和点迹损失率。但该方法在综合特征因子求取时,加权因子的确定依赖经验值,影响了算法的运算效率和杂波抑制效果。文献[5]提出了一种基于杂波图的杂波抑制方法,分别对单部雷达和组网雷达进行杂波抑制。但该方法需要对杂波区域进行判别、划分,根据不同杂波区选取不同的判别门限,在组网时要考虑不同雷达的融合权值,计算过程较为复杂。文献[6]在研究了雷达信号处理中的动目标显示和动目标检测2种杂波抑制技术的基础上,应用了K近邻算法对目标和杂波进行判别,但是该方法的杂波剩余点迹抑制率不到70%,杂波点迹识别率还有待提高。文献[7]设计了5层BP神经网络分类器,采用L-M算法对分类器进行训练,较K近邻算法和支持向量机提高了分类精度。但是该方法的神经网络过于复杂,识别时间较长,不太适用于雷达剩余杂波的快速识别。
本文针对现有BP神经网络算法学习速度慢,杂波识别率较低的问题,提出了一种改进的BP神经网络抑制杂波的方法。选取多普勒速度、目标原始幅度、杂噪比等8个特征作为输入,设计雷达点迹分类器,引入弹性BP算法提高神经网络的收敛速度,并对网络结构进行优化。结果表明,改进后的BP神经网络算法既节省了识别时间,也提升了杂波抑制的效果。
2 BP神经网络
BP神经网络是一种由输入层、隐含层和输出层组成的多层前馈网络[8-9]。BP神经网络的隐含层数量和各层的节点数可以是一个或者多个,一个包含单个隐含层的BP神经网络可以实现M维到N维的非线性映射,如图1所示[10]。
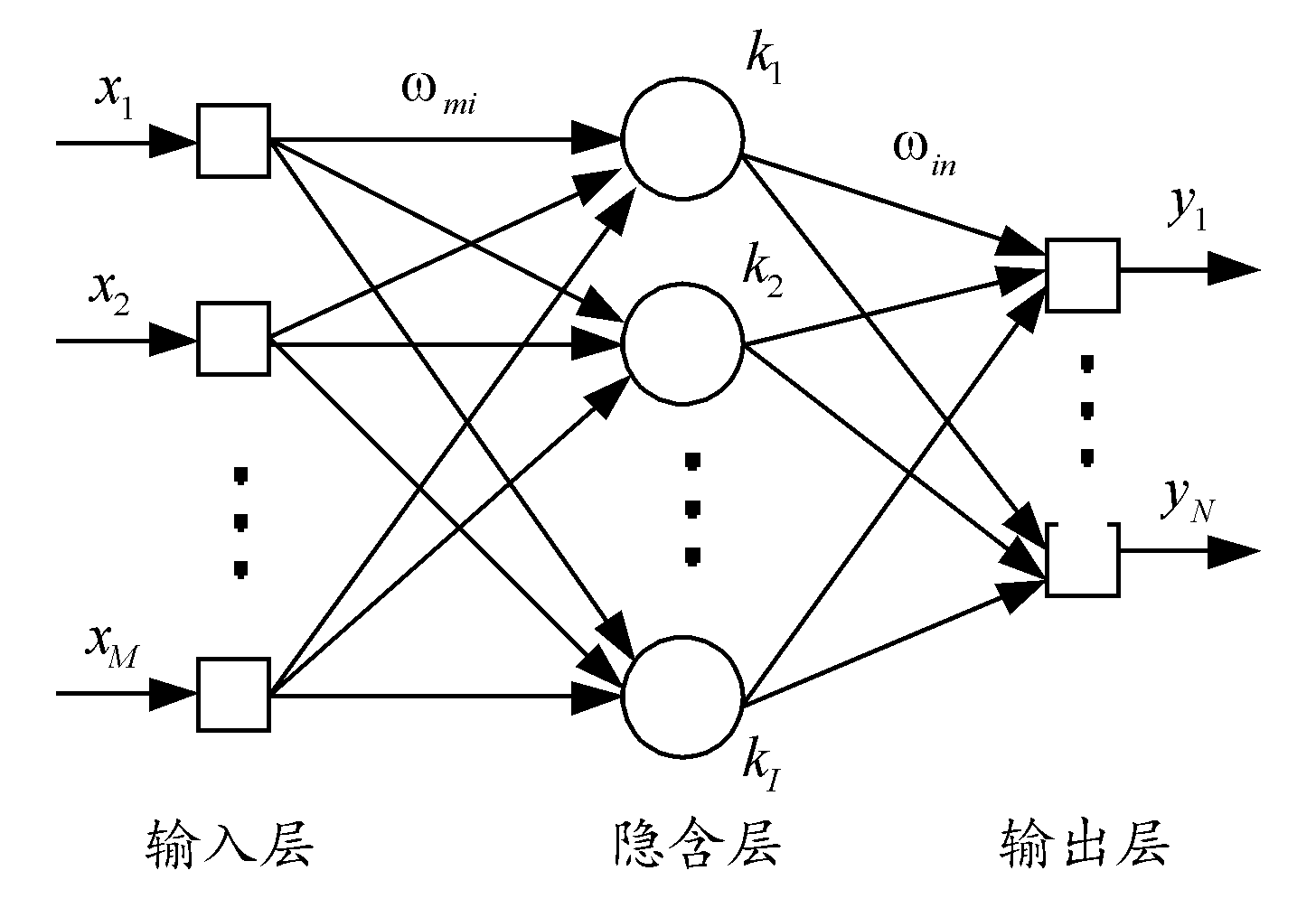
图1 BP神经网络示意图
Fig.1 Schematic diagram of BP neural network
BP神经网络各层之间全连接,同一层的神经元相互不连接。在BP神经网络中,数据按照输入层-隐含层-输出层的顺序,逐层向后传播。在对网络的权值进行训练时,沿着误差减小的方向,按照反向顺序,逐层向前修正权值,通过多次的学习训练,最终的误差逐渐缩小至符合要求的范围,此时神经网络训练完成。
图1中的BP神经网络,输入层的神经元数量为M,隐含层神经元数量为I,输出层神经元数量为N。输入层的第m个神经元为Xm,隐含层第i个神经元为Ki,输出层第n个神经元为Yn。从Xm到Ki的连接权值为ωmi,从Ki到Yn的连接权值为ωin。该网络的输入数据为M维的向量,输出数据为N维的向量。用u和v分别表示每一层的输入和输出,例如![]() 表示隐含层第一个神经元的输入。迭代次数为s,网络的实际输出为:
表示隐含层第一个神经元的输入。迭代次数为s,网络的实际输出为:
(1)
网络的期望输出为:
d(s)=[d1,d2,…,dJ]
(2)
2.1 工作信号正向传播
神经网络中输入层的节点数为输入向量的维数,输入层的输出为神经网络的输入信号。假设输入信号为x(s),则输入层第m个神经元的输出为:
(3)
隐含层第i个神经元的输入为:
(4)
假设隐含层传递函数为f(·),则隐含层第i个神经元的输出为:
![]()
(5)
输出层第n个神经元的输入为:
(6)
假设输出层传递函数为g(·),则输出层第n个神经元的输出为:
![]()
(7)
输出层第n个神经元的误差为:
(8)
神经网络的总误差为:
![]()
(9)
2.2 误差信号反向传播
神经网络在调整权值时,按照网络逐层反向调整。隐含层与输出层之间的权值调整为:
ωin(s+1)=ωin(s)+Δωin(s)
(10)
输入层与隐含层之间的权值调整为:
ωmi(s+1)=ωmi(s)+Δωmi(s)
(11)
式中,Δωin(s)、Δωmi(s)分别为隐含层与输出层之间和输入层与隐含层之间的权值调整量,其大小取决于训练算法。
3 改进前后的BP神经网络模型
BP神经网络包含训练和学习2个过程[11]。网络训练时,数据通过输入层进入网络,然后传递至隐含层各神经元,数据经过传递函数变换后传递到输出层输出。当实际输出值与期望值误差较大时,误差反向经过隐含层传递到输入层,传递时将误差分配至每一层,各层的神经元权值根据误差进行调整,直至满足训练停止条件。网络学习时,先对网络进行初始化设置,分配连接权值,确定学习次数、误差函数。然后输入训练数据,计算隐含层的输入输出,调整权值。最后计算全局误差,直至误差满足停止条件[12]。
BP神经网络的设计包含网络层数、输入层节点数、隐含层节点数、输出层节点数、传递函数、训练方法和训练参数设置等内容[13]。
3.1 经典BP神经网络模型
1)网络层数
BP神经网络包含一个或多个隐含层。文献[7]中构建了5层神经网络,其中包含一个输入层、3个隐含层和一个输出层。
2)输入层节点数
输入层的节点数取决于输入数据的维数。文献[7]中选取的数据特征为方位、距离、信噪比、幅度、方位跨度和距离跨度等6维特征,因此输入层节点数为6个。
3)隐含层节点数
文献[7]中第1个隐含层有10个节点,第2个隐含层有20个节点,第3个隐含层有10个节点。
4)输出层节点数
输出层的节点数取决于输出数据的维数。在雷达剩余杂波抑制的过程中,需要根据BP神经网络来识别雷达点迹为目标还是杂波,输出数据为一维数据,因此输出层节点数为1个。
5)传递函数和训练参数
BP神经网络的传递函数必须可微[14]。文献[7]中隐含层传递函数为tansig函数,输出层为logsig函数。
6)训练方法
标准BP神经网络的训练算法为最速下降法,但该算法的收敛速度慢,易陷入局部极小。文献[7]中采用了L-M算法,使训练速度得到了一定的提升。
3.2 本文改进BP神经网络模型
1)网络层数
文献[7]中构建的网络结构过于复杂,导致雷达点迹判别耗时较长,无法快速抑制杂波。经理论证实,单个隐含层结构的网络可以实现任意非线性映射[15]。因此,本文构建了3层BP神经网络,包含一个输入层、一个隐含层和一个输出层,简化了网络结构,提高了模型的识别速度。
2)输入层节点数
本文选取的数据特征为多普勒速度、目标原始幅度、目标背景幅度、滤波标志、恒虚警类型、杂噪比、滤波器组选择和EP质量等8维特征,因此输入层节点数为8个。
3)隐含层节点数
隐含层的节点数对BP神经网络的性能影响巨大,隐含层节点数增多可以提高网络的性能,但也会延长训练时间。文献[7]中设计隐含层节点数时未给出设计的依据,存在一定的随意性。本文隐含层节点数采取下式确定:
(12)
式中,M和N分别为输入层和输出层节点数,a是[0,10]之间的常数。本文中输入层和输出层节点数分别为8个和1个,a取值为10,因此隐含层节点数为13个。
4)输出层节点数
本文中,网络输出为0或1的一维数据,0代表该雷达点迹识别为杂波,1代表该雷达点迹识别为目标,因此输出层节点数为1个。
5)传递函数和训练参数
本文选用Tan-Sigmoid函数为隐含层传递函数,线性函数purelin函数为输出层传递函数。网络学习率为0.01,目标误差为10-7,最大迭代次数为1 000次。
6)训练方法
文献[7]中采用了L-M算法,模型的识别时间仍然较长,识别率较低。本文引入弹性BP算法,以提高神经网络的训练速度和识别率。弹性BP算法在调整权值时,仅使用了偏导的符号,而未使用偏导的幅值,这样权值的调整量就与幅值无关,可消除梯度幅度的不良影响。权值调整量的大小由下式决定:
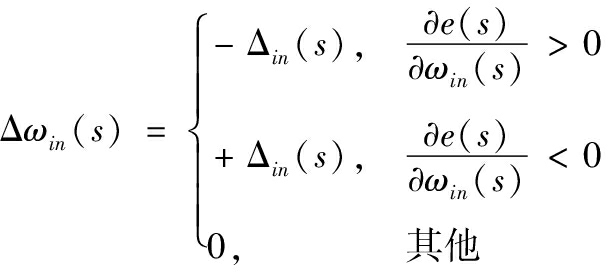
(13)
权值的调整遵循以下原则,如果偏导为正,则权值减小,如果偏导为负,则权值增加。下一次迭代的权值调整量为:
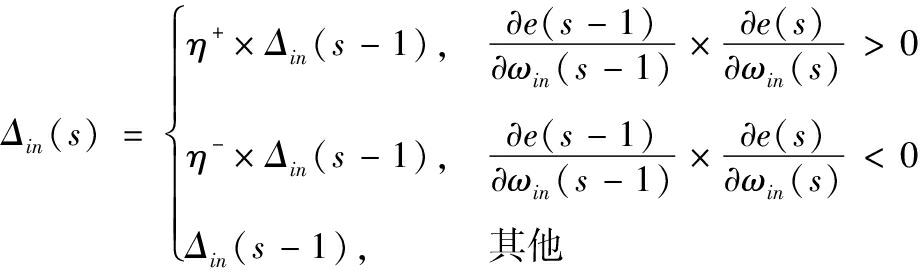
(14)
式中,Δin(s)为权值的调整步长,Δin(s)∈[Δmin,Δmax],0<η-<1<η+为调整系数。
与以学习率为基础的其他算法不同的是,弹性BP算法直接修改调整权值,因此不会导致因为无法预期的梯度变化而使修改后的网络性能下降。当训练发生振荡时,弹性BP算法的权值调整量将减小,在多次迭代中权值朝相同方向变化时,权值调整量增大。因此,弹性BP算法的收敛速度更快。
3.3 BP神经网络训练与分类
将雷达点迹训练数据输入设计好的BP神经网络中进行训练,当分类精度满足要求时,网络训练完成。将雷达点迹测试数据输入训练好的网络中,通过输出识别雷达点迹为目标还是杂波,若识别为杂波,则滤除该点迹,以达到抑制杂波的目的。
文中所提雷达剩余杂波抑制方法的流程如图2所示。
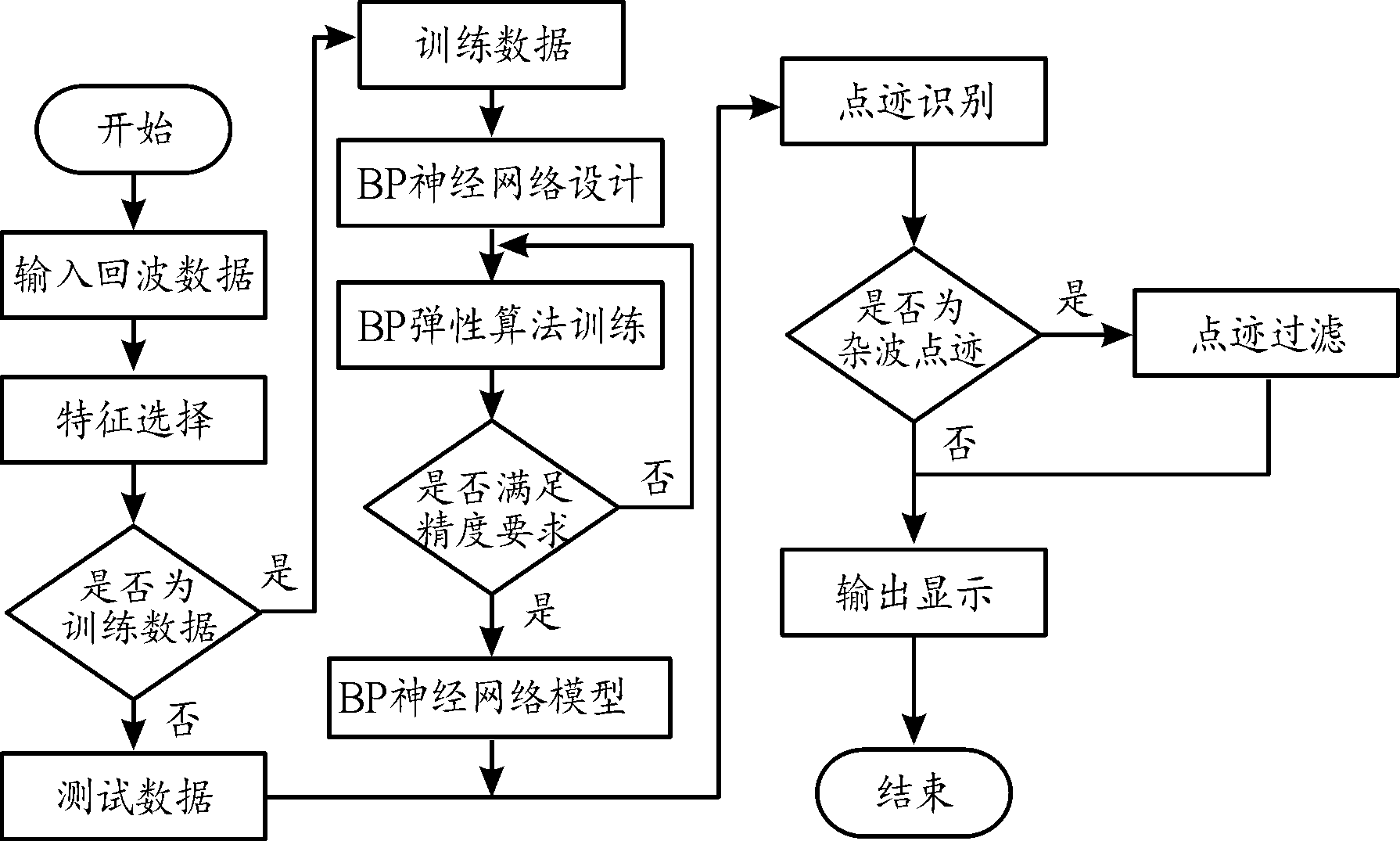
图2 基于BP神经网络的雷达剩余杂波抑制流程框图
Fig.2 Flow diagram of radar residual clutter suppression based on BP neural network
4 实验结果与分析
采集某型空管雷达的30 000个点迹实测数据,选取24 000个作为训练样本,其中目标点迹和杂波点迹各12 000个,剩余6 000个作为测试样本,其中目标点迹和杂波点迹各3 000个。数据分布如表1所示。
表1 数据分布
Table 1 Data distribution
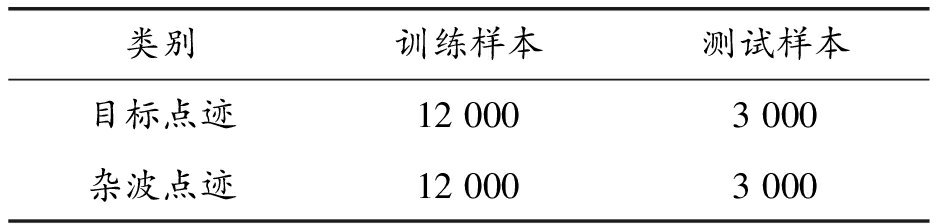
类别训练样本测试样本目标点迹120003000杂波点迹120003000
实验内容分为2个部分,实验1通过设计的BP神经网络测试不同特征组合时的雷达点迹识别率,选取最优的特征组合作为点迹识别模型的输入数据;实验2将本文提出的方法与文献[7]中的方法进行对比分析。
4.1 最优特征组合的选取
从采集的雷达点迹特征中选取8个特征进行测试,分别为:多普勒速度、目标原始幅度、目标背景幅度、滤波标志、恒虚警类型、杂噪比、滤波器组选择和EP质量。对单个特征或者多个特征组合时BP神经网络模型的识别率进行研究,不同特征下的识别率如表2所示。
表2 不同特征下的识别率(%)
Table 2 Recognition rate under different features(%)
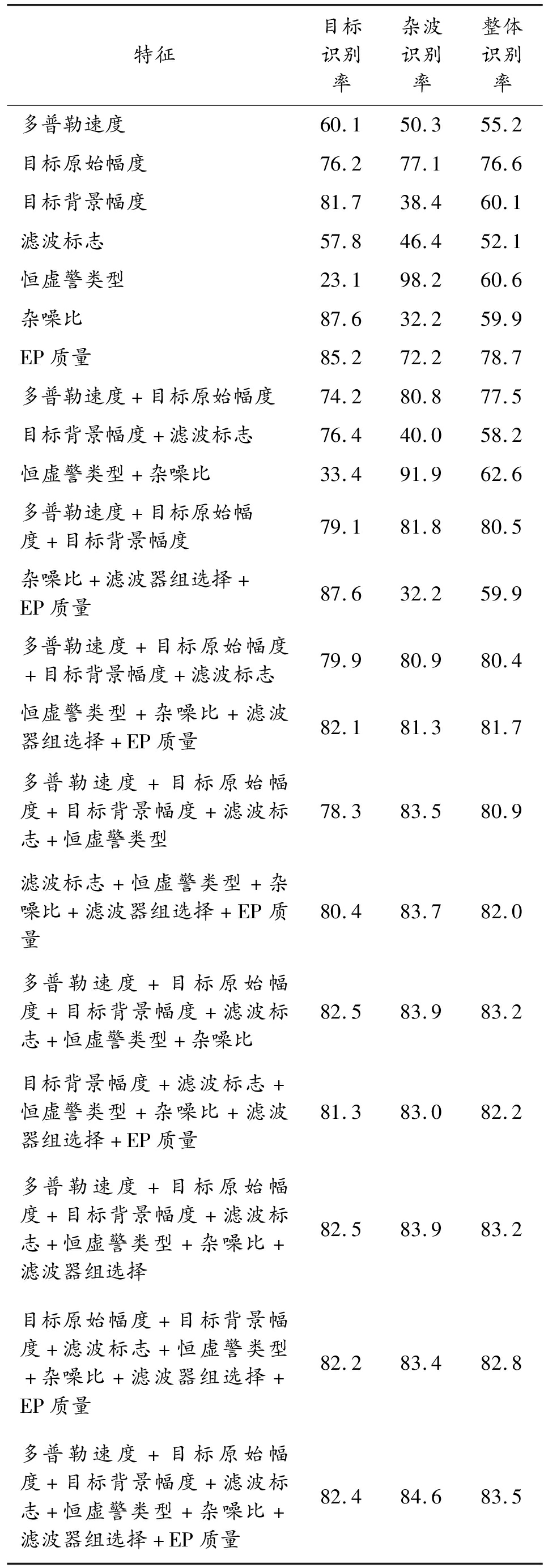
特征目标识别率杂波识别率整体识别率多普勒速度60.150.355.2目标原始幅度76.277.176.6目标背景幅度81.738.460.1滤波标志57.846.452.1恒虚警类型23.198.260.6杂噪比87.632.259.9EP质量85.272.278.7多普勒速度+目标原始幅度74.280.877.5目标背景幅度+滤波标志76.440.058.2恒虚警类型+杂噪比33.491.962.6多普勒速度+目标原始幅度+目标背景幅度79.181.880.5杂噪比+滤波器组选择+EP质量87.632.259.9多普勒速度+目标原始幅度+目标背景幅度+滤波标志79.980.980.4恒虚警类型+杂噪比+滤波器组选择+EP质量82.181.381.7多普勒速度+目标原始幅度+目标背景幅度+滤波标志+恒虚警类型78.383.580.9滤波标志+恒虚警类型+杂噪比+滤波器组选择+EP质量80.483.782.0多普勒速度+目标原始幅度+目标背景幅度+滤波标志+恒虚警类型+杂噪比82.583.983.2目标背景幅度+滤波标志+恒虚警类型+杂噪比+滤波器组选择+EP质量81.383.082.2多普勒速度+目标原始幅度+目标背景幅度+滤波标志+恒虚警类型+杂噪比+滤波器组选择82.583.983.2目标原始幅度+目标背景幅度+滤波标志+恒虚警类型+杂噪比+滤波器组选择+EP质量82.283.482.8多普勒速度+目标原始幅度+目标背景幅度+滤波标志+恒虚警类型+杂噪比+滤波器组选择+EP质量82.484.683.5
由表2可知,在特征组合为“多普勒速度+目标原始幅度+目标背景幅度+滤波标志+恒虚警类型+杂噪比+滤波器组选择+EP质量”时模型的识别率最高,目标识别率为82.4%,杂波识别率为84.6%,整体识别率为83.5%。因此,该组合为最优特征组合。
4.2 2种方法对比
由最优特征组合中特征的数量可知,BP神经网络的输入数据维数为8维,因此输入层节点数为8个。已知输出层节点数为1,由式(12)可知,隐含层节点数范围为[3,13]。经过验证,隐含层节点为13时的效果最好。因此,本文的BP神经网络由8个节点的输入层、13个节点的隐含层和1个节点的输出层构成。如图3所示,本文设计的神经网络结构比文献[7]中的神经网络更加简单。

图3 2种BP神经网络结构示意图
Fig.3 Schematic diagram of two kinds of BP neural network structure
为了对比2种BP神经网络的识别时间和杂波抑制效果,采取相同的训练数据对2种BP神经网络进行训练,利用相同的测试数据对训练好的模型分别进行测试,得到的识别时间如图4所示,均方误差如图5所示。
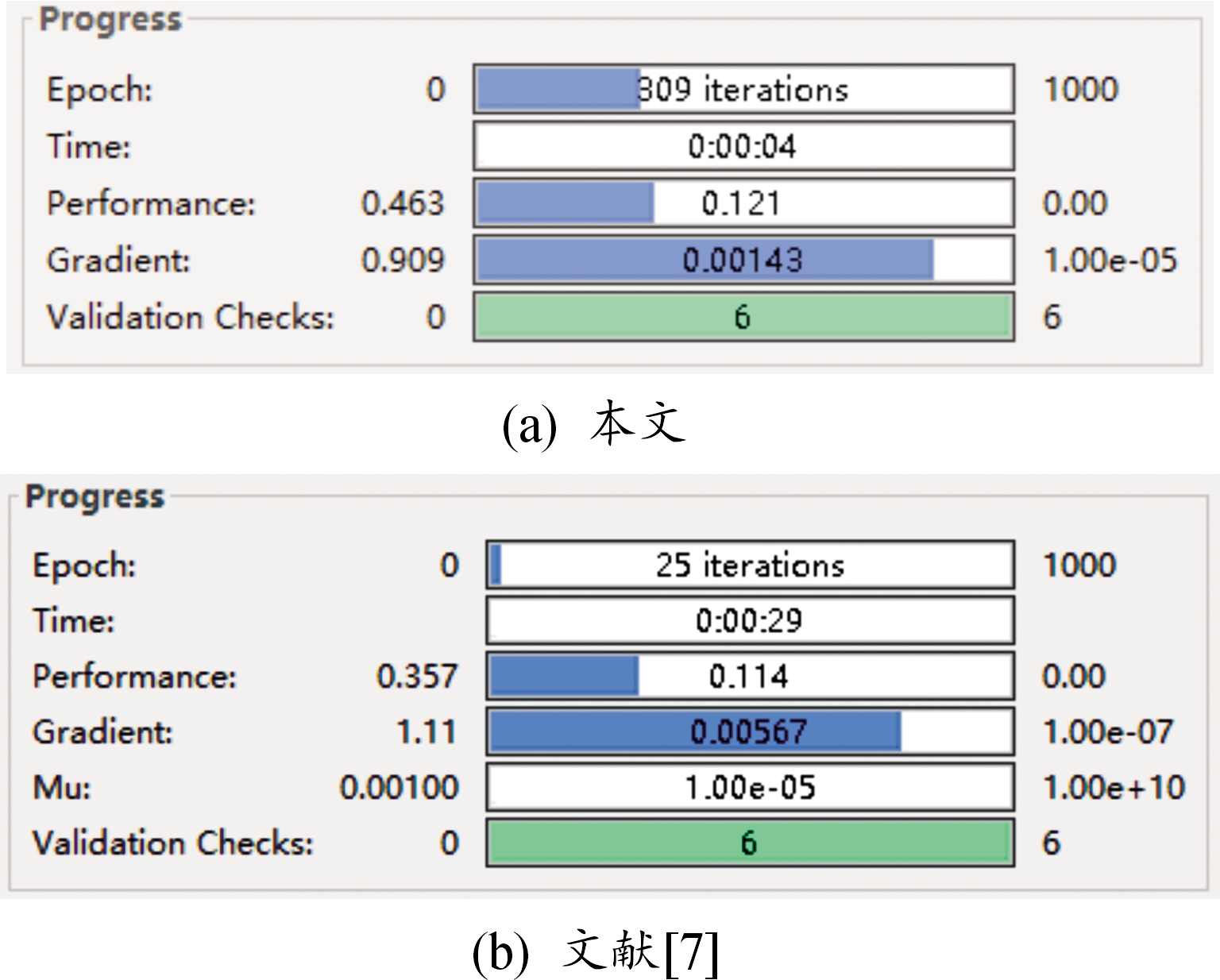
图4 2种BP神经网络结构识别时间界面
Fig.4 Recognition time of two kinds of BP neural network structures
从图4中可以看出,本文方法BP神经网络识别时间为4 s,文献[7]中BP神经网络的识别时间为29 s,前者比后者的识别时间节省了86%。从图5中可以看出,本文方法神经网络在迭代303次时均方误差最低,误差为0.117 49,文献[7]中BP神经网络在迭代19次时的均方误差最低,误差为0.121 21,前者在更短的时间内迭代次数更多且误差下降更快最优误差更小。通过图4和图5可以说明,本文方法收敛速度更快,精度更高,显著提高了雷达点迹识别的效率,在雷达这种对情报实时性要求较高的装备中,本文方法具有更好的适用性。
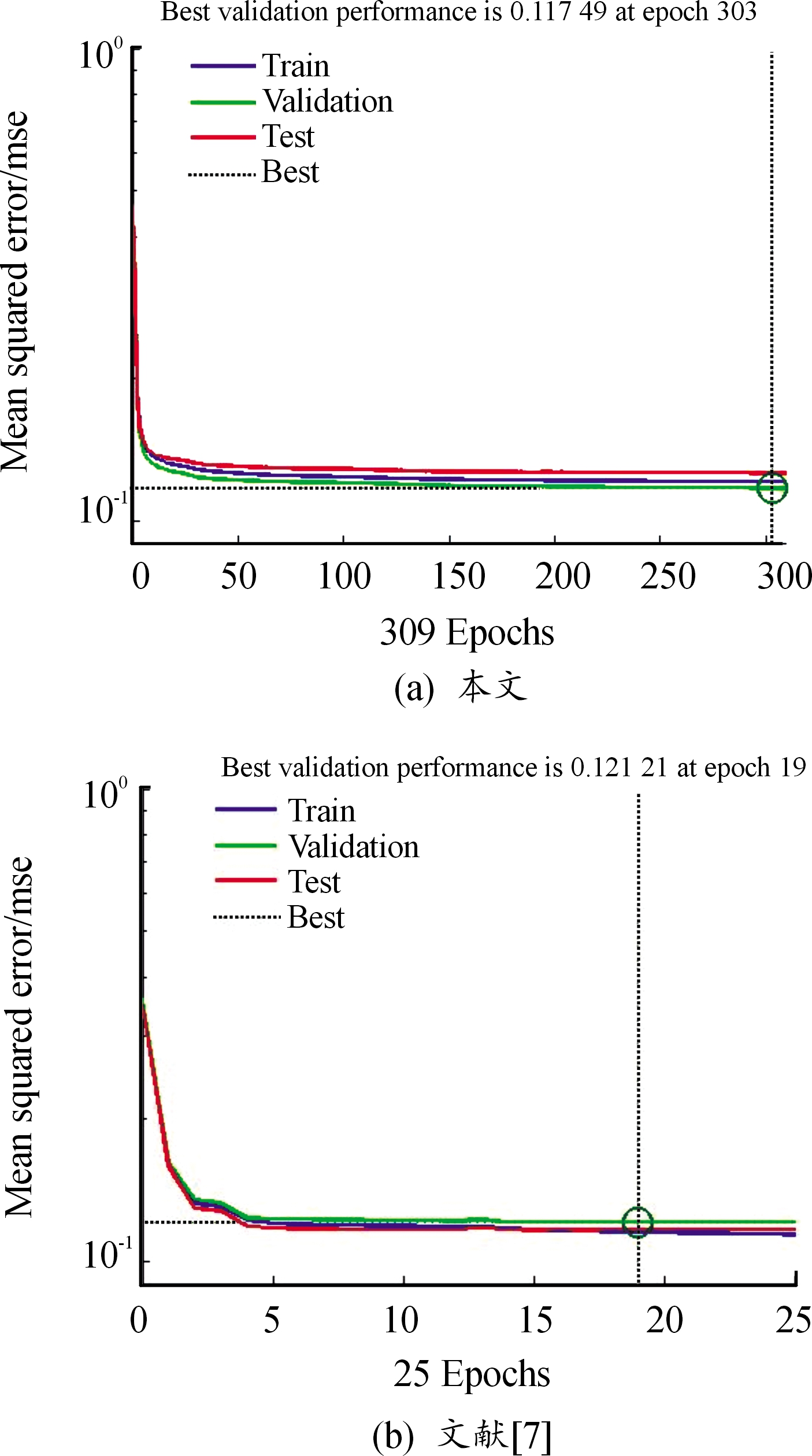
图5 2种BP神经网络均方误差曲线
Fig.5 Mean square error of two kinds of BP neural network
图6为3 000个测试样本在分类识别前的分布图,横坐标为方位,纵坐标为距离,绿色点代表目标点迹,红色点代表杂波点迹。

图6 测试样本空间分布图
Fig.6 Spatial distribution of test samples
图7为采取2种BP神经网络杂波抑制后的效果图,前者为本文方法杂波抑制后的效果,后者为文献[7]中方法杂波抑制后的效果。从图6和图7的对比中可以看出,采取2种BP神经网络后大部分杂波都被成功抑制。从图7可以看出,在圆框内的区域中,本文方法剩余的杂波点迹更少,杂波抑制的效果更好。
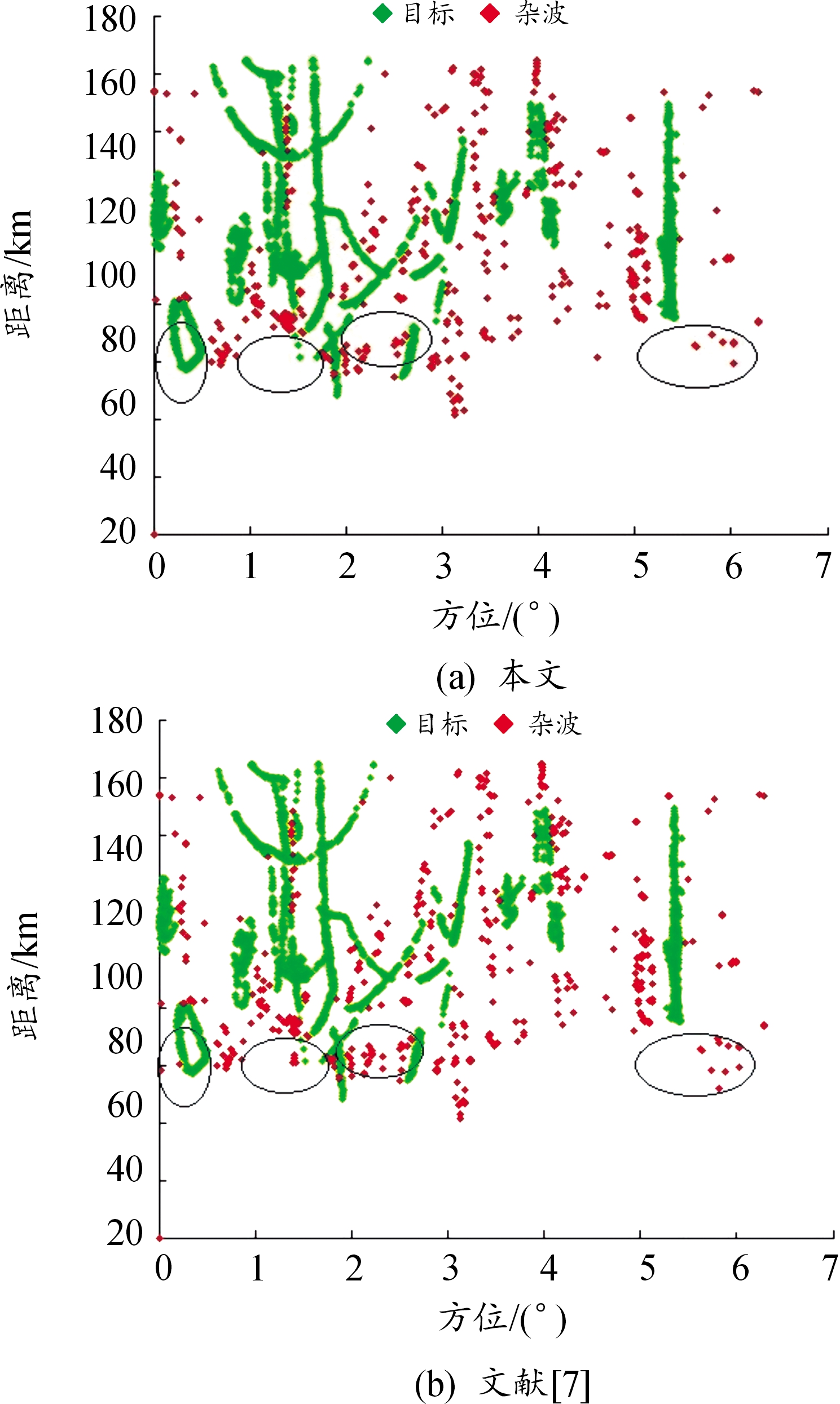
图7 2种方法杂波抑制效果图
Fig.7 Effect of clutter suppression by two methods
2种方法的识别率如表3所示。由表3可知,本文方法比文献[7]中方法杂波点迹识别率提升了1.6%,整体点迹识别率提升了0.2%,识别精度更高,杂波抑制效果更好。
表3 2种方法的识别率(%)
Table 3 Recognition rate of the two methods(%)
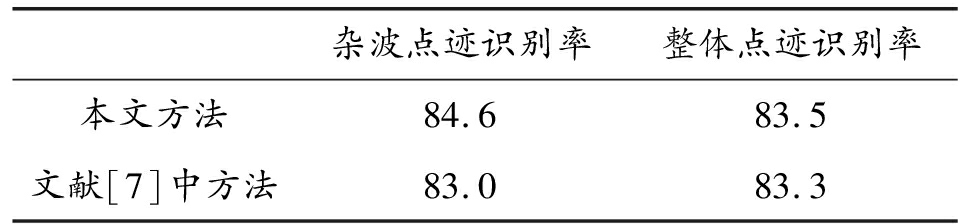
杂波点迹识别率整体点迹识别率本文方法84.683.5文献[7]中方法83.083.3
5 结论
本文引入弹性BP算法,改进现有的BP神经网络训练算法,提升了网络收敛速度。通过分析隐含层的层数和节点数,减少了现有神经网络中隐含层层数和节点数的数量,简化了BP神经网络的结构,提高了雷达点迹识别率。通过计算雷达实测数据,证明本文提出的雷达剩余杂波抑制方法,不仅缩短了识别时间,也提高了杂波的抑制效果,对雷达装备在实际工作中快速高效地抑制剩余杂波具有指导作用。
[1] 林坚鑫,沈学勇,楼奇哲,等.基于AdaBoost的雷达剩余杂波抑制方法[J].电光与控制,2020,27(06):53-57.
Lin J X,Shen X Y,Lou Q Z,et al.An AdaBoost based method for suppression of radar residual clutter[J].Electronics Optics & Control,2020,27(06):53-57.
[2] Shang S,He K N,Wang Z B,et al.Sea clutter suppression method of HFSWR based on RBF neural network model optimized by improved GWO algorithm[J].Computational Intelligence and Neuroscience,2020,2020:8842390.
[3] Li H,Ren J W,Han J G,et al.Ground clutter suppression method based on FNN for dual-polarisation weather radar[J].The Journal of Engineering,2019,2019(19):6043-6047.
[4] 史建涛,杨予昊,孙俊,等.基于杂波特征评估的雷达目标点迹过滤方法[J].太赫兹科学与电子信息学报,2019,17(06):988-993.
Shi J T,Yang Y H,Sun J,et al.A plots filtering method for radar targets based on clutter feature evaluation[J].Journal of Terahertz Science and Electronic Information Technology,2019,17(06):988-993.
[5] 罗兴旺,张伯彦,刘嘉,等.雷达数据处理中的杂波抑制方法[J].系统工程与电子技术,2016,38(01):37-44.
Luo X W,Zhang B Y,Liu J,et al.Researches on the method of clutter suppression in radar data processing[J].Systems Engineering and Electronics,2016,38(01):37-44.
[6] 韦涛.杂波抑制与真假目标判别[D].西安:西安电子科技大学,2017.
Wei T.Clutter suppression and true-false target discrimination[D].Xi’an:XIDIAN University,2017.
[7] 李松,汪圣利.基于BP神经网络的雷达点迹分类方法[J].现代雷达,2018,40(12):52-56.
Li S,Wang S L.Radar plots classification method based on BP neural network[J].Modern Radar,2018,40(12):52-56.
[8] 周璐,顾均元,冯玉光.基于模糊理论与BP神经网络的导弹质量评估研究[J].兵器装备工程学报,2020,41(04):52-57.
Zhou L,Gu J Y,Feng Y G.Missile quality assessment based on fuzzy theory and BP neural network[J].Journal of Ordnance Equipment Engineering,2020,41(04):52-57.
[9] Zhang D H,Lou S.The application research of neural network and BP algorithm in stock price pattern classification and prediction[J].Future Generation Computer Systems,2021,115:872-879.
[10] DAI H,XU Q,XIONG Y,et al.Improved prediction of michaelis constants in CYP450-mediated reactions by resilient back propagation algorithm[J].Current Drug Metabolism,2016,17(07):673-680.
[11] 迟明祎,侯兴明,陈小卫,等.基于BP神经网络的某反装甲武器系统打击效果预测[J].兵器装备工程学报,2020,41(08):52-57.
Chi M Y,Hou X M,Chen X W,et al.Prediction of strike effect of an anti-armor weapon system based on BP neural network[J].Journal of Ordnance Equipment Engineering,2020,41(08):52-57.
[12] 樊剑,李志刚,李立国.基于改进BP-小波神经网络法的分药故障检测[J].兵器装备工程学报,2018,39(06):155-158.
Fan J,Li Z G,Li L G.Fault detection of modular dispensing based on improved wavelet-BP neural network[J].Journal of Ordnance Equipment Engineering,2018,39(06):155-158.
[13] 陈明.MATLAB神经网络原理与实例精讲[M].北京:清华大学出版社,2013.
Chen M.Principle and example of MATLAB neural network[M].Beijing:Tsinghua university Press,2013.
[14] Wen F,Jing F S,Zhao W H,et al.Research on optimal receiver radius of wireless power transfer system based on BP neural network[J].Energy Reports,2020,6(09):1450-1455.
[15] 王国辉,张宝栋,李向荣.基于BP神经网络的身管磨损量监测系统设计[J].兵器装备工程学报,2020,41(06):126-131.
Wang G H,Zhang B D,Li X R.Design of body tube wear monitoring system based on BP neural network[J].Journal of Ordnance Equipment Engineering,2020,41(06):126-131.