1 引言
利用装药聚能作用,药型罩在爆轰压力作用下可快速形成具有一定初速度的侵彻体[1-3]。目前,多点起爆超压成型与爆轰波相互碰撞作用分析已成为当前EFP领域内研究热点,已证实爆轰波碰撞超压可提高装药利用率与弹丸的初速度,优化EFP尾翼从而使其具有更好的空气动力学稳定性[4-5]。在爆轰波相互碰撞作用下形成EFP的研究近年来更为细致,利用碰撞形成的超压马赫区域加载到药型罩表面驱动其形成不同形态尾翼的EFP。在PAN[6]的研究试验中观察到正规斜反射碰撞点作用在金属铜上所造成的凹坑边缘光滑,而马赫反射所造成的凹坑边缘及表面却很粗糙,马赫杆上强度不一致,进一步说明正规斜反射碰撞点区域压力比马赫杆压力稳定,并且缺少对正规斜反射碰撞点区域作用于药型罩的详细研究。为此,利用LS-DYNA 有限元软件并结合三波理论,分析了单元装药结构下爆轰波相互作用以及与双向曲率药型罩的碰撞过程,通过数值模拟和理论计算得到药型罩表面超压分布,之后阐述两点起爆误差对EFP的成型及尾翼的影响规律,确定出成型较好EFP的两点最大同步起爆误差。
2 单元装药结构及有限元模型建立
2.1 单元装药结构几何尺寸有限元模型建立
本研究对象为一个单元装药结构[7-8],如图1所示,主视图与左视图显示药型罩为双向曲率的线性圆弧结构。装药长度L=70 mm,装药宽度W=26 mm,装药高度H=30 mm,药型罩外曲率半径Ro=120 mm,内曲率半径 Ri=117.5 mm,侧向曲率半径Rr=15 mm,厚度δ=2.5 mm,宽度w=20 mm。装药顶部两端中点设置为起爆点,采用两点同时或延迟起爆。有限元模型中炸药、药型罩采用拉格朗日算法,二者之间边界定义滑移接触算法。炸药为RDX基,采用HIGH_EXPLOSIVE_BURN材料模型和JWL状态方程,无氧铜罩采用Johnson Cook材料模型和Gruneisen状态方程;具体材料参数[9-10]见表1。
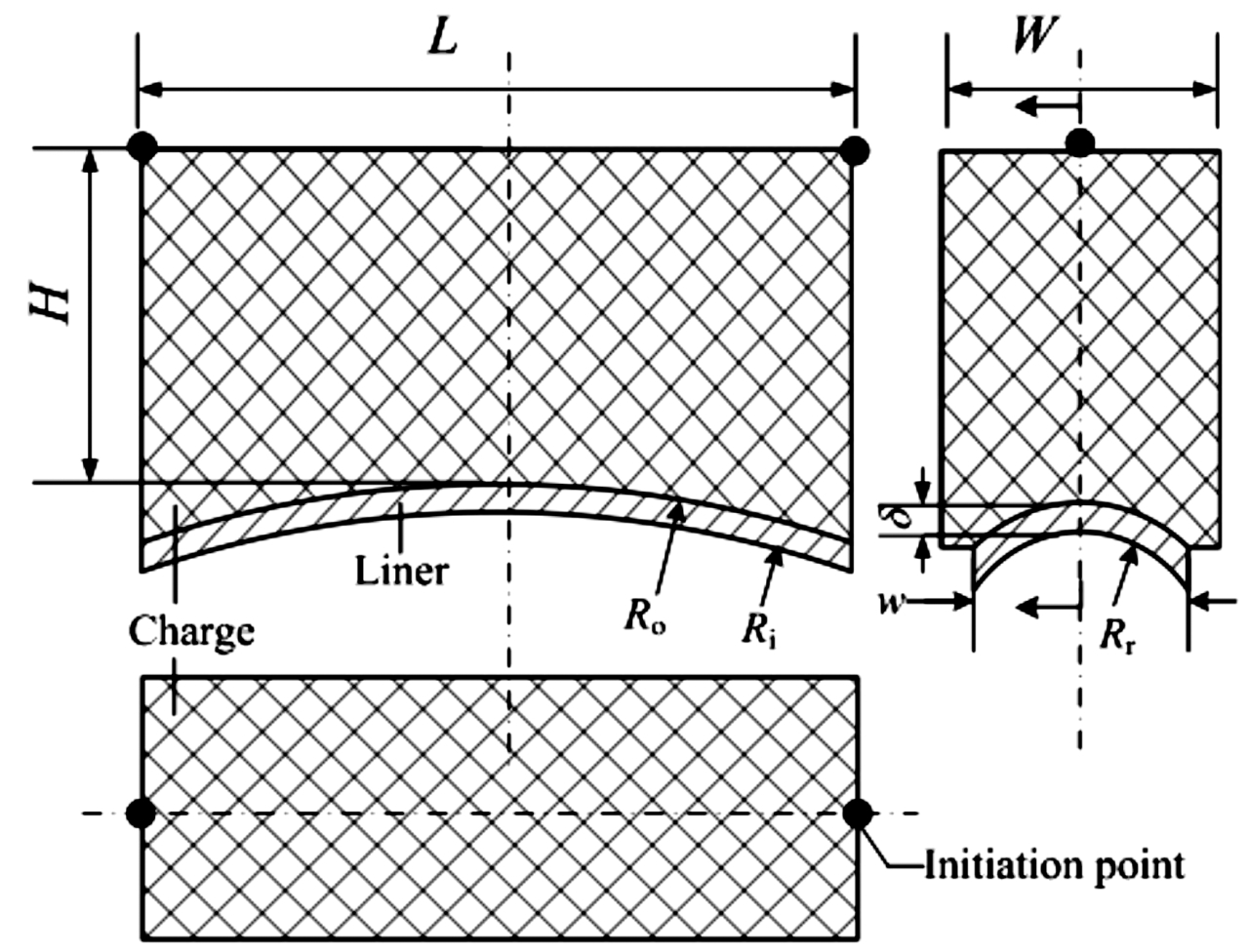
图1 单元装药结构示意图
Fig.1 Schematic representation of the unit-shaped charge
2.2 数值模拟与试验验证
根据图2中x-ray试验[8]与数值模拟结果,EFP前端存在凸起,中部主体粗大,主体和尾翼之间存在一定的径向扩张,EFP在初期成型中的形状为扇形,此后EFP尾翼逐渐发展为四翼,试验和数值模拟中均能反映出EFP成型以及尾翼闭合的形态,说明数值计算结果和试验结果吻合较好,进一步说明建立的有限元模型能有效反映出此装药结构形成EFP的成型过程。
表1 仿真用材料参数
Table 1 Material parameters used for the numerical simulation
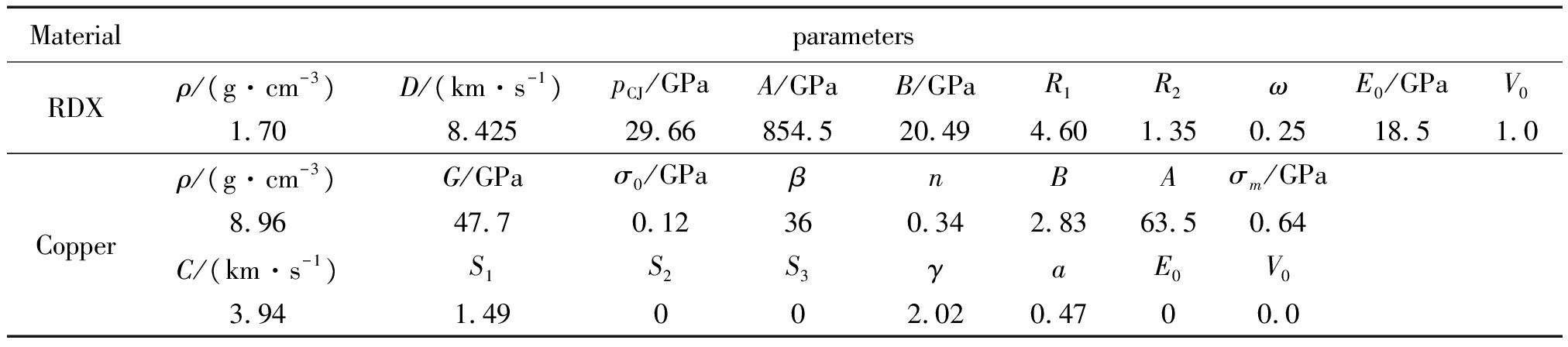
MaterialparametersRDXρ/(g·cm-3)D/(km·s-1)pCJ/GPaA/GPaB/GPaR1R2ωE0/GPaV01.708.42529.66854.520.494.601.350.2518.51.0Copperρ/(g·cm-3)G/GPaσ0/GPaβnBAσm/GPa8.9647.70.12360.342.8363.50.64C/(km·s-1)S1S2S3γaE0V03.941.49002.020.4700.0

图2 EFP的x-ray试验与数值模拟结果图
Fig.2 Comparison between x-ray test and numerical simulation of EFP
3 爆轰波传播相互作用分析
3.1 爆轰波与药型罩作用分析
图3所示的xoy为有限元模型对称平面,起爆点分布在x轴线上,2个起爆点坐标值分别为(L/2,0,0)和(-L/2,0,0),两点距离为装药长度L。在xoy平面内,爆轰波从起爆点各自以球面爆轰波独立传播,已知爆速DCJ和传播时间t,装药各个单元中心离起爆点位置的距离即为tDCJ,存在多个起爆点则各单元起爆时间按照最近起爆点距离计算。

图3 有限元模型及药型罩上表面爆轰波传播与碰撞示意图
Fig.3 Finite element model of the charge and schematic representation of the detonation wave propagation
2个爆轰波在坐标原点o位置开始接触并发生正碰撞,之后碰撞点沿着y轴正方向进行移动,正碰撞则转变为正规斜反射过程。为此,计算图3(a)中波阵面切线与y轴之间形成入射角φ1,根据几何关系可得:
(1)
在xoy平面内,2个爆轰波碰撞的入射角变化如图4所示,入射角随着碰撞点从o点运动至药型罩上表面并最先接触药型罩外曲率半径Ro弧顶中点,整个过程中入射角逐渐增大,其变化范围为0~40.2°。
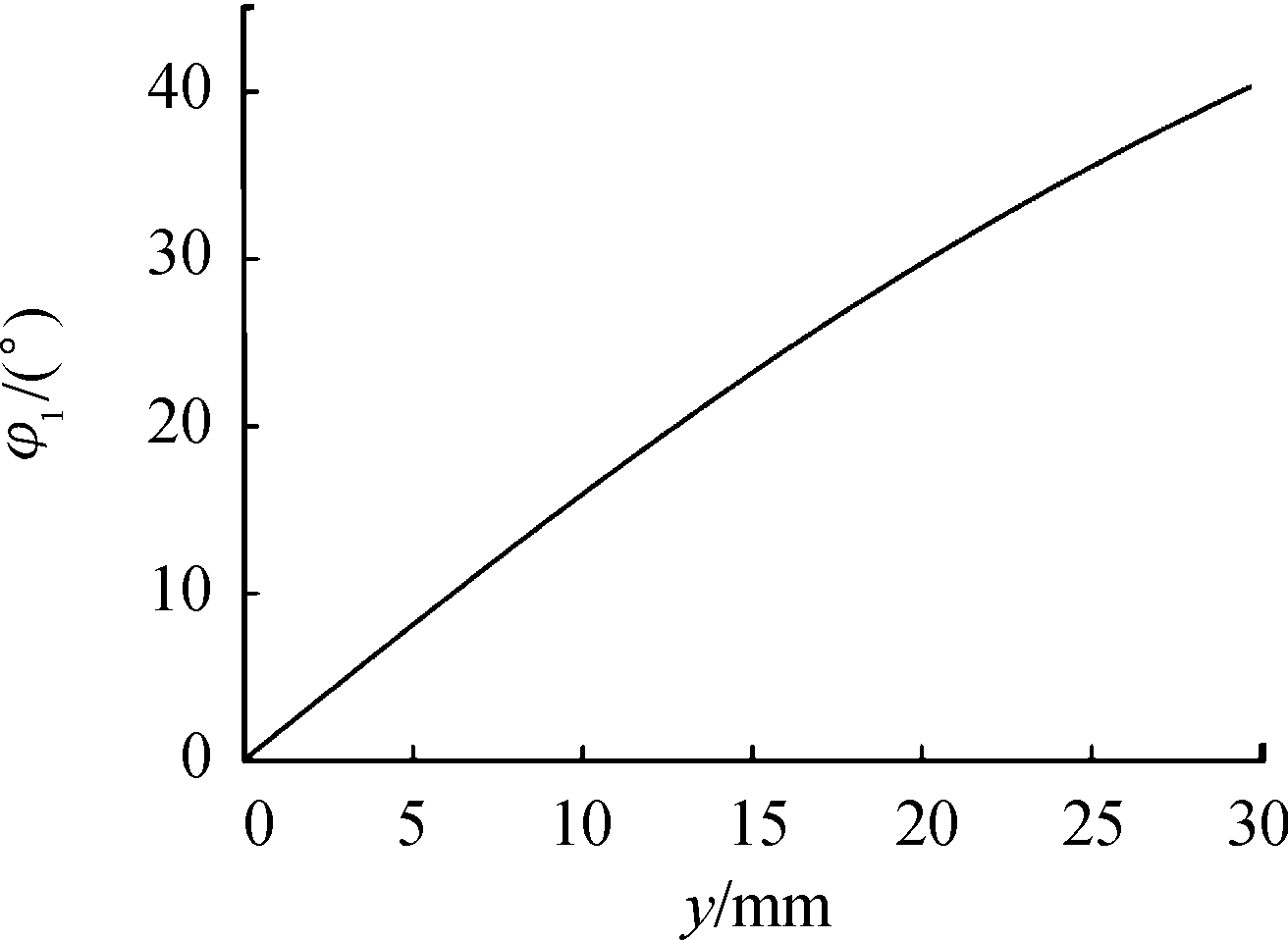
图4 沿y轴爆轰波碰撞入射角变化曲线
Fig.4 Incident angle of the detonation wave collision along the y-axis
根据图3(a)明确波阵面首先碰撞到药型罩上表面两端的位置,然后爆轰波沿着药型罩上表面外曲率半径向对称中心进行传播,并在药型罩弧顶中线进行碰撞,如图3(b),其中药型罩的短对称弧线为弧顶中线,给出药型罩上表面爆轰波碰撞点的运动轨迹线,沿着药型罩的侧向曲率半径Rr方向,由于药型罩具有对称结构,故给出局部示意图。
计算中做如下假设爆轰波近似球面传播,根据几何关系有波阵面运动方程为:
(2)
式中:xd为起爆点坐标值±L/2。
根据药型罩双向曲率几何结构,在三维直角坐标系中得到药型罩上表面的曲面方程:
![]()
(3)
根据几何关系,有:
y0= H+ Ro
(4)
yr= Rr+ Hr+H
(5)
![]()
(6)
当爆轰波作用于药型罩上表面后,即波阵面方程(2)与药型罩上表面曲面方程(3)相交,因此可得到二者的相交线。在图3(b)中,2个爆轰波与药型罩的相交线在对称中线接触并发生碰撞,药型罩弧顶中线为相交线碰撞点轨迹线,中间起点坐标(0,H,0),轨迹线终点坐标为![]() 正规斜反射碰撞点沿轨迹线运动的波阵面入射角随药型罩侧向曲率半径Rr发生变化,如图5所示,入射角的变化范围在0~42.6°。
正规斜反射碰撞点沿轨迹线运动的波阵面入射角随药型罩侧向曲率半径Rr发生变化,如图5所示,入射角的变化范围在0~42.6°。
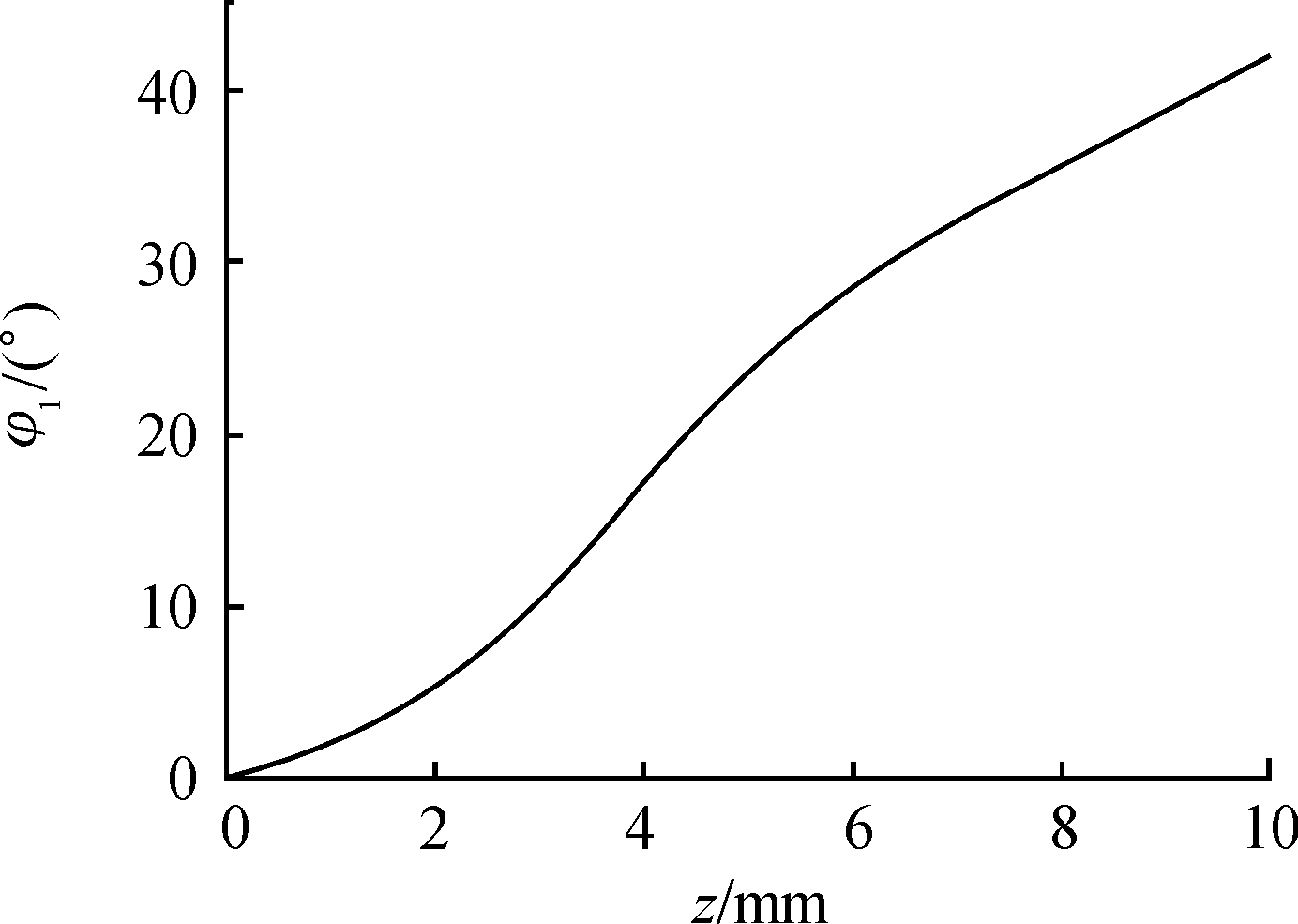
图5 药型罩弧顶中线爆轰波碰撞入射角变化曲线
Fig.5 Incidence angle of the wave front at the midline in the top arc of the liner
3.2 爆轰波碰撞作用分析
在装药结构中通过调整装药结构尺寸或者起爆直径等可以控制爆轰波碰撞类型。根据波系几何结构和Rayleigh-Hugoniot 关系得到反射角与转折角的关系[10]:
(7)
式中:γ=3为多方指数。
反射波后区域(2)压力与入射波后区域(1)的压力比值,
![]()
(8)
根据上述理论公式(7)分析,计算可得正规斜反射转马赫反射的临界角φc=44.59°,与图4、图5入射角的变化范围进行比较可知,本装药中爆轰波碰撞过程保持在正规斜反射区域。
根据式(8)可得到爆轰波正规斜反射碰撞点处的压力强度变化情况,如图6,压力强度随着入射角增大基本保持稳定在2.3-2.4,当接近临界角时,强度增速较快并会产生跳跃。因此,通过对单元装药结构的设计,控制入射角在临界角以下并稳定压力比值在2.4以上,因此可以利用正规斜反射产生的较为稳定的超压作用。
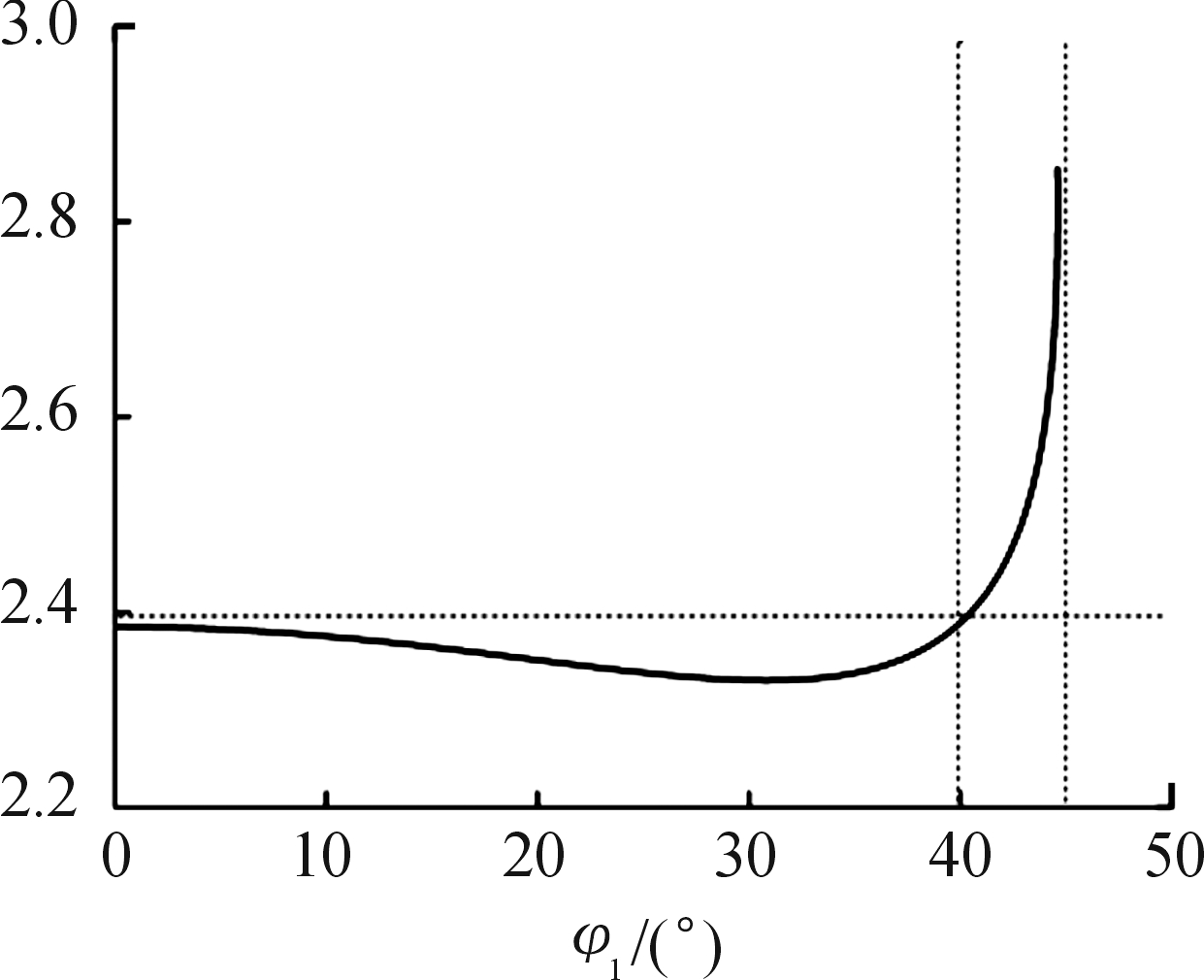
图6 正规斜反射爆轰波强度曲线
Fig.6 Intensity of the regular oblique reflection
为得到药型罩表面爆轰波压力分布,提取有限元模型y轴与药型罩弧顶中线上分布的压力测量点,然后结合上述理论计算,可以确定爆轰波作用于药型罩表面的压力分布,如图7,因此,超压分布导致药型罩沿外曲率半径方向上产生压力梯度,超压作用区域形成EFP头部并使得药型罩翻转,不同压力区域为椭圆形,压力大小随椭圆面积增大依次减小。

图7 药型罩表面超压分布曲线
Fig.7 Overpressure distribution on the surface of the liner
4 两点同步起爆误差分析
4.1 两点起爆误差工况设定
所利用同步起爆仪的起爆误差为1 μs,同时考虑到导爆索及传爆药加工尺寸误差,因此后续分析两点同步起爆误差设置偏差±0.5 μs内,由于实际中两点起爆网络的同步起爆误差具有一定的随机性,为观察两点起爆同步误差对EFP成型控制以及影响规律,将延迟起爆时间Δt(μs)分别设定为0、0.05、0.1等8种工况,如表2所示。
表2 两点同步起爆误差工况
Table 2 Two-point synchronous initiation error

同步起爆误差工况N=1N=2N=3N=4Δt/μs00.050.10.15同步起爆误差工况N=5N=6N=7N=8Δt/μs0.30.51.01.5
图8中可以看出,在无起爆误差情况下,正规反射碰撞点压力正好在双曲率药型罩的顶部,随着起爆误差的增大,碰撞点的位置相对于药型罩的弧顶中线发生偏移,随着起爆误差的增大,偏移量也随之增加。

图8 同步起爆误差下爆轰波碰撞作用过程示意图
Fig.8 Schematic diagram of detonation wave collision process under synchronous initiation error
4.2 两点起爆误差对 EFP尾翼及成型影响
图9中展示了EFP的后尾翼过程,可以看出,在N=0与N=0.05工况下EFP的尾翼呈现标准的十字形,在中间位置尾翼闭合良好;当从N=0.1开始,EFP左右两侧的尾翼开始发生偏转,四尾翼的交叉点开始移动,同时带动上下的尾翼之间开口增大,随着N的逐渐增大,四尾翼的交点偏移幅度明显增大,左右两侧尾翼偏转亦更加显著。因此,在实际中控制两点起爆误差在0.5 μs内,可较好的保证EFP四翼具有良好的十字形中心位置。
图10中展示了在不同工况下药型罩在形成EFP时存在折叠过程,其具有良好的长径比,并且为四翼型,四尾翼逐渐闭合并形成扁平结构,尾翼存在情况下有利于EFP的飞行稳定性,其中在y-z平面内所显示的两翼较长,而在x-y平面内观察两翼则相对较短,但在长度方向上EFP成型为变截面,造成在x方向和z方向宽度相差较大。在N=0时,药型罩进行折叠形成四翼型,有利于保持飞行稳定性;随着N的增大,在y-z平面内所显示的两翼长度缓慢加长,而且开口夹角略有增大。
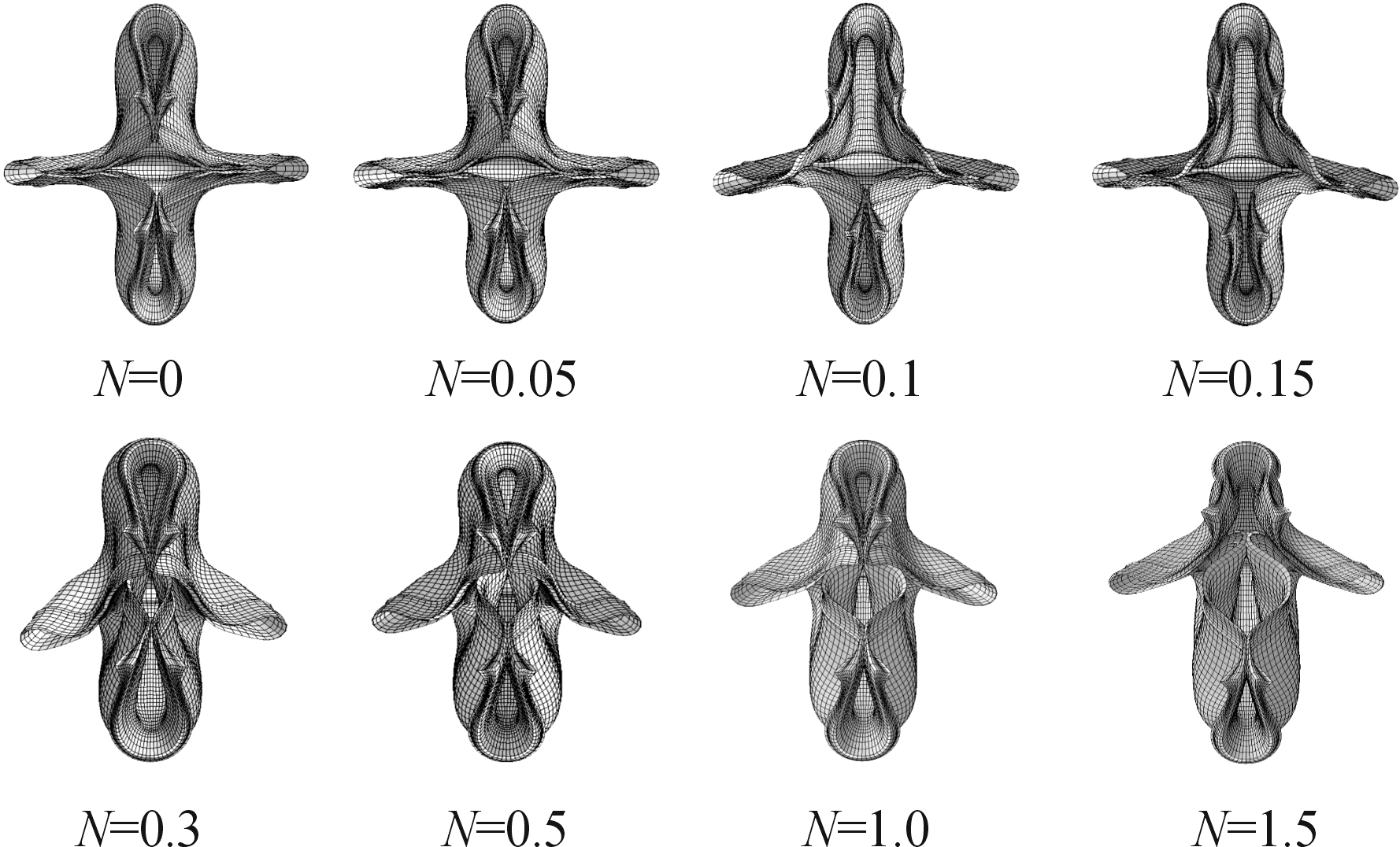
图9 两点同步起爆误差EFP尾翼成型过程 示意图(俯视图)
Fig.9 Schematic diagram of EFP tail forming process with two-point synchronous initiation error (top view)

图10 两点同步起爆误差EFP成型过程示意图
Fig.10 Schematic diagram of EFP forming process of two-point synchronous initiation error
从图11看出,侧向速度随起爆同步误差增大而增加,其二者变化规律基本一致。只有延迟起爆时间在0~0.3 μs,即两点几乎同时起爆,所造成的侧向分速度偏差较小,所形成的EFP尾翼更加规则对称。同时,随同步起爆误差的增大,对偏移速度的影响更加明显,基本成线性增加,不利于EFP的远距离飞行,因此,当两点延迟时间约为最长延迟时间1.5 μs的1/5时,侧向分速度影响较小。
在起爆点位置确定的情况下,当Δt在0~0.3 μs时,略有下降,而当Δt在0.3~1.5 μs时,降幅较大,结合同步起爆误差的对EFP四尾翼的影响,在实际中尽量保证起爆点误差Δt在0.3μs内,以提高四翼远距离飞行的稳定性。
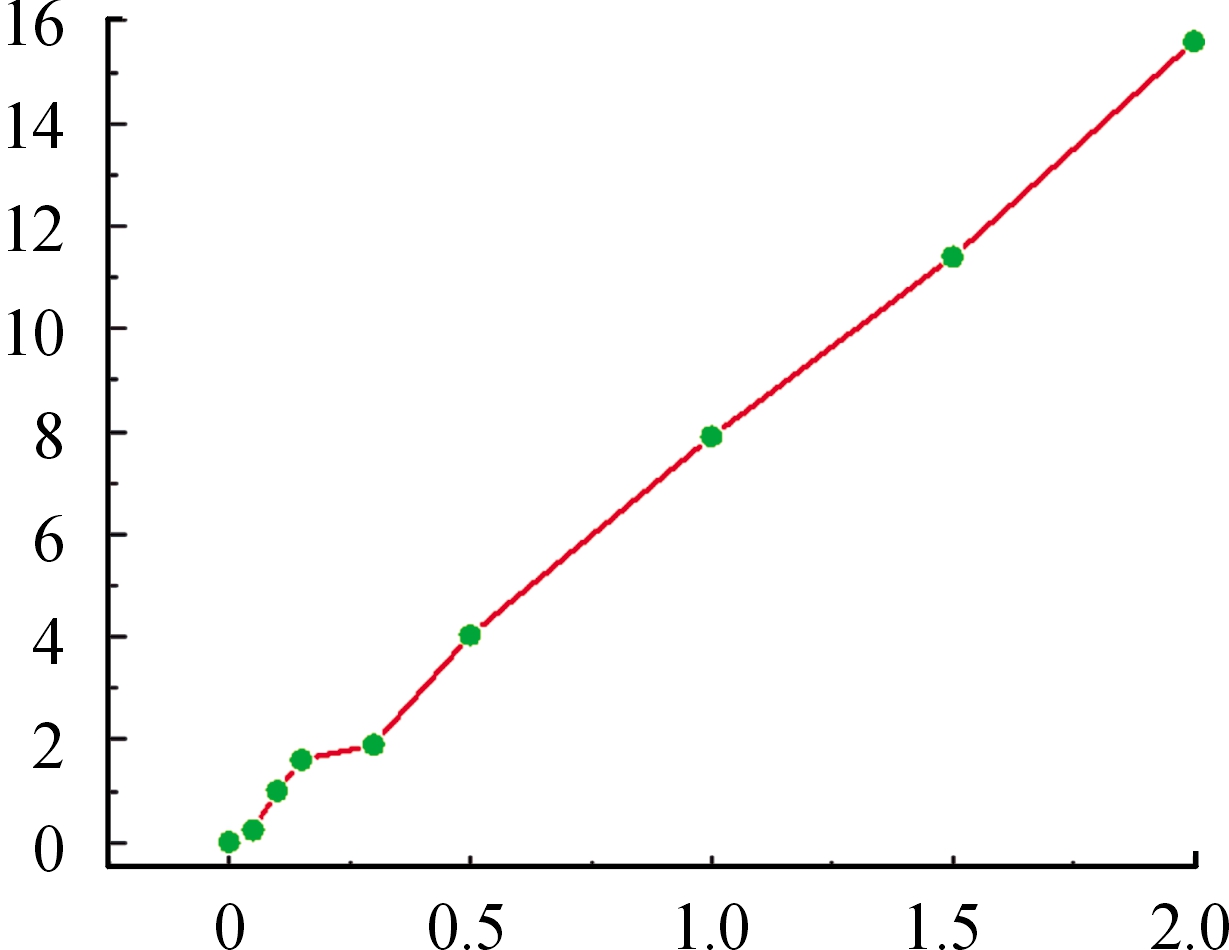
图11 侧向分速度变化曲线
Fig.11 Variation curve of lateral velocity of EFP
5 结论
1) 设定单元装药结构尺寸使得爆轰波碰撞入射角在正规斜反射区域,双向曲率药型罩表面压力区域为椭圆形,压力大小随椭圆面积增大依次减小。
2) 相比于四尾翼的交点偏移幅度,EFP的侧向偏移速度对两点同步起爆产生的误差更加敏感。两点延迟时间约为最长延迟时间的1/5时,可保证EFP四翼具有良好的十字形中心位置。
[1] BOOKOUT L,MULLIGAN P,BAIRD J.Explosively Formed Projectile Soft-recovery Force Analysis[J].Procedia Engineering,2013,58:560-569.
[2] Zhu C S,Huang Z X,Zu X D,et al.Mach Wave Control in Explosively Formed Projectile Warhead[J].Propellants Explosives Pyrotechnics,2014,39(6):909-915.
[3] 白利红,苗成,武海玲,等.EFP成型数值模拟及侵彻威力试验研究[J].兵器装备工程学报,2019,40(10):75-79.
Bai L H,Miao C,Wu H L,et al.Numerical Simulation of EFP Forming Characteristic and Experimental Study on EFP Penetration Ability[J].Journal of Ordnance Equipment Engineering,2019,40(10):75-79.
[4] Li R,Li W B,Wang X M.Effects of control parameters of three-point initiation on the formation of an explosively formed projectile with fins[J].Shock Waves,2017,28(5):1-14.
[5] Xiao Q Q,Huang Z X,Jia X,et al.Shaped charge penetrator into soil-concrete double-layered target[J].International Journal of Impact Engineering,2017,109-121.
[6] PAN J,ZHANG X,HE Y,et al.Theoretical and Experimental Study on Detonation Wave Propagation in Cylindrical High Explosive Charges with a Wave-shaper[J].Central European Journal of Energetic Materials,2016,13(3):658-676.
[7] 陈曦,刘杰,杜忠华,等.两端起爆下曲率药型罩线性装药的成型特性[J].火炸药学报,2018,41(5):441-446.
Chen X,Liu J,Du Z H,et al.Forming Characteristics of Linear Charge with Curved Liner under Two-end Initiation[J].Chinese Journal of Explosives & Propellants,2018,41(5):441-446.
[8] Liu J,Chen X,Du Z H.A study on the surface overpressure distribution and formation of a double curvature liner under a two-point initiation,Defence Technology,https://doi.org/10.1016/j.dt.2020.10.004.
[9] CARDOSO D.TEIXEIRA-DIAS F.Modeling the formation of explosively formed projectile ( EFP )[J].International Journal of Impact Engineering,2016,93:116-127.
[10] Liu Y,Yin J,Wang Z.Study on the overdriven detonation wave propagation in double-layer shaped charge[J].Physics of Fluids,2019,31(9):1-14.