1 引言
为满足未来海上高技术战争需求，精确打击功能要素对于舰炮已经越来越重要。舰炮精确打击的实现不仅取决于目标定位精度，更与射击诸元精度[1]有关。通过解弹道方程进行舰炮射击诸元求解时，舰船摇摆运动导致目标相对舰炮射击中心的运动状态发生变化[2]，引起的舰炮指向扰动对求解过程产生较大的影响。因此，有必要明确摇摆作用下舰炮指向扰动规律，并将它作为稳定系统的动力学环节进行补偿，以获得正确完整的舰炮射击诸元。
目前，国内外学者对舰船摇摆条件下舰炮射击诸元求解模型进行了大量的研究[3-8]，基于二分法和落点诸元信息的弹道解算方法等研究较为成熟。但是，现有研究大多直接采用舰船摇摆角获得实际瞄准角或摇摆误差角，却较少考虑地球惯性系和舰船非惯性系的变换关系，没有完全消除舰炮指向运动误差叠加形成的射击诸元误差，在摇摆补偿时也鲜有计及弹丸初始扰动的影响。针对该问题，本文面向舰炮多体系统的串联运动链，建立了摇摆作用下的舰炮指向运动误差模型，明确炮口指向在静水—摇摆条件下的绝对误差及相对误差。从串联机构角度构造了舰炮位姿补偿模型，从目标方位一致性角度推导了炮口姿态补偿模型，从弹道轨迹预测角度给出了舰炮射击瞄准点的补偿解算流程。通过仿真验证获得了摇摆条件下舰炮指向误差补偿特性，为各类精确打击状态的舰炮射击诸元解算提供参考。
2 摇摆作用下舰炮指向运动误差模型
基于多体系统方法[9]，首先建立舰船摇摆条件下的舰炮串联运动链如图1所示。其中，惯性系{E}原点设置在舰船摇心处，并假定随舰船匀速运动。舰体系{W}原点初始与摇心重合，WX指向舰艏方向，WZ沿着甲板法向，WY按右手法则建立，此处主要计及对舰炮影响最大的横摇、纵摇和垂荡运动。舰炮系{F}的原点与甲板炮位中心重合，轴向与舰体系的坐标轴一致。工具系{T}原点位于炮口中心，TX正向与身管轴向一致，TZ正向位于身管(射击平面)纵截面且与TX垂直，TY按右手法则建立。
在惯性系{E}中，γ、θ、η分别表示横摇角、纵摇角和垂荡位移，
分别表示舰炮方位、高低和后坐运动旋量。舰炮系{F}相对惯性系{E}的齐次变换矩阵可采用摇荡运动变量和结构矢量L表示为:
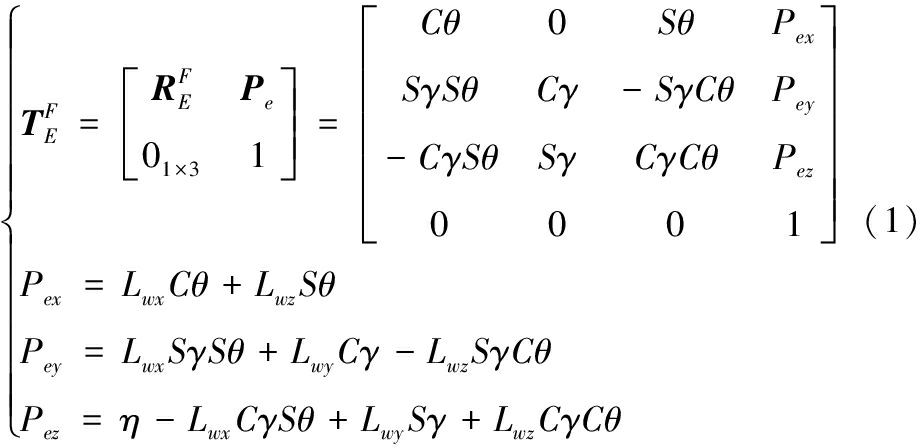
式(1)中：Lwx，Lwy，Lwz是L在舰体系{W}的位置坐标；符号缩写C=cos，S=sin。
根据旋量坐标不变性，采用指数积公式[10]给出舰炮工具系{T}相对舰炮系{F}的位姿变换矩阵模型为：
gft(θ)=exp(θ11)exp(θ22)exp(θ33)gft(fx，fy，fz)
(2)
式(2)中：exp(·)是运动旋量的指数积算子；gft(·)是初始位姿矩阵， fx、 fy、 fz是工具系原点在舰炮系的位置坐标，并且fy分量通常假定为零值； θ1、θ2是转动关节变量， θ3是移动关节变量，初始都为零值。
图1 基于多体系统的舰炮串联运动链示意图
Fig.1 Serial kinematic chain model of naval gun
根据坐标变换关系，推导出摇摆作用下，工具系{T}相对惯性系{E}的位姿模型为：
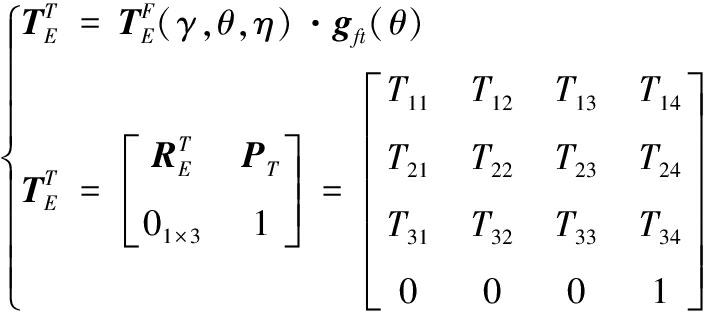
(3)
式(3)中，各矩阵元素分别为
(4)
为再明确舰船摇摆引起的指向扰动，构造出静水条件下，工具系{T}的位姿模型为：
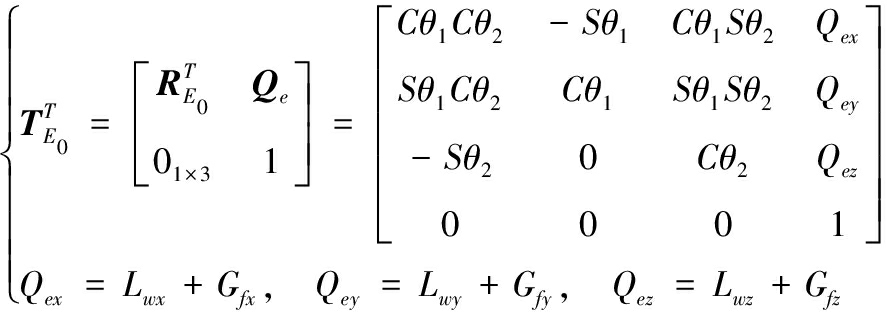
(5)
此时，根据式(3)和式(5)推导出惯性系中炮口中心扰动ΔX、ΔY、ΔZ及指向扰动δWX、δWY、δWZ分别为：
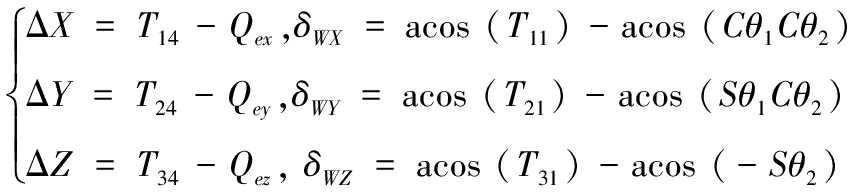
(6)
式(6)给出了惯性系中的舰炮指向误差模型，代入舰炮瞄准跟踪或发射时的舰炮运动变量，即可获得摇摆作用下炮口最大可能扰动域。
为便于误差合成分析，再采用误差旋量[10-11]对惯性系描述的工具系位姿误差进行转换，如图2所示。
图2 舰炮指向扰动的误差旋量模型示意图
Fig.2 Pointing error screw model of naval gun
在惯性系中，基于工具系移动关节误差旋量dpp和转动关节误差旋量
推导出：
(7)
式(7)中：ep是移动关节轴线的单位矢量；wr是转动轴线单位矢量；er是旋量轴对原点的矩；
根据旋量伴随变换定义，再将式(7)转换为理想工具系{T}中表示的误差旋量，得出：
(8)
通过改写式(8)，得出不同于式(6)扰动参数描述的炮口工具系位姿误差为：
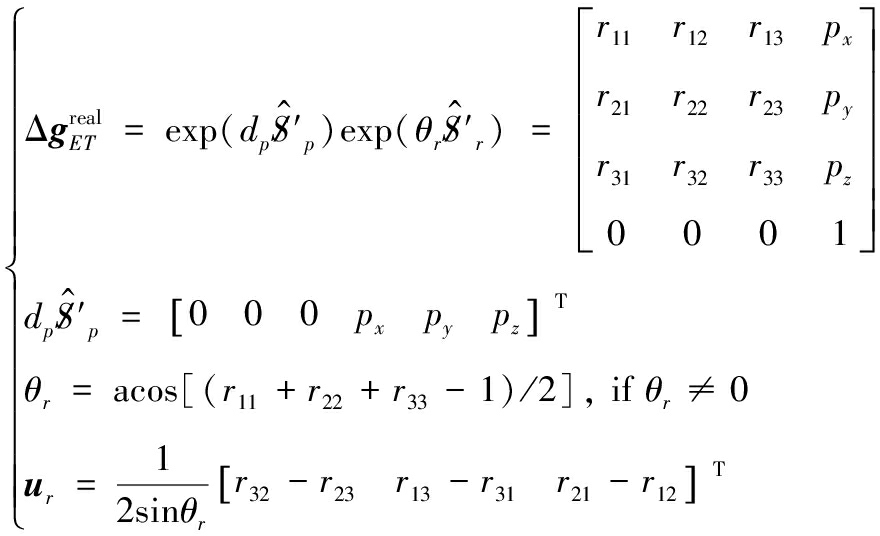
(9)
式(9)中：px、py、pz分别是炮口位置误差在工具系描述时的轴向分量； θr是姿态误差合成量；ur是姿态误差旋量轴在理想工具系中的方向余弦。
3 摇摆作用下舰炮指向误差补偿模型
3.1 基于舰炮串联运动链的指向误差补偿
在获得舰炮指向误差的基础上，根据舰炮串联运动链构造出瞄准跟踪过程的指向补偿模型为：
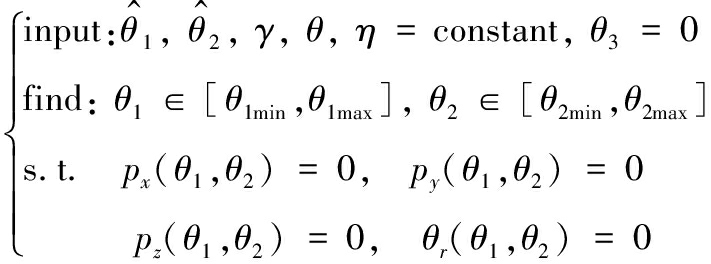
(10)
式(10)中：
为理想关节变量； θ1、θ2为带有关节补偿的实际关节变量，受舰炮射角范围约束。
式(10)给出舰炮指向补偿模型的一般表达式，包含4个约束方程、2个未知变量，误差补偿效果取决于超静定方程组的逼近精度[12]，解析方程在此省略。
在舰炮瞄准跟踪时，若假设已知某目标相对惯性系{E}的Z-Y-Z欧拉角(μ1，μ2，μ3)，则根据舰炮指向TX轴夹角与目标方位角的一致性得出：
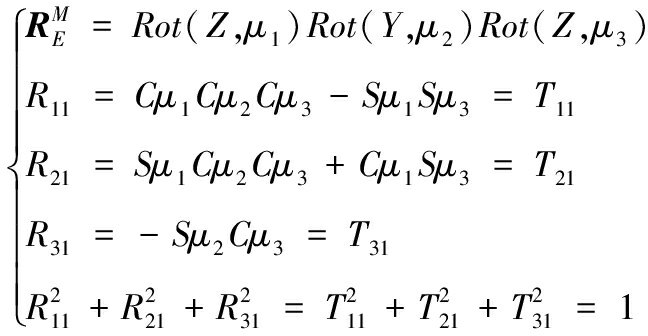
(11)
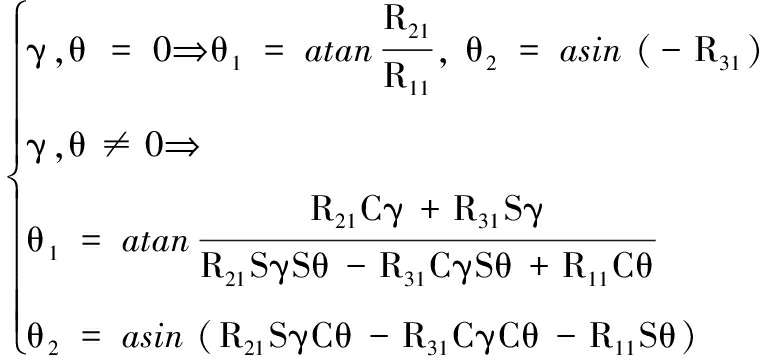
(12)
对于舰炮发射过程，虽然利用式(10)的后坐关节变量也可构造出相似的指向补偿模型，但由于弹丸膛内运动时间通常小于舰炮方位和高低运动响应时间，因此很难主动控制，也无法应用于指向补偿，这里不再赘述。
3.2 基于弹道解算的舰炮指向误差补偿
由于高海况下舰船摇摆运动较为严苛，其引起的炮口指向扰动量甚至会超越舰炮理想工作空间，因此很难对舰炮指向运动误差进行“完全”补偿。但根据大口径舰炮弹道轨迹可以看出，即使对炮口指向进行部分补偿时，也能够实现精确打击目标，如图3所示。
为实现舰炮指向运动误差的局部补偿，不妨再设置补偿系{Tc}和弹丸速度系{S}。并假设已知目标点在惯性系中的运动方程、弹丸在速度系中的质点弹道模型，给出射击瞄准点的补偿解算流程如下。
图3 舰炮指向运动误差补偿模型示意图
Fig.3 Pointing error compensation model of naval gun
1) 炮口切向运动转换。
已知炮口工具系相对惯性系的旋转矩阵
在每个瞬时都存在一个转轴(单位矢量k描述)和一个转角φ，使得旋转矩阵相等
因此，该瞬时转角的变化率所引起的变换率可表示为：
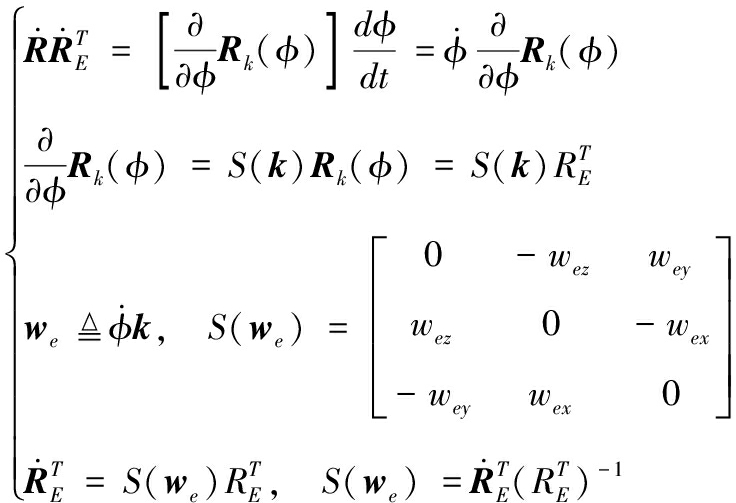
(13)
式(13)中: we是工具系在惯性系中的角速度矢量；再采用矢量求导法则可得出角加速度为
若将舰炮后坐运动转换为工具系的位矢xA(沿着舰炮指向TX轴)，则在弹丸出炮口瞬时，根据矢量运算[13]可推导出炮口中心点在惯性系{E}中的切向运动为:
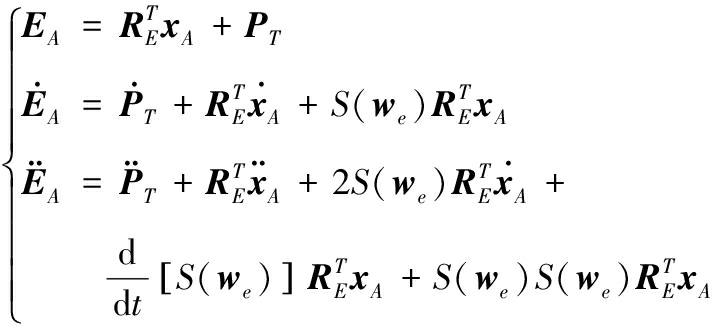
(14)
2) 坐标系齐次变换。
将待解的舰炮射击诸元(θ1，θ2，tf)代入式(3)，得出补偿系{Tc}相对惯性系的位姿矩阵；再将弹丸出炮口瞬时的摇荡参数、后坐位矢代入式(14)，得出炮口切向速度vex，vey，vez并推导速度系相对惯性系的变换矩阵为：
(15)
式(15)中：vd是弹丸膛内运动速度；vα是根据弹炮切向速度合成得出的弹丸初速，沿着速度系XS轴方向。
3) 弹丸质点运动转换。
弹丸出炮口瞬时，质点位于速度系原点，tf时刻弹丸在速度系OSXSZS平面的弹道轨迹模型为：
(16)
式(16)中：gs为重力加速度在速度系中的Z向分量； ρ为弹丸速度矢量夹角；C为弹道系数；H为空气密度函数； F为阻力函数。数学模型详见文献[14-15]。
采用龙格库塔法求解微分方程，得出弹丸飞行tf时的落点位置p(xp，0，zp)。当式(16)改写为弹丸的刚体弹道模型时，也可求解出更精确的落点位置。
4) 弹道命中方程。
将速度系中的弹丸落点位置转换至惯性系，计算其与目标未来点(xm，ym，zm)位置的相对距离，得出舰炮修正射击诸元下的射击瞄准偏差Δs为：
(17)
当弹丸落点偏差Δs小于规定值
时，当前舰炮射击诸元即可满足与目标未来点吻合的精确度。
5) 舰炮修正射击诸元优化计算。
联立式(15)至式(17)，得出弹丸命中期望下的射击瞄准变量优化模型为：
(18)
采用PLS算法或NSGA算法对式(18)的多目标优化模型进行求解，得出的Pareto最优解集，即能对舰炮指向误差进行局部补偿，从而实现精确打击的目标。
4 仿真验证
4.1 舰炮指向运动误差分析
以某舰船装载的大口径舰炮为对象，假定高海况下舰船摇摆谱参数[8]、舰炮零位对准时的结构矢量、方位角和高低角范围、后坐运动/弹丸膛内运动参数等分别为：
对于舰炮瞄准跟踪过程，设置方位驱动在6 s内由零位调转至120°，高低驱动在2 s内由零位调转60°，后坐驱动保持为零值。根据式(6)得出惯性系中描述的舰炮原点轨迹误差和指向误差不再展示，根据式(9)得出工具系描述的舰炮指向误差如图4所示，包络最值是各点轨迹(摇摆参数组合确定)下的最大值和最小值。
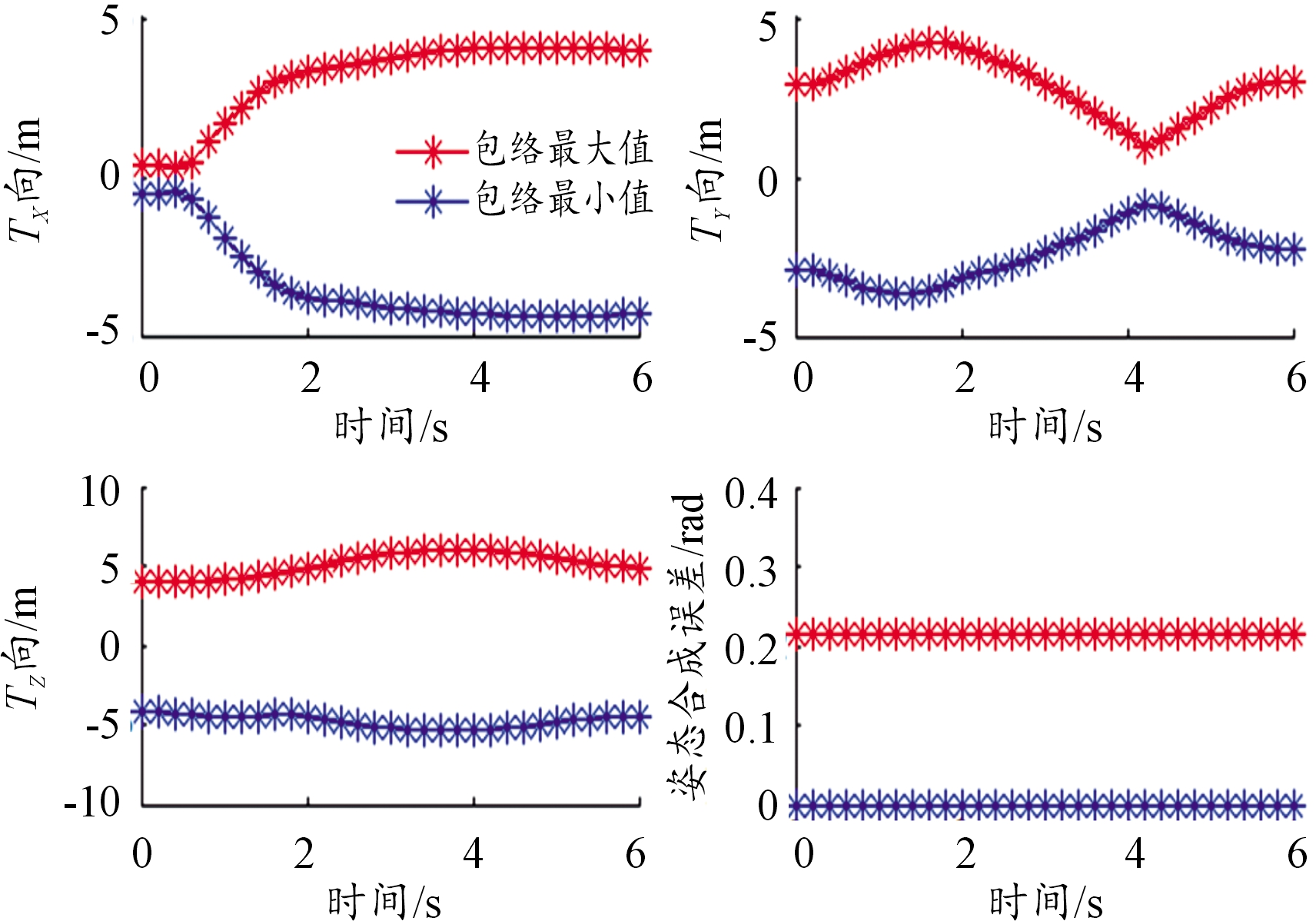
图4 摇摆作用下炮口轨迹误差和指向误差曲线
Fig.4 Muzzle trajectory error and pointing error of naval gun under ship swaying condition
由图4可以看出：舰船摇摆运动作用于舰炮串联运动链的虚拟连杆副，其引起的叠加扰动域导致炮口绝对轨迹出现了较大的偏移；所建指向误差模型能够准确预测舰炮的最大可能扰动域，明确摇摆作用下舰炮指令信号响应。
4.2 舰炮指向误差补偿分析
在明确舰炮指向误差之后，采用PLS算法对超静定方程组进行数值逼近，图5给出了采用全约束解的舰炮指向补偿效果。其中理想方位角0°、高低角60°，横轴是横纵摇和垂荡运动参数的独立组合。
由图5可以看出：通过求解超静定方程组得出舰炮关节运动变量时，姿态误差角零值的前置条件是r11+r22+r23=3，即需满足姿态误差矩阵为单位阵I3×3的隐含约束；但由于舰炮不具有横纵摇和垂荡方向的自由度，因此从串联系统的角度摇荡运动引起的舰炮指向误差无法完全补偿；在不同的摇荡组合参数下：① 姿态误差和Y向误差逼近零值，其余两向位置残余误差相比无补偿值减小约40%，② 若位置误差都逼近零值时，姿态残余误差减小约67%，相对实际炮口指向，位姿补偿效果总体接近34%左右。
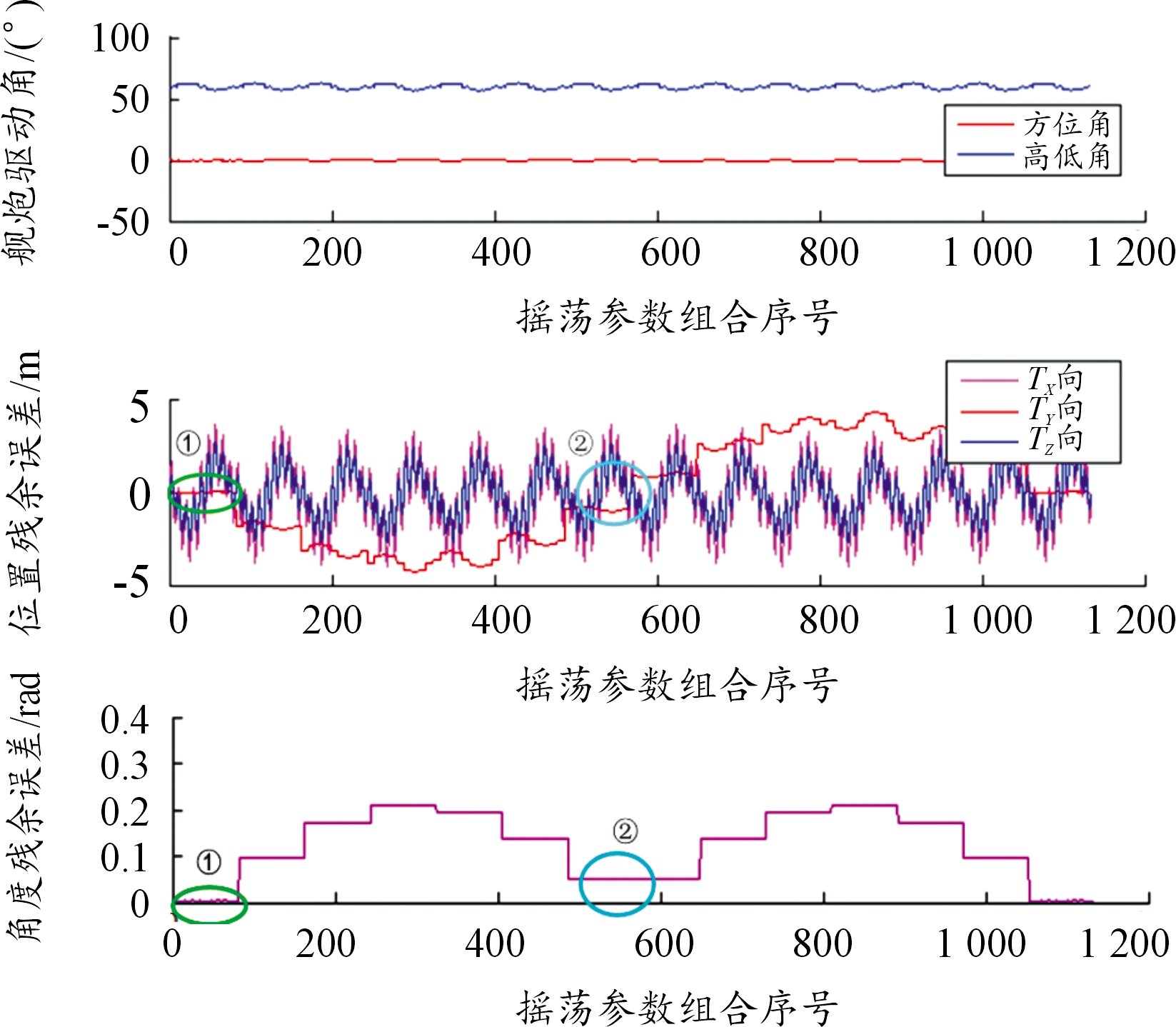
图5 基于舰炮串联运动链的指向误差补偿效果曲线
Fig.5 Pointing error compensation effect based on the serial kinematic chain of naval gun
若假定目标方位角(-60°，30°，30°)时，根据指向一致性得出不同摇荡参数组合条件下，舰炮方位和高低角如图6所示。由图6可以看出：解析模型能够获得与摇荡参数对应的精确值，炮口姿态补偿效果可达到100%。
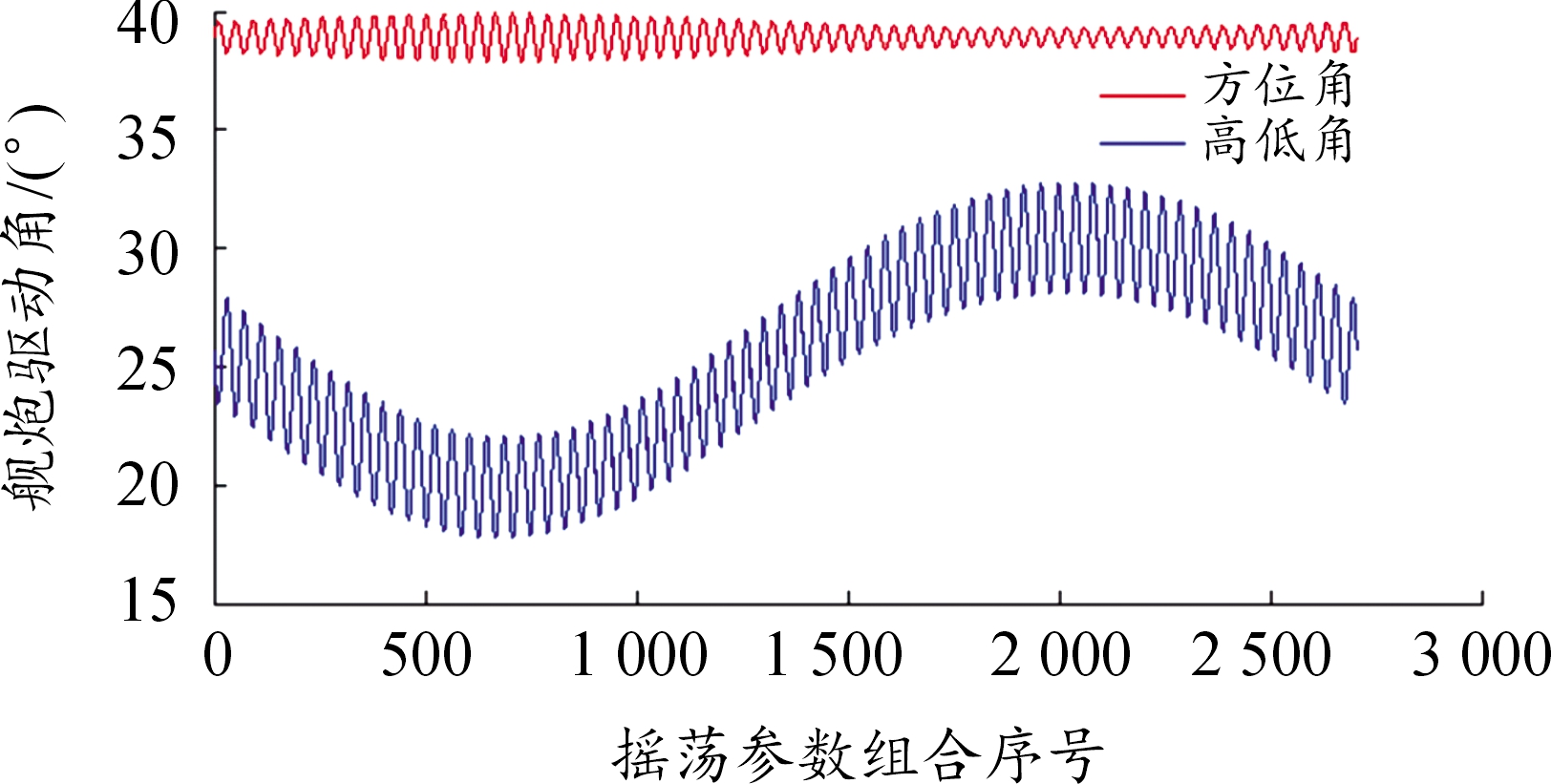
图6 舰炮指向目标方位补偿曲线
Fig.6 Target azimuth compensation effect of naval gun
假设弹丸质点运动按照标准气象弹道条件，根据舰船摇摆参数、方位驱动(-6°，6°)、高低驱动(25°，55°)以及后坐运动30 ms的条件，弹丸初速850 m/s、飞行时间60 s，设置某目标未来点在惯性系中的坐标(25，0，0)km、弹着散布半径为30 m时，根据射击瞄准点的补偿解算流程得出弹道轨迹如图7所示。其中，可行概率表示指定射击诸元下满足精度要求的摇摆条件。
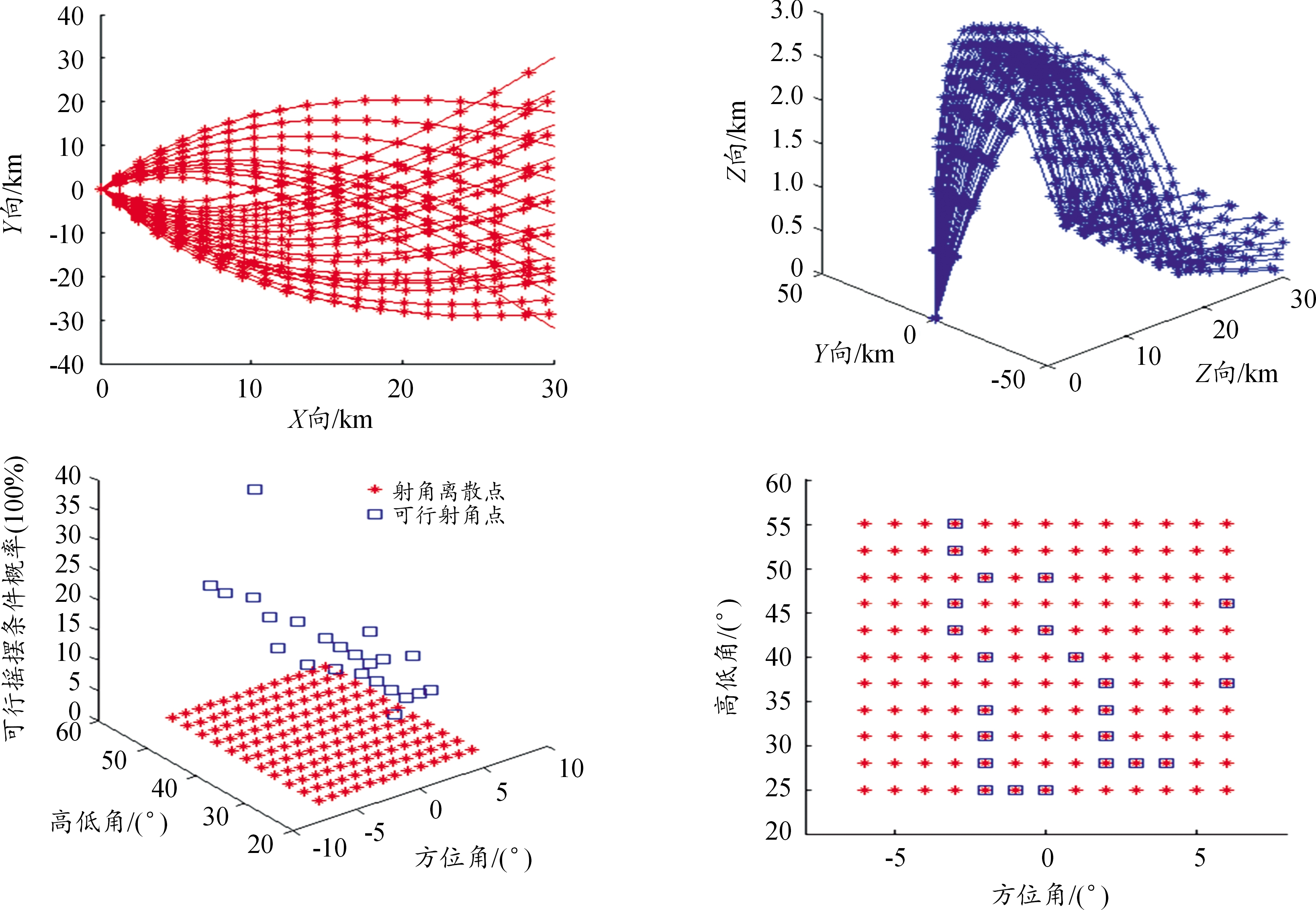
图7 舰炮射击瞄准解算的弹道轨迹图
Fig.7 Ballistic trajectory and firing data calculation of naval gun under ship swaying condition
由图7可以看出：弹丸飞行时间越长(以落点至水平面为截止时间)，舰船摇摆对弹丸飞行轨迹的影响越大，在摇荡参数组合条件下，同组射击诸元的弹丸落点范围较大；对于指定目标点，虽能够得出23组修正射击诸元，但可行摇摆条件概率最大仅为40%，表明该射击诸元下预设的10组摇摆组合参数中仅有4组能够满足弹着点要求；通过与143组弹道轨迹数目比对，炮口指向局部补偿效果约为16%左右，当摇摆运动较为剧烈时，射击瞄准补偿的无解情形更多。
5 结论
为保障舰炮射击诸元求解精度，根据舰炮多体系统串联运动链建立了摇摆作用下的指向误差模型，根据机构运动精度及弹道方程分别构造了舰炮指向补偿模型，并对摇摆补偿解算流程进行仿真验证。仿真结果表明：指向误差模型能够描述摇摆作用下舰炮瞄准跟踪、定点及跟踪射击时的炮口最大扰动域；对于摇摆补偿，舰炮串联系统不具备与摇荡运动关节对应的“主动”自由度，舰船摇摆引起的指向扰动属于不可完全补偿误差，位姿补偿总体效果约为34%；通过目标方位一致性或解弹道方程对指向误差进行局部补偿，计及炮口非惯性系中的弹丸初始扰动和累积效应，射击瞄准补偿效果约为16%，可以获得满足落点弹丸偏差裕度要求的舰炮射击诸元，实现摇摆条件下的舰炮精确打击功能。
[1] 潘红华，胡家升，杨绍清，等.解弹道方程求解舰炮武器系统射击诸元的数学模型[J].兵工学报，2003，24(01):23-26.
Pan H H，Hu J S，Yang S Q，et al.Model for finding firing data of shipborne gun weapon system by solving external ballistic equation[J].Acta Armamentarii，2003，24(01):23-26.
[2] 程晗，陈维义，周敏佳.舰艇摇摆作用下火炮射击诸元求解模型分析[J].系统工程与电子技术，2017，39(11):2484-2490.
Cheng H，Chen W Y，Zhou M J.Analysis on model for solving firing data under influence of ship swaying[J].Systems Engineering and Electronics，2017，39(11):2484-2490.
[3] 王立红，宋军.高海情对反导舰炮命中概率的影响[J].指挥控制与仿真，2016，38(01):53-56.
Wang L H，Song J.Hit probability of antimissile naval gun under high sea state[J].Command Control&Simulation，2016，38(01):53-56.
[4] 余戌曈，吴玲，卢发兴.舰艇摇摆下射界动态变化对武器目标分配的影响[J].兵工学报，2015，36(09):1819-1824.
Yu X T，Wu L，Lu F X.The influence of dynamically changing firing zone on weapon-target assignment under ship swaying[J].Acta Armamentarii，2015，36(09):1819-1824.
[5] 吴威，吴玲，卢发兴.基于最大命中概率的新型舰炮对海射击火控解算技术[J].电光与控制，2019，26(03):44-48.
Wu W，Wu L，Lu F X.Maximum hitting probability based fire control calculation for new shipboard gun against sea target[J].Electronics Optics&Control，2019，26(03):44-48.
[6] 王光源，毛世超，孙涛，等.基于舰艇摇摆的垂发型舰空导弹三维弹道仿真[J].火力与指挥控制，2020，45(03)：64-68.
Wang G Y，Mao S C，Sun T，et al.Three dimensional trajectory simulation of vertical launching ship to air missile based on warship swaying [J].Fire Control & Command Control， 2020，45(3)：64-68.
[7] Ma P，Zhou Y C，Shang X B，et al.Firing accuracy evaluation of electromagnetic railgun based on multicriteria optimal latin hypercube design[J].IEEE Transactions on Plasma Science，2017，45(07):1503-1511.
[8] 陈维义，程晗，刘国强，等.基于改进弹丸追踪法的舰炮校射方法研究[J].兵器装备工程学报，2019，40(05):10-14.
Chen W Y，Cheng H，Liu G Q，et al.Study on firing correction method for naval gun based on improved projectile tracking method[J].Journal of Ordnance Equipment Engineering，2019，40(05):10-14.
[9] 王德石，史跃东.火炮振动分析与多体系统模型研究[J].动力学与控制学报，2012，10(04):303-324.
Wang D S，Shi Y D.Research on guns vibration and modeling methods by multibody dynamics[J].Journal of Dynamics and Control，2012，10(04):303-324.
[10] Sun T，Lian B B，Yang S F，et al.Kinematic calibration of serial and parallel robots based on finite and instantaneous screw theory[J].IEEE Transactions on Robotics，2020，36(03):816-834.
[11] 黄勇刚，杜力，黄茂林.基于旋量理论的机器人误差建模方法[J].哈尔滨工业大学学报，2010，42(03):484-489.
Huang Y G，Du L，Huang M L.Screw theory based error modeling method of robot mechanisms[J].Journal of Harbin Institute of Technology，2010，42(03):484-489.
[12] Riccardo M，Paolo F.A PLS-based statistical approach for fault detection and isolation of robotic manipulators[J].IEEE Transactions on Industrial Electronics，2012，59(08):3167-3175.
[13] 霍伟.机器人动力学与控制[M].北京:高等教育出版社，2004.
Huo W.Robot dynamics and control[M].Beijing:Higher Education Press，2004.
[14] 韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社，2008.
Han Z P.Exterior ballistics of projectiles and rockets[M].Beijing:Beijing Institute of Technology Press，2008.
[15] 普承恩，王良明，傅健.基于EKF落点预测的二维弹道修正弹制导方法[J].兵器装备工程学报，2018，39(06):52-57.
Pu C E，Wang L M，Fu J.A guidance method for two dimensional trajectory correction projectile based on impact point prediction of EKF[J].Journal of Ordnance Equipment Engineering，2018，39(06):52-57.