1 引言
制导弹药是现代战争中实现精准打击的重要武器手段，滚转角是其姿态控制中必不可少的参数。地磁测姿技术作为一种全自主导航系统，凭借其稳定性高、体积小、成本低、误差不累积的特点[1]，广泛应用于制导弹药滚转角信息的获取。理想条件下，以磁传感器为核心构建的磁测系统在使用时，通过测量地磁场矢量在其三轴的分量而实现对滚转角的解算[2]。在制导弹药滚转角的解算过程中，测量精度除受传感器自身零偏、灵敏度、不正交角等相关参数偏移的影响外，还受到弹体磁场影响导致滚转角测量不准确。弹体干扰磁场主要由弹体结构中存在的钢合金等硬磁性材料产生，受发射时的高过载环境和储存环境的磁场影响，弹体磁场容易发生变化，且发射时引起的磁场变化无法事先标定，需要采用实时在线的方式对其进行补偿。
针对弹体磁场干扰的校准，杨宇彬等[3]提出了异常磁信号滤除算法,异常磁信号滤除算法适用于制导弹药实际工作环境中的工程问题，通过最优线性移动平滑算法对飞行过程中的采样数据进行估计，从而实现对出现的异常磁信号即野值进行滤除，但该方法适用于干扰信号中类脉冲信号的消除，对弹体飞行过程中长时间存在的干扰磁场量无法滤除。狄素素，曾成等[4]提出了两步校正算法,两步校正算法在地面能够将实现将磁测系统所在结构的固定磁场干扰进行标定，其通过场矢量在传感器各轴上的投影关系，在不同测量轴所在平面进行转动即可实现标定，可用于制导弹药弹体结构的干扰磁场所造成的偏移，但在发射高过载环境影响后弹体磁场已经发生改变，使用事先地面标定参数解算的滚转角不准确，需要对其进行在线修正。
因此，本文提出一种基于实时滤波的弹体磁场在线补偿方法，可实现在旋转弹药飞行过程的极短时间内完成测量量的实时修正，以解决发射高过载环境后弹体磁场变化引起的滚转角解算误差问题。
2 磁测系统测量模型
利用磁场信息解算滚转角时，需要将发射系下磁场三分量转换为弹体系下的磁场三分量。定义发射坐标系为f系， f系中的三分量以Hf表示，弹体坐标系为b系，b系中的三分量以Hb表示。根据典型弹道规律，弹药在发射后基本处于弹道射击平面内，旋转弹药飞行轨迹符合零偏航假设，在飞行过程中，偏航角不发生改变，滚转角与俯仰角变化。则弹体坐标系与发射坐标系间存在如下转换关系：
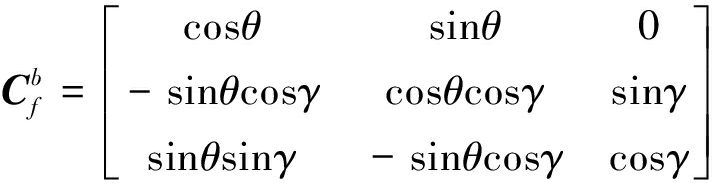
(1)
式中：
表示由发射坐标系到弹体坐标系的转换矩阵，θ为俯仰角，γ为滚转角。则可得到弹体坐标系下三轴测量量，可表示为
(2)
三分量形式为
(3)
其中，
旋转弹弹体存在的干扰磁场分为固定磁场和感应磁场。其中，固定磁场主要由弹体铁磁材料外壳及其他铁磁材料部件产生，这类材料属于硬磁材料，具有高矫顽力与剩磁值，一经外界磁场磁化后，其剩磁可保留较长时间不消失。弹体在储存期间，较长时间保持在某一固定地点的固定方位上，持续受该位置地磁场影响使得弹体中的硬磁材料被磁化而具有较强的磁性，即干扰磁场中的固定磁场，而发射高过载环境还会引起这类固定磁场的变化，发射后的固定磁场主要为热电池等电气元件在激活使用时产生的固定磁场，这一类电气元件在弹体结构上使用时其位置固定，设备电流稳定，由此产生的干扰磁场为一常量，也可以归类为固定磁场引起的误差问题，固定磁场造成的误差可视作测量值偏移量。感应磁场主要由弹体结构中存在的软磁材料产生，软磁材料具有低矫顽力和高磁导率，易于磁化，也易于退磁。感应磁场造成的误差可以将其视为对三轴灵敏度的误差，需要有感应磁场的等效灵敏度矩阵对其进行补偿。综合弹体存在的干扰误差源，则实际测量值表示为
Hs=KinduceHb+Hbia
(4)
其中，
为感应磁场的等效灵敏度矩阵，
为固定磁场在三轴方向分量。
3 误差分析
根据以上分析可知,高旋弹体在飞行过程中的磁测系统实际测量值可以用式(4)表示，其中包含固定磁场和感应磁场两类干扰磁场。由于弹体外形一般为圆柱体，其在飞行过程中通过切割地磁场磁力线产生的感应磁场强度很小，即Kinduce可视为单位矩阵，感应磁场造成的干扰磁场在分析时可以忽略不计，系统测量误差的主要来源为弹体上存在的固定磁场Hbia，三分量实际测量值表示为
Hs=I3×3Hb+Hbia
(5)
以滚转角速率为自变量的形式如下：
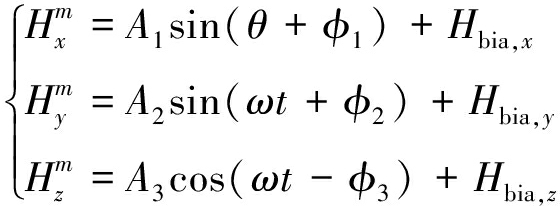
(6)
其中，
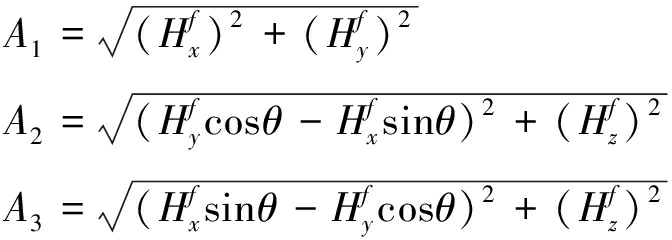
高速旋转弹体在飞行中俯仰角θ变化缓慢，短时间内可看作常量，则
和
为类正弦信号与干扰磁场常量的叠加信号。其中，X轴理想测量值为变化缓慢的类正弦信号，可采用在发射前采集初始分量Hinitial,x，测量过程中计算得出干扰磁场值的方式对测量值进行补偿，即
(7)
(8)
根据式(6)中的分析，Y轴信号与Z轴信号中理想测量量与滚转角速率有关，使用高通滤波的方式对其进行干扰补偿，滤除干扰磁场引起的偏移误差，即可得到准确的弹体坐标系下的磁场测量量。
为保证对原始数据的高精度实时处理，在设计时选用IIR滤波器，实现对测量值原始数据的高精度实时补偿。通过对旋转弹实际飞行状态的运动特性分析，可以得出，旋转弹药在飞行时，角速率一般可达到5 r/s及以上，根据旋转速率与信号周期对应关系，可计算得到径向磁场测量值频率为5 Hz及以上，则可通过IIR高通滤波器实现对径向两轴测量量内存在的固定磁场干扰量进行滤除。
4 实验
4.1 仿真验证
为验证上述补偿方案，结合弹体飞行时姿态变化规律，旋转弹药飞行时偏航角由初始射向决定，发射后不发生变化，俯仰角与滚转角变化曲线如图1。
图1 飞行姿态曲线
Fig.1 Diagram of attitude during flight
由图1并结合上述分析可以得出，当系统采样频率为一步1 kHz时，单位采样时间内俯仰角度变化约为0.002°，在滚转角转动一个周期时，俯仰角变化相较于滚转角变化很小，约为滚转角变化量的0.001倍，则可以在对径向磁场值高通滤波时将其视作常量。
根据以上条件假设磁测系统在稳定地磁场中Y轴，Z轴测量值峰值分别为[40 000,40 000]nT，根据旋转弹药飞行时的运动状态实际情况，Y、Z轴信号频率为5 Hz。在原始信号值上添加一定的干扰磁场值，作为初始值。干扰磁场值分布如图2所示，初始值如图3所示。
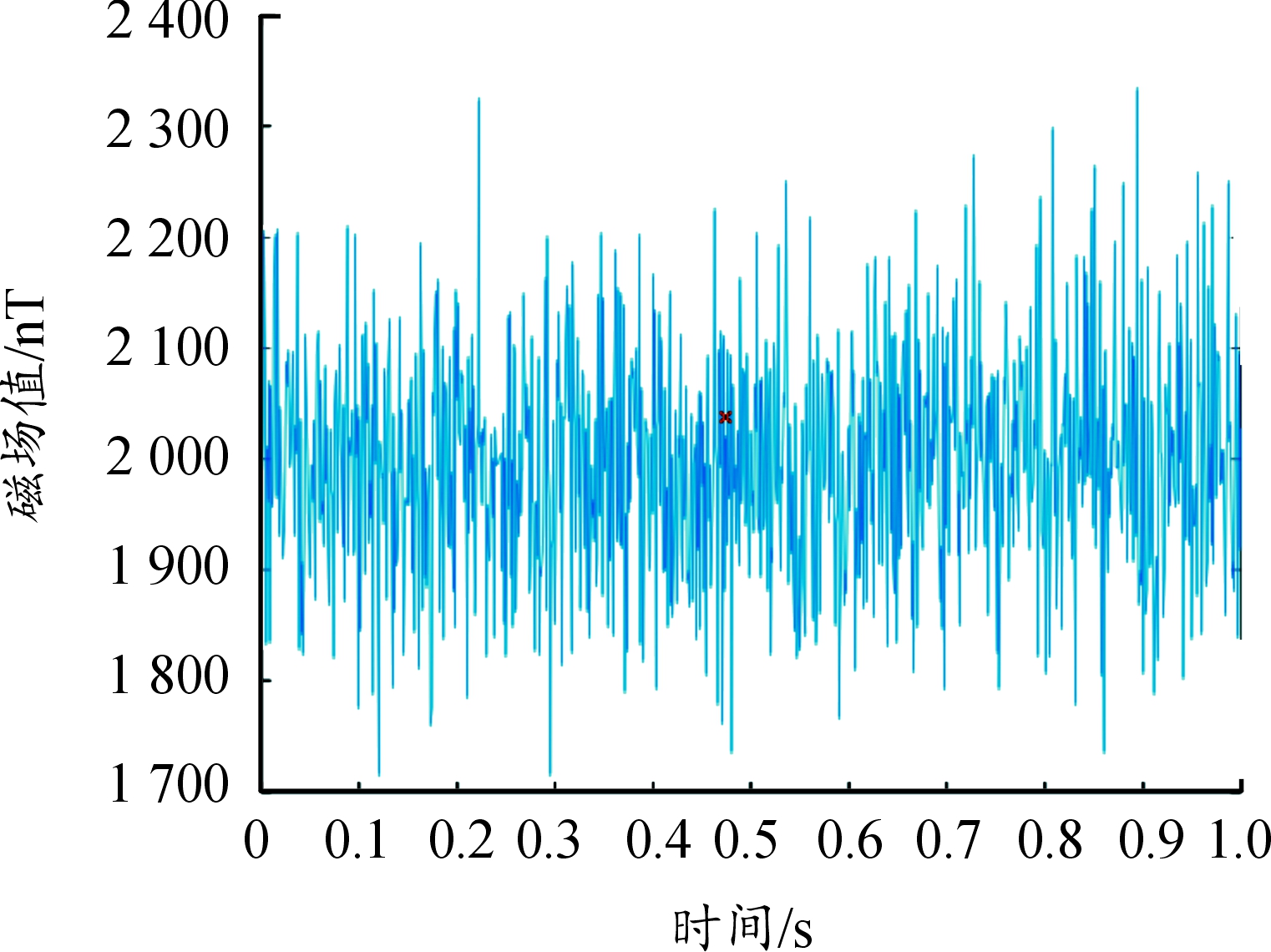
图2 干扰磁场值分布曲线
Fig.2 Interfering magnetic field
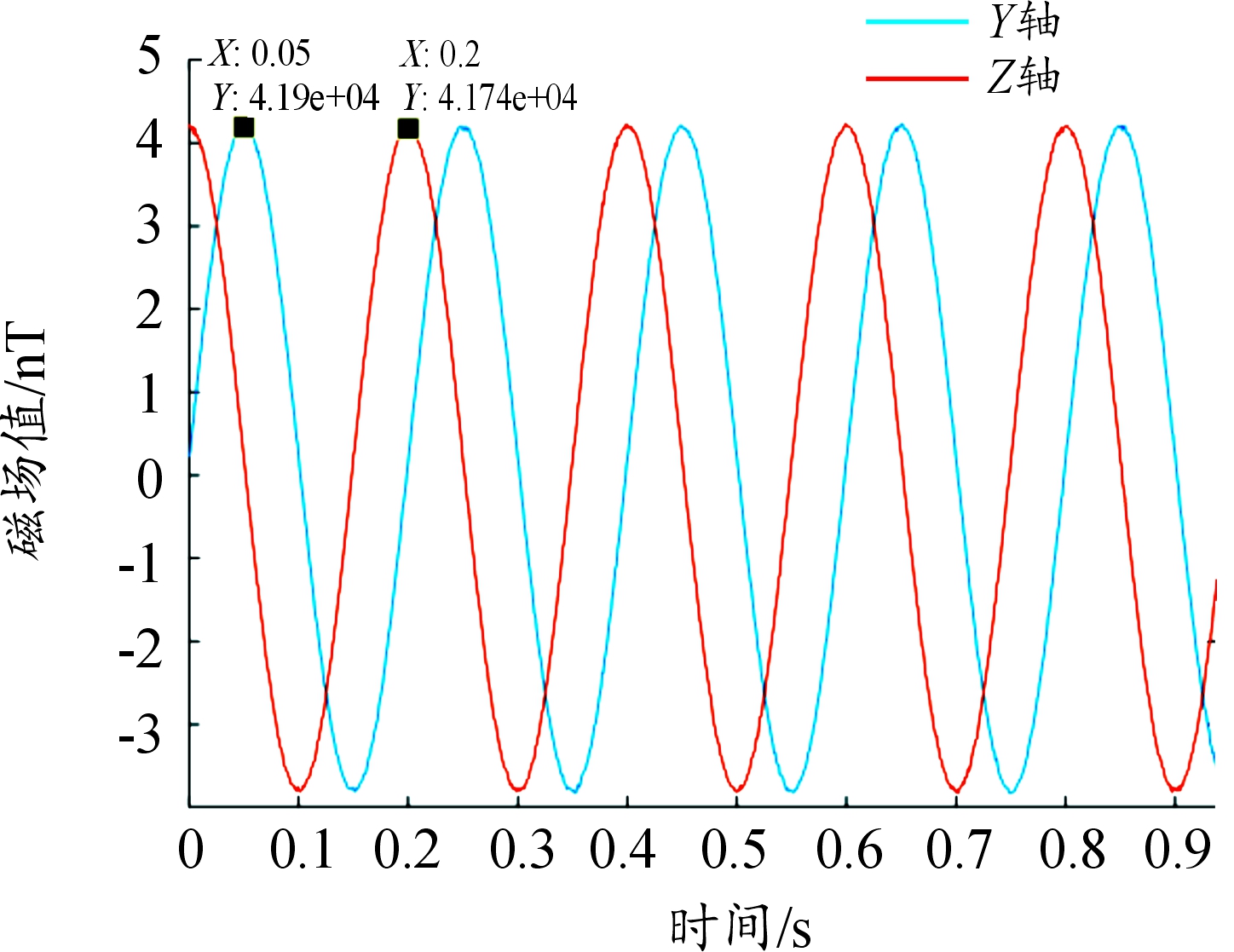
图3 仿真数据初始值曲线
Fig.3 Initial value of simulation data
初始值峰值分别为41 925 nT和41 744 nT，误差值分别为1 925 nT和1 744 nT，将初始值按照上述补偿方案进行高通滤波处理，滤波器选用IIR高通滤波器，对于理想高通滤波器条件，通带与阻带之间不存在过渡，但实际滤波器较理想情况过度缓慢，通带与阻带之间存在一定频率范围的过渡带，其截止频率设计为1 Hz。滤波器采样频率根据奈奎斯特采样定理，为保证采样之后的数字信号能够完整保留原始信号信息，设置为50 Hz。滤波器阶数与滤波器效果有关，同时较高阶数需要的计算量大，会造成数据处理时的较大时延，为保证滤波器的滤波效果同时较小时延要求，设计为2阶滤波器，所设计IIR高通滤波器参数如表1所示，幅频特性如图4所示。
表1 滤波器参数
Table 1 Coefficients of filter
分子系数分母系数1,-2,11,-1.822 694,0.837 186 5
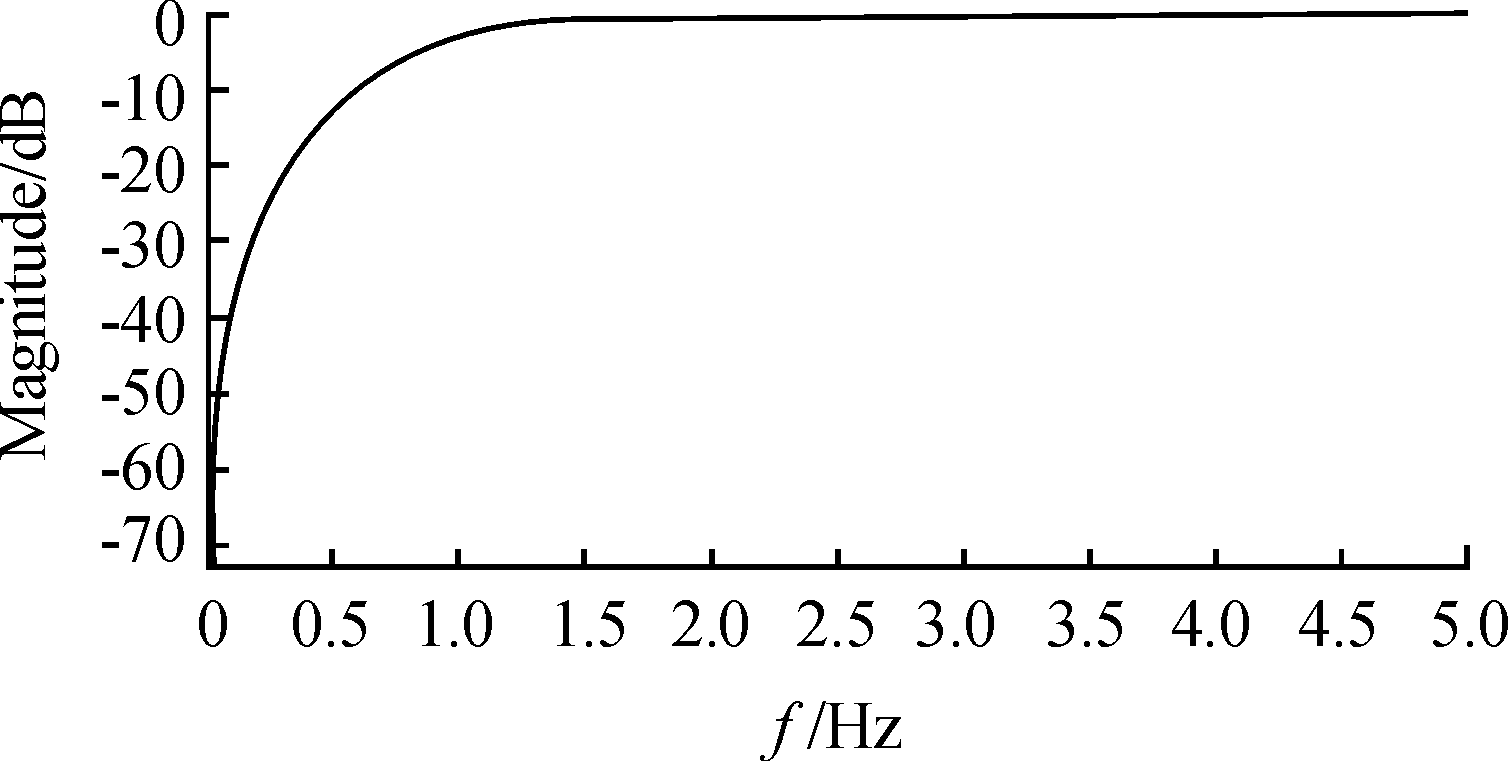
图4 滤波器幅频特性曲线
Fig.4 Characteristics of filter amplitude-frequency
得到补偿后的测量值如图5所示。由图5、图6可以看出：根据上述方案对干扰磁场引起的误差值进行补偿后，测量值误差明显减小，Y轴误差值减少为27 nT，Z轴误差值减少为38 nT。补偿前Y-Z轴磁场值零点受干扰磁场影响发生偏移，补偿后零点位置准确，验证了补偿模型的准确性。
图5 补偿后的测量值曲线
Fig.5 Simulation data after filtering
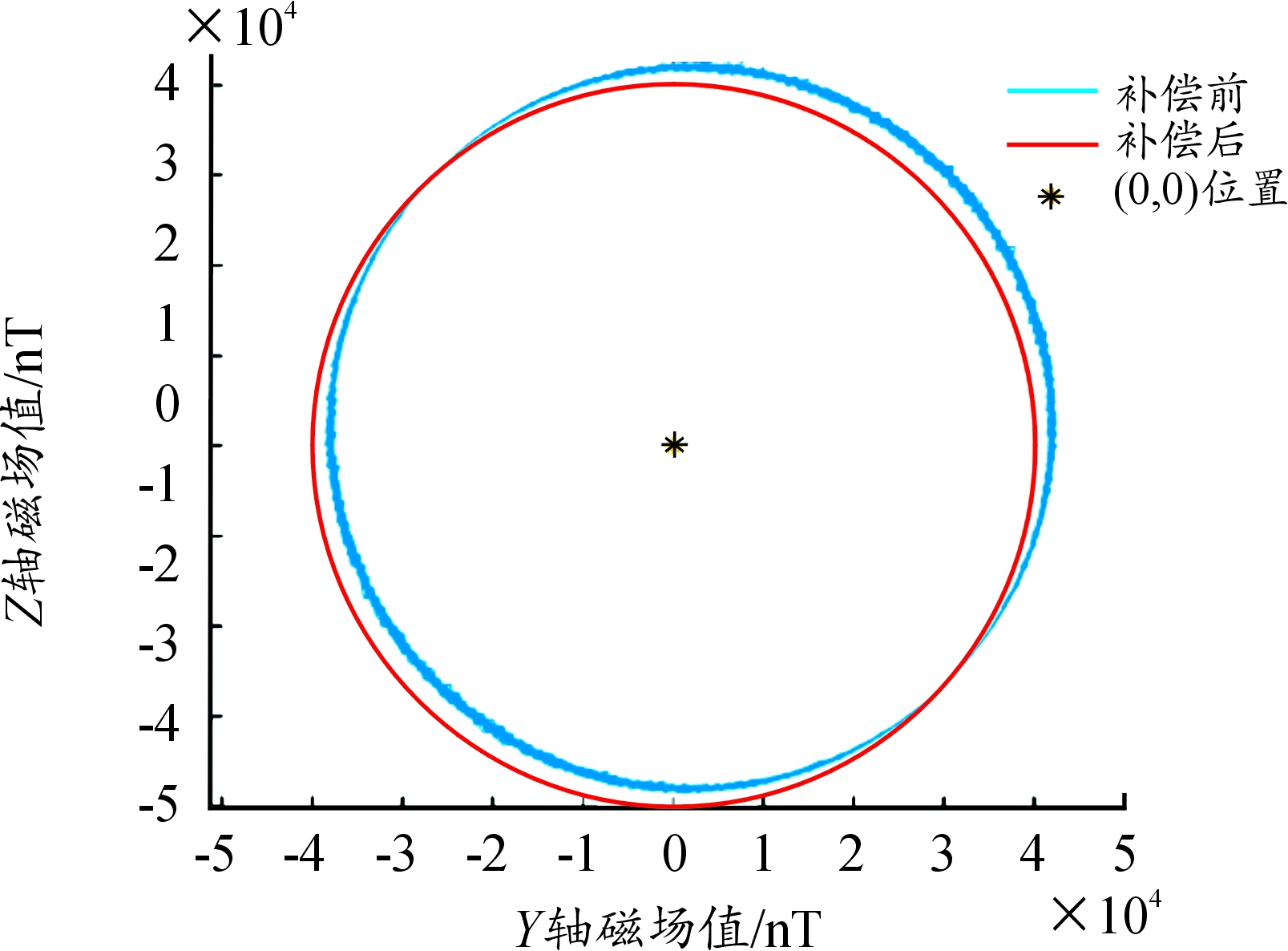
图6 零点位置变化曲线
Fig.6 The change of zero-point position
由于截止频率对滤波器效果有直接影响，调整截止频率再次补偿，进行对比。
1) 截止频率为2 Hz(图7)。
图7 截止频率为2 Hz补偿曲线
Fig.7 Compensation when cutoff frequency is 2 Hz
2) 截止频率为3 Hz(图8)。
图8 截止频率为3 Hz补偿曲线
Fig.8 Compensation when cutoff frequency is 3 Hz
由图7、图8可以看出，当调整滤波器频率分别为2 Hz和3 Hz时，Y轴峰值分别为37 118 nT和36 197 nT，Z轴峰值分别为36 891 nT和36 180 nT，滤波后得到的补偿值误差较1 Hz滤波显著增大，证明截止频率与有用信号频率差值越小，得到的补偿结果误差越大，则在设计时应遵循截止频率与有用信号频率差值尽可能大的原则。
4.2 半物理实验
选用以三轴磁传感器HMC1053作为磁敏感单元，STM32作为MCU的磁测系统进行试验，将磁测系统安装在三轴高速模拟飞行转台上如图9所示，将俯仰角与偏航角调整为0°。
图9 磁测系统安装状态图
Fig.9 Installed state of magnetic measurement system
控制模拟飞行转台使磁测系统仅绕X轴做滚转运动，得到磁测系统径向测量值如图10所示。
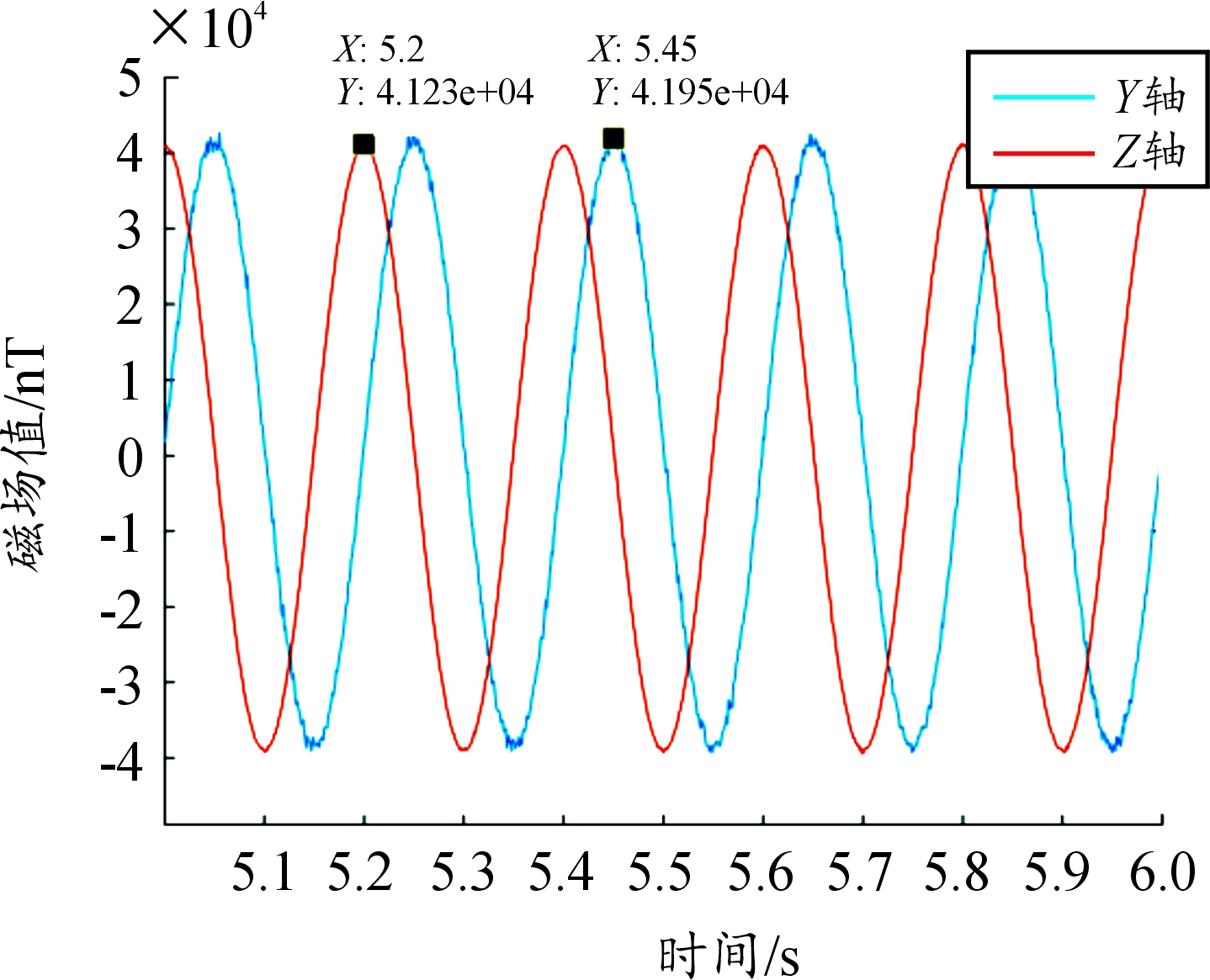
图10 补偿前测量值曲线
Fig.10 Measured value before compensation
将测量值进行滚转角解算，与飞行转台反馈标准滚转角度数变化曲线对比，即可得到补偿前的滚转角解算误差。通过分析滚转角角速率得到信号频率，对测量数据进行滤波后得到补偿后的测量值峰值分别由41 235 nT和41 957 nT减小为39 853 nT和40 142 nT，如图11所示。
重新进行滚转角解算，再次与飞行转台反馈标准滚转角度数变化曲线对比得到滚转角解算误差，误差曲线如图12，误差统计值如表2所示。
综合图12和表2可以得出：当弹体的俯仰角与偏航角均为0°，仅处于绕轴向的高速旋转状态时，由于干扰磁场的存在，直接使用地面标定参数进行滚转角解算得到的滚转角误差值峰值达到9.4°，误差均值为3.418°，且误差值呈周期性变化。而使用文中所述的方案对三轴磁场测量值进行补偿后，得到的滚转角误差值明显减小，误差峰值减小至2°以内，误差均值为0.371°，误差随机分布，不具有周期特性，滚转角精度提高6倍，可以满足制导弹药对滚转角精度的要求。
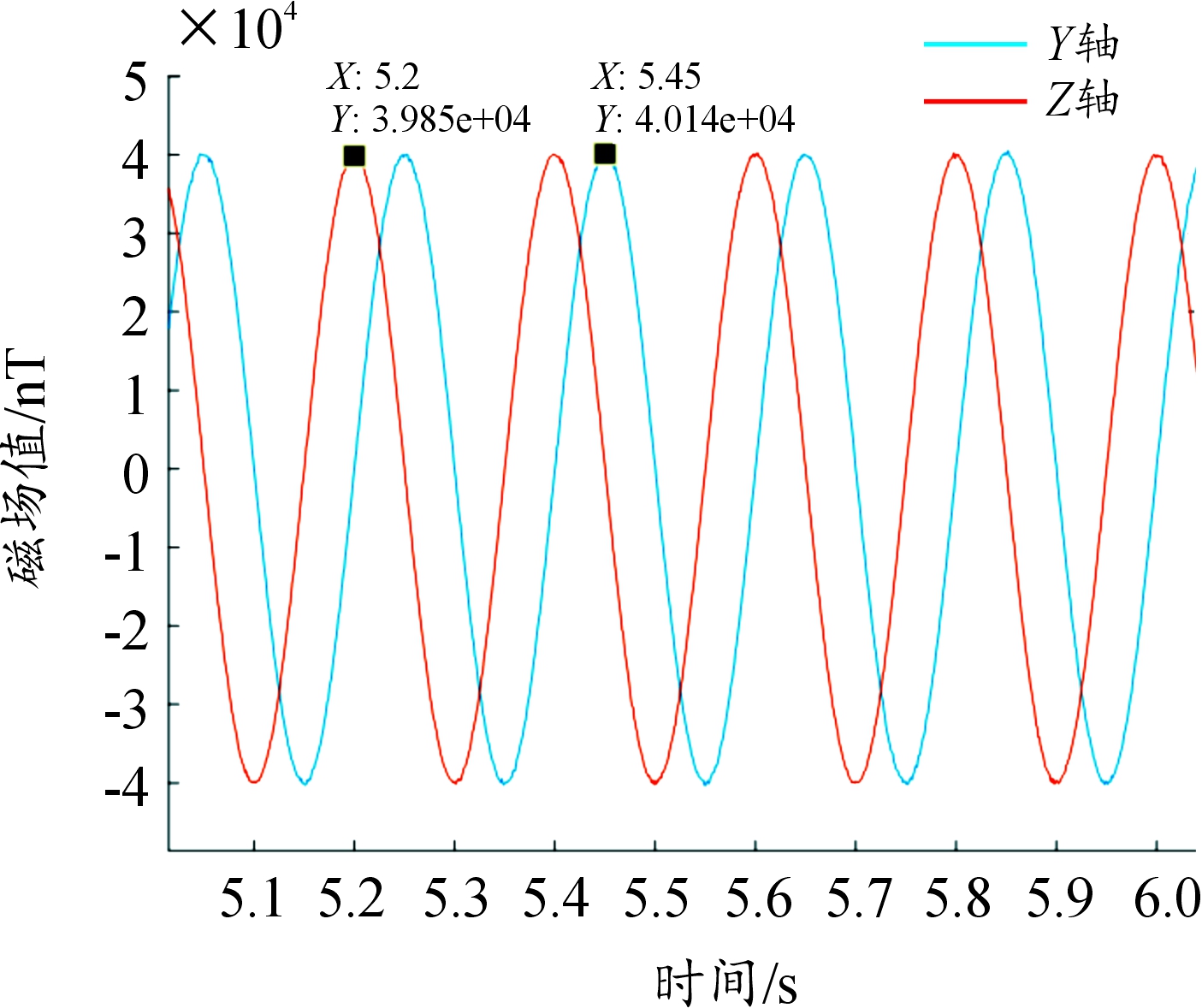
图11 补偿后测量值曲线
Fig.11 Measured value after compensation
图12 滚转角误差曲线
Fig.12 Comparison of roll angle error
表2 误差值
Table 2 Comparison of error
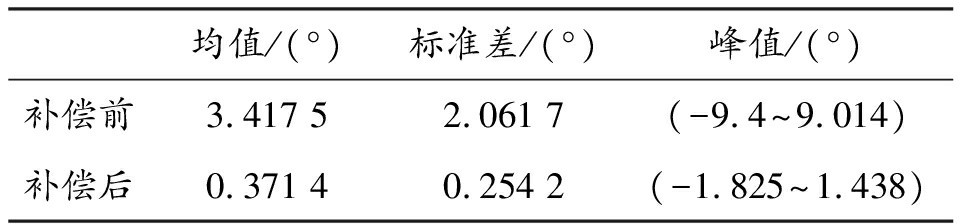
均值/(°)标准差/(°)峰值/(°)补偿前3.417 52.061 7(-9.4～9.014)补偿后0.371 40.254 2(-1.825～1.438)
5 结论
本文针对旋转弹弹体干扰磁场引起的滚转角解算不准确问题，提出了一种基于实时滤波的在线补偿方法。通过分析磁测系统中滚转角解算原理得到三轴磁场测量值与滚转角之间的数学关系，利用角速度得到径向信号在高速旋转过程中的频率参数，设计IIR高通滤波器对其进行补偿。通过仿真实验表明，该方法可应用于对存在弹体干扰磁场的磁测系统进行测量值补偿，能够有效减小弹体干扰磁场引起的磁场值误差。通过分析半物理实验数据可以得出，当弹体做高速旋转运动时，经过该方案补偿后得到的滚转角精度提高，误差值可达到2°以内，该方案中的补偿方式计算量小，实时性好，在STM32单片机上可实现对信号的实时补偿，满足制导弹药的滚转角精度及时延性需求，对于提高磁测系中滚转角统解算精度，满足高速旋转弹的测姿需求有较高的应用价值。
[1] 鲍广建,丁立波,张合.弹丸姿态解算初始地磁分量误差分析[J].兵器装备工程学报,2019,40(01):74-77.
Bao G J,Ding L B,Zhang H.Error Analysis of Initial Geomagnetic Component in Ammunition Attitude Angle Solution[J].Journal of Ordnance Equipment Engineering,2019,40(01):74-77.
[2] 段偲丽,管雪元,李文胜.基于磁传感器的炮弹姿态测量解算[J].电子测量技术,2018,41(02):31-36.
Duan S L,Guan X Y,Li W S.Attitude Measurement of Projectile Based on Magnetic Sensor[J].Electronic Measurement Technology,2018,41(02):31-36.
[3] 杨宇彬,汤国建,包为民.地磁姿态探测器的实时标定方法研究[J].飞行力学,2014,32(01):93-96.
Yang Y B,Tang G J,Bao W M.Read-time Calibration Method of Magnetometer[J].Flight Dynamics,2014,32(01):93-96.
[4] 狄素素,曾成,张梦影.航姿参考系统三轴磁强计的两步校正算法[J].火力与指挥控制,2018,43(09):40-43.
Di S S,Zeng C,Zhang M Y.Two-step Calibration Algorithm of Three-axis Magnetometerin Attitude an Heading Reference System[J].Fire Control & Command Control,2018,43(09):40-43.
[5] 李翔,刘晓琴,宋百麒.航姿系统三轴磁强计动态校正研究[J].电子器件,2020,43(04):913-917.
Li X,Liu X,Song B Q.Research on Dynamic Calibration of Tri-axial Magnetometer in Attitude and Heading Reference system[J].Chinese Journal of Electronic Devices,2020,43(04):913-917.
[6] 施国兴,杨树兴,苏中.地磁信息的旋转弹姿态算法研究[J].弹箭与制导学报,2011,31(05):33-35,38.
Shi G X,Yang S X,Su Z.The Study on Attitude Algorithm of Rolling Projectile Using Geomagnetic Information[J].Journal of Projectiles Rockets Missiles & Guidance,2011,31(5):33-35,38.
[7] 嵇绍康,高艳丽.地磁信号误差模型分析及补偿算法[J].舰船电子工程,2019,39(12):43-47.
Ji S K,Gao Y L.Error Model Analysis and Compensation Algorithm for Geomagnetic Signal[J].Ship Electronic Engineering,2019,39(12):43-47.
[8] 刘宗源,高敏,宋卫东等.基于地磁测姿的误差建模及仿真分析[J].火力与指挥控制,2019,44(09):149-152,158.
Liu Z Y,Gao M,Song W D,et al.Error Modeling and Simulation Analysis Based on Geomagnetic Measurement[J].Fire Control&Command Control,2019,44(09):149-152,158.
[9] Li S P,et al.An Improved Calibration Method for the Misalignment Error of a Triaxial Magnetometer and Inertial Navigation System in a Three-Component Magnetic Survey System[J].Applied Sciences,2020,10(19):6707-6707.
[10] Cao G C,Xu X,Xu D C.Real-Time Calibration of Magnetometers Using the RLS/ML Algorithm[J].Sensors,2020,20(02)：535-549.
[11] Yin Y,Zhou B Q,et al.Comprehensive influence of modulated and bias magnetic fields on an atomic magnetometer[J].Measurement Science and Technology,2021,32(05)：4-9.
[12] Wang Y J,Li Z,Li X.External Disturbances Rejection for Vector Field Sensors in Attitude and Heading Reference Systems.[J].Micromachines,2020,11(09)：803-817.
[13] InvenSense Inc.“Method And System For Magnetometer Calibration” in Patent Application Approval Process (USPTO 20200142008)[J].Technology & Business Journal,2020(10s)：57-65.
[14] Opromolla R.Magnetometer Calibration for Small Unmanned Aerial Vehicles Using Cooperative Flight Data.[J].Sensors (Basel,Switzerland),2020,20(02)：538-554.