1 引言
大型运载火箭发射平台有一次投入多次使用的特点,在高密度使用需求下,对发射平台的使用寿命需极为关注。潘玉竹等[1]对火箭发射工况燃气流载荷下发射平台钢结构进行了动响应分析,并对发射平台钢结构进行了优化和改进;饶毅[2]将发射平台核心指标结构应力转化为火箭发射平台结构强度可靠性,建立了火箭发射平台可靠性评价的多级模糊评价数字模型;平仕良等[3]通过结构动态响应数据分析、评判及时发现发射台主体结构损伤风险,实现对发射台结构可靠性的评估。但均未对发射平台进行损伤分析及寿命预测。在大型结构疲劳寿命研究中,目前广泛使用的方法主要有A-N曲线法[4]、S-N曲线法[5-6],但A-N曲线法无法直接用作材料的疲劳性能指标,对疲劳寿命不能采用定量的计算[7],对于重要的典型焊接箱梁结构,通常采用结构级的疲劳试验研究来确定结构的疲劳寿命[8]。基于可靠性的疲劳寿命研究是从可靠性要求出发,对结构疲劳问题用随机的概念和统计的方法研究一定存活率下的寿命分布规律和分布特性,建立p-S-N曲线的理论预测模型有效预测材料的疲劳寿命[9-11]。对于实际的工程应用研究,通过结构所受的载荷谱,利用有限元仿真软件计算出关键特征位置的动力特性,结合疲劳累积损伤理论,可预测结构的疲劳寿命[12-13],用nCodeGlyghworks等软件可快速有效地实现结构载荷谱编制、疲劳设计以及疲劳损伤分析[14]。
大型运载火箭发射平台在发射流程中,受到火箭加注载荷逐渐积累、箭体起飞载荷释放、发射燃气流场的热力环境等循环作用,多次使用后结构可能出现疲劳失效,影响发射平台使用寿命。但现有研究对运载火箭发射平台疲劳分析及寿命预测的较少,故以CZ-X运载火箭的发射平台主结构为研究对象,综合运用平台力学环境实测数据分析和有限元分析的方法对其进行主结构细节特征及载荷谱识别研究;利用雨流分析技术有效识别单次任务下平台结构的疲劳载荷循环次数,对发射平台载荷工况进行分类分析,结合结构几何、应力集中、焊接细节等特征对基于可靠性的疲劳曲线p-S-N进行修正;结合CZ-X运载火箭Y1、Y2任务的测试数据,对加注建压、起飞阶段不同载荷情况进行疲劳损伤分析及寿命预测。
2 发射平台主结构力学特性分析
2.1 有限元计算模型
根据发射平台的结构形式、发射环境下载荷分布以及约束位置,采用对称模型进行计算以降低总体网格数量及计算时间,采用实体单元进行建模考虑了焊接梁结构的厚度效应,平台主结构有限元模型如图1所示。
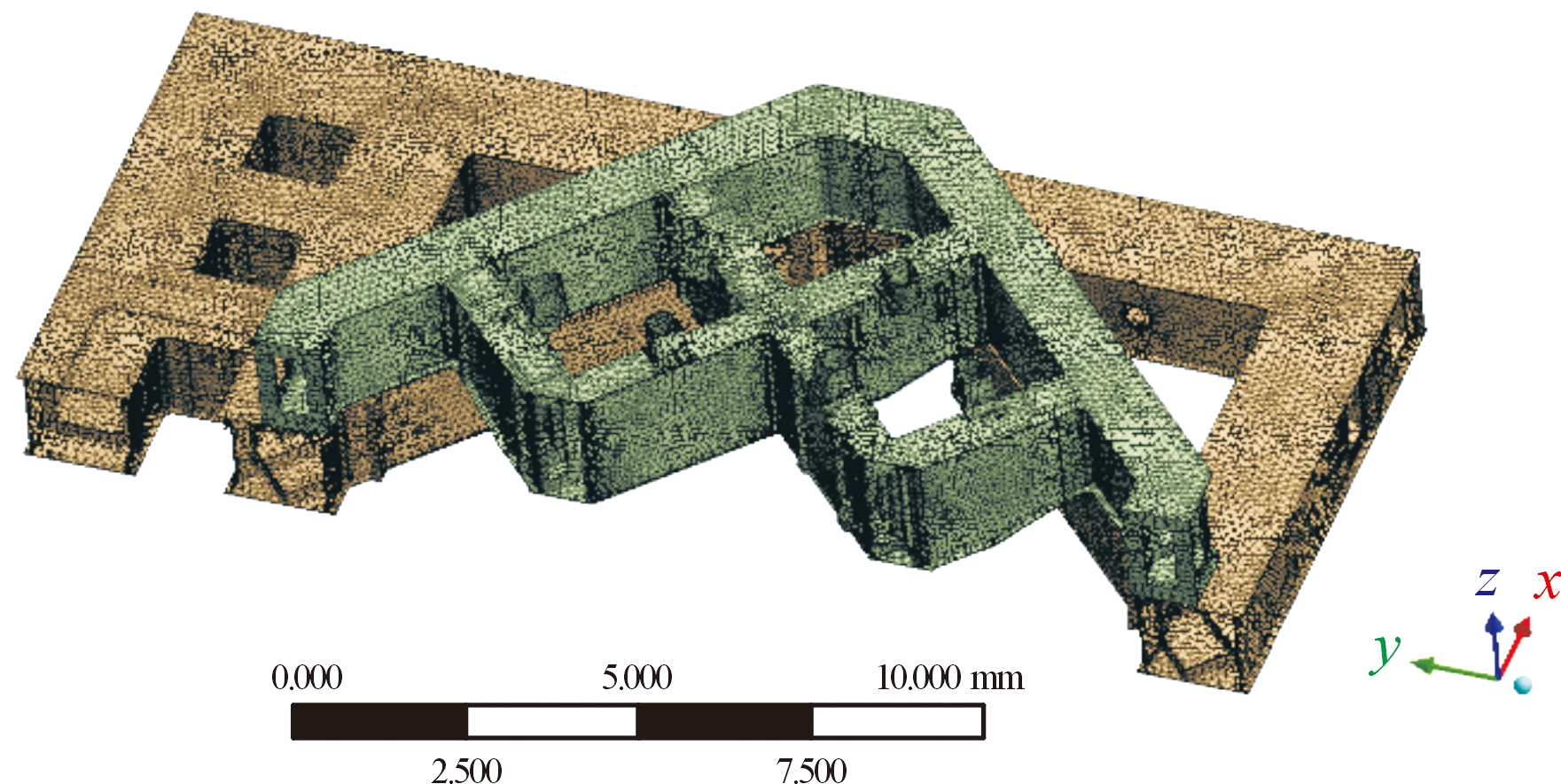
图1 发射平台主结构1/2有限元模型示意图
Fig.1 Finite element model of 1/2 launch pad main structure
模型简化后结构自重约1 640 t,脐带塔质量250 t以面载荷形式施加于脐带塔安装板上方。
2.2 载荷工况及边界条件
在发射前支承状态下,箭体静态重力载荷、风载荷通过发射平台承载机构支撑,由主体结构进行承载,并最终由球铰型的承力装置与地面连接。有限元模型中建立球铰承力装置相应位置的连接板,进行远端球铰约束(只约束平动位移),同时在对称面施加对称约束,模型载荷施加及约束如图2所示。
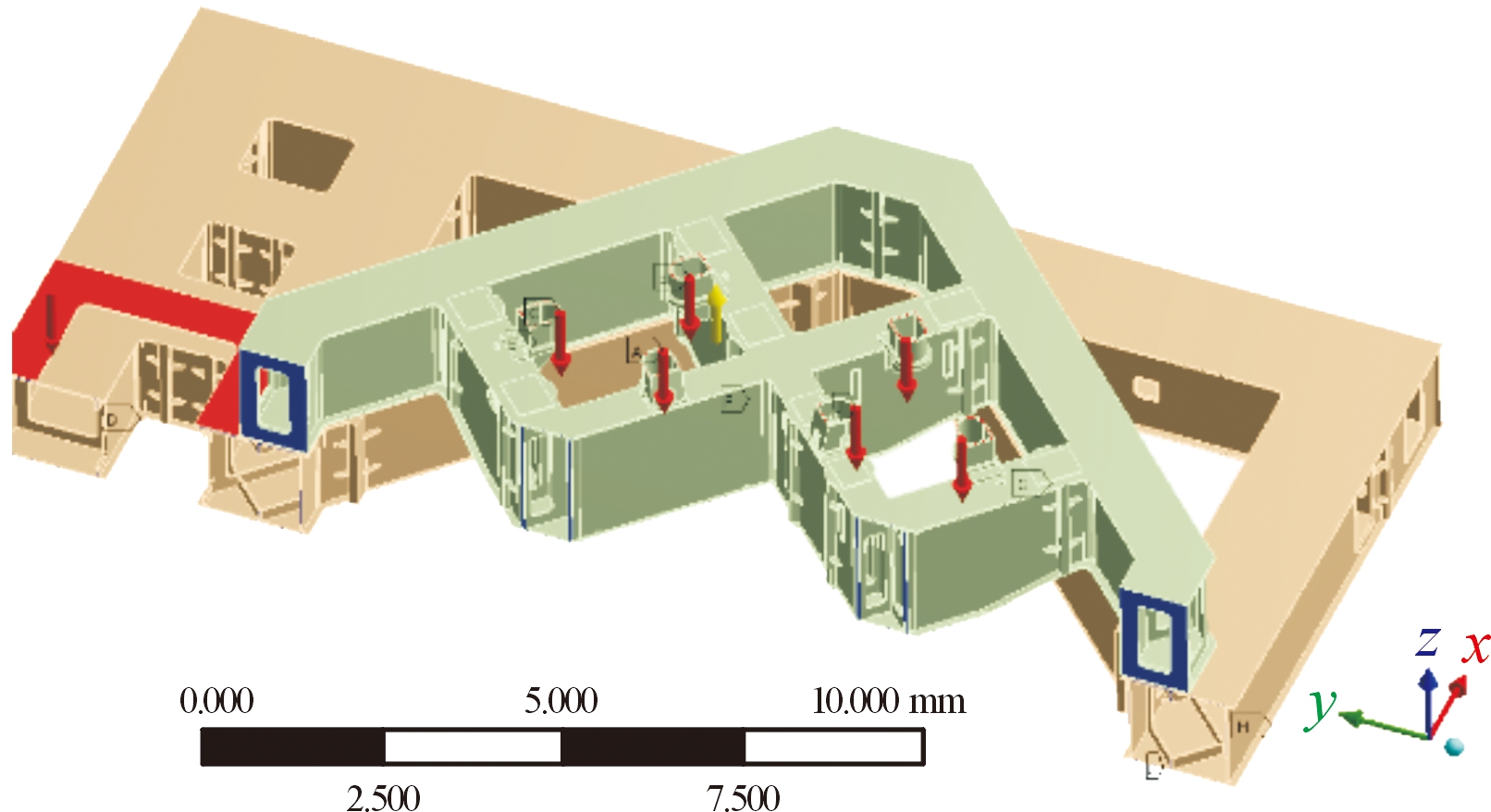
图2 静态承载载荷的模型及边界条件示意图
Fig.2 Static load condition and constrains
火箭起飞后,与承载机构脱离,发射平台台体不再承受箭体自重载荷。起飞初期,燃气流由发射平台导流孔进行排导,起飞至一定高度,燃气流作用至台面,如图3所示。根据燃气流仿真结果,随起飞高度上升,燃气流作用核心区域逐渐扩张,但面压随高度的增加而下降。以典型计算工况,起飞燃气流作用到台面最大面压为1.12 MPa。
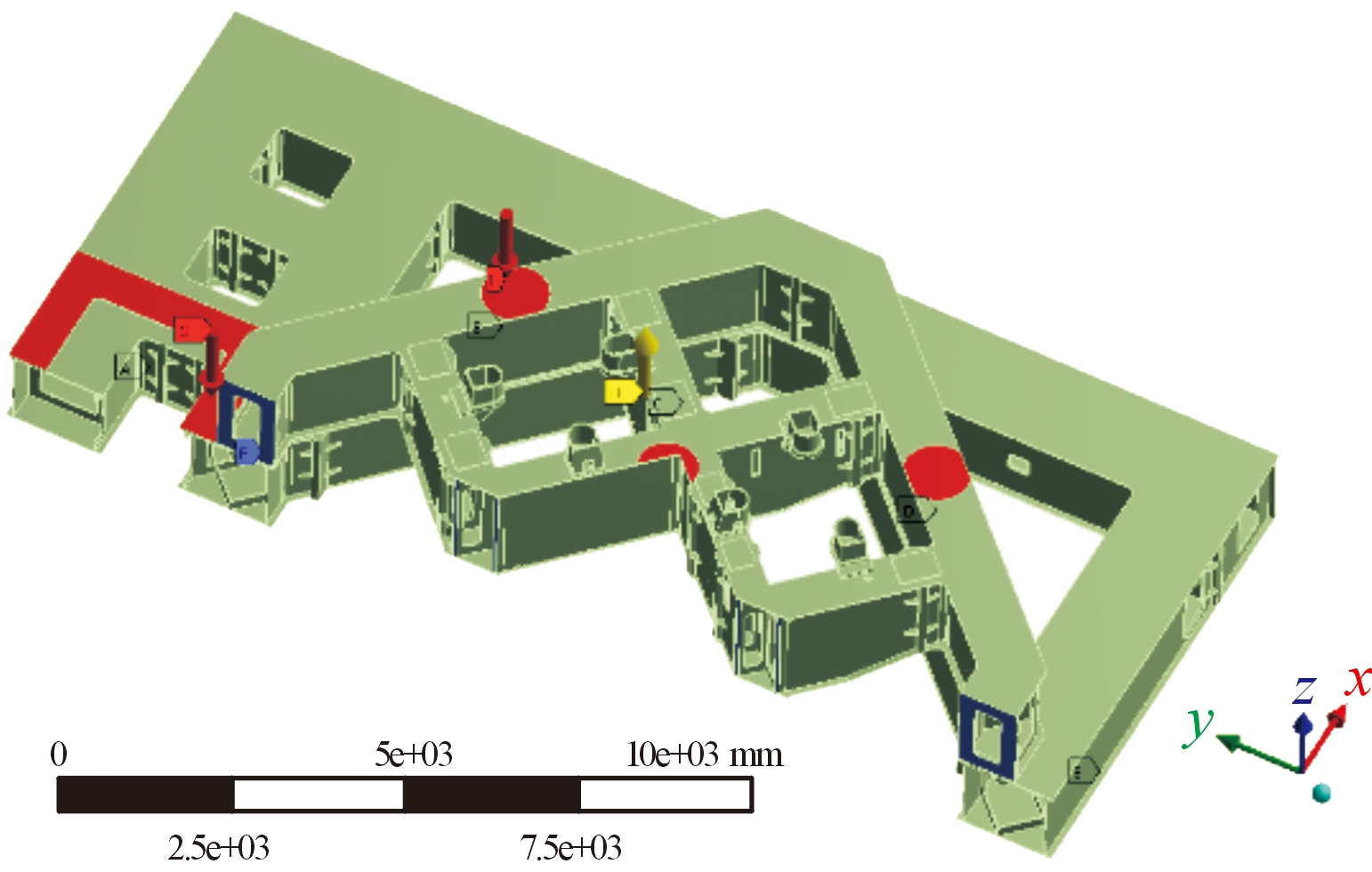
图3 发射载荷的模型及边界条件示意图
Fig.3 Launching load condition and constrains
2.3 静力学特性计算分析
通过对不同工况下台体主结构进行静力学计算,获取了台体结构的应力分布云图。如图4、图5所示,在静态承载下,主体结构最大等效应力为239 MPa,位于中间梁上面板相交的内侧圆角处。在发射燃气流载荷作用下,主体结构最大等效应力为208 MPa,要略小于静态承载下的最大应力,且最大应力位置位于主体结构约束上方的内部筋板。
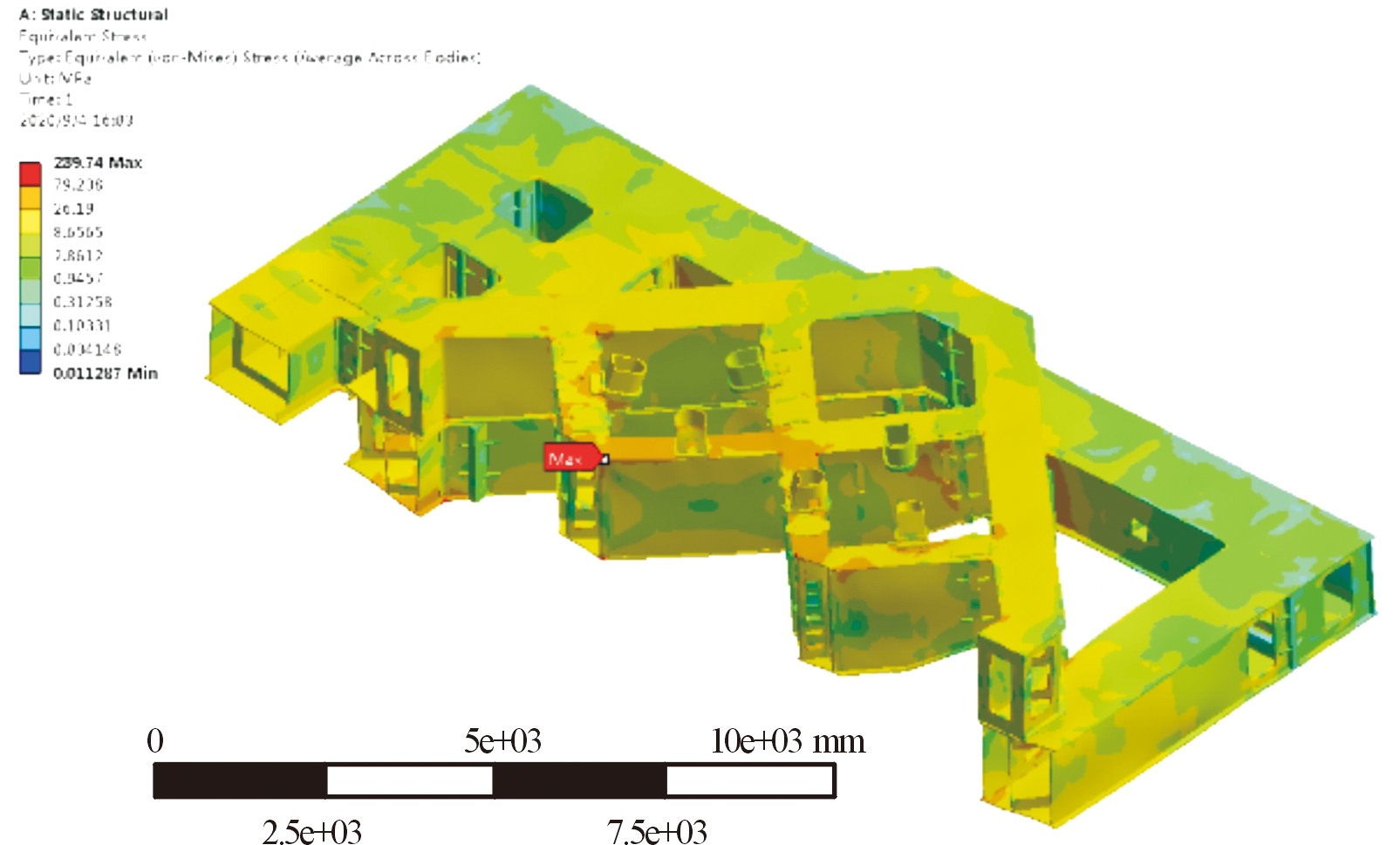
图4 静态承载下台体等效应力云图
Fig.4 Equivalent stress under static load condition
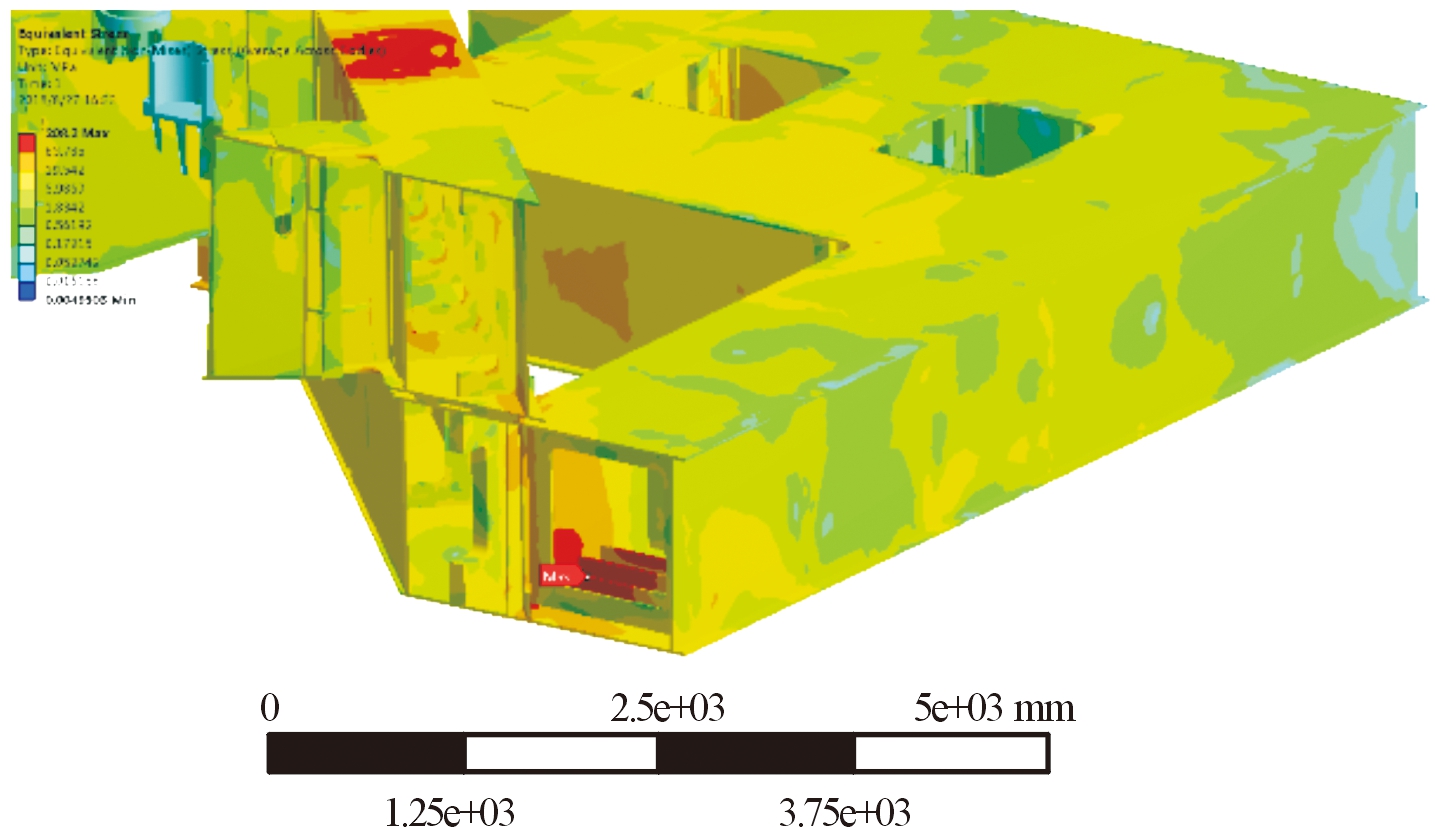
图5 发射载荷下台体等效应力云图
Fig.5 Equivalent stress under launching load condition
实测载荷谱通常在设备实际使用中采取结构应变测量的方式获取,以便于更真实地掌握结构的实际受力情况。测试中采用单向应变片进行测量,应变片方向平行于井字梁结构,各测点处的变形处于材料弹性范围内,Y1测点位置如图6所示,![]() 为Y2新增测点,其中
为Y2新增测点,其中![]() 为同一位置的互成90°方向,
为同一位置的互成90°方向,![]() 为同一位置的互成90°方向。
为同一位置的互成90°方向。
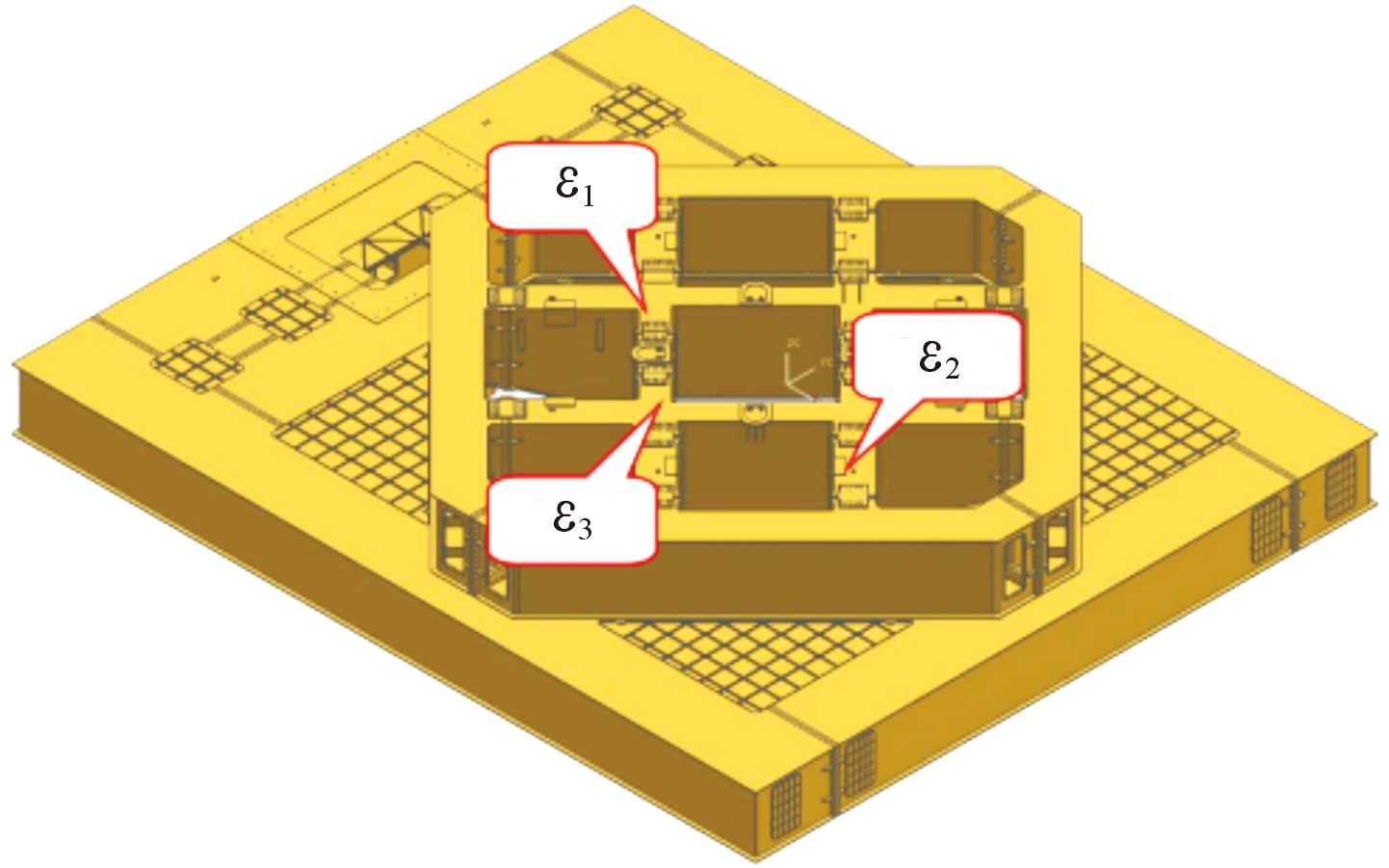
图6 发射平台应变测试测点位置示意图
Fig.6 Stain measurement locations of the launch pad
根据发射平台在某两次实际使用中测试的时统分析、测试数据清理的处理情况,对两次测试的多个测点进行合并分析。根据测点布置位置,测点处结构应力为拉应力,实际应力值为正值。随着起飞过程逐渐卸载,应力值具有明显下降过程。由于测试前,各测点处的应变被设置为零位,随后逐渐卸载。
根据如图7所示测试结果分析可知,起始段发射平台主结构的应力水平保持一个稳定值,为静态承载状态;直至发动机建压后,逐渐卸载至静态载荷完全消失;在火箭起飞后的0.5 s内,燃气流由发射平台导流孔进行导流,发射平台应力基本保持稳定;起飞4 s后,随着燃气流开始作用于发射平台结构上表面,部分测点应力值出现增加趋势;当燃气流中心作用到台面,应力值出现峰值,此后随燃气流的减弱,应力值下降。需要指出的是,Y1测试中发射平台应变测点仅在台体井字梁和摆杆桁架上布置,考虑到发射过程中发射平台钢架结构被燃气流破坏引起结构失效(对应图7(a)中测试曲线10 s后变大),在Y2测试中增加钢架结构立柱上的应变测点![]() 用于获取发射过程中钢架结构立柱的受力情况。
用于获取发射过程中钢架结构立柱的受力情况。
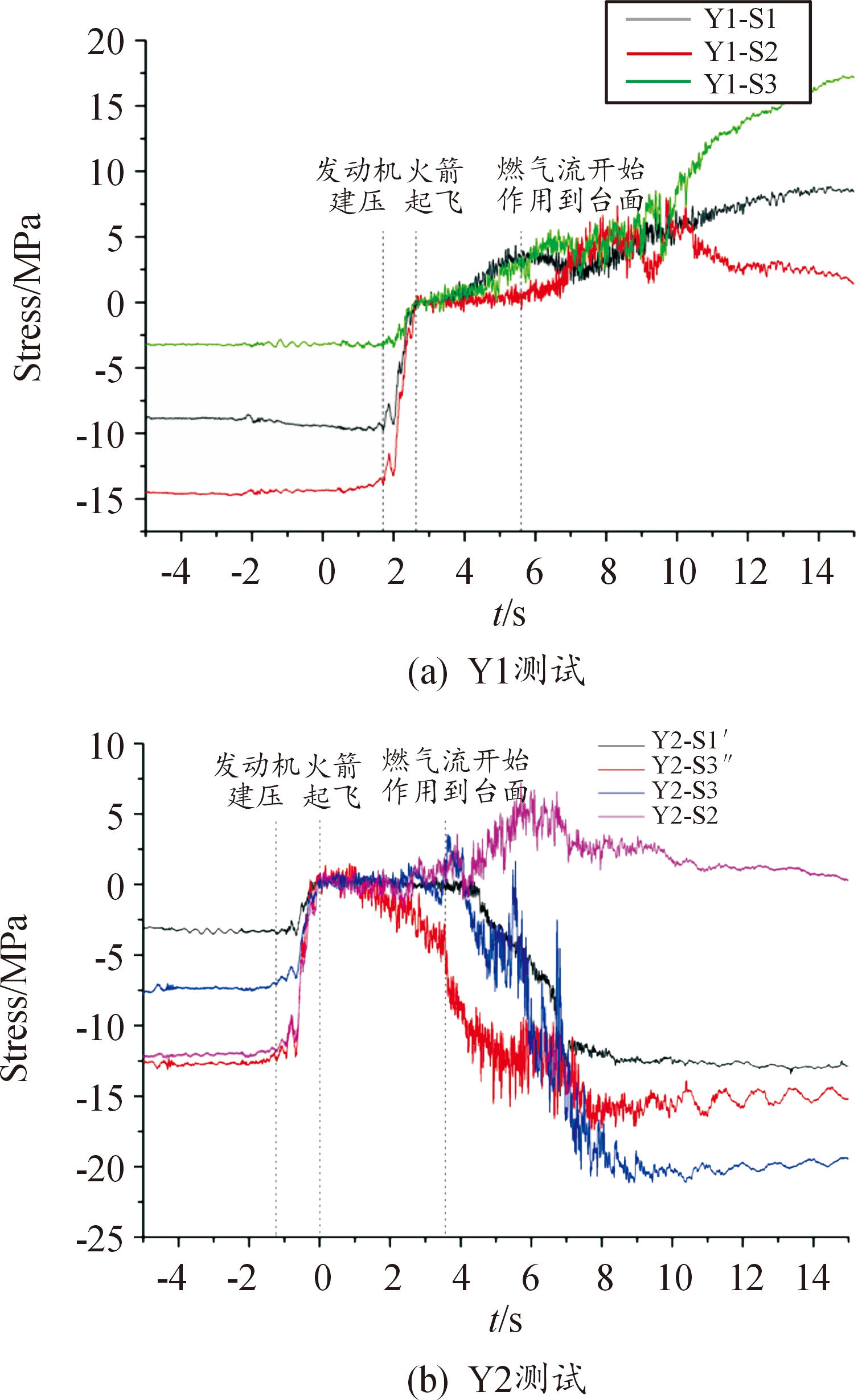
图7 测试应力随起飞时间历程的变化曲线
Fig.7 Variation of measured stress under launching time course
根据温度传感器测试结果,台面最大热流为15.32 MW/m2、最大空气温度为2 489 ℃、最大压力为1.07 MPa,从测点热流、空气温度、压力峰值出现的时刻来看,15.32 MW/m2出现在火箭起飞2.97 s,此时空气温度、压力尚未达到峰值,可见温度对结构板材的影响较为滞后,燃气流瞬间冲刷产生的热量逐渐传导至结构,可忽略高温对应力测试的影响。
3 不同可靠度下的构件疲劳寿命曲线
3.1 材料p-S-N疲劳曲线表达方式
发射平台主承载结构应具备可靠性考核要求,因此要想全面表达各种存活率下的疲劳寿命与应力水平间的关系,可使用p-S-N曲线。工程上一般认为在同级应力水平下的疲劳寿命服从双对数正态分布或威尔分布。不少试验已证实,一旦在结构或部件中萌生了裂纹,低于疲劳极限的应力循环也能导致裂纹扩展,并产生疲劳损伤。且低于疲劳极限的应力循环在载荷谱中所占的百分比很高,对疲劳损伤肯定有影响。为考虑低于疲劳极限应力循环所引起的损伤,必须将p-S-N曲线作必要的修正[9]。对小于疲劳极限部分的p-S-N曲线(对数曲线),用斜率(bp-2)的斜线来代替原来的水平线,此时p-S-N曲线的表达式为:
(1)
结合疲劳设计手册,对Q345材料疲劳p-S-N曲线超过107次疲劳循环后段曲线的修正,修正后的材料疲劳p-S-N曲线如图8所示。
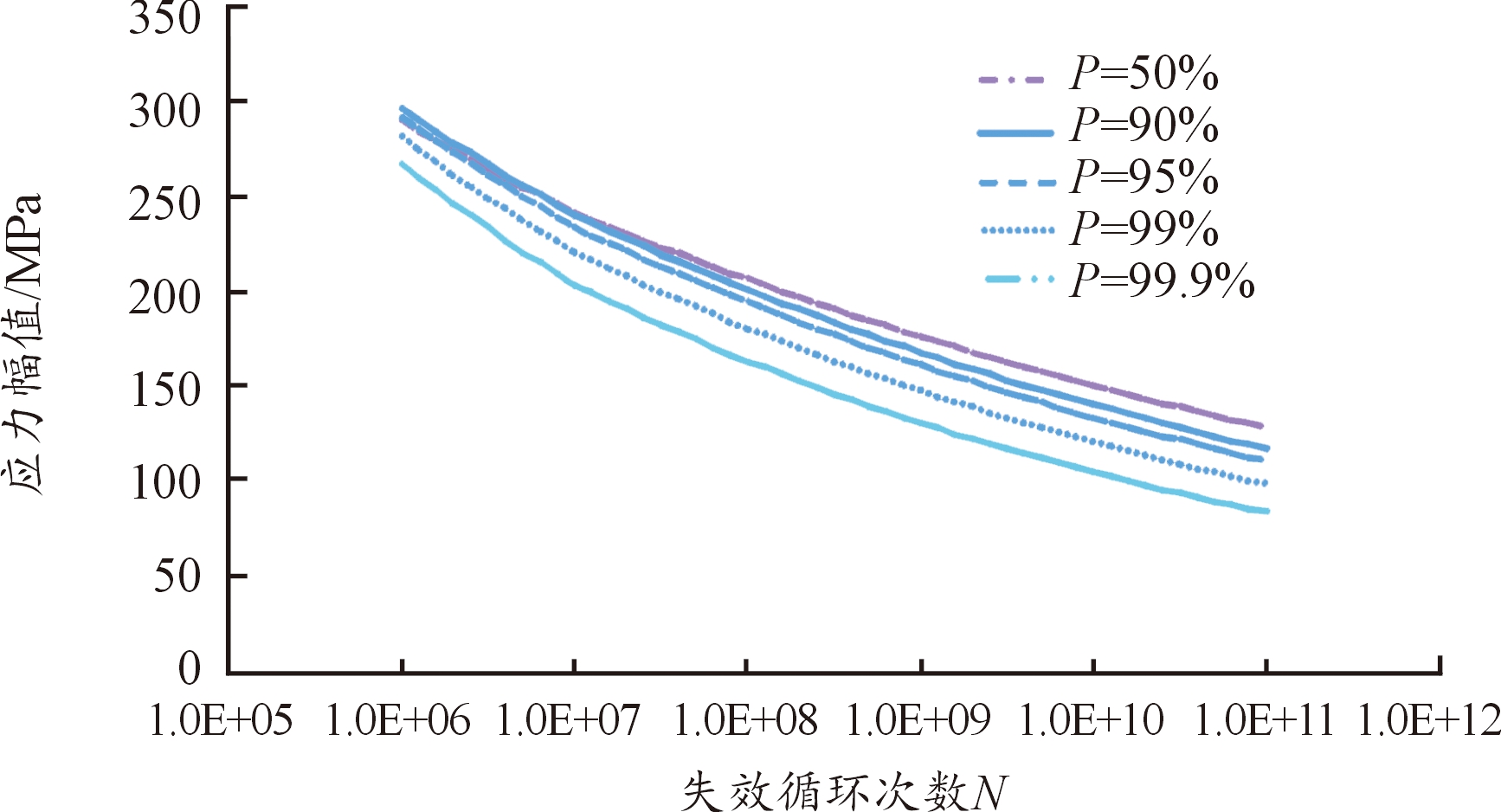
图8 Q345材料修正后p-S-N曲线
Fig.8 Modified p-S-N curve of Q345 material
3.2 焊接箱型梁p-S-N疲劳曲线表达方式
考虑真实构件的状态,包括尺寸、表面粗糙度、结构连接焊接细节特征、载荷等,对疲劳曲线具有一定的影响。箱型梁疲劳寿命N的分布,基本符合双参数对数正态分布模型,箱型钢结构主梁p-S-N曲线簇的数学表达式如下[7]:
lgN=lgC+βlgδ-mlgS
(2)
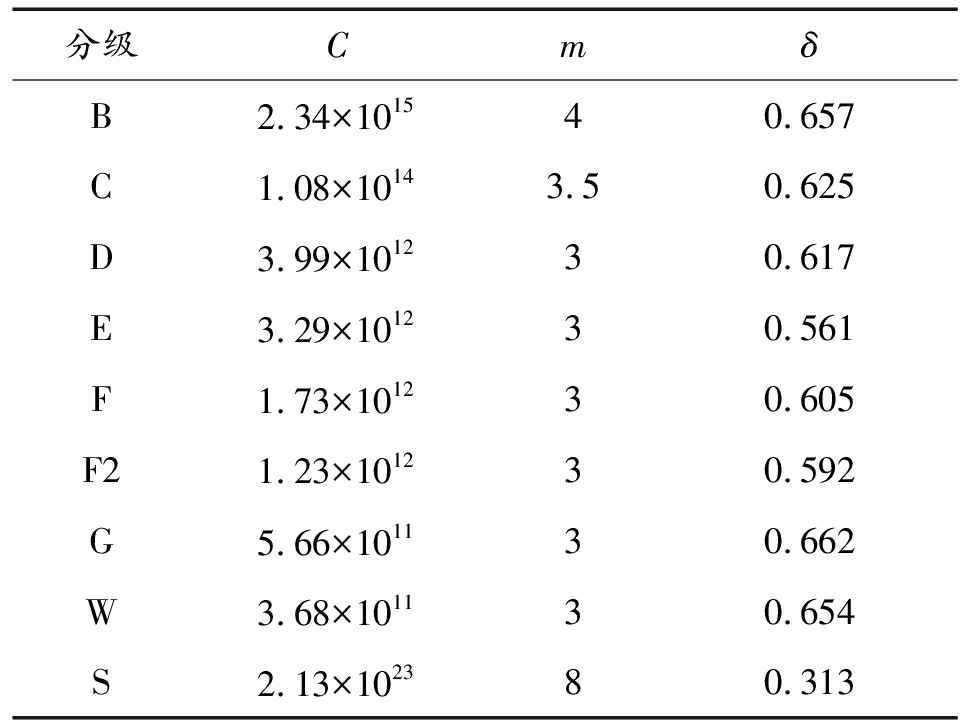
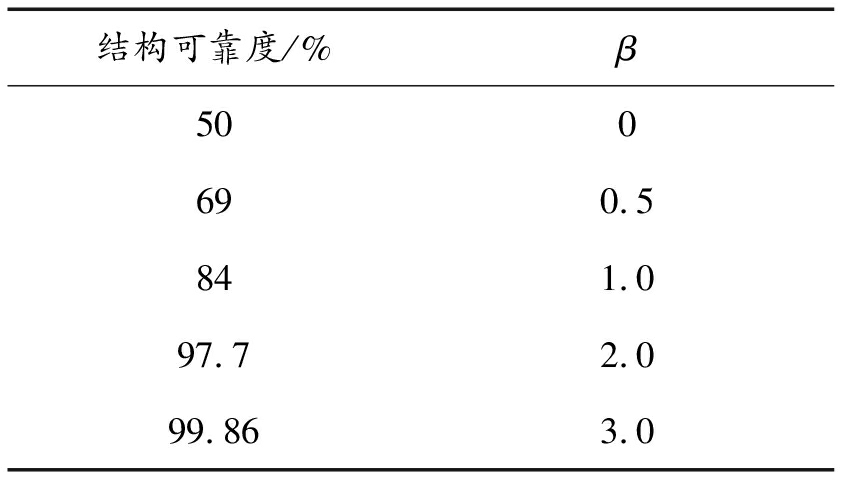
式中: β为工程中常用于反映结构可靠度的指标,对于某一条p-S-N曲线而言为常量;δ为寿命分布标准差,m为p-S-N曲线在双对数坐标内的负斜率,lgC-βlgδ为p-S-N曲线在双对数坐标系内的截距。根据英国桥梁设计规范BS5400,具体各参数表征值、可靠度指标如表1、表2所示。
依据BS5400规范中对箱型梁结构特征、概率性疲劳、焊接细节疲劳特性等的定义,发射平台主结构以主结构板材、垫板连接结构、孔洞结构以及其他螺栓连接结构等的特征居多,更适用于特征分类中的D级构造。以往发射平台结构设计,以安全系数2进行结构安全性及可靠性评价,当平台主结构仿真结果确认安全系数均在2以上,则平台可靠度为100%。依据设计手册,结构疲劳可靠度划分为多个等级,通常50%为常规疲劳设计,而目前其他行业如桥梁钢结构、起重机钢结构,考虑到结构服役及迭代成本,较多使用97.73%作为可靠度指标,鉴于运载火箭发射对可靠性、安全性的高要求,平台主结构的可靠度可依据99.87%进行评价。如图9所示为推导出的D级构造下,发射平台主结构箱型梁在不同可靠度下的p-S-N曲线,随着应力幅的上升,失效循环次数显著增加,且在不同可靠度下的差异性逐渐增加。
表1 不同结构疲劳等级分类下的参数特征值(BS5400)
Table 1 Parameters under different classification of structure fatigue grades (BS5400)
分级CmδB2.34×101540.657C1.08×10143.50.625D3.99×101230.617E3.29×101230.561F1.73×101230.605F21.23×101230.592G5.66×101130.662W3.68×101130.654S2.13×102380.313
表2 不同可靠度下的分布标准差β
Table 2 Distribution standard deviation β under different reliability
结构可靠度/%β500690.5841.097.72.099.863.0
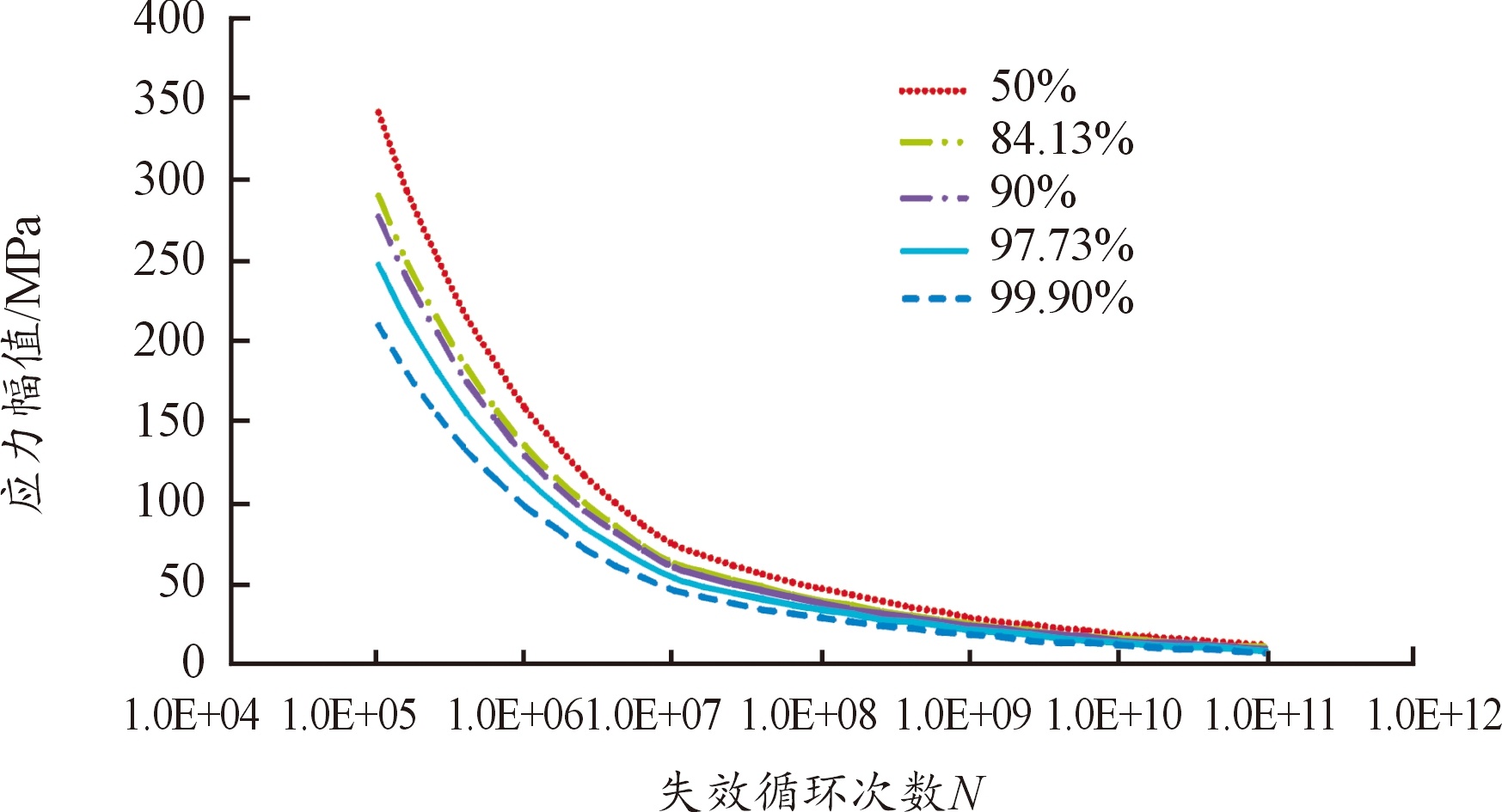
图9 发射平台箱型梁不同可靠度下p-S-N曲线
Fig.9 p-S-N curve of box girder of the launch pad under different reliability
4 发射平台疲劳寿命预测
4.1 疲劳线性累计损伤理论
线性疲劳累积损伤理论中最具代表性的就是Miner损伤理论,它假定结构或构件的疲劳损伤度与应力循环次数成线性关系:
(3)
式中:ni为第i级应力水平下的循环次数;Ni为第i级应力水平下的疲劳寿命。根据线性损伤理论,应力σi每作用一次对材料的损伤D/Ni,则经过ni次后,对材料造成的总损伤为niD/ Ni。当各级应力对材料的损伤综合达到临界值D时,材料即发生破坏。
4.2 名义应力法疲劳寿命分析流程
名义应力法的基本假设是:对相同材料制成的任意2个构件,只要应力集中系数相同,载荷谱相同,则它们的疲劳寿命相同。用名义应力法估算平台结构疲劳寿命的分析步骤如图10所示。
1) 识别平台点火阶段、起飞阶段力学载荷工况;
2) 结合实测应力数据,利用有限元分析确定结构中的疲劳危险部位;
3) 确定危险部位的名义应力谱;
4) 确定不同可靠度下Q345箱型梁结构p-S-N曲线;
5) 应用雨流计数法、Miner疲劳损伤累积理论,求出平台结构危险部位的疲劳寿命。
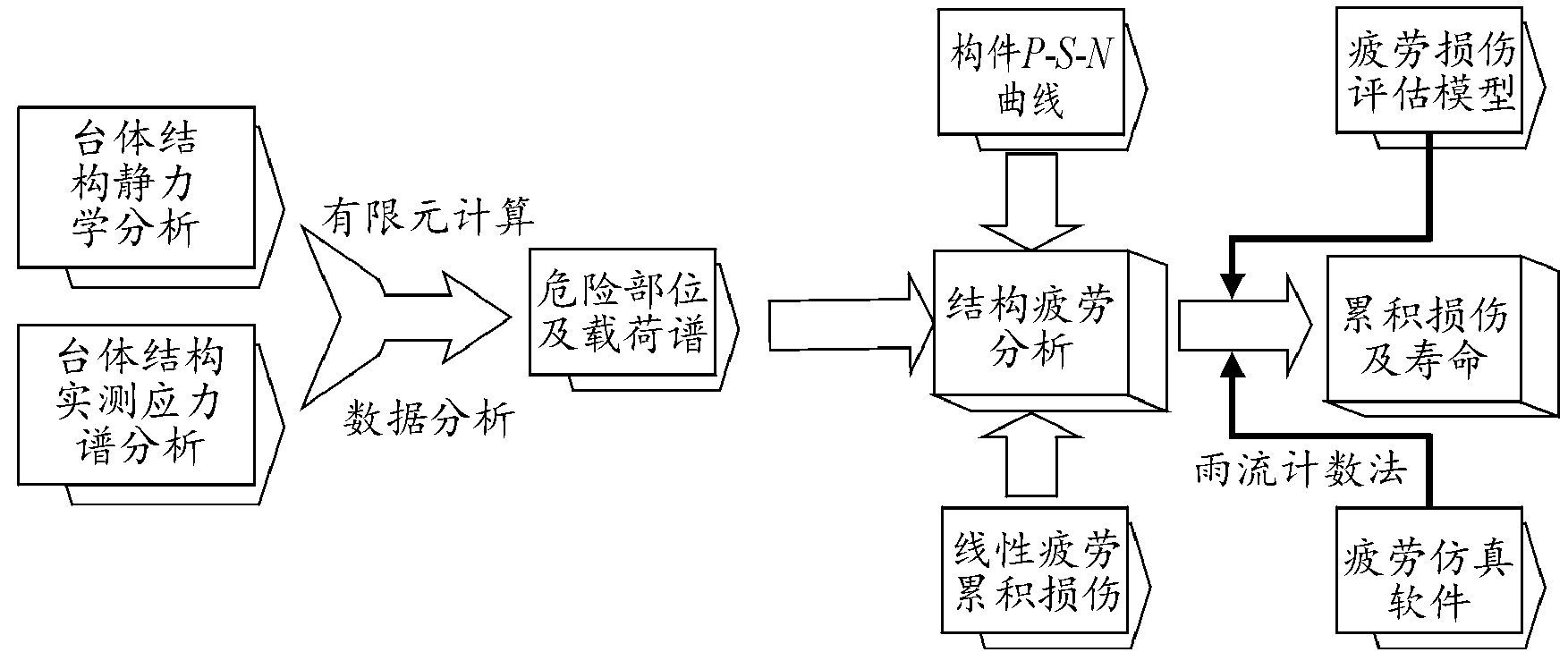
图10 平台台体结构疲劳寿命预测分析步骤框图
Fig.10 Structure fatigue life analysis method of launch pad
p-S-N曲线都在对称循环应力(即循环应力比R=-1)的试验下得到的,但在现实中,完全对称的循环载荷或应力是没有的,当试验循环应力比R改变时,平均应力Sm也跟着发生变化,所得到的S-N曲线也发生改变。对于Goodman平均应力修正,应力幅和平均应力用于计算平均应力为零时的等效应力幅S-1。
S-1=σbSa/(σb-|Sm|)
(4)
式中:S-1为等效零均值应力;Sa为应力幅值;Sm为应力均值,σb为拉伸强度极限,σb=490 MPa。
4.3 疲劳载荷计数-雨流计数法
雨流计数法[15]为一种用于载荷时间历程计数的方法,可反映材料的记忆特性,与材料的应力-应变行为具有一致性,力学概念明确。
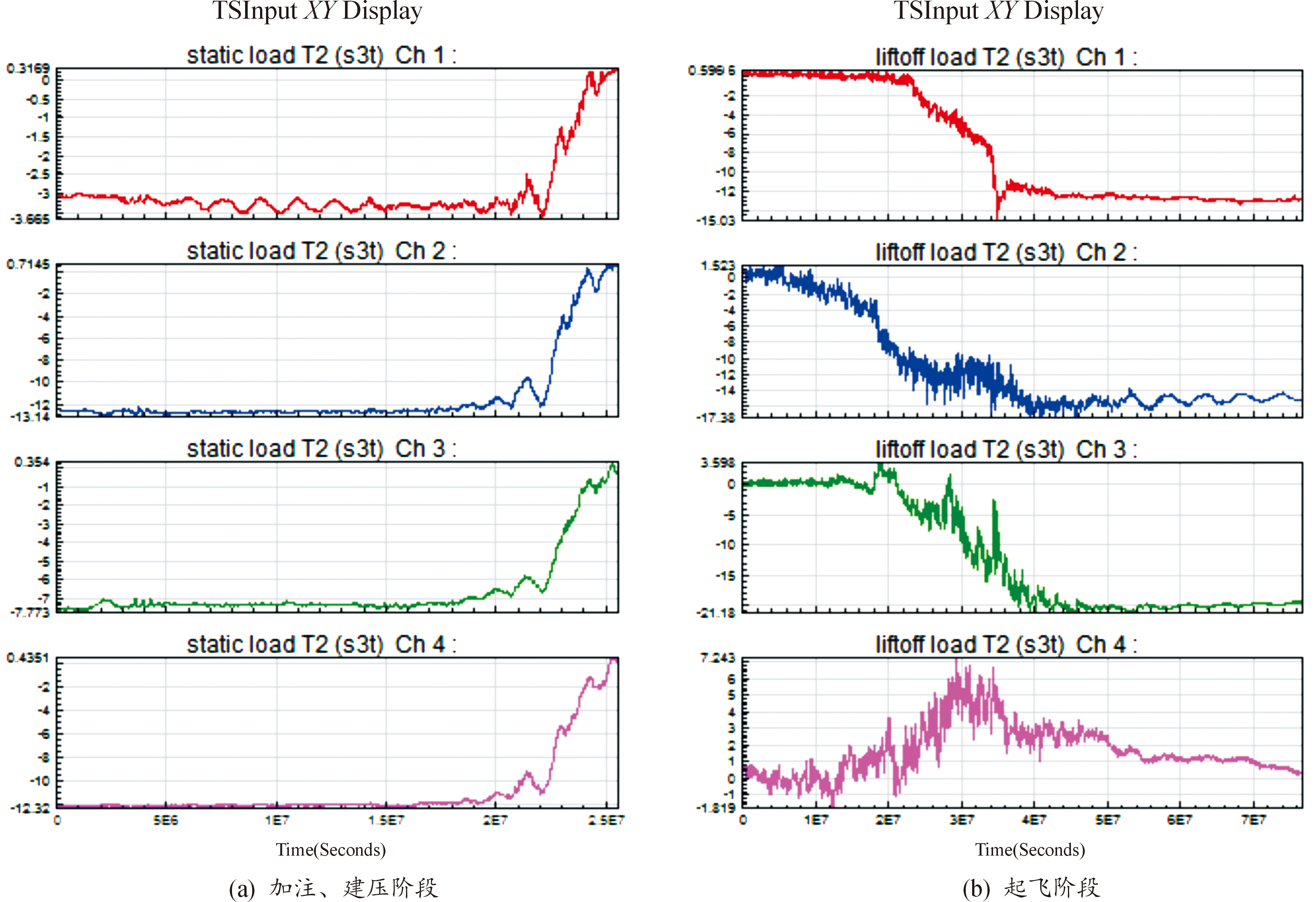
图11 平台测点载荷谱
Fig.11 Load spectrum of measurement locations on launch pad

图12 平台测点载荷计数结果曲线
Fig.12 Load counting of measurement locations on launch pad
对CZ-X运载火箭Y2飞行任务中各测点的载荷谱进行雨流计数分析,结果如图11~图12、表3所示。
表3 Y2任务中各测点应力谱统计(截取)
Table 3 Stress spectrum statistics of measurement locations in Y2 mission

序号载荷工况测点编号应力幅值/MPa应力均值/MPa等效零均值应力幅值/MPa循环次数1234加 注 后 承 载ε′10.031-3.198 00.031 2 334ε20.109-12.597 30.111 8734ε30.064-7.320 00.064 9830ε″30.100-12.018 50.102 56125678起 飞 阶 段ε′10.123-12.9560.126 31 246ε20.149-14.5780.153 5495ε30.195 5-19.8230.203 7894ε″30.7151.0800.716 5346
根据雨流计数统计分析:
1) 平台在加注建压、起飞阶段,循环次数较多的应力幅值均比较小,与CZ-3B动响应分析结果规律相接近[1];
2) 加注建压阶段的高周次应力均值较小,而起飞阶段的的高周次应力均值较大,但均为超过疲劳应力极限。
4.4 测点疲劳寿命计算
根据雨流计数分析,对所有测点的零均值应力幅值进行等效计算,获取不同p-S-N曲线计算出对应应力幅值下的破坏次数及损伤度。以CZ-X运载火箭Y2飞行任务中测点ε1'举例。
由于对结构可靠度要求的增加,结构的疲劳寿命曲线趋于严格,如图13所示。99.87%可靠度下的损伤度比50%的损伤度增加约59.26%。根据钢结构桥梁的使用经验,通常对97.73%可靠度下的结构疲劳进行评估。
根据线性疲劳损伤理论,测点处的累积损伤度为:
(5)
预计疲劳寿命为:
(6)
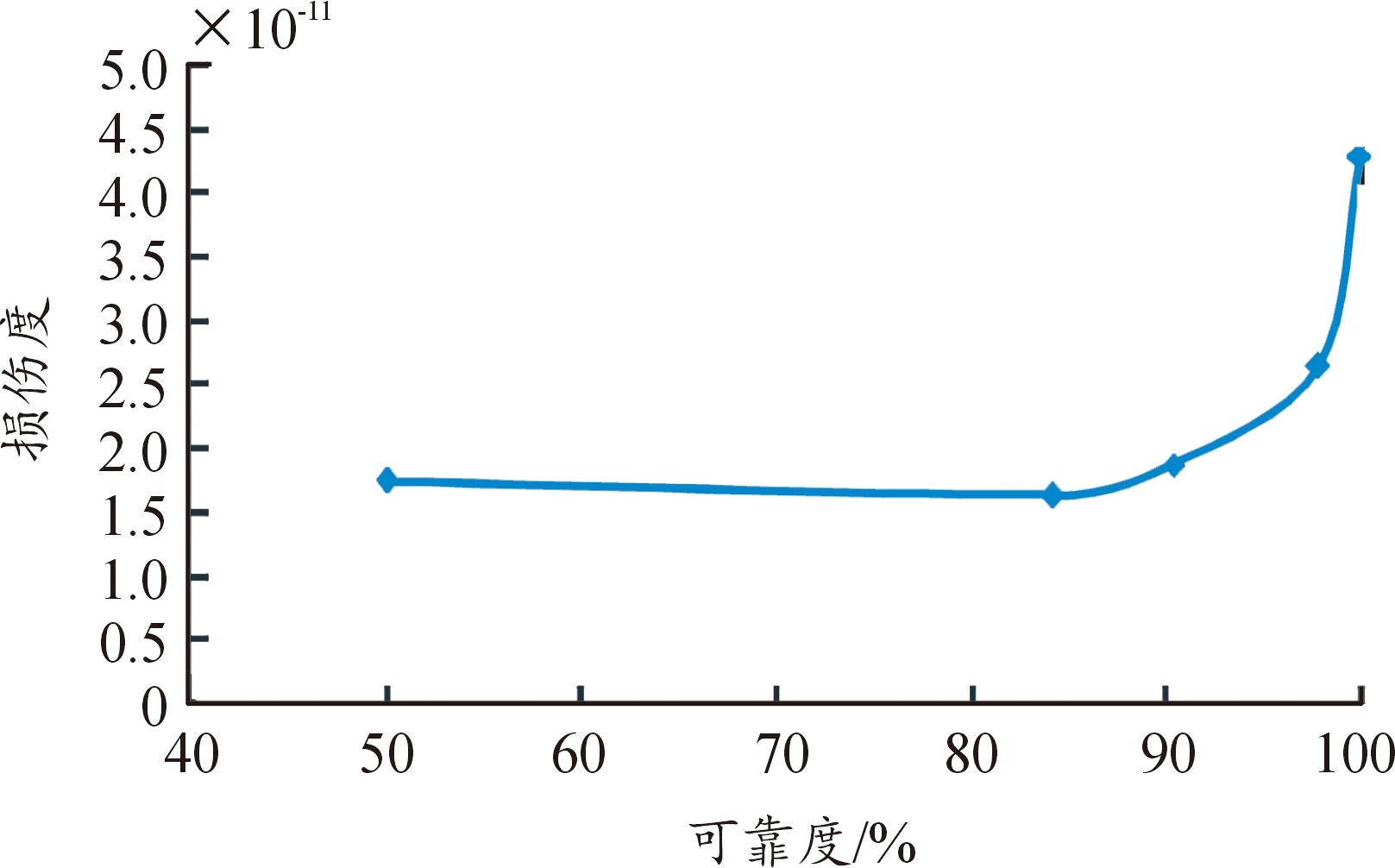
图13 测点损伤度随可靠度指标的变化曲线
Fig.13 Trend of measurement locations’ damage degree with reliability
如图14、图15所示,由以上2种工况实测数据与计算数据对比,加注及点火建压阶段,箭体支承臂承载下结构计算应力大于实测应力,约1.72~3.9倍;起飞阶段燃气流作用下,计算应力小于实测应力,约1.5倍,可推断起飞20 m并非燃气流对台体作用的最大压力高度。然而由于起飞燃气流作用载荷计算数据暂时无法利用于瞬态有限元计算,本研究中暂取20 m高度的应力比例进行估算。
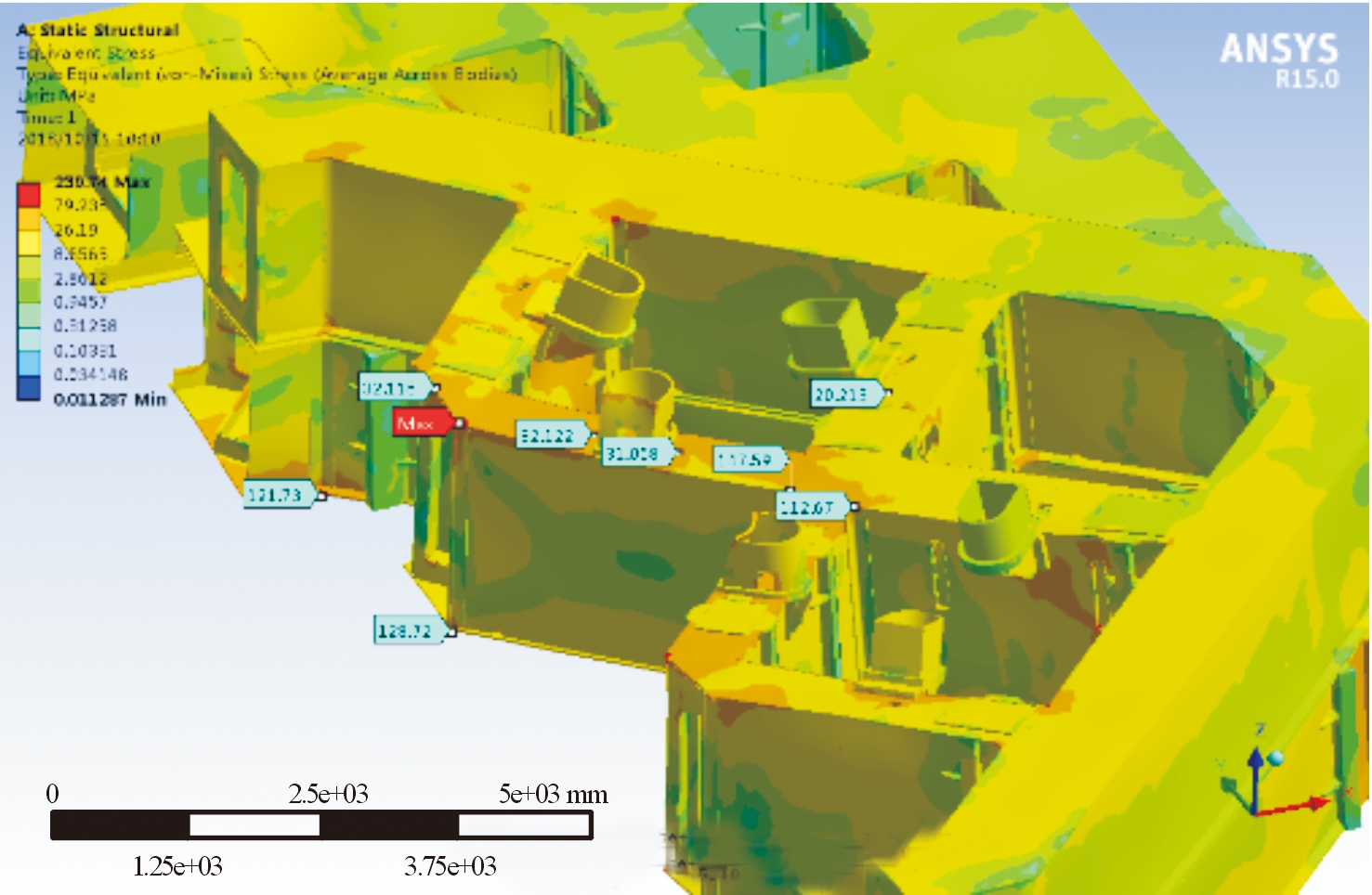
图14 加注、点火建压阶段测点位置应力值及 危险点示意图
Fig.14 The stress value of corresponding measurement locations,and dangerous locations when injecting and igniting pressure
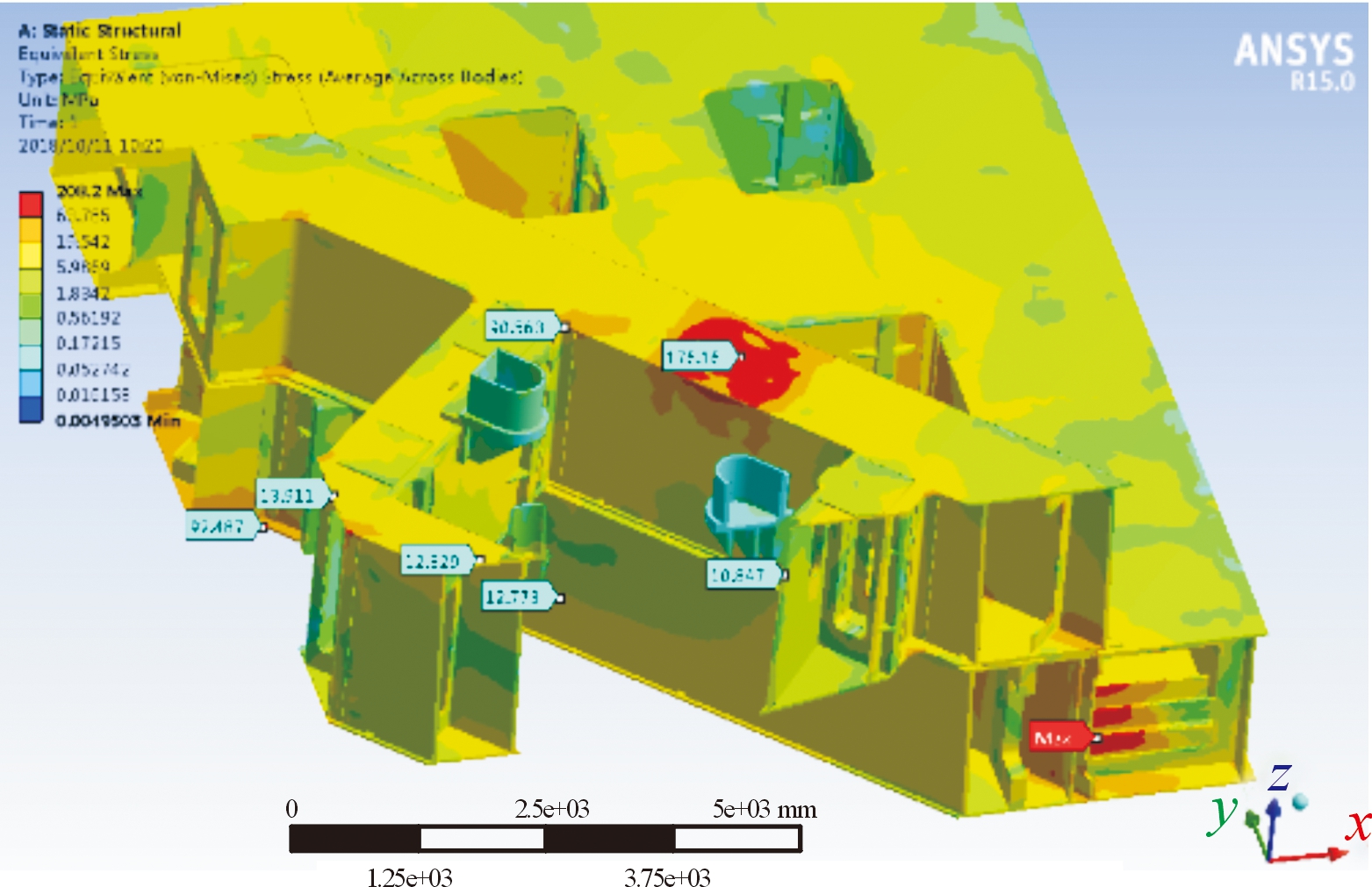
图15 起飞20 m时测点位置应力值及危险点示意图
Fig.15 The stress value of corresponding measurement locations,and dangerous locations when taking off 20 m
平台在加注建压阶段,最大应力239 MPa,位于十字梁交叉处,为应力尖点,其他位置较大应力值为147.59 MPa、128.72 MPa,均位于结构过渡拐角(圆角)处。起飞燃气流作用阶段,平台上台体边梁受燃气流正压作用,出现局部较大应力176.16 MPa,而台体最大应力出现于下台体内筋板,应力值为208.2 MPa。因此,从危险点的累积疲劳损伤数据对比分析,发射平台在起飞阶段燃气流作用下的危险点位置疲劳损伤度较高,预计疲劳寿命低于其他危险点。
假设各危险点应力均值与测点处一致,应力幅值根据测试、计算结果推演:
S-1危险=S-1测σ危险/σ测试
(7)
其中:σ为计算应力值,S-1为应力幅值。可得到危险点应力幅值与对应应力循环次数关系如图16所示。不同可靠度下的累计疲劳损伤度及预测寿命见表4。
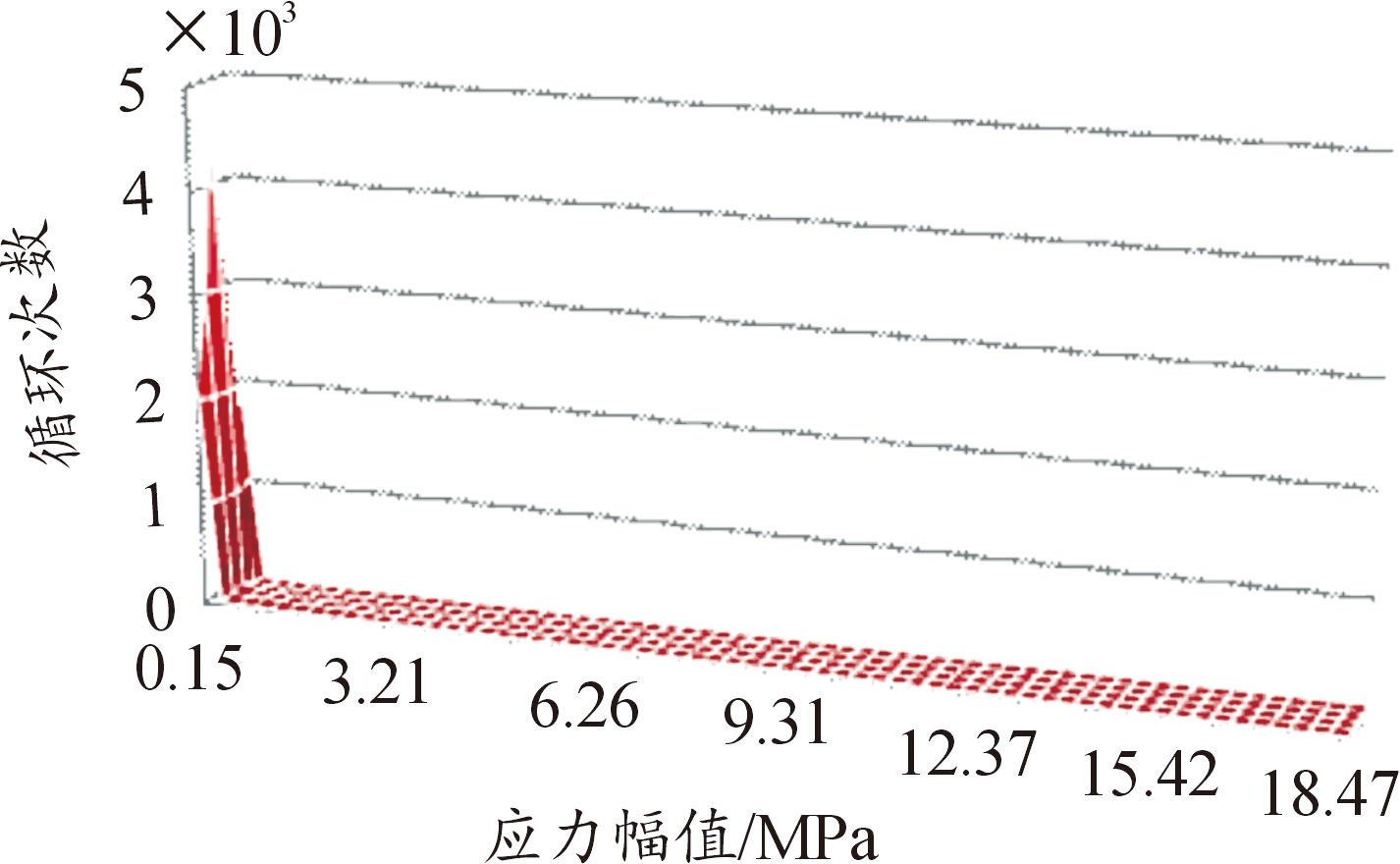
图16 危险点应力幅值与对应应力循环次数关系
Fig.16 Relationship between dangerous location’s stress amplitude and corresponding stress cycle times
表4 不同可靠度下的累计疲劳损伤度及预测寿命
Table 4 Cumulative fatigue damage degree and life prediction under different reliability
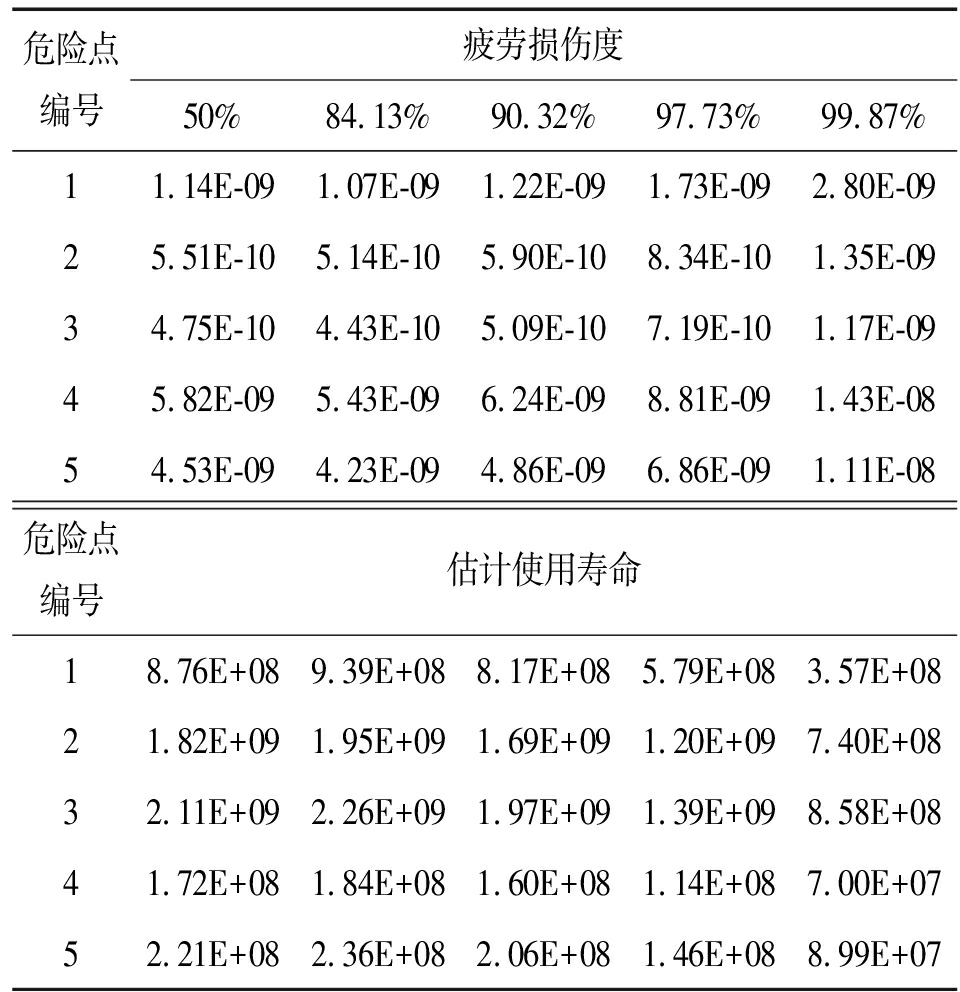
危险点编号疲劳损伤度50%84.13%90.32%97.73%99.87%11.14E-091.07E-091.22E-091.73E-092.80E-0925.51E-105.14E-105.90E-108.34E-101.35E-0934.75E-104.43E-105.09E-107.19E-101.17E-0945.82E-095.43E-096.24E-098.81E-091.43E-0854.53E-094.23E-094.86E-096.86E-091.11E-08危险点编号估计使用寿命18.76E+089.39E+088.17E+085.79E+083.57E+0821.82E+091.95E+091.69E+091.20E+097.40E+0832.11E+092.26E+091.97E+091.39E+098.58E+0841.72E+081.84E+081.60E+081.14E+087.00E+0752.21E+082.36E+082.06E+081.46E+088.99E+07
5 结论
1) 根据所测试验及仿真结果,推测危险点的累积疲劳损伤程度,给出了不同可靠度下的疲劳损伤度及估计使用寿命,发射平台的估测疲劳寿命按照危险点中最低使用次数进行估测,99.87%结构可靠度下疲劳寿命约7×107次,疲劳寿命次数与发射次数对应。
2) 从危险点的累积疲劳损伤数据对比分析,发射平台在起飞阶段燃气流作用下的危险点位置疲劳损伤度较高,预计疲劳寿命低于其他危险点。
3) 从整体数据分析,发射平台主结构较高的应力循环数集中于较低的应力循环幅值下,因此不论从加注建压工况、发射燃气流作用工况下,疲劳损伤度均较低,根据现有的发射平台使用寿命设计,在使用寿命期限内,出现主结构疲劳破坏的可能性较低。
[1] 潘玉竹,陈世业,赵劲彪,等.运载火箭发射平台钢结构强度分析方法研究[J].现代机械,2019(03):10-12.
Pan Y Z,Chen S Y,Zhao J B,et al.The research on the analytical method of steel-frame structure of launch vehicle launch pad[J].Modern Machinery,2019(03):10-12.
[2] 饶毅.基于层次分析法的火箭发射台可靠性模糊综合评价[D].武汉:武汉理工大学,2018.
Rao Y.Fuzzy comprehensive evaluation of the launch pad’s reliability based on AHP[D].Wuhan:Wuhan University of Technology,2018.
[3] 平仕良,冯超,徐铮,等.运载火箭发射台主体结构可靠性评估方法研究[J].导弹与航天运载技术,2019,5(04):93-97.
Ping S L,Feng C,Xu Z,et al.Research on reliability assessment method of launch vehicle launch pad[J].Missiles and Space Vehicle,2019,5(04):93-97.
[4] Johnson D N,Johnson A A.The low cycle impact fatigue properties of pearlitic plain carbon steel[J].Fatigue & Fracture of Engineering Materials & Structures,1985,8(03):287-294.
[5] Chandran KSR.A physical model and constitutive equations for complete characterization of S-N fatigue behavior of metals[J].Acta Mater,2016,121:85-103.
[6] 杨高伟,王惠源,黄少保,等.闭锁块偏转式机心强度和疲劳寿命分析[J].兵器装备工程学报,2020,41(11):112-116,181.
Yang G W,Wang H Y,Huang S B,et al.Analysis of strength and fatigue life of breech with tilting locking block[J].Journal of Ordnance Equipment Engineering,2020,41(11):112-116,181.
[7] 张遥辉.钢铁材料冲击疲劳行为综述[J].中国设备工程,2020,(06):211-216.
Zhang Y H.An overview of Impact fatigue behavior of steel materials[J].China Plant Engineering,2020(06):211-216.
[8] 张清华,崔闯,卜一之,等.港珠澳大桥正交异性钢桥面板疲劳特性研究[J].土木工程学报,2014,47(09):110-119.
Zhang Q H,Cui C,Bu Y Z,et al.Study on fatigue features of orthotropic decks in steel box girder of Hong Kong-Zhuhai-Macao Bridge[J].China Civil Engineering Journal,2014,47(09):110-119.
[9] 刘嘉,李静,杨友社,等.给定存活率下45钢的疲劳寿命估算[J].空军工程大学学报,2011,12(06):79-82.
Liu J,Li J,Yang Y S,et al.Fatigue life Prediction of 45 steel with given survivability[J].Journal of Air Force Engineering University:Natural Science Edition,2011,12(06):79-82.
[10]Bai X,Zhang P,Zhang Z J,et al.New method for determining p-S-N curves in terms of equivalent fatigue lives[J].Fatigue FractEng Mater Stuct,2019,1-14.
[11]方红荣,薛立鹏,李朝晖.基于有限元法的运载火箭管路随机振动疲劳寿命分析[J].导弹与航天运载技术,2017(04):107-110.
Fang H R,Xue L P,Li Z H.Research on simulation of launch vehicle pipeline structure’s random vibration fatigue lifetime based on finite element method[J].Missiles and Space Vehicle,2017(04):107-110.
[12]王海峰,王新刚,胡福豪.疲劳和刚度失效模式下矿井提升机主轴系统的可靠性研究[J].兵器装备工程学报,2019,40(11):199-206.
Wang H F,Wang X G,Hu F H,et al.Frequency reliability and sensitivity analysis of double servo turret system[J].Journal of Ordnance Equipment Engineering,2019,40(11):199-206.
[13]Sai H,De Q G,Chao P L,et al.Fatigue life of welded structures under Random load study on frequency domain method[C]//The 7th International Conference on Environmental Science and Civil Engineering,2021:1-6.
[14]Li X C,Hu X B,Li Y,et al.Research on fatigue life Prediction of heavy lifting equipment based on nCode Design-Life[J].Machinery,2017,44(08):1-6.
[15]Tatsuo E,Koichi M,Kiyohumi T,et al.Damage evaluation of metals for random or varying loading-three aspects of rain flow method[C]//IProceedings of 1974 symposium on mechanical behavior of materials,21-24 August 1974 Japan,The society of Materials Science,1974:371-380.