1 引言
转管武器自动机设计过程中,机心上主滚轮与凸轮曲线槽相配合,凸轮曲线的设计对于自动机的性能好坏起着决定性作用。为提高自动机性能,需要设计出转管武器自动机凸轮机构的轮廓曲线。对于转管武器的凸轮曲线,通过比较正弦曲线和梯形曲线的性能参数,确定了从单纯的正弦曲线变为在正弦曲线中插入一段二次曲线的形式,降低了加速度和跃度[1],在进一步的研究中,也出现了取消斜直线段,通过平分角度来设计凸轮曲线[2],徐健等[3-4]又通过增加其过渡段角度,减小前直线段对应角度从而对凸轮性能进行了改进,后来也通过应用3次样条进行改进,获得了改进结果;李世康等[5]通过应用5次曲线代替正弦曲线;李强等[6]使用线性加权法优化修正正弦曲线,其方法通过对优化变量施加权重系数来实现,在优化自动机的过程中,应用模拟退火算法和线性加权法对自动机结构进行优化;熊镐等[7]应用线性规划方法优化凸轮曲线,线性加权法优点在于优化方法简单,可通过应用优化求解工具箱直接求解,但易陷入局部最优解,在加速度下降的同时跃度上升,在降低机心与凸轮曲线的撞击力的同时振动加剧,不能满足工程中对于高速凸轮应具有优良综合性能的要求[8]。
葛荣雨等[9]提出应用遗传算法进行凸轮曲线的多目标优化,本文运用理想点法建立优化的理论模型,按照转管武器凸轮机构的工作要求,应用遗传算法求解,分配过渡段角度及其推程,从而在降低机心和凸轮曲线撞击力、提高机心和凸轮曲线寿命的同时,降低机心跃度和电机驱动功率,优化设计出凸轮轮廓。
2 曲线槽与机心运动
2.1 凸轮曲线与机心运动
由多根身管组成的转管武器具有多个机心,机心上主滚轮与凸轮曲线槽相配合,从而完成装弹、推弹、击发、抛壳的动作。
图1为转管武器机心的理论运动轨迹。θ1、θ3、θ5、θ7为曲线过渡段,θ4、θ8为前直线段和后直线段,θ2、θ6为斜直线段,h为机心推程,h1、h2为过渡段的轴向长度。

图1 转管武器机心的理论运动轨迹
Fig.1 Diagram of the theoretical movement trajectory of Gatling gun movement
2.2 修正正弦加速度曲线槽
图2为修正正弦加速度曲线。修正正弦加速度曲线由2段正弦曲线(θA、θC)、2次曲线(θB)拼接而成[10]。
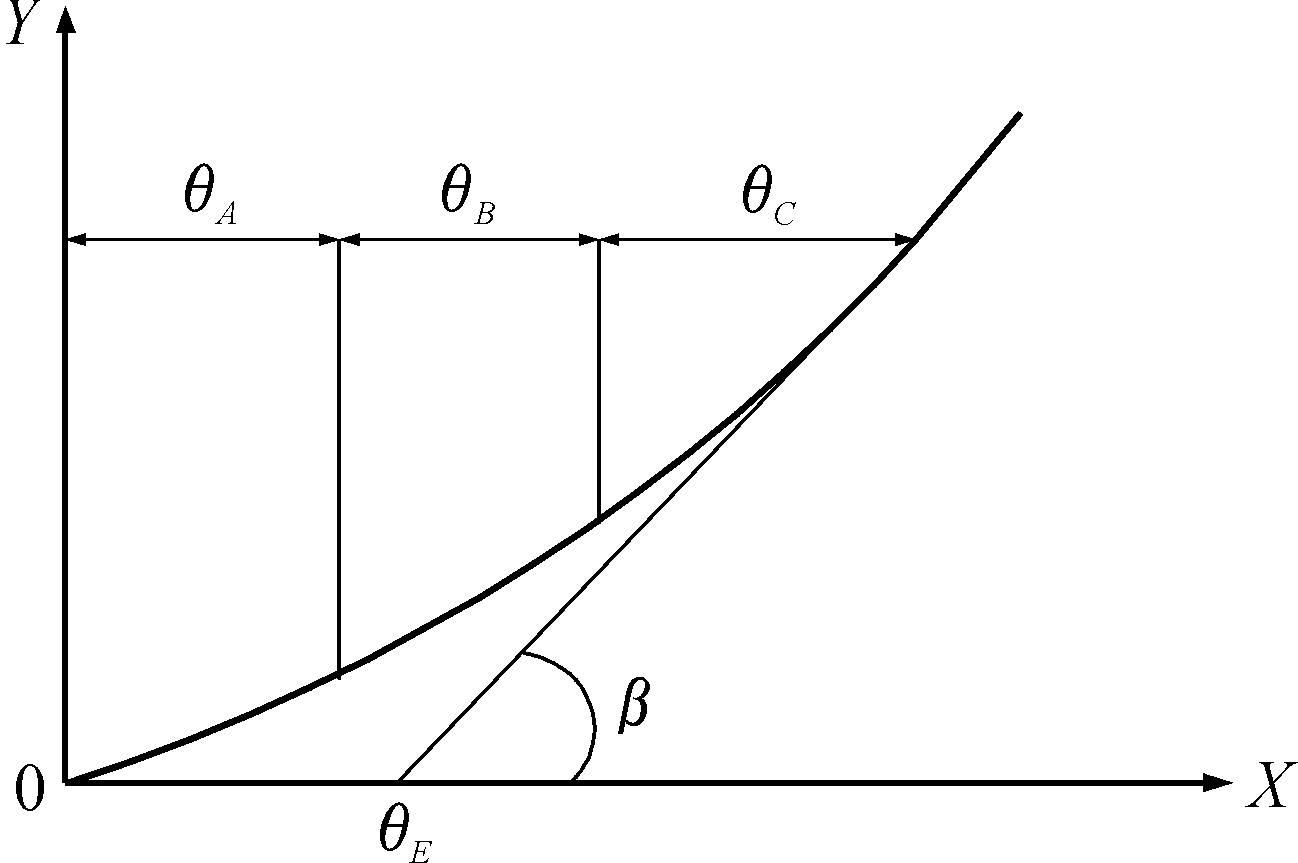
图2 修正正弦加速度曲线
Fig.2 Modified sine acceleration curve constitute
正弦曲线(θA)的位移、类速度、类加速度、类跃度为[10]:
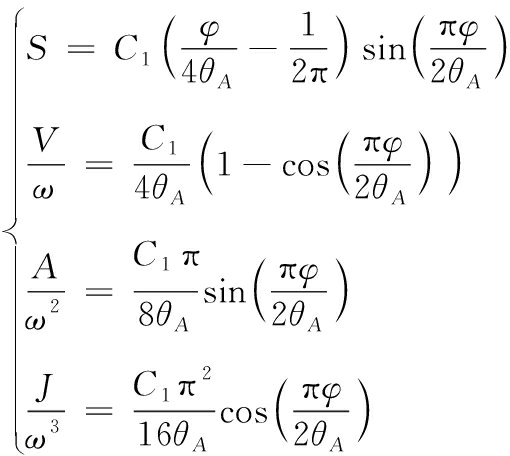
(1)
2次曲线(θB)段为:
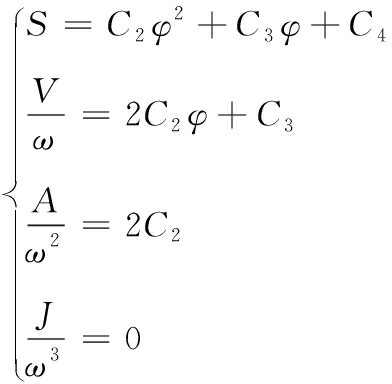
(2)
正弦曲线(θC)段为:

(3)
式(1)~(3)中,ω为凸轮的角速度。
2条正弦曲线和2次曲线所占角度的分配关系为:
(4)
整理后:
θB=2θET
(5)
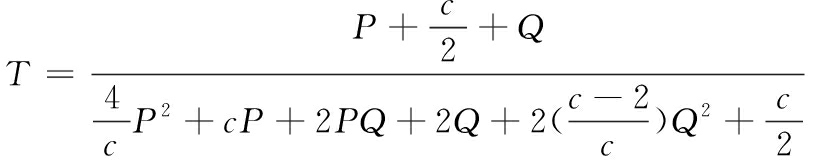
(6)
同时根据拼接条件,修正段的凸轮转角θ1、θ3与其对应的机心位移量h1、h2的关系式为:
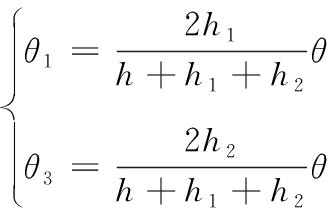
(7)
或

(8)
3 遗传算法优化计算设计
遗传算法抽象于生物体的进化过程,通过全面的模拟自然选择和遗传机制,形成的一种具有“生成+检验”特征的搜索算法。遗传算法以编码空间代替问题的参数空间,以适应度函数为评价标准,以编码群体为进化基础,以对群体中个体位串的遗传操作实现选择和遗传机制,建立起一个迭代过程。在这一过程中,通过随机重组编码位串中重要的基因,使新一代的位串集合优于老一代的位串集合,群体的个体不断进化,逐渐接近最优解,最终达到求解问题的目的。在遗传算法(GA)的应用过程中,往往结合问题特征和领域知识对标准遗传算法(SGA)进行各种改变,形成各具特色的GA,使得GA具有求解不同类型问题的能力,以及强大的全局搜索能力[11]。遗传算法流程如图3所示。
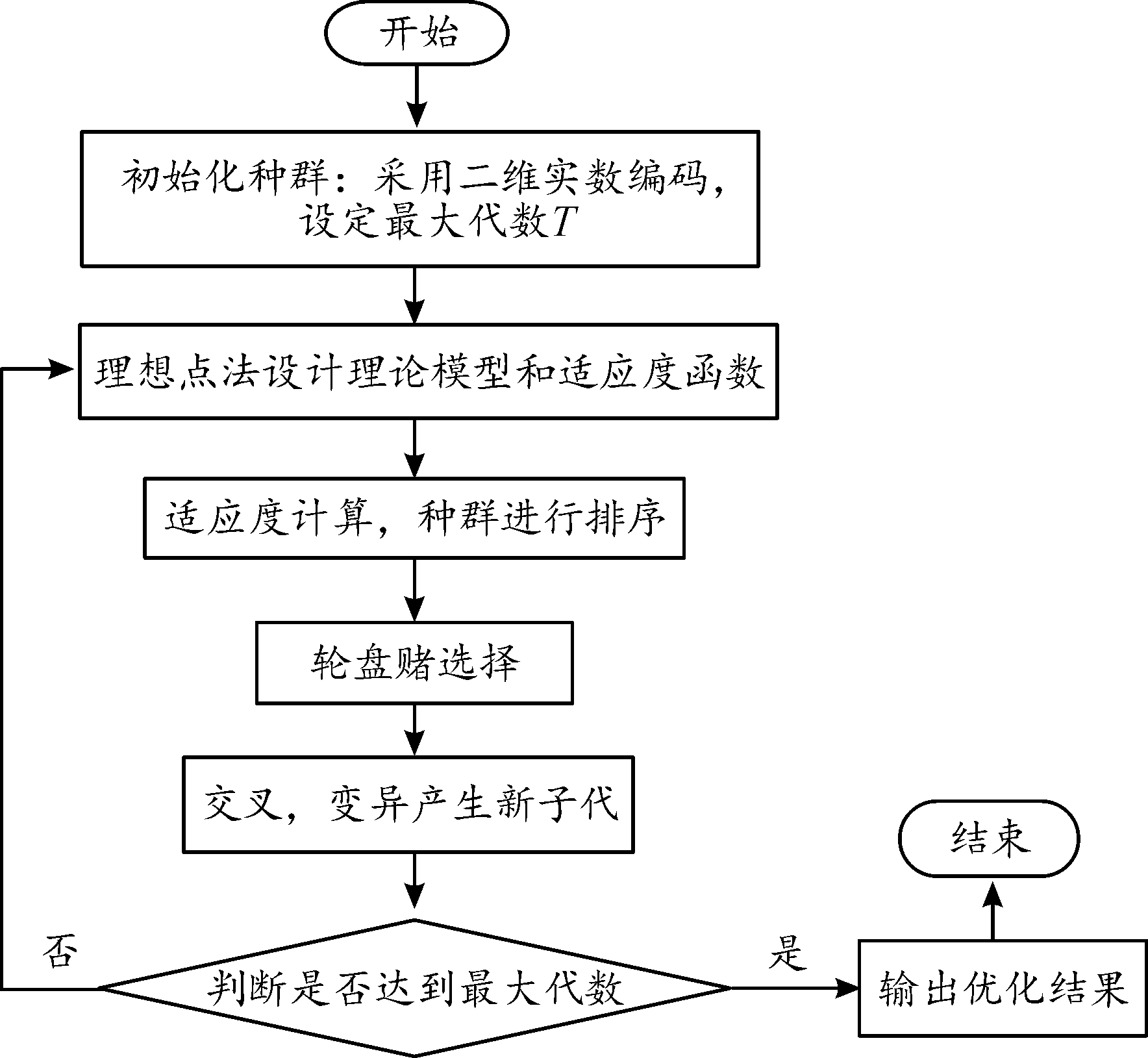
图3 遗传算法流程框图
Fig.3 Flowing diagram of genetic algorithm
3.1 优化目标
由转管武器的动力性能优化目标如下:
1) 机心最大速度Vm:机心最大速度和压力角成正比,影响传动效率[12]。
2) 机心最大加速度Am:根据自动机动力学,加速度和机心与曲线槽的碰撞力大小成正比,直接影响机心使用寿命。
3) 机心最大跃度Jm:在转管武器高射速情况下,机心的跃度影响机心的振动和冲击。
凸轮曲线槽和机心的横越冲击速度为[13]:
(9)
式(9)中, μ为间隙值。
4) 最大无量纲惯性矩Qm:在转管武器达到稳定射频时,电机的驱动功率和最大无量纲惯性矩相关,根据驱动功率选取适合的电机[14]。
Qm=AV
(10)
3.2 种群编码与初始化
由于凸轮曲线性能优化属于二维优化变量,编码方式采用实数编码,整体凸轮曲线采用对称结构,因此一种可行的编码方式[(θ1,h1),(θ2,h2),…,(θn,hn)],获得一个规模为n的初始种群。
3.3 选择方法
需要对优秀的个体进行筛选,采用轮盘赌选择方法,假设在种群中某个个体的适应度的fi,则被选中的概率Pi为:
(11)
3.4 适应度计算方法
机心的最大速度Vm、最大加速度Am、最大跃度Jm之间并不是独立存在,相互之间存在联系,所以为了获得更好的优化效果,需要基于多目标优化的思想来解决问题。有学者使用线性加权方法进行优化,但线性加权方法的权重系数并没给出完整且合理的分配,结果也往往优化有限。这里使用理想点法,将多目标优化转化为单目标优化函数,令其成为遗传算法中的适应度函数,获得优化结果并和使用线性加权法的结果进行比较来判断方法的优劣。
根据理想点法,需要先获得每一个优化目标的最优理想值![]() 和最优理想点
和最优理想点![]() 一般各个目标难于都能达到最小值,但能让各个目标都逼近最优值,从而得出最优解[15]。
一般各个目标难于都能达到最小值,但能让各个目标都逼近最优值,从而得出最优解[15]。
通过这种方法把多目标优化变为单目标优化,把求解最小函数值函数变为求解各值逼近最优解程度的函数,解决了最小函数值问题中Vm、Am、Jm之间量纲不同所带来的问题。
(12)
修正段的凸轮转角θ1、θ3与其对应的机心位移量h1、h2的关系式如下。
修正正弦曲线为:

(13)
各变量在该条件下的最小值为:
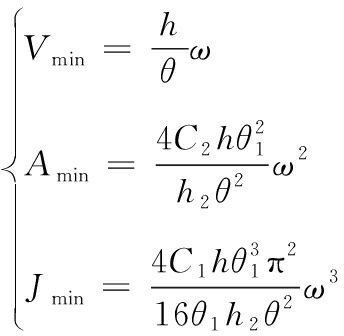
(14)
构造目标函数为:
(15)
故该转管武器的凸轮优化模型为:
(16)
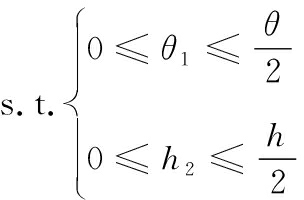
(17)
3.5 交叉和变异操作
交叉和变异操作能扩展新的搜索空间,帮助跳出局部最优解,增加种群多样性[16]。
交叉方式由父代个体A、B提供第i个基因进行交叉计算产生新个体xi,即:
xi=rai+(1-r)bi
(18)
式(18)中,xi为区间(0,1)的随机数。
变异操作为加上一随机数c,即:
xi=xi+c
(19)
4 优化结果对比
现阶段,针对转管武器凸轮曲线优化主要方法为线性加权法,通过人为施加权重系数,建立理论模型,应用最优解优化工具箱求解,本文与该方法的优化结果[7]进行对比。
利用遗传算法优化6管6 000发/min的转管武器凸轮曲线,选出文献[7]中每一种权重分配中的修正正弦加速度曲线,和本研究优化的3条曲线共计5条曲线进行比较。
文献[7]中的曲线分别为Case 1[7]、Case 2[7];本研究优化的3条曲线分别为Case 3、Case 4、Case 5。
本文采用理想点法进行适应度函数的编写,没有针对单一或几个变量,而是求取全局最优解,因为过渡段角度和推程越相似,其性能特性也更相似,根据各曲线的过渡段所占角度和推程数值大小相似度匹配对比对象,故选用Case 3和Case 1[7]、Case 4、Case 5和Case 2[7]进行对比。各曲线角度分配关系如表1所示。
由于转管武器的供弹、击发等功能的要求,各工作区间角度已进行分配,从图4中凸轮曲线形状可以看出,优化前后的凸轮曲线整体结构没有发生变化,凸轮曲线在优化后对转管武器其他结构没有影响。
表1 凸轮曲线角度分配
Table 1 Angle distribution of cam curve
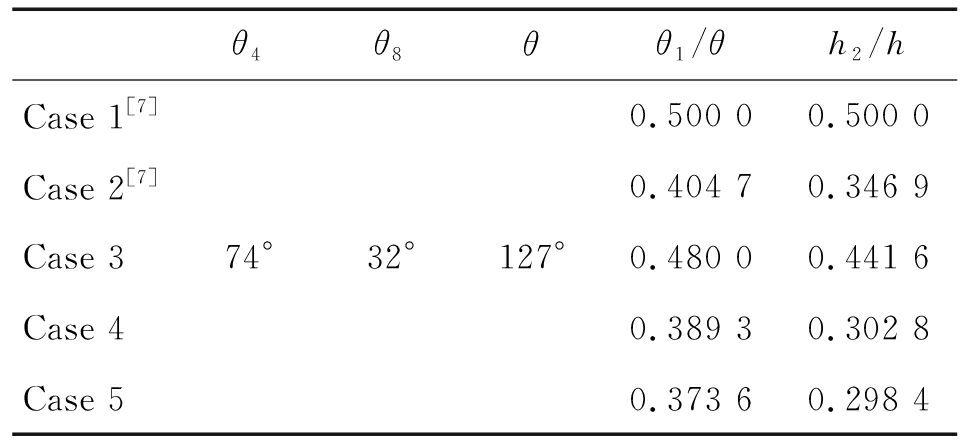
θ4θ8θθ1/θh2/hCase 1[7]Case 2[7]Case 3Case 4Case 574°32°127°0.500 00.500 00.404 70.346 90.480 00.441 60.389 30.302 80.373 60.298 4
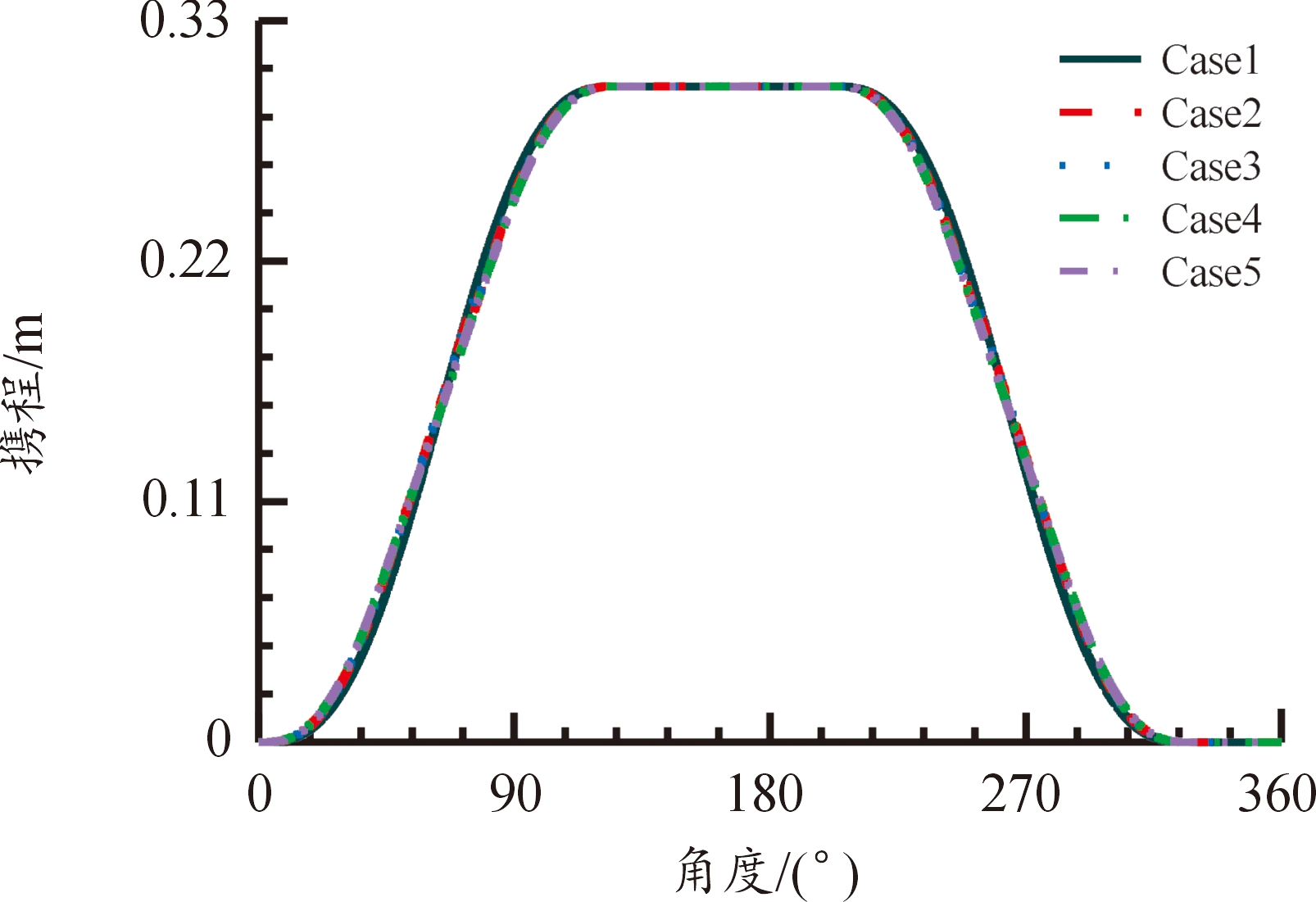
图4 转管武器凸轮曲线
Fig.4 Cam curve of the Gatling gun
优化后的Case 3相比于Case 1[7]最大速度下降7.80%,速度的下降提升了传动效率。Case 4、Case 5相比于Case 2[7]最大速度分别下降0.10%、0.60%,速度的下降降低了最大压力角,在转管武器高射速、高转速的情况下,提升了自动机的传动效率。各曲线速度变化情况如图5所示。
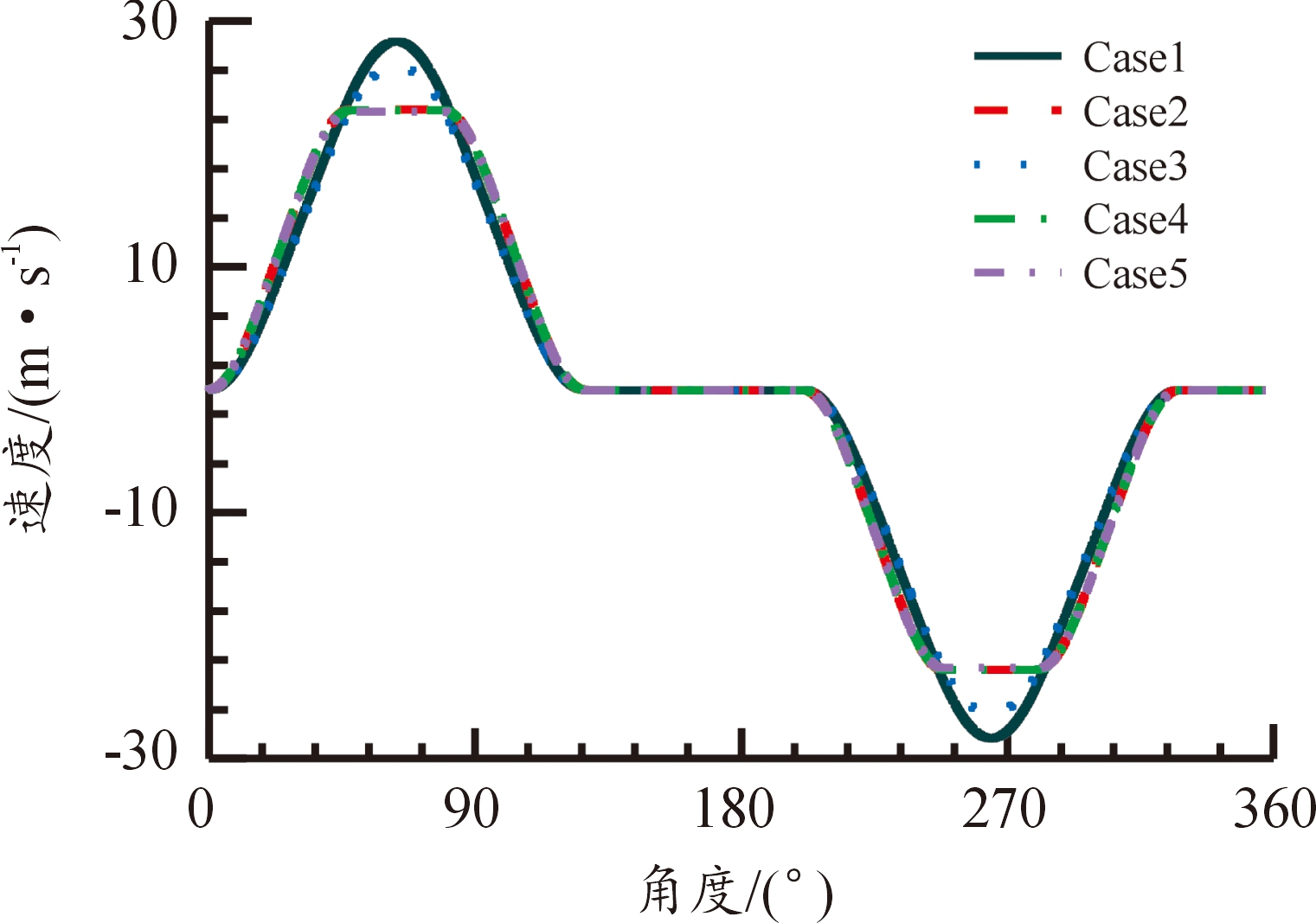
图5 速度曲线
Fig.5 Velocity of different curves
优化后的Case 3相比于Case 1[7]最大加速度下降4.03%,Case 4、Case 5相比于Case 2[7]最大加速度分别下降1.83%、1.37%。最大加速度下降,机心主滚轮和凸轮曲线槽之间由于存在间隙故而会发生碰撞,最大加速度下降,机心主滚轮与凸轮曲线槽之间的最大冲击力减小,降低机心主滚轮与凸轮曲线槽之间的磨损,延长机心和凸轮曲线槽的使用寿命。各曲线加速度变化情况如图6所示。
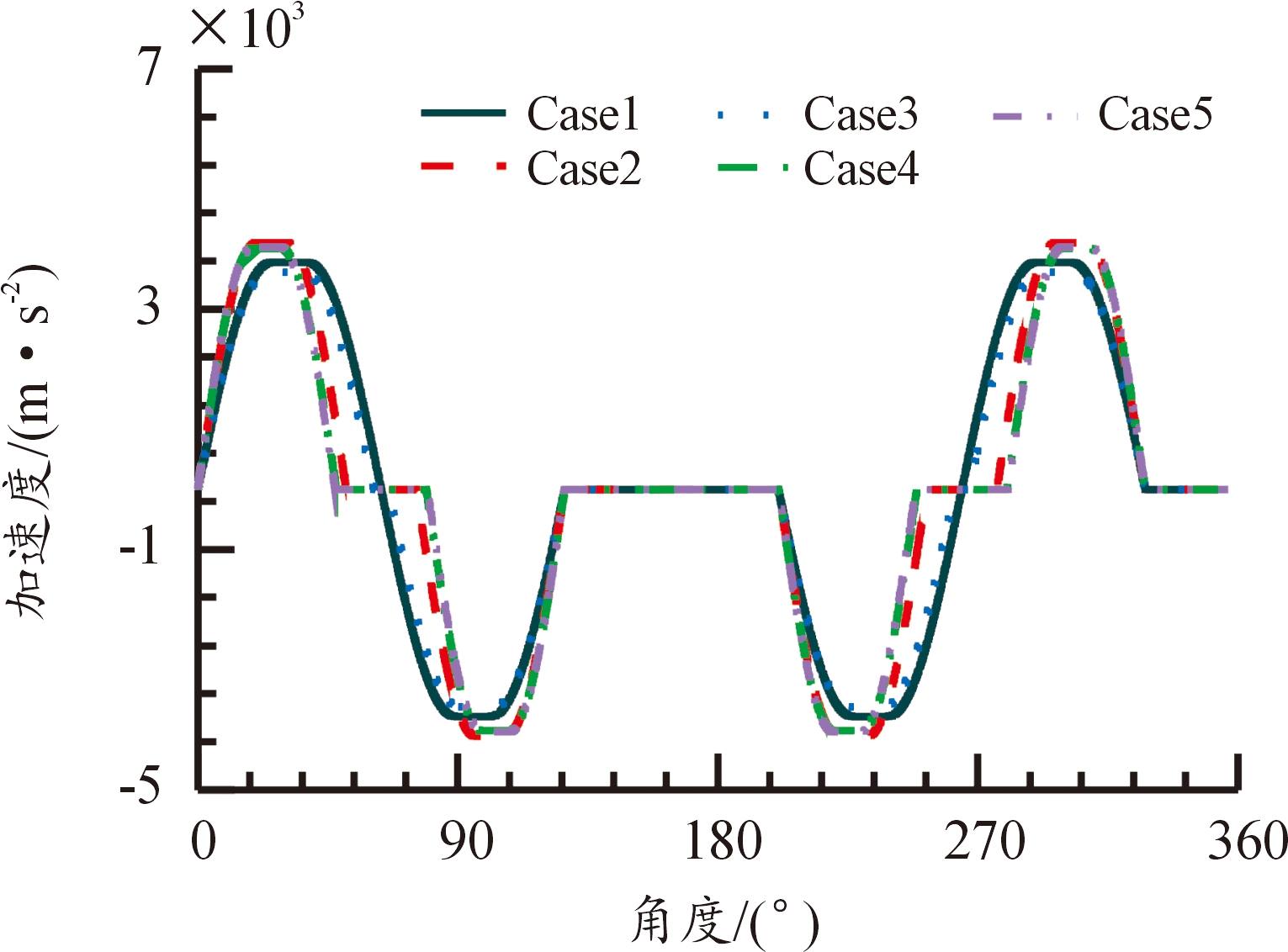
图6 加速度曲线
Fig.6 Acceleration curve
优化后的Case 3相比于Case 1[7]最大跃度下降0.50%,Case 4、Case 5相比于Case 2[7]最大跃度分别下降20.33%、19.18%。在转管武器超高射频的情况下,凸轮曲线槽和机心的横越冲击速度减小,振动降低。各曲线跃度变化情况如图7所示。

图7 跃度曲线
Fig.7 Jerk curve for different
优化后的Case 3相比于Case 1[7]最大无量纲惯性矩下降11.78%,Case 4、Case 5相比于Case 2[7]最大无量纲惯性矩分别下降1.90%、1.97%。最大无量纲惯性矩直接反应对于外能源驱动电机功率的要求,降低电机的驱动功率,扩大电机选择范围。各曲线计算结果如表2所示。
通过以上各曲线速度、加速度计算得出对应机心滚轮正应力变化情况如图8所示。
在各峰值下降的同时,优化后的Case 3相比于Case 1[7],最大正压力由34 433 N下降为31 845 N,下降7.51%,Case 4、Case 5相比于Case 2[7],最大正压力由36 339 N分别下降为30 646 N和30 634 N,分别下降15.66%、15.69%,降低机心滚轮正压力,减少机心主滚轮与凸轮曲线槽之间的磨损,延长机心和凸轮曲线槽的使用寿命。
表2 各曲线计算结果
Table 2 Calculation results of each curve
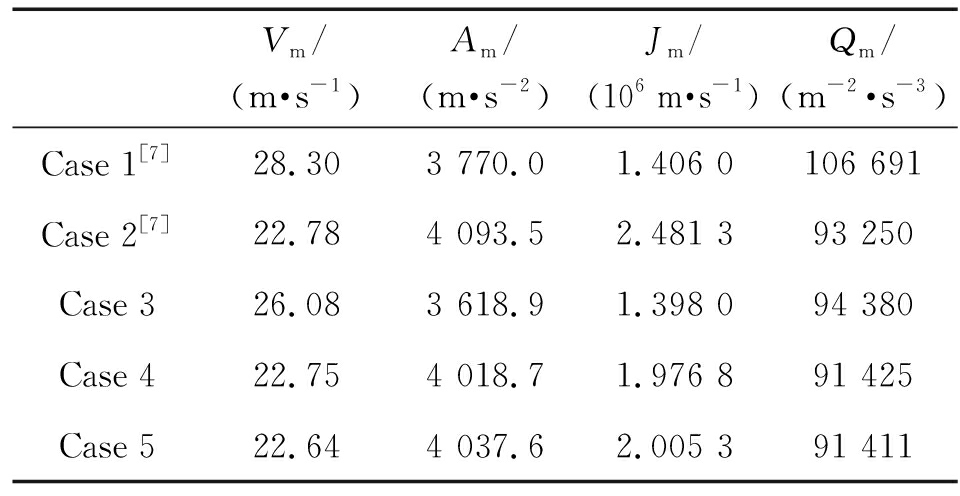
Vm/(m·s-1)Am/(m·s-2)Jm/(106 m·s-1)Qm/(m-2·s-3)Case 1[7]28.303 770.01.406 0106 691Case 2[7]22.784 093.52.481 393 250Case 326.083 618.91.398 094 380Case 422.754 018.71.976 891 425Case 522.644 037.62.005 391 411

图8 正应力曲线
Fig.8 Normal force curve
5 结论
将遗传算法应用于优化转管武器凸轮曲线,通过遗传算法对优化模型进行求解。针对修正正弦加速度转管武器凸轮曲线进行优化,并和现有线性加权法的优化结果进行比较,Case 3相比于Case 1在最大跃度下降的同时,最大加速度、速度、无量纲惯性矩,机心滚轮正应力下降明显;Case 4、Case 5相比于Case 2,在最大速度和加速度小幅下降的同时,最大跃度、机心滚轮正应力下降明显,降低机心滚轮与凸轮曲线槽之间的撞击和振动;相比于线性加权法人为施加权重系数,该方法则是通过种群适应度计算等操作不断接近全局最优解,得出的结果更加合理,取得了更加优秀的凸轮曲线。
[1] 刘绍奎,张清,薄玉成.转管机枪凸轮曲线设计[J].华北工学院学报,1999,20(03):262-265.
Liu S K,Zhang Q,Bo Y C.Design of the cam curve groove for rate gatling gun[J].Journal of North China institute of technology,1999,20(03):262-265.
[2] 徐健,薄玉成,常学芳.超高射速转管炮新型低功耗凸轮曲线设计[J].弹道学报,2009,21(02):70-73.
Xu J,Bo Y C,Chang X F.New type of power consumption cam curve designed for super-high fire ratio gatling gun[J].Journal of Ballistics,2009,21(02):70-73.
[3] 徐健,薄玉成,常学芳.超高射速转管跑凸轮曲线槽分析与改进[J].火炮发射与控制学报,2007(04):43-46.
Xu J,Bo Y C,Chang X F.Analysis and improvement for cam curve groove for super-high fire rate gatling gun[J].Journal of Gun Launch & Control,2007(04):43-46.
[4] 徐健,常学芳,薄玉成.三次样条在转管武器凸轮曲线中的应用[J].机械工程师,2007(07):83-84.
Xu J,Chang X F,Bo Y C.Application of cubic spline in gatling gun’s cam curve[J].Mechanical Engineer,2007(07):83-84.
[5] 李世康,李强,安俊斌,等.高射速转管炮凸轮曲线槽的优化与设计[J].火炮发射与控制学报,2017,38(02):40-43.
Li S K,Li Q,An J B,et al.Optimization and design of the cam curve groove for high fire rate gatling gun[J].Journal of Gun Launch & Control,2017,38(02):40-43.
[6] 李强,程驰青,李博.基于UG与MATLAB的圆柱凸轮曲线槽设计[J].机械设计,2016,33(09):66-69.
Li Q,Cheng C Q,Li B.Design of cylindrical cam curve groove based on UG and MATLAB[J].Journal of Machine Design,2016,33(09):66-69.
[7] 熊镐,王惠源.基于线性规划的转管武器曲线槽优化设计[J].兵器装备工程学报,2019,40(02):80-85.
Xiong H,Wang H Y.Optimization and design of cam curve groove for gatling gun based on linear programming[J].Journal of Ordnance Equipment Engineering,2019,40(02):80-85.
[8] 王惠源,薄玉成,杨志良,等.转管武器机心加速度测试实验[J].火炮发射与控制学报,2008(03):75-77.
Wang H Y,Bo Y C,Yang Z L,et al.Gatling gun bolt acceleration test experiment[J].Journal of Gun Launch & Control,2008(03):75-77.
[9] 葛荣雨,李世伟,刘莉.柔性凸轮曲线NURBS表达与多目标遗传算法优化[J].农业机械学报,2008,39(02):155-158.
Ge R Y,Li S W,Liu L.Flexible cam curve expressed by NURBS and multi-objective optimization based on genetic algorithm[J].Transaction of the Chinese Society for Agricultural Machinery,2008,39(02):155-158.
[10] 戴成勋.自动武器设计新编[M].北京:国防工业出版社,1990.
Dai C X.New edition of automatic weapon design[M].National Defense Industry Press,1990.
[11] 李敏强.遗传算法的基本理论与应用[M].北京:科学出版社,2002.
Li M Q.Principle and application of genetic algorithms[M].Beijing:Science Press,2002.
[12] 王海旭,张鹏军,杨一帆,等.转管武器机心主滚轮滚动特性动力学分析[J].兵器装备工程学报,2020,41(07):14-17.
Wang H X,Zhang P J,Yang Y F,et al.Dynamic analysis of rolling characteristics of roller system for gatling gun[J].Journal of Ordnance Equipment Engineering,2020,41(07):14-17.
[13] 何雪明,何楷,武美萍,等.基于冲击模型的含间隙高速凸轮机构动力学分析[J].食品与机械,2017,33(09):84-89.
He X M,He K,Wu M P,et al.Dynamic analysis of high speed cam mechanism with clearance based on impact model[J].Food & Machinery,2017,33(09):84-89.
[14] 张志明.凸轮升降台的设计制造及结构分析[D].烟台:烟台大学,2016.
Zhang Z M.Design manufacture and structure analysis of cam elevator[D].Yantai:Yan Tai University,2016.
[15] 严升明.机械优化设计[M].徐州:中国矿业大学出版社,2003.
Yan S M.Mechanical optimization design[M].Xuzhou:China University of Mining and Technology Press,2003.
[16] 王红梅.算法设计与分析[M].北京:清华大学出版社,2006.
Wang H M.Algorithm design and analysis[M].Beijing:Tsinghua University Press,2006.