1 引言
对于采用脉冲推力弹道修正方案弹丸来说，如采用脉冲矢量发动机、射流类修正机构[1-2]等，在弹道修正阶段，弹体将受到多次离散的具有一定大小且持续一段时间的脉冲力，对弹丸的运动产生一定的影响，改变其弹道轨迹[3-6]。脉冲推力修正有较强的横向修正能力和快速响应优势，但是由于作用力具有瞬时性，弹体的攻角和侧滑角会发生很严重的振荡，严重的时候可能导致弹体失稳。因此针对类似瞬时脉冲力强干扰对弹丸的飞行姿态和稳定性影响研究是弹道轨迹控制过程中不可缺少的重要内容[7-12]。
杨红伟等[13]在对弹丸运动方程进行线性化的基础上，针对低旋尾翼稳定弹在受强干扰扰动后的稳定性进行了建模分析，结果表明其动态稳定性不仅与冲量修正初始条件有关，还与弹丸本身参数相关，其中对允许攻角的幅值限制，可以对脉冲发动机的冲量设计提供重要理论依据。戴明祥等[14]采用“小扰动”和“系数冻结法”建立了脉冲发动机修正的弹道模型的传递函数，区别于数值计算的方法，对弹丸的动态稳定性进行分析，分析表明静稳定裕度越大，发动机产生的直接力对弹体姿态的扰动影响越小，这也是脉冲发动机直接力控制与舵机控制方式典型的不同之处。Cooper[15]通过对基于弹丸线性理论的方程求解，直观地揭示了弹丸在横向脉冲力作用下对方向改变的影响程度，分析表明空气动力瞬变量减小的速率与脉冲持续的时间密切相关，这也是由于脉冲力作用后续的影响，这一影响会随着脉冲作用时间的延长而显著。
综上可知，对于瞬时脉冲力强干扰对弹丸的飞行姿态和稳定性影响研究基本从理论进行定性分析，而在设计参数的定量分析上不足以解决脉冲力修正器参数难以与弹丸适配的问题。本研究中则针对某口径对空弹道修正的低旋尾翼弹，根据其采用的一种“由火药气体燃烧产生的高压推出具有一定质量的质量块，对弹体产生反作用力”的修正器的离散短时脉冲推力作用特性，从理论和仿真分析两方面着手，详细研究了弹丸参数和修正器设计参数对弹丸角运动和修正效果的影响，为设计修正器参数提供理论数值参考。
2 脉冲强干扰产生的角运动理论分析
研究对象为参照某口径制式底凹弹的基础上根据实际需求进行了结构改进后的对空低旋尾翼修正弹，整弹外形示意图如图1所示，除船尾部的结构有所变化，其他外形基本与制式弹一致，弹头部周向安装诺干个修正器。其修正力产生原理为：装有质量块和特制火药的力产生机构在点火头起爆后，由火药气体燃烧产生的高压推出具有一定质量的质量块，对弹体产生反作用力，形成弹道修正所需的修正力或修正力矩，来改变弹丸的姿态或位置，称之为动量修正机构。单个动量修正机构的部分结构原理如图2所示，与常用的脉冲矢量发动机产生的推力原理不同，但是也可以获得一个短时推力，对飞行弹体的稳定性形成一种短时脉冲强干扰。
1.头部组件；2.修正机构；3.弹体；4.尾部组件
图1 某口径对空低旋尾翼修正弹外形示意图
Fig.1 Configuration of a certain caliber fin-stabilized trajectory correction projectile
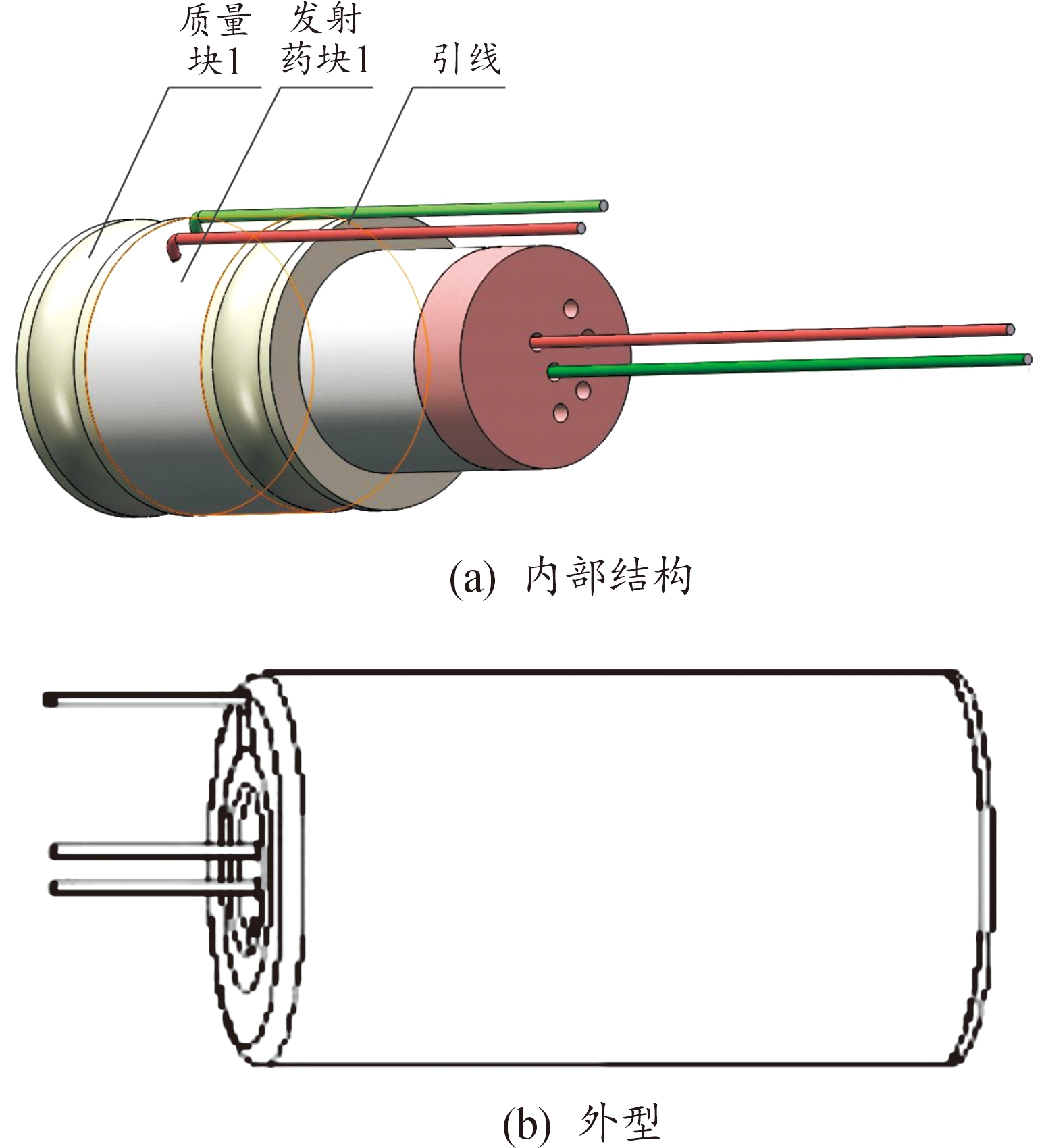
图2 动量修正机构示意图 Fig.2 Momentum correction mechanism
对于第i个动量修正机构，假设修正力的时间常数为τ，修正力大小为Fi，修正起始时刻tsi，修正相位角为αi。在做单个修正力特性理论分析时，做简化处理：每触发一次横向修正，则弹丸运动状态将发生突变，突变量大小可由式(1)计算，其中，Ix2、 Iy2、 Iz2表示作用力获得的冲量在速度坐标系3个坐标上的分量。
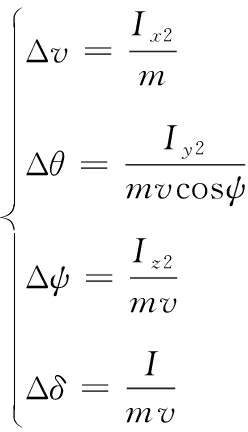
(1)
根据文献[16]中弹箭运动的一般方程组可推导具有轴向偏心的脉冲推力强干扰下的扰动弹道角运动简化方程：
(2)
其中：
气动升力偏心角的模值，γ10为起始方位角； βD=βD1+iβD2，ΔM0=δM0eiγ20，γ20为气动偏心起始方位角。其中Δ′为Δ对弹道弧长s的导数。即有
其他参数定义详情见文献[16]。
在仅考虑脉冲力产生的强干扰扰动对角运动的影响以及造成的落点偏差时，根据文献[16]中弹箭的角运动方程可知，攻角的齐次方程为：
Δ″+(H-iP)Δ′-(M+iPT)Δ=0
(3)
对于低旋尾翼稳定弹来说，静力矩系数kz<0[16]，选择起始条件为脉冲力作用的起始时刻弹丸的状态，分析从定义的起始时刻到单个脉冲推力作用完成后的一段时间内弹丸的角运动。
齐次方程的特征方程为：
l2+(H-iP)l-(M+iPT)=0
(4)
解式(4)可得：
l1,2=λ1,2+iω1,2=
(5)
得攻角的齐次方程通解为：
Δ=C1e(λ1+iω1)s+C2e(λ2+iω2)s
(6)
式中: C1、C2为待定系数，亦为复数，由起始条件确定。
已知起始时刻t=t0，s=s0，γ=γ0时，是强扰动作用的前一时刻，此时有：
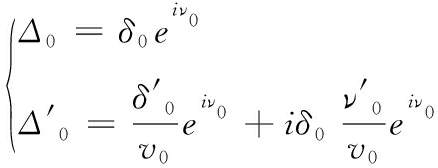
(7)
解得待定系数为：
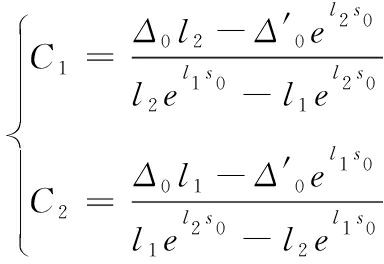
(8)
存在强扰动因素时，考虑强扰动时，低旋尾翼稳定弹的角运动方程写为：
Δ″+(H-iP)Δ′-(M+iPT)Δ=
(9)
其中： 记fM(αi)表示Mη+iMζ的幅角，是关于αi的函数； fF(αi,δ1,δ2)是Fy2+iFz2的幅角，是关于αi,δ1,δ2的函数。假设特解具有齐次方程通解的形式，但待定系数为弧长s的函数：
ΔF=C1(s)e(λ1+iω1)s+C2(s)e(λ2+iω2)s
(10)
则
(11)
令：
(12)
则有：
C1(s)(λ1+iω1)2e(λ1+iω1)s+
C2(s)(λ2+iω2)2e(λ2+iω2)s
(13)
将
和
代入非齐次微分方程式(9)中，结合韦达定理的结论l1+l2=-(H-iP)，l1l2=-(M+iPT)。得到方程：
(14)
结合式(12)联立，解得：
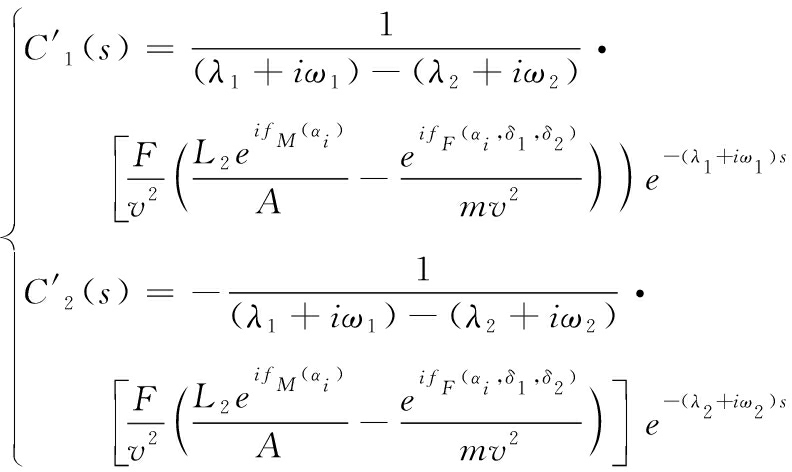
(15)
分别积分
和
得式(16)：
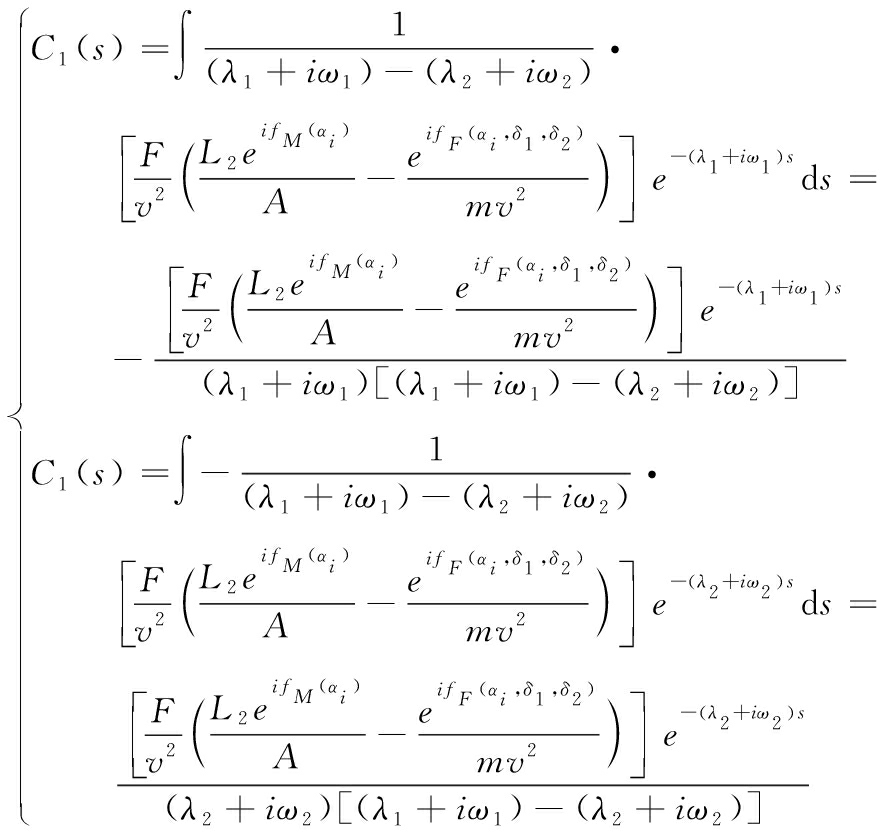
(16)
将和代入特解式中得：
ΔF=C1(s)e(λ1+iω1)s+C2(s)e(λ2+iω2)s=
(17)
攻角的存在会产生马格努斯力和升力，升力在攻角平面内，马格努斯力垂直于攻角平面，如只考虑最大升力项，则偏角方程简化为：
(18)
求解并积分Ψ得：
(19)
偏角计算结果中包含周期变化项和不变项，对不变项在剩余弹道弧长上积分落点偏差Δpoint，Δδ=ΔF，如下式，
(20)
其中，
由式(20)可知，落点偏差量与有直接关系，并与修正起始条件相关。起始时刻越早，即sc越大，落点偏差Δpoint越大，则弹丸获得的修正量越大；由式(1)可知Δδ由推力总冲量决定，在考虑飞行稳定性时需要对Δ(即Δδ)进行限制，即推力冲量不能过大。式(20)的结论并不能直观得出修正起始条件和修正量之间的关系，下文将通过仿真来进一步讨论两者之间的关系。
3 修正效果和攻角变化仿真分析
根据理论分析可知弹丸和修正机构参数对对空修正效果和攻角变化都有影响。定性分析可知，具有偏心的修正力具有更大的修正能力，同时也会造成攻角更剧烈的变化。对于动量修正机构这样力作用时间极短的机构，单个修正力产生的冲量也是微小的，直接作用于质心就可能存在修正能力不足的情况。因此在以下初步对各个因素的分析中以安装不存在径向偏心距为基本条件，但考虑根据弹丸结构空间确定的最大可能轴向偏移量(200 mm)来进行展开。
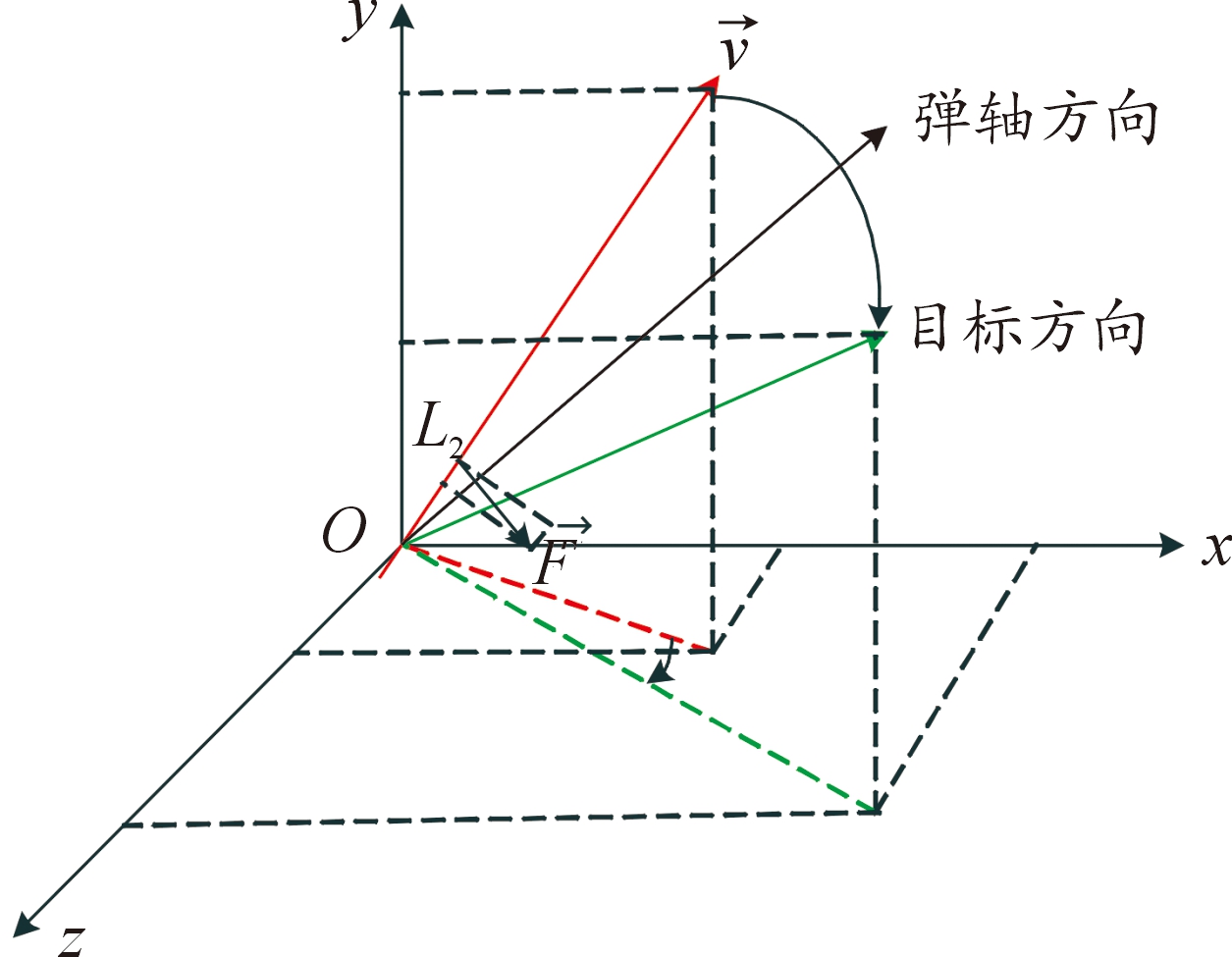
图3 弹目位矢与速度之间角度差示意图
Fig.3 Diagram of the angle difference between position vector and velocity direction
3.1 自转速度的影响
增加动量修正机构和尾翼组件后的弹丸，其低旋主要是利用斜置尾翼或者尾翼端面斜切来实现的。根据修正弹道数学模型可知，不考虑径向偏心下，当极阻尼力矩和导转力矩大小相等时，弹丸转速达到平衡，转速为
为导转角，除出炮口附近瞬时转速与平衡转速有差异，在随后的弹道上，弹丸瞬时转速与平衡转速可视为相同。因此确定的转速也就确定了导转角的大小。
以修正相位角αi= 90°，起始修正时刻在达到1 km射程处(修正起始时刻ts=1.542 s)nξ0= 0.1 r/s，Δnξ0=0.5 r/s，τ= 6 ms，Fi=2 000 N，L2=-200 mm为算例初始条件，在y=4 200 m高空位置得到的横向修正量、最大攻角以及速度方位角变化量如表1所示。由表可知由于动量修正机构产生的是极短时力，因此转速在小范围内变化对固定射高平面的修正量影响不大，主要是对最大攻角的影响，小于3.1 r/s的范围最大攻角随之有减小趋势，在大于3.1 r/s的转速后，弹丸最大攻角则随之增大。另外，随着转速的增大，速度方向角的改变量有减小的趋势，这是因为弹丸自转速度影响了修正力作用的角度区间Δαi，当自转速度增大时，Δαi随之增大，因此实际有效作用力Fi′将比理论作用力Fi延迟，此时Fi′在有效修正力分量方向就有一定损失。
表1 单个脉冲推力作用影响
Table 1 Influence of a single impulse thrust
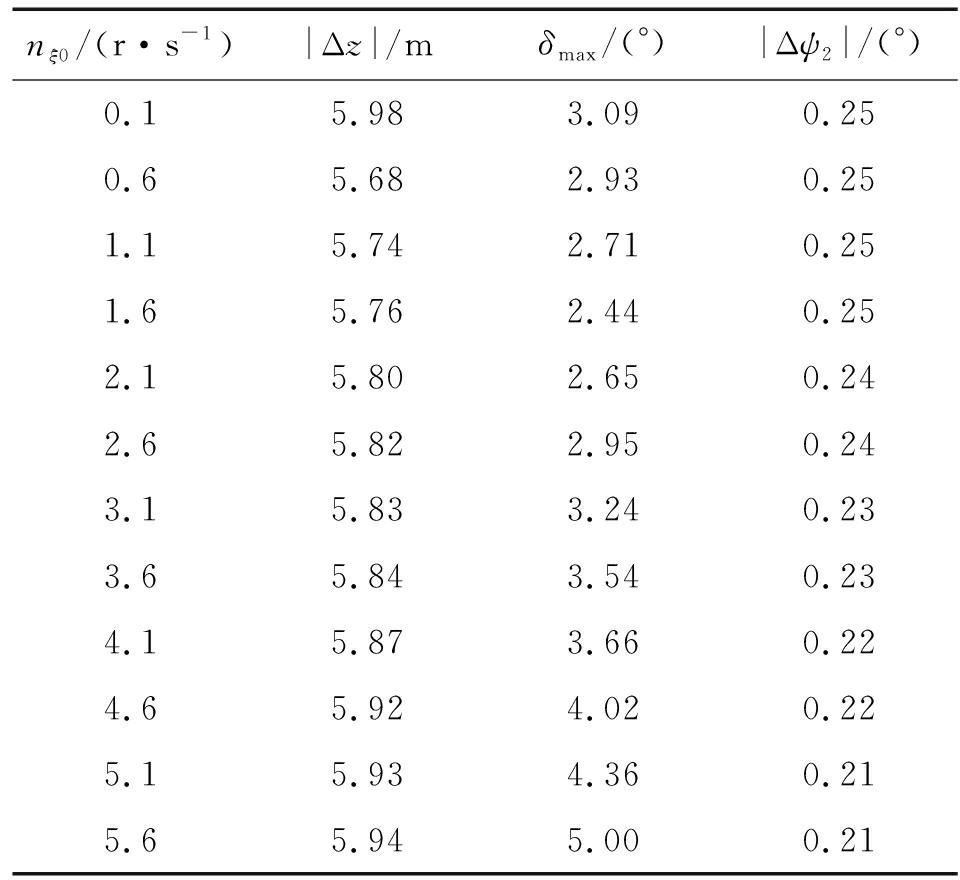
nξ0/(r·s-1)|Δz|/mδmax/(°)|Δψ2|/(°)0.15.983.090.250.65.682.930.251.15.742.710.251.65.762.440.252.15.802.650.242.65.822.950.243.15.833.240.233.65.843.540.234.15.873.660.224.65.924.020.225.15.934.360.215.65.945.000.21
由分析可知，单次修正机构作用后，随着时间的延续，弹丸的飞行可以在作用力结束后稳定下来，且对最大攻角的影响小于工程经验值。然而，如果连续多个修正力的作用，弹丸在还未恢复到稳定状态时可能再次受到修正力作用而导致攻角发生突变。相同仿真条件下，此时在1 km后，弹丸有12*2次机会在90°修正相位角处作用，实时检测角度位置，连续触发满足角度要求的修正机构直到到达终止高度，为了使同一数量级下对比明显，将修正量缩比1/10，得到结果如图4所示。
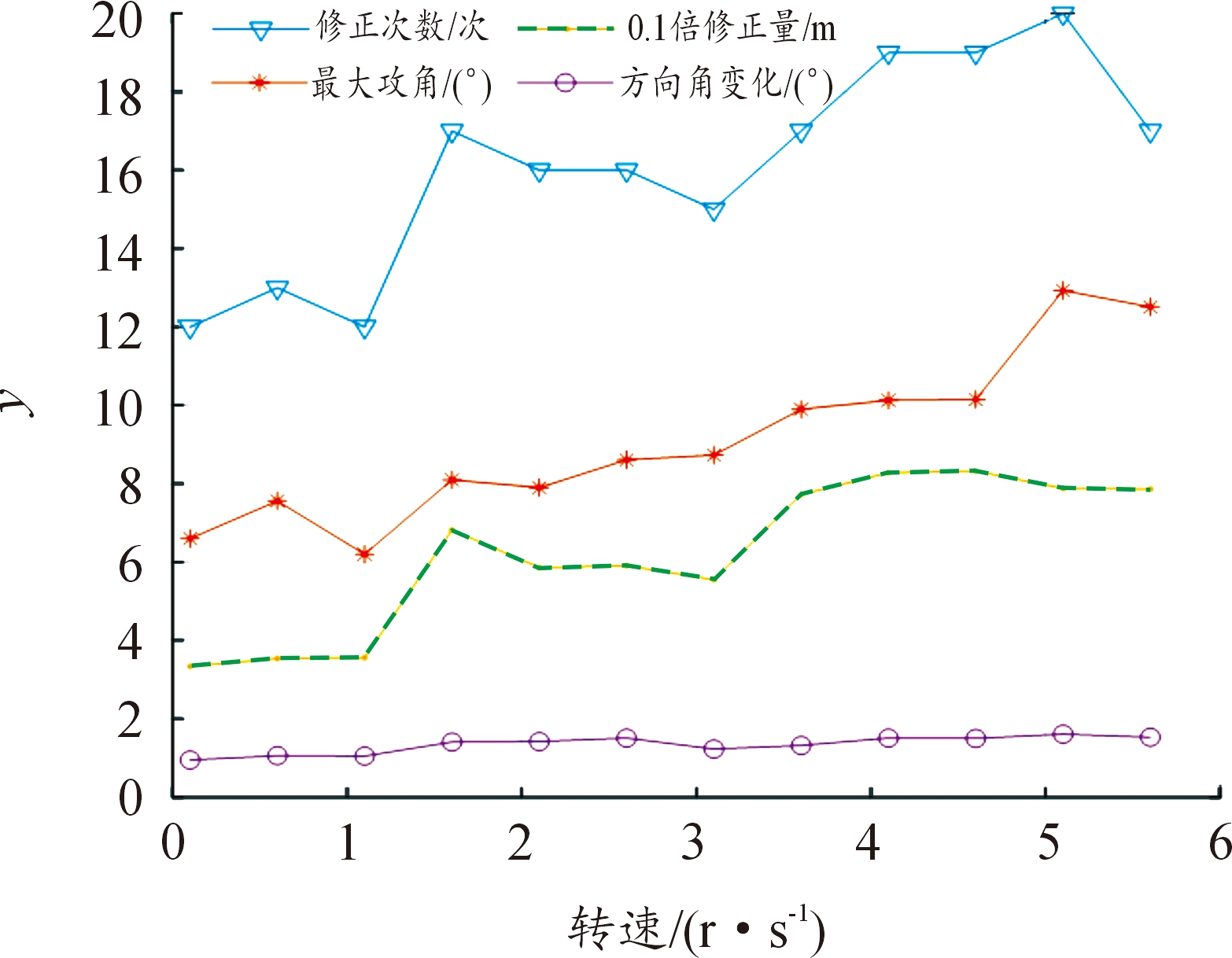
图4 转速对多次修正力作用效果
Fig.4 The effect of spin speed on multiple pulse thrusts
分析图4可知，相同作用次数下，对于对空修正来说，对修正量的影响并不非常明显，转速的小增量增大时，修正量的增量也较小，只有转速发生明显变化时，对修正量的影响才比较明显；此外，同一修正次数下，转速在小于3.1 r/s时，对最大攻角的影响相比高转速下更小，接近工程经验值，因此，在保证修正能力的条件下，应将弹丸低转速控制在较低范围，以确保修正过程弹丸的飞行稳定性。
3.2 脉冲力大小与起始时刻的影响
考虑单次修正机构作用力Fs=0～3 000 N变化时，修正力具有最大轴向偏心距离，起始修正点分别在1、1.5、2、2.5、3 km射程处时，对空中弹丸上升段H=4 200 m处高度平面得到的最大横向修正能力，此时弹丸射程达4.4 82 km。假设τ=6 ms，转速2.6 r/s，则得到如图5、图6所示的修正起始时刻、修正力大小与最大横向绝对修正量和最大攻角之间的关系。由图5可知，修正力越大，获得的修正量越大，而起始修正时刻越早获得的修正量也越大。从图6可知，修正力增大引起攻角变化增大；而在初始阶段和修正终点附近的修正力作用造成攻角变化影响较小。在仿真条件下，0～3 000 N单个修正力作用下，弹丸总攻角均未超过8.5°。当连续进行修正，作用所有满足修正相位角的修正机构时，得到了如图7所示的修正力大小、起始修正时刻与最大攻角关系曲线，由图可知过大的修正力连续作用会迅速使攻角变化，在超过2 000 N时，连续作用将是弹丸攻角超出允许范围，弹丸极可能失稳。
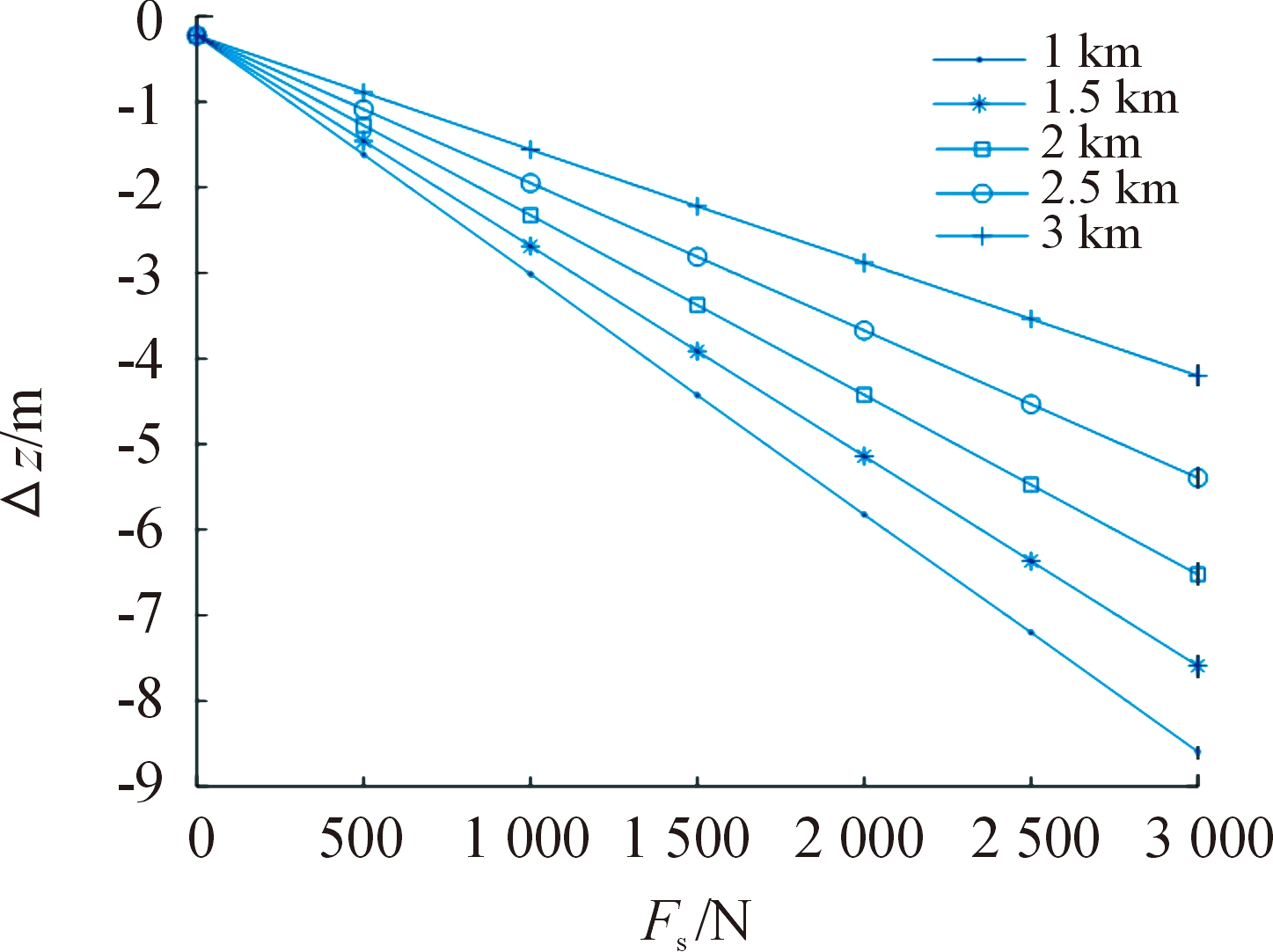
图5 单个修正力大小、修正起始时刻与修正量关系
Fig.5 The relationship between the magnitude of single pulse
thrust, the starting time of correction and the correction
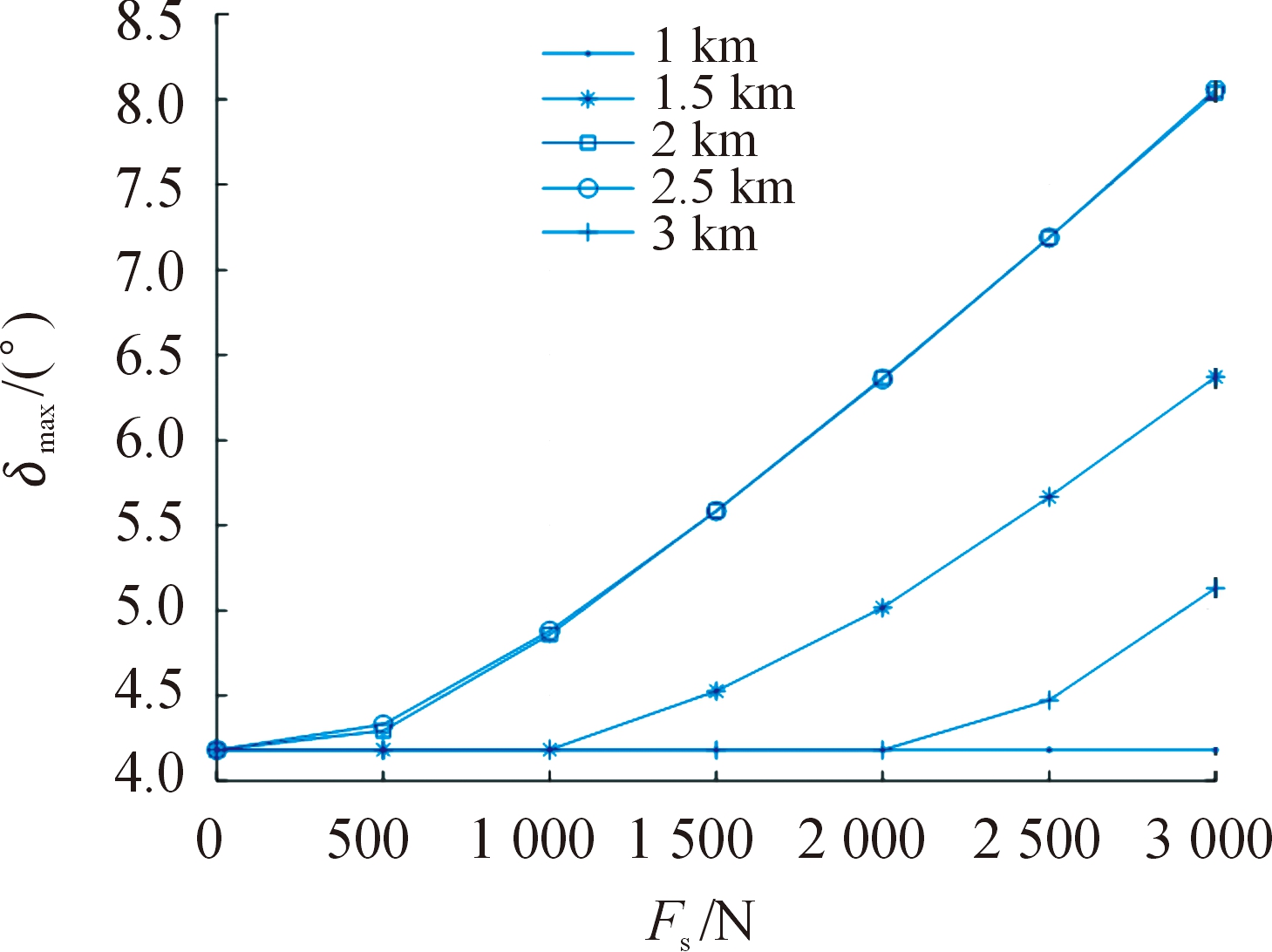
图6 单个修正力大小、修正起始时刻与最大攻角关系
Fig.6 The relationship between the magnitude of single pulse thrust, the starting time of correction and the maximum angle of attack
图7 连续修正力作用时修正力大小、修正起始时刻 与最大攻角关系
Fig.7 The relationship between the magnitude of multiple pulse thrusts, the starting time of correction and the maximum angle of attack
考虑到具有轴向偏心的修正力产生的冲击力矩将对弹丸的飞行稳定性产生影响，因此还需要考虑修正力产生的修正力矩对弹丸的角运动稳定性的影响。取修正力最大和轴向偏心距最大时，研究单个和相同修正相位角下连续多个短时修正力作用时弹丸的横向运动。由于此时间段内空气动力矩的量值远小于修正力矩，则前者可忽略，因此，根据第2节的分析得到弹丸的转动动力学方程可简化为
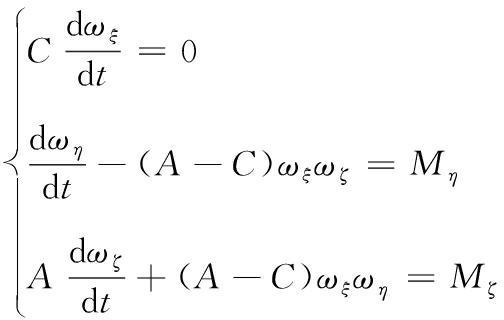
(21)
以自转转速γ为自变量，则
其中(j～η,ζ)，ωj′表示对γ求导，则式(21)可写为
(22)
其中：
引进复数m=mη+imζ，ω=ωη+iωζ，将式(22)的第2个方程乘以i在加上第1个方程得到式(22)的复数形式
ω′+iμω=m(γ)
(23)
其解的形式为
ω=e-iμγ(ω0+
m(φ)e-iμφdφ)
(24)
ω0表示修正开始瞬间是弹丸的摆动角速度。
利用狄克拉函数表示连续的短时修正力矩作用
M(t)=∑Mjδ(t-tj)
(25)
其中：tj表示第j个修正力矩的触发时间；Mj则为其量值，则解式(24)可以写为
(26)
引入阶跃函数
(27)
则式(26)的一般形式为
(28)
式(28)修正力作用后短时间内弹轴的摆动情况。根据仿真初始条件，采用数值计算式(28)可以得到不加修正力下弹轴角运动的状态变化，根据式(28)可知，此时只有第一项，得到ω复合量的变化情况如图8(a)—图8(b)所示，其中ω在初始阶段大约0～2.5 s内具有一定横摆动速度，但是弹轴的振动很小，并且随时间而消失。假设在该区间内作用单个或多个动量修正机构，修正力取前文分析的临界值2 000 N，且机构安装在最大偏心距离处。取起始时刻t0=1 s，单个修正力作用的相位角为90°，通过计算得到tj=1.362 s，得到弹丸横向摆动的变化如图9(a)，横摆运动随时间变化如图9(b)，可见突变的振动随着修正力矩的消失而逐渐收敛直至消失，弹轴运动恢复稳定。当在修正相位角为90°附近连续作用多次动量修正机构，tj=[1.000 0,1.026 0,1.278 0,1.308 0]，则得到如图10(a)—图10(b)，在连续的作用下，弹丸的横摆更加剧烈，但是连续作用完成后，振动同样随时间而消失，但是，在实际情况中，这样剧烈的角运动变化仍然极有可能导致弹丸飞行剧烈失稳而失去攻击能力。
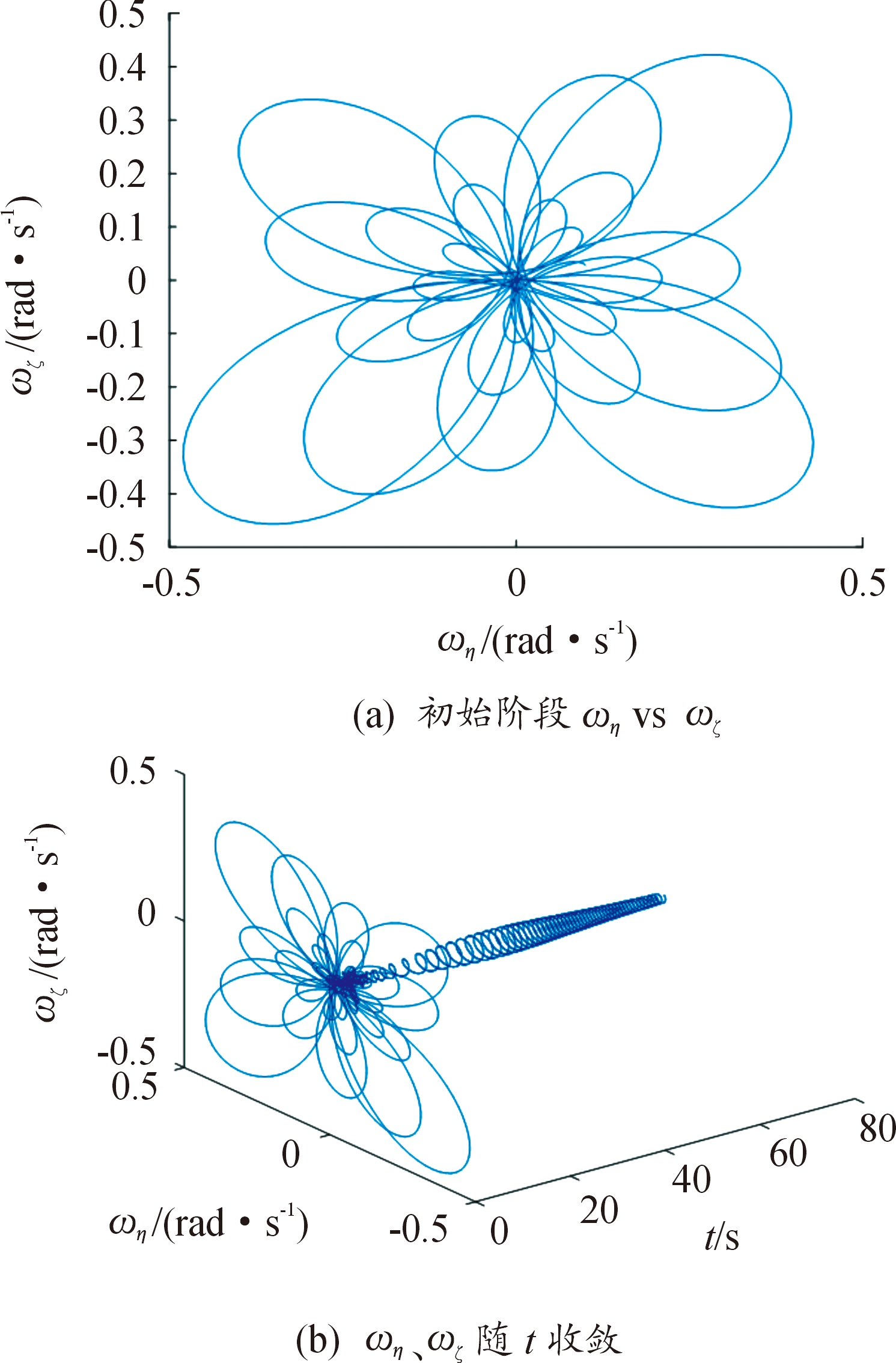
图8 不加修正力下弹轴角运动的状态变化
Fig.8 The state change of angular motion of projectile axis without pulse thrust
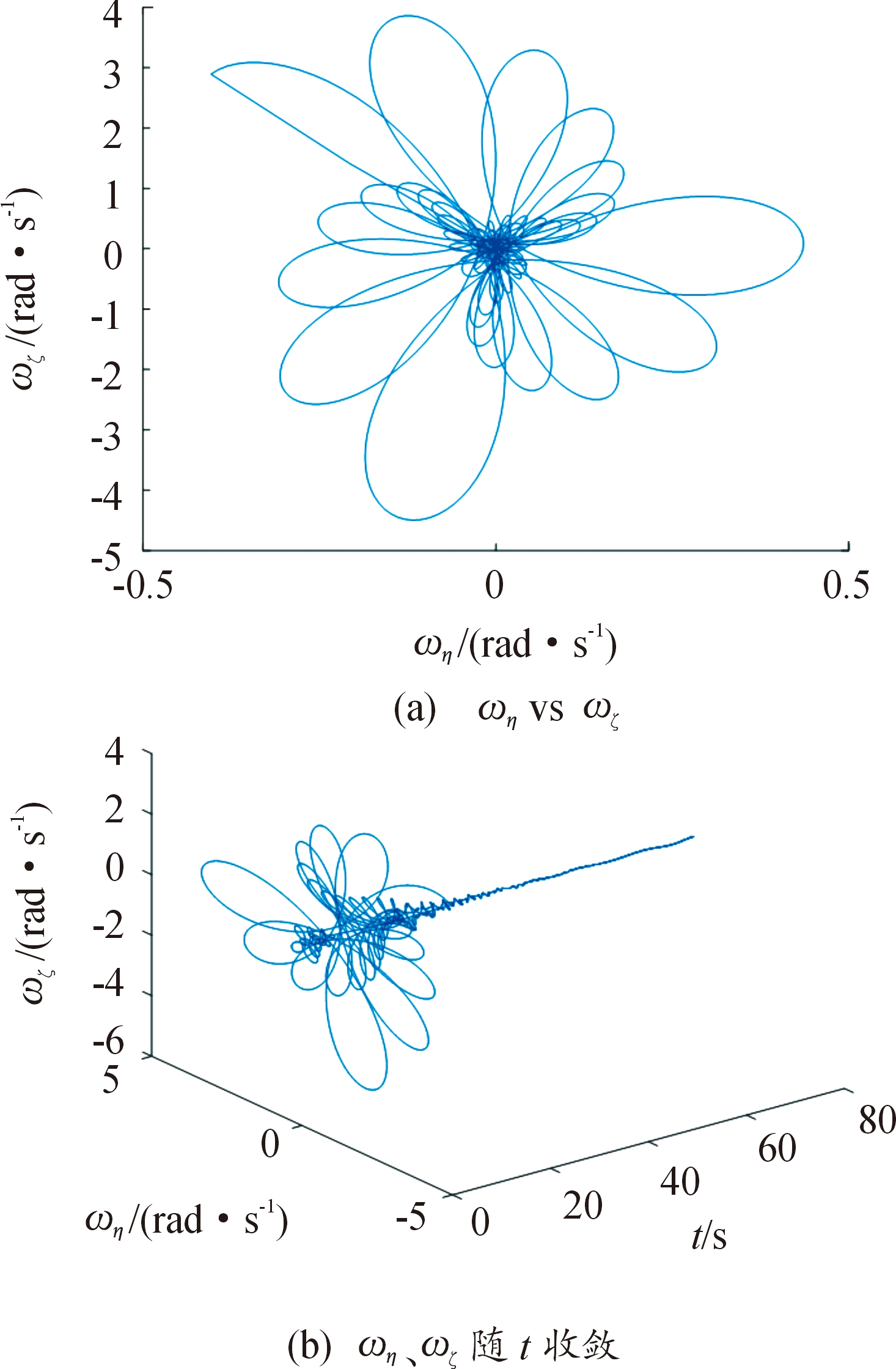
图9 单个最大修正力矩作用下弹轴角运动的状态变化
Fig.9 The state change of angular motion of projectile axis with a single pulse thrust
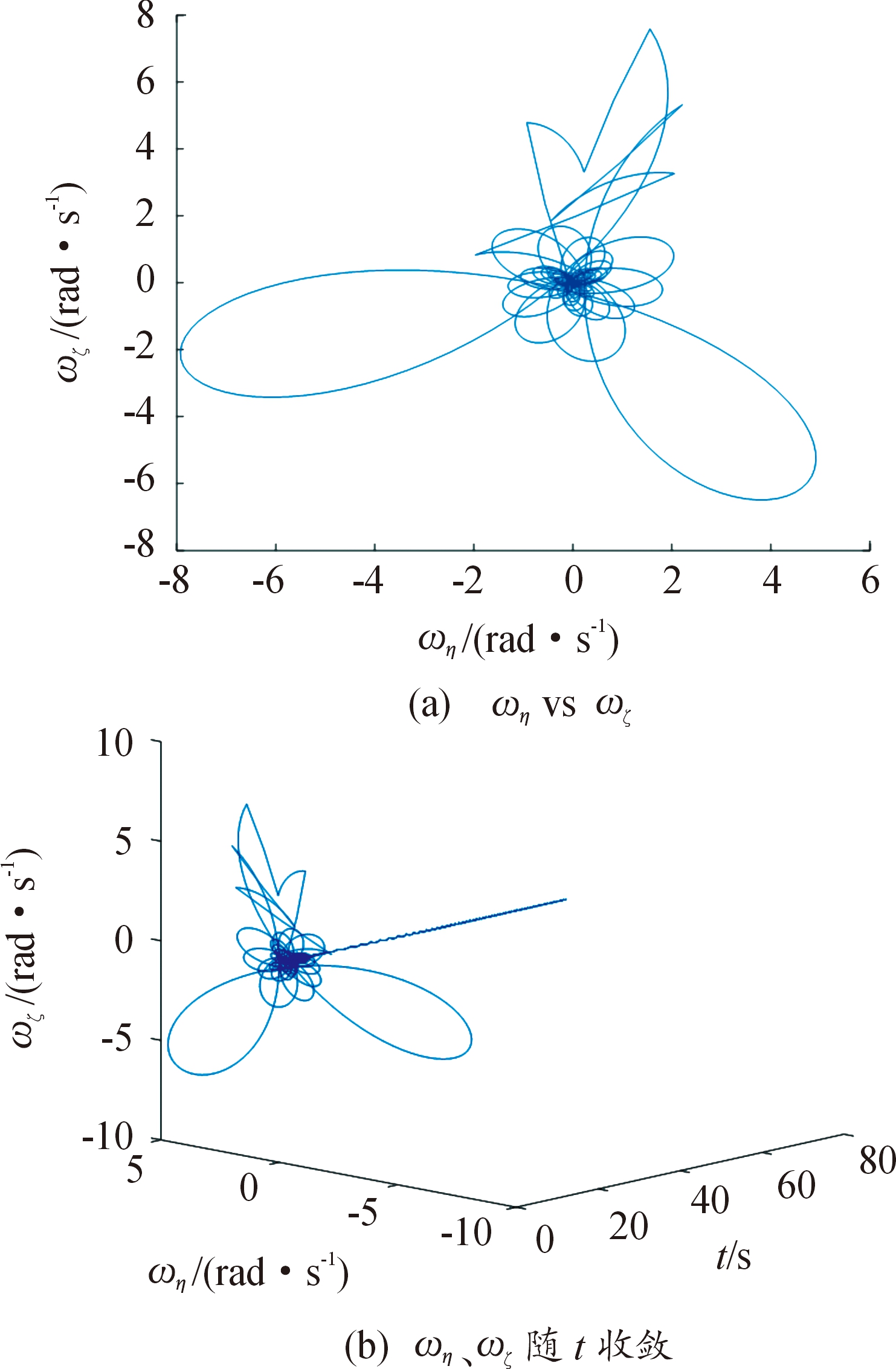
图10 连续多个修正力矩作用下弹轴角运动的状态变化
Fig.10 The state change of angular motion of projectile axis with multiple pulse thrusts
由上述结论可知在连续修正力和力矩作用下，弹丸的横摆振动加剧，另一方面，攻角幅值也会发生变化。弹丸由于多次连续外力和力矩的作用也会导致攻角不稳定，出现较大幅度的波动，实际中，攻角过大的情况非常有可能引起弹丸的失去飞行稳定，甚至出现翻转或掉弹情况，这是不允许的。因此，在确定修正机构提供的直接力大小时不仅需要考虑最大化其修正能力，同时还要保证弹丸的飞行稳定性，根据本小节的分析可知在最大轴向偏心距下，修正力不宜超过2 000 N。
3.3 轴向偏心距离的影响
当修正起始时刻固定，修正力设定为2 000 N时，仿真分析了单个修正力作用于质心前后以及过质心时，不同修正相位角条件下，在弹丸上升段一定高度平面上最大纵、横向修正量的变化规律如图11所示，图11中3种条件下的起始修正时刻均为0 s。由图可知，修正力处于质心处和质心之后时，修正相位角对纵向、横向修正量的影响相对于修正力处于质心前的情况较小。3种情况下，当修正力处于质心之前时，可以获得更大的修正量。宜将修正机构安装于质心之前，此时，纵向、横向修正量具有大的修正能力并呈现一定变化规律；取修正相位角为90°或270°附近时，可获得最大横向修正量；而取修正相位角为0°或者180°附近时，可获得最大纵向修正量，角度不同，修正量的正负性不同。
图11 修正相位角对纵向、横向修正量的影响 (初速960 m/s，H= 4 200 m)
Fig.11 Effect of correction phase angle on longitudinal and lateral correction (with initial speed 960 m/s, H=4 200 m)
根据上述分析确定脉冲修正推力宜置于质心之前，此时脉冲推力具有轴向偏心时除了产生修正力，还会由于偏心而产生了修正力矩，根据3.2小节的分析可知，单个修正力作用在最大轴向偏心距条件下时，弹轴振动虽然加剧，但是弹丸在修正力作用完成后可以恢复到正常的飞行状态。在此，考虑连续作用修正力，轴向偏心距对横向修正效果和最大攻角的影响。
根据3.1小节的分析，选择一个合理的转速1.6 r/s，修正力2 000 N，力持续时间6 ms，在1 km处连续多次横向修正，修正次数由修正相位角判定，取轴向偏心距离L2大小在0～200 mm变化时，对空中高度H=4 200 m处平面的最大横向修正量(修正相位角90°或270°)之间的变化关系如图12、图13所示。由其中曲线分析可知，轴向偏心越大获得的修正量越大，而最大攻角也随之增大，在仿真条件下最大偏心距处的最大攻角约8.1°。说明在仿真条件下，最大偏心距安装是可以满足攻角限制条件并获得最大修正量。但是在实际中，在确定安装轴向偏心距时，不仅要考虑弹丸的修正能力和飞行稳定性，还要考虑实际情况下弹丸整体结构和弹体内部其他组成元素(主要是战斗部、引信等结构的位置和占比)位置的合理性。
图12 轴向偏心距离对横向修正量影响
Fig.12 Influence of installation axial eccentricity on lateral correction
图13 轴向偏心距离对最大攻角影响
Fig.13 Influence of installation axial eccentricity on maximum angle of attack
4 结论
根据外弹道理论，主要分析了脉冲推力强干扰对某口径低旋尾翼弹修正效果和弹丸角运动以及攻角变化的影响。得到了如下结论：
1) 推导了修正推力强干扰下弹丸角运动变化和修正落点偏差公式，分析了单次脉冲推力的修正特性。
2) 弹丸的主要参数弹丸转速nξ、修正力大小F、修正力作用时间τ、以及轴向安装偏心距L2等对修正能力以及攻角的影响是相互制衡，在设计修正器参数时应该考虑以保证弹丸飞行稳定的条件下最大化弹丸的修正能力为优化目标。
3) 对于本文的研究对象，对空修正的情况下、同一修正次数下，转速应小于3.1 r/s；修正力应作用于质心之前；起始修正时刻越早，获得的修正量越大；而在最大轴向偏心距下，修正力不宜超过2 000 N。
[1] 张德键,张健,焦志刚,等.二维弹道修正弹修正机构气动特性研究[J].弹道学报,2021,33(02):34-39.
Zhang D J,Zhang J,Jiao Z G,et al.Research on aerodynamic characteristics of correction mechanismof two-dimensional trajectory correction projectile[J].Journal Of Ballistics,2021,33(02):34-39.
[2] 丛戎飞，吴军强，张长丰，等.扰流片式推力矢量喷管气动特性数值模拟研究[J].空气动力学学报，2019，37(02)：234-241.
Cong R F,Wu J Q,Zhang C F,et al.Numerical research on jet tab thrust vector nozzle aerodynamic characteristic[J].Acta Aerodynamica Sinica,2019,37(02):234-241.
[3] Jacewicz M,Lichota P,Miedziński D,et al.Study of model uncertainties influence on the impact point dispersion for a gasodynamicaly controlled projectile[J].Sensors,2022,22(09):1-20.
[4] Yang Z W,Wang L M.Movement characteristics of a dual-spin guided projectile subjected to a lateral ompulse[J].Aerospace,2021,8(10):1:17.
[5] Glebocki R,Jacewicz M.Parametric study of guidance of a 160 mm projectile steered with lateral thrusters[J].Aerospace 2020,7(05):1-27.
[6] Yang Z W,Wang L M,Zhong Y W.Calculation method for the nonlinear angular motion attraction domain of spin-stabilized projectile[J].Acta Armamentarii.2021,42(06),1195-1203.
[7] 赵群.基于新型主动流动控制技术的推力矢量喷管特性研究[D].南京：南京航空航天大学,2020.
Zhao Q.Research on thrust vector nozzle based on new methods of active flow control[D].Nanjing：Nanjing University of Aeronautics and Astronautics,2020.
[8] 龚东升.基于微型涡喷发动机的无源流体推力矢量喷管的研究[D].南京：南京航空航天大学,2020.
Gong D S.Research on passive fluid thrust vectornozzle based on micro turbojet engine[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2020.
[9] 王晓辉,刘志勇,褚学森.扰流片式推力矢量控制的气动力学研究[J].船舶力学,2019,23(07):791-801.
Wang X H,Liu Zh Y,et al.Gas dynamics research on thrust vector control with spoiler[J].Journal of Ship Mechanics,2019,23(07):791-801.
[10] 王钰.固定鸭舵式二维弹道修正炮弹控制规律和修正策略研究[D].南京：南京理工大学,2019.
Wang Y.Analysis of guidance and corrective strategy for a spin-stabilized projectile equipped with fixed canards[D].Nanjing：Nanjing University of Science and Technology,2019.
[11] 邢炳楠,张志安,高光发,等.基于某推力机构弹道修正弹角运动稳定性分析[J].火力与指挥控制,2019,44(03):96-101.
Xing B N,Zhang Z A,Gao G F,et al.Stability analysis of angular motion based on a thrust mechanism trajectory correction projectile[J].Fire Control and Command Control,2019,44(03):96-101.
[12] 柯知非,高敏,王毅,等.基于二维修正组件的弹道修正弹稳定性分析与仿真研究[J].火炮发射与控制学报,2019,40(02):26-32.
Ke Z F,Gao M,Wang Y,et al.Stability analysis and simulation of the trajectory correction projectile based on 2-D correction fuze[J].Journal of Gun Launch and Control,2019,40(02):26-32.
[13] 杨红伟,窦丽华,甘明刚.具侧向脉冲力制导炮弹的非线性稳定性分析[J].北京航空航天大学学报,2011,37(07):772-776.
Yang H W,Dou L H,Gan M G.Analysis of non-linear stability of guided projectile using lateral impulsive thrust[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(07):772-776.
[14] 戴明祥,杨新民,易文俊.脉冲修正弹药动态稳定性分析[J].弹道学报,2011,23(03):63-68.
Dai M X,Yang X M,Yi W J.Analysis of the dynamic stability of pulse correction projectile[J].Journal of Ballistics,2011,23(03):63-68.
[15] Cooper G R.Projectile aerodynamic jump due to lateral impulses[R].Maryland:Army Research Lab,2003.
[16] 韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008:23-83.
Han Z P.Ballistics of projectiles[M].Beijing:Beijing Institute of Technology Press,2008:23-83.