0 引言
装药发射安定性是指在弹体和其他零件在强度上满足要求时,炸药等装填物不发生危险。但在实际发射过程中,弹体受多种载荷作用使战斗部壳体产生应力和变形,从而使装药内部产生应力和缝隙。为保证弹丸能够安全发射完成作战要求,对于发射过程中的弹丸装药安定性的分析尤为重要。
近些年来,有许多学者针对弹丸发射过程中的装药安定性进行了研究[1-4]。如芮筱亭等研究了发射装药引起膛炸的机理和装药发射安定性的评估方法,建立了我国首个基于发射装药起始动态活度比的发射装药发射安全性评定方法兵器行业标准和国家军用标准[5-8];徐赫阳等[9]运用LS-DYNA软件建立了战斗部在膛内运动的模型,分析了战斗部在不同运动阶段下的应力、应变曲线等,最终该模型模拟结果与实弹测试结果基本吻合;许耀峰等[10]通过数值模拟分析对比了不同膛线形式和膛线深度下,制导炮弹在挤进阶段和膛内运动过程中的弹炮应力、挤进阻力以及弹炮动力学响应,获得了大口径火炮膛线结构对滑动弹带制导弹丸膛内运动的影响关系;王韫泽等[11]考虑到异物阻滞导致炸膛的情况并设定了2种典型异物阻塞形式,在模拟分析多种不同的工况后得出结论,弹体膛内突然受阻和速度急剧下降,导致底部燃气中形成激波和局部高压区,其存在可造成膛炸;弹体膛内近炮口处高速冲击沙土,身管受到复杂的强动载荷作用并可造成膛炸;李文彬等[12-14]从装药缝隙影响的角度出发,采用数值模拟的方式得出结论,底隙对装药应力分布影响中,气隙厚度是主要因素、在发射载荷作用下,特定尺寸的孔隙不会导致战斗部内装药的早爆以及当B炸药中的孔隙尺寸小于0.3 mm时,其对落锤撞击感度的影响可以忽略;彭嘉诚等[15]采用LS-DYNA仿真模拟并结合Matlab计算得出结论,在无摩擦或摩擦因数大到弹体与装药间不发生相对转动时,装药温度无明显变化;高温发射条件下,膛内炸药装药与弹体出现显著相对转动,常温条件下装药与弹体基本不发生相对转动;张涛等[16]对不同装药工艺对装药安定性的影响进行了研究,结果表明,在装药其他条件相同的情况下,压装药相对钝感,其安定性优于注装药及浇注药;由上述研究可知,国内外的学者针对装药发射安定性做出了很多成果,但缺少对高速旋转弹丸在膛内发射过程中装药应力分布的研究。
本文中使用数值模拟分析的方法研究高转速下膛内装药发射安定性,通过模拟分析在改变膛压、摩擦因数以及装药底隙大小3个限定条件的情况下对装药应力变化的影响,可为高转速下膛内装药安定性分析研究提供参考依据。
1 发射时弹丸临界状态
魏惠之等人发现弹丸在发射过程中存在3个临界状态[17],要研究膛内装药发射安定性可以先通过数值模拟结果观察3种临界状态下装药的应力分布情况。
第一临界状态,弹带嵌入完毕,弹带压力达到最大值的时刻。此状态下弹内装药所受应力分布如图1所示,此时装药受力集中在底部与侧面,装药应力值处于安全值。
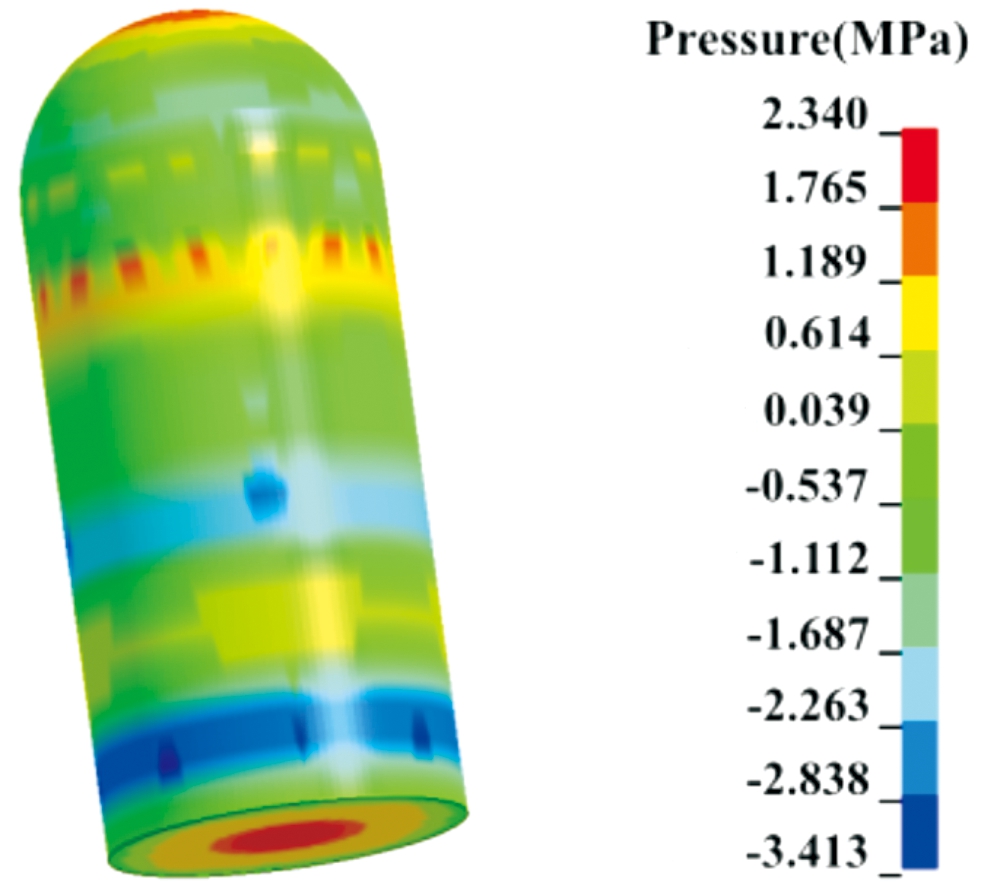
图1 弹带挤进膛线时装药应力分布(t=480 μs)
Fig.1 Charge stress distribution when the elastic belt is squeezed into the rifling(t=480 μs)
第二临界状态,最大膛压时期。这种状态下的特点是膛内火药气体压力达到最大,由加速度引起的惯性力等均达到最大,同时这一状态下弹体的变形也极大,会对内部装药造成挤压产生应力,此状态下的装药应力分布如图2所示,此时装药受力最大,装药应力值处于相对危险的状态。
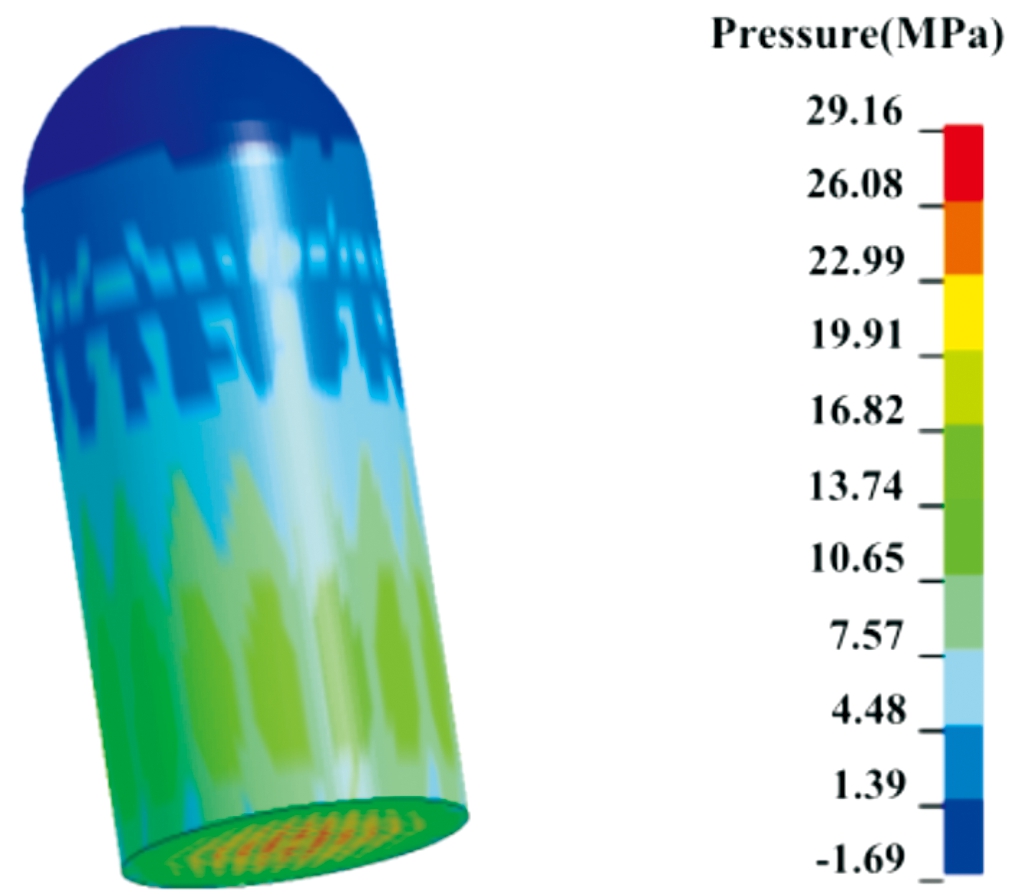
图2 最大膛压时期装药应力分布(t=1 300 μs)
Fig.2 Charge stress distribution during maximum chamber pressure(t=1 300 μs)
第三临界状态,弹丸出炮口的时刻。首先弹丸的旋转角速度达到最大,与角速度相关的载荷达到最大值,但与弹体强度有关的膛内火药气体压力等载荷迅速减小,弹体上变形也相应变小。其次弹丸出炮口瞬间,大部分载荷突然卸载,由此产生的拉伸应力对弹体会造成影响,进而影响内部装药的稳定性,此状态下装药应力分布如图3所示,此时装药应力值虽不如最大膛压时刻,但也相对较大。

图3 出炮口时装药应力分布(t=5 280 μs)
Fig.3 Stress distribution of propellant at the exit of the gun(t=5 280 μs)
2 建立仿真模型
2.1 有限元模型
利用TRUEGRID软件进行仿真建模以及网格划分,弹丸分为装药、弹体、引信和弹带4个部分(见图4)。其中弹丸弹径为37 mm,弹长为138 mm,炮管膛线为渐速膛线。整个仿真需要炮管与弹丸共同完成,炮管的模型(见图5)。

图4 弹丸剖面模型(左)弹丸完整模型(右)
Fig.4 Projectile profile model (left) Projectile complete model (right)

图5 炮管剖面模型(左) 炮管完整模型(右)
Fig.5 Barrel profile model (left) Barrel complete model (right)
2.2 材料及计算模型
利用TRUEGRID建立模型后,开始定义模型部位的算法与接触类型。其中弹带采用SPH算法,弹带与弹体间采用点-面绑定接触,弹带与炮管间采用点-面自动接触。其余部分采用拉格朗日算法,弹底引信与弹体采用面-面绑定接触,其余各部分均采用面-面自动接触。本文数值模拟中装药材料模型为ELASTIC_PLASTIC_HYDRO,状态方程为IGNITION_AND_GROWTH_OF_REACTION_IN_HE,装药部分主要参数见表1。炮管为刚体,材料模型为RIGID。其余部分材料模型均为PLASTIC_KINEMATIC,主要参数见表2。
表1 炸药参数
Table 1 Parameters of explosive

ρ/(g·cm-3)ABXP1XP2GSIGY1.65.240.0774.21.10.0350.002
表2 其他部分材料参数
Table 2 Parameters of other parts
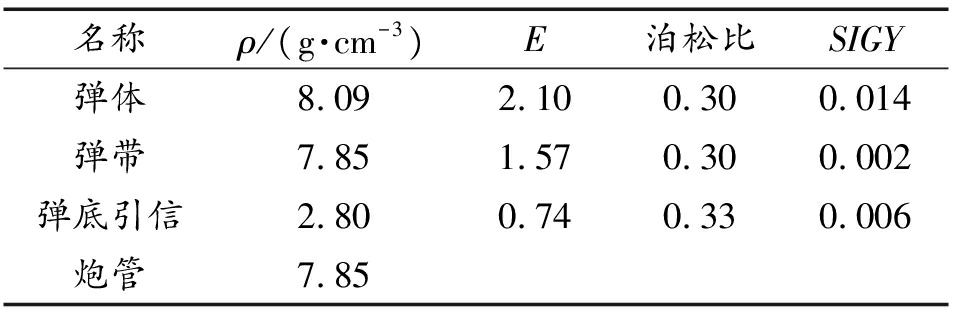
名称ρ/(g·cm-3)E泊松比SIGY弹体8.092.100.300.014弹带7.851.570.300.002弹底引信2.800.740.330.006炮管7.85
其中:A,B,XP1,XP2为JWL状态方程中的常数;G为剪切模量;E为弹性模量;SIGY为屈服应力。
2.3 发射过程中的装药安定性分析
弹丸在膛内运动期间,弹丸整体做轴向运动的同时绕弹轴高速旋转,当摩擦因数较小时,膛内弹体与装药还会发生相对旋转,因此,需研究弹丸分别在直线运动和旋转运动时弹体与装药的状态,分析装药安定性的影响因素。
2.3.1 直线运动下装药安定性分析
设定弹体在膛压曲线的作用下做直线运动,此过程中的应力分布如图6所示。从图中可以看出,由于惯性作用装药会向后移动,作用力集中在装药底部。由于装配过程中存在系统误差、人为误差等因素,装药与弹底引信间会存在间隙。由李文彬等人的研究可知,底隙的存在必然会对装药底部应力产生影响[12],因此在仿真模拟研究中将底隙大小作为变量之一。
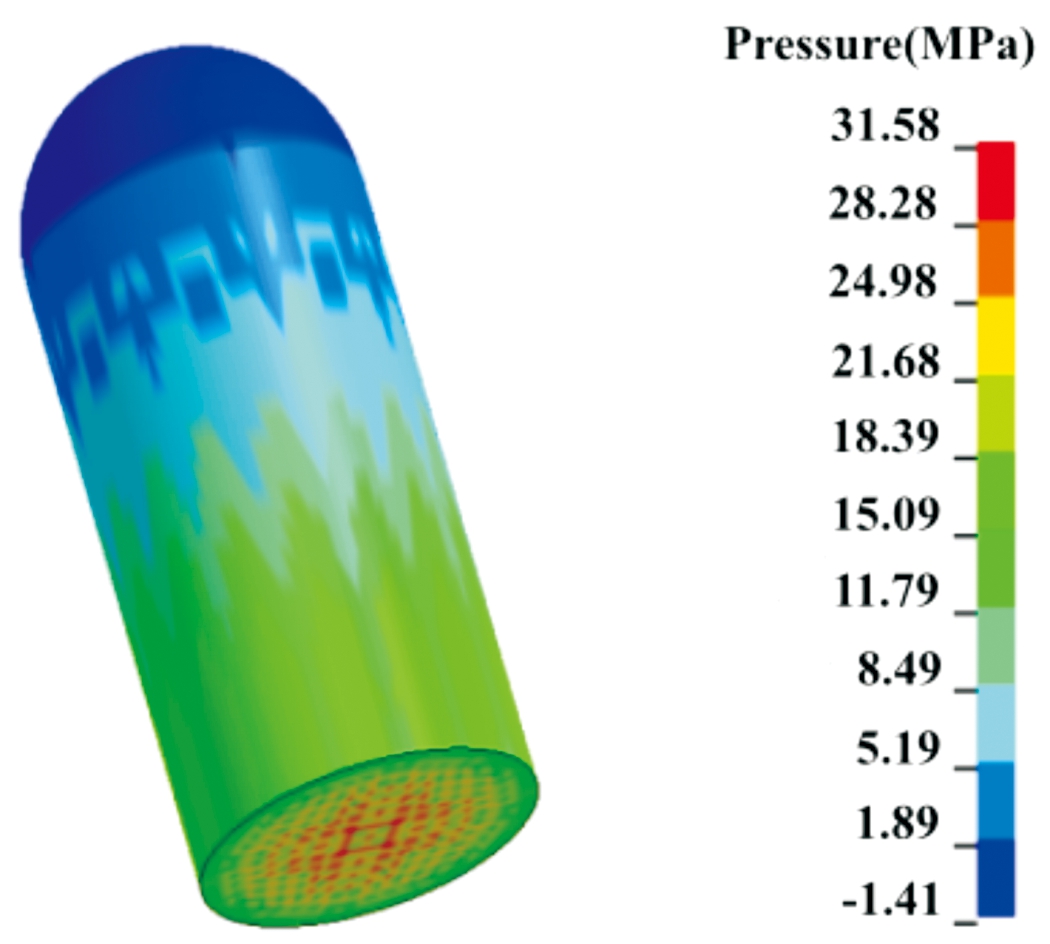
图6 直线运动中装药的应力分布
Fig.6 Stress distribution of charge in linear motion
2.3.2 旋转运动下装药安定性分析
给弹体施加扭矩模拟膛内转动,令弹体在原处旋转,同时弹体与装药间的摩擦因数设为0.02,此过程中弹体和装药会发生相对旋转,由于摩擦力的原因,弹体侧面也会产生应力集中的区域(见图7),选取装药侧表面的一列单元(后续分析装药侧面应力时也采用同一列单元,如图8所示),得到对应的应力-时间曲线(见图9),通过LSPREPOST软件中的Mearsure板块获取弹体与装药在膛内运动中的转速曲线(见图10)。

图7 旋转运动中装药的应力分布
Fig.7 Stress distribution of charge in rotating motion
图8 装药侧表面选取的单元
Fig.8 Element for selecting charge side surface
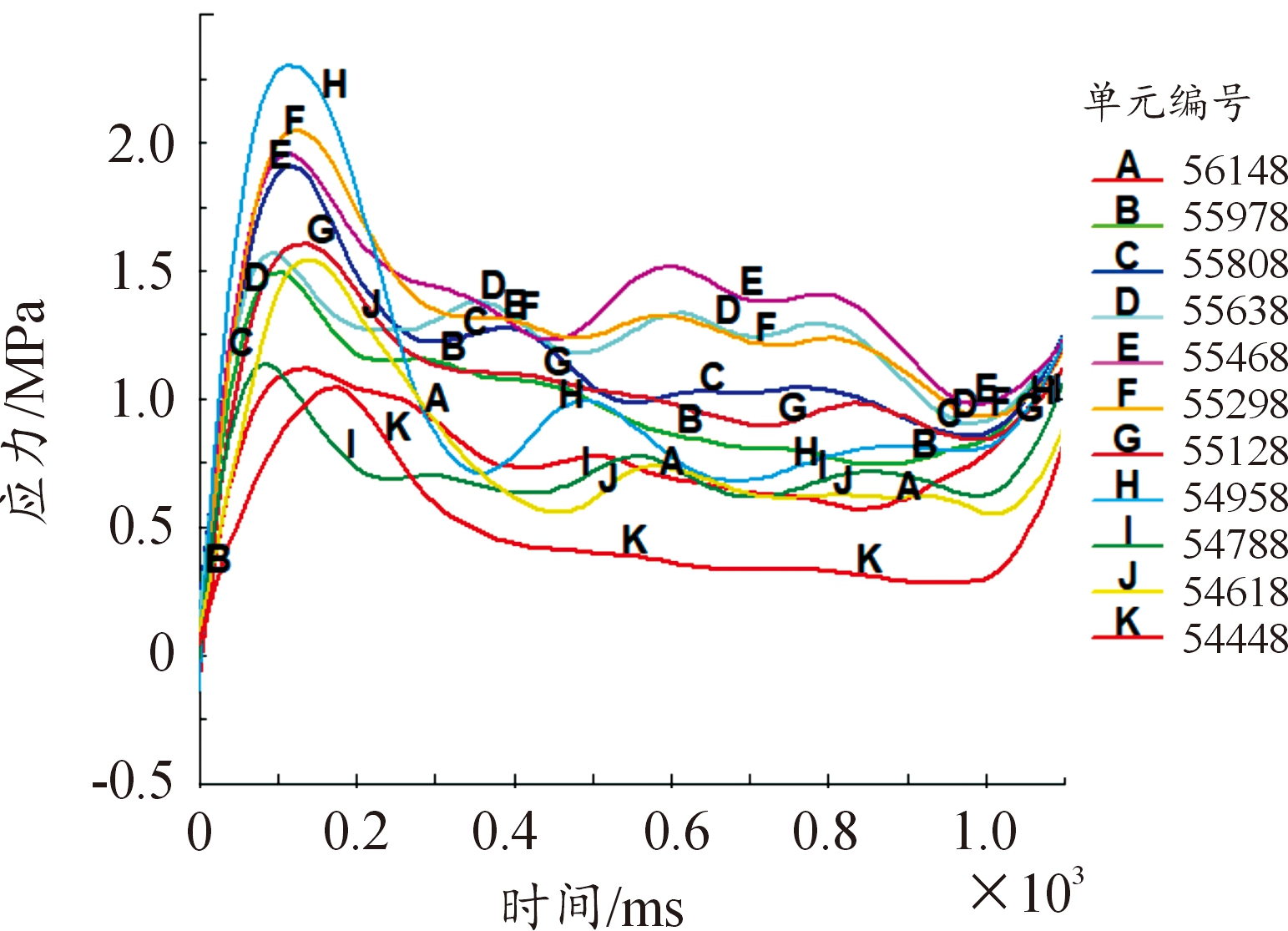
图9 施加扭矩下装药侧面应力变化曲线
Fig.9 Side stress curve of charge under applied torque

图10 装药与弹体的相对转速
Fig.10 Relative rotational speed of charge and projectile
可以发现,装药所受的应力先增大后趋于稳定,这种现象是弹体在扭矩的作用下做变加速旋转运动,与装药间的摩擦由静摩擦转化为动摩擦导致的。从图中还可以发现,应力曲线后半段虽趋于稳定但仍有波动,这是由于在仿真过程中装药模型会发生晃动。
可以看出弹体在扭矩的作用下呈加速旋转趋势,装药也因摩擦力的作用发生转动,但由于摩擦因数偏小,转动并不明显。
2.3.3 膛内装药安定性分析
对膛内弹药进行仿真分析,观察其与单一因子下的异同,进一步确定膛压对装药应力变化与转速的影响,其中装药在运动过程中的应力分布如图11所示,装药侧面应力曲线如图12所示,弹体与装药的相对转速如图13所示。
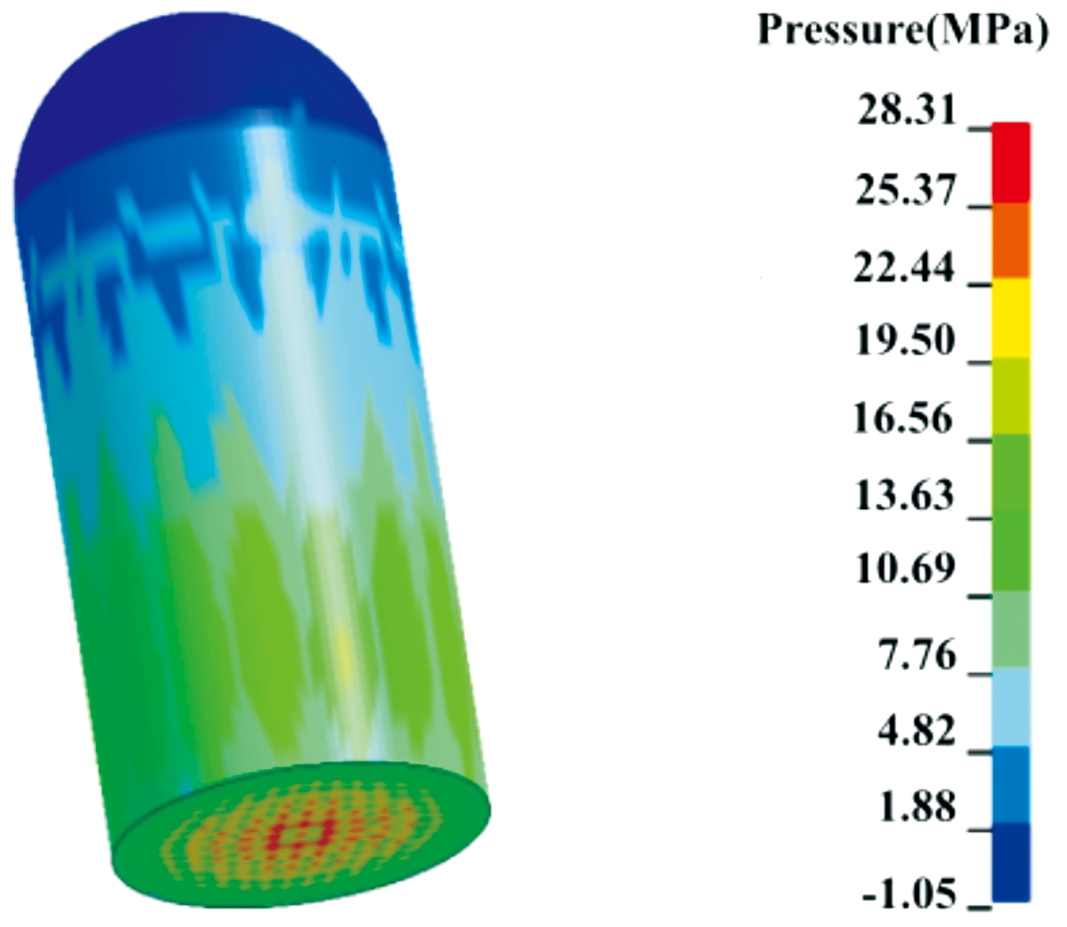
图11 膛内装药应力分布
Fig.11 Stress distribution of charge in bore

图12 装药侧面应力变化曲线
Fig.12 Side stress curve of charge
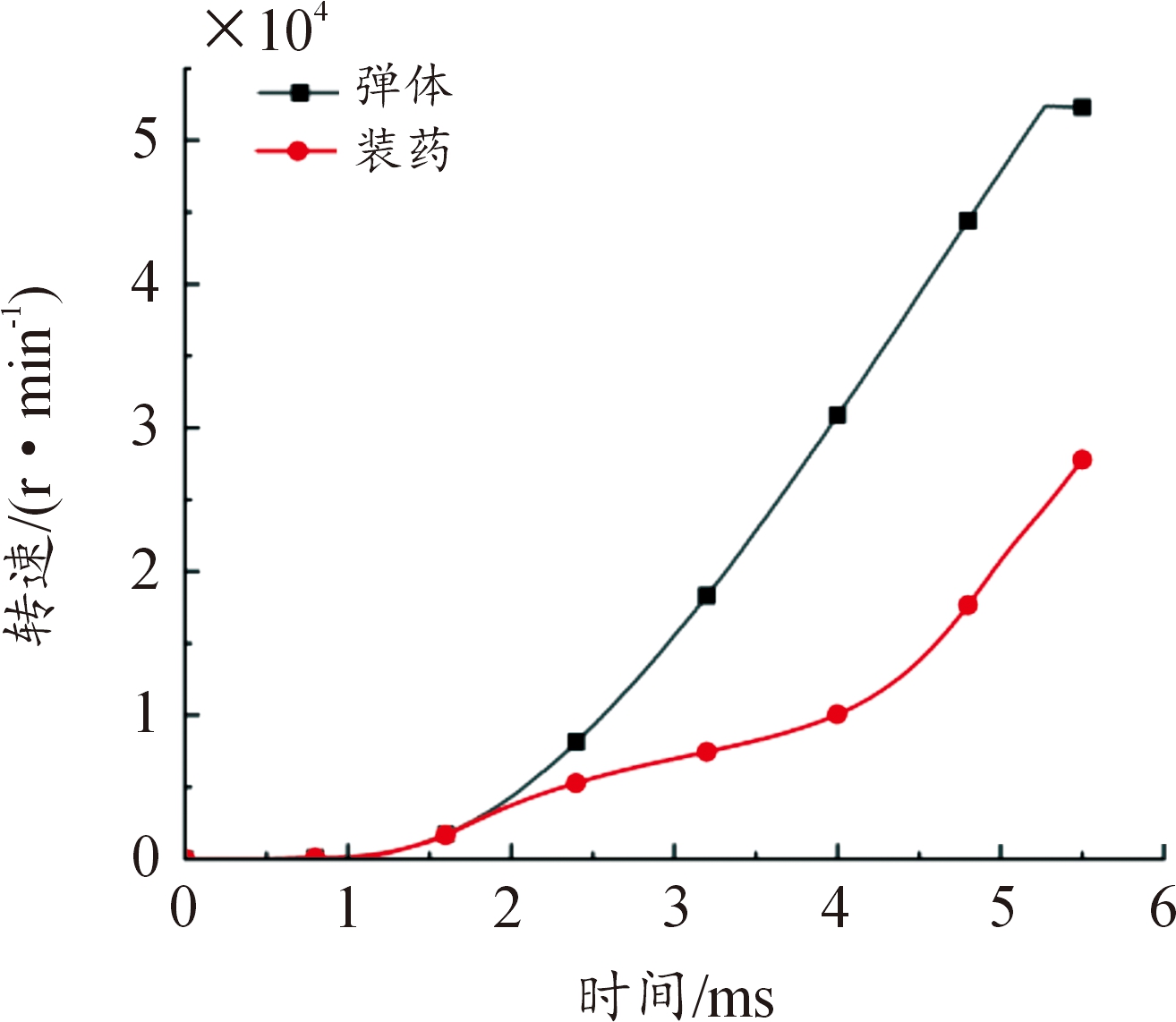
图13 膛内弹体与装药转速
Fig.13 Projectile body and charge speed in bore
通过观察膛内运动中装药侧面的应力变化曲线,可以明显发现其与扭矩作用下的不同,由于膛压的作用,装药侧面应力呈先增大后减小的趋势。通过上述单一因子分析和膛内分析的对比我们可以发现,装药的应力都集中于弹底,在膛压存在的情况下,弹体与装药间的相对转动会缩小,装药侧面应力的变化趋势由单扭矩情况下的先增大后趋于稳定变为先增大后减小。综上所述,在仿真模拟研究中涉及的变量有3个,分别是底隙、摩擦因数和膛压。但底隙、摩擦因数和膛压都会对装药应力产生影响,因此在研究装药应力的变化规律时,采用控制变量法单独研究每个变量。
3 数值模拟研究
3.1 底隙影响分析
在只改变膛压和装药底隙的条件下,探究装药底隙变化对装药底部应力的影响,同时也能反映出膛压变化对装药底部应力的影响。首先设定5组膛压曲线以及5组装药与弹底引信间的缝隙大小,其中5组膛压曲线的峰值分别为334.5、357.9、383、409.8、438.5 MPa,6组装药底隙分别是0、0.3、0.6、0.9、1.2、1.5 mm。此时为了保持理想状态,设定弹体与装药间摩擦因数为0。
经LS-DYNA仿真及数据处理后,不同膛压曲线峰值下,不同底隙下的装药应力峰值曲线如图14所示。
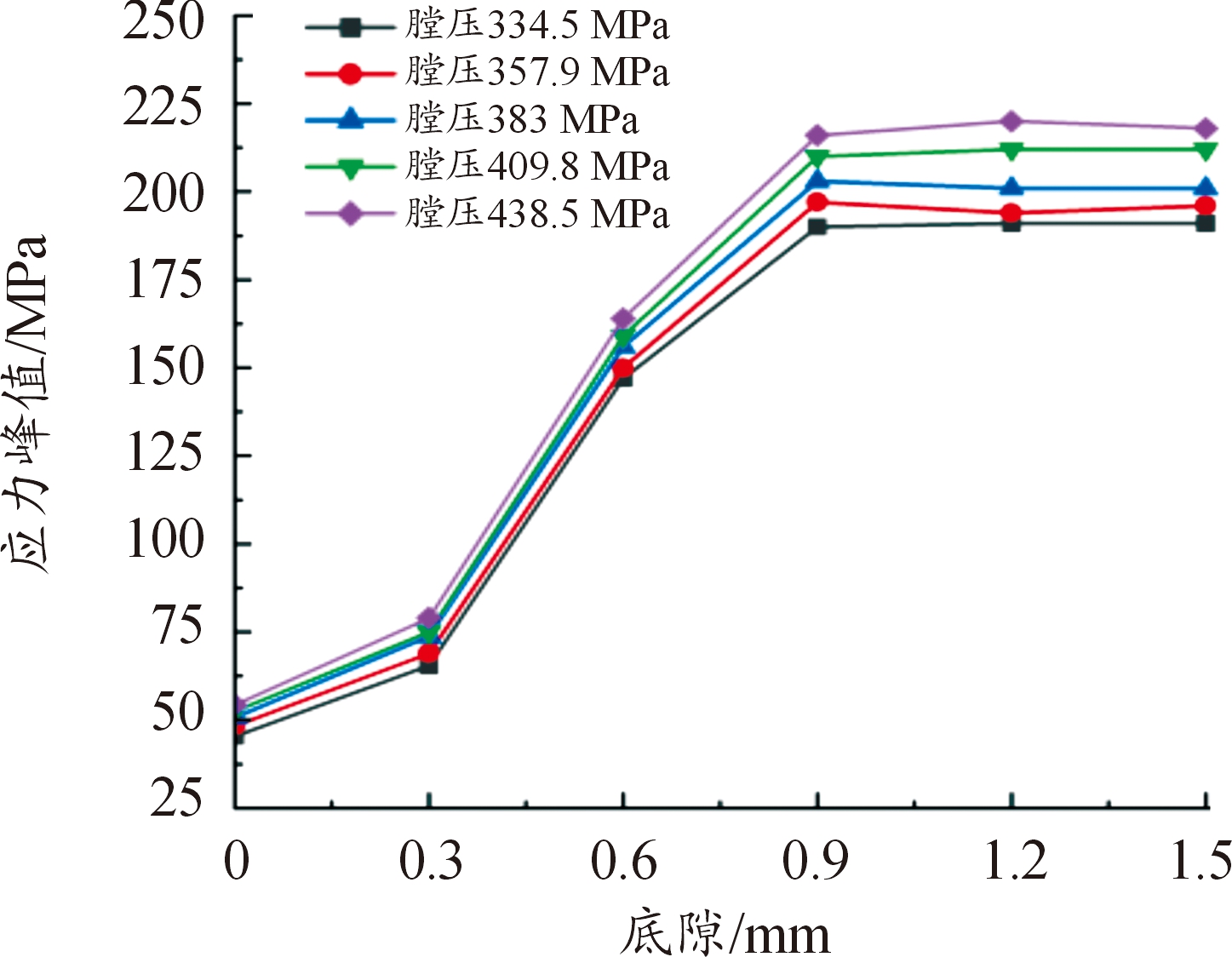
图14 不同膛压不同底隙下应力峰值曲线
Fig.14 Stress peak curve under different chamber pressure and different bottom gap
可以看出,随着底隙的增大,装药底部应力呈先增大后趋于稳定值,同时膛压越大,装药底部应力也越大。
3.2 摩擦影响分析
由上述2.3.2旋转运动下装药安定性分析中得知,当摩擦因数较小时,装药与弹体会发生相对转动,同时装药侧表面也会受到摩擦力的作用。为了更好地观察摩擦力作用的变化规律,通过改变膛压与摩擦因数探究摩擦力变化对装药安定性的影响,在装药表面建立Segment集合(见图15),并施加大小为20 MPa的预应力,在此条件下选取装药侧表面的一列单元研究其应力变化曲线(与图8中所取单元一致),同时也能得到装药与弹体的相对转速变化。同样需要设置5组膛压曲线以及6组摩擦因数,膛压曲线峰值与上述一致,静动摩擦因数分别为0.01/0.005、0.02/0.015、0.03/0.025、0.04/0.035、0.06/0.055。同时装药底隙保持理想状态即为0 mm。
图15 装药侧表面Segment集合
Fig.15 Segment set of charge side surface
当膛压大小为334.5 MPa时,选取装药与弹体2个部件收集其转速数据,得到各组摩擦因数条件下装药与弹体的转速曲线如图16所示。选取装药侧表面的单元(见图8)收集其应力变化数据,得到各组摩擦因数条件下装药侧面应力变化曲线如图17所示。
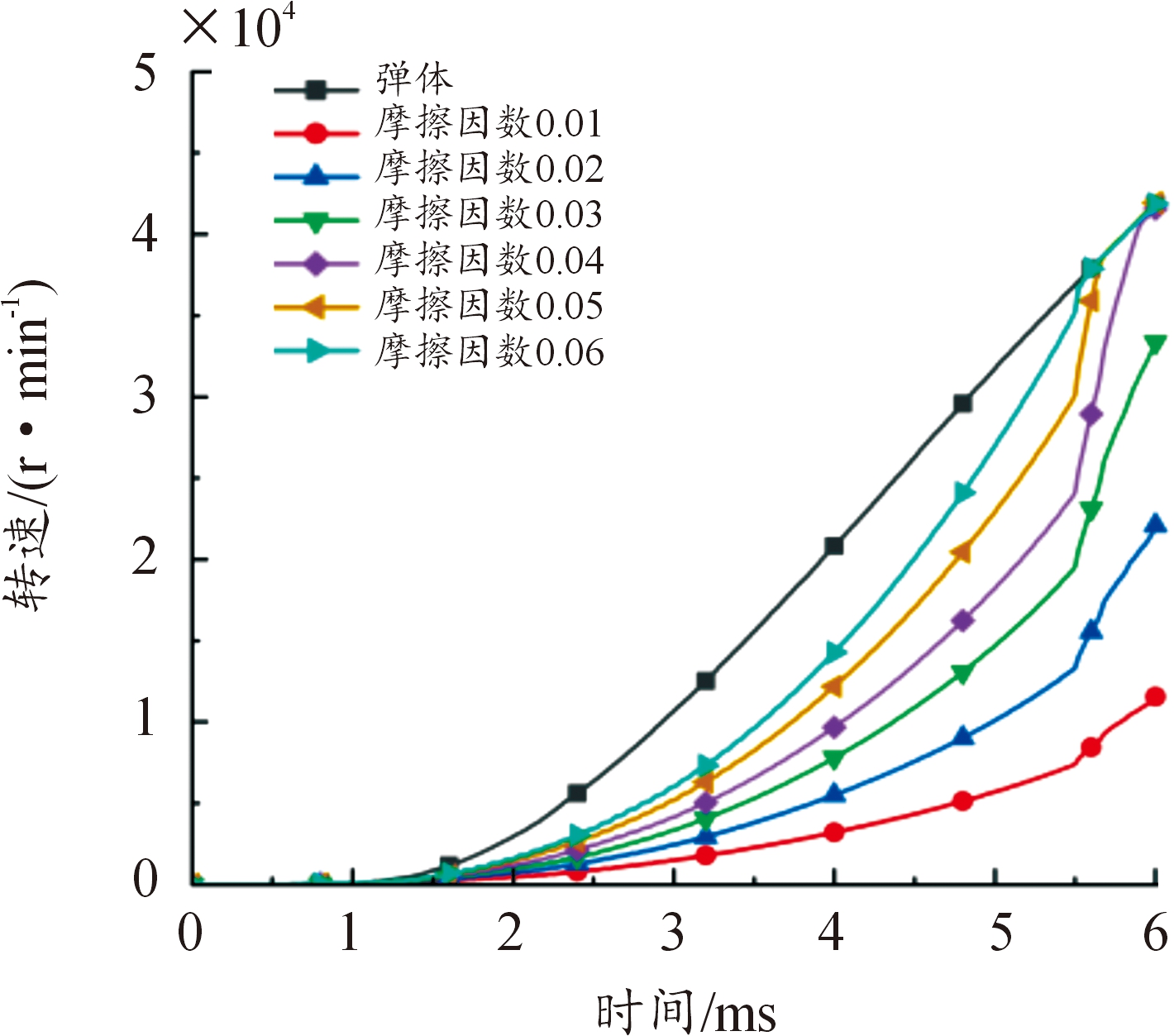
图16 334.5 MPa时各组摩擦因数的转速
Fig.16 Rotational speed of each group offrictional coefficients at 334.5 MPa

图17 334.5 MPa时各组摩擦因数条件下装药侧面应力曲线
Fig.17 Side stress curve of charge under each group of coefficients at 334.5 MPa
从图16中可以看出,当弹体与装药间摩擦因数较小时,装药与弹体会发生相对转动,随着摩擦因数的增大装药与弹体间的相对转速会减小。从图17中可以看出装药侧面所受应力均呈先增大后减小的趋势,这是由于膛压对装药侧面的作用,装药侧面存在应力集中的单元,其编号为54448(图8中位于最底部的单元)。
当膛压大小为357.9 MPa时,选取装药与弹体2个部件收集其转速数据,得到各组摩擦因数条件下装药与弹体的转速曲线如图18所示。选取装药侧表面的单元(如图8)收集其应力变化数据,得到各组摩擦因数条件下装药侧面应力变化曲线如图19所示。
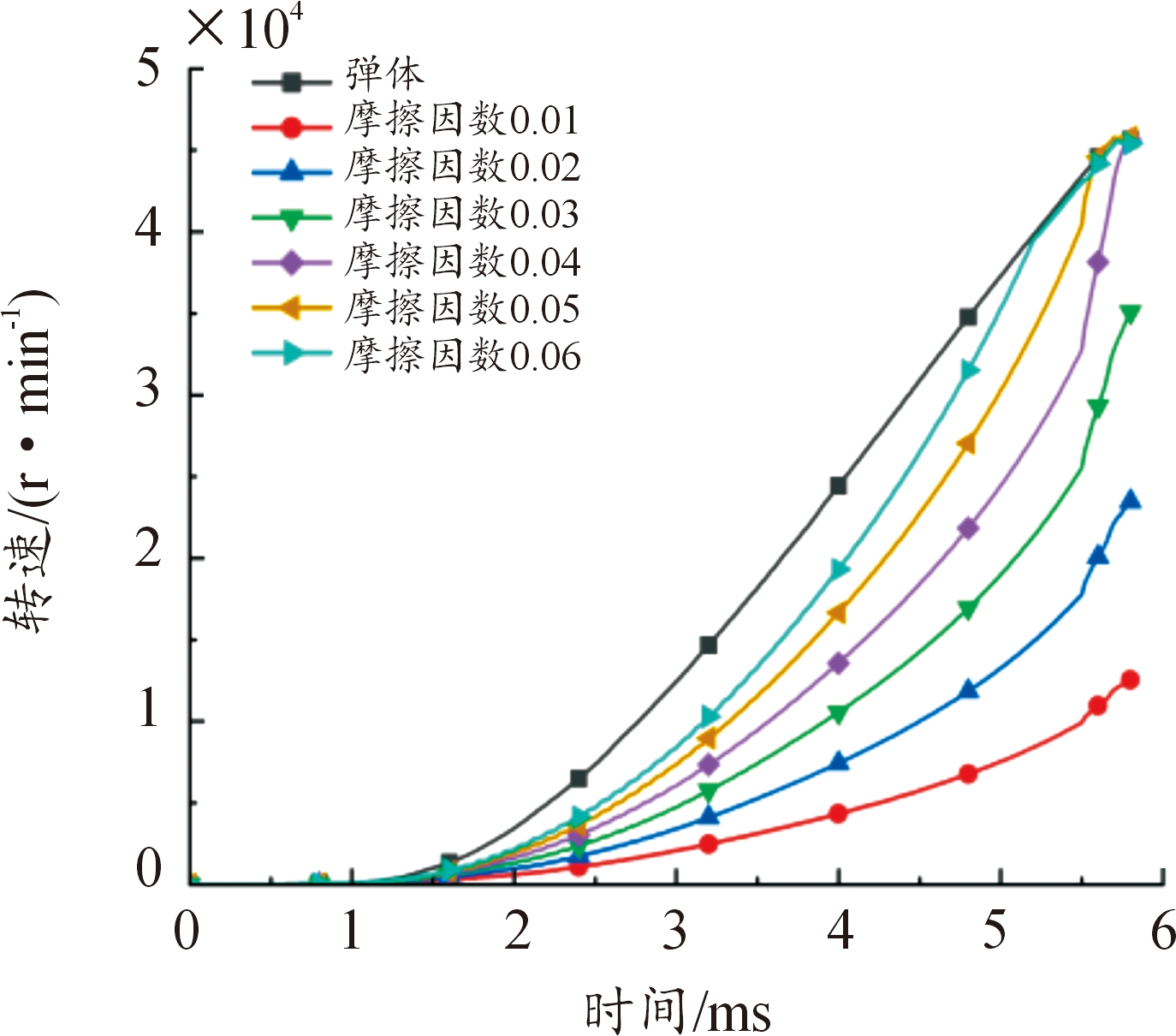
图18 357.9 MPa时各组摩擦因数的转速
Fig.18 Rotational speed of each group offrictional coefficients at 357.9 MPa

图19 357.9 MPa时各组摩擦因数条件下装药侧面应力曲线
Fig.19 Side stress curve of charge under each group of coefficients at 357.9 MPa
从357.9 MPa膛压下的转速图中可以发现,装药与弹体间的相对转速对比334.5 MPa膛压下的情况有减小趋势,表明膛压增大可以改善弹体与装药间的相对转动,从而减小装药产生的摩擦热。观察357.9 MPa膛压下的装药侧面应力变化图可以发现,其规律基本与334.5 MPa膛压的情况下一致,其中应力集中的位置仍是编号为54448的单元(图8中位于最底部的单元)。
当膛压大小为383 MPa时,选取装药与弹体2个部件收集其转速数据,得到各组摩擦因数条件下装药与弹体的转速曲线如图20所示。选取装药侧表面的单元(见图8)收集其应力变化数据,得到各组摩擦因数条件下装药侧面应力变化曲线如图21所示。
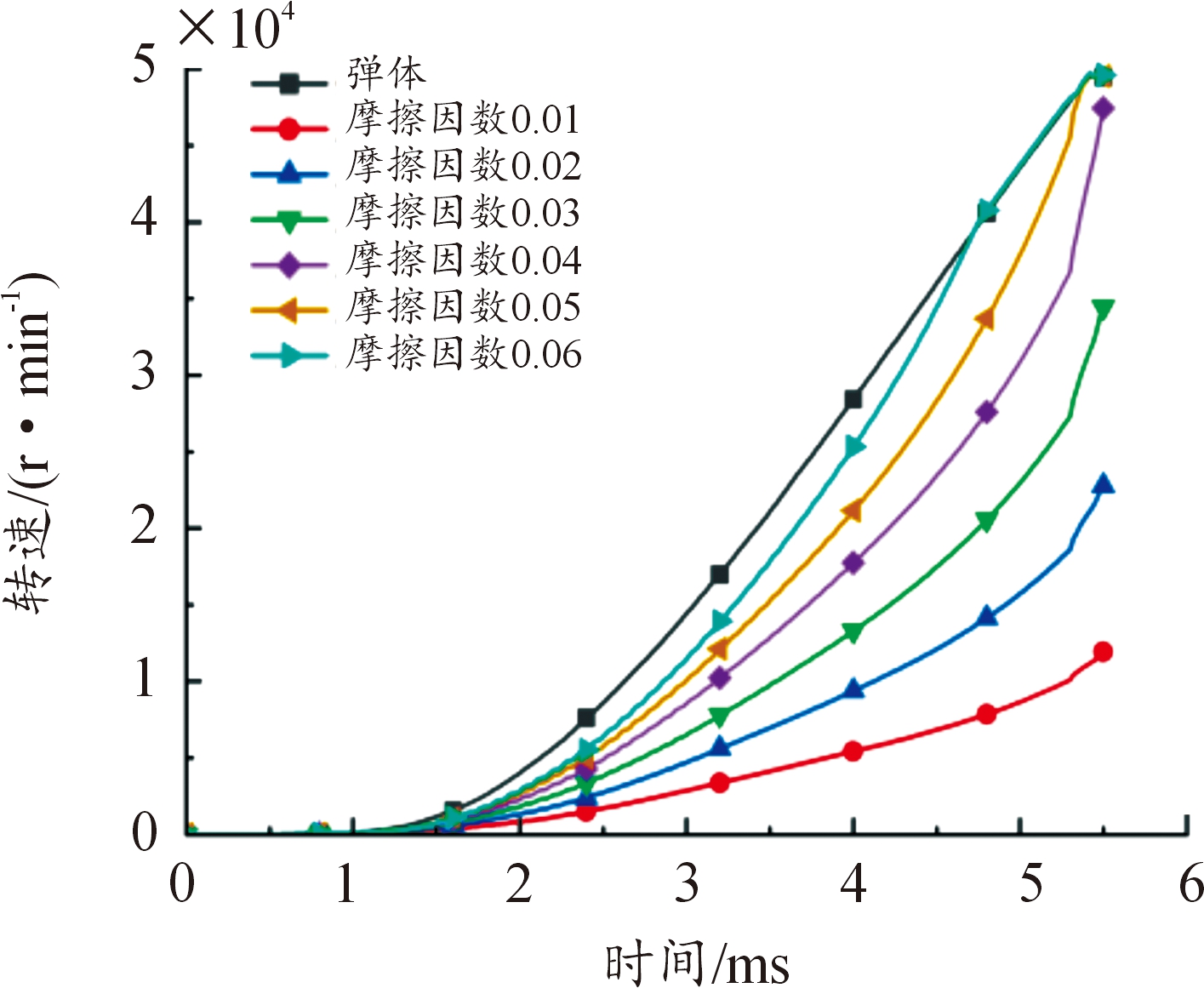
图20 383 MPa时各组摩擦因数的转速
Fig.20 Rotational speed of each group offrictional coefficients at 383 MPa

图21 383 MPa时各组摩擦因数条件下装药侧面应力曲线
Fig.21 Side stress curve of charge under each group of coefficients at 383 MPa
从图20中可以发现,装药转速的变化规律与上述一致,进一步验证膛压增大可以减少弹体与装药间相对旋转的规律。同样,图21中所示的应力变化规律也与上述一致。
当膛压大小为409.8 MPa时,选取装药与弹体2个部件收集其转速数据,得到各组摩擦因数条件下装药与弹体的转速曲线如图22所示。选取装药侧表面的单元(见如图8)收集其应力变化数据,得到各组摩擦因数条件下装药侧面应力变化曲线如图23所示。
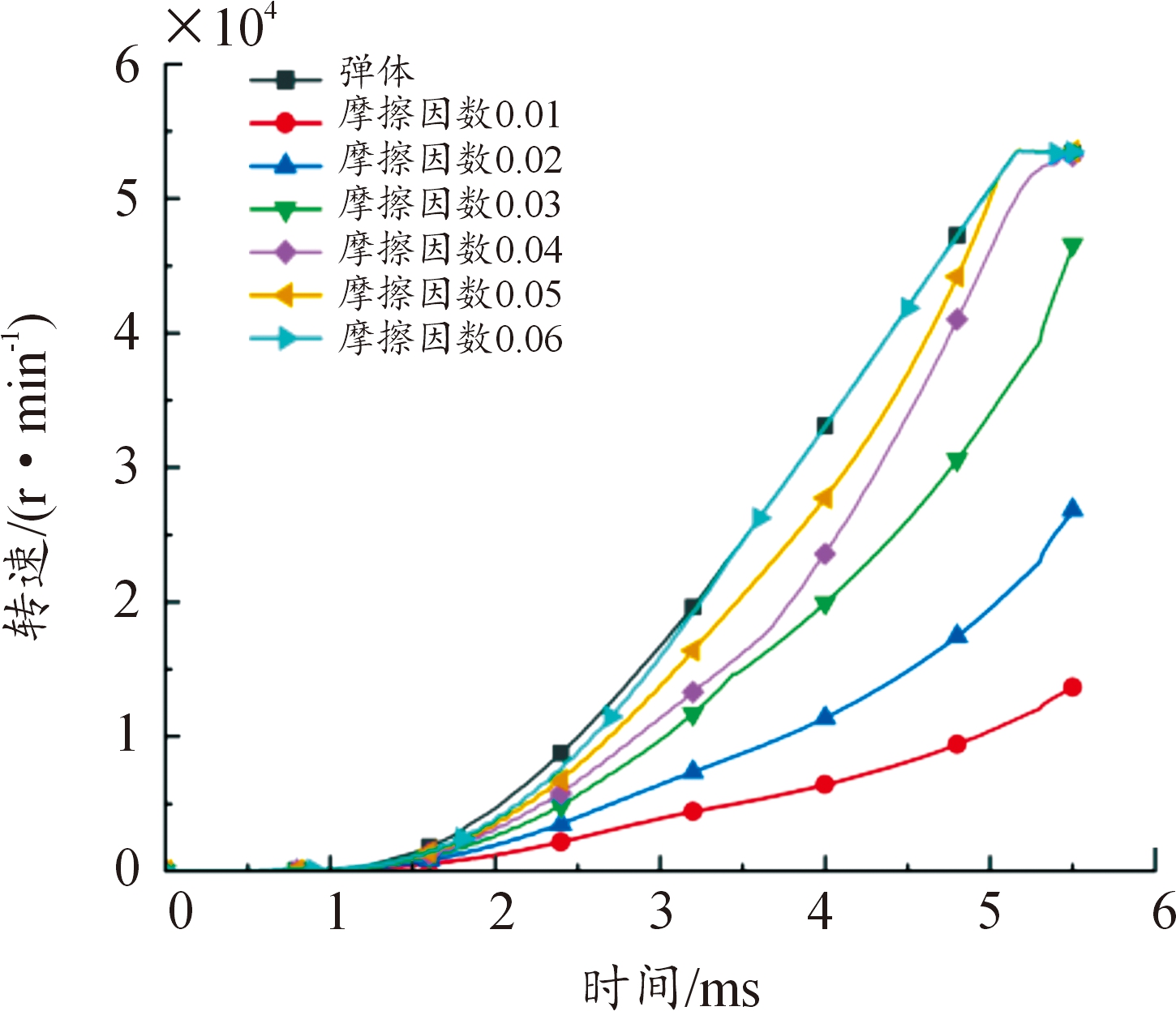
图22 409.8 MPa时各组摩擦因数的转速
Fig.22 Rotational speed of each group offrictional coefficients at 409.8 MPa

图23 409.8 MPa时各组摩擦因数条件下装药侧面应力曲线
Fig.23 Side stress curve of charge under each group of coefficients at 409.8 MPa
从409.8 MPa膛压下的装药转速图可以看出,在摩擦因数为0.06的条件下,装药转速基本与弹体一致,装药与弹体间的摩擦开始向静摩擦转变,随着膛压的增大,装药可以在更小的摩擦因数下实现与弹体的零相对转动,除此之外的规律均与上述一致。
膛压大小为438.5 MPa时,选取装药与弹体两个部件收集其转速数据,得到各组摩擦因数条件下装药与弹体的转速曲线如图24所示。选取装药侧表面的单元(见图8)收集其应力变化数据,得到各组摩擦因数条件下装药侧面应力变化曲线如图25所示。
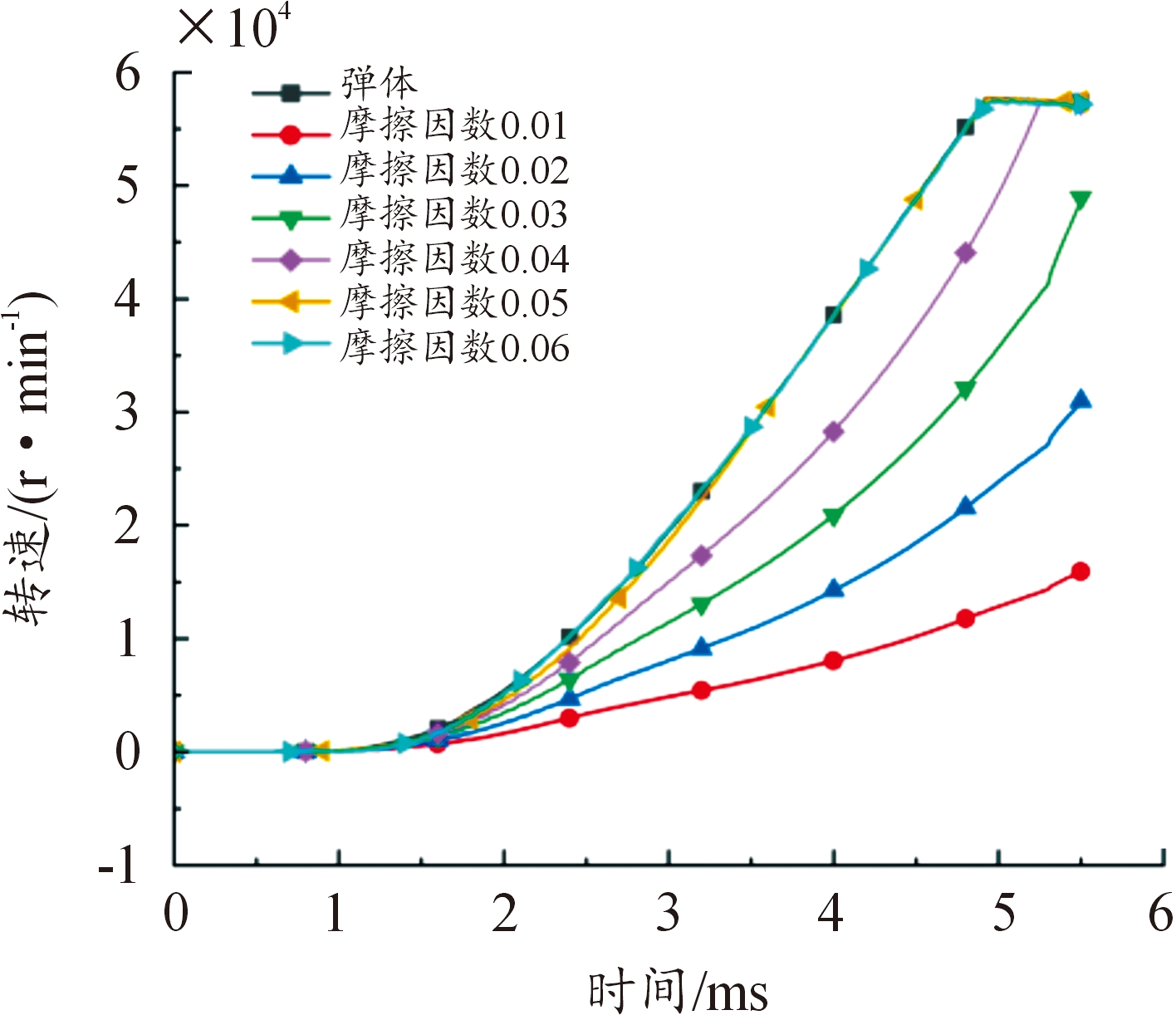
图24 438.5 MPa时各组摩擦因数的转速
Fig.24 Rotational speed of each group offrictional coefficients at 438.5 MPa

图25 438.5 MPa时各组摩擦因数条件下装药侧面应力曲线
Fig.25 Side stress curve of charge under each group of coefficients at 438.5 MPa
通过上述一系列膛压下的仿真数据分析,在膛内运动过程中装药侧面所受的应力均呈先增大后减小的趋势,且在装药底部存在一个受力最大的单元,编号为54448(图8中位于最底部的单元);随着摩擦因数的增大,装药侧面所受的应力峰值整体呈增长趋势,结合装药与弹体的相对转速图可以看出,装药与弹体间大都为动摩擦,在膛压增大后,一部分摩擦因数较大的情况下,装药与弹体间转化为静摩擦,但总体所受的摩擦力作用都呈增长趋势;同时,从各膛压下装药与弹体的转速图中可以发现,摩擦因数相同的条件下,膛压越大弹体及装药的转速越大,装药与弹体间的相对转速越小。
3.3 膛压影响分析
将3.1底隙影响分析中各膛压下的装药应力峰值整合,得到装药在不同膛压下的应力峰值曲线如图26所示。
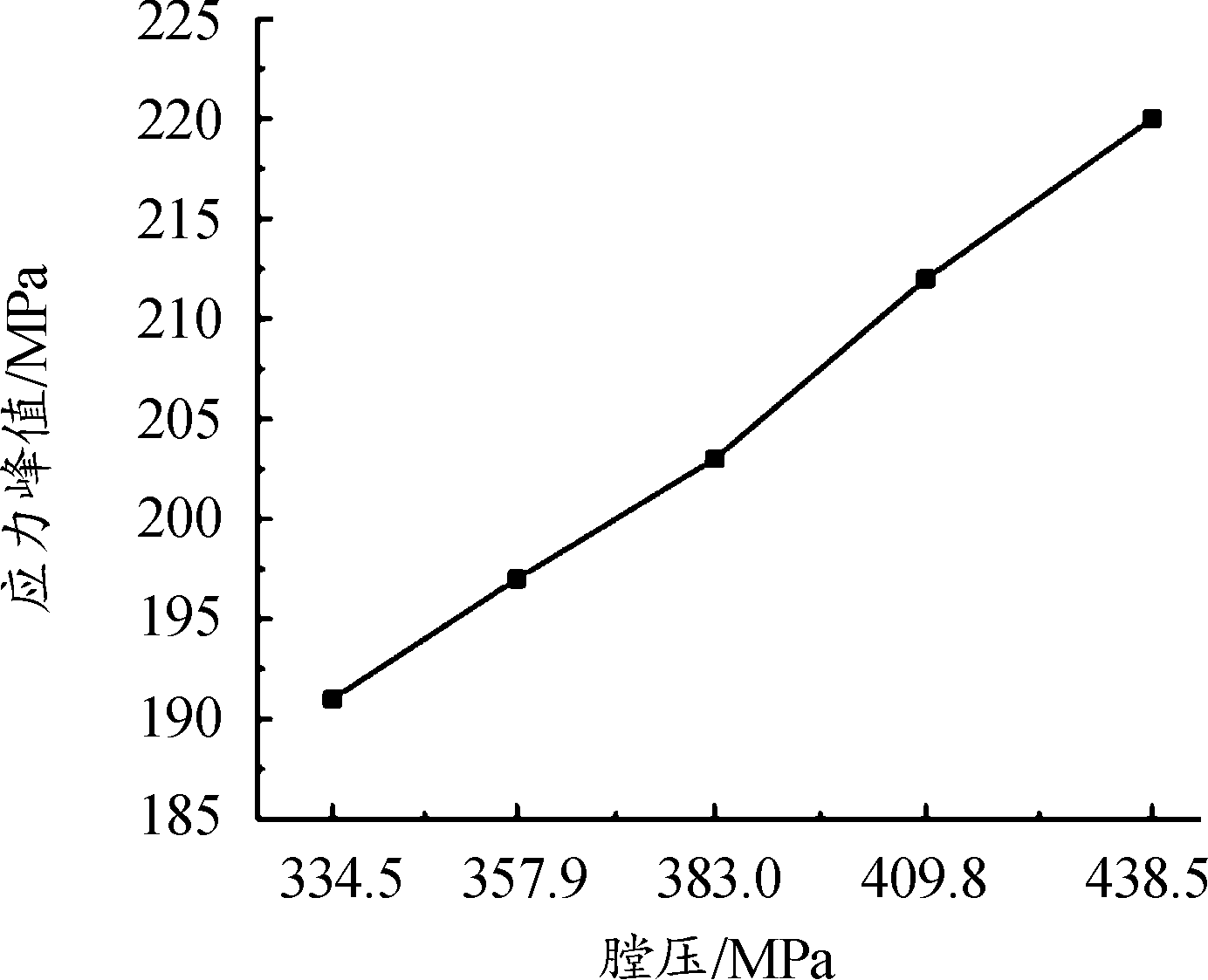
图26 不同膛压下装药底部应力峰值曲线
Fig.26 Peak stress curve of charge bottom under different chamber pressures
将3.2摩擦影响分析中装药侧面受力最大的单元提取出来,给定摩擦因数条件,将其在各膛压下的应力变化曲线整合(见图27)。
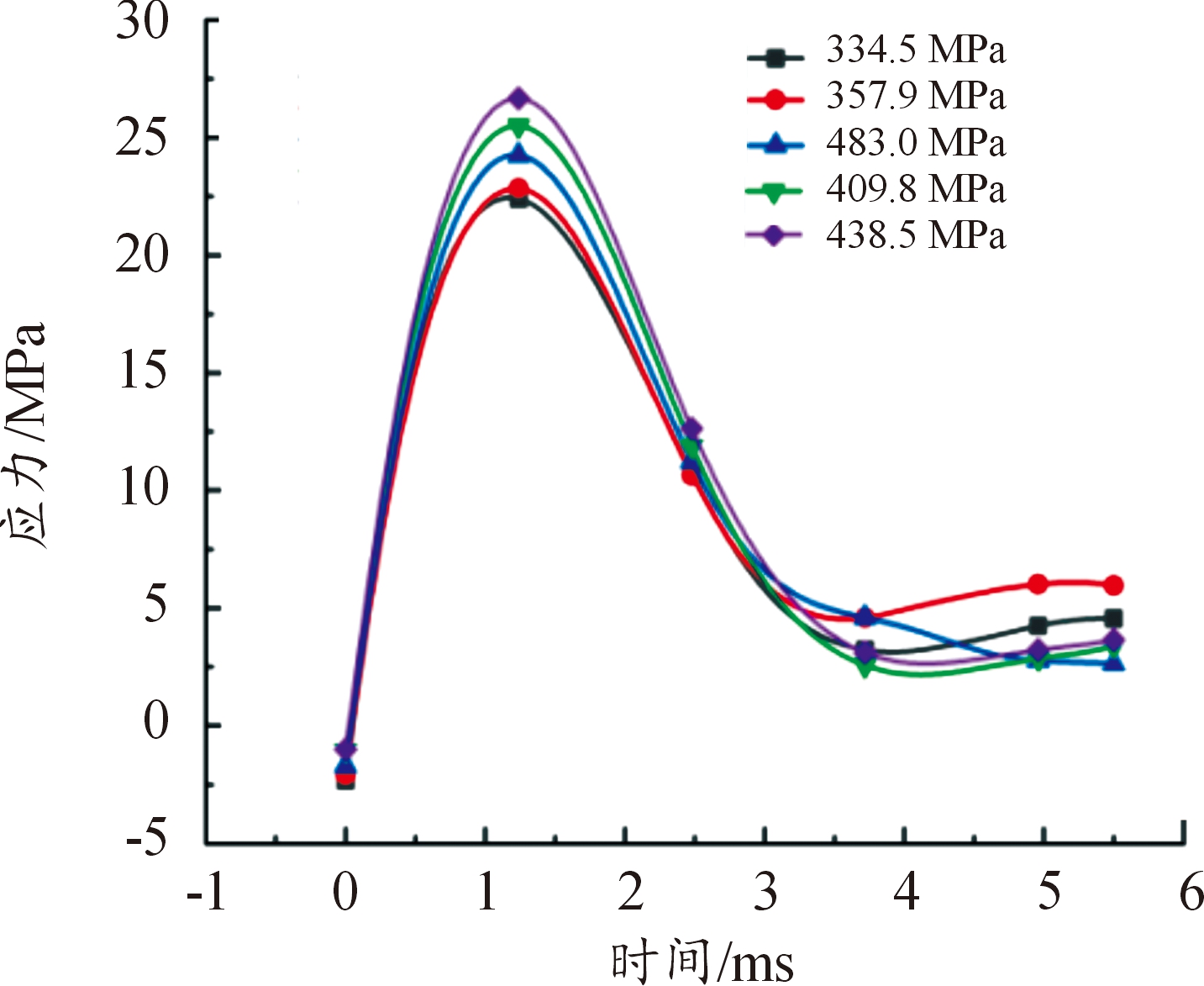
图27 不同膛压下装药侧面应力曲线
Fig.27 Side stress curves of charge under different chamber pressures
从两图中的应力变化曲线可以看出,膛压越大,装药所受的应力峰值越大,对装药安全性的危害越大。因此在设计该类型弹丸时应慎重考虑膛压的大小。
4 结论
1) 装药底面应力峰值随底隙的增大先增大后趋于稳定,过大的应力会造成装药出现散落、早炸的后果,严重影响发射安定性,减小装药底隙是降低膛内发射过程中装药应力的有效措施。
2) 装药侧面应力峰值随摩擦因数的增大而增大,而从时间历程来看,小摩擦因数情况下,运动初期弹体与装药之间出现相对转动,装药侧面所受的应力随时间呈先增大后减小的趋势。过小的摩擦因数易导致二者相对转动,造成热量积累,对装药造成威胁,提高二者之间的摩擦因数,减小摩擦力做功,能有效提高发射过程中的装药安定性。
3) 装药应力峰值随膛压的增大而增大,在底隙和摩擦因数不变的前提下,较大的膛压更易导致装药出现危险,但膛压的增大有利于减小弹体与装药之间的相对转动,降低热量累积,因此,合理优化底隙和摩擦因数,是提高膛压,提高炮口初速和转速的必要前提。
4) 从改变底隙和摩擦因数2种条件对装药应力影响的研究中可以发现,装药底部所受的应力最大,因此在设计弹药时,应多关注装药底部的安定性。
[1] 郭俊行,李艳利.某大口径火炮发射弹丸启动压力研究[J].弹道学报,2022,34(2):80-85.
GUO Junhang,LI Yangli.A study on initial pressure of projectile engraving process for large calibr gun[J].Journal of Ballistics,2022,34(2):80-85.
[2] 孙全兆,杨国来,王鹏,等.某大口径榴弹炮弹带挤进过程数值模拟研究[J].兵工学报,2015,36(2):206-213.
SUN Quanzhao,YANG Guolai,WANG Peng,et al.Numerical simulation of projectile belt extrusion of a large caliberhowitzer[J].Acta Armamentarii,2015,36(2):206-213.
[3] 丁传俊,张相炎.基于热力耦合有限元模型的弹带挤进过程及内弹道过程的仿真研究[J].兵工学报,2015,36(12):2254-2261.
DING Chuanjun,ZHANG Xiangyan.Simulation study on projectilebelt extrusion and interior ballistics based on thermomechanical coupling finite element model[J].Acta Armamentarii,2015,36(12):2254-2261.
[4] 李淼,钱林方,孙河样.某大口径弹带热力耦合挤进运动学数值模拟研究[J].兵工学报,2016,37(10):1804-1813.
LI Miao,QIAN Linfang,SUN Heyang.Numerical simulation of thermomechanical coupling squeezing kinematics of a large caliber projectile belt[J].Acta Armamentarii,2016,37(10):1804-1813.
[5] 来峰,芮筱亭,王浩,等.对发射装药引起膛炸机理的讨论[J].兵工学报,2007(2):153-157.
LAI Feng,RUI Xiaoting,WANG Hao,et al.Discussion on the mechanism of chamber explosion caused by propellant charge[J].Acta Armamentarii,2007(2):153-157.
[6] 芮筱亭,冯宾宾,王燕,等.发射装药发射安全性评定方法研究[J].兵工学报,2015,36(1):1-11.
RUI Xiaoting,FENG Binbin,WANG Yan,et al.Study on launch safety evaluation of propellant charge[J].Acta Armamentarii,2015,36(1):1-11.
[7] 顾健,芮筱亭,刘飞飞,等.模拟发射环境下炸药装药发射安全性试验研究[C]//第一届机械系统动力学国际会议论文集.南京,2022.
GU Jian,RUI Xiaoting,LIU Feifei,et al.Research on the launch safety test of explosive charge under simulated launch environment[C]//1st International Conference on Mechanical System Dynamics.Nanjing,2022.
[8] 赵鑫,芮筱亭,黎超等.基于支持向量回归的发射装药发射安全性评估与预测方法[J].应用软计算,第 109 卷,2021年9月.
ZHAO Xin,RUI Xiaoting,LI Chao,et al.Evaluation and prediction methods for launch safety of propellant charge based on support vector regression[J].Applied Soft Computing,September 2021,Volume 109.
[9] 徐赫阳,乔相信,郭克强,等.某线膛火炮战斗部发射强度数值模拟[J].沈阳理工大学学报,2016,35(3):75-78,106.
XU Haoyang,QIAO Xiangxin,GUO Keqiang,et al.Numerical simulation of firing intensity of a line-bore gun warhead[J].Journal of Shenyang Ligong University,2016,35(3):75-78,106.
[10] 许耀峰,丁宏民,徐坚,等.大口径火炮膛线结构对滑动弹带弹丸膛内运动影响的数值分析[J].兵工学报,2016,37(11):2148-2156.
XU Yaofeng,DING Hongmin,XU Jian,et al.Numerical value of the influence of rifling structure of large caliber gun on the motion of sliding projectile in bore[J].Acta Armamentarii,2016,37(11):2148-2156.
[11] 王韫泽,王树山,魏平亮,等.穿甲弹异物阻滞膛炸机理数值仿真分析[J].兵工学报,2018,39(5):859-866.
WANG Yunze,WANG Shushan,WEI Pingliang,et al.Numerical simulation of foreign body blocking bore explosion mechanism of armorpiercing projectile[J].Acta Armamentarii,2018,39(5):859-866.
[12] 李文彬,王晓鸣,赵国志,等.装药底隙对弹底应力及发射安全性影响研究[J].弹道学报,2001(3):64-67,72.
LI Wenbin,WANG Xiaoming,ZHAO Guozhi,et al.Study on the influence of charge bottom gap on projectile bottom stress and launch safety[J].Journal of Ballistics,2001(3):64-67,72.
[13] 李文,阎华,张琦,等.发射载荷下弹头炸药内孔隙的压缩过程[J].国防科学杂志,2010,60(3):244-250.
LI Wen,YAN Hua,ZHANG Qi,et al.Compression process of pore inside explosive charge in a warheadunder launching Load[J].Defence Science Journal,2010,60(3):244-250.
[14] 张琦,胡少桥,梁慧敏,等.落锤冲击下B炸药孔隙对感度的影响[J].国防科学杂志,2013,63(1):108-113.
ZHANG Qi,HU Shaoqiao,LING Huimin,et al.Effect of porein composition-B explosive on sensitivity under impact of drop weight[J].Defence Science Journal,2013,63(1):108-113.
[15] 彭嘉诚,蒋建伟,廖伟.高速旋转弹丸炸药装药在膛内运动中底层温度的数值模拟[J].兵工学报,2020,41(9):1783-1791.
PENG Jiacheng,JIANG Jianwei,LIAO Wei.Numerical simulation of bottom layer temperature during the motion of high-speed rotating projectile explosive charge in the chamber[J].Acta Armamentarii,2020,41(9):1783-1791.
[16] 张涛,肖洋,郭晓红,等.不同装药工艺对装药安定性的影响[J].弹箭与制导学报,2011,31(2):86-88.
ZHANG Tao,XIAO Yang,GUO Xiaohong,et al.Influence of different charge processes on charge stability[J].Journal of Projectiles,Rockets,Missiles and Guidance,2011,31(2):86-88.
[17] 魏惠之,朱鹤松,汪东晖,等.弹丸设计理论[M].北京:国防工业出版社,1985:122-123.
WEI Huizhi,ZHU Hesong,WANG Donghui,et al.Projectile design theory[M].Beijing:National Defense Industry Press,1985:122-123.