0 引言
滚动轴承作为旋转机械结构的核心部件,其特殊的结构和承力方式致使其非常容易退化失效,是旋转机械结构中较为薄弱的部分,因此,开展滚动轴承的剩余寿命研究,对滚动轴承的剩余寿命进行精准预测可有效保证设备的运行状态,降低设备的维护成本[1-3]。
滚动轴承的剩余寿命预测主要包括特征指标的提取与融合和预测模型的建立2个部分[4]。但目前这两部分面临着特征提取困难和寿命分布获取困难的问题。
特征指标的提取与融合即构建性能退化因子目前主要有2种思路,一种是利用统计学或信号处理的方法构建物理退化因子,一种是通过机器学习方法构建虚拟退化因子。文献[5]中通过小波包变换提取节点能量构建物理退化因子。文献[6]中通过提取时间序列排列熵构建物理退化因子。随着计算机技术不断发展和传感器监测数据类型的丰富多样,基于深度学习方法构建虚拟退化因子逐渐成为研究热点。基于深度学习的性能退化因子构建方法具有深度学习的优点,可提取更深层次性能退化特征信息,更完整地表征设备性能退化过程。文献[7]中通过堆叠去噪自编码器构建虚拟退化因子。文献[8]中通过快速傅里叶变换得到滚动轴承的时频图,并构建一种多尺度卷积神经网络模型来得到性能退化因子。文献[9]中提出一种卷积神经网络和长短时记忆网络相结合的方法,通过卷积神经网络提取滚动轴承深层退化特征信息作为输入,利用长短时记忆网络与标签数据映射得到性能退化因子。
对于预测模型的建立,考虑到滚动轴承的退化过程是在外界应力影响下的发生的一种渐进变化过程,属于随机过程,运用随机过程理论建立预测模型更容易获取设备寿命分布且更加符合工程实际。文献[10]中提出利用Logistic回归模型结合PCA的方法实现滚动轴承剩余寿命预测。文献[1]建立基于广义Wiener过程的退化模型实现滚动轴承的剩余寿命预测。文献[11]中提出一种指数模型和贝叶斯更新相结合的滚动轴承剩余寿命预测方法。文献[12]中利用伽玛过程建立状态空间模型实现滚动轴承剩余寿命预测。
本文中结合深度学习和随机过程的优点,将深度学习(Deep Learning)方法和伽玛过程(Gamma Process)结合,采用深度卷积神经网络和双向长短时记忆网络结合的混合输入网络构建性能退化因子,针对性能退化因子单调递增趋势良好的特点采用伽玛过程建立预测模型,实现对滚动轴承剩余寿命的预测,有效解决特征提取困难和寿命分布难以获得的问题。
1 原理介绍
1.1 深度卷积神经网络
深度卷积神经网络(deep convolution neural network,DCNN)是由卷积神经网络改进得到。卷积神经网络(convolution neural networks,CNN)是通过对猫的视觉皮层细胞研究而得到一种类似于神经认知机的人工网络模型,其本质是多层感知机(multi-layer perceptron,MLP)[13]。一个完整的卷积神经网络包括输入层、卷积层、池化层、全连接层和输出层,深度卷积神经网络在此基础上通过增加卷积层和池化层,并将其交替连接来实现对深层次特征的学习,其基本结构如图1所示。随着计算机技术不断发展,深度卷积神经网络规模越来越大,其应用范围也越来越广泛。
图1 DCNN基本结构
Fig.1 Basic structure of DCNN
卷积层的任务是提取输入的不同特征,其对特征的提取类似人类通过观察事物某个部分判别事物整体,可将输入数据分成不同部分来提取典型特征,此时需要引入卷积运算。卷积运算是指在三维的输入特征图上通过滑动窗口提取三维的特征图块来与权重矩阵(即卷积核)做张量积得到一维的张量,随后将这些张量输入至激活函数进行非线性映射得到三维的输出特征图。卷积过程的计算公式为
xl= f(∑xl-1*kl+bl)
(1)
式中:xl为l层的特征图;xl-1为l-1层的特征图;kl为l层的卷积核;bl为l层的偏置项; f为激活函数,常用的激活函数包括Sigmoid、Softmax、Tanh、ReLU等。
池化层的作用是对特征图进行采样,减少特征图在空间上的运算,其运算过程与卷积类似。其中最大池化是最常用的池化方法,它通过从输入特征图中提取窗口取最大值来实现池化。
全连接层的作用是得到最终的输出特征,前面经过卷积层和池化层的输出特征图要经过展平处理变为一维张量,最后输入至全连接层得到输出。
全连接层的输出可表示为
O= f (∑xFω+b)
(2)
式中:O为最终输出值;xF为全连接层的神经元;ω为神经元和输出层的权重;b为偏置项; f为激活函数。
DCNN网络展平层可表示为
Omul_layer=f(∑xpoolωpool+b)
(3)
式中:Omul_layer为展平层的输出值; xpool和ωpool分别为最后一层池化层的神经元和权重;b为偏置项; f为sigmoid激活函数。
1.2 双向长短时记忆网络
卷积神经网络在处理数据时要将数据变为张量,网络内部对所处理数据并不会产生记忆,属于前馈网络(feedforward network)。针对时间序列数据需要网络模型动态地对数据进行遍历和更新,循环神经网络(recurrent neural network,RNN)便可很好实现这一目的。RNN是一种具有内部环的神经网络,可对遍历过的数据产生记忆并保存一个内部模型,且这一模型可随着新数据不断输入而更新。但RNN内部结构过于简单,处理长序列时可能会产生梯度消失问题(vanishing gradient problem),为解决这一问题,长短时记忆网络(long-short term memory network,LSTM)应运而生。LSTM由RNN演变过来,其在网络内部加入一条历史信息传送带,可将历史信息跨越多个时间步进行携带,历史信息可从任意单元输入至传送带上,这样就可以放置早期信息在序列处理过程中消失。LSTM网络结构如图2所示。
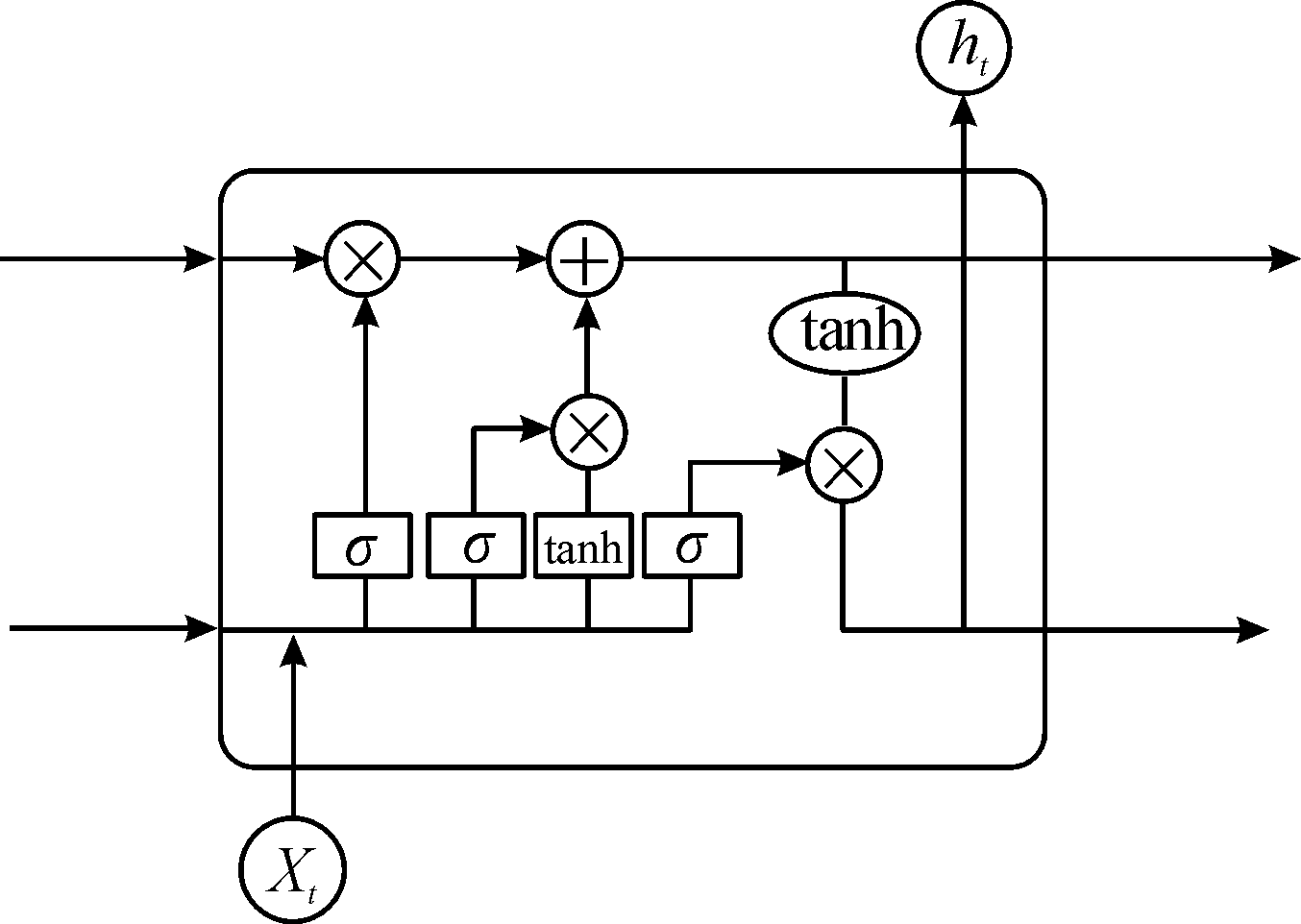
图2 LSTM网络结构
Fig.2 LSTM network structure
LSTM每个记忆单元主要有遗忘门、更新门、输出门组成,式(4)表示遗忘门工作过程,式(5)—式(7)表示更新门工作过程,式(8)和式(9)表示输出门过程。
ft=σ(Wf·[ht-1,xt]+bf)
(4)
it=σ(Wi·[ht-1,xt]+bi)
(5)
(6)
(7)
ot=σ(Wo·[ht-1,xt]+bo)
(8)
ht=ot*tanh(Ct)
(9)
式中:ft为遗忘门的输出值;
为更新门输出的更新值;ot、ht为输出门的输出值和隐藏层的输出值;Wf、Wi、Wc、Wo为权重矩阵;bf、bi、bc、bo为偏置项。
在LSTM基础上,双向长短时记忆网络(bi-directional long-short term memory network,Bi-LSTM)内部包含2个LSTM模型,分别按照时间正序和时间逆序对数据进行处理,Bi-LSTM工作原理如图3所示。相对于基本的LSTM,Bi-LSTM可捕捉单一正向序列遍历忽略的信息特征。
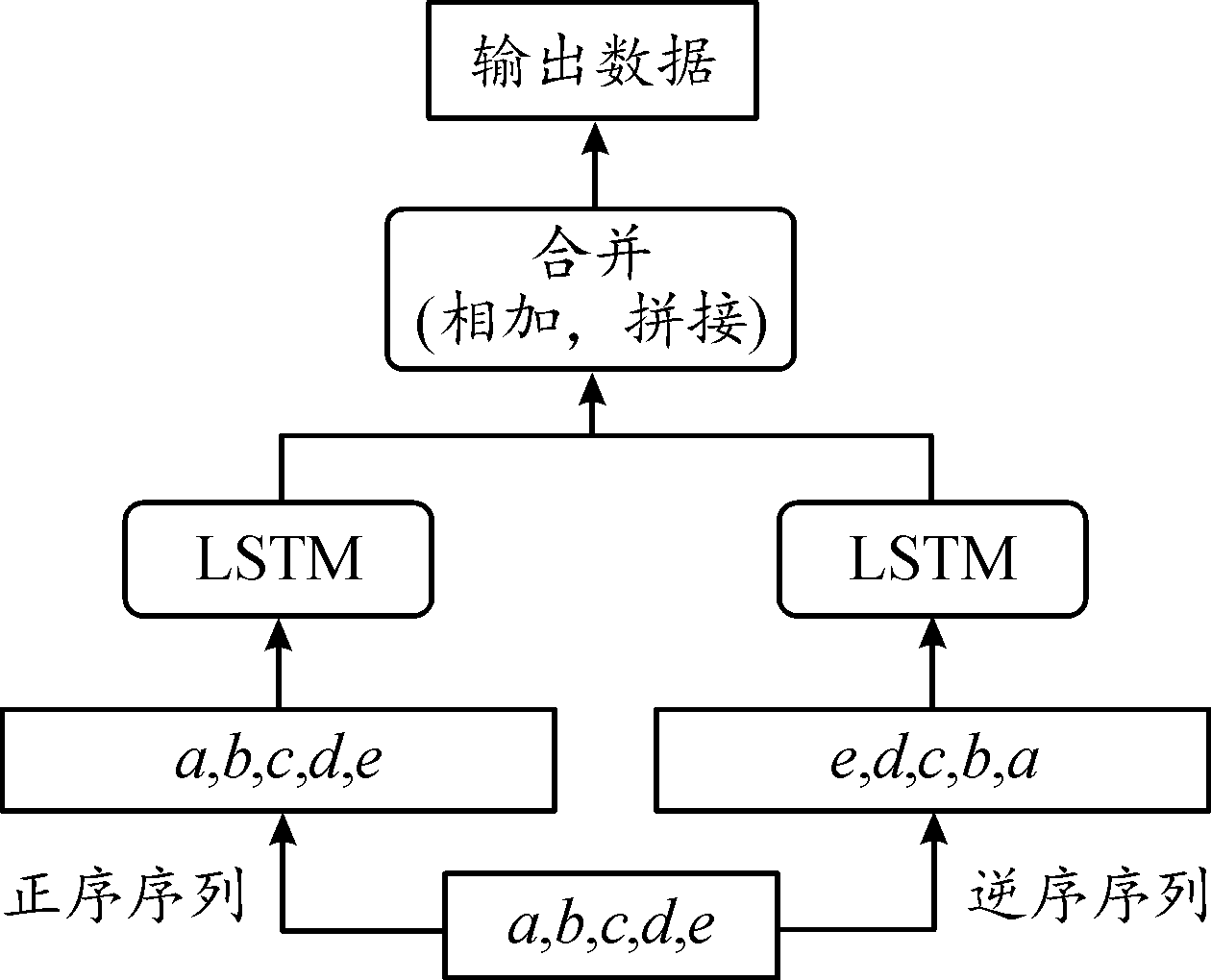
图3 Bi-LSTM工作原理框图
Fig.3 Bi-LSTM working principle diagram
1.3 伽玛过程
了解伽玛过程首先要了解伽玛分布,伽玛分布(Gamma Distribution)是一种连续概率函数,其代表随机事件中第n个事件发生概率的分布,其定义与泊松过程(poisson process)和指数分布(exponential distribution)分不开。指数分布是泊松过程中事件间隔的分布,由此可将伽玛分布直观地理解为n倍的指数分布,即伽玛分布是泊松分布在正实数上的连续化版本。伽玛分布的概率密度函数如式(10)所示,式中α>0为形状参数,β>0为尺度参数,式(11)是α>0时的伽玛函数。
(10)
Γ(α)=
tα-1e-tdt
(11)
伽玛过程是一种增量服从具有恒等尺度参数伽玛分布的连续时间随机过程。在伽玛分布的基础上,伽玛过程的形状参数α(t)随时间t发生变化,尺度参数β保持不变,其概率密度函数为:
fX(t)(x)=Ga(x|α(t),β)
(12)
其均值和方差为:
(13)
(14)
对均值求导可得
可见形状参数α(t)的导数反映的是设备的平均退化速率,当形状参数α(t)跟时间t呈线性关系时,设备的退化过程为平稳退化过程。
1.4 参数估计
对于伽玛退化过程的形状参数和尺度参数常采用矩估计法和极大似然估计法对其进行估计[14],由于本文中选用的性能退化因子的样本量较为充足,所以采用矩估计法对参数进行估计。对于非平稳伽玛退化过程的参数估计首先要将其转化为平稳伽玛过程再进行参数估计。通常情况下非平稳伽玛退化过程的期望退化水平可表示为式(15),在工程运用中常采用式(16)将退化过程的均值和方差表示为式(17)和式(18),这样关于时间t的非平稳伽玛退化过程就转变为关于时间z 的平稳伽玛退化过程。
(15)
z(t)=tb
(16)
(17)
(18)
针对参数b的估计可采用最小二乘法,首先对式(15)两边取对数得式(19),这样便可将参数b的求解转换为求解直线的斜率,根据最小二乘法可得式(20)对参数b进行求解。
logE[X(t)]=blogt+log(c/β)
(19)
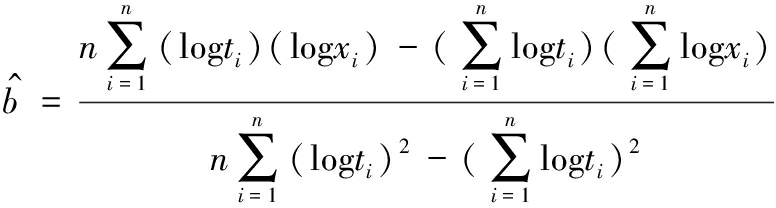
(20)
矩估计法属于点估计的一种,其核心思想为利用样本矩估计总体矩,即样本矩收敛于相应的总体矩,样本矩的连续函数收敛于总体矩的连续函数。设Δxi=xi-xi-1,Δzi=zi-zi-1,用Δxi/Δzi定义退化率,根据伽玛过程的性质,其退化率服从伽玛分布。经计算可得退化率的样本均值和样本方差为:
(21)
根据矩估计的思想和式(21)可得:
(22)
因此可得到总体方差为:
(23)
联系矩估计的思想根据上式可得
(24)
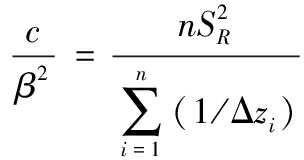
(25)
求解式(24)和式(25)可得参数的估计值为:
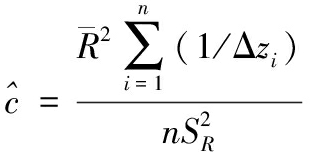
(26)
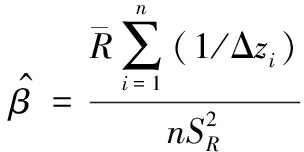
(27)
1.5 剩余寿命分布
通常情况下,设备在性能退化值到达某一阈值时即认定为设备失效,这种失效称为首次通过型失效,在这种失效情况下设备的寿命值是设备从开始运转到首次到达失效时刻的时间长度。当设备的退化过程符合伽玛过程时,设备的寿命分布为式(28)。其中,ζ表示设备的失效阈值,γ(a,x)表示上不完全伽玛函数,表达式为式(29)。
(28)
γ(a,x)=
ta-1e-tdt
(29)
得到设备的寿命分布后,寿命的一阶矩和二阶矩表示为:
E[T]=
[1-FT(t)]dt
(30)
E[T2]=2t[1-FT(t)]dt
(31)
对于寿命的一阶矩和二阶矩通常可采用泊松近似的方法求解。设qn=Pr{tn<Tξ≤tn+1},令tn=n/α(n=0,1,2,…),再对式(28)进行离散时间近似,得到式(32)。
(32)
通过式(32)可以看出,设备在区间(n/α,(n+1)/α]发生失效的概可以近似为泊松分布,该分布的均值为ζβ/α,方差为ζβ/α2。
若已知设备当前的工作周期tc,通常情况下设备的剩余寿命分布可表示为式(33)。但用式(33)对表示剩余寿命分布只考虑了设备的已工作时间,若想得到更为准确的剩余寿命分布还应考虑到设备的已退化程度,代入已退化程度,设备的剩余寿命表示为式(34)。
FT(t|tc)=Pr(T≤t∣T>tc)=
(33)
FT(t∣tc)=Pr(T≤t∣X(tc)=xc)=
Pr(X(t)-X(tc)≥ζ-xc)=
(34)
对于伽玛退化过程寿命分布的t时刻的可靠度函数可表示为式(35)。式中γl(a,x)=
ta-1e-tdt,x≥0,a≥0称为下不完全伽玛函数。
R(t)=P(T≥t)=P{X(t)≤ζ}=
(35)
2 方法流程
混合网络的结构如图4所示。输入层包括2部分,一部分是原始数据典型时域频域特征组成的一维时间序列数据,一部分是利用连续小波变换得到的原始数据时频图组成的二维图像序列数据。本文中选取文献[15]中提出的24个典型时域频域特征。将一维时间序列数据和二维图像序列数据分别输入Bi-LSTM和DCNN中,输出结果展平连接后输入至全连接层得到性能退化因子。
图4 混合网络结构
Fig.4 Hybrid network structure
基于DL-Gamma的滚动轴承剩余寿命预测方法具体步骤如下:
Step1:提取原始数据典型时域频域特征作为一维时间序列数据;
Step2:对原始数据进行连续小波变换得到时频图作为二维图像序列数据;
Step3:划分训练集和测试集,训练混合网络;
Step4:将测试集输入训练好的网络得到性能退化因子;
Step5:对性能退化因子曲线进行拟合,并利用矩估计法对退化曲线进行参数估计;
Step6:根据参数估计结果得到设备的剩余寿命分布,预测设备的剩余寿命。
3 试验验证
3.1 性能退化因子构建
本试验采用FEMTO-ST数据集[16],试验平台为FEMTO-ST搭建的PROGNOSTIA平台,试验平台主要有3部分组成:旋转部分、负载部分、测试部分,如图5所示。旋转部分主要由电机控制,电机功率为250 W,最高转速可达2 830 r/min;负载部分由气动千斤顶提供4 000 N的动载荷;测试部分主要由2个振动传感器和一个温度传感器组成,2个振动传感器沿径向放置在轴承外圈上,一个放置在水平轴,一个放置在垂直轴,采样频率为25.6 kHz,采样周期设置为每10 s采样一次,每次采集2 560个点即采样时长为0.1 s。
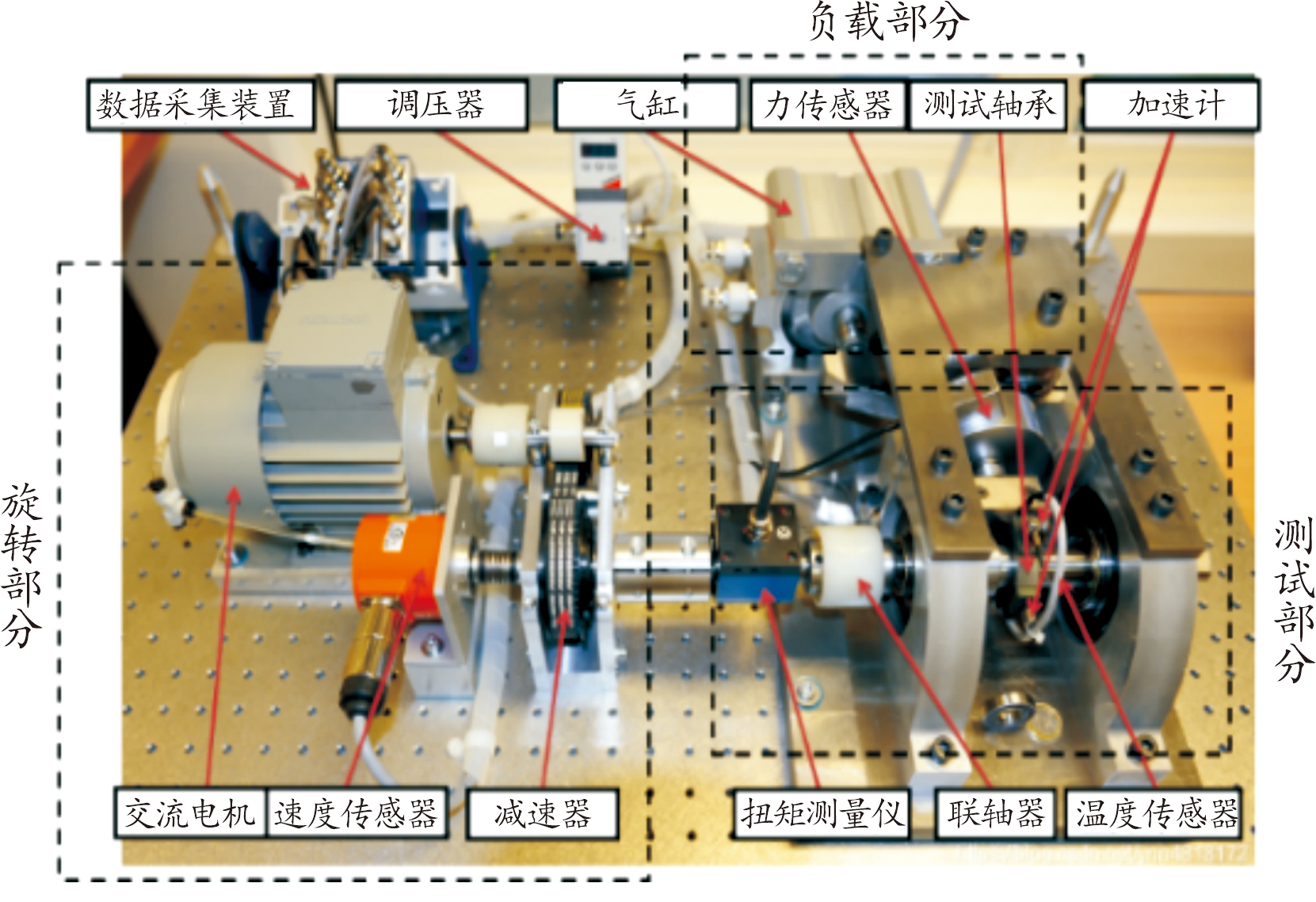
图5 PROGNOSTIA轴承全寿命周期测试平台
Fig.5 PROGNOSTIA bearing life cycle testing platform
本文中随机选取工况1(负载4 000 N,转速1 800 r/min)下Bearing1_3和Bearing1_5作为训练集,Bearing1_1作为测试集。混合输入数据中一维时间序列数据由24个时域和频域特征组成,二维图像数据由连续小波变换得到的时频图组成,具体输入可表示为
其中
表示t时间周期内振动信号的时频域特征向量,
表示为t时间周期的时频图,时频图尺寸设置为100×100,yt∈[0,1]表示为t时间周期内设备的性能退化程度即训练标签。本文中按照线性过程对训练标签进行设置,以0表示为轴承的起始状态,以1表示为轴承的失效状态,T表示为轴承的寿命,则t周期轴承的性能退化程度为yt=t/T。经过不断调整与优化后,网络的参数如表1所示。
表1 网络参数
Table 1 Network parameter
网络层参数输入层二维图像数据:尺寸:[100×100],通道数:3一维时间数据:尺寸:[24×1]卷积层1卷积核尺寸:[11×11],步长:4,通道数:96池化层1卷积核尺寸:[3×3],步长:2,通道数:96卷积层2卷积核尺寸:[5×5],步长:1,通道数:256池化层2卷积核尺寸:[3×3],步长:2,通道数:256卷积层3卷积核尺寸:[3×3],步长:1,通道数:384卷积层4卷积核尺寸:[3×3],步长:1,通道数:384卷积层5卷积核尺寸:[3×3],步长:1,通道数:256池化层5卷积核尺寸:[3×3],步长:2,通道数:256CNN展平层通道数:1 024Bi-LSTM层单元数:160
续表(表1)
网络层参数CNN+Bi-LSTM连接层节点数:1 184(1 024+160)全连接层1通道数:800全连接层2通道数:200全连接层3通道数:20输出层通道数:1
将测试集输入网络后得到的性能退化因子结果如图6所示,图中横坐标代表滚动轴承的运行周期,纵坐标代表得到的性能退化因子值。
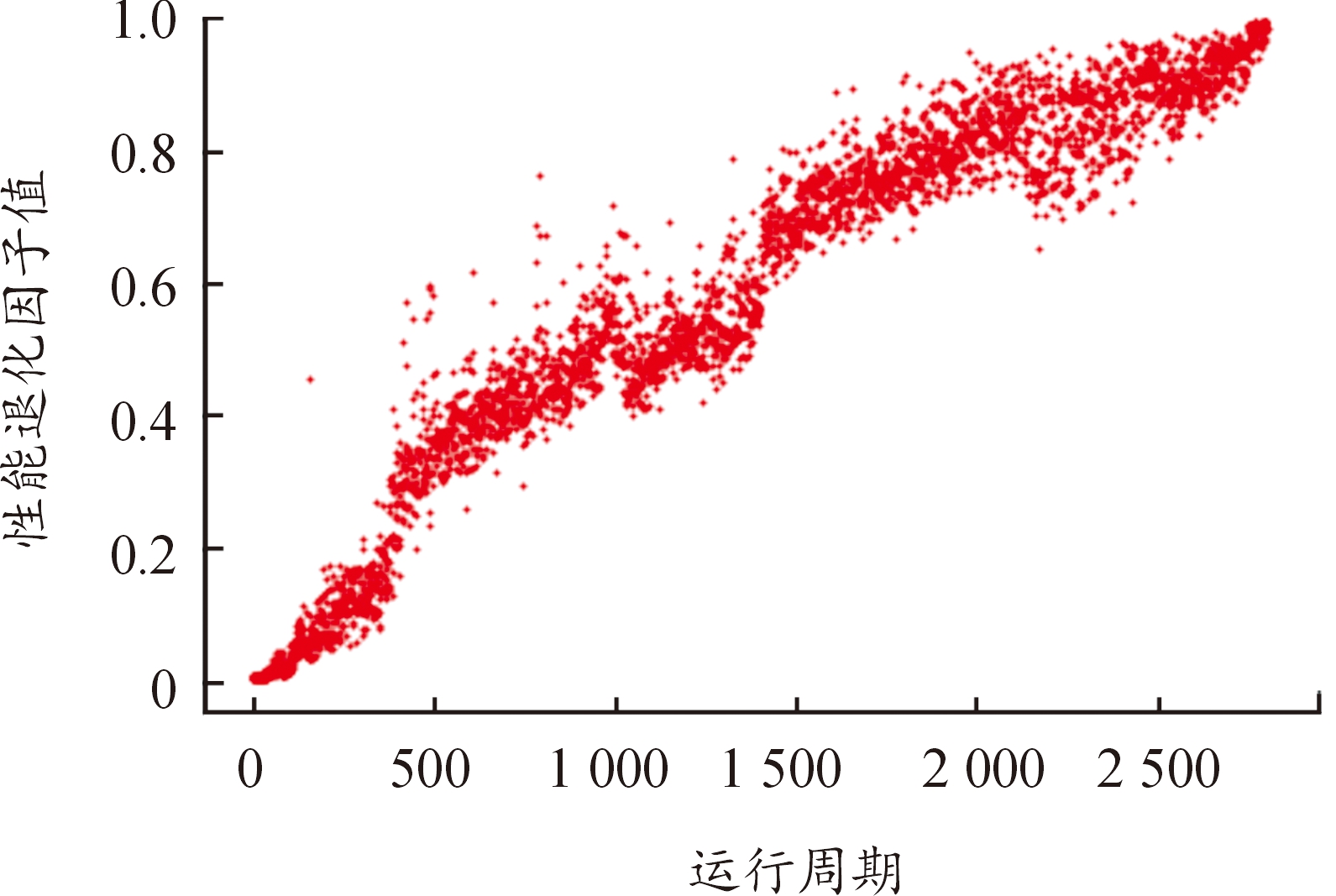
图6 Bearing1_1性能退化因子分布图
Fig.6 Bearing1_1 performance degradation factor distribution
3.2 性能退化因子构建方法对比
为充分证明本文中性能退化因子构建方法的有效性,本节选取文献[17]和文献[18]中运用的单调性、预测性、鲁棒性分别对单一DCNN网络、单一Bi-LSTM网络和混合输入网络得到的性能退化因子进行评估,评估结果如图7所示。
图7 不同方法构建性能退化因子评估对比
Fig.7 Comparison of performance degradation factor evaluation by different methods
从评估结果可以看出,混合网络对比单一网络,虽然单调性不如单一DCNN网络,但综合3个性质来看,混合网络效果更好一些。
3.3 剩余寿命预测模型构建
对性能退化因子的分布进行曲线拟合,因利用混合网络对性能退化因子进行构建时根据线性过程设置训练标签,所以性能退化因子分布具有良好的趋势性,故采用多项式拟合方法便可对性能退化因子分布进行效果较好地拟合,且多项式拟合得到的曲线也可满足伽玛退化过程恒单调递增不可逆的性质,拟合后的曲线如图8所示。
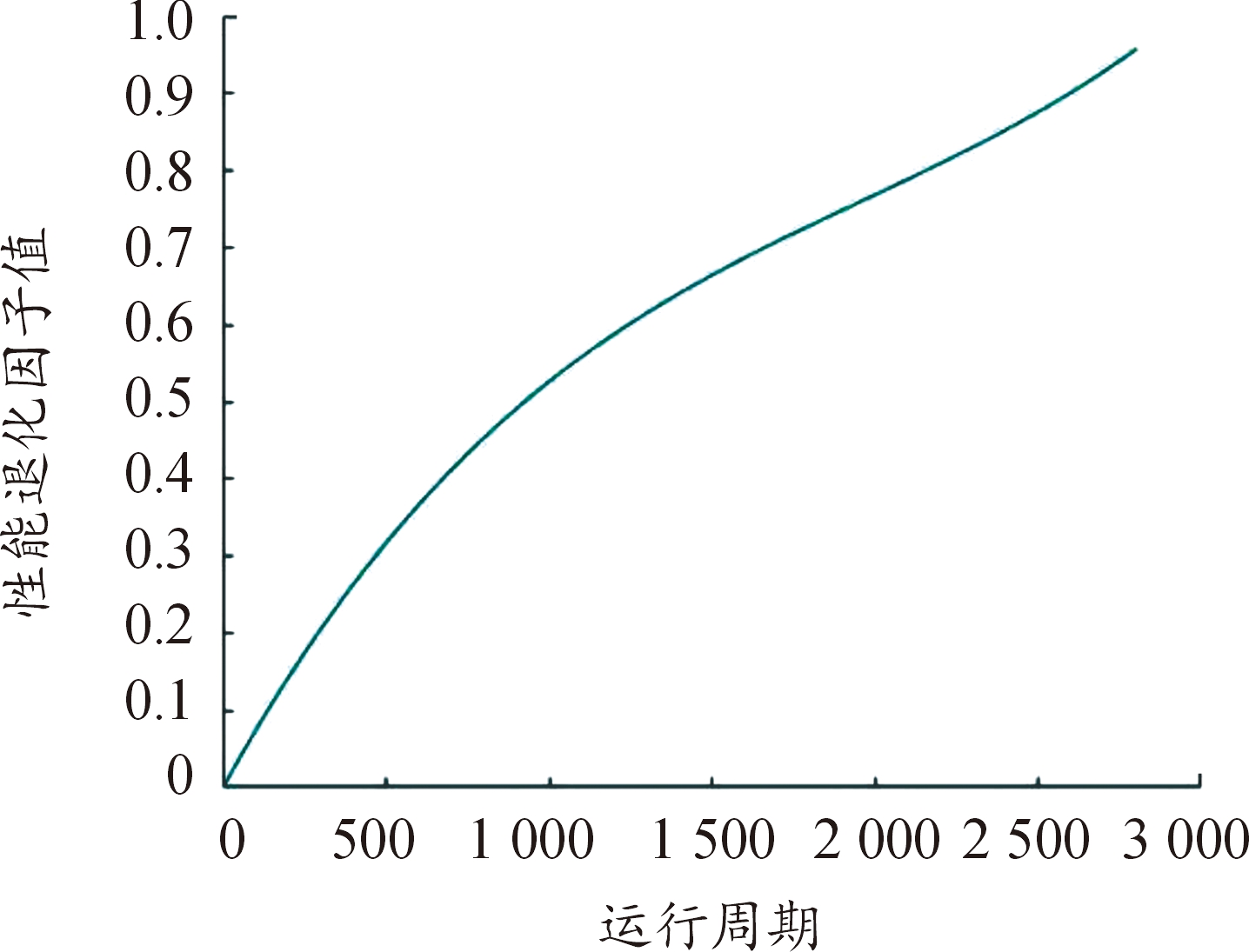
图8 Bearing1_1性能退化因子拟合曲线
Fig.8 Bearing1_1 performance degradation factor fitting curve
得到拟合曲线后,对其退化过程进行参数估计,得到的参数估计结果如表2所示。
表2 伽玛过程参数估计值
Table 2 Parameter estimation of gamma process
参数估计值b ^0.773 3^c80.111 1β ^39 522.017 2
由于利用伽玛退化过程进行建模是会存在初期不稳定情形,本节选取第500周期为起始监测周期,根据估计得到的参数绘制出的寿命分布的概率密度函数如图9所示。
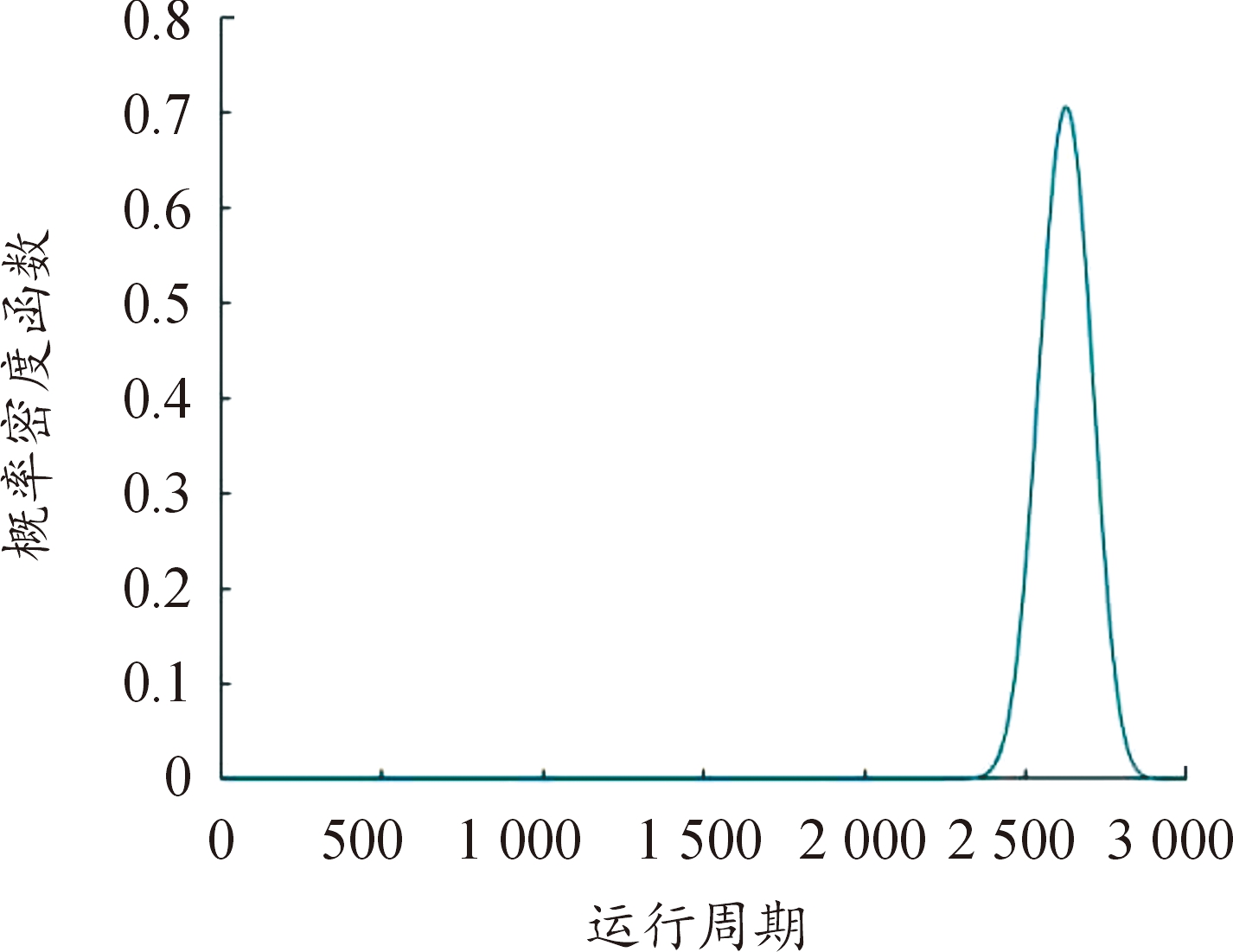
图9 寿命分布的概率密度函数
Fig.9 Probability density function of life distribution
根据概率密度曲线可以看出,在周期2 400～2 900,曲线的形状与泊松分布类似。由构建性能退化因子的标签设定可知失效阈值ζ=1,根据计算,预测出的设备失效周期为2 626,实际设备失效周期为2 803,相差177个周期,误差为6.31%,虽然结果具有一定误差,但可为实际应用提供一定参考。
在此基础上,选取设备运行周期2 400绘制出其剩余寿命分布的累积分布函数和可靠度函数,如图所10示。剩余寿命分布的累积分布函数表示设备剩余寿命分布的积分,其到达1时证明设备失效的概率为1。可靠度表示设备能够正常运行的概率。通过图10可进一步得知设备的性能退化情况,随剩余寿命周期增加,其剩余寿命分布概率值接近于1,可靠度概率值接近于0,证明随着设备运转其失效的概率越大。取剩余寿命分布的累计分布函数值和可靠度函数值同为0.5即二者相交的点,根据寿命分布近似与泊松分布的性质,在该点设备发生失效的概率最大,图中相交的点周期为256,根据计算由图10预测的设备失效周期为2 656,和根据概率密度曲线预测的寿命大致相同。
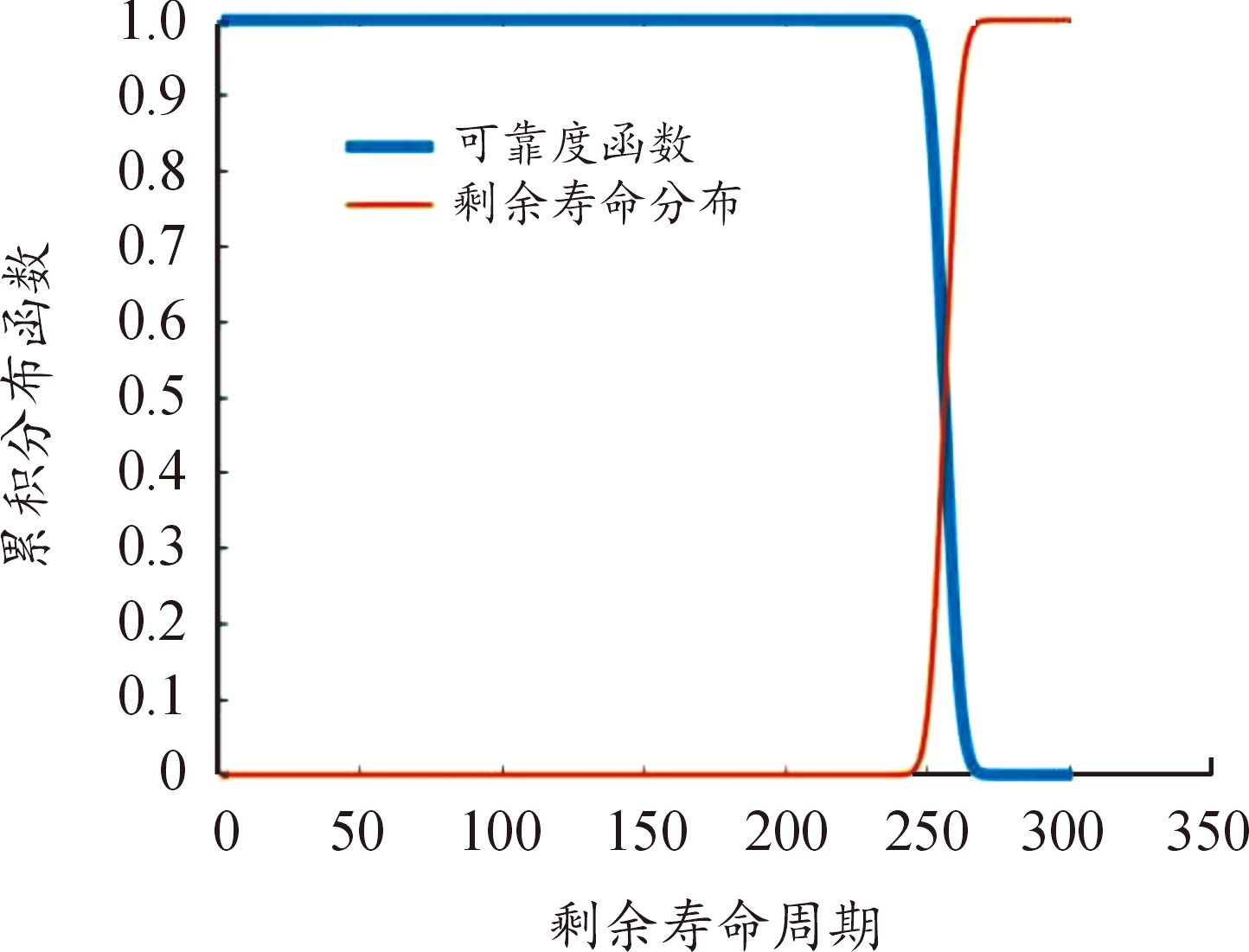
图10 剩余寿命分布和可靠度函数
Fig.10 Residual lifetime distribution and reliability function
根据上述结果,以2 200周期为起点截取性能退化因子拟合曲线进行计算,对比分析预测的剩余寿命和实际的剩余寿命,实际剩余寿命采用前文4.1节中线性退化过程进行设置,随着监测周期增加,其预测的剩余寿命如图11所示。
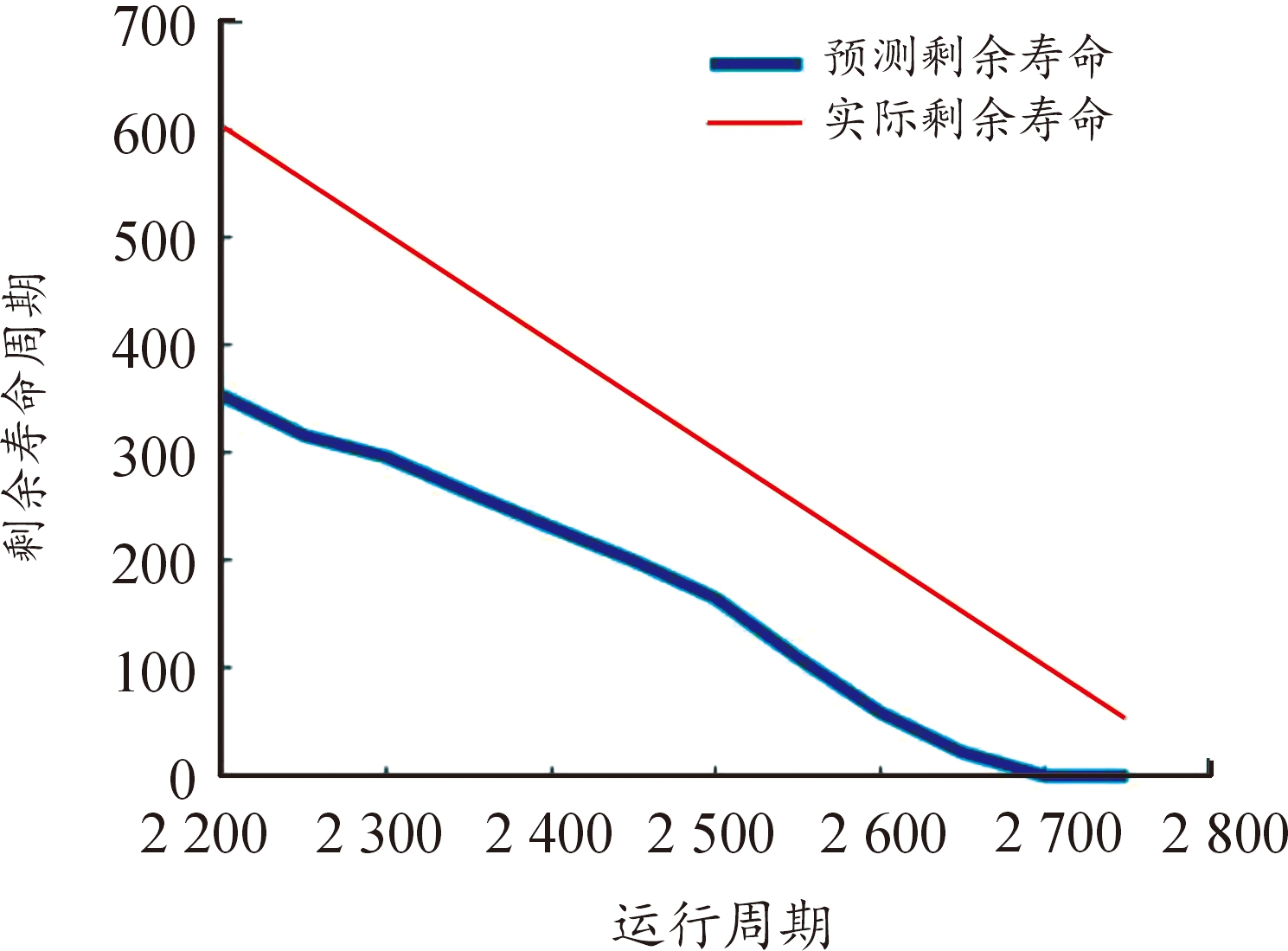
图11 不同监测周期剩余寿命预测结果
Fig.11 Residual lifetime prediction results of different monitoring periods
由图11可知,随着监测周期的增加,其预测的剩余寿命和实际的剩余寿命误差越来越小,这与监测的数据量更丰富有一定关系。除此之外,从图11中可以看出,预测的剩余寿命始终小于实际剩余寿命,证明由该方法得到的预测结果留有一定余量,预测滞后性不明显。剩余寿命预测滞后性明显会导致设备在运行中未达到预测的失效时刻便提前故障,容易造成安全事故,本文中方法的预测滞后性不明显更有利于实际工程运用。
4 结论
本文中以滚动轴承为研究对象,将深度学习和伽玛过程结合实现对滚动轴承的寿命预测,结论包括以下几条:
1) 构建一种基于DCNN和Bi-LSTM的混合输入网络性能退化因子提取方法,有效提取滚动轴承运行各阶段的性能退化特征;
2) 根据性能退化因子单调递增性质利用伽玛过程建模,准确预测滚动轴承剩余寿命;
3) 本文中方法预测的滚动轴承剩余寿命滞后性不明显,符合实际运用中安全需求。
[1] 李军星,黄嘉鸿,邱明,等.基于广义Wiener过程的滚动轴承剩余寿命预测[J/OL].计算机集成制造系统:1-17[2022-06-21].
LI Junxing,HUANG Jiahong,QIU Ming,et al.The residual life prediction of rolling bearings based on generalized Wiener process[J/OL].Computer Integrated Manufacturing System:1-17[2022-06-21].
[2] 张小丽,王保建,马猛,等.滚动轴承寿命预测综述[J].机械设计与制造,2015(10):221-224.
ZHANG Xiaoli,WANG Baojian,MA Meng,et al.Overview of rolling bearing life prediction[J].Mechanical Design and Manufacturing,2015(10):221-224.
[3] 韩晓娟.不同条件下滚动轴承寿命的分析计算方法[J].机械设计与制造,2005(9):31-32.
HAN Xiaojuan.Analysis and calculation method of rolling bearing life under different conditions[J].Mechanical Design and Manufacturing,2005(9):31-32.
[4] 马尧辉.基于特征融合的滚动轴承剩余寿命预测[D].武汉:华中科技大学,2020.
MA Yaohui.The remaining life prediction of rolling bearings based on feature fusion[D].Wuhan:Huazhong University of Science and Technology,2020.
[5] 肖文斌,陈进,周宇,等.小波包变换和隐马尔可夫模型在轴承性能退化评估中的应用[J].振动与冲击,2011,30(8):32-35.
XIAO Wenbin,CHEN Jin,ZHOU Yu,et al.Application of wavelet packet transform and hidden Markov model in bearing performance degradation assessment[J].Vibration and Impact,2011,30(8):32-35.
[6] RUQIANG YAN,YONGBIN LIU,ROBERT X.GAO.Permutation entropy:A nonlinear statistical measure for status characterization of rotary machines[J].Mechanical Systems and Signal Processing,2012,29:474-484.
[7] 赵光权,刘小勇,姜泽东,等.基于深度学习的轴承健康因子无监督构建方法[J].仪器仪表学报,2018,39(6):82-88.
ZHAO Guangquan,LIU Xiaoyong,JIANG Zedong,et al.The unsupervised construction method of bearing health factor based on deep learning[J].Journal of Instruments,2018,39(6):82-88.
[8] LI Xian,ZHANG Wei,DING Qian.Deep learning-based remaining useful life estimation of bearings using multi-scale feature extraction[J].Reliability Engineering and System Safety,2019,182:208-218.
[9] 王玉静,李少鹏,康守强,等.结合CNN和LSTM的滚动轴承剩余使用寿命预测方法[J].振动,测试与诊断,2021,41(3):439-446,617.
WANG Yujing,LI Shaopeng,KANG Shouqiang,et al.Combined with CNN and LSTM rolling bearing residual life prediction method[J].Vibration,Test and Diagnosis,2021,41 (3):439-446,617.
[10] 王贝.基于改进Logistic回归模型航空发动机滚动轴承寿命预测[D].大连:大连理工大学,2017.
WANG Bei.Life prediction of aeroengine rolling bearing based on improved Logistic regression model[D].Dalian:Dalian University of Technology,2017.
[11] 邱明,牛凯岑,李军星,等.多重应力下滚动轴承剩余寿命预测[J].航空动力学报,2022,37(5):980-988.
QIU Ming,NIU Kaicen,LI Junxing,et al.Prediction of residual life of rolling bearings under multiple stresses[J].Aerodynamics,2022,37(5):980-988.
[12] 谷玉波,贾云献,张英波.基于Gamma退化过程的剩余寿命预测及维修决策优化模型研究[J].轴承,2013(4):44-49.
GU Yubo,JIA Yunxian,ZHANG Yingbo.The residual life prediction and maintenance decision optimization model based on Gamma degradation process[J].Bearings,2013(4):44-49.
[13] 周楠,欧阳鑫玉.卷积神经网络发展[J].辽宁科技大学学报,2021,44(5):349-356.
ZHOU Nan,OUYANG Xinyu.Development of convolutional neural network[J].Journal of Liaoning University of Science and Technology,2021,44(5):349-356.
[14] 胡昌华,樊红东,王兆强.设备剩余寿命预测与最优维修决策[M].北京:国防工业出版社,2018.
HU Changhua,FAN Hongdong,WANG Zhaoqiang.Equipment remaining life prediction and optimal maintenance decision[M].Beijing:Defense Industry Press,2018.
[15] 雷亚国,何正嘉,訾艳阳.基于混合智能新模型的故障诊断[J].机械工程学报,2008(7):112-117.
LEI Yaguo,HE Zhengjia,ZI Yanyang.Fault diagnosis based on hybrid intelligent new model[J].Mechanical Engineering Journal,2008 (7):112-117.
[16] PATRICK N,RAFAEL G,KAMAL M R,et al.PRONOSTIA:An Experimental platform for bearings accelerated life test[C]//IEEE International Conference on Prognostics and Health Management.Denver,CO,USA,2012.
[17] 刘胜兰,高凌寒,杜剑维,等.基于自适应顺序的滚动轴承最优特征选取与寿命预测[J].舰船科学技术,2019,41(21):71-76.
LIU Shenglan,GAO Linghan,DU Jianwei,et al.The optimal feature selection and life prediction of rolling bearings based on adaptive sequence[J].Ship Science and Technology,2019,41 (21):71-76.
[18] 孙世岩,张钢,田福庆,等.多输入混合深度学习网络的健康因子构建方法[J].系统工程与电子技术,2020,42(10):2390-2398.
SUN Shiyan,ZHANG Gang,TIAN Fuqing,et al.Health factor construction method of multi-input hybrid deep learning network[J].System Engineering and Electronic Technology,2020,42(10):2390-2398.