0 引言
现代高科技战争中,新式制导武器精度的提高,使得坑道目标受到战斗部打击产生毁伤的可能性越来越高[1],而爆炸冲击波是坑道目标主要的毁伤因素之一[2],因此研究爆炸冲击波作用下坑道目标易损性是军事领域的热点问题,而坑道目标易损性研究过程中需要通过坑道毁伤试验获取真实数据。地下防护工程预选场址大多数都是在花岗岩等Ⅰ-Ⅱ类天然岩体中,天然岩体节理纵横交错,岩块构成的结构体不属于均质材料,不确定性很高,很难满足毁伤试验要求[3],因此在研究坑道目标防护层结构易损性时,可采用等效靶进行研究[4],而人工浇筑的混凝土材料质地均匀,同时,混凝土与岩石均为脆性材料,岩石材料的宏观力学特性与混凝土比较接近,且混凝土材料较易获得。在等效靶研究方面,Farrand等[5]研究了靶板等效的定义,建立了等效靶毁伤等效准则,同时给出靶板等效设计方法流程。Bourget、Baillargeon等[6]从易损性损伤的角度,将人员等效为多层金属薄板。徐辉等[4]采用能量消耗原则,建立了坚固目标等效靶模型。黄松等[7]采用试验与数值仿真相结合的方法,建立了船舰等效模型。苗朝阳等[8]使用ANSYS/LS-DYNA软件,研究了原型坑道和模型坑道爆炸冲击波下的毁伤相似律。邓国强等[3]采用钢筋混凝土靶来代替侵彻作用下的自然岩体。鉴于目前爆炸冲击波作用下坑道靶标材料等效关系研究没有较合理的理论依据,亟需开展坑道靶标材料的毁伤相似性研究。
为了获得在爆炸冲击波作用下坑道目标的花岗岩和混凝土2种材料之间的等效关系,本研究中以靶标最大位移公式为指导,以目标特性和毁伤效应为基础,以靶标等效设计准则为依据,对花岗岩的坑道原模型等效为C50混凝土、C35混凝土的等效靶模型进行科学合理设计的一个完整过程,以确保等效靶模型相对于原模型具有充分的等效性和代表性[9]。
1 靶标材料等效方法
爆炸冲击波作用下,靶标的毁伤主要表现为塑性大变形或者产生凹形炸坑。在发生塑性大变形时主要的量化指标是靶板的挠度值[10],因此爆炸冲击波作用下的等效原则采用挠度原则,即相同炸药当量和相同爆炸距离的情况下原模型和等效靶模型在爆炸冲击波作用下的挠度值是相同的,则该等效靶的尺寸为等效几何尺寸[11]。因此,采用毁伤挠度值进行分析,推导原型与等效靶的厚度尺寸等效系数。
1.1 建立相似准则
坑道目标的原型材料选择花岗岩,等效靶材料分别选择C50混凝土和C35混凝土。
针对本研究中的工况条件,根据学者Talor等[7]得到了靶标在爆炸冲击波作用下靶标中心最大位移估算公式为
![]()
(1)
式(1)中:ω为毁伤挠度值;I为作用在靶标上的总冲量;t为靶板的厚度尺寸;L为靶标边长;ρ为材料密度;σ为抗压强度。
同工况下,密度差距很小,因此仅考虑材料的抗压强度不同时,根据该估算公式可得材料间毁伤挠度值比值满足
![]()
(2)
C50混凝土抗压强度为50 MPa,C35混凝土抗压强度为35 MPa,花岗岩抗压强度为90 MPa,因此,毁伤挠度值的理论比值为 ![]()
同样可以推导出,在相同工况下,要使原型与等效靶之间发生相同的挠度,则需要靶标的厚度尺寸满足
![]()
(3)
所以花岗岩与C50混凝土、C35混凝土的靶板厚度尺寸等效系数理论值为1.342、1.600。
采用式(1)的推导结果与采用王芳等[12]的靶板中心最大位移估算公式进行推导也可印证。
由于本研究中理论推导的靶板的形状不是严格意义上的理论假设条件,从而达不到理论情况下的结果,下文将进行数值仿真试验,来推导花岗岩与C50混凝土、C35混凝土的厚度尺寸等效关系。
1.2 爆炸冲击波作用下坑道靶标材料设计流程
采用数值模拟计算分析不同材料下的原型与等效靶之间动力响应特征,建立原型与等效靶的之间的材料等效关系。并通过材料等效关系建立原模型与等效靶的爆炸毁伤试验,验证原型与等效靶在爆炸冲击波下的毁伤相似性,得到具有毁伤相似性的坑道等效靶模型,具体步骤为:
1) 通过爆炸冲击波作用下坑道靶标的构造特性分析,确定坑道靶标的结构参数、材料参数、边界条件;
2) 使用ANSYS/LS-DYNA软件,建立爆炸冲击波下坑道靶标计算模型,并对比现有的爆炸冲击波作用下坑道的毁伤结果相关数据,验证数值仿真试验的可靠性;
3) 设计多组不同炸药当量下的原型与等效靶数值仿真试验,建立不同TNT当量与毁伤挠度值之间的函数关系,得到原型与等效靶之间的毁伤挠度值的比值,为后边推导坑道靶标厚度尺寸等效系数提供依据;
4) 根据在爆炸冲击波作用下靶标中心最大位移的估算公式,得到坑道靶标厚度尺寸与毁伤挠度值之间存在函数关系。通过上述3)中原型与等效靶毁伤挠度值的比值,可推导靶标材料厚度尺寸等效系数;
5) 按照上述4)得到的材料厚度尺寸等效系数设计原型与等效靶的毁伤数值仿真试验,对比毁伤效应参量,验证原型与等效靶之间的毁伤相似性。靶标流程如图1所示。
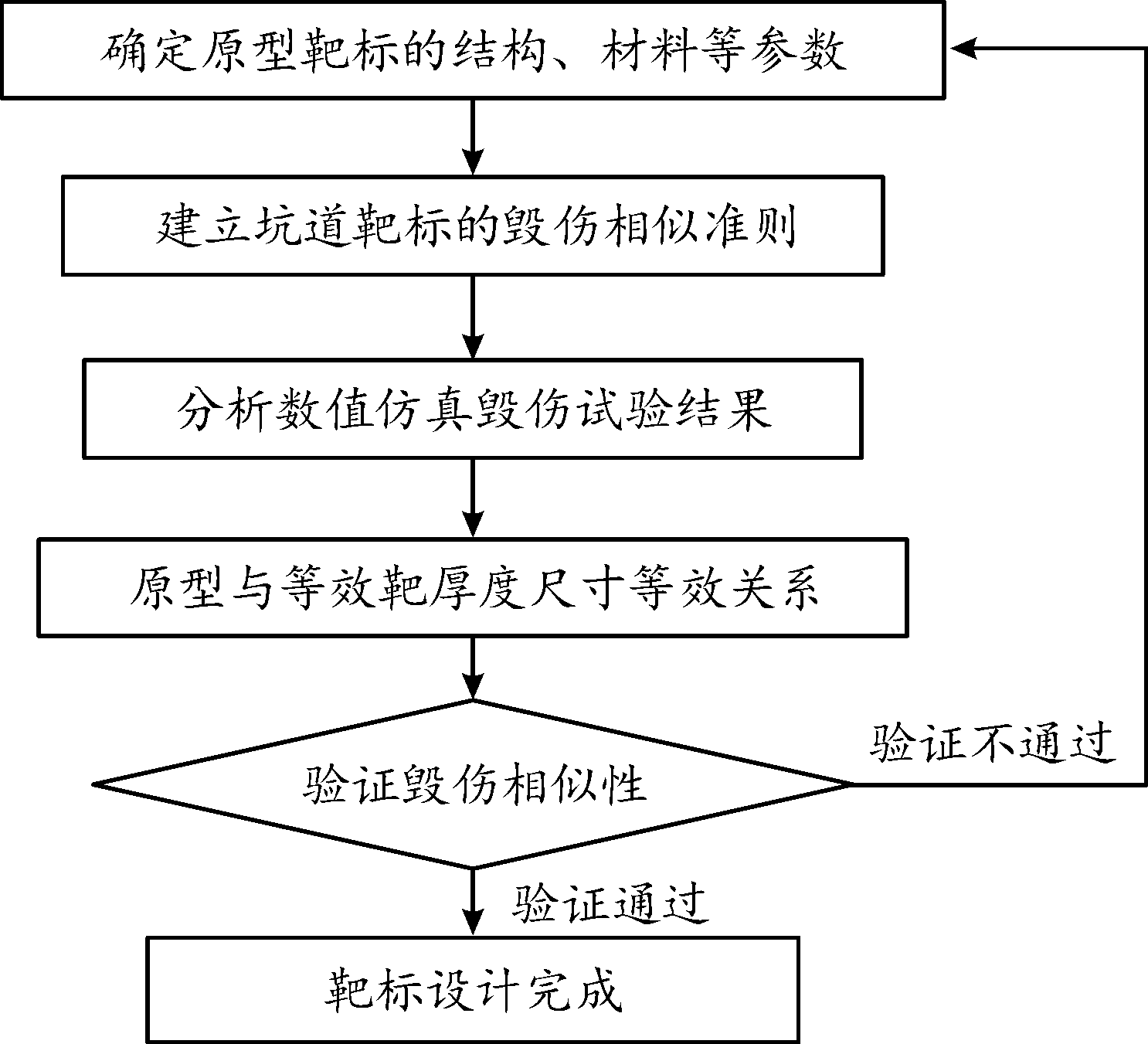
图1 靶标设计流程
Fig.1 Flow chart of equivalent target design
2 计算模型的建立与可靠性分析
2.1 有限元模型
建立的有限元模型主要有3部分:靶标、TNT炸药和空气。靶标采取坑道目标,坑道目标的结构为直墙圆拱形构造[13],净跨为8.0 m,直墙高度为4 m,拱高2.0 m,拱顶上方的岩石防护层厚度为10 m,为便于分析,坑道模型宽度取20 m,纵向长度取60 m。坑道目标模型如图2所示。
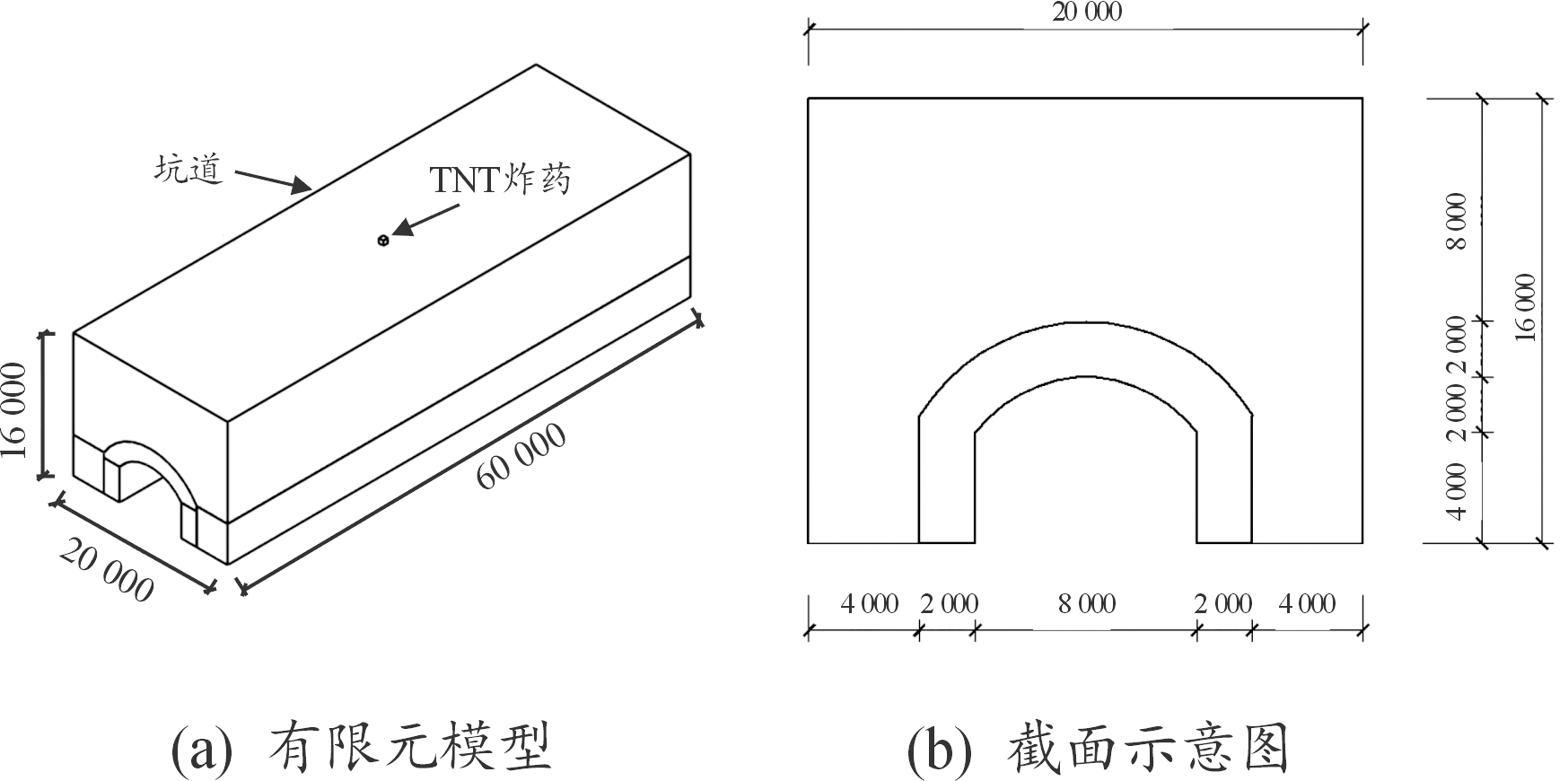
图2 坑道目标模型(mm)
Fig.2 Finite element model of tunnel target
原模型材料选用90 MPa花岗岩,等效靶材料选用C50混凝土、C35混凝土,材料参数如表1所示。为了简化叙述,C50混凝土、C35混凝土使用简称C50、C35代替。
表1 花岗岩、C50、C35材料参数
Table 1 Material parameter

材料密度/(kg·m-3)弹性模量/GPa泊松比抗压强度/MPa抗拉强度/MPa花岗岩2 66028.70.159012.20C502 50034.50.20502.64C352 40031.50.20352.20
2.2 建立计算模型及边界条件
2.2.1 原型材料本构模型和等效材料本构模型
采用流固耦合方法[14],数值模拟仿真采用全尺寸模型,结合坑道目标模型的构造特性,设置模型的底面和围岩的两边为固定约束,空气采用无边界约束条件。
采用*MAT_JOHNSON_HOLMQUIST_CONRETE模型作为花岗岩的本构模型[15]。
采用*MAT_BRITTLE_DAMAGE模型作为C50、C35的本构模型[16]。
2.2.2 空气本构模型及状态方程
空气采用*MAT_NULL材料模型,采用*EOS_LINEAR_POLYNOMAL定义状态方程[17],计算公式为
P=C0+C1u+C2u2+C3u3+
C4E+C5uE+C6u2E
(4)
![]()
(5)
其中:C0、C1、C2、C3、C4、C5、C6状态方程参数;p为压力;u为体积应变;v相对体积;E材料内能。
对于空气C0=-1×10-6,C1=C2=C3=C6=0,C4=C5=0.4;密度取1.293 kg/m3,E=0.25 MPa[17]。
2.2.3 炸药本构模型及状态方程
采用*MAT_HIGH_EXPLOSIVE_BURN定义炸药材料模型。用JWL方程作为炸药的状态方程[18],其状态方程表示为:
![]()
(6)
式(6)中: A、B、R1、R2、ω为材料常数;P为爆轰压力;v为相对体积;E为单位体积内能。
对于TNT炸药,密度取1.63×103 kg/m3,初始爆轰速度为6.93 km/s,爆压为27 GPa,A=371 GPa,B=7.43 GPa,R1=4.15,R2=0.95,ω=0.3,E=7 GJ/m3,v=1[18]。
2.3 计算模型的可靠性分析
借鉴文献[18]中坑道模型结构在爆炸冲击波作用下的破坏结果进行验证。文献中坑道模型长2.4 m,纵深长0.4 m,高2.3 m,跨度0.60 m的几何模型,TNT布置在拱顶中心上部83 cm处,TNT的质量为50 g。文献中结构模型如图3(a)所示,根据文献中的结构参数建立坑道结构的几何模型如图3(b)所示。
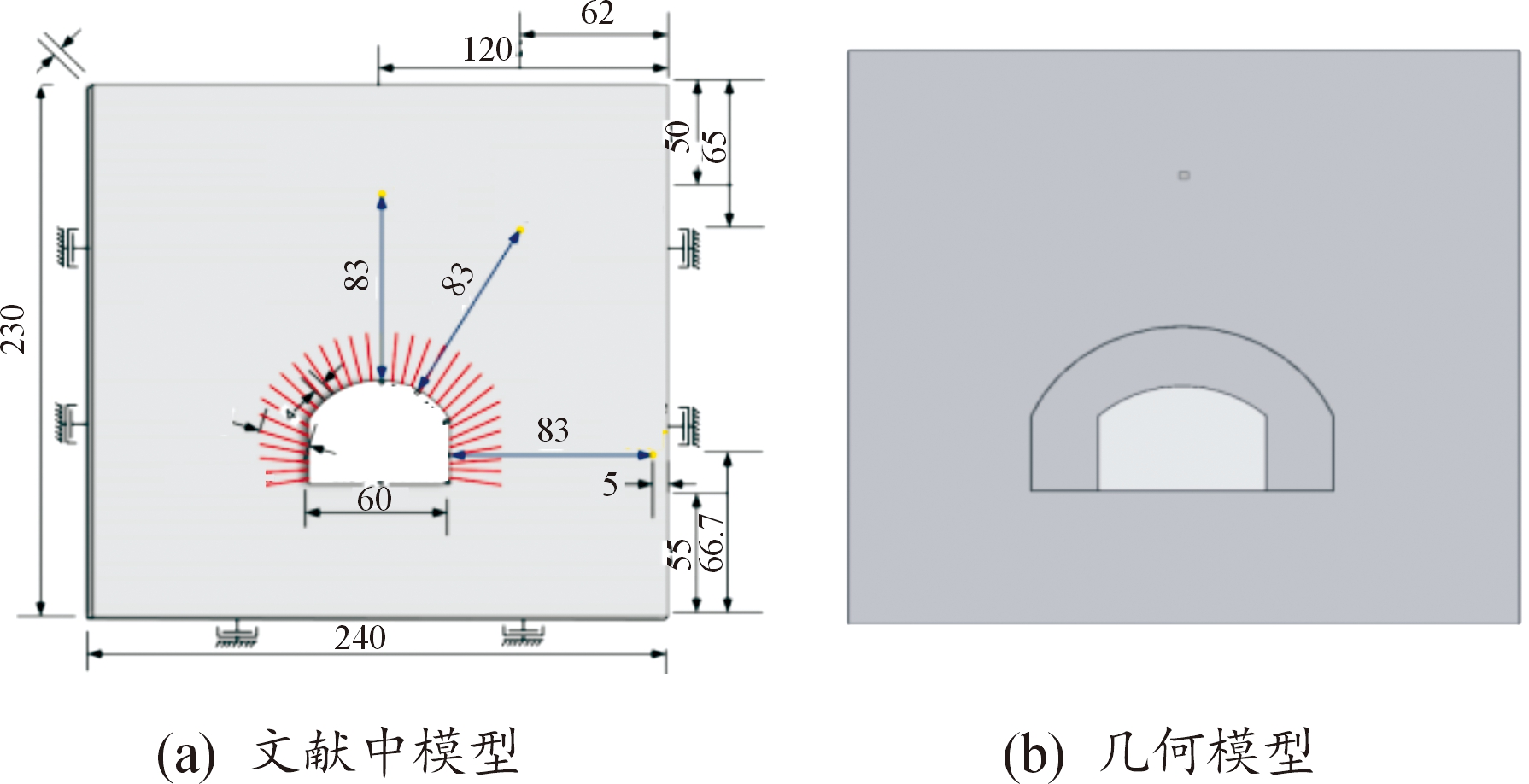
图3 坑道结构对比模型图
Fig.3 Tunnel target comparison model
依据已有文献具体材料参数设置几何模型,文献[18]中岩石材料参数见表2所示,并进行爆炸数值仿真模拟,可得数值模拟毁伤破坏图如图4(b)所示,与图4(a)已有文献中爆炸冲击波作用下的毁伤破坏结果进行比较。
表2 文献中岩石材料参数
Table 2
Table of rock material parameters in literature
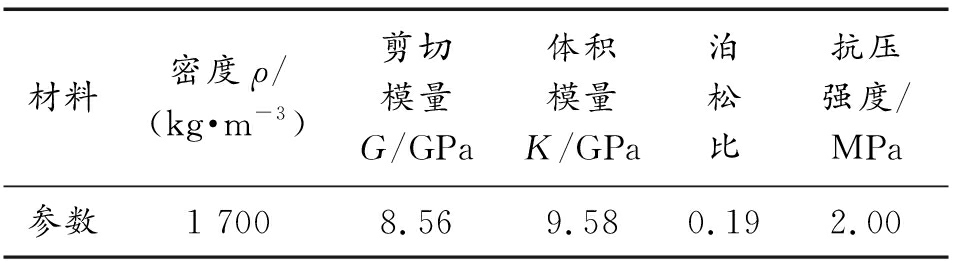
材料密度ρ/(kg·m-3)剪切模量G/GPa体积模量K/GPa泊松比抗压强度/MPa参数1 7008.569.580.192.00
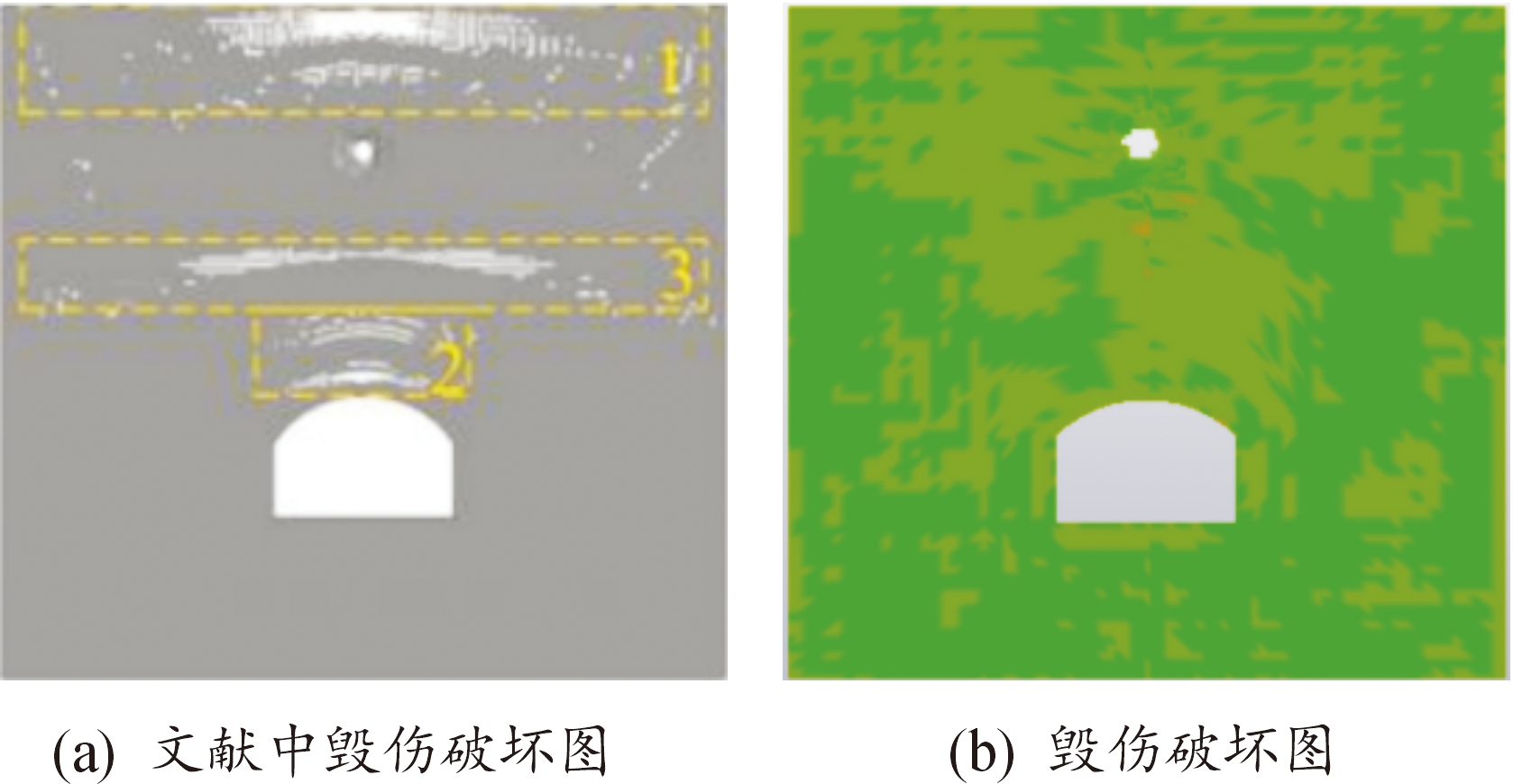
图4 毁伤破坏对比图
Fig.4 Comparison chart of damage effect
从图4可以看出,爆炸冲击波作用下形成贯穿洞,通过Matlab图像识别技术进行像素处理对比,得到洞的尺寸及形状较相似,并提取有限元模型炸药正下方83 m处拱顶位置的位移值进行分析,得到位移时程曲线如图5所示。

图5 位移时程曲线
Fig.5 Displacement time history curve diagram
从图5可知,数值模拟位移曲线峰值为4.86 mm,已有文献中同位置测得的位移峰值为4.46 mm,两者的误差为8.9%,在工程允许误差范围内。
由以上结果表明,利用已选择的相关本构模型进行有限元计算能够较好地模拟出爆炸冲击波作用下坑道靶标的毁伤效应,可为下一步的有限元数值模拟分析提供依据。
3 靶标材料的毁伤相似性分析
3.1 毁伤效果分析
利用2.1节的有限元模型,进行不同炸药当量(100、150、200、250、300、400 kg)的数值模拟,炸药的填充形状都是正方体,炸药安置在坑道顶部中心位置。分别赋予坑道靶标(花岗岩、C50、C35)3种材料属性。有效应变云图如图6所示,左边、中间、右边分别为花岗岩、C50、C35的有效应变云图。

图6 坑道目标有效应变云图
Fig.6 Effective strain cloud map of tunnel target
从图6可以得到,爆炸后在坑道顶部产生了一个很大的炸坑。随着炸药当量的增加,毁伤情况也逐渐增加,在相同炸药的情况下,花岗岩的炸毁情况较小,C50的炸毁情况中等,C35的炸毁情况较大。
使用LS-PrePost后处理软件,提取坑道拱顶中心毁伤挠度参量,得到了不同TNT炸药当量下花岗岩、C50和C35的坑道拱顶中心毁伤挠度值,如图7所示。

图7 毁伤挠度值随炸药当量变化关系图
Fig.7 Relationship between damage deflection value and explosive equivalent
从图7可知,坑道拱顶中心毁伤挠度值变化随TNT当量的增加而变大,分析相同炸药当量下的花岗岩与C50、C35坑道拱顶中心毁伤挠度值,得到的比值关系,如表3所示。
表3 毁伤挠度值比值
Table 3 Damage deflection value ratio
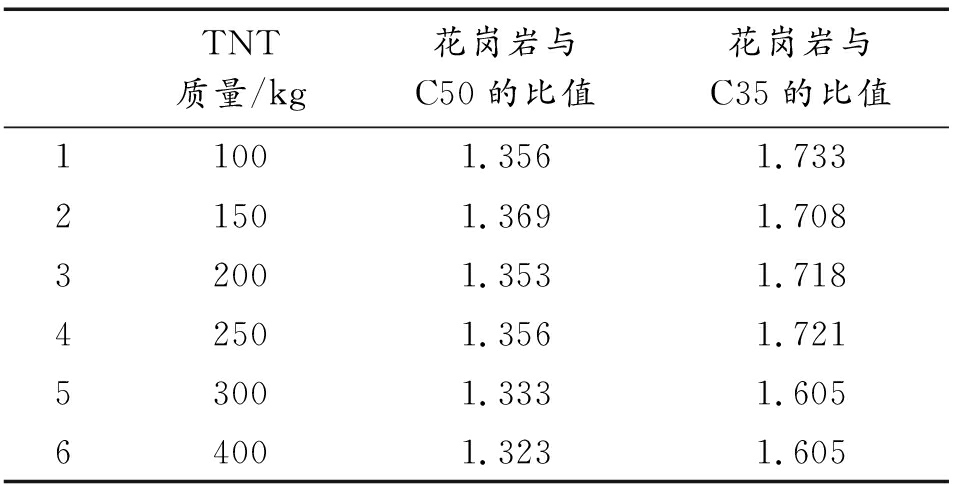
TNT质量/kg花岗岩与C50的比值花岗岩与C35的比值11001.356 1.733 21501.369 1.708 32001.353 1.718 42501.356 1.721 53001.333 1.605 64001.323 1.605
从表3可得,花岗岩与C50、C35的坑道拱顶中心毁伤挠度比值的平均值分别为:1.348、1.682。
3.2 推导等效材料的厚度尺寸等效关系
六组数值仿真结果中花岗岩与C50、C35的毁伤挠度值之间的比值分别是:1.348、1.682,依据式(3),推导出不同材料间的厚度尺寸与毁伤挠度值满足下列关系:
![]()
(7)
![]()
(8)
从式(7)与式(8)可知花岗岩与C50、C35厚度尺寸等效系数分别为1.348、1.682。
所得数值模拟结果与已有估算式(3)的误差分别为-0.45%、-5.13%,均符合工程允许误差要求。
3.3 等效材料厚度的毁伤仿真验证
以2.1节中所示坑道目标为原型靶标,则按照上述花岗岩与C50、C35材料之间的厚度尺寸等效关系设计等效靶,所建立的等效靶厚度对应关系为:C50、C35对应拱顶上层的防护层厚度分别为13.48 m、16.82 m。炸药当量选择300 kg TNT,炸药紧贴在坑道顶部中心位置,数值模拟得到的有效应变云图如图8所示。
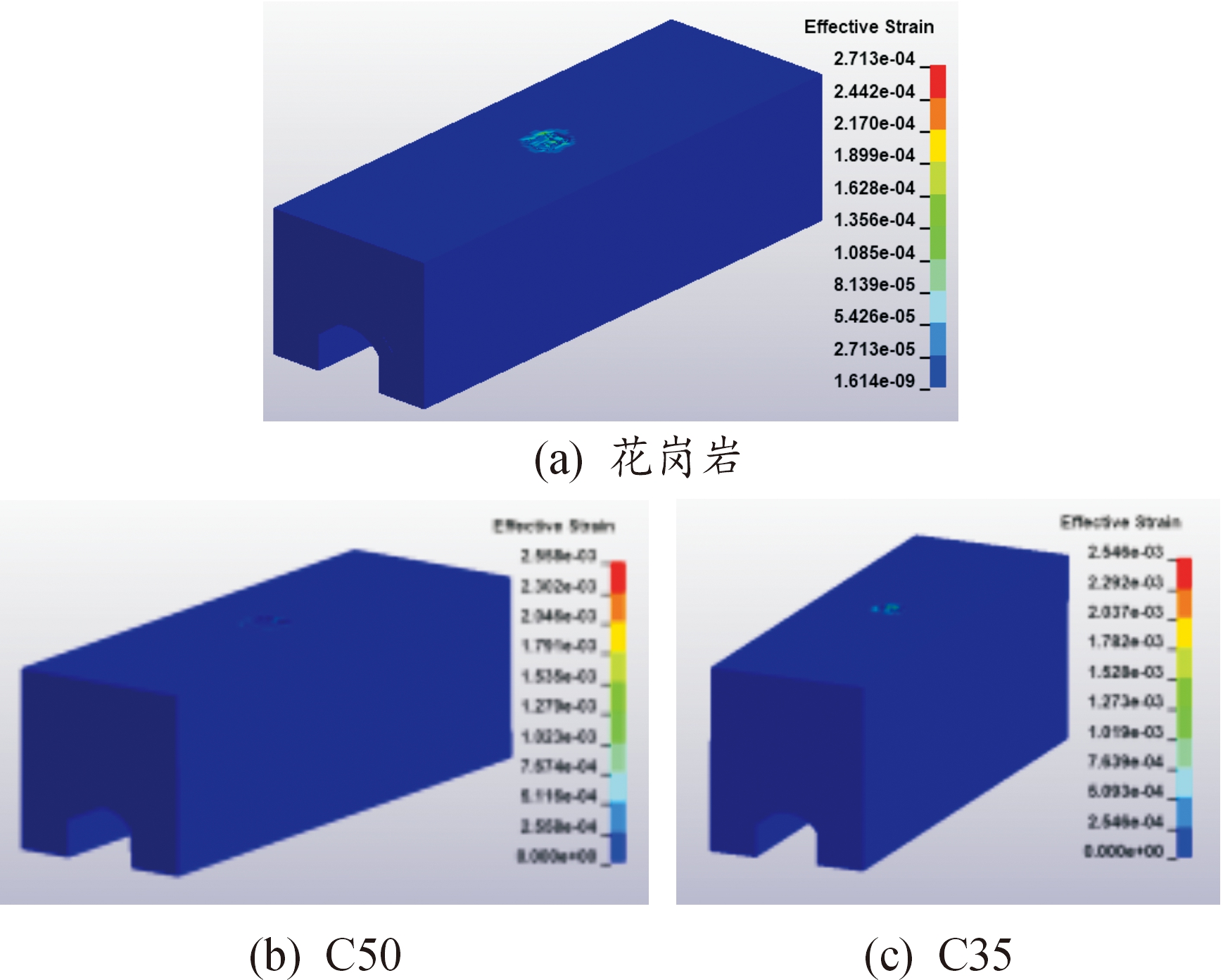
图8 坑道目标有效应变对比云图
Fig.8 Comparative cloud chart of effective plastic strain of tunnel target
选取原型与等效靶的坑道拱顶中心位置特征点A,提取其超压时程曲线和位移时程曲线进行对比分析,如图9所示。
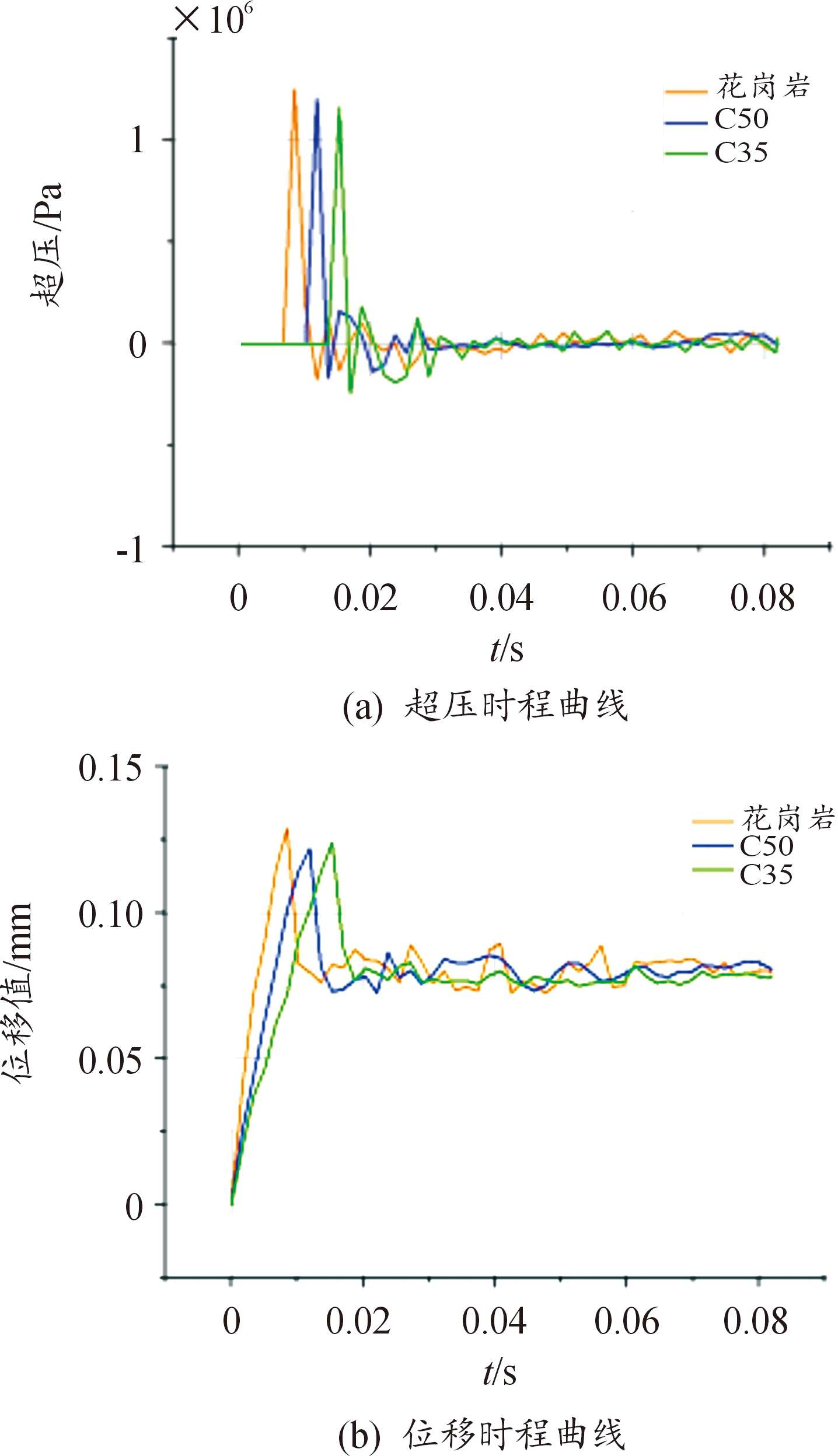
图9 特征点A的毁伤参量曲线对比图
Fig.9 The damage parameter curve comparison diagram of the characteristic point A
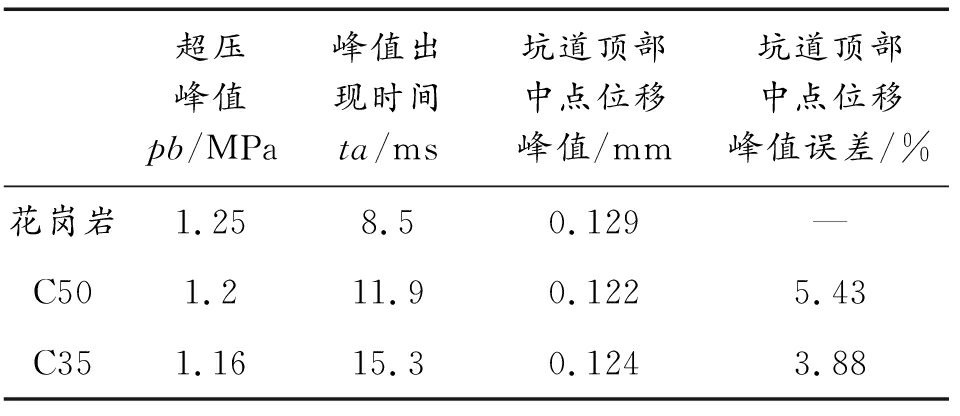
从图9可以看出,特征点A在不同材料下的超压时程曲线与位移时程曲线变化规律较相似。提取图9中原型与等效靶在特征点A的爆炸冲击波的超压峰值、超压峰值出现时间,坑道拱顶中点位移峰值等,进行误差分析,具体数值如表4所示。
表4 特征点A的爆炸毁伤效应参量数据
Table 4 Explosion damage effect parameter data at feature point A
超压峰值pb/MPa峰值出现时间ta/ms坑道顶部中点位移峰值/mm坑道顶部中点位移峰值误差/%花岗岩1.258.50.129—C501.211.90.1225.43C351.1615.30.1243.88
由表6可以看出,随着等效靶厚度尺寸的增加,超压峰值在减小,峰值出现时间推后,花岗岩和C50、C35的坑道拱顶中心位移值误差分别为5.43%、3.88%,误差均在工程允许范围±10%以内,满足设计要求。
所以在爆炸冲击波作用下坑道靶标材料(花岗岩与C50、C35)之间的厚度尺寸等效系数分别为1.348、1.682。
4 结论
1) 以靶板结构在爆炸冲击波作用下毁伤相似性为准则,提出了具有毁伤相似性的坑道靶标材料设计流程。
2) 基于靶板最大位移的估算公式,得到了爆炸冲击波作用下坑道靶标材料的厚度尺寸等效系数与毁伤挠度值比值之间的联系。
3) 在坑道靶标材料设计流程中,由原型与等效靶的毁伤挠度值之间的比值,推导了花岗岩与C50混凝土、C35混凝土之间的厚度尺寸等效系数分别为1.348、1.682,与已有估算公式的误差分别为-0.45%、-5.13%,均符合工程允许误差要求。
4) 根据花岗岩与C50混凝土、C35混凝土材料之间的厚度尺寸等效系数,设计了原型与等效靶的毁伤数值仿真试验,验证了材料的厚度尺寸等效关系的毁伤相似性,为后续的坑道靶标设计相关研究提供了参考。
[1] 刘祥,孙宇新,钟垂琦.隧道口部爆炸冲击波传播规律数值仿真分析[J].防护工程,2020,42(1):12-13.
LIU Xiang,SUN Yuxin,ZHONG Chuiqi.Numerical simulation analysis of propagation law of explosion shock wave at tunnel entrance[J].Shield and Seal Ball Bearing Engineering,2020,42(1):12-13.
[2] 马荣华,贾波,杨丽,等.坑道截面形状对爆炸冲击波传播规律的影响[J].兵器装备工程学报,2022,43(2):92-96.
MA Ronghua,JIA Bo,YANG Li,et al.The influence of tunnel section shape on the propagation law of explosion shock wave[J].Journal of Weapon Equipment Engineering,2022,43(2):92-96.
[3] 邓国强,黄魅.混凝土靶标等效岩体有效性分析[J].防护工程,2017,39(1):19-20.
DENG Guoqiang,HUANG Mei.Effectiveness analysis of equivalent rock mass of concrete target[J].Shield and Seal Ball Bearing Engineering,2017,39(1):19-20.
[4] 徐辉,李加财.坚硬目标防护层等效素混凝土靶的方法[J].工程技术,2008:29.
XU Hui,LI Jiacai.Method of equivalent plain concrete target to hard target protective layer[J].Engineering Technology,2008:29.
[5] FARRAND T,MAGNESS L,BURKINS M.Definition and uses of RHA equivalences for medium caliber targets[C]//19th International Symposium of Ballistics.Interlaken,Switzerland,2001:1159-1165.
[6] BOURGET D,BAILLARGEON Y,NORTHROP S.Witness pack calibration for human vulnerability assessment[C]//Jeo Carleone.20th International Symposium on Ballistics(II).Florida:National Defense Industrial Association,2002.
[7] 黄松.舰船易损性分析中船用钢的等效靶研究[D].广州:中山大学,2019.
HUANG Song.Research on target of ship steel in ship vulnerability analysis[D].Guangzhou:Zhongshan University,2019.
[8] 苗朝阳,李秀地,杨森,等.坑道内爆炸冲击波相似律问题探讨[J].爆破,2016,33(1):131-135.
MIAO Chaoyang,LI Xiudi,YANG Shen,et al.Discussion on similarity law of explosion shock wave in tunnel[J].Blasting,2016,33(1):131-135.
[9] 曹兵.靶板等效方法研究[J].弹箭与制导学报,2003,23(3):122.
CAO Bing.Study on equivalent target experimental methods[J].Journal of Projectiles,Rockets,Missiles and Guidance,2003,23(3):122.
[10] 傅辉刚.效应靶在爆炸冲击波毁伤评估中的应用研究[D].南京:南京理工大学,2015:8-9.
FU Huigang.Study on the application of effect target in blast wave damage assessment[D].Nanjing:Nanjing University of Science &Technology,2015:8-9.
[11] PEI Y,SONG B F,HAN Q,et al.A generic calculation model for aircraft single hit vulnerability assessment based on equivalent target[J].Chinese Journal of Aeronautics,2006.
[12] 王芳,冯顺民,俞为民.爆炸冲击波作用下靶板的塑性大变形响应研究[J].中国安全科学学报,2003,13(3):58-61.
WANG Fang,FENG Shunmin,YU Weimin.Study on plastic large deformation response of target plate under explosion shock wave[J].China Safety Science,2003,13(3):58-61.
[13] 李加贵,边小华,张雷,等.爆炸冲击波传播的数值模拟与试验数据对比[J].山西建筑,2006,32(8):106-107.
LI Jiagui,BIAN Xiaohua,ZHANG Lei,et al.Comparison of numerical simulation and experimental data of explosion shock wave propagation[J].Shanxi Architectu,2006,32(8):106.
[14] 张世臣,米双山.爆炸冲击波损伤祀板问题中的流固稱合算法[J].科学技术与工程,2008,87:1655-1664.
ZHANG Shichen,MI Shuangshan.Fluid-solid coupling algorithm in the problem of blast shock wave damage sacrificial plate[J].Science Technology and Engineering,2008,87:1655-1664.
[15] 黄佑鹏.基于HJC本构的岩石爆破损伤演化规律数值模拟[D].合肥:合肥工业大学,2020.
HUANG Youpeng.Numerical simulation of rock blasting damage evolution based on HJC constitutive model[D].Hefei:Hefei University,2009,5(29):142-144.
[16] 李天华.爆炸荷载下钢筋混凝土板的动态响应及损伤评估[D].西安:长安大学,2012.
LI Tianhua.Dynamic response and damage assessment of reinforced concrete slabs under blast loading[D].Xi’an:Chang’an University,2012.
[17] 侯满义,范惠林.爆炸波对靶板冲击损伤的动力有限元模拟[J].弹箭与制导工程学报,2009,29(5):142-144.
HOU Manyi,FAN Huilin.Dynamic finite element simulation of blast wave impact damage on target plate[J].Journal of Missile and Guidance Engineering,2009,5(29):142-144.
[18] WANG G Y,CAO A S,WANG X Y,et al.Numerical simulation of the dynamic responses and damage of underground cavern under multiple explosion sources[J].Engineering Failure Analysis,2021,120:1-3.