0 引言
在现代战争中,掌握战场制空权可以在地面装备无显著优势的情况下起到扭转战局的作用[1]。因此各个国家对于空中力量的建设均十分重视,空中目标的不断发展使防空反导压力不断提升。破片杀伤战斗部作为对空中目标进行毁伤的重要战斗部类型,在空天攻防中起着至关重要的作用。
破片杀伤战斗部多采用预制破片,通过提高破片飞散速度和密度来增强对目标的毁伤能力。其中聚焦战斗部通过改变装药曲线使破片汇聚以提高破片密度,达到远高于普通杀伤战斗部的毁伤效果[2-5]。为更进一步提升对空中目标的打击能力,梁争峰等[6]提出了动态线列式破片战斗部,该战斗部通过控制装药曲线和预制破片排布方式实现破片轴向飞散速度一致和目标靶落点穿孔的线列式分布,将破片对目标的毁伤效果由聚焦战斗部的“带切割”模式进一步强化为“线切割”模式。王宝成等[7]对面对导弹目标时线列式战斗部的结构毁伤效应进行了分析,以剩余强度系数对气动因素或爆炸冲击作用下目标解体的难易程度进行了评价,结果表明线列式战斗部的结构毁伤能力优于聚焦战斗部。舒张忆南等[8]对聚焦和线列式毁伤模式下飞机外壳等效靶标承受弯曲载荷的能力进行了比较,相较于聚焦式毁伤,线列式毁伤模式下目标结构内部最大平均应力提高,而达到屈服破坏所需载荷减小。
上述研究对不同目标受到线列式结构毁伤的效果进行了对比,但仅考虑了某一特定情形下的破片分布情况,而在实际作战中,受导弹精度和目标机动影响,破片命中情况复杂,在不同弹目交会条件下,战斗部起爆时与目标间的距离不同,在目标上形成的破片穿孔分布状况亦有差异,需要考虑不同破片分布情况下线列式战斗部对目标的毁伤效应。
因此,为研究线列式破片分布对典型靶标的毁伤效应,分析了聚焦及线列式战斗部造成的破片穿孔分布特点,设置了不同的破片穿孔分布间距来模拟战斗部在不同起爆距离下对目标的毁伤情况。采用LS-DYNA软件进行仿真计算,对典型靶标在不同破片穿孔分布下的抗拉和抗弯强度变化进行了研究,对比了线列式和聚焦战斗部对目标的毁伤能力,总结了线列式破片穿孔分布对典型靶标毁伤效应的影响规律。
1 理论分析
1.1 破片穿孔特点
聚焦战斗部一般通过内凹的装药曲线使破片在轴向汇聚,形成一定宽度的聚焦杀伤带,进而在目标上形成密集的破片穿孔,图1即为较为典型的聚焦战斗部破片穿孔分布。
线列式战斗部则在聚焦战斗部的基础上,通过预设破片初始斜置角实现破片在战斗部周向的连续均匀分布,进而对目标造成如图2所示的周期线列的破片穿孔毁伤效果。相较于聚焦战斗部片破片穿孔,线列式战斗部破片穿孔整体呈线性分布,破片毁伤带更窄。

图1 聚焦战斗部破片穿孔分布
Fig.1 Fragmentation perforation of focused warhead

图2 线列式战斗部破片穿孔分布
Fig.2 Fragmentation perforation of linear warhead
线列式战斗部仅改变了预制破片初始的排列方式,破片排布密度与尺寸等并未发生变化,在同种战斗部结构与弹目交会条件下,若起爆距离相同,其在目标上形成的破片穿孔数量与聚焦战斗部保持一致。
在实际作战中,防空反导导弹在攻击目标时存在一定的精度误差,难以确保每次起爆时与目标间的距离相同,多数情况下起爆距离会在一定范围内发生变化。在不同起爆距离下,破片在目标上造成的穿孔间距也会随之变化,对应的变化规律如图3所示。

图3 不同起爆距离下破片穿孔间距示意图
Fig.3 Diagram of fragment perforation spacing varying with distance
从图3中不难看出,破片穿孔间距d与战斗部起爆时弹靶间的距离L呈等比例增加关系,即起爆距离L变为原来的k倍时,破片穿孔间距d也变为原来的k倍,同理聚焦战斗部破片聚焦带宽度与起爆距离也呈等比例增加的关系。
依据2种战斗部命中目标后形成破片穿孔数量相同,且破片穿孔间距和聚焦带宽度随起爆距离等比例变化的特点,可以对破片命中目标后形成的含孔结构的应力集中效应进行分析。
1.2 含孔结构的应力集中效应
战斗部起爆产生的高速破片在命中目标后形成的穿孔使目标截面受力面积减小,同时在穿孔周围产生应力集中现象,使得孔边应力急剧增加,远高于同种受力情况下无孔时的应力,同时也远高于距穿孔较远处的应力[9-12]。可采用应力集中系数Ksc来反映这种局部应力增长的现象:
![]()
(1)
式(1)中:σmax为拉伸或弯曲条件下的局部应力峰值,σn为不考虑应力集中效应时的应力,可根据孔径与含孔结构的宽度对应力集中系数Ksc进行计算[13]:
![]()
(2)
式(2)中: β=a/b,即穿孔直径a与含孔结构宽度b之间的比值。对于含孔结构,a与b均为大于0的数,且孔径a不会大于含孔结构宽度b,因此β的值在0至1之间变动。在取值范围内,Ksc随β的增加不断增加,且增幅逐渐提升。对于预制破片杀伤战斗部,其破片尺寸一致,在目标上造成的穿孔直径基本相同,β仅随穿孔附近相对结构宽度的变化发生改变。随着起爆距离减小,目标上破片穿孔间距减小,每个穿孔附近相对结构宽度发生下降,β值相应增加,孔边应力集中现象更为明显,应力峰值增幅逐渐提升。
在相同起爆距离下,线列式战斗部造成的破片穿孔与聚焦战斗部数量相同,但线列式的穿孔分布特点使得目标上相邻穿孔的间距更小,β值更大,孔边由于应力集中导致的应力增幅较大,更易到达材料的屈服强度进而对目标造成毁伤。当起爆距离减小时,破片间距等比例减小,由于线列式战斗部在破片穿孔间距上的优势,其应力集中系数的提升幅度较大,应力提升更为明显,对目标的毁伤能力随穿孔间距减小产生的增幅更大。
2 仿真计算
2.1 典型标靶模型建立
飞机与导弹作为典型空中目标,结构复杂,在进行分析时难以直接计算,需对目标进行简化。考虑到破片尺寸相较于目标往往很小,且破片穿孔仅能影响目标壳体局部区域,因此采用带孔平板作为典型靶标来对空中目标受杀伤战斗部破片毁伤后的外壳结构进行等效处理。根据聚焦战斗部与线列式战斗部破片穿孔的分布特点,采用如图4所示在靶标中心线按破片穿孔间距平均打孔的方式来模拟线列式战斗部毁伤模式,在等效靶中部取一定范围聚焦带后在聚焦带内均匀打孔的方式模拟聚焦战斗部的毁伤模式。在战斗部参数相同的情况下,同一区域内2种毁伤模式对应靶标的破片穿孔数量相同,仅存在分布位置上的差异。
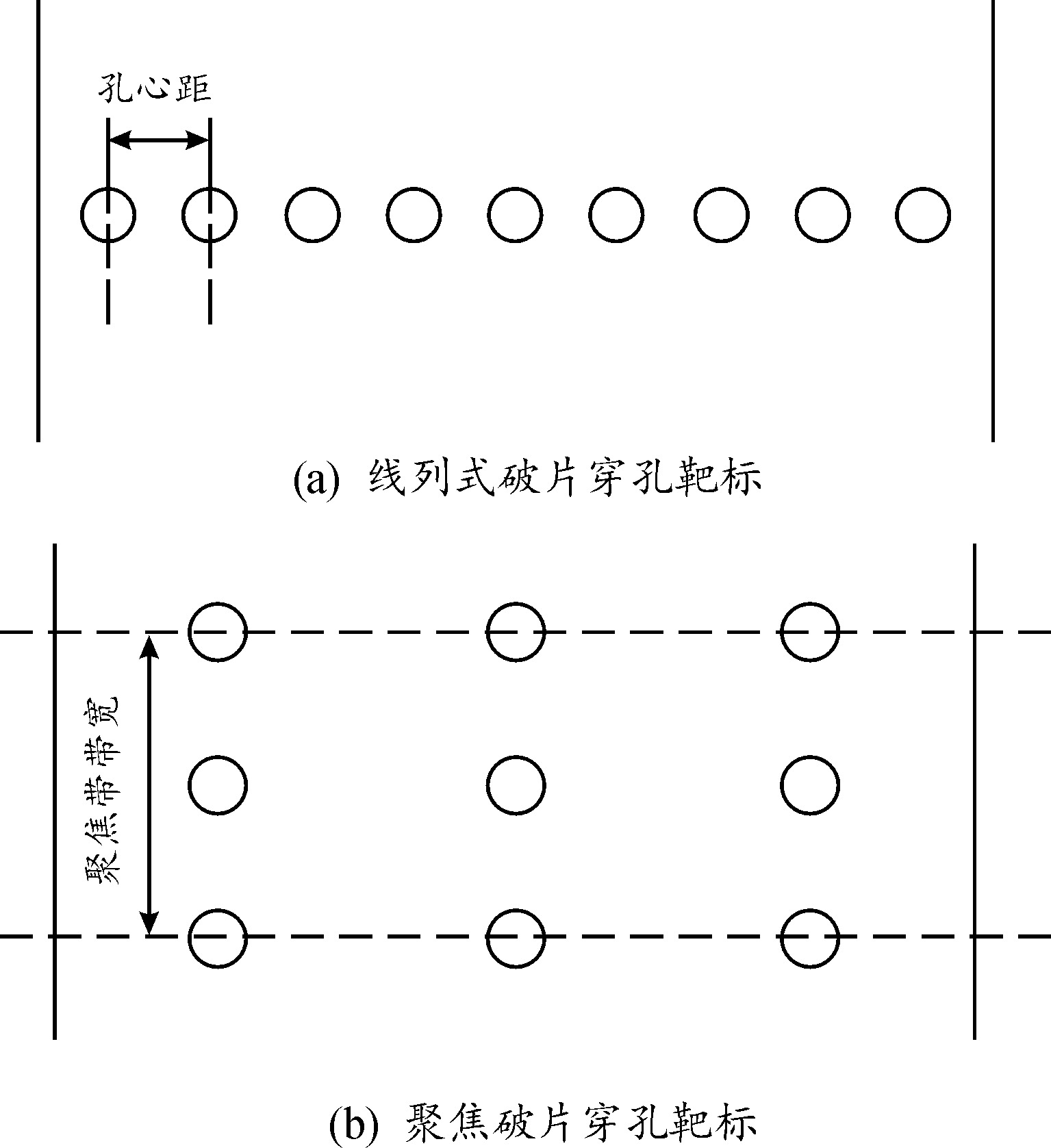
图4 典型靶标破片穿孔分布示意图
Fig.4 Distribution of fragment perforations on typical target
2.2 仿真工况设计
为具体设计不同起爆距离下的典型靶标工况,需得知任一距离处2种战斗部起爆后破片的飞散特性,因此进行了相同尺寸与结构的聚焦及线列式战斗部静爆试验,并在距战斗部10 m处放置靶板以得到破片穿孔分布的相关参数。试验靶板的破片穿孔情况如图5所示,2种靶标的关键设计参数在表1中列出。
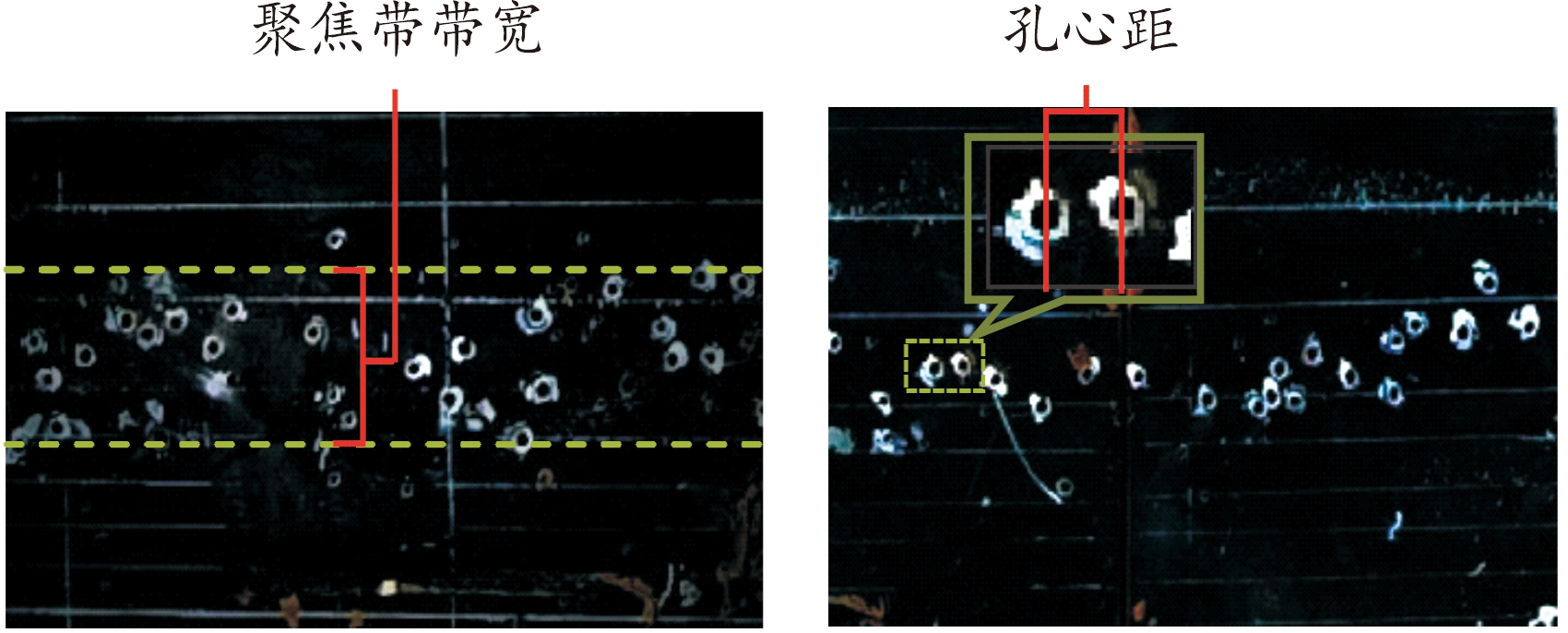
图5 起爆距离10 m处靶板破片穿孔分布情况
Fig.5 Distribution of fragment perforation at detonation distance of 10 m
表1 起爆距离10 m处破片穿孔分布关键参数
Table 1 Distribution parameters of fragment perforation at detonation distance of 10 m

战斗部类型平均穿孔直径/mm平均穿孔孔心距/mm聚焦带带宽/mm聚焦8.0-334.6线列式8.033.7-
在选取起爆距离时需考虑导弹精度对弹目交会距离的影响,而导弹精度通常采用圆周概率误差(circular error probable。CEP)进行衡量[14-15],取CEP=5 m,对3倍CEP范围内不同起爆距离下的破片穿孔分布情况进行研究,典型靶标则选取尺寸550 mm×300 mm,板厚为3 mm的平板结构。依据1.1节理论分析及表1的试验数据计算得出不同起爆距离下等效靶标的穿孔分布情况,以此为基础设计表2所列各仿真工况,同时设置一无穿孔靶标作为对照组进行后续的对比分析。
表2 2种靶标破片穿孔工况
Table 2 Fragmentation perforation conditions of typical targets
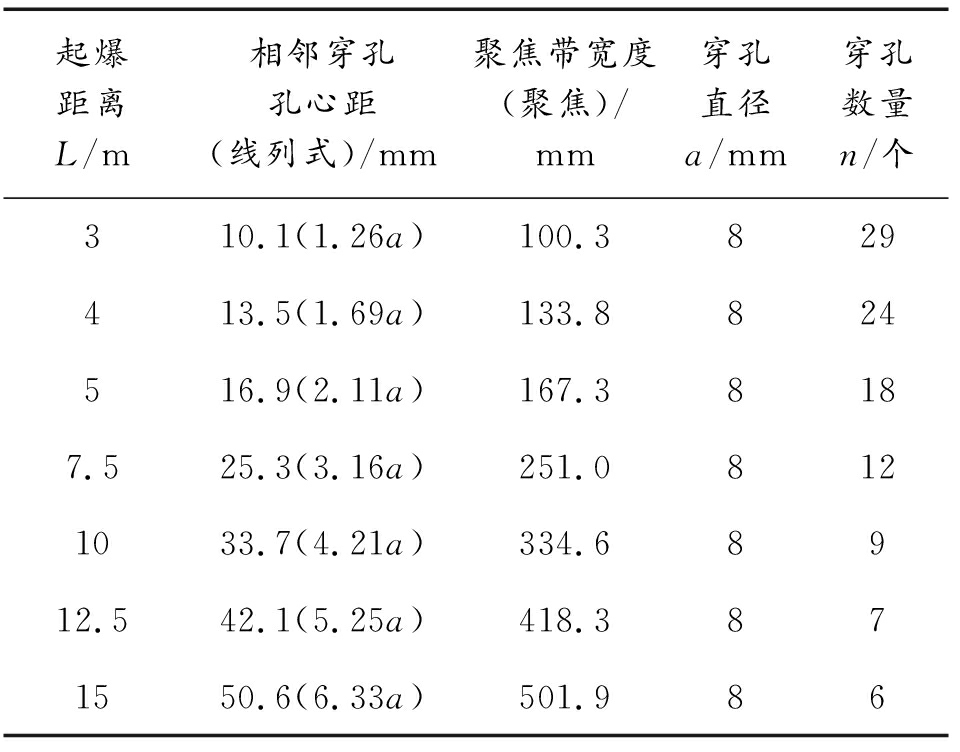
起爆距离L/m相邻穿孔孔心距(线列式)/mm聚焦带宽度(聚焦)/mm穿孔直径a/mm穿孔数量n/个310.1(1.26a)100.3829413.5(1.69a)133.8824516.9(2.11a)167.38187.525.3(3.16a)251.08121033.7(4.21a)334.68912.542.1(5.25a)418.3871550.6(6.33a)501.986
2.3 模型参数及加载方式
采用LS-DYNA软件对所设计的工况进行仿真计算,选取高强度铝合金作为典型靶标材料,采用MAT_JOHNSON_COOK模型和GRUNEISEN状态方程[16]进行描述,具体参数在表3给出。
表3 典型靶标材料参数
Table 3 Material parameters of typical target
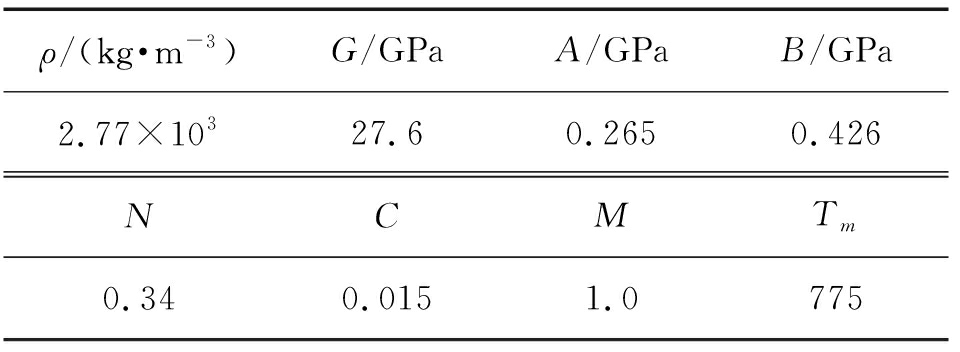
ρ/(kg·m-3)G/GPaA/GPaB/GPa2.77×10327.60.2650.426NCMTm0.340.0151.0775
由于孔周的应力集中现象,穿孔附近应力变化较为剧烈,因此对模型穿孔附近的网格进行局部加密,以得到更为精确的计算结果。为研究不同工况下典型靶标的抗弯和抗拉性能,设计两类加载方式,通过将标靶一端固支,在另一端施加平行于靶标长边的强制位移的方式来研究其抗拉能力;通过将标靶两端固支,在靶标中心处施加垂直于靶标的强制位移的方式来研究其抗弯性能。以5 m处靶标为例,对应模型网格划分情况和加载方式如图6所示。
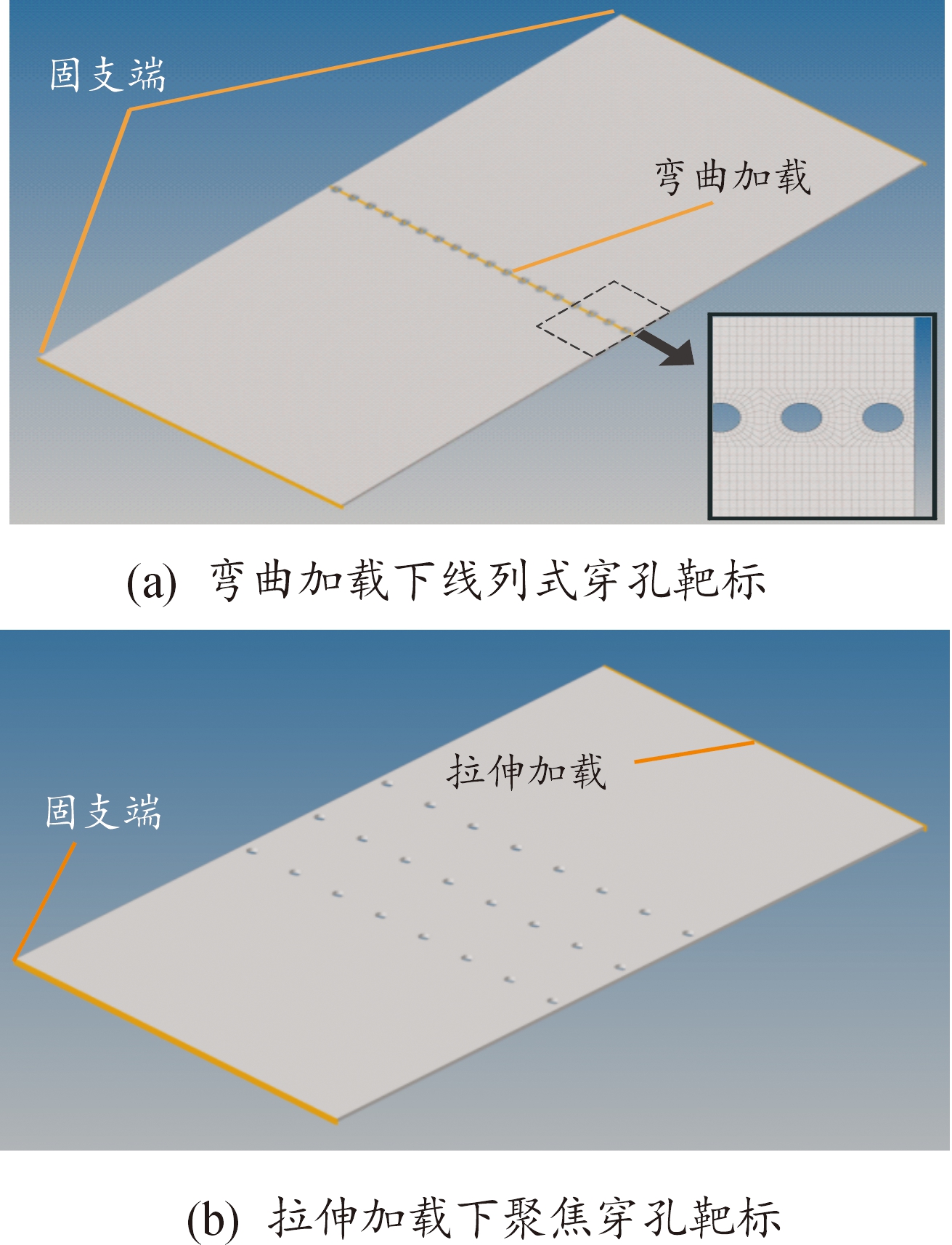
图6 典型靶标的网格划分及加载方式
Fig.6 Meshing and loading methods of typical target
3 结果分析
3.1 拉伸加载
在拉伸加载的仿真计算中,采用一端固支一端加载的方式对各工况的靶标施加强制位移直至其被拉断,以起爆距离为5 m时2种靶标为例,其在拉伸加载下的应力云图如图7所示。
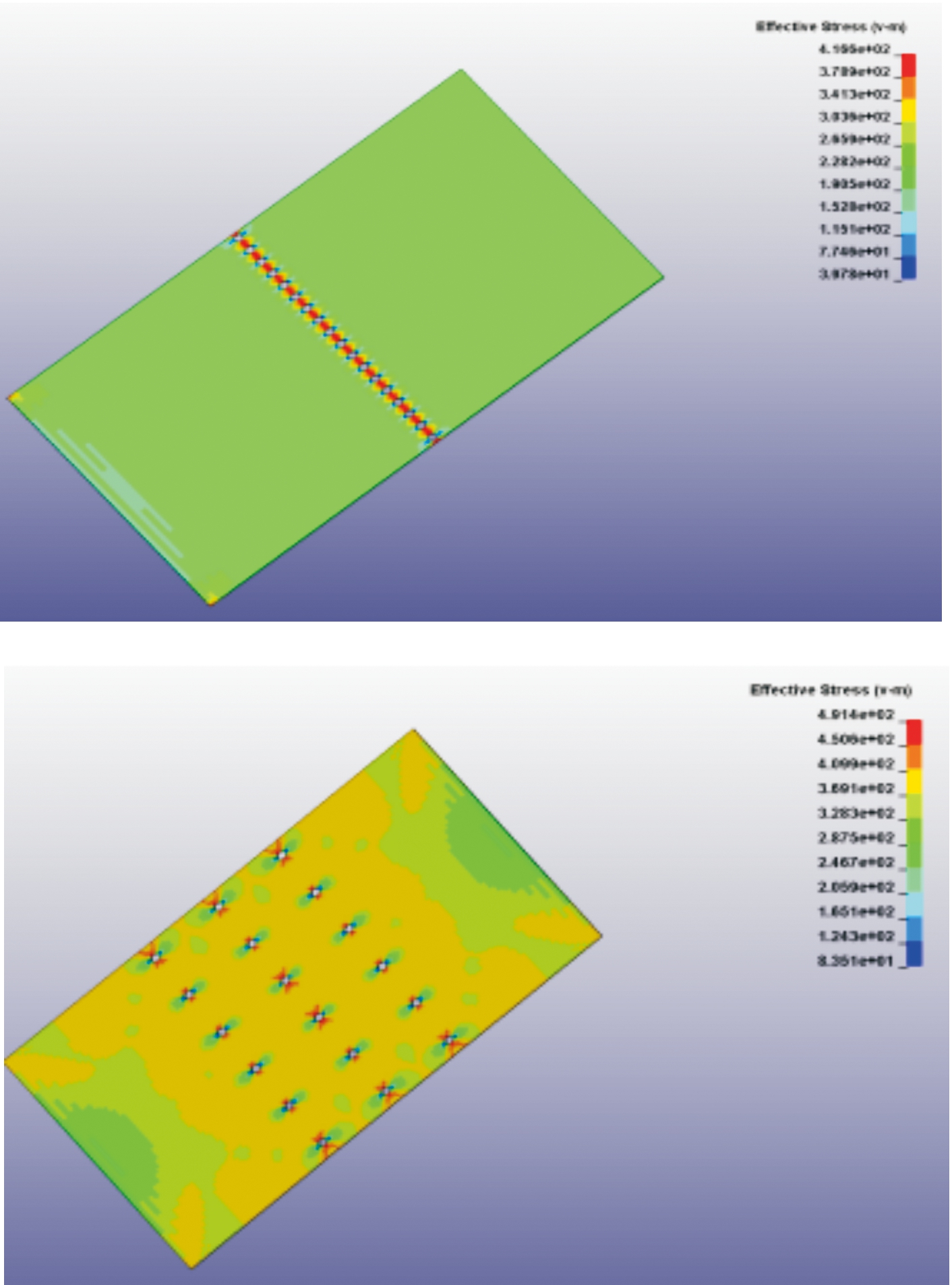
图7 拉伸加载下典型靶标应力云图
Fig.7 Stress nephogram of target under tensile loading
由仿真结果可以看出,2种带孔靶标在受到拉伸载荷时在孔周均出现应力集中现象,其中线列式穿孔靶标中心由于各孔应力集中后的耦合形成了线性的应力集中区域。由于孔周应力集中现象造成的应力大幅上升,材料在局部快速达到强度极限,产生裂纹,最终随裂纹发展整个靶标完全断裂。在5 m起爆距离下,线列式破片穿孔靶标在加载时长相同时应力峰值的增幅更大,应力集中更加明显,线列式穿孔孔周快速的应力增长以及应力集中区域的耦合使对应靶标达到屈服极限的时间相较于聚焦破片穿孔靶标缩短了1.76 s,在其余工况下,若起爆距离相同,线列式破片穿孔靶标出现失效的时间均早于聚焦破片穿孔靶标。
在靶标加载过程中,随着加载时长的增加,固支端上的支反力逐渐增加。当靶标产生裂痕,力无法从加载端再传递至固支端,支反力快速下降直至靶标断裂,最终变为0 N,可通过靶标断裂前对应的最大支反力来评价其抗拉能力。含孔靶标断裂时固支端最大支反力越小,与对照组之间的差值越大,说明在对应距离处,该类型破片穿孔下靶标的抗拉能力越弱,该类型战斗部对目标的毁伤效果越好。
对表2工况下的仿真结果进行统计,其固支端最大支反力随起爆距离的增加逐渐增加,具体结果在表4中列出。
表4 最大支反力统计结果
Table 4 Statistical result of the maximum counterforce

起爆距离/m固支端最大支反力/(105 N)聚焦破片穿孔靶标线列式破片穿孔靶标对照组无穿孔靶标33.291.1343.341.6753.442.407.53.483.18103.543.4012.53.563.48153.573.505.25
相较于无穿孔情况下的对照组,不同起爆距离下线列式和聚焦破片穿孔均使得靶标最大支反力下降。在弹靶距离相同时,线列式穿孔下靶标最大支反力总是小于聚焦破片穿孔下的靶标,即线列式战斗部对空中典型目标的毁伤能力总是优于同种参数的聚焦战斗部。
对于2种穿孔下的靶标,最大支反力的下降幅度对应着抗拉强度的损失比:
![]()
(3)
式(3)中:RΔTS为靶标的抗拉强度损失比; Ftc为对照组最大支反力; Ft为带孔靶标最大支反力。抗拉强度损失比反映了不同破片穿孔分布下典型目标受到某一类型战斗部破片命中毁伤后抗拉强度的损失情况,抗拉强度损失比越大,则战斗部对目标的毁伤能力越强。对各工况下靶标的抗拉强度损失比进行计算,其随破片穿孔孔心距的变化趋势如图8所示。
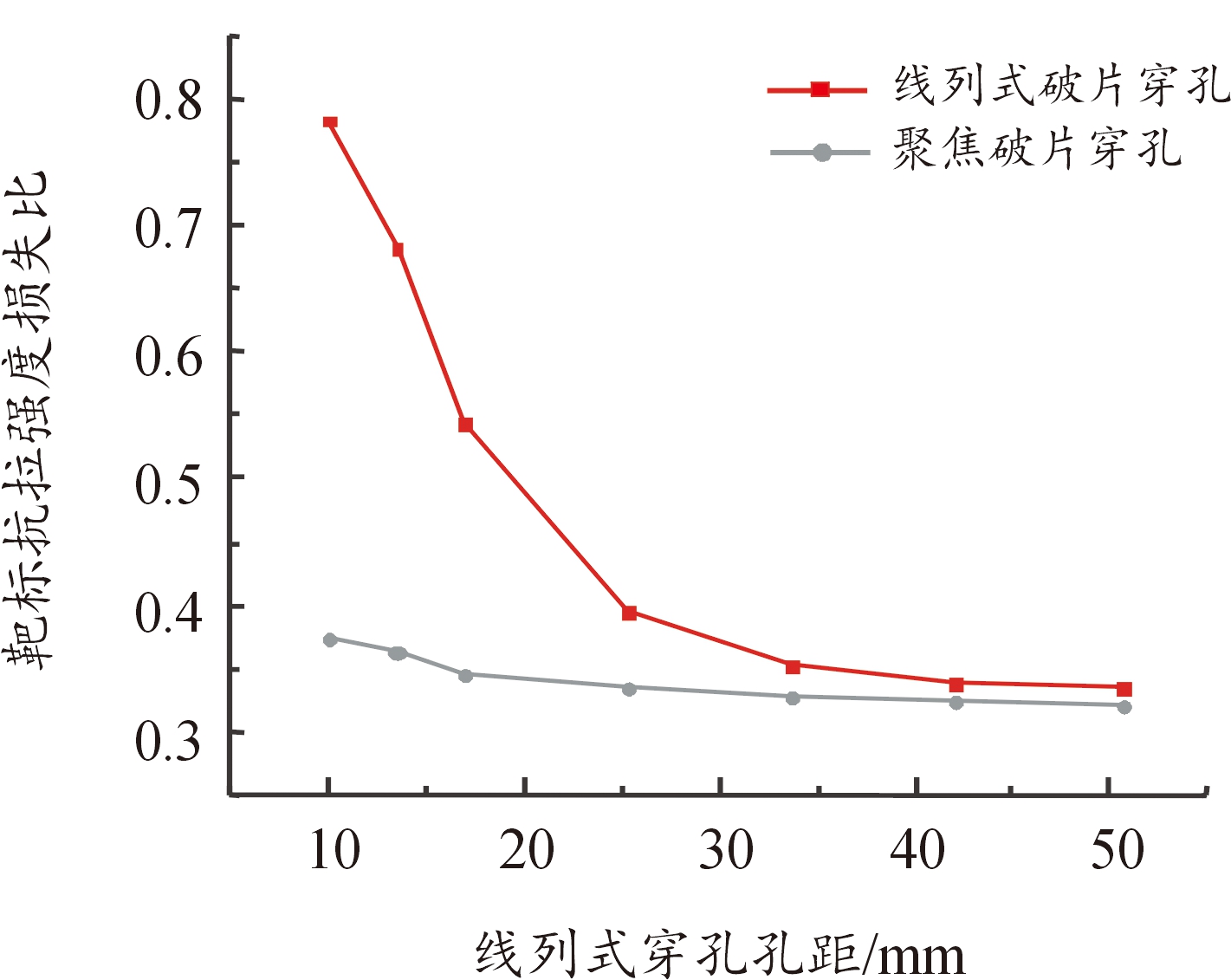
图8 靶标抗拉强度损失比变化趋势
Fig.8 Variation trend of tensile strength loss ratio
在设计工况下线列式和聚焦破片穿孔下靶标抗拉强度损失比均在0.32以上。随着穿孔孔心距的减小,线列式破片穿孔靶标的抗拉强度损失比迅速增大,在穿孔孔心距缩小至1.26倍孔径,即起爆距离减小至3 m时,对应靶标的抗拉强度损失比高达0.785。与之相比,聚焦破片穿孔靶标抗拉强度损失比增长缓慢,仅从起爆距离为15 m时的0.320增加至3 m时的0.373,战斗部毁伤能力提升并不显著。通过同一起爆距离下2种靶标的抗拉强度损失比的比值对不同破片穿孔分布下线列式战斗部的毁伤优势进行分析,结果如图9所示、以靶标的抗拉强度损失比评价2种战斗部对目标的毁伤能力时,随着破片穿孔孔心距减小,线列式战斗部相对聚焦战斗部在毁伤能力上的优势逐渐增强,当穿孔孔心距较小时,其对典型靶标的毁伤能力可以达到聚焦模式下的2.1倍。当起爆距离超过10 m后,其对典型靶标的毁伤能力约为普通聚焦模式的1.1倍,即当线列式破片穿孔孔心距超过4.21倍孔径后,线列式战斗部相对聚焦战斗部的毁伤优势约为10%,并不再随孔心距的增加发生大幅度的减小。
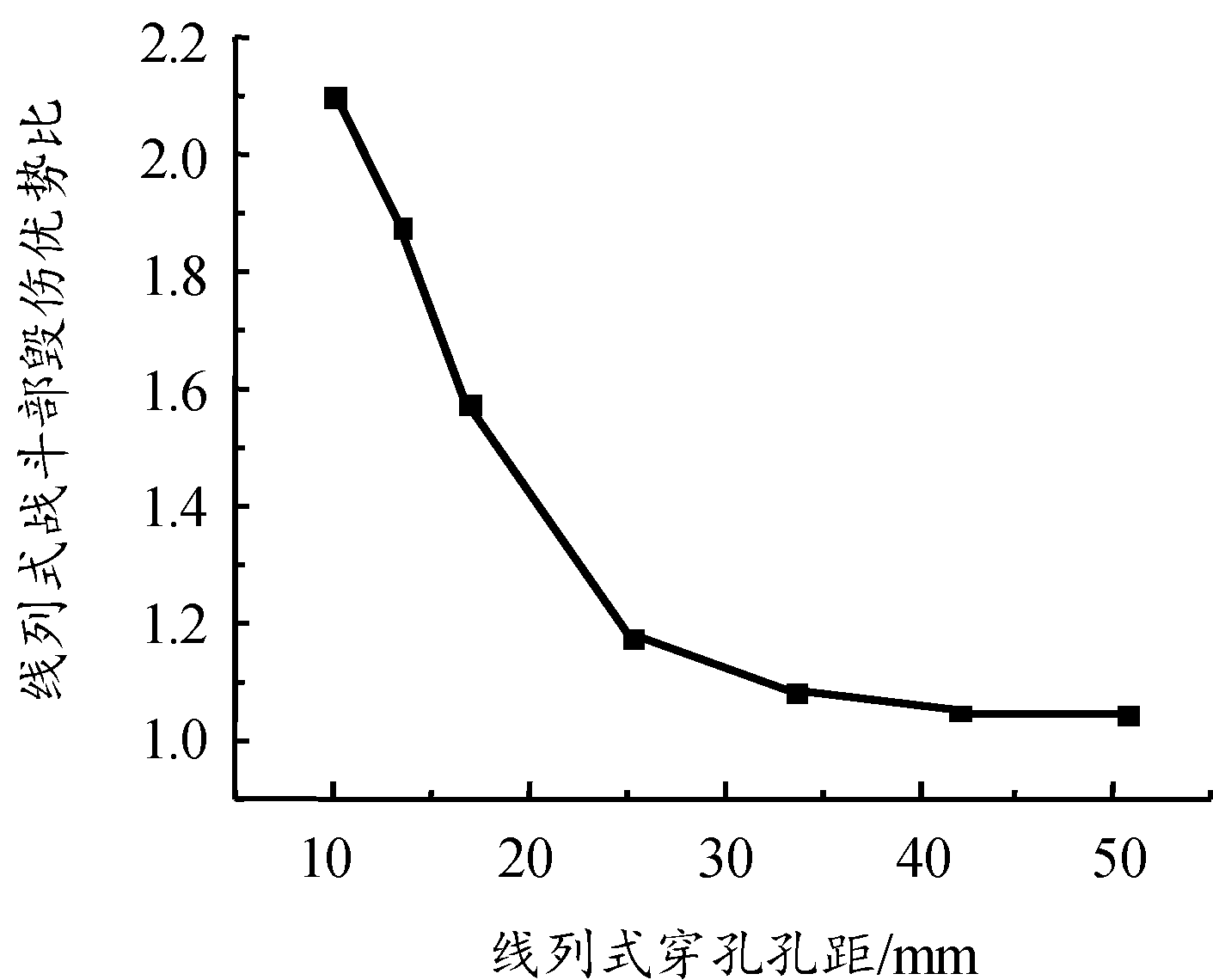
图9 线列式战斗部毁伤优势(抗拉)变化趋势
Fig.9 Variation trend of damage odds (tensile strength) ratio
3.2 弯曲加载
在施加弯曲载荷时以类似于三点弯曲的方式进行加载,2种靶标在受到弯曲加载时加载区域附近穿孔在孔周出现明显的应力集中现象,图10为5 m起爆距离下2种靶标受弯时对应的应力分布情况。
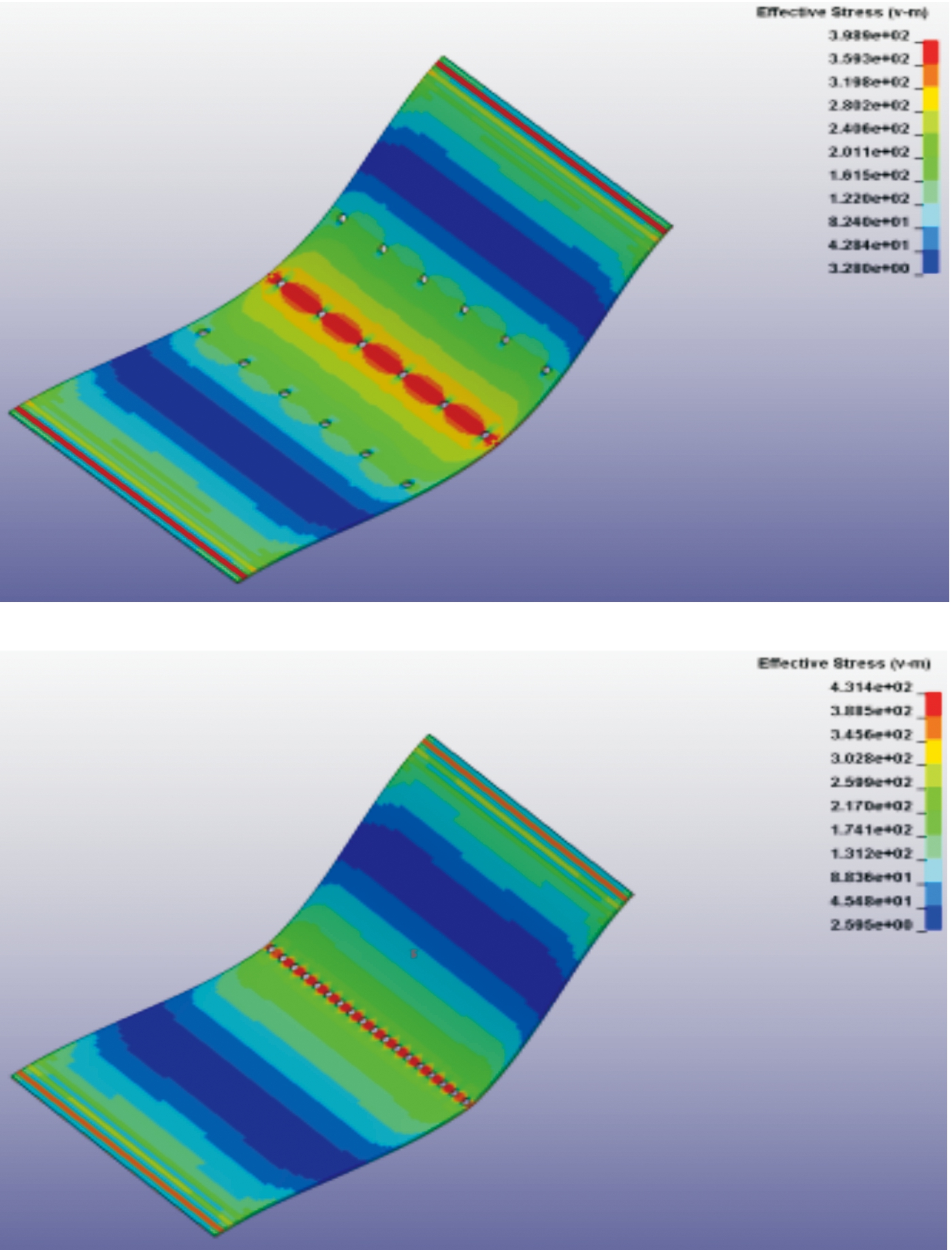
图10 弯曲加载下典型靶标应力云图
Fig.10 Stress nephogram of target under bending loading
靶标受弯曲载荷作用时载荷施加处的应力高于其他区域,在加载区域,穿孔附近的应力高于其他位置。对于2种不同穿孔情况的靶标而言,当加载时长相同,即靶标弯曲情况一致时,线列式穿孔孔周应力更大且相邻孔间应力集中耦合,加载内沿破片穿孔形成了线性的应力集中区域。可以看出,当靶标上有线列式破片穿孔时,在弯曲加载下局部应力提升更为明显。记录弯曲加载时不同穿孔分布情况下靶标受载区域位移达到100 mm所需力的大小来对靶标的抗弯能力进行评价,在各靶标加载方式与弯曲形变相同的前提下,达到该弯曲变形所需要的力越大,则对应靶标的抗弯能力越强,靶标越不容易发生弯曲变形,当达到该弯曲变形所需要的力越小,则靶标的抗弯能力越弱。对表2中各工况下靶标弯曲变形达到100 mm的所需力进行统计,结果如表5所示。
表5 靶标达到预设形变所需力统计结果
Table 5 Statistical result of the required counterforce

起爆距离/m弯曲加载所需力/(103 N)聚焦破片穿孔靶标线列式破片穿孔靶标对照组无穿孔靶标35.741.9345.872.5156.103.137.56.193.44106.374.8212.56.435.01156.485.117.90
与无穿孔情况的对照组靶标相比,在弯曲变形程度相同时,不同弹靶距离下的2种穿孔模式均使得靶标变形所需要的力下降,靶标抗弯强度降低。以产生100 mm弯曲变形时所需力的下降幅度为靶标的抗弯强度损失比进行计算:
![]()
(4)
式(4)中:RΔBS为靶标的抗弯强度损失比; Fbc为无穿孔靶标达到预设弯曲变形所需要的力; Fb为带孔靶标达到预设弯曲变形所需要的力。抗弯强度损失比是对不同破片穿孔分布下典型目标受到杀伤战斗部破片命中后抗弯强度的损失情况的评价,抗弯强度损失比越大,则目标受损越严重,各工况下靶标抗弯强度损失比如图11所示。
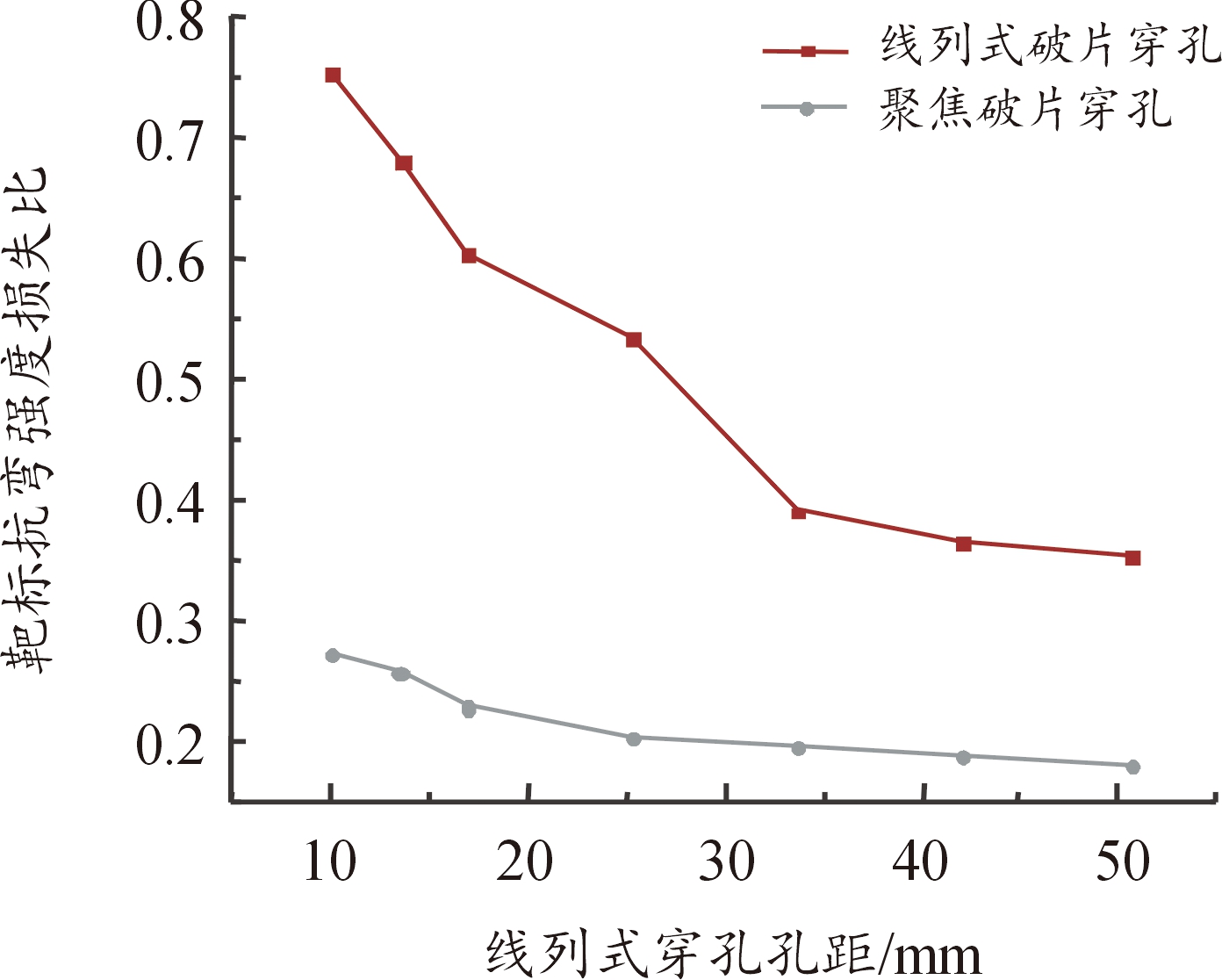
图11 靶标抗弯强度损失比变化趋势
Fig.11 Variation trend of bending strength loss ratio
2种破片穿孔类型的靶标抗弯强度均出现不同程度的下降,线列式穿孔靶标的抗弯强度损失比在预设工况内均高于聚焦式穿孔靶标。随着起爆距离的减小,即破片穿孔间距减小,靶标的抗弯强度损失比逐渐提升,线列式穿孔靶标的抗弯强度损失比提升幅度大于聚焦式破片穿孔靶标。在起爆距离为3 m时,线列式穿孔靶标的强度损失比达到0.756而聚焦式穿孔靶标强度损失比仅为0.273,当起爆距离增加到15 m时,线列式靶标和聚焦式靶标的抗弯强度损失比分别下降至0.353和0.179。以不同弹靶距离下靶标抗弯强度损失比的比值对2种类型战斗部对典型靶标的毁伤能力进行比较,结果如图12所示。

图12 线列式战斗部毁伤优势(抗弯)变化趋势
Fig.12 Variation trend of damage odds (bending strength) ratio
起爆距离在7.5 m以内时,线列式穿孔靶标的抗弯强度损失比为对应距离下聚焦式穿孔靶标的2.6倍以上,在3 m距离处可达2.8倍。当起爆距离增加至10 m后,线列式靶标的抗弯强度损失比下降至聚焦式靶标的2倍左右,并趋于稳定。以不同穿孔分布下典型靶标的抗弯强度损失比对2种战斗部的毁伤能力进行评估,当线列式穿孔孔心距在4.21倍孔径以上时,线列式战斗部相对聚焦战斗部的毁伤威力优势维持在98%左右;而当线列式破片穿孔孔心距减小至3.16倍的孔径以下时,线列式战斗部较于聚焦战斗部有着163%以上的显著毁伤优势,
4 结论
为了研究线列式破片穿孔分布对典型靶标的毁伤效应,本文中分析了线列式及聚焦战斗部破片穿孔特点,考虑导弹制导精度误差引起的起爆距离差异,设计了不同穿孔分布下2种战斗部对应靶标仿真工况并对仿真计算结果进行了对比总结。得到结论如下:
1) 破片命中目标后形成的穿孔附近产生应力集中效应,在起爆距离相同的前提下,线列式破片穿孔的应力集中现象更为明显,应力集中系数Ksc随孔心距减小时的增幅更高;
2) 当起爆距离在15 m之内时,线列式破片穿孔靶标的抗拉与抗弯强度损失比均高于聚焦破片穿孔靶标,线列式战斗部毁伤效果总是优于聚焦战斗部;
3) 随着起爆距离的减小,即随着线列式破片穿孔分布距离的减小,线列式战斗部对典型靶标的毁伤优势逐渐增加。当破片穿孔孔心距小于3.16倍的孔径时,线列式战斗部毁伤优势明显,对应靶标的抗拉及抗弯强度损失比可达聚焦破片穿孔靶标的2.1倍及2.8倍。
[1] 张阳.纳卡冲突中无人机攻防装备运用及典型作战场景分析[J].指挥控制与仿真,2022,44(5):31-37.
ZHANG Yang.Analysis of the application of UAV attack and defense equipment and typical operational scenarios in the Nagorno-Karabakh conflict[J].Command Control& Simulation,2022,44(5):31-37.
[2] 徐梦林,印立魁,黄文龙,等.轴向聚焦式预制破片战斗部破片飞散角研究[J].弹箭与制导学报,2022,42(4):108-113.
XU Menglin,YIN Likui,HUANG Wenlong,et al.Study on fragment dispersion angle of axial focusing prefabricated fragment warhead[J].Journal of Projectiles,Rockets,Missiles and Guidance,2022,42(4):108-113.
[3] 梁安定,郑雄伟,孙兴昀.一种防空导弹用破片战斗部技术[J].弹箭与制导学报,2021,41(5):86-90.
LIANG Anding,ZHENG Xiongwei,SUN Xingyun.A fragment warhead technology on air defense missile[J].Journal of Projectiles,Rockets,Missiles and Guidance,2021,41 (5):86-90.
[4] 张绍兴,李翔宇,丁亮亮,等.聚焦式战斗部破片轴向飞散控制技术[J].高压物理学报,2018,32(1):140-147.
ZHANG Shaoxing,LI Xiangyu,DING Liangliang,et al.Axial dispersion control of focusing fragment warhead[J].Chinese journal of high pressure physics 2018,32 (1):140-147.
[5] 苗春壮,梁增友,邓德志,等.曲率半径对聚焦战斗部影响的数值仿真[J].兵工自动化,2018,37(12):93-96.
MIAO Chunzhuang,LIANG Zengyou,DENG Dezhi,et al.Numerical simulation influence of curvature radius on focusing warhead[J].Ordnance Industry Automation,2018,37 (12):93-96.
[6] 梁争峰,袁宝慧,程淑杰,等.动态线列式破片战斗部技术探索[J].火炸药学报,2011,34(3):42-44.
LIANG Zhengfeng,YUAN Baohui,CHENG Shujie,et al.Engineering design of dynamic linear distribution fragmentation warhead[J].Chinese Journal of Explosives &Propellants,2011,34(3):42-44.
[7] 王宝成,程淑杰,梁争峰,等.线列式战斗部对目标结构毁伤效应研究[J].四川兵工学报,2015,36(6):15-17,24.
WANG Baocheng,CHENG Shujie,LIANG Zhengfeng,et al.Study on structure damage effect of target for linear distribution fragmentation warhead[J].Journal of Sichuan Ordnance,2015,36 (6):15-17,24.
[8] 舒张忆南,梁争峰,程淑杰,等.线列式结构毁伤在弯曲载荷下的增益[J].科学技术与工程,2022,22(15):6106-6112.
SHU Zhangyinan,LIANG Zhengfeng,CHENG Shujie,et al.Damage gain of linear structures under bending load[J].Science Technology and Engineering,2022,22 (15):6106-6112.
[9] 石多奇,张恒斌,李振磊,等.孔间非均匀应力影响下的带孔薄板破坏行为[J].航空动力学报,2022,37(11):2353-2361.
SHI Duoqi,ZHANG Hengbin,LI Zhenlei,et al.Effect of nonuniform stress between holes on failure behavior ofthin plate with holes[J].Journal of Aerospace Powe,2022,37(11):2353-2361.
[10] SANTOS A.Determination of stress concentration factors on flat plates of structural steel[J].Journal of Physics:Conference Series,2013.
[11] CHENG B,WANG J,LI C.Compression tests and numerical analysis of perforated plates containing slotted holes in steel pylons[J].Thin-Walled Structures,2013,67(2):129-143.
[12] 王绍波.含孔复合材料结构应力集中的广义混合法[D].天津:中国民航大学,2019.
WANG Shaobo.Generalized mixed finite element methodfor stress concentration around a circle holein composite structure[D].Tianjin:Civil Aviation University of China,2019.
[13] 李云松,陈小安,江德智.带孔薄板孔边应力集中系数的改进算法[J].机械设计与制造,2017(6):42-45.
LI Yunsong,CHEN Xiaoan,JIANG Dezhi.Improved algorithm for stress concentration factor of perforated thin plate[J].Machinery Design &Manufacture,2017(6):42-45.
[14] 张乐,李武周,巨养锋,等.基于圆概率误差的定位精度评定办法[J].指挥控制与仿真,2013,35(1):111-114.
ZHANG Le,LI Wuzhou,JU Yangfeng,et al.Positioning accuracy evaluation method based on CEP[J].Commandcontrol &Simulation,2013,35(1):111-114.
[15] 刘国国,王鹏辉,周旭宜.导弹圆周概率误差的仿真评估[J].电子质量,2019(6):29-31.
LIU Guoguo,WANG Penghui,ZHOU Xuyi.Simulation evaluation of missile circumference probability error[J].Electronics Quality,2019(6):29-31.
[16] 张子群,姜兆亮,魏清月.2219铝合金动态力学性能及其本构关系[J].材料工程,2017,45(10):47-51.
ZHANG Ziqun,JIANG Zhaoliang,WEI Qingyue.Dynamic mechanical properties and constitutive relation of 2219 aluminum alloy[J].Journal of Materials Engineering,2017,45 (10):47-51.