0 引言
在军事设施的建造与爆炸防护领域,研发轻质高强、具有一定爆炸冲击防护能力的板材一直是该领域的研究热点。通常采用夹芯结构板材来抵抗爆炸荷载的作用,其主要通过芯层塑性大变形将爆炸产生的能量转化为其他形式的能量,对于芯层力学性能的要求较高。目前国内外大多采用多孔金属材料[1]作为夹芯结构的芯层,其具有相对密度小、耗能性好等特点。依据内部单元是否周期性排布,多孔金属材料可分为泡沫多孔金属材料和周期性多孔金属材料2大类。其中,由于后者具有更高的比强度与比刚度[2],更能满足爆炸冲击防护的需要。
目前常见的制备周期性多孔金属材料的方法主要有熔模铸造法[3]、塑性变形法[4]、增材制造法[5]、三维编织法[6]等。其中三维编织法通过对成品金属丝进行弯折、绕织制成所需拓扑构型,具有制备工艺简单,材料易得,可快速大批量制备等特点,近年来在国内外得到了广泛关注。如Kang等[7]基于三维编织法提出了Circular Spring Kagome、Hexagonal Spring Kagome、Dual Wired Octet、Zigzag、Three dimensional woven wire structure(3DWT)等编织结构构型,并提出了相应的静力学性能指标计算公式。此外,随着金属制造行业的发展,一些高强金属材料也被应用于编织结构中,例如陈鹏等[8]采用三维编织法设计了一种由三角螺旋式高强钢丝与螺旋双绞线组成编织结构芯层,静压试验结果表明芯层高度增加时,其压缩力学性能增大而吸能特性减小。
尽管国内外学者对三维编织法的制备工艺进行了大量的研究,并提出了多种拓扑构型,但对于三维编织结构的研究集中于静力学领域,对于其在爆炸荷载作用下的响应分析仍较少。国内外学者针对其他类型夹芯结构的动力响应展开了大量研究,例如邓旭辉等[9]运用数值模拟的方法分析了蜂窝结构夹芯板在爆炸荷载作用下的响应,并将响应过程划分为爆炸发生、力的传递和结构变形3个阶段。张豪等[10]通过提取背板中心点的速度,分析了夹芯结构各组成部分之间作用力的传递规律,结果表明:背板的变形主要源于芯层传递的作用力因此在进行夹芯结构设计时应根据荷载选择合适的芯层。姚梦雷等[11]分析了不同面板与芯层刚度组合的Y型夹芯板在舱内爆炸荷载作用下的变形模式,发现面板与芯层刚度之间的相对强弱关系是影响Y型夹芯板变形模式的主要原因。Feng等[12]对比了采用沙漏型芯层与金字塔型芯层的夹芯结构在水下爆炸荷载作用下的响应,虽然2种芯层的抗压强度基本相同,但是前者具有更好的抗面板拉伸和撕裂性能,表明了可以通过对芯层进行拓扑优化提高结构整体的抗爆性能。亓昌等[13]对比了金字塔型夹芯板芯层腹杆分别采用实体单元与梁单元时的仿真精度,发现爆炸点高度在一定范围内时,梁单元简化模型的仿真精度高于实体单元模型,并且前者计算时间能够减少99%。易建坤等[14]研究发现改变质量及载荷条件,结构几何参数对复合结构夹芯板抗爆性能影响趋势也会随之改变,因此需要针对特定的质量、荷载参数分析几何参数的影响规律。
总体来看,在爆炸荷载作用下夹芯结构的抗爆性能受芯层参数、芯层与面板之间的相互作用等因素的影响。因此,对于编织结构夹芯板抗爆性能的研究,不能只关注静态条件下芯层的力学性能,为此本文中在高强钢丝编织结构夹芯板抗爆试验的基础之上,采用数值模拟的方法研究了结构响应的过程,对比不同芯层高度的高强钢丝编织结构夹芯板的响应模式,分析不同芯层参数对于高强钢丝编织结构夹芯板抗爆性能的影响规律。根据无量纲冲量与无量纲变形量的计算公式,进一步推导高强钢丝编织结构夹芯板设计指导公式。研究可为高强钢丝编织结构夹芯板抗爆性能的优化设计提供参考。
1 抗爆性能试验
1.1 试验装置
如图1所示,设计制作的爆炸试验台主要由“回”型盖板及支撑底座组成。
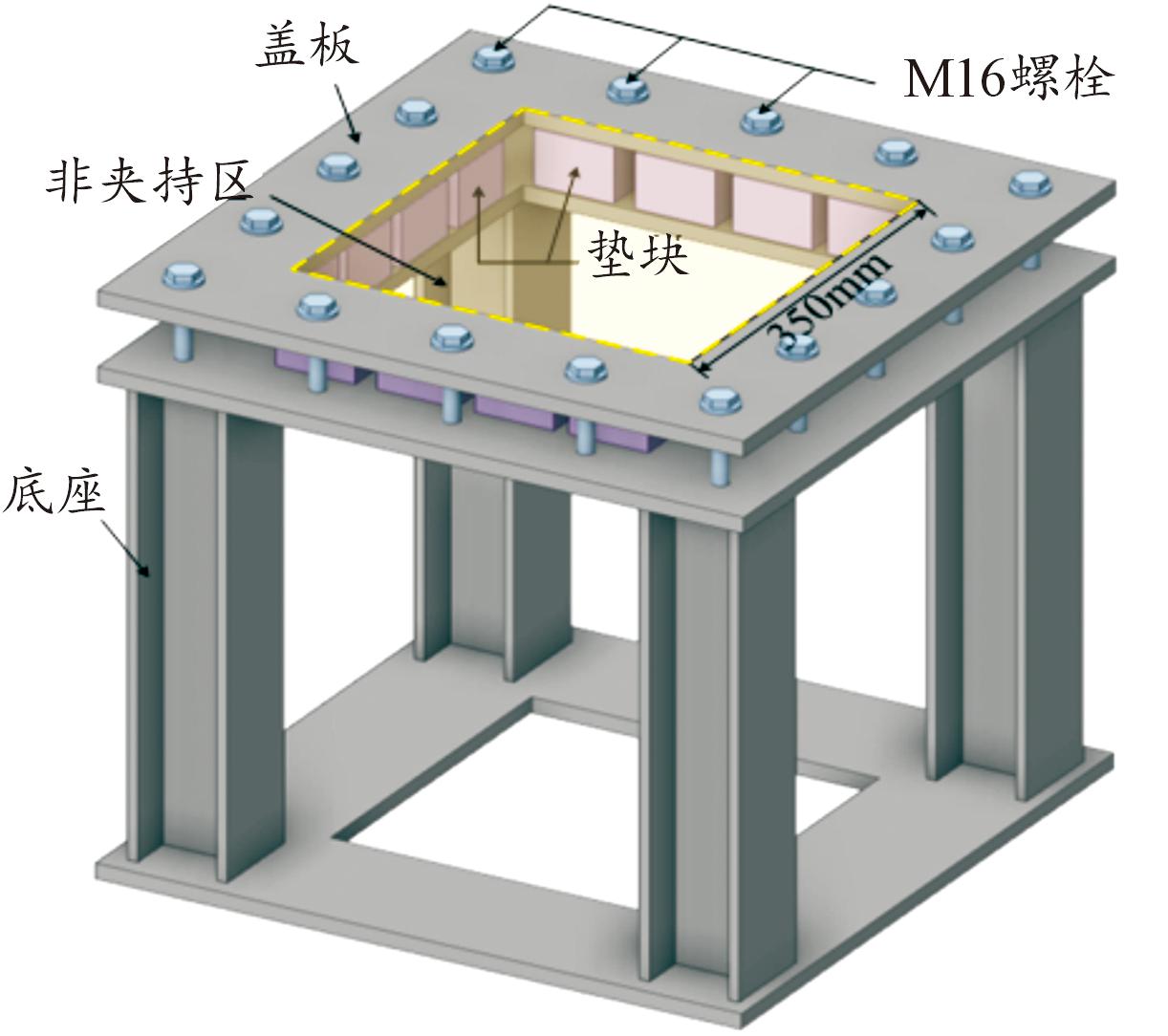
图1 爆炸试验台
Fig.1 The blast test-bed
其中,中央镂空面积为350 mm×350 mm,试验时先将夹芯板试件置于中央镂空区,再采用与芯层等高的垫块填充于夹芯板试件迎爆面、背爆面板中间,最后采用M16螺栓将底座与盖板连接以确保对试件的有效夹持。需说明的是,本文中的试验、数值模拟及相关分析讨论均针对试件的非夹持区域展开。
1.2 制备工艺
制备高强钢丝编织结构夹芯板试件时,首先利用折弯机将钢丝弯折成螺旋式三角形(高强钢丝弯折处倒角半径为2 mm)。然后将螺旋三角钢丝段正反向错位拼接组成,利用压条和螺栓将芯层与上下面板连接,制备流程如图2所示。试件芯层相对密度ρrel,即单个胞元内芯层钢丝所占体积的百分比,计算公式如式(1)所示。
![]()
(1)
式(1)中:r为芯层钢丝半径(mm);θ为钢丝偏折角;Hc为芯层高度。具体几何参数见图3。
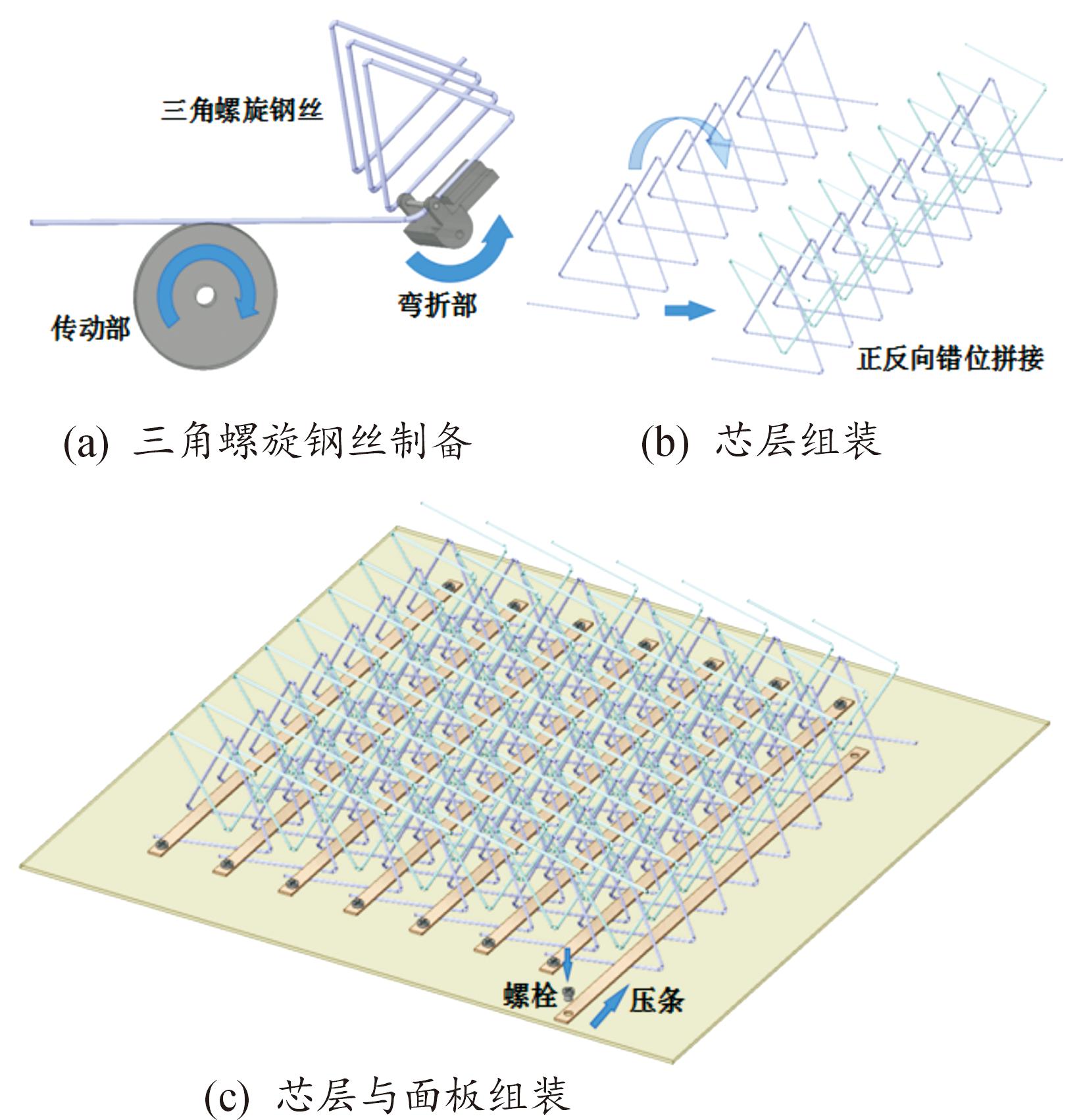
图2 夹芯板制备工艺
Fig.2 Preparation technology of sandwich panel
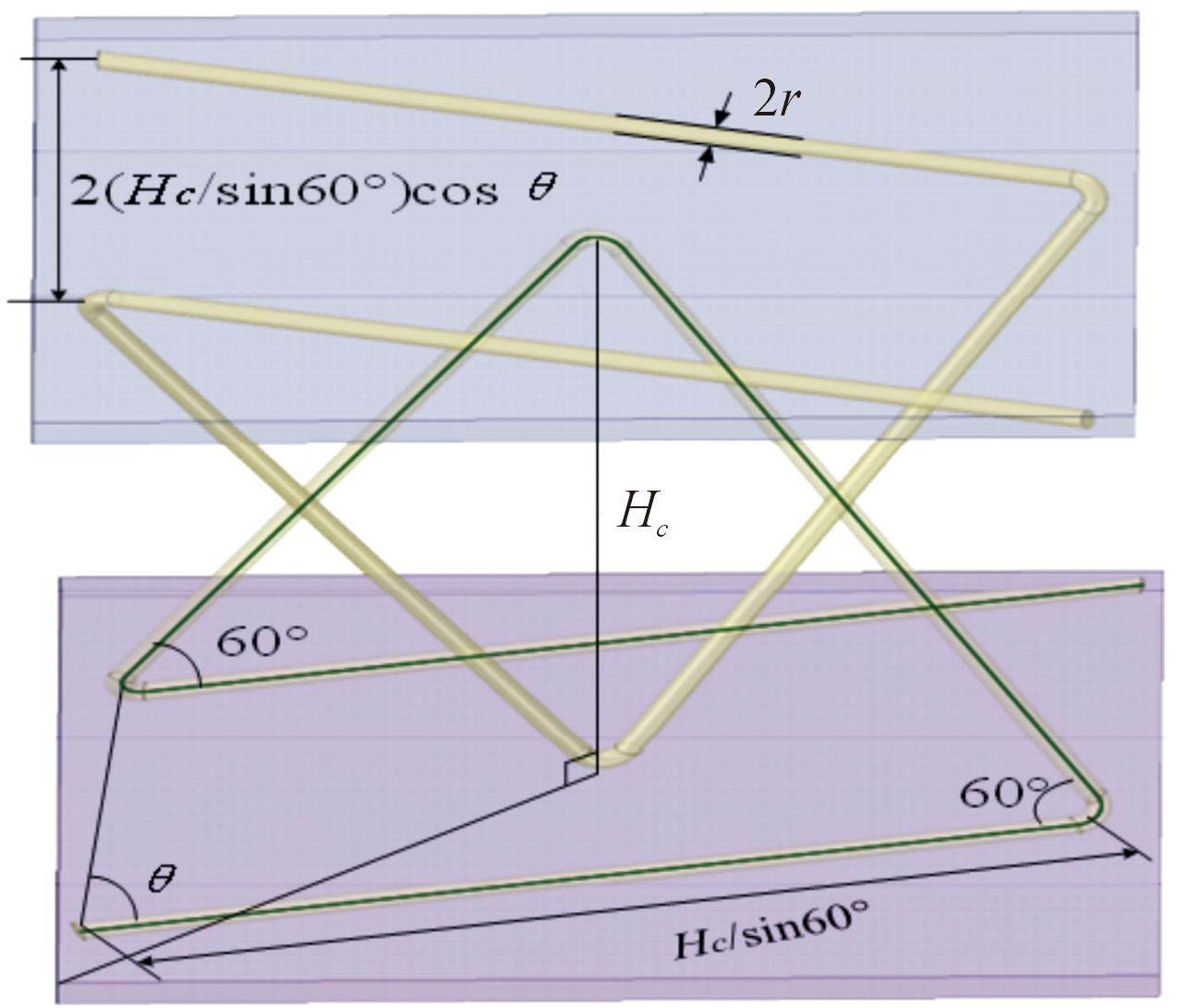
图3 几何参数示意图
Fig.3 Geometric parameter diagram
本文中采用的高强钢丝编织结构芯层制备工艺,支持芯层高度的设计区间为48~88 mm,调整间隔为10 mm;钢丝偏折角的设计区间为70~80 °。
对于编织结构芯层的抗压强度σ0,采用Kang等[13]基于芯层金属丝段均是理想的直杆且节点不堆积的假设,提出的芯层抗压强度σ0是芯层金属材料强度σc和芯层相对密度ρrel的函数,如式(2)所示。
σ0=cρrelσc
(2)
式(2)中:σ0为芯层抗压强度,MPa;σc为高强钢丝极限强度;c为无量纲系数,参考对于不同规格的高强钢丝编织结构芯层准静态压缩试验[8]结果,发现c值的大小与芯层钢丝直径有关,在数值上等于0.67r。
1.3 试验方法
制作了3个高强钢丝编织结构夹芯板试件用于开展实爆试验,如图4所示。试件面板材料为Q235钢,厚度为2.5 mm,尺寸为500 mm×500 mm,其中受爆炸荷载作用区域长度为350 mm,两端为固定支撑区域,长度均为75 mm。芯层参数见表1。

图4 高强钢丝编织结构夹芯板
Fig.4 High-strength steel wire woven structure sandwich panel
表1 试件芯层参数
Table 1 Parameters of samples core layer
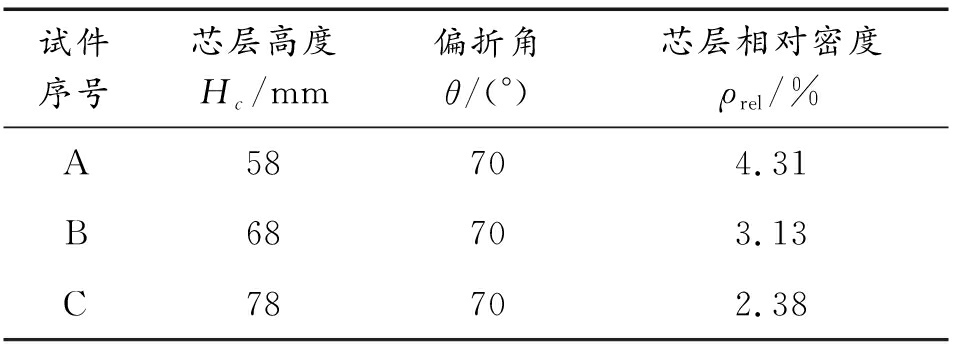
试件序号芯层高度Hc/mm偏折角θ/(°)芯层相对密度ρrel/%A58704.31B68703.13C78702.38
爆炸试验采用2号岩石乳化炸药圆球形药包,质量为350 g,采用8号瞬发电雷管嵌入药包内部起爆,药包中心与上面板中心距离为15 cm,如图5所示。
2 高强钢丝材料力学性能
2.1 准静态、动态拉伸试验
为了能够准确描述高强钢丝的力学性能,参考GB/T228.1—2010[15]制作了2个准静态拉伸试验试件。利用WDW-50C微机控制电子万能试验机进行常温下准静态拉伸试验,如图6所示。

图5 球形药包爆炸试验布置现场
Fig.5 The spherical charge blast test layout site

图6 准静态拉伸试验
Fig.6 Quasi-static tensile test
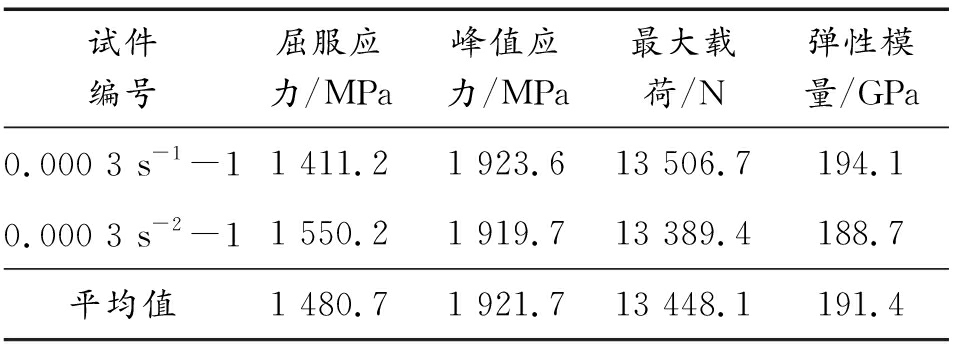
准静态拉伸试验结果如表2所示,可以看出高强钢丝的屈服应力为1 480.7 MPa,峰值应力为1 921.7 MPa,能够承受的最大载荷为13 448.1 N,弹性模量为191.4 GPa。
表2 准静态拉伸试验结果
Table 2 Quasi-static tensile test results
试件编号屈服应力/MPa峰值应力/MPa最大载荷/N弹性模量/GPa0.000 3 s-1-11 411.21 923.613 506.7194.10.000 3 s-2-11 550.21 919.713 389.4188.7平均值1 480.71 921.713 448.1191.4
为了获得高强钢丝的动态力学性能,在分离式霍普金森拉杆上进行不同应变率下的动态拉伸试验,如图7所示。

图7 分离式霍普金森拉杆试验
Fig.7 SHTB test
将试验得到的工程应力-应变数据转换为真实应力-应变,得到高强钢丝的真实应力-应变曲线,如图8所示。可以看出,高强钢丝峰值应力随着应变率的增加而增加,表明其为应变率敏感材料。
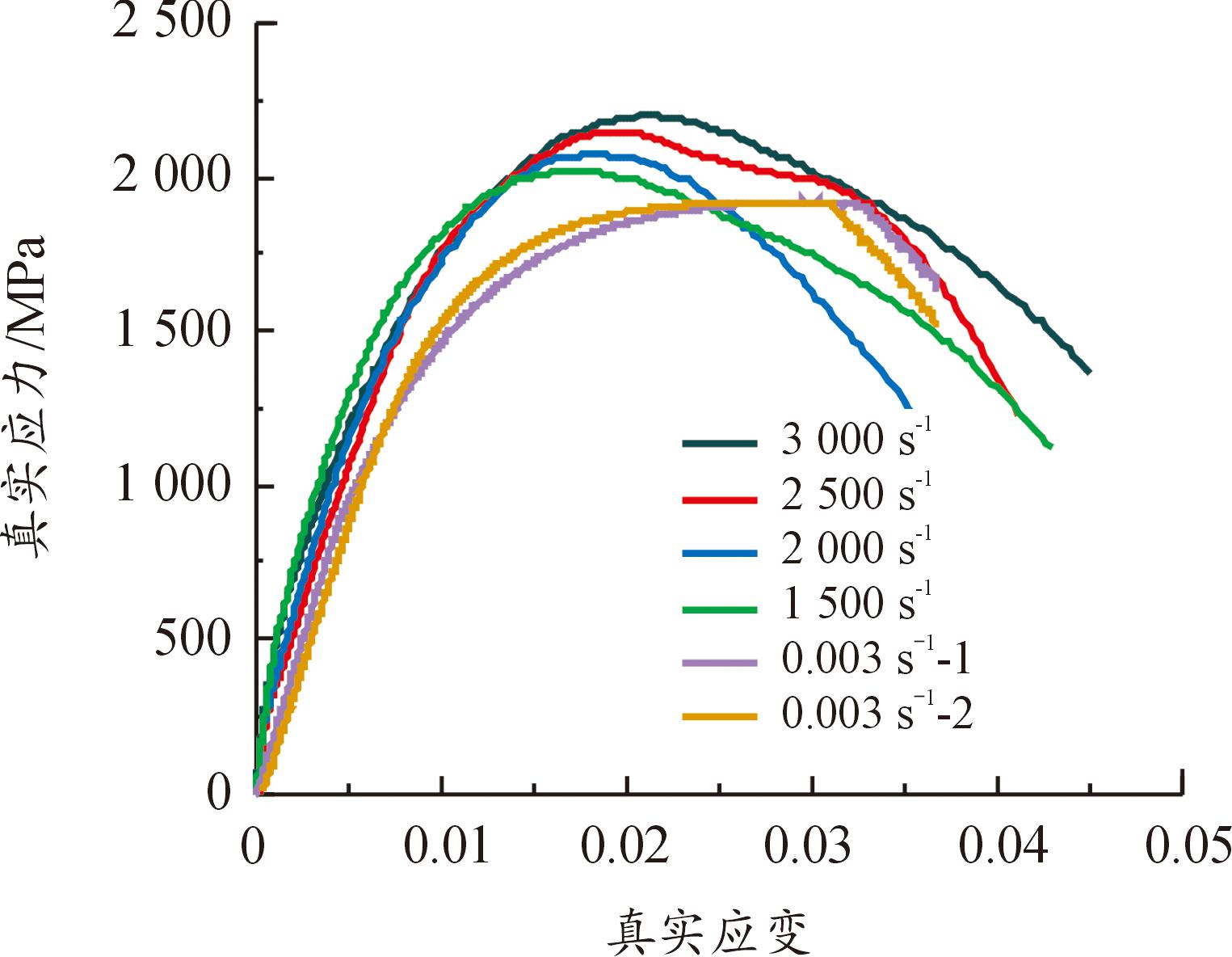
图8 不同应变率下的真实应力-应变曲线
Fig.8 True stress-true train curves at different strain-rates
2.2 Johnson-Cook本构模型参数拟合
Johnson-Cook本构模型[16]作为典型的经验型本构模型,综合考虑了应变、应变速率和温度对材料塑性流动的耦合效应,能够较好地预测大变形、高应变速率和高温下材料的力学响应。Johnson-Cook本构模型描述材料动态力学性能,表达式如下所示:
![]()
(3)
式(3)中:σeq为等效应力;εeq为等效塑性应变;![]() 为等效应变率;
为等效应变率;![]() 为参考应变率(取准静态拉伸应变率);A、B、n为静态力学相关参数;C为应变速率相关参数。m为温度软化系数;无量纲温度T*=(T-Tr)/(Tm-Tr),Tm为材料熔点温度;Tr为室温。此处不考虑温度软化项,此时式(3)可简化为:,简化后的本构方程对应LS-DYNA软件中98号材料卡片*MAT_Simplified_Johnson-Cook,简化后的表达式如式(4)所示:
为参考应变率(取准静态拉伸应变率);A、B、n为静态力学相关参数;C为应变速率相关参数。m为温度软化系数;无量纲温度T*=(T-Tr)/(Tm-Tr),Tm为材料熔点温度;Tr为室温。此处不考虑温度软化项,此时式(3)可简化为:,简化后的本构方程对应LS-DYNA软件中98号材料卡片*MAT_Simplified_Johnson-Cook,简化后的表达式如式(4)所示:
![]()
(4)
在此基础上,利用2.1节的试验数据对式(4)进行拟合,即可得到高强钢丝的Simplified Johnson-Cook本构模型材料参数,如表3所示。
表3 Johnson-Cook本构模型材料参数
Table 3 Parameters of Johnson-Cook model

A/MPaB/MPanC1 480.72 573.00.450.013 3
3 有限元模拟
3.1 有限元模型
基于1.3节的试件参数,利用SpaceClaim和DesignModeler软件对高强钢丝编织结构夹芯板进行建模分析,如图9所示。
其中芯层与面板连接处采用共节点的方式进行处理,边界约束条件为四周固支。面板采用SHELL单元,芯层钢丝采用BEAM单元。利用LS-DYNA软件使用任意拉格朗日欧拉(ALE)算法模拟炸药爆炸冲击波对夹芯板的作用,起爆方式为中心起爆。
为节约计算机资源,将空气域的覆盖范围设置为400 mm×400 mm×350 mm,并在表面施加无反射边界条件以模拟自由空气域。高强钢丝编织结构夹芯板试件模型的网格尺寸为5 mm,其余部分均为10 mm。
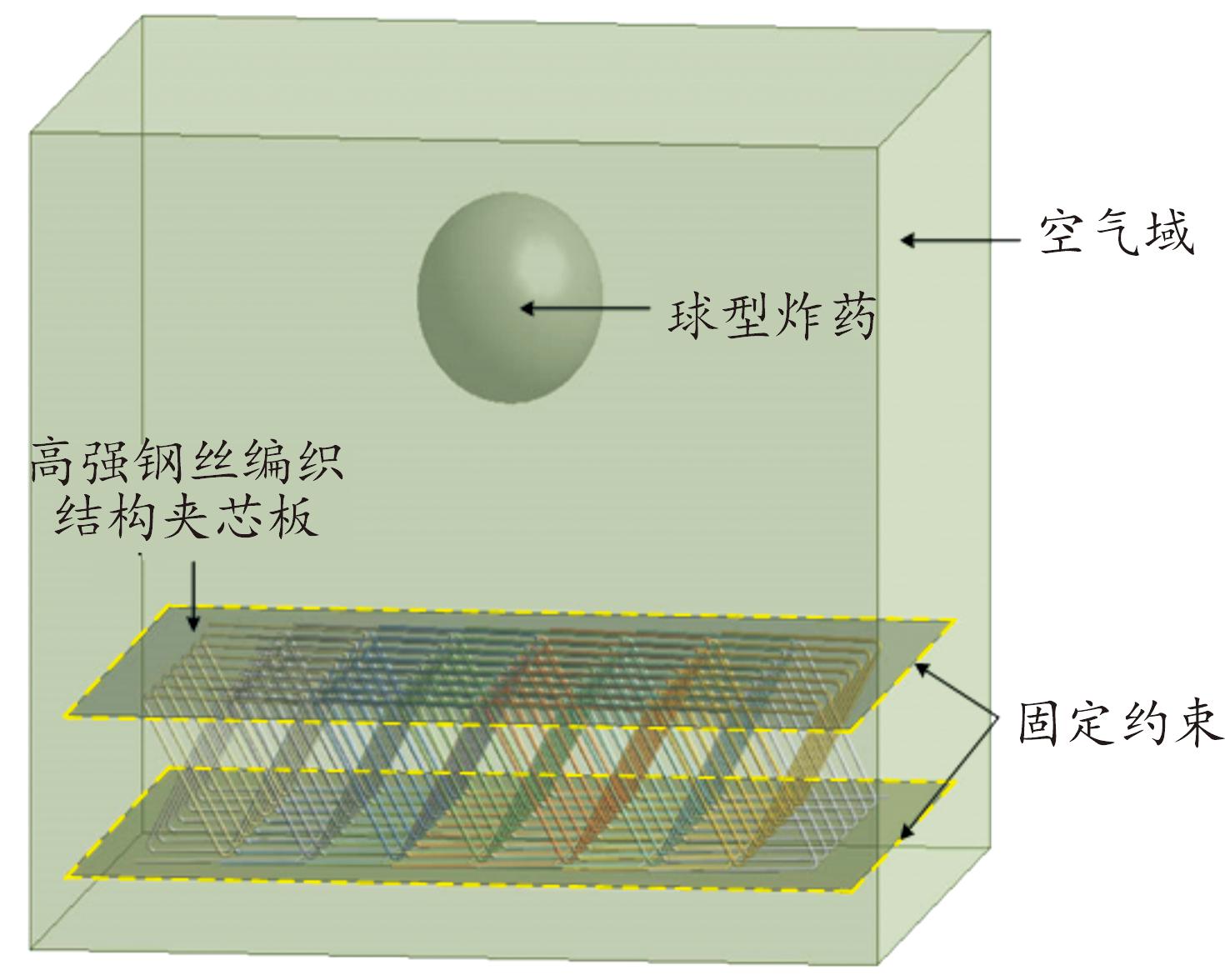
图9 有限元模型
Fig.9 FEA model
3.2 材料模型
炸药选用*MAT_HIGH_EXPLOSIVE_BURN本构模型,爆轰产物膨胀选用*EOS_JWL状态方程描述:
![]()
(5)
式(5)中:PCJ为爆轰产物的压力;A1、B1、R1、R2、ω均为炸药参数;V为炸药相对体积;E0为单位体积初始内能,具体参数见表4。
表4 炸药状态方程参数
Table 4 EOS Parameters of explosive

A1/GPaB1/GPaR1R2ωE0/GPaV373.83.7474.150.90.356.01
空气选用*MAT_NULL本构模型,理想气体选用*EOS_LINEAR_POLYNOMIAL状态方程描述:
P=C0+C1μ+C2μ2+C3μ2+
(C4+C5μ+C6μ2)E0
(6)
式(6)中:P为压力;C0、C1、C2、C3、C4、C5、C6为多项式方程系数;E0为单位体积初始内能; μ为空气相对体积, μ=1/V-1,具体参数见表5。
迎爆、背爆面板为Q235钢,选用Simplified Johnson-Cook本构模型描述,具体参数见表6。
表5 空气状态方程参数
Table 5 EOS Parameters of air

密度/(kg·m-3)C0/MPaC1=C2=C3C4=C51.29000.4C6E0/(kJ·m-3)V02.5×1051
表6 Q235钢本构模型参数
Table 6 Constitutive model parameters of Q235
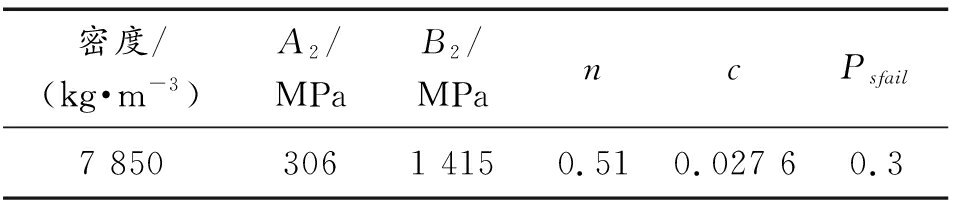
密度/(kg·m-3)A2/MPaB2/MPancPsfail7 8503061 4150.510.027 60.3
芯层高强钢丝材料选用Simplified Johnson-Cook本构模型描述,具体参数见表3。由于在实爆试验时没有发现芯层高强钢丝断裂失效的现象,故在数值模拟过程中不考虑BEAM单元的失效。
3.3 数值模拟方法准确性验证
将数值计算得到的试件迎爆面、背爆面及芯层变形情况与试验结果进行对比,如图10所示。同时提取数值计算模型中试件背爆面的最终变形量与试验结果进行比较,如表7所示。

图10 试验变形与模拟变形情况对比
Fig.10 Comparison between test deformation and simulated deformation
表7 背爆面最终变形量对比
Table 7 Comparison of final deformation of the back explosive surface

试件编号试验值/mm模拟值/mm误差/%A15.618.116.0B14.515.46.2C12.214.418.0
可以看出,数值模拟得到的迎、背爆面及芯层的变形情况与试验结果基本一致,且背爆面最终变形量与试验获得的数据平均误差为13.4 %,满足精度要求。因此,可以认为该数值模拟方法能够较好模拟高强钢丝编织结构夹芯板在爆炸荷载作用下的响应过程。
4 结构响应研究
为了探究夹芯结构在爆炸荷载作用下的响应模式,建立了25组具有不同芯层几何参数的高强钢丝编织结构夹芯板有限元模型,各试件的芯层参数见表8。采用第3节中的数值模拟方法模拟不同试件模型在爆炸荷载作用下的响应过程。
表8 各试件参数及响应模式
Table 8 Parameters and response model of each panel
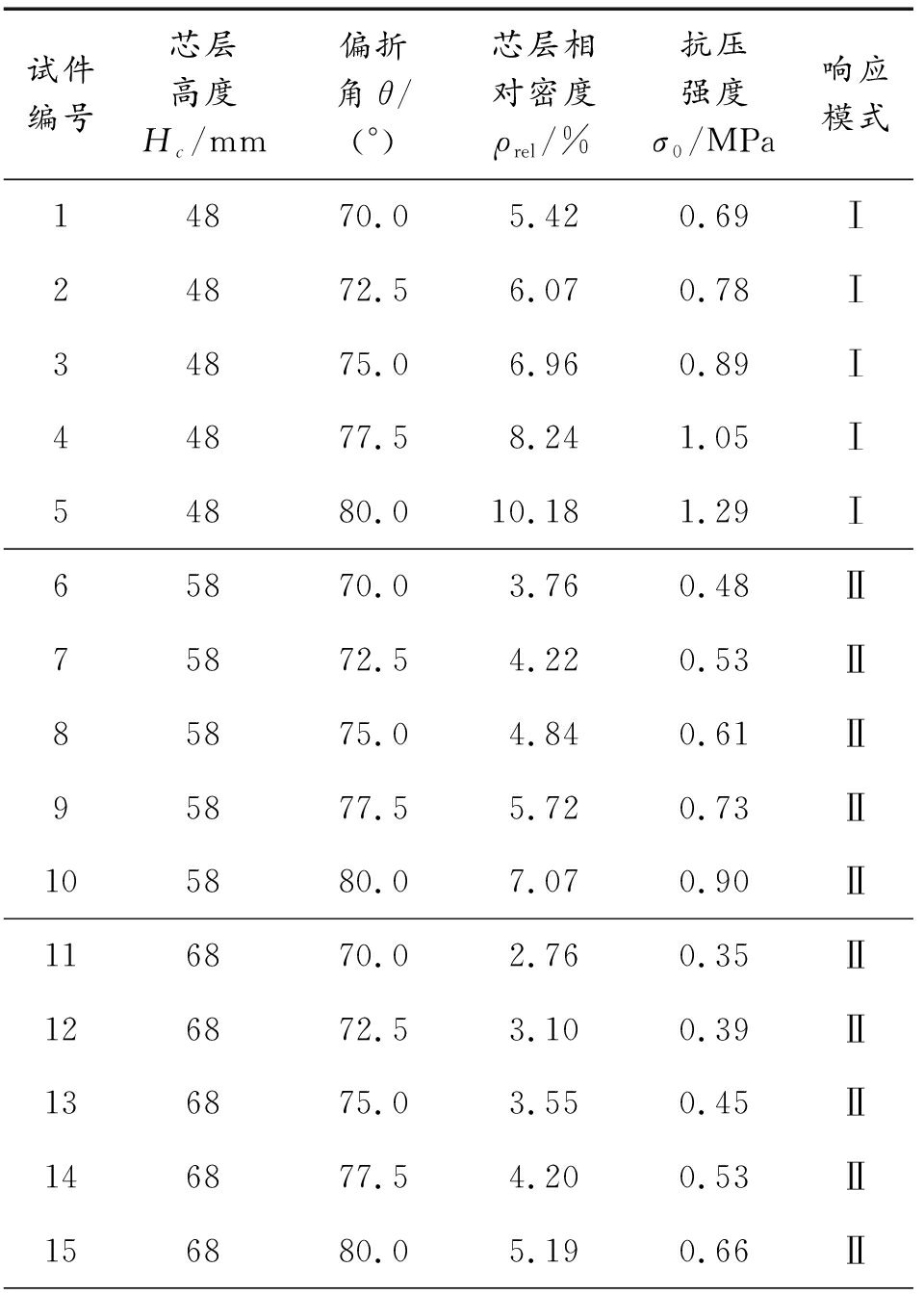
试件编号芯层高度Hc/mm偏折角θ/(°)芯层相对密度ρrel/%抗压强度σ0/MPa响应模式14870.05.420.69Ⅰ24872.56.070.78Ⅰ34875.06.960.89Ⅰ44877.58.241.05Ⅰ54880.010.181.29Ⅰ65870.03.760.48Ⅱ75872.54.220.53Ⅱ85875.04.840.61Ⅱ95877.55.720.73Ⅱ105880.07.070.90Ⅱ116870.02.760.35Ⅱ126872.53.100.39Ⅱ136875.03.550.45Ⅱ146877.54.200.53Ⅱ156880.05.190.66Ⅱ
续表(表8)
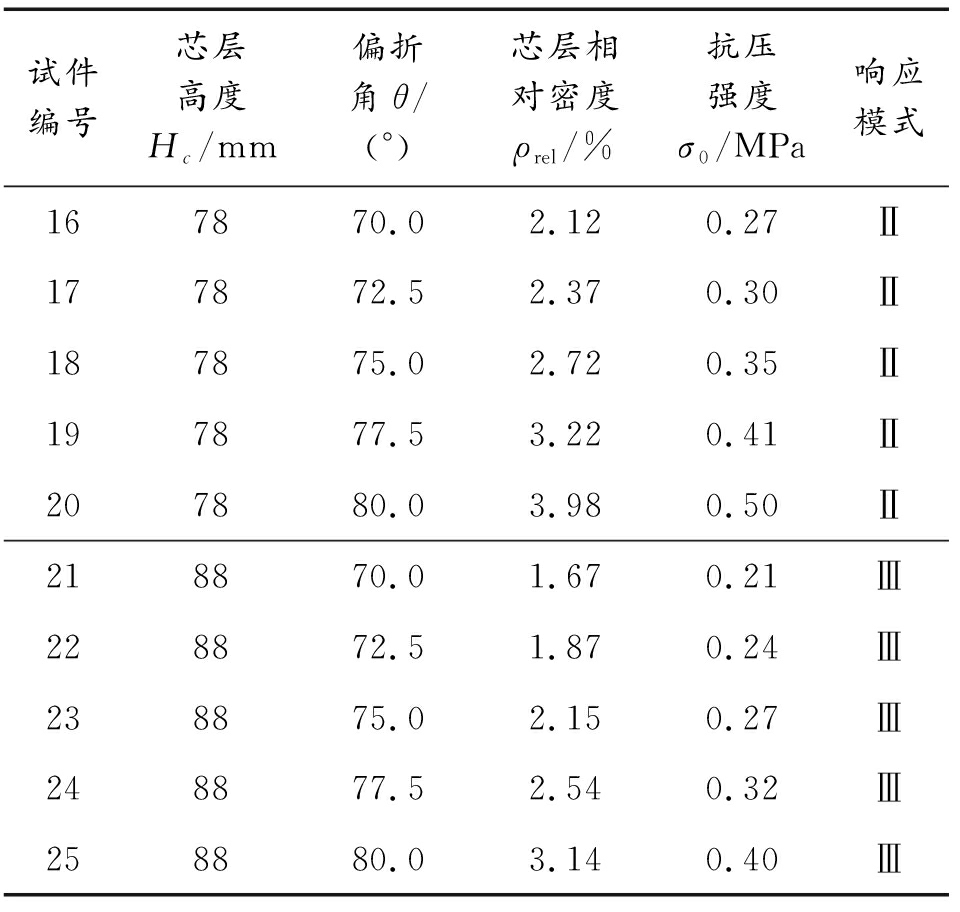
试件编号芯层高度Hc/mm偏折角θ/(°)芯层相对密度ρrel/%抗压强度σ0/MPa响应模式167870.02.120.27Ⅱ177872.52.370.30Ⅱ187875.02.720.35Ⅱ197877.53.220.41Ⅱ207880.03.980.50Ⅱ218870.01.670.21Ⅲ228872.51.870.24Ⅲ238875.02.150.27Ⅲ248877.52.540.32Ⅲ258880.03.140.40Ⅲ
4.1 响应过程分析
采用文献[9]的方法,将炸药起爆到结构整体响应结束的过程分为3个阶段:
第1个阶段为爆轰产物在空气中传播的阶段。0~30 μs,炸药爆炸瞬间产生高压冲击波并迅速向外传播。
第2阶段为爆轰产物与结构相互作用的阶段。30~50 μs,爆炸产生的高压冲击波首先作用于夹芯板的迎爆面板为其提供了巨大的加速度,使其开始向下运动,推动并压缩芯层高强钢丝;芯层高强钢丝获得了动能之后向下推动背爆面板,因此背爆面板的动响应滞后于芯层与迎爆面板,并以相对较小的速度向下变形。
第3阶段为夹芯板结构自身响应的过程。50 μs之后炸药与结构的相互作用已经消失。虽然没有外部荷载的作用,但是由于自身的惯性作用,夹芯板仍然向下变形,不同芯层高度的试件在此阶段出现了不同的响应模式。
4.2 响应模式对比
数值模拟结果表明,高强钢丝编织结构夹芯板的响应模式主要3种:① 迎爆面板局部破坏,背爆面板变形量达到峰值之后小幅振荡;② 迎爆面板未发生局部破坏,背爆面板变形量达到峰值之后小幅振荡; ③ 迎爆面板未发生局部破坏,背爆面板变形量始终在一定范围内大幅振荡。
芯层高度为48 mm的试件响应模式为Ⅰ,芯层高度为58 mm、68 mm以及78 mm的试件响应模式为Ⅱ,芯层高度为88 mm的试件响应模式为Ⅲ。以试件1、试件11以及试件21为例,采用文献10的方法,通过提取背板中心点的速度对3种不同的响应模式进行分析。
对于48 mm层高的试件1(图11(a)),0.275 ms时刻迎爆面板向下变形的速度达到最大值88 m/s,0.50 ms时刻芯层压缩量达到最大,此后背爆面向下变形的速度超过了迎爆面板,0.624 ms时刻速度达到最大值48.2 m/s,被压缩的芯层钢丝从0.50 ms时刻开始向下打开直至0.74 ms时刻迎爆面板开始向上变形,芯层钢丝出现了向上打开的现象,大约0.1 ms之后背爆面变形方向开始变化。在1 ms左右,夹芯板结构开始整体的轻微震荡,最终恢复静止状态,直至响应结束。
68 mm层高的试件11整体动态响应与试件1(图11(b))相似,但是迎爆面板向下运动的速度最大值为82.7 m/s,在0.47 ms时刻芯层压缩量就已经达到最大,同时背爆面向下变形速度也达到最大值40.4 m/s。在0.65 ms时刻,迎爆面板开始向上变形,出现了“拉动”芯层高强钢丝向上变形的现象。在1 ms时刻左右,夹芯板结构开始整体的轻微震荡。
88 mm层高的试件21迎爆面(图11(c))在0.25 ms时刻向下变形的速度达到了峰值112.6 m/s,远高于另外2个试件,而背爆面向下变形的速度小于另外2个试件,并且背爆面速度变化的周期明显大于迎爆面,并没有出现上述2个试件在1 ms之后出现的小幅震荡的现象。
通过对比3个夹芯板试件迎爆面、背爆面板中心变形量时程曲线(图12)可以看出,试件1、试件11的迎、背爆面板由于出现了弹性卸载现象,导致残余变形量小于峰值变形量,而试件21的迎爆面板在变形量达到峰值之后就开始了小幅振荡,而背爆面板始终在弹性范围内振荡,且振荡周期远远大于迎爆面。试件1的迎、背爆面的峰值变形量与残余变形量均大于试件11;试件21迎爆面的峰值变形量最大,为46.0 mm。
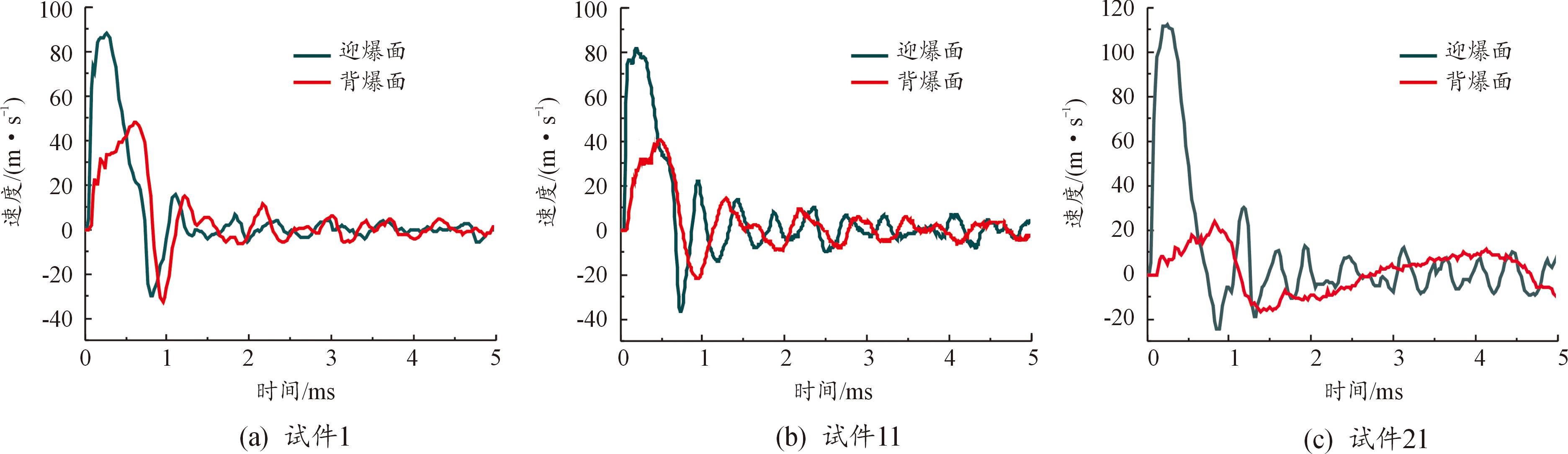
图11 迎、背爆面板中心速度曲线
Fig.11 Velocity curves of centers of front sheet and back sheet
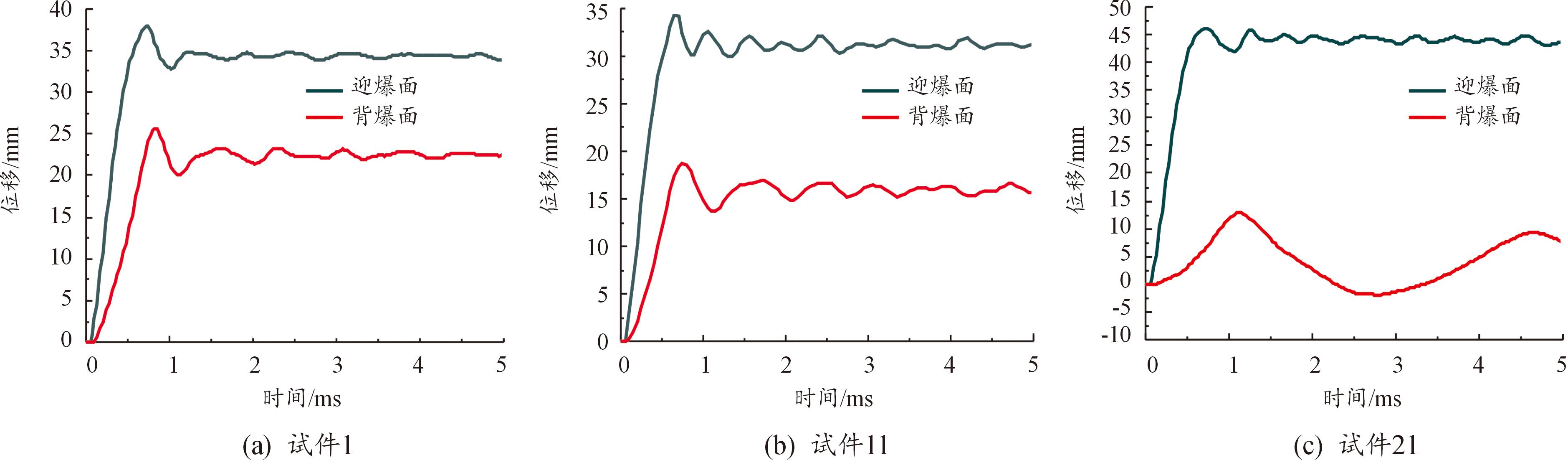
图12 迎、背爆面板中心变形量曲线
Fig.12 Deformation curves of centers of front sheet and back sheet
进一步比较3个夹芯板试件各部分吸能占比图(图13)可以看出:随着芯层高度的增加,迎爆面吸能占比越大,芯层吸能占比越小,背爆面吸能占比越小。试件21的迎爆面板吸收了79%的能量,高于试件1(47%)以及试件11(60%),且芯层吸能占比最低为17 %,说明在整个动响应过程中芯层承载力过低,难以发挥吸能作用,主要依赖迎爆面板吸能,导致夹芯板试件在爆炸荷载作用下不能作为一个整体发挥抗爆性能。
另外,试件1的迎爆面出现了局部破坏的现象,如图14所示。由于试件1的芯层强度过高,且芯层高度较小,在迎爆面板向下压缩芯层的过程中,面板与芯层连接处容易被顶破。由于芯层不易被充分压缩,所以传递了较多的上部荷载到达背爆面,使背爆面产生了较大变形,进而使得结构整体的变形较大。

图13 夹芯板各部分能量吸收占比
Fig.13 Proportion of energy absorbed by each part of sandwich panel
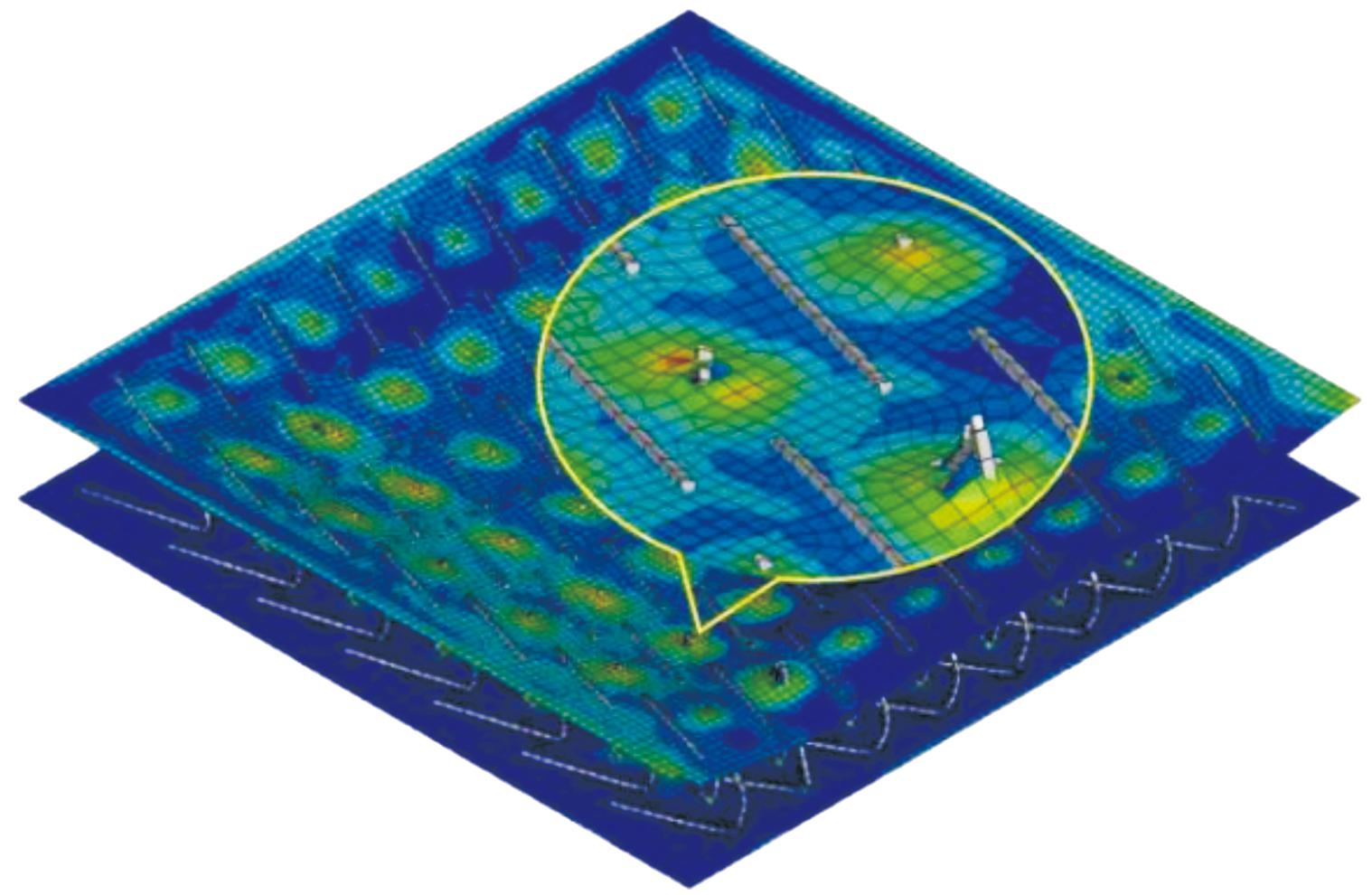
图14 迎爆面板局部破坏
Fig.14 Partial failure of front sheet
图15为芯层高度与芯层抗压强度之间的关系图,可以看出芯层抗压强度在0.27~0.90 MPa之间时,不同芯层高度的试件会有不同的响应模式。说芯层抗压强度与芯层高度存在耦合作用共同影响夹芯板在爆炸荷载作用下的响应过程。
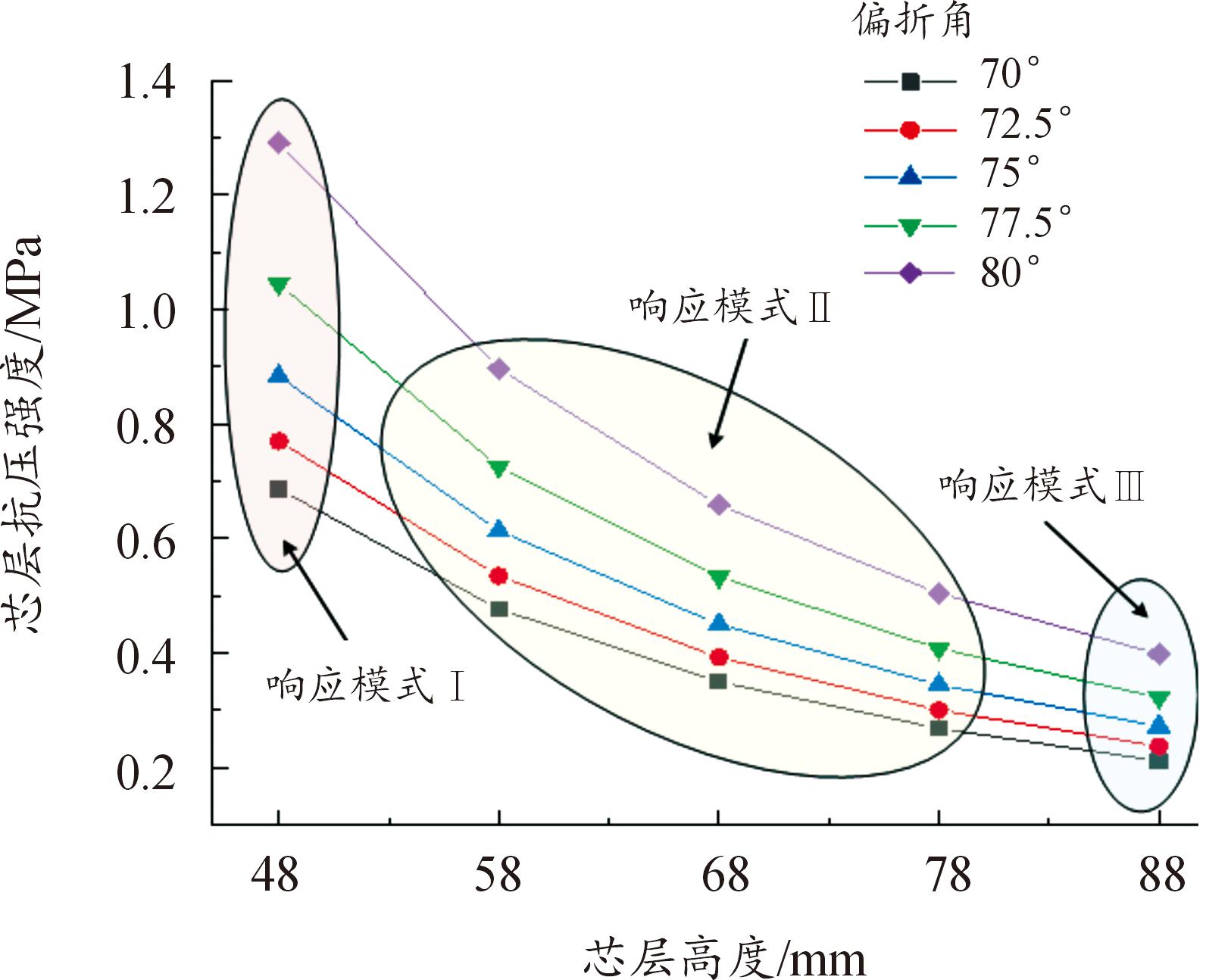
图15 芯层高度与芯层抗压强度关系图
Fig.15 Figure of relationship between core height and core compressive strength
5 芯层几何参数对夹芯板抗爆性能的影响
在爆炸荷载作用下,48 mm层高试件会出现面板局部破坏的现象;88 mm层高试件不能作为一个整体发挥抗爆性能,所以以芯层高度在58~78 mm之间的试件作为研究对象,分析芯层几何参数对于高强钢丝编织结构夹芯板抗爆性能的影响。
5.1 抗爆性能评价指标
由于不同规格高强钢丝编织结构夹芯板试件的芯层相对密度不同,所以采用无量纲变形量与无量纲冲量[17]的比值K来衡量夹芯板结构的抗爆性能,计算公式如式(7)所示。K值越小代表夹芯板在承受了相同冲量时产生的变形量越小,所以抗爆性能越好。
![]()
(7)
式(7)中:![]() 为无量纲变形量,计算公式如式(8)所示;
为无量纲变形量,计算公式如式(8)所示;![]() 为无量纲冲量,计算公式如式(9)所示。
为无量纲冲量,计算公式如式(9)所示。
![]()
(8)
式(8)中:δmax为背爆面板最大变形量;L为试件边长。
![]()
(9)
式(9)中:I为作用在迎爆面板中心点的比冲量[18],对于本文中炸药布置情况,I=5.4 kPa·s;M为夹芯板单位面积的质量,计算公式如式(10)所示;σy为面板屈服强度,取σy=300 MPa;ρ为面板材料密度,取ρ=7 850 kg/m3。
M=(2hfρ+ρrelρcHc)
(10)
式(10)中:hf为面板厚度,取hf=2.5 mm; ρc为芯层高强钢丝材料密度,取ρc=7 850 kg/m3。
将式(8)—式(10)代入式(7)可以得到无量纲变形量与无量纲冲量的比值K的具体表达式,如式(11)。
![]()
(11)
由式(2)可知芯层抗压强度σ0是关于芯层相对密度ρrel的函数,所以将式(2)代入式(11)中,得到式(12)。
![]()
(12)
联立式(1)和式(2)得到式(13)。可以看出σ0是关于Hc、θ等芯层几何参数的函数。
![]()
(13)
将式(13)代入式(12)得到式(14),可以看出无量纲变形量与无量纲冲量的比值K与芯层几何参数Hc、θ有关。
![]()
(14)
下节将进一步分析芯层几何参数对高强钢丝编织结构夹芯板抗爆性能的影响规律。
5.2 芯层高度对抗爆性能的影响
提取数值模拟的结果,得到无量纲变形量与无量纲冲量的比值K随着芯层高度变化的曲线,如图16所示。可以看出,K值随着芯层高度的增加而减小,偏折角不变时,随着芯层高度的增加,芯层抗压强度变小,芯层更容易被压缩,更容易将爆炸产生的能量转换为自身的塑性应变能,传递到背爆面的能量较少,无量纲化变形量与无量纲化冲量的比值K也相应减少。
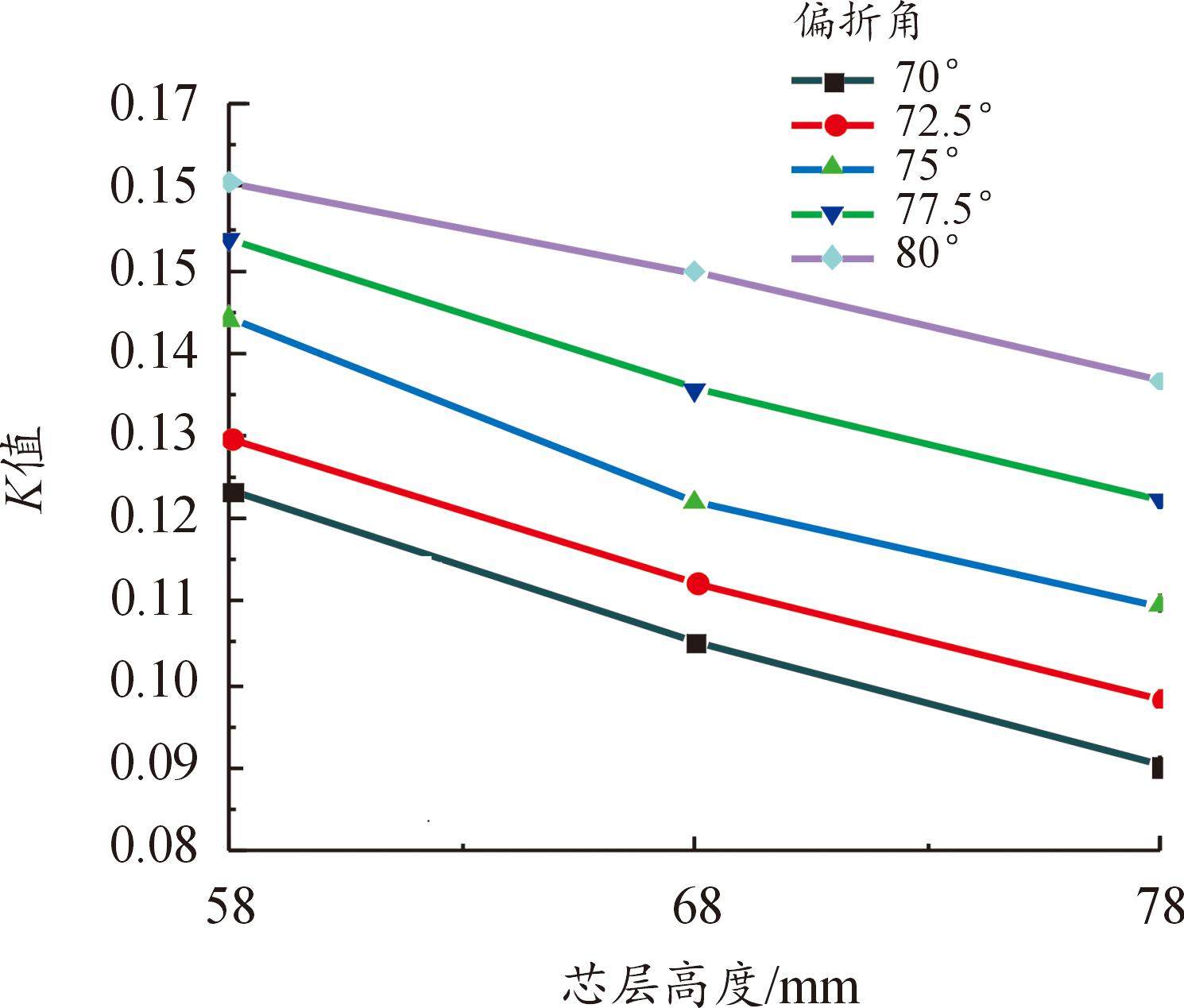
图16 芯层高度与K值关系曲线
Fig.16 Relationship curves between core height and K value
5.3 偏折角对于结构响应的影响
无量纲变形量与无量纲冲量的比值K随着偏折角变化的曲线如图17所示。可以看出,K值随着偏折角的增加而增加,芯层高度不变时,随着偏折角的增加,单位体积内能够容纳更多的高强钢丝,相对密度增加,芯层抗压强度也逐渐增加。在承受爆炸荷载时,芯层不易被压缩吸能,芯层缓冲作用较弱,传递了较多的能量到达背爆面。

图17 偏折角与K值关系曲线
Fig.17 Relationship curves between deflection angle and K value
综上,芯层高度越高、偏折角越小,高强钢丝编织结构夹芯板抗爆性能越好,所以在设计高强钢丝编织结构夹芯板芯层时,在芯层布置过多的高强钢丝会使芯层抗压强度过高,不能得到较好的抗爆性能。
5.4 高强钢丝编织结构夹芯板设计指导公式
将式(14)变换可以得到背爆面无量纲变形量δmax/L的理论计算公式即高强钢丝编织结构夹芯板设计指导公式,如式(15)所示。
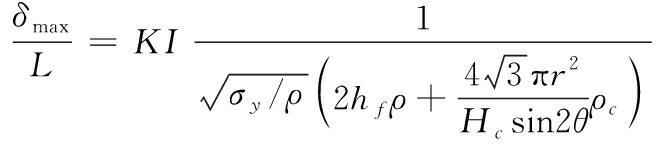
(15)
等式右边依次分为3个部分:抗爆性能设计值即无量纲化变形量与无量纲化冲量的比值K、荷载项以及夹芯板参数项。在进行高强钢丝编织结构夹芯板设计时,首先假定背爆面最大变形量δmax以及抗爆性能设计值,通过数值模拟等手段获得炸药作用在迎爆面板中心点的比冲量I之后,可以根据式(15)确定夹芯板各项参数的影响规律指导夹芯板设计。需要注意的是,对于不同的炸药布置情况以及面板参数,设计芯层高度存在一定的限制,芯层强度过高或者过低都不利于发挥高强钢丝编织结构夹芯板整体的抗爆性能。
6 结论
本文中在高强钢丝编织结构夹芯板抗爆性能试验的基础上,开展爆炸荷载作用下夹芯板结构响应研究。主要结论如下:
1) 在夹芯板结构自身响应阶段,不同芯层高度的试件出现了3种响应模式:① 迎爆面板局部破坏,背爆面板变形量达到峰值之后小幅振荡;② 迎爆面板未发生局部破坏,背爆面板变形量达到峰值之后小幅振荡;③ 迎爆面板未发生局部破坏,背爆面板变形量始终在一定范围内大幅振荡。
2) 当夹芯板芯层高度在58~78 mm之间,且偏折角不变时,增加芯层高度可有效提升夹芯板的抗爆性能;当芯层高度不变,增加偏折角会降低夹芯板的抗爆性能。
3) 提出了高强钢丝编织结构夹芯板的设计指导公式,在确定背爆面最大变形量、抗爆性能设计值以及比冲量I后,可根据公式设计夹芯板的几何参数。
[1] 敬霖,王志华,赵隆茂.多孔金属及其夹芯结构力学性能的研究进展[J].力学与实践,2015,37(1):1-24.
JING Lin,WANG Zhihua,ZHAO Longmao.Advances in studies of the mechanical performance of cellular metals and related sandwich structures[J].Mechanics in Engineering,2015,37(1):1-24.
[2] 赵著杰,侯海量,李典.填充多胞元抗冲击防护结构动力学特性及防护性能研究进展[J].中国舰船研究,2021,16(3):96-111.
ZHAO Zhujie,HOU Hailiang,LI Dian.Research progress on dynamic characteristics and protective performance of multicellular filled impact resistant protective structure[J].Chinese Journal of Ship Research,2021,16(3):96-111.
[3] 薛金涛,韩福生,黄英杰,等.熔模铸造点阵Al的力学行为及吸能特性[J].特种铸造及有色合金,2021,41(6):734-737.
XUE Jintao,HAN Fusheng,HUANG Yingjie,et al.Mechanical behavior and energy absorption of investment casting lattice Al[J].Special Casting and Nonferrous Alloys,2021,41(6):734-737.
[4] WADLEY H G N,DHARMASENA K P,et al.Compressive response of multilayered pyramidal lattices during underwater shock loading[J].International Journal of Impact Engineering,2008,35:1102-1114.
[5] 柏龙,熊飞,陈晓红,等.SLM制备的Ti6Al4V轻质点阵结构多目标结构优化设计研究[J].机械工程学报,2018,54(5):156-165.
BO Long,XIONG Fei,CHEN Xiaohong,et al.Multi-objective structural optimization design of Ti6Al4V lattice structure formed by SLM[J].Journal of Mechanical Engineering,2018,54(5):156-165.
[6] WALLACH J C,GIBSON L J.Truss core sandwich panels and methods for making same[P].US patent no.6,644,535 B2,November11,2003.
[7] KANG K J.Wire-woven cellular metals:The present and future[J].Progress in Materials Science,2015(69):213-307.
[8] 陈鹏,汪敏,陈辉国,等.高强钢丝编织点阵结构材料的制备及其静压试验研究[J].重庆理工大学学报(自然科学),2021,35(10):120-126.
CHEN Peng,WANG Min,CHEN Huiguo,et al.Research on the preparation and static pressure test of high strength steel wire woven lattice structural materials[J].Journal of Chongqing University of Technology (Natural Science),2021,35(10):120-126.
[9] 邓旭辉,李亚斌,董琪,等.爆炸荷载作用下方形夹芯板动力学响应与优化设计数值分析[J].应用力学学报,2020,37(1):339-343.
DENG Xuhui,LI Yabin,DONG Qi,et al.Numerical analysis of dynamic response and optimization design of square sandwich panel under explosion load[J].Chinese Journal of Applied Mechanics,2020,37(1):339-343.
[10] 张豪,常白雪,赵凯,等.三种蜂窝夹芯板的抗爆性能分析[J].北京理工大学学报,2022,42(6):557-566.
ZHANG Hao,CHANG Baixue,ZHAO Kai,et al.Anti-explosion analysis of honeycomb sandwich panels with three kinds of core structures[J].Transactions of Beijing Institute of Technology,2022,42(6):557-566.
[11] 姚梦雷,侯海量,李典,等.舱内爆炸荷载下Y型夹层板动响应及抗爆性能影响因素[J].兵工学报,2022.
YAO Menglei,HOU Hailiang,LI Dian,et al.Dynamic response of Y-shaped sandwich plate and the influence factors anti explosion performance under the explosion load in the cabin[J].Acta Aramamentarii,2022.
[12] FENG L J,WEI G T,YU G C,et al.Underwater blast behaviors of enhanced lattice truss sandwich panels[J].International Journal of Mechanical Sciences,2019(150):238-246.
[13] 亓昌,郝鹏程,舒剑,等.金字塔型点阵材料夹芯板抗爆性能仿真与优化[J].振动与冲击,2019,38(16):246-252.
QI Chang,HAO Pengcheng,SHU Jian,et al.Simulation and optimization for blast-resistant performances of pyramidal lattice cored sandwich panels[J].Journal of Vibration and Shock,2019,38(16):246-252.
[14] 易建坤,艾云平,张东红,等.结构几何参数对填充泡沫铝的金字塔形点阵金属夹芯方板抗爆性能的影响[J].材料科学与工程学报,2015(1):66-70.
YI Jiankun,AI Yunping,ZHANG Donghong,et al.Effects of geometrical parameters of pyramid lattice sandwich square plate filled with aluminum foam material on its blast resistance[J].Journal of Materials Science and Engineering,2015(1):66-70.
[15] 中华人民共和国国家质量监督检验检疫总局,中国标准化管理委员会.金属材料 拉伸试验 第1部分:室温试验6方法:GB/T 228.1—2010[S].
General Administration of Quality Supervision,Inspection and Quarantine of the People’s Republic of China,Standardization Administration of the People’s Republic of China.Metallic materials-Tensile testing-Part 1:Method of test at room temperature:GB/T 228.1—2010[S].Beijing,China:Standards Press of China,2011.
[16] JOHNSON G R,COOK W H.A constitutive model and data for metals subjected to large strains,high strain rates and high temperatures[C]//Proceedings of the 7th International Symposium on Ballistics.Hague,the Netherlands:IBC,1983:541-547.
[17] XUE Zhyini,HUTCHINSON J W.A comparative study of impulse-resistant metal sandwich plates[J].International Journal of Impact Engineering,2004,30(10):1283-1305.
[18] 赵猛,戴开达,向召,等.近爆荷载下PVC泡沫夹芯板的动力学模型研究[J].兵工学报,2022.
ZHAO Meng,DAI Kaida,XIANG Zhao,et al.Dynamic model study of PVC foam sandwich panels under close blast loading[J].Acta Aramamentarii,2022.