0 引言
弹丸击发后火药燃烧生成火药气体,使内膛压力不断增大,在达到一定值时,开始推动弹丸克服摩擦阻力和挤进阻力运动,弹带也开始挤入坡膛,产生塑性变形。对于弹丸挤进的分析,可以使用有限元方法模拟弹丸挤进过程,获得弹带刻痕的塑性应变及等效应力变化规律[1-4]。对于内弹道性能的影响因素,胡朝斌[5]在内弹道精细化建模中,研究了弹带宽度对内弹道的影响,弹带宽度的增加导致膛压和弹丸运动阻力的增大;彭松江[6]对不同坡膛结构为研究对象,坡膛采取小坡度,导致挤进阻力减小,最大膛压降低。对于弹丸挤进的影响因素,何行[7]研究了坡膛在不同锥度下的受力过程;孙河洋[8]引入考虑粘塑性及韧性损伤耦合的本构模型,对不同坡膛结构下弹丸的挤进过程进行研究;李淼[9]研究了不同卡膛速度、弹炮径向间隙和初始摆角对挤进过程挤进阻力和挤进后弹丸摆角的影响。
基于相关工程实践中,由于身管存在加工误差,弹丸定位后与坡膛的距离发生改变,弹丸挤进前的自由行程发生变化,最终反映到弹丸出膛口速度的变化,使用有限元算法,并通过VUAMP子程序进行二次开发,将内弹道方程嵌入有限元模型,计算弹丸在膛内运动过程,计算分析弹丸相对坡膛不同卡膛位置对于内弹道的影响,并解决相关问题。
1 有限元模型建立
1.1 弹炮匹配模型
某小口径火炮身管坡膛结构如图1所示,弹膛与药筒采用斜肩定位,机匣结构确定后,弹丸位置随之确定,弹丸与身管尾端面的距离也随之确定,α为坡膛起始处到身管尾端面的距离,α值的变化会引起弹丸与坡膛起始处轴向距离的改变,对坡膛径向尺寸无影响。弹带与身管的装配关系如图2,由于加工误差,弹丸定位后,与坡膛的轴向距离发生变化。在正常加工尺寸下,弹带凸起与坡膛起始处之间存在一定的轴向间隙,本文中轴向间隙值设置为0.4 mm,如图2位置1;加工误差为负值时,导致弹带与坡膛起始处的距离缩短,弹丸在挤进前的自由行程减少,如加工误差为-0.2 mm时,弹丸与坡膛距离缩短0.2 mm,弹丸在挤进前的自由行程缩短0.2 mm;误差较大时也可能导致弹丸定位后弹带凸起与坡膛起始处开始接触,如图2中的位置2,此时加工误差为-0.4 mm,弹丸与坡膛距离缩短了0.4 mm;另一方面,加工误差为正值时,会导致弹丸与坡膛距离增大,弹丸挤进前的自由行程增加,如图2中的位置3。在实际工程实践中,α=15±0.3 mm,本文中α值的误差取±0.4 mm,图2中位置2加工误差为-0.4 mm,位置3加工误差为+0.4 mm。

图1 斜肩定位式弹炮匹配示意图
Fig.1 Diagram of projectile-barrel matching with oblique shoulder positioning
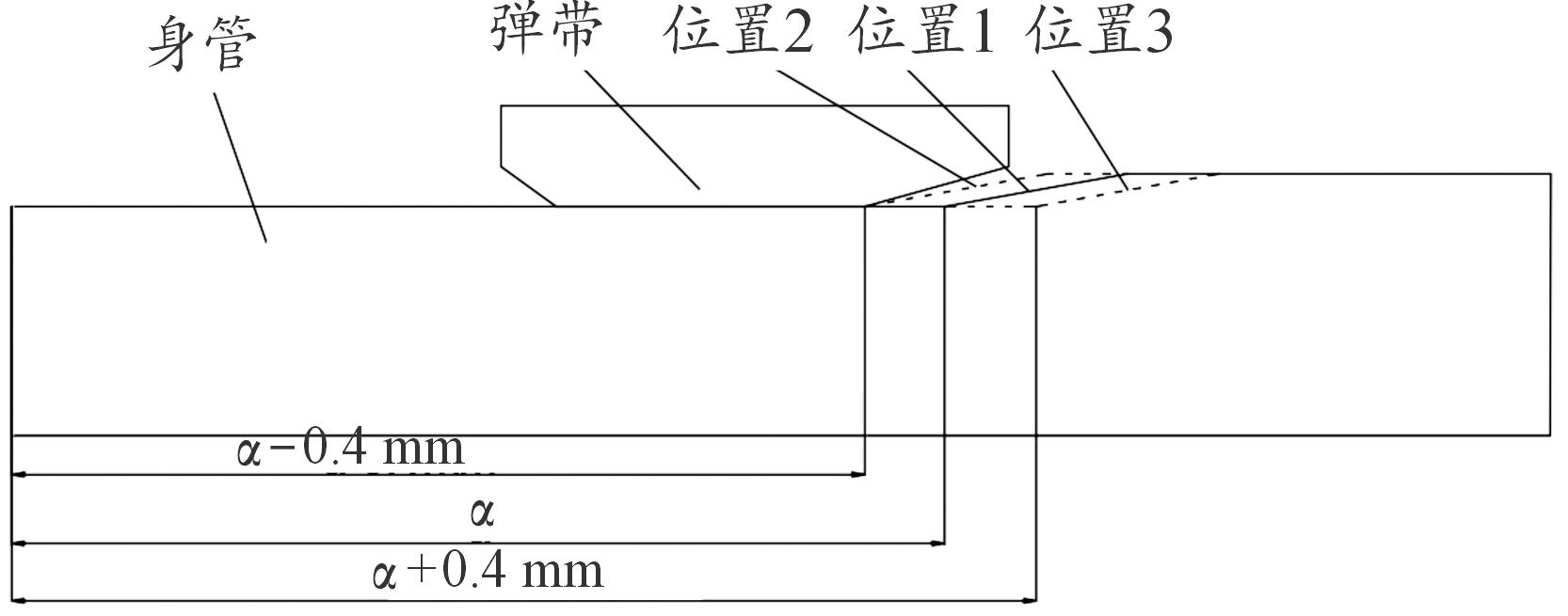
图2 弹带位置示意图
Fig.2 Diagram of the location of rotating band
1.2 有限元模型
建立弹炮匹配模型,分别建立身管、弹丸和弹带的有限元模型,单元类型使用8节点六面体线性缩减积分单元(C3D8R)。弹带采用细化网格,根据模型试算收敛性确定网格的基本尺寸。身管有限元模型如图3所示,弹炮匹配有限元模型如图4所示,不同加工误差下弹带与坡膛的装配关系如图5所示(加工误差依次为+0.4 mm,0,-0.4 mm)。

图3 身管有限元模型
Fig.3 Finite element model of barrel

图4 弹炮匹配有限元模型
Fig.4 Finite element model of projectile-barrel matching
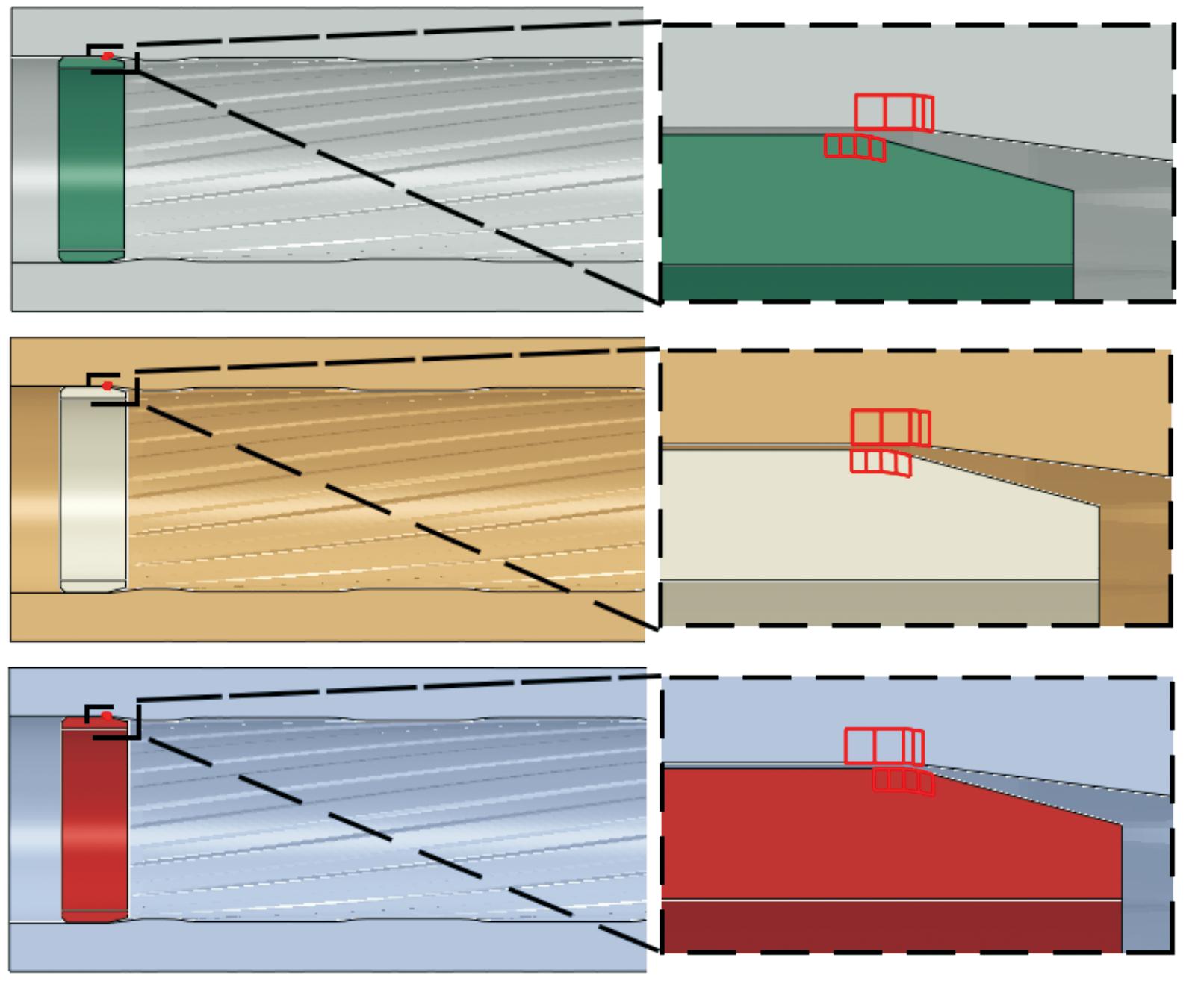
图5 不同加工误差下弹带与坡膛装配关系
Fig.5 Assembly between rotating band and forcing cone with different machining errors
1.3 材料模型
该弹带挤进计算中,身管基体材料为炮钢,炮钢型号为30SiMn2MoVA,弹带材料为黄铜,弹带挤进过程中,产生塑性变形和摩擦生热,适用Johnson-Cook材料模型[10-11],该模型用于描述大应变、高应变率和高温的条件下材料的极限强度和变形行为,故采用Johnson-Cook本构模型及其失效本构模型,其表达式为:
σ = (A + BεPn)(1 + Clnε*)(1-T*n)
(1)
式(1)中:![]() 和
和![]() 分别为等效应力、应变率和参考应变率;εP为等效塑性应变;Α、Β、C、m和n为材料常数;T为试验温度;Tr为参考温度;Tm为材料的熔化温度。
分别为等效应力、应变率和参考应变率;εP为等效塑性应变;Α、Β、C、m和n为材料常数;T为试验温度;Tr为参考温度;Tm为材料的熔化温度。
Johson-Cook损伤本构模型用于描述弹带挤进过程中的损伤情况,用等效塑性临界应变εD作为损伤依据。
εD=(d1+d2ed3σ*)(1+d4lnε*)(1+d5T*)
(2)
式(2)中:d1~d5为材料失效参数;σ*为应力三轴度
通过查阅材料手册[12]和文献[13],得到炮钢和弹带的材料模型参数如表1、表2所示。
表1 材料属性参数
Table 1 Material property parameter
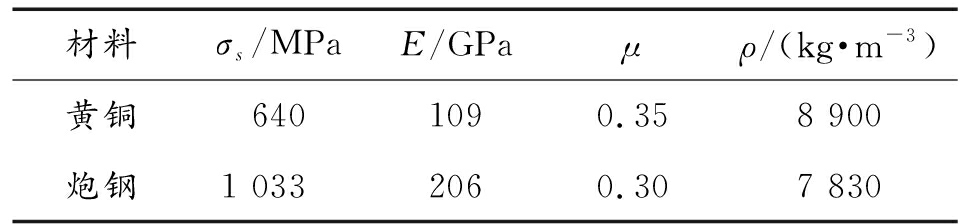
材料σs/MPaE/GPaμρ/(kg·m-3)黄铜6401090.358 900炮钢1 0332060.307 830
表2 弹带与炮钢材料的Johnson-Cook模型参数
Table 2 Johnson-Cook model parameters of rotating band and gun steel material

材料A/MPaB/MPancd1d2d3d4d5m黄铜1125050.420.010.544.89-3.030.0141.21.68炮钢1 5001 6000.25-0.002 1-----1.5
1.4 载荷条件
弹带挤进过程中,弹底受到火药燃气压力的作用,其值由内弹道方程求解获得,经典内弹道方程组为[14]
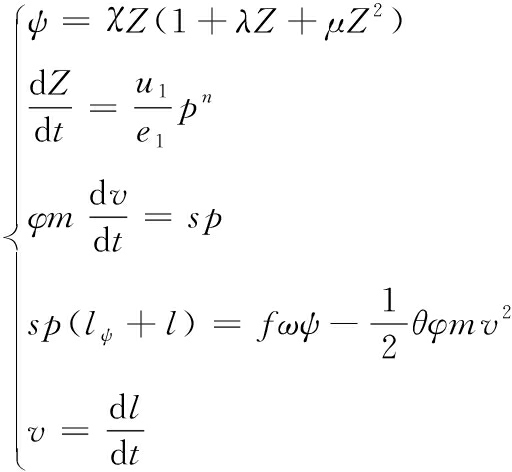
(3)
式(3)中:ψ为火药已燃百分数;u1为火药燃速系数;e1为火药1/2厚度;p为平均压力;φ为次要功计算系数;m为弹丸质量;v为弹丸沿膛运动速度;s为弹膛横截面积; f为火药力;ω为装药量;θ=k-1,k为绝热指数;n为压力指数;l为弹丸行程。
其中,![]() 为药室缩径长; ρ为火药密度;
为药室缩径长; ρ为火药密度;![]() 为装填密度,V0为药室容积;α为火药气体余容。
为装填密度,V0为药室容积;α为火药气体余容。
基于几何燃烧定律多孔火药燃烧方程:
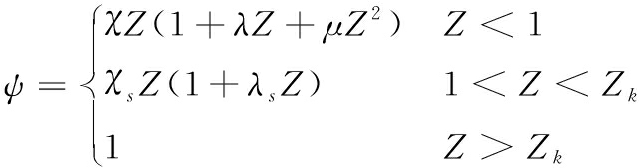
(4)
式(4)中: χ、λ、μ、χs、λs 为火药形状特征量,Z为火药已燃相对厚度,Zk=(e1+ρ)/e1为火药燃烧结束时的相对燃烧厚度。
弹底压力pd与平均压力的关系为
![]()
(5)
式(5)中,φ1为运动阻力系数。
通过ABAQUS的内部子程序VUAMP可以在每个增量步开始前获得弹丸的速度v和行程l,代入式(3),对内弹道方程组进行改写,内弹道方程组变为一个微分方程和一个代数方程:
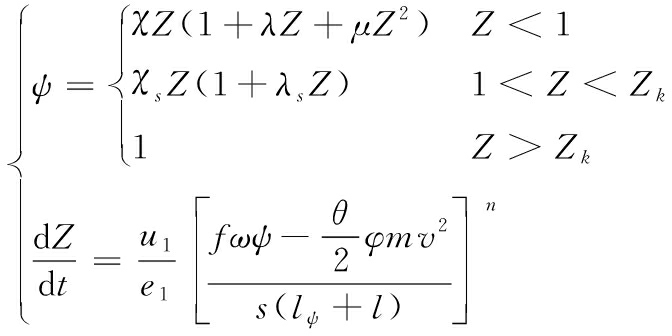
(6)
通过读取有限元模型中每一个增量步的弹丸的速度v和行程l,使用四阶龙格库塔公式对式(6)进行求解,得出火药燃烧的相对厚度,进一步计算出平均压力p,再由式(5)解得弹底压力pd,对有限元模型中的弹底压力载荷进行更新,使弹丸膛内运动过程中通过位移情况解算出载荷情况。
2 仿真结果
2.1 弹带的应力云图
弹带在刻槽开始时和刻槽结束的应力云图如图6和图7所示,弹带与坡膛存在间隙,弹带在自由行程后开始刻槽,自由行程的大小反映到刻槽起始时刻的不同,加工误差为-0.40 mm的工况(工况5)与正常加工工况(工况3)相差0.029 ms。弹带刻槽完成的时刻,不同工况下都在0.3 ms左右,表明坡膛起始处与身管尾端距离短、间隙小的身管,其弹带刻槽所用的时间更长,也表明此工况下弹丸在挤进时期速度更慢。

图6 弹带在刻槽开始时的应力云图
Fig.6 Stress cloud image of rotating band at the beginning of engraving
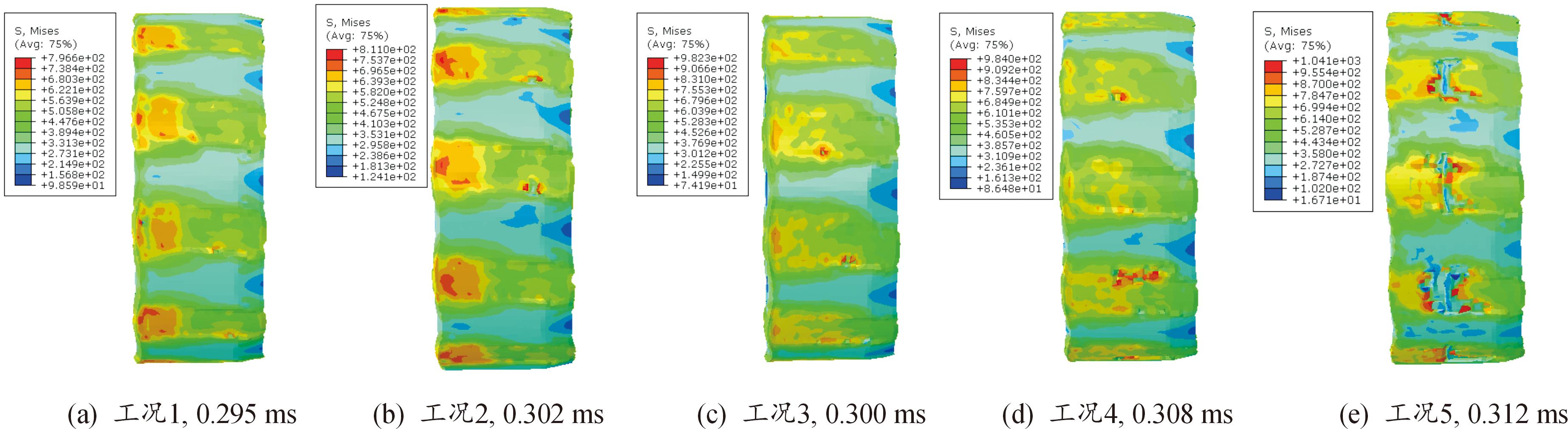
图7 弹带在刻槽完成下的应力云图
Fig.7 Stress cloud image of rotating band after engraving
2.2 弹丸挤进时期
弹丸在挤进时期的挤进阻力如图8所示,加工误差为-0.20 mm和-0.40 mm的身管,弹丸在挤进时期受到更大的阻力,其峰值分别为142.94 kN和150 kN,其他3个工况挤进阻力峰值在110~130 kN。在弹丸挤进初期,加工误差为负值的情况下,弹带与坡膛间隙小,弹带更早接触坡膛,导致相同时刻下弹丸的挤进阻力大,加速度小。
弹丸在挤进时刻的速度和加速度如图9和图10,在挤进过程,误差为负值的身管,其弹丸速度小于误差为正值的身管。弹丸初始速度均为0,则在挤进过程中,误差为负值的身管,其弹丸加速度也小于误差为正值的身管。在约0.6 ms后,坡膛加工误差为负值的身管,其弹丸初速大于加工误差为正值的身管,表明挤进后加工误差为负值的身管弹丸加速度大于误差为正值的身管。
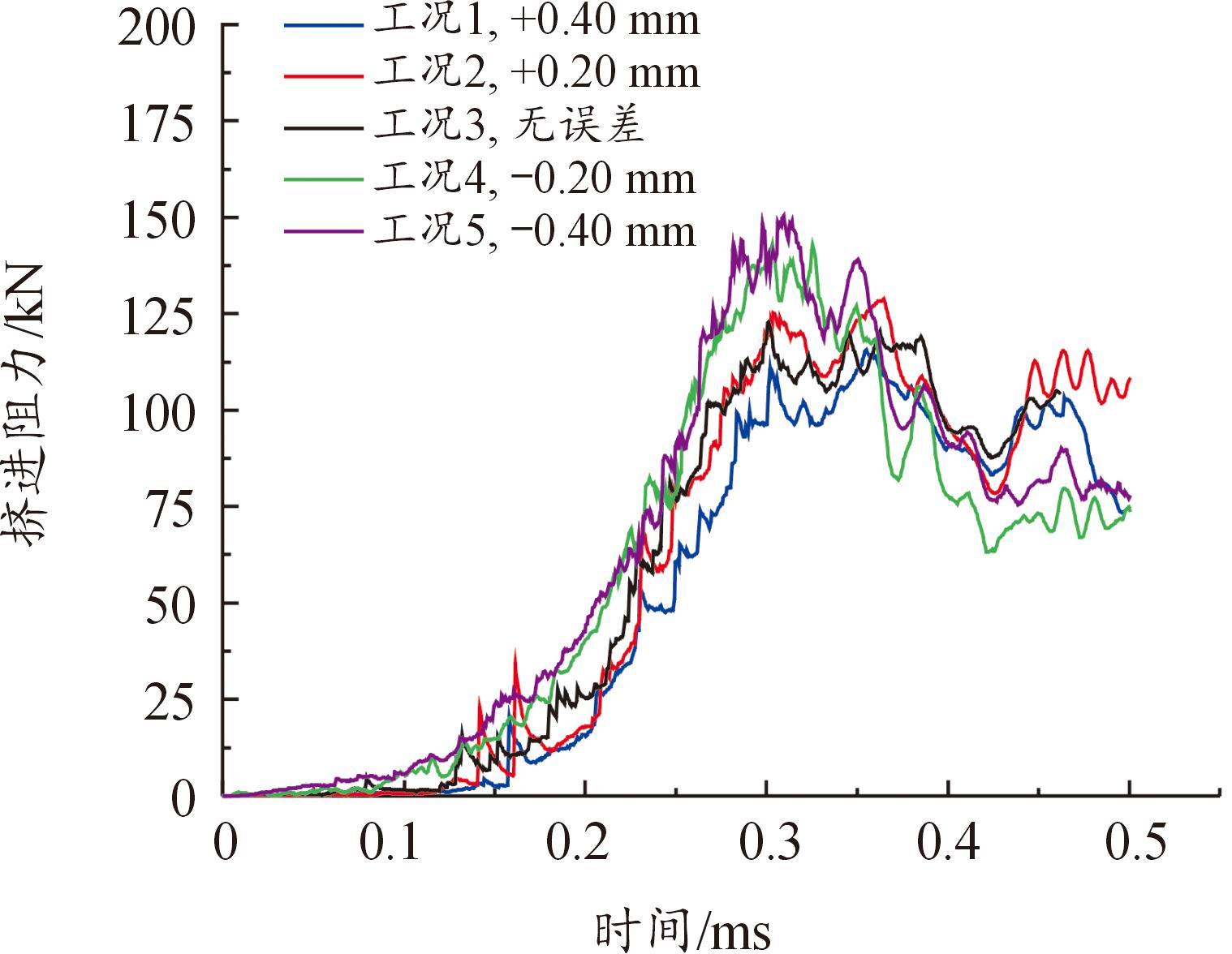
图8 挤进阻力曲线
Fig.8 Curves of engraving resistances
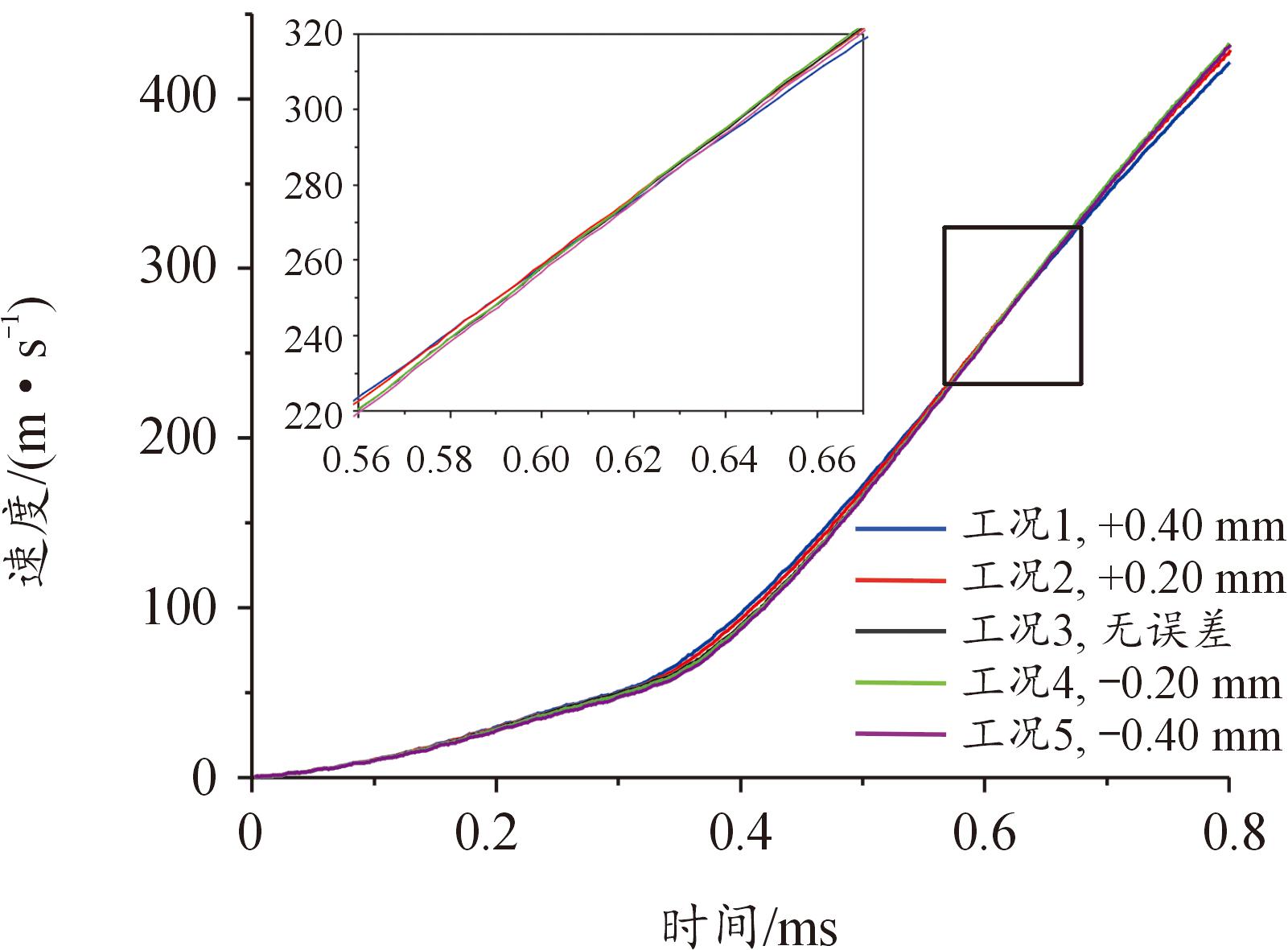
图9 挤进时期速度曲线
Fig.9 Curves of engraving velocity
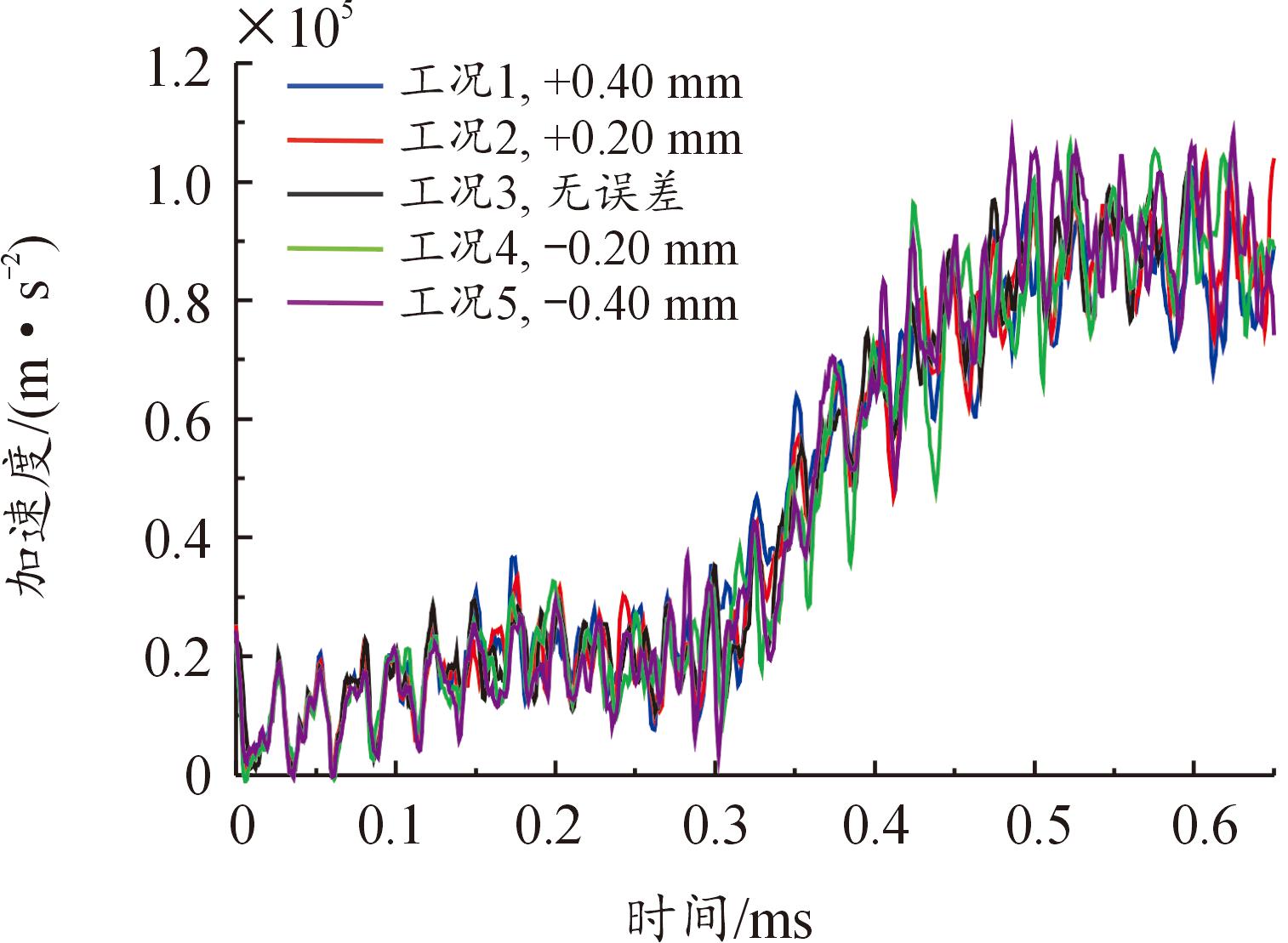
图10 挤进时期加速度曲线
Fig.10 Curves of engraving acceleration
2.3 弹丸膛内运动
在不同加工误差下,弹丸在膛内运动过程的速度,如图11、图12所示,平均膛压曲线图如图13、图14所示,出膛口速度和最大膛压随着弹丸与坡膛距离的缩短而增大。
由弹丸挤进时期运动分析可知,加工误差为负值的情况下,弹丸的挤进阻力大,加速度小。从而导致弹后容积增加的速率小,根据火药燃烧定律,在火药燃烧了相同时刻的情况下,膛压增加速率更快,最终导致膛压的峰值更高,从而使弹丸出膛口速度更快。
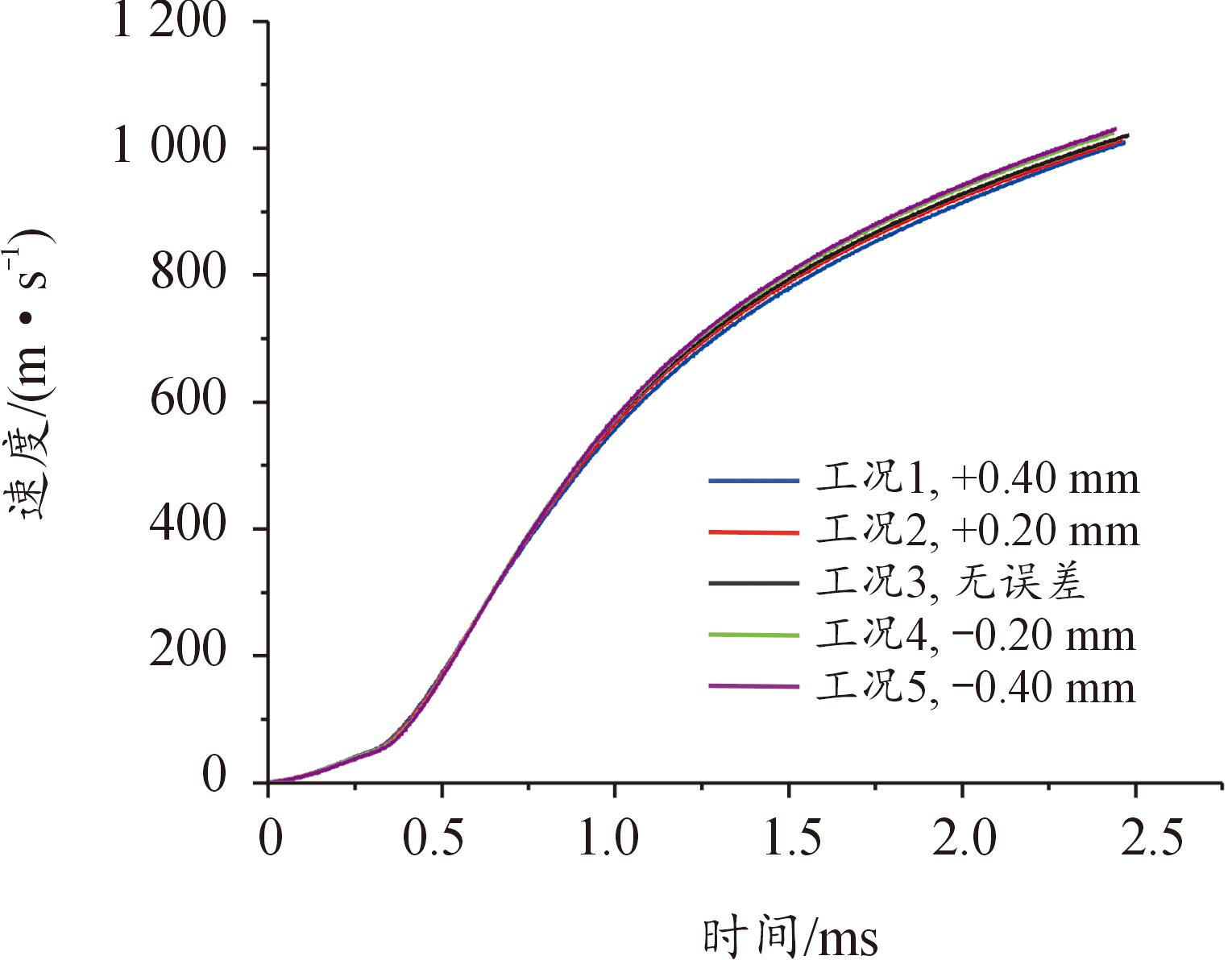
图11 速度-时间曲线
Fig.11 Velocity-time curves
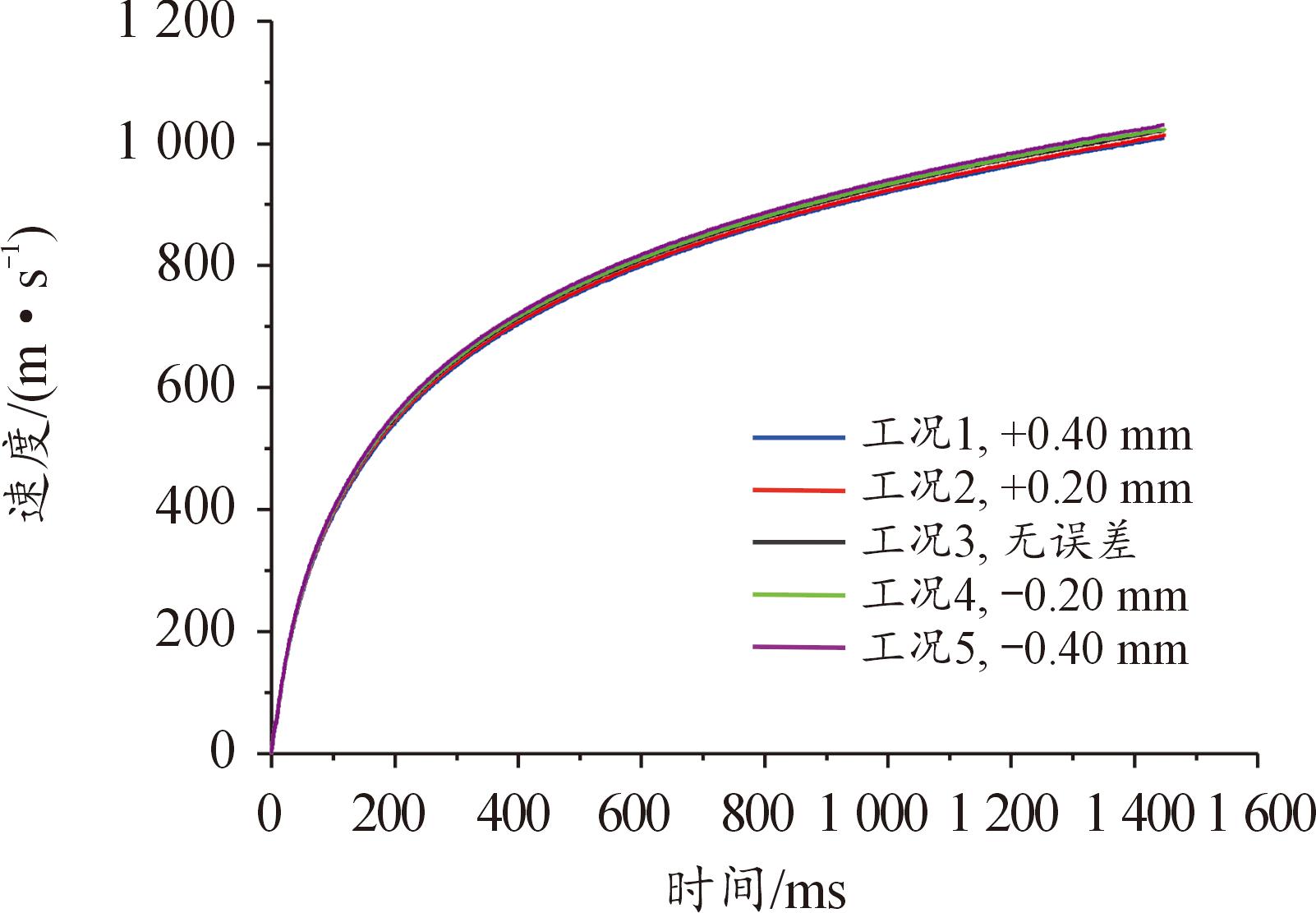
图12 速度-位移曲线
Fig.12 Velocity-displacement curves
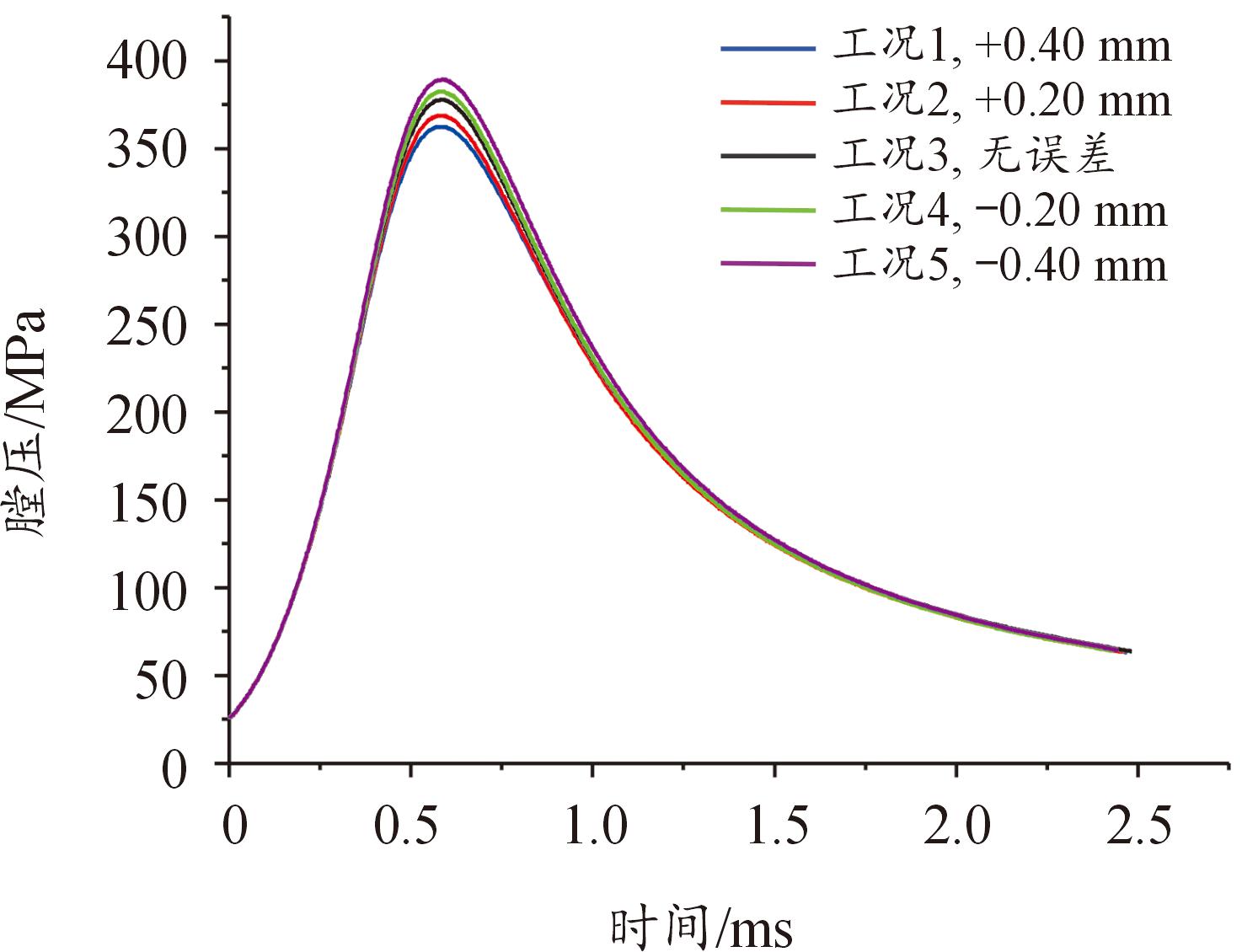
图13 膛压-时间曲线
Fig.13 Chamber pressure-time curves

图14 膛压与位移曲线
Fig.14 Chamber pressure-displacement curves
没有加工误差工况下,弹丸出膛口速度为1 021.5 m/s,最大膛压为377.8 MPa;加工误差-0.2 mm工况下的弹丸出膛口速度为1 024.2 m/s,最大膛压为382.4 MPa;加工误差为-0.4 mm工况下的弹丸出膛口速度为1 030.4 m/s,最大膛压为389.2 MPa。与没有加工误差工况相比,加工误差为-0.2 mm和-0.4 mm工况的弹丸出膛口速度分别增大了2.7 m/s和8.9 m/s,相对增大了0.26%和0.87%。最大膛压增大了4.6 MPa和11.4 MPa。弹丸出膛口速度和最大膛压随加工误差的变化情况如图15所示。
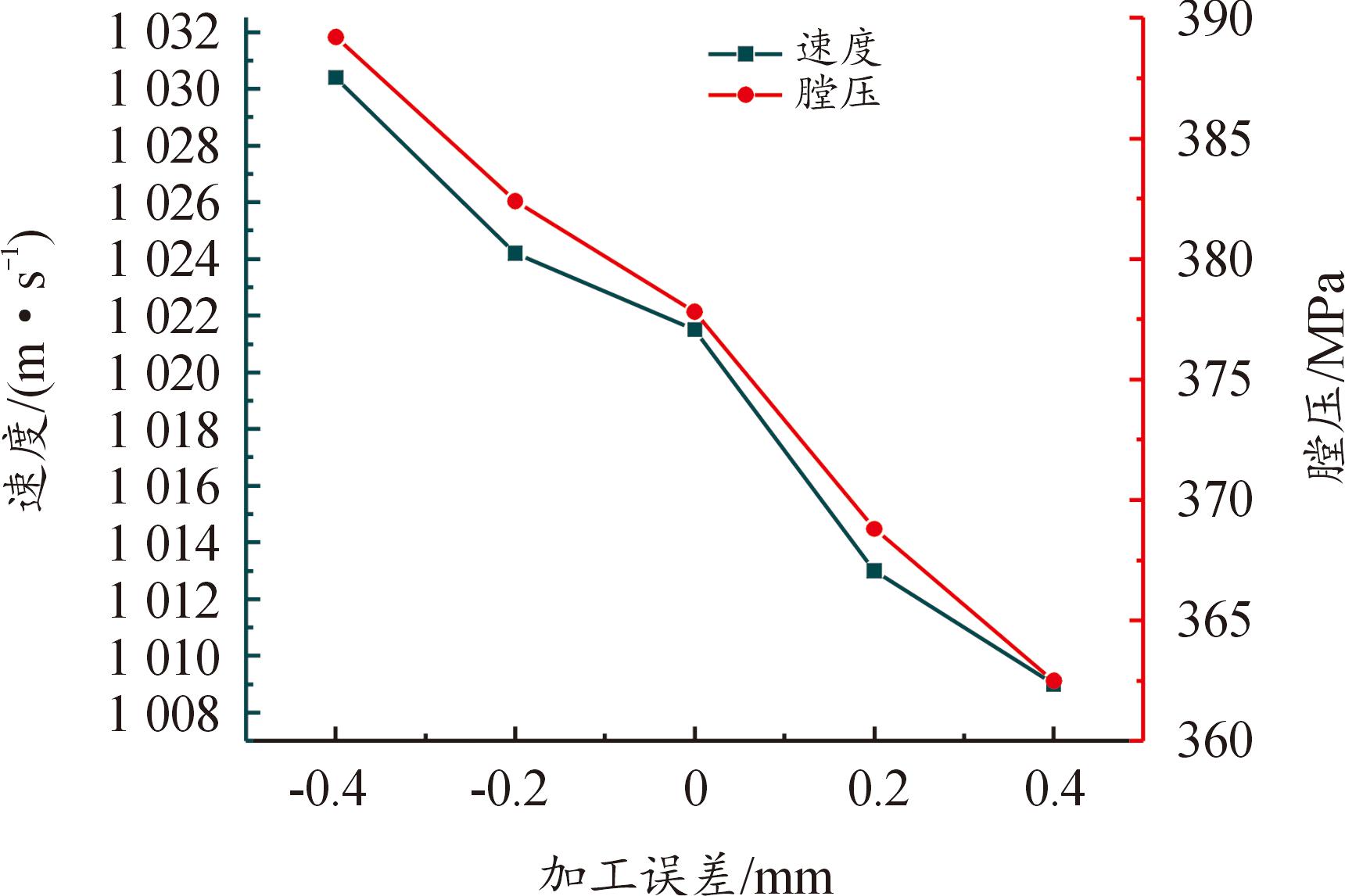
图15 弹丸初速和最大膛压随加工误差变化曲线
Fig.15 Curves of projectile muzzle velocity and maximum bore pressure change with machining error
通过对不同加工误差的身管进行实弹射击试验获得的弹丸出膛口速度如表3。
表3 不同加工误差的身管实弹射击初速
Table 3 Projectile velocity of barrel with different machining errors
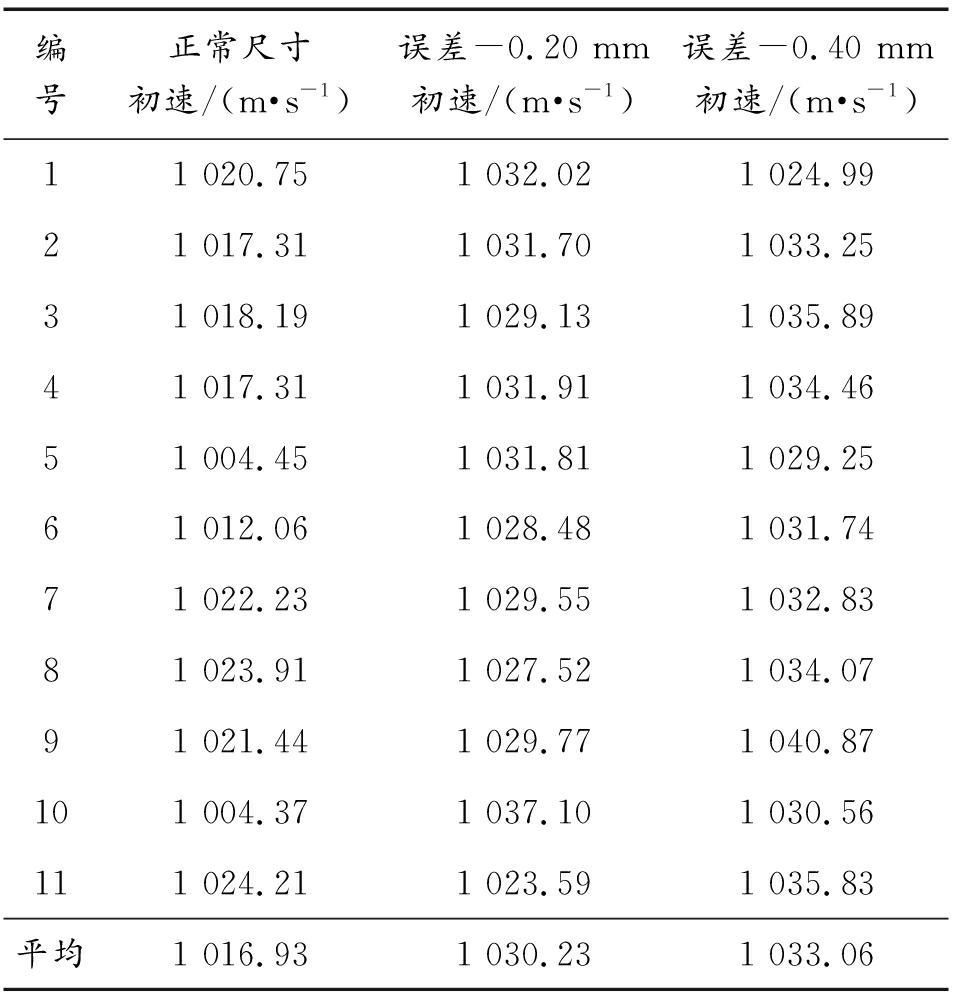
编号正常尺寸初速/(m·s-1)误差-0.20 mm初速/(m·s-1)误差-0.40 mm初速/(m·s-1)11 020.751 032.021 024.9921 017.311 031.701 033.2531 018.191 029.131 035.8941 017.311 031.911 034.4651 004.451 031.811 029.2561 012.061 028.481 031.7471 022.231 029.551 032.8381 023.911 027.521 034.0791 021.441 029.771 040.87101 004.371 037.101 030.56111 024.211 023.591 035.83平均1 016.931 030.231 033.06
根据实弹射击条件下,计算出不同加工误差下11发弹丸出膛口速度的平均值,正常内膛、弹丸与坡膛距离缩短0.20 mm和缩短0.40 mm的身管,分别为1 016.93、1 030.23、1 033.06 m/s,相差13.30 m/s和16.13 m/s,速度相对误差为1.31%和1.59%。
仿真分析的结果与试验数据进行对比,弹丸出膛口速度的变化规律基本一致,弹丸出膛口速度随弹丸与坡膛距离的缩短而增大。
3 结论
对不同加工误差导致弹丸与坡膛沿身管轴线方向距离变短后的弹丸膛内运动进行仿真计算,计算结果表明,在弹丸开始运动后,弹带与坡膛间的间隙减小,自由行程减少甚至没有自由行程,使弹带更早地接触坡膛起始处,也使在火药燃烧相同的时刻后,弹带受到更大的阻力,从而使弹丸加速度更小,也对弹后容积的增加速率有减缓作用,弹后容积小导致此刻膛内压力相较于正常加工状况下的膛内压力更大。最终在整个内弹道期间,加工误差大、坡膛起始处与弹丸距离短的身管,弹丸的出膛口速度增大,膛压峰值增大。不同加工误差下身管初速试验也得到了与结论一致的规律。
[1] 邹利波,于存贵,冯广斌,等.弹丸连续挤进过程中身管坡膛受力和磨损分析[J].北京理工大学学报,2021,41(5):487-493.
ZOU Libo,YU Cungui,FENG Guangbin,et al.Analysis of the friction and wear of the barrel bore during the continuous engraving process[J].Transactions of Beijing Institute of Technology,2021(5):487-493.
[2] DONG Y,SUN J,GONG L,et al.Numerical analysis of nylon projectile engraving into rifle[J].IOP Conference Series:Materials Science and Engineering,2019,688(3).
[3] 梁兴旺,李强,安俊斌,等.弹丸挤进过程中弹带变形仿真分析[J].兵器装备工程学报,2019,40(1):94-97.
LIANG Xingwang,LI Qiang,AN Junbin,et al.Deformation simulation analysis of rotating band in engraving process[J].Journal of Ordnance Equipment Engineering,2019(1):94-97.
[4] 侯文伟,杨臻,蓝维彬,等.弹丸被甲材料对弹丸挤进的影响分析[J].兵工自动化,2018,37(12):58-62,66.
HOU Wenwei,YANG Zhen,LAN Weibin,et al.Influence analysis of bullet shell material on projectile extrusion[J].Ordnance Industry Automation,2018,37(12):58-62,66.
[5] 胡朝斌.内弹道精细化建模及其在身管烧蚀磨损研究中的应用[D].南京:南京理工大学,2020.
HU Chaobin.Refined modeling of interior ballistics and its application in the study of erosion and wear in gun bores[D].Nanjing:Nanjing University of Science and Technology,2020.
[6] 彭松江,陈亮,何行,等.某舰炮典型坡膛结构的受力和内弹道特性分析[J].火炮发射与控制学报,2020,41(4):27-31.
PENG Songjiang,CHEN Liang,HE Hang,et al.Analysis of force and interior ballistic performance of the typical forcing cone structure of a naval gun[J].Journal of Gun Launch &Control,2020,41(4):27-31.
[7] 何行,彭松江,邱群先,等.不同坡膛锥度对弹丸挤进过程影响仿真研究[J].兵器装备工程学报,2020,41(11):141-146.
HE Hang,PENG Songjiang,QIU Qunxian,et al.Simulation study on impact of different tapers on projectile squeezing pross[J].Journal of Ordnance Equipment Engineering,2020,41(11):141-146.
[8] 孙河洋,马吉胜,李伟,等.坡膛结构变化对火炮内弹道性能影响的研究[J].兵工学报,2012,33(6):669-675.
SUN Heyang,MA Jisheng,LI Wei,et al.Study on influence of bore structure on gun’s interior ballistic performances[J].Acta Armamentarii,2012,33(6):669-675.
[9] 李淼.弹丸膛内起始运动过程瞬态特性研究[D].南京:南京理工大学,2017.
LI Miao.Dynamic characteristics study of the projectile initial motion in bore[D].Nanjing:Nanjing University of Science and Technology,2017.
[10] MEYERS M A.材料的动力学行为[M].张庆明,刘彦,黄风雷,等译.北京:国防工业出版社,2006:226-228.
MEYERS M A.Dynamic behavior of materials[M].Beijing:National Defense Industry Press,2006:226-228.
[11] JOHNSON GORDON R,COOK WILLIAM H.Fracture characteristics ofthree metals subjected to various strains,strain rates,temperatures and pressures[J].Engineering Fracture Mechanics,1985,21(1).
[12] 辛春亮,薛再清,涂建,等.有限元分析常用材料参数手册[M].北京:机械工业出版社,2020,266.
XIN Chunliang,XUE Zaiqing,TU Jian,et al.Handbook of common material parameters for finite element analysis[M].Beijing:China Machine Press,2020:266.
[13] 曾志银,高小科,刘朋科,等.炮钢材料动态本构模型及其验证[J].兵工学报,2015,36(11):2038-2044.
ZENG Zhiyin,GAO Xiaoke,LIU Pengke,et al.Dynamic constitutive model of gun steel material and its verification[J].Acta Armamentarii,2015,36(11):2038-2044.
[14] 张小兵,金志明.枪炮内弹道学[M].北京:北京理工大学出版社,2014:351-365.
ZHANG Xiaobing,JIN Zhiming.Gun interior ballistics[M].Beijing:Beijing Institute of Technology Press,2014:351-365.
[15] 丁传俊,张相炎.基于热力耦合有限元模型的弹带挤进过程及内弹道过程的仿真研究[J].兵工学报,2015,36(12):2254-2261.
DING Chuanjun,ZHANG Xiangyan.Simulation study of bearing band engraving process and interior ballistic process based on thermo-mechanical coupling FEA model[J].Acta Armamentarii,2015,36(12):2254-2261.