0 引言
随着我国现代通用航空事业迅速发展,研制综合性能更高的通用航空飞机以满足国民多种需求,成为实现我国现代化至关重要的一环。飞机的质量直接影响飞机的各种性能,飞行器各部件结构质量的减少,意味有效载荷、飞行速度、飞行距离的增加[1]。襟翼作为机翼重要的增升装置,在通航飞机中占据非常重要的地位,该关键部位的轻量化设计有助于提升整机的最大升力系数,使飞机具有良好的低速起降性能和失速特性,更好地适应不同的起降环境,应用更加广泛。
拓扑优化是一种设计满足约束条件的最优材料布置形式和结构轻量化的优化方法,可分为离散体结构和连续体结构拓扑优化。连续体结构拓扑优化模型复杂,计算量大,近几十年才取得了快速发展。目前,连续体结构拓扑优化方法主要包括均匀化方法、渐进结构优化法、独立连续映射法、变密度法、变厚度法和水平集法[2]。其中变密度法被广泛应用于航空航天领域各种航空器的结构拓扑优化中,能使结构优化的周期缩短,材料成本降低,设计的科学性提高[3]。
但拓扑优化问题的设计变量数目庞大,计算规模较大,并且目标函数与约束函数之间一般为设计变量的非线性、非单调的隐式函数,因此求解时需要选择收敛速度较快、求解简单有效的算法。国内外学者对此做了大量的研究,演化出优化准则法、数学规划法以及智能算法3大类[2],其中,数学规划算法有严密的理论基础,适用于多数结构拓扑优化问题,该优化方法不需要重新初始化步骤,在一定条件下能收敛到问题的最优解,使拓扑优化计算效率得到提高,收敛速度加快。俞燎宏[4]在桥梁结构设计过程中利用光滑对偶算法引进拉格朗日乘子对新的优化模型进行计算,在确保计算结果的最优化前提下,大大减少了计算量,最终结果可稳健地获得清晰的0/1拓扑优化分布。赖松[5]进行拓扑优化设计过程中采用反应扩散方程的水平集结构拓扑优化方法,通过理论推导给出算法中的参数选择建议,生成新的孔洞。在航空航天领域中,纪斌[6]运用数学规划法中的移动渐进法将飞机翼肋拓扑优化的原问题的凸近似函数进行改进,得到翼肋的最佳材料分布形式。许华旸[7]以数学规划法中的拉格朗日方程为基础引入导重法,对飞行器模拟器大臂结构进行变密度法拓扑优化,使得在惯性载荷作用下的拓扑优化迭代公式更合理,得到的优化结果更具有参考意义。
飞机中薄壁构件作为主要承载结构,需具备强承载能力、超高精度、超轻量化等特性[8],拓扑优化过程中计算量大,现有研究中关于该类结构拓扑优化的算法优化较少。采用Optistruct软件完成整个优化过程,根据某型通航飞机襟翼的工作特性,模拟襟翼在最大弯度工况下受到的气动载荷环境,采用变密度法进行多约束拓扑优化设计,并在优化过程中采用可分凸逼近对偶优化算法进行计算,以提高计算效率,更快更好地实现襟翼材料最佳分布和轻量化设计的目标。对襟翼结构进行拓扑优化设计能够有效针对襟翼的工作特性以及受力特点得到符合飞行设计要求的拓扑结构,不仅能够实现襟翼的轻量化设计目标,还能对同类型结构优化有一定的参考意义。
1 基于可分凸逼近对偶优化的变密度拓扑优化法
1.1 变密度法的结构拓扑优化模型
采用变密度法应用在襟翼薄壁结构拓扑优化中。变密度法假设材料的密度为“伪密度”,通过构建该材料的物理属性(如弹性模量、许用应力)与伪密度之间函数显式表达式构建材料模型,利用近似方案建立伪密度与目标函数和约束函数之间的关系,用一系列显式近似子问题代替初始隐式问题的解,最终用简单的0/1来表示材料的有无,直观地呈现出结构的最佳材料分布。变密度法将拓扑优化从关于0和1的非连续取舍问题转化为一个在{0,1}之间取值的连续变量优化问题,为了尽可能好的消除中间密度材料对拓扑优化的影响,变密度法通过惩罚因子对伪密度在{0,1}之间的中间密度值进行惩罚,使连续变量的拓扑优化模型能更好地逼近传统的0和1的离散变量的拓扑优化模型[9]。针对襟翼的工况,最终建立数学求解模型,如式(1)所示。
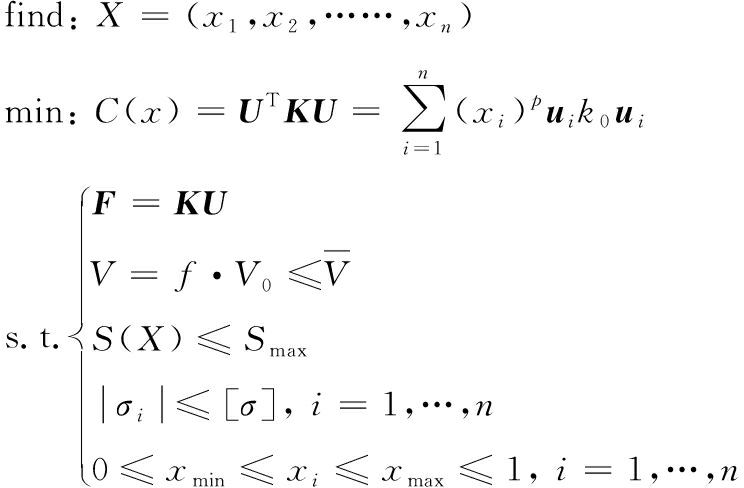
(1)
式(1)中: V为优化后结构体积,C为结构的总柔顺性,U为结构的位移向量,K为结构的刚度矩阵,xi为单元的伪密度, k0为单元刚度矩阵, ui为单元位移向量,F为结构的载荷向量,V0为结构设计域的初始体积,![]() 为优化后需要保留的结构体积,xmin、xmax是为了防止总体刚度矩阵奇异的最小、最大伪密度约束, f为优化的体积比率因子,S表示位移,Smax表示位移的最大值,|σi|为结构强度,[σ]为材料的许用应力,n为结构有限单元数目,p为惩罚因子。
为优化后需要保留的结构体积,xmin、xmax是为了防止总体刚度矩阵奇异的最小、最大伪密度约束, f为优化的体积比率因子,S表示位移,Smax表示位移的最大值,|σi|为结构强度,[σ]为材料的许用应力,n为结构有限单元数目,p为惩罚因子。
该模型用各向同性材料惩罚模型SIMP对中间变量进行惩罚,则其材料的弹性模量根据伪密度的变化而变化,如式(2)所示。
![]()
(2)
式(2)中:Ei为第i号单元的弹性模量,E0为结构材料的弹性模量,Emin为删除材料单元的弹性模量值[9]。
1.2 可分凸逼近的对偶优化算法
拓扑优化过程中计算量大,网格数量以及设计区域使得设计变量数目庞大,求解过程中,计算量也随之增大,针对多变量多约束的情况,采用的是基于可分凸逼近的对偶优化法(DUAL)。该算法对薄壁结构的综合优化具有针对性的效果,通过近似与对偶相结合求解结构最小质量设计方法即近似概念,将结构问题的数学规划问题转换为一组可分离的显式原始问题,这些问题通过构造显式对偶函数来解决,而对偶函数在对偶变量的非负性约束下最大化[10]。
对偶方法将原问题通过拉格朗日函数重新定义为一个无约束问题,将约束函数与目标函数通过拉格朗日乘子分配,从而将约束问题无约束化。对于可分离离散问题其拉格朗日函数也可分离,根据式(1)可构造拉格朗日方程,如式(3)所示。
L=C+λ1(V-fV0)+λ2(KU-F)+![]()
![]()
![]()
![]()
(3)
式(3)中: λ1、λ2、λ3、λ4、β为Lagrange乘子,![]() 为松弛因子。
为松弛因子。
得到对偶函数l(λ),对于给定的λ,拉格朗日函数可以分解为n个单变量问题,每个问题都与可行集X上的一个xi有关,对偶相当于给当前的优化问题找到了一个下界,通过提升这个下界来找到原问题的最优解,即对这个对偶函数通过梯度上升迭代法进行最大化求解。如果对偶函数在当前对偶点处是可微的,则用基于梯度的方法计算。否则,使用基于次梯度的方法。该过程反复进行,直至达到最优,从已有的可能性集合中选较优的原始值组合。
对于任何对偶函数,不管是凸且处处可微的,还是非凸的对偶函数并非处处可微,次梯度可表示为
![]()
(4)
当l(λ)在λ处可微时,p=0,β是常数,对于不可微的对偶点λ存在p个一阶导数间断的平面,有2p个不同的次梯度被原始约束影响,因此,在λ处的次微分由这2p个次梯度的凸包决定。根据求解的次梯度得到最大上升方向从而求解出每一步的对偶问题的最优解,根据迭代条件直至求出最符合设计要求的拓扑形状[10]。
2 飞机襟翼肋板的建模与分析
2.1 对襟翼进行参数化建模
选用某通航飞机固定翼襟翼作为拓扑优化设计对象,其主要结构部件包括蒙皮、主梁、肋板、后墙、连接件及接头,如图1所示。襟翼总体长度为2 000 mm,蒙皮厚度为0.8 mm,接头处厚度为5 mm,梁腹板厚度为1 mm,缘条厚度为0.8 mm。其中,肋板分为加强肋和普通肋,以自身刚度给桁条和蒙皮起支撑作用,提高蒙皮的抗失稳能力,而加强肋用来承受平面内的集中载荷,将其转化为分散载荷传给蒙皮、翼梁等,因此普通肋版厚度为1 mm,而加强肋版为1.2 mm[11]。
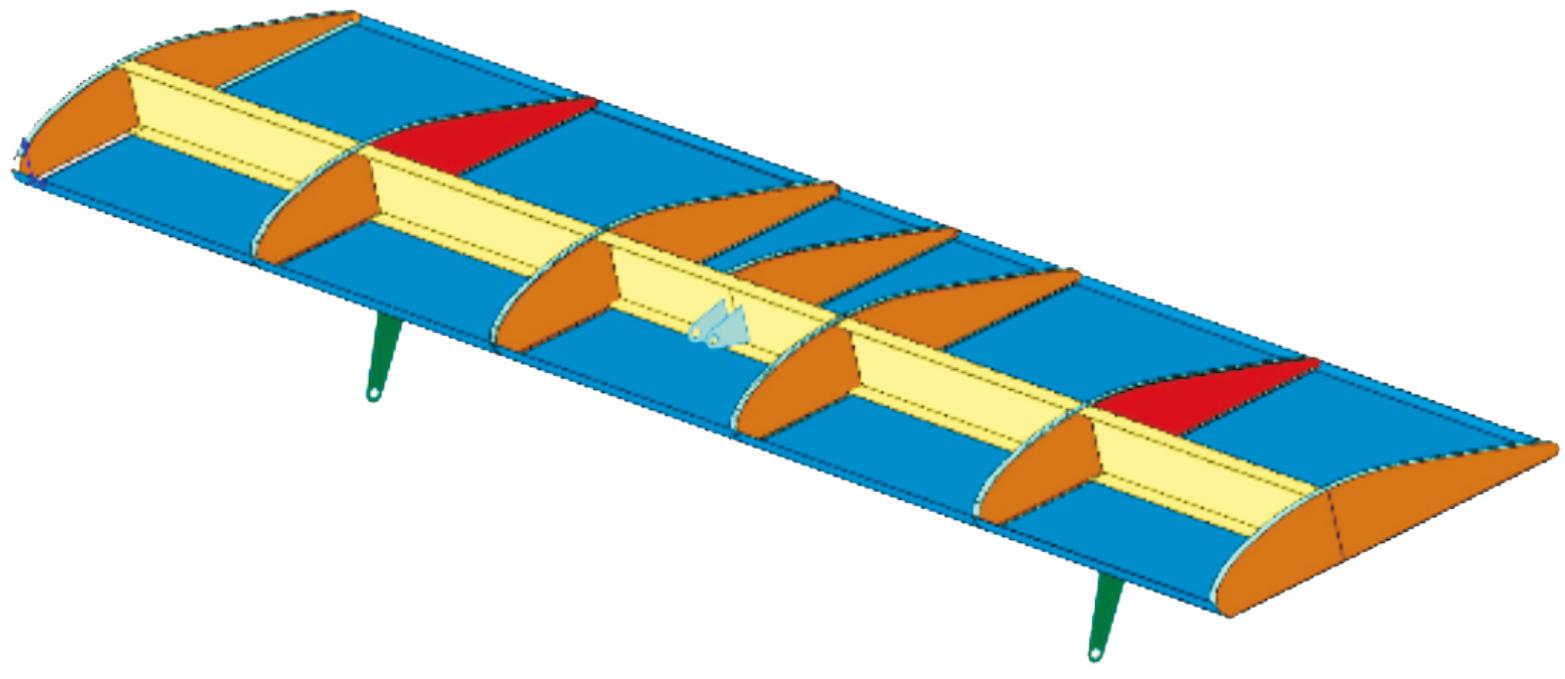
图1 襟翼模型
Fig.1 Flap model
襟翼的材料为2024-T3铝合金,该系列铝合金主要用于飞机结构中疲劳和损伤容限问题比较突出的承拉结构,并且具有质量轻、强度高、耐腐蚀性等优点,在航空航天领域应用广泛[11],材料属性如表1所示,该铝合金材料的极限应力为485 MPa,当材料应力超过该极限值时发生失效。襟翼模型的有限元网格划分根据结构特点,选用四边形壳单元进行划分,单元尺寸为3 mm。划分网格时应对模型进行清理,去除倒角、圆角以及不完整线条,利于后续中面抽取的完整性。设置网格划分结果中jacobian为0.7,skew为40,warpage为15,min size为2,最终划分网格共计233 766个,如图2所示,综合网格质量(comp.QI)为0.01,该值越小表示网格质量越好。
表1 2024-T3铝合金材料属性
Table 1 2024-T3 aluminum alloy material properties

属性值杨氏模量E/MPa72 400剪切模量G/MPa28 000泊松比μ0.33质量密度ρ/(t·mm-3)3.064 425×10-9极限应力σu/MPa485屈服应力σy/MPa345剪切极限应力u/MPa291
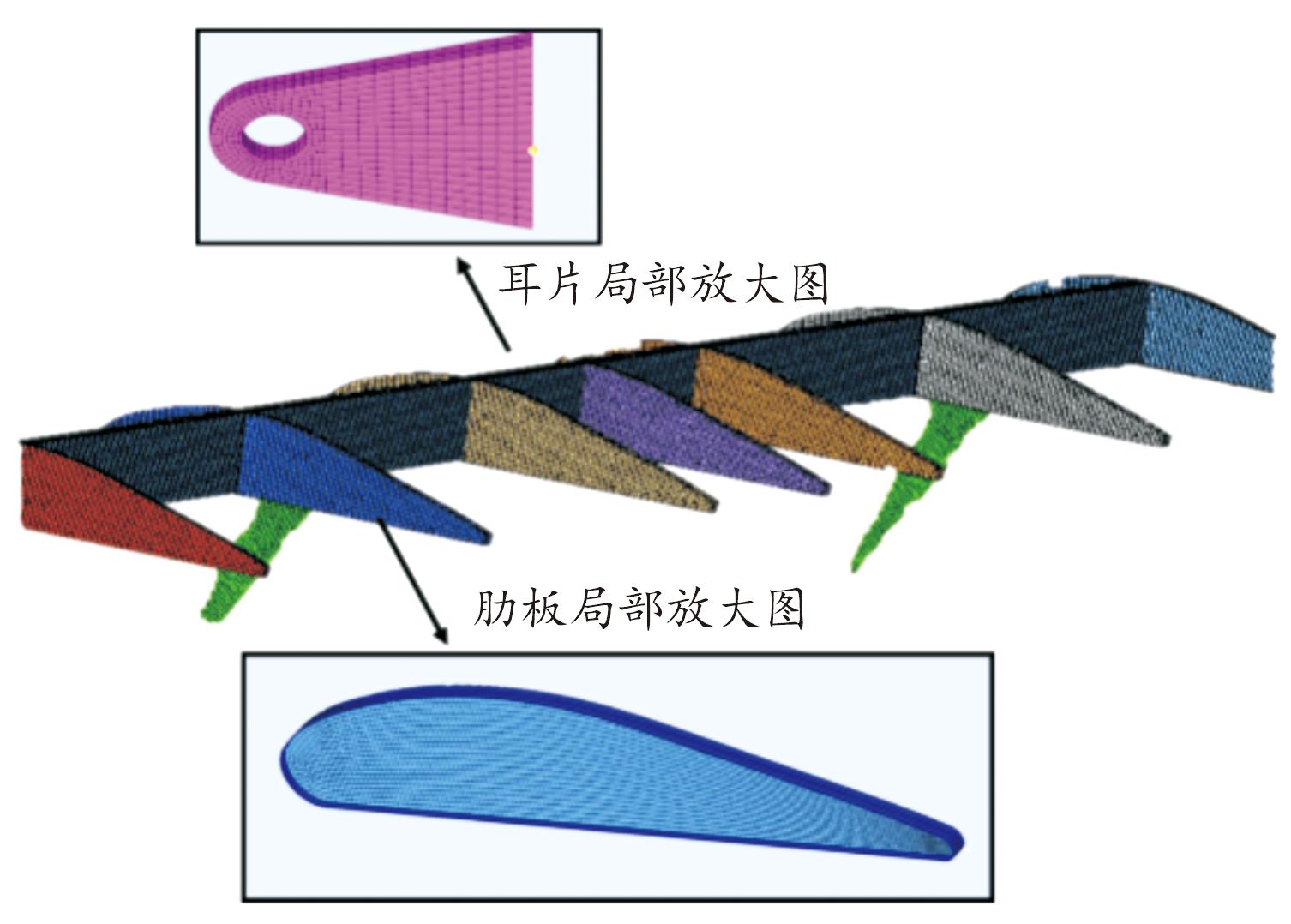
图2 网格划分
Fig.2 Meshing
襟翼作为航空器重要的增升操纵面,与机翼由传动机构相连接,在其驱动下伸出向后下方偏转,从而增大机翼表面积来获得升力[12]。本文中主要研究襟翼翼面,因此将传动机构简化为旋转接头和操纵接头。为了模拟旋转接头向下偏转的运动,在旋转接头和操纵接头的螺栓孔处定义局部坐标系coord1,以操纵接头的轴向方向为X轴正向,以横向方向为Z轴正向,根据来流方向的右侧为Y轴正向。在接头孔洞处建立RBE2连接并以局部坐标系coord1为基准约束旋转接头和操纵接头其3个平动方向位移,仅释放平行于翼面方向的转动位移,如图3所示。以达到模拟襟翼向下偏转的运动方式,释放其在局部坐标系的Z轴方向的位移,以免出现过约束的情况。
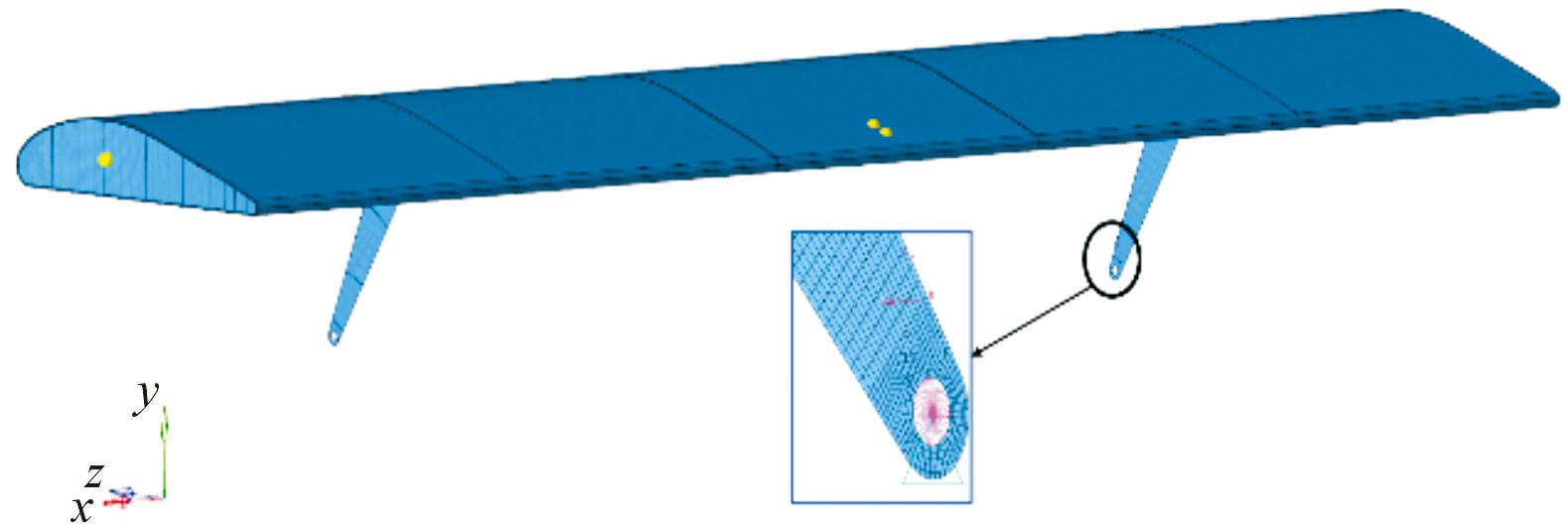
图3 旋转接头处局部坐标系coord1以及边界条件
Fig.3 Local coordinate system coord1 at rotating joint and boundary conditions
襟翼在伸出后(偏转角度为33°)主要承受气动载荷,并以剪流的方式传递给梁、肋板等,为了得到襟翼在该工况下的真实气动载荷分布,利用fluent进行空气动力学分析,来流速度设置为50 m/s,来流方向为z方向cos(-33°),y方向为sin(33°),x方向为0。湍流模型选用SST k-ω模型,相较于k-ω模型,该模型更适合近壁自有流,湍流粘度也考虑到了湍流剪应力的传播,这些改进使得SST k-ω模型比标准k-ω模型在广泛的流动领域中有更高的精度和可信度[13]。得到襟翼的压力云图如图4所示,初始模型承受最大主应力为41.29 MPa,远低于材料的极限应力485 MPa,襟翼在极限工况下应力大小远小于材料的许用应力。

图4 33°偏角襟翼压力云图
Fig.4 33°flap pressure cloud nephogram
襟翼的气动载荷加载采用插值拟合样条曲面的方法,拟合得到蒙皮表面的压力分布曲面,然后再在单元上积分得到结点载荷[14]。将fluent中得到的襟翼表面压力载荷结果导入tecplot软件中利用切片提取作用在翼面上的三维离散压强场,最终得到上表面与下表面的压强函数曲线,该软件具有强大的数据分析以及可视化处理功能,并且与fluent软件有专门的数据接口,方便操作,简单易行,可准确将气动载荷反映到有限元模型上,为有限元计算提供可靠的输入。将处理后的襟翼面三维压强以函数形式加载到hypermesh的有限元模型上,得到襟翼在伸出偏角为33°时其载荷函数如表2所示。
表2 襟翼载荷公式
Table 2 Load formula of flap
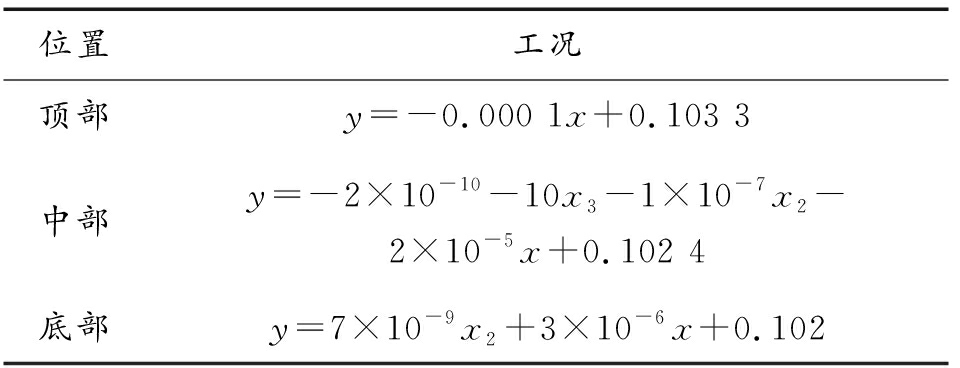
位置工况顶部y=-0.000 1x+0.103 3中部y=-2×10-10-10x3-1×10-7x2-2×10-5x+0.102 4底部y=7×10-9x2+3×10-6x+0.102
2.2 对襟翼进行拓扑优化
利用变密度法对襟翼进行拓扑优化,主要流程如图5所示。
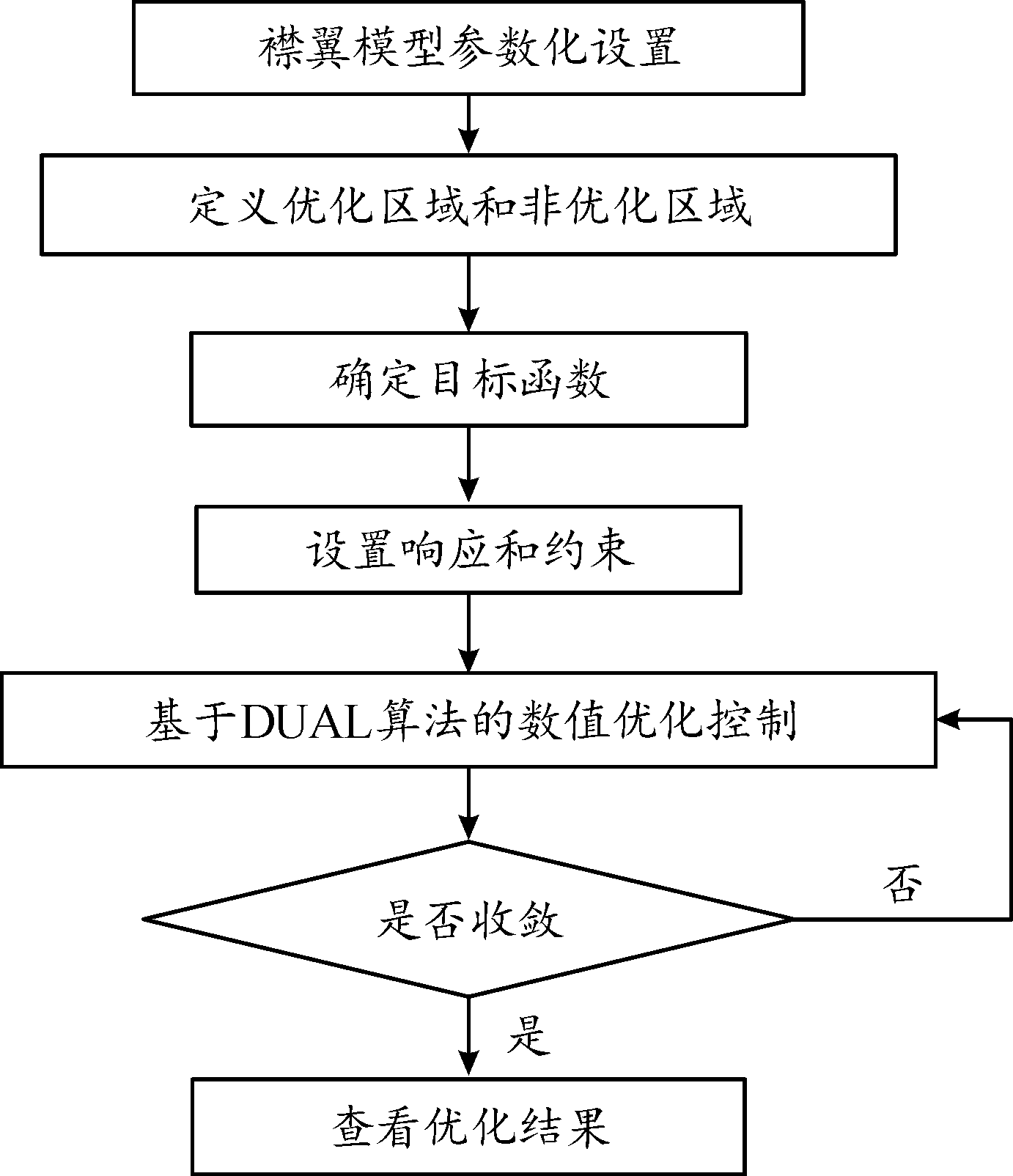
图5 拓扑优化流程框图
Fig.5 Flow chart of topology optimization
首先需要进行优化区域和非优化区域的设定。襟翼蒙皮质量占总质量的66.87%,根据结构的外在设计准则和气动特性,蒙皮为非设计区域;而主梁只占总质量的15.2%,相对于肋板的占比,其优化效果不理想,因此,将肋板定义为设计区域。其次,应用变密度法即以单元密度作为设计变量,以柔度最小为设计目标,对肋板模型进行位移约束、剪切应力约束和体积分数约束,由于蒙皮主要承受剪力,因此对蒙皮以及肋板进行剪切应力约束,其剪切极限应力为291 MPa,最大位移约束为4 mm,代入求解模型式(1);求解过程中运用式(3)所示DUAL算法将约束问题无约束化,多次迭代得到最优拓扑优化结果。
3 优化结果分析
在优化过程中会出现棋盘格现象,由于伪密度是在0~1之间变化,而拓扑优化结果作为一种概念设计,其体现的是材料在传力路径上的最优分布,不能得到各部分的具体尺寸,因此会出现棋盘格现象,对现实制造加工增加难度,难以实现,因此需要对此现象进行控制,增加制造性约束。通过改变最大、最小单元尺寸改善棋盘格现象,最终确定最小单元尺寸为4 mm,比网格划分单元尺寸略大,保证优化后的单元可见,最大尺寸为15 mm;本研究中采用优化控制中的CHECKER进行全局控制,减小中间伪密度值,控制棋盘格现象。
体积比率因子在(0,1)之间取值,为了得到拓扑优化的最优结果,将体积比率因子作为变量,通过改变该值来控制襟翼肋板最终保留的体积分数,当f分别取值0.7、0.6、0.5、0.3时肋板拓扑优化的结果如图6所示。
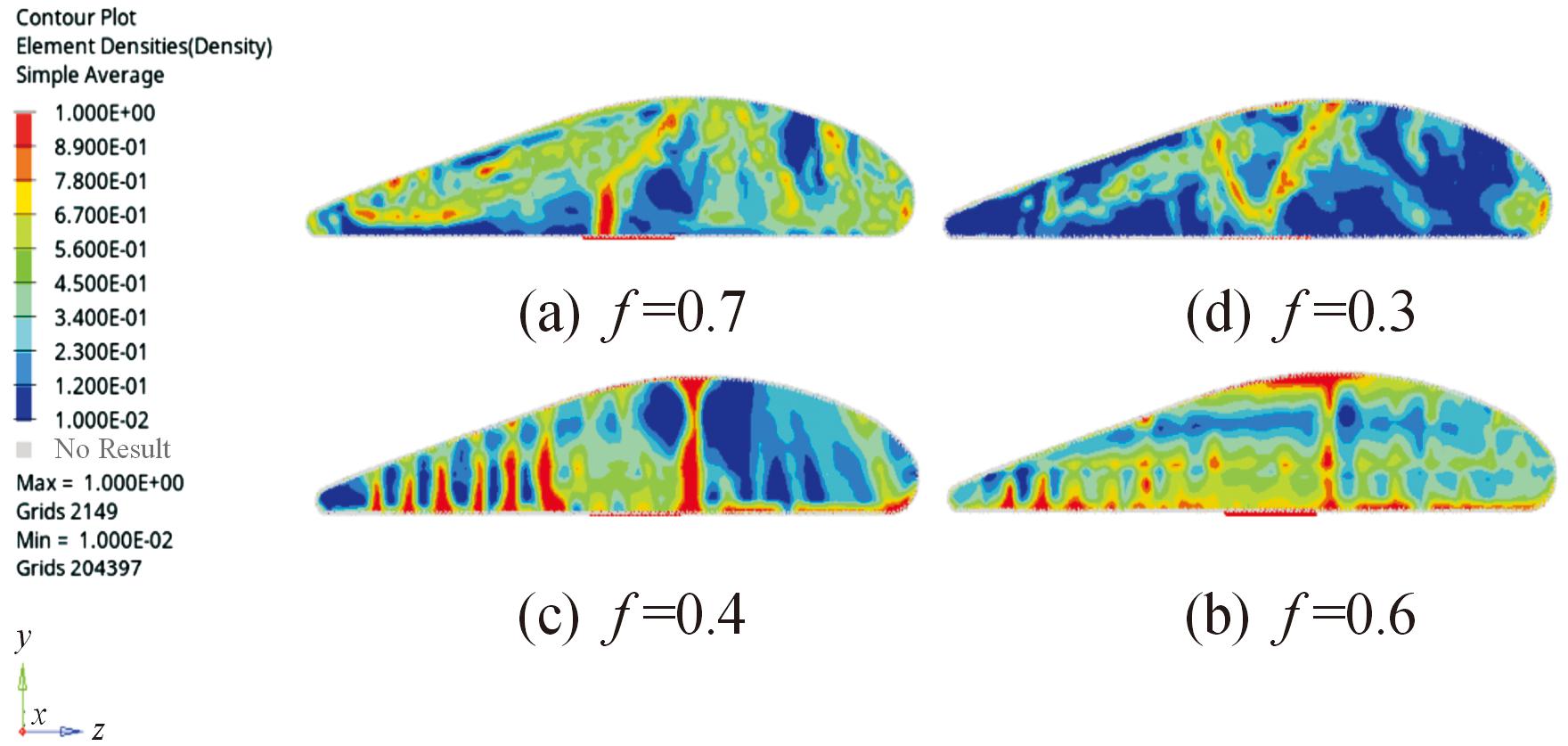
图6 拓扑优化结果图
Fig.6 Optimization results
当f=0.4时,收敛结果如图7所示,优化结果如图8所示。根据结果分析得出:当f>0.4时,肋板的大部分材料被保留,且柔度变化较小,结构质量变化较小,当f<0.4时中间变量太多,不能达到收敛。因此,为了达到轻量化设计目标,使结构质量尽可能小,经过多次调整,最终确定体积质量分数选取0.4最为合适。经过80步迭代优化,与优化前相比柔度减小了约30%。红色部分代表伪密度为1的材料,需保留;蓝色部分代表伪密度为0的材料,需去除,而中间密度的材料有选择性地保留。
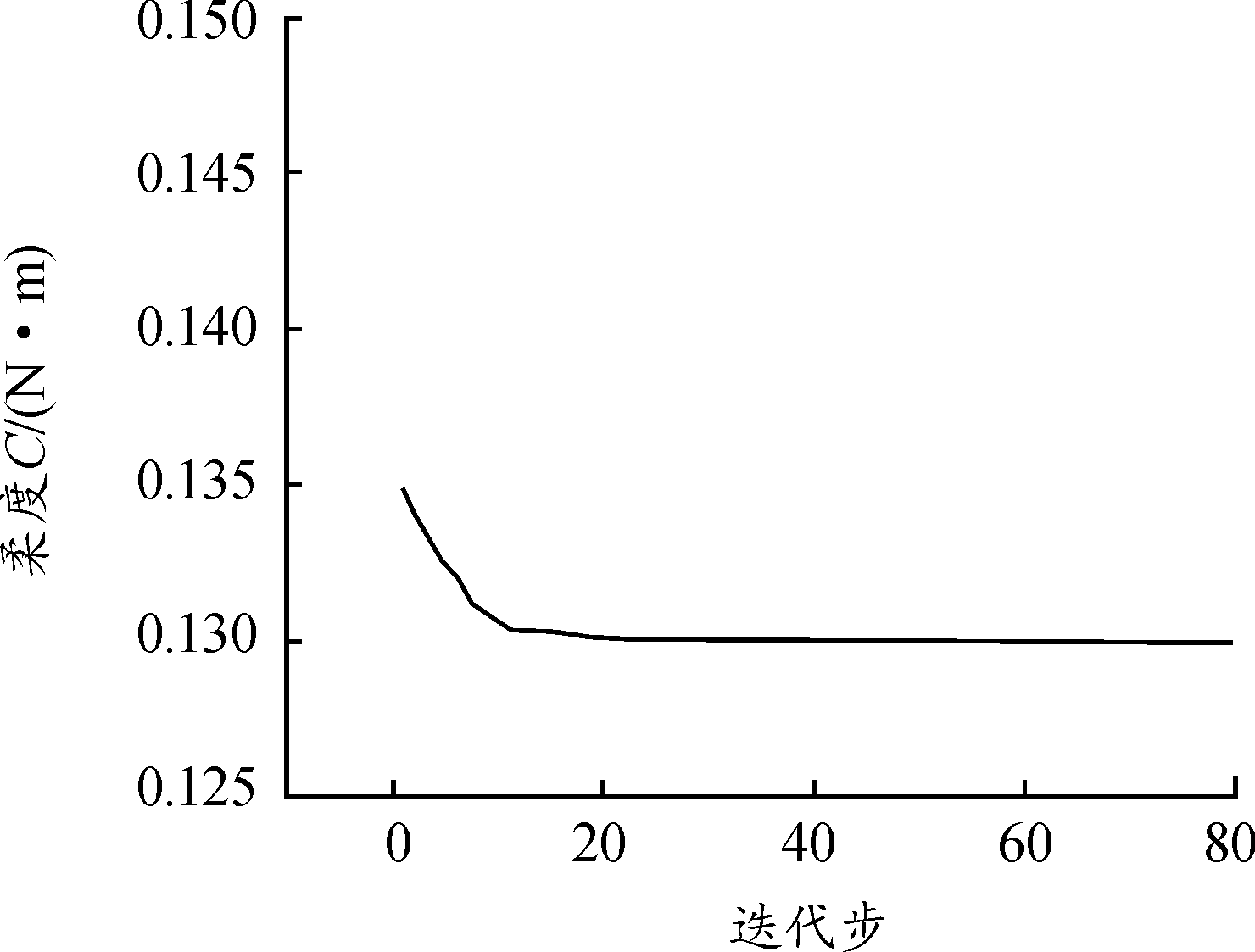
图7 柔度迭代曲线
Fig.7 Complianceiteration curve
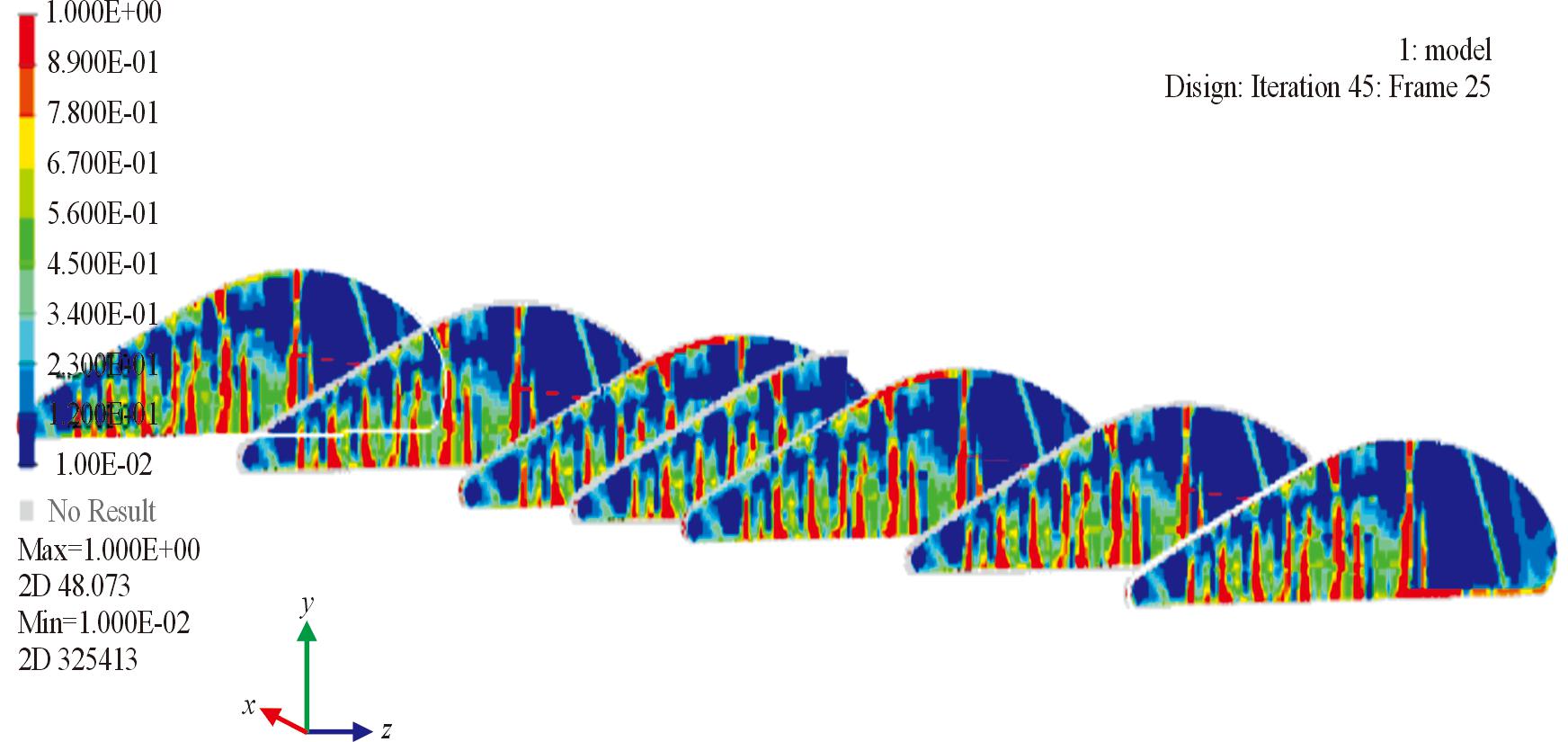
图8 拓扑优化结果
Fig.8 Optimization results
对于DUAL算法,通过构建拉格朗日方程将襟翼的约束问题无约束化,使这种薄壁结构的多约束问题求解通用性更好,求解效率更高。
对拓扑优化后的襟翼进行静力学分析,由于襟翼蒙皮属于薄壳结构,厚度较小,抗弯能力较小,而肋板主要受到来自蒙皮传递的剪流,主要承受剪切载荷,因此主要对襟翼的剪切受力进行分析。从图9所示的优化后襟翼的剪切应力云图中可以看出,最大剪切应力出现在肋板附近,肋板是剪切应力的主要承载结构,最大剪应力值为39.26 MPa,远小于襟翼的最大剪切极限应力值291 MPa。襟翼在33°偏角工况下,翼面中部主要受到垂直于翼面的载荷,而肋板主要承受来自蒙皮传递的剪切应力,因此,在中部需要支撑的材料更多,需要保留的部分就越多。随着迭代步数的增加,目标函数柔度呈现下降趋势,并且最终收敛,柔度越小说明刚度越大,优化结果符合预期。
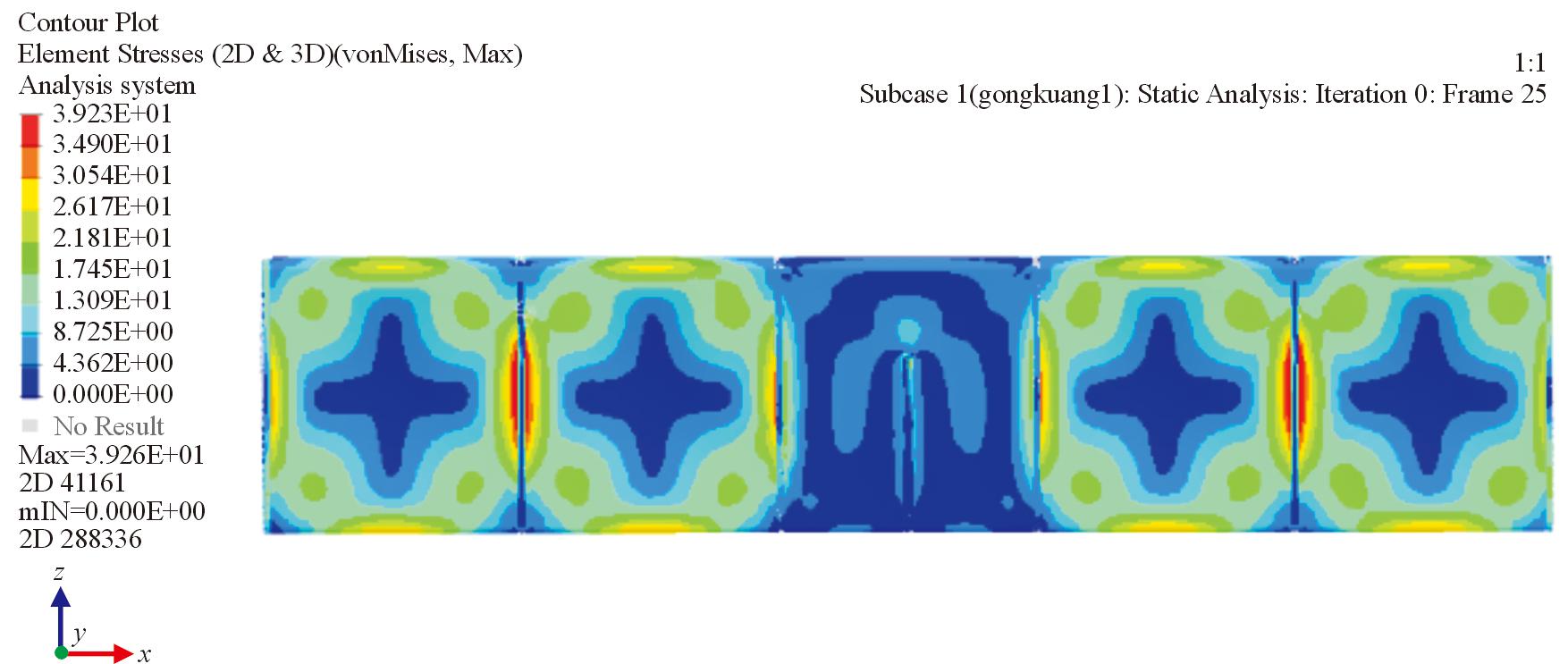
图9 优化后襟翼的剪切应力云图
Fig.9 Optimized flap shear stress cloud nephogram
对经过拓扑优化后的模型进行静力学分析,得到襟翼在33°工况下的应力云图,如图10所示。

图10 优化后33°偏角下的应力云图
Fig.10 Stress nephogram at 33° deflection angle after optimization
根据应力云图可知,优化后的襟翼的最大应力同样发生在肋板与蒙皮的连接处,以及旋转接头与蒙皮的连接处。在33°工况下最大应力为321.1 MPa,均未超过铝合金的极限应力,符合静强度设计准则。
4 结论
1) 根据襟翼最大偏转角度的受载情况,基于样条插值原理得到襟翼在最大偏角(33°)下受到的表面载荷,并且以数学公式的形式加载到有限元分析软件Hypermesh中,为后续优化设计提供最真实的载荷工况,确保优化结果与实际情况的贴合度。
2) 基于拓扑优化方法中的变密度法对襟翼进行了结构优化设计,并且在优化过程中选用可分凸逼近的对偶优化算法专门针对薄壁结构优化过程进行算法优化,最终优化结果在初始模型的基础上质量减少了23%,达到轻量化设计的阶段性目标。最后通过静力学分析得到结构应力大小,确定其主要承载力为剪应力,并对优化后的结构进行剪应力校核,确保结构的安全性。
本研究中的工作为后续襟翼的轻量化设计提出了优化方案和具体做法。所用的优化方法对薄壳类结构优化具有一定的可借鉴性,优化过程中所用到的方法对襟翼后续的轻量化设计有一定的参考意义。
[1]苏胜伟.基于Optistruct拓扑优化的应用研究[D].哈尔滨:哈尔滨工程大学,2008.
SU Shengwei.Plication and research of topology optimization with optistruct[D].Harbin:Harbin Engineering University,2008.
[2]季武强.飞机机翼结构拓扑优化方法研究及其实现[D].沈阳:沈阳航空航天大学,2013.
JI Wuqiang.Researchand implementation on topology optimization methods of aircraft wing structure[D].Shenyang:Shenyang Aerospace University,2013.
[3]郭文杰.飞行器多舱段多组件结构系统布局优化设计[D].西安:西北工业大学,2017.
GUO Wenjie.Integrated layout and topology optimizationdesign of multi-frame and multi-component fuselage structure systems[D].Xi’an:Northwestern Polytechnical University,2017.
[4]俞燎宏,荣见华,赵志军,等.多工况载荷下连续体结构柔顺度拓扑优化问题的新的求解方法[J].机械工程学报,2018,54(5):210-219.
YU Liaohong,RONG Jianhua,ZHAO Zhijun,et al.A newsolving method of the compliance topology optimizationproblem of continuum structures under multiple load cases[J].Journal of Mechanical Engineering,2018,54(5):210-219.
[5]赖松,王坤.基于反应扩散方程的水平集结构拓扑优化方法与实现[J].计算机辅助工程,2021,30(2):9-15.
LAI Song,WANG Kun.Topology optimization method and-its implement of level set structure using reaction diffusion equation[J].Computer Aided Engineering,2021,30(2):9-15.
[6]纪斌.柔性变形机翼关键结构的拓扑优化[D].南京:南京航空航天大学,2017.
JI Bin.Topology optimization of key structures of flexible morphing wing[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2017.
[7]许华旸,关立文,王立平,等.惯性载荷下飞行模拟器大臂结构的拓扑优化[J].机械工程学报,2014,50(9):14-23.
XU Huayang,GUAN Liwen,WANG Liping,et al.Topology optimization for the arm of flight simulator under inertial loads[J].Journal of Mechanical Engineering,2014,50(9):14-23.
[8]张卫红,周涵,李韶英,等.航天高性能薄壁构件的材料-结构一体化设计[J].航空学报,2022,43(10):1-19.
ZHANG Weihong,ZHOU Han,LI Shaoying,et al.Material structure integrated design for high-performance aerospace thin-walled component[J].Acta Aeronautica et Astronautica Sinica,2022,43(10):1-19.
[9]沈思源.超轻复合材料机翼模型结构优化设计[D].大连:大连理工大学,2014.
SHEN Siyuan.Structure optimization of ultra-light composite wing model[D].Dalian:Dalian University of Technology,2014.
[10]MURIEL B.Dual methods for discrete structural optimization problems[J].International Journal for Numerical Methods in Engineering,2000,48(12):1761-1784.
[11]韩观林.某通航飞机襟翼的有限元模拟及静强度校核[D].南昌:南昌航空大学,2019.
HAN Guanlin.Finite element simulation and static strength check of a navigation aircraft flap[D].Nanchang:Nanchang Hangkong University,2019.
[12]王一飞,李庆飞,陈建华,等.大型客机复合材料襟翼刚度设计技术[J].中国科技信息,2016(19):88-92.
WANG Yifei,LI Qingfei,CHEN Jianhua,et al.Stiffness design technology of composite flap for large airliner[J].China Science and Technology Information,2016(19):88-92.
[13]曹九发.大型风力机非定常载荷计算及其减缓研究[D].南京:南京航空航天大学,2015.
CAO Jiufa.Investigation of large scalewind turbine unsteady loads calculation and alleviation[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2015.
[14]李力,王天.基于薄板样条插值函数的气动分布载荷插值计算方法[J].中国科技信息,2021(22):26-27.
LI Li,WANG Tian.Aerodynamic distributed load interpolation calculation method based on thin plate spline interpolation function[J].ChinaScience and Technology Information,2021(22):26-27.