0 引言
在枪炮发射时,炮口处会在初始射流、火药燃气射流以及弹丸的共同作用之下产生复杂的炮口流场系,炮口流场是诸多影响火炮射击精度的因素之一。在双身管齐射时,由于身管之间距离较小,各自所产生的流场会相互干扰,形成复杂的叠加流场,对弹丸侧面压力分布产生影响,形成侧向合力,从而导致武器的射击精度受到影响。
随着计算流体力学的发展,数值模拟已成为研究膛口流场的重要手段。张焕好等[1]应用Roe格式及结构化动网格技术,模拟了弹丸飞离制退器过程中的膛口流场。张海龙等[2]对航炮在吊舱中的不同安装位置进行稳态数值模拟和膛口流场瞬态数值模拟。李善吉等[3]利用动网格技术分别模拟了在吊舱内部是否使用偏流装置的航炮发射时膛口流场。刘欣宁等[4]运用三维非定常Euler方程并结合Roe格式,数值模拟分析了弹丸飞出炮口制退器过程中的膛口流场的变化过程。汤傲等[5]对小口径尾翼弹飞出膛口及尾翼张开过程中的膛口流场进行了数值模拟。郭则庆等[6]基于ALE方程的有限体积方法,对复杂形状弹丸的膛口流场进行了数值模拟。黄欢等[7]采用整体分块网格和结构化网格动态层变方法数值模拟分析了迫击炮弹丸出炮口后的流场。
针对单个身管炮口流场计算,现已有广泛的研究,但对于双身管齐射时炮口流场对弹丸受力的研究较少。本文中根据三维非定常Euler方程,运用结构化动网格技术,建立双管自动迫击炮齐射时三维数值模拟模型,对双管自动迫击炮的炮口流场进行数值仿真,分析双身管齐射时的炮口处流场的叠加过程,以及叠加后的炮口流场对弹丸侧向合力和轴向力的影响。
1 膛内过程计算
1.1 基本假设及内弹道计算模型
根据迫击炮的装药及内弹道过程特点提出以下假设[8]:
1) 尾管未破孔之前,基本装药在尾管内定容燃烧,打开传火孔以后,燃气从尾管中流出并点燃辅助装药。在基本装药未燃完之前,按基本装药和辅助装药构成的混合装药处理。基本装药燃完后,辅助装药单独燃烧,直至燃完。
2) 基本装药和辅助装药按各自燃烧规律燃烧,燃速公式采用指数燃烧定律。
3) 热损失不作直接计算,通过减小火药力的方法,间接修正热损失的影响。
4) 气体从间隙中流出时,满足临界状态的条件。对于装有闭气环的情况,可令SΔ=0。
根据上述假设,迫击炮内弹道计算方程组为[9]
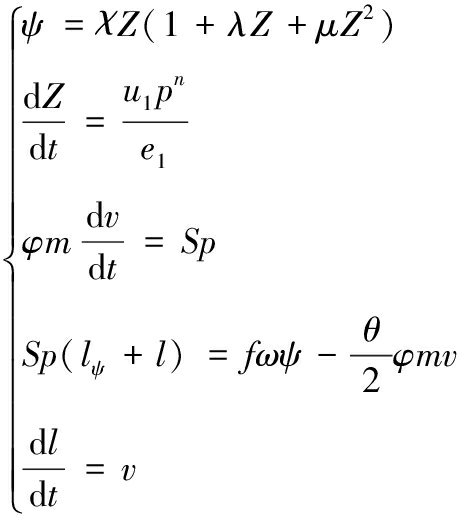
(1)
式(1)中: ψ为火药装药烧去的百分比; χ、λ为火药的形状特征量; μ1为燃速常数;n为燃速指数; φ为次要功系数;m为弹丸质量;S为炮膛横断面积;p为膛内平均压力;lψ为药室自由容积缩颈长; f为平均火药力;ω为装药质量;v为弹丸运动速度。
1.2 内弹道计算结果
膛内平均压力随时间的变化规律曲线如图1所示。内弹道计算膛内最大平均压力为54.62 MPa。弹丸的速度随时间变化规律如图2所示,弹丸在身管内运动时间约为9 ms,计算获得弹丸出炮口时的初速为319.57 m/s。该计算结果将用于炮口流场数值模拟的参数初始化。
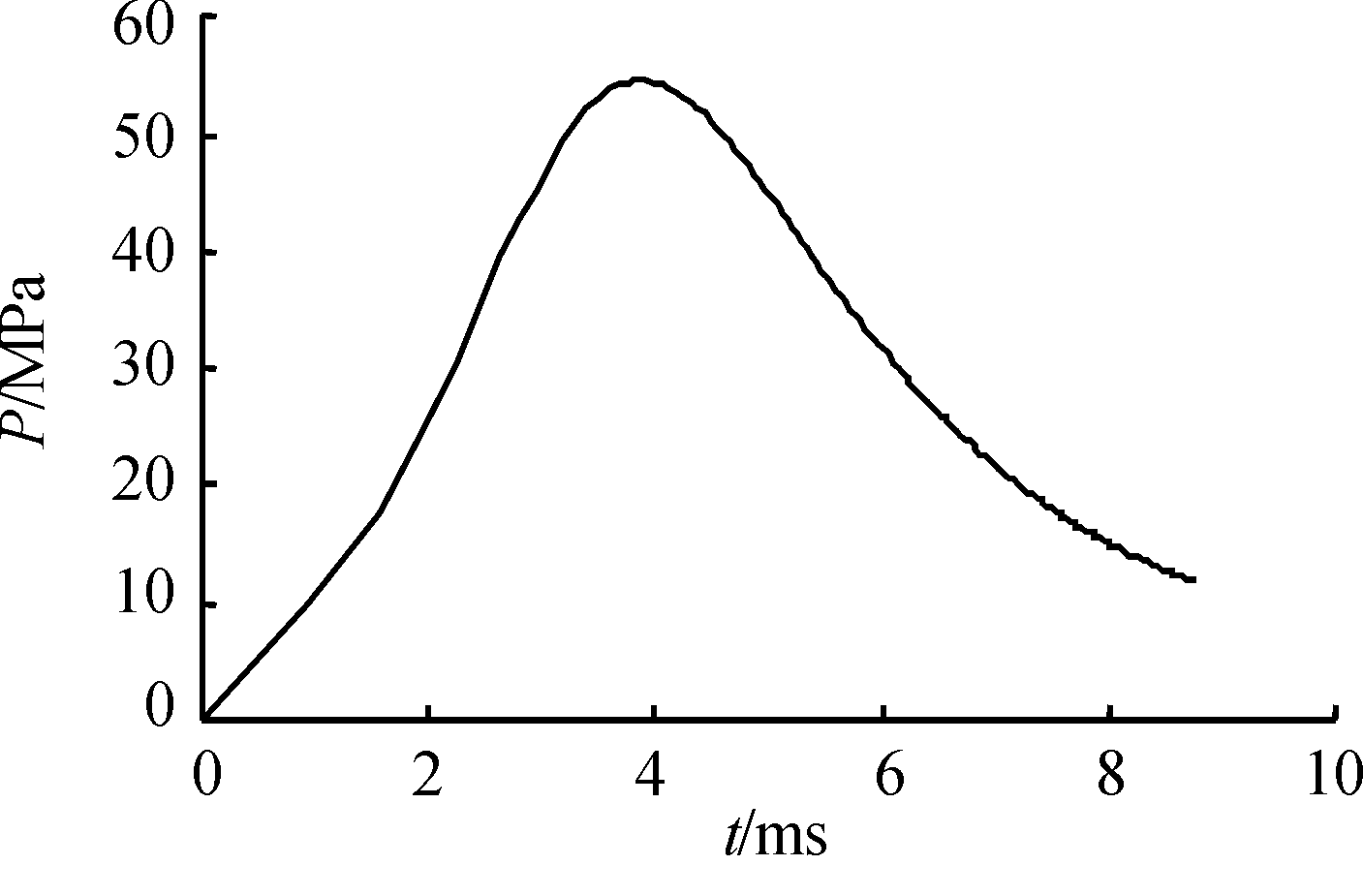
图1 膛内平均压力随时间的变化规律
Fig.1 The variation pattern of average pressure in the bore over time

图2 弹丸速度随时间变化规律
Fig.2 The variation of projectile velocity over time
2 数值模拟方法
2.1 控制方程
选用三维非定常Euler方程[10]
![]()
(2)
其中:
U=[ρ, ρu, ρv, ρw,E]T
F=[ρu, ρu2+p, ρuv, ρuw,(E+p)u]T
G=[ρu, ρuv, ρv2, ρvw,(E+p)v]T
H=[ρw,ρuw,ρvw,ρw2+p,(E+p)w]T
式(2)中:ρ为气体密度;u、v、w分别为x、y、z 3个方向的速度分量;E为单位质量气体的总能量。E的表达式为
![]()
(3)
式(3)中,λ为理想气体绝热指数。理想气体状态方程为
p=ρRT
(4)
式(4)中, R为通用气体常数,取R=287.4 J/(kg·K)。
由于弹丸运动导致网格运动,计算流场内控制体会发生改变,控制方程为
![]()
(5)
式(5)中:V为运动区域控制体;∂V为运动区域控制体边界;φ为通变量;u为控制体运动速度矢量;uw网格运动速度矢量;Γ为广义扩散系数;Sφ为φ的源项;A为面积矢量。
湍流模型采用Realizable k-ε模型,该模型对逆压梯度作用的边界层分离、流线弯曲、旋涡流等现象非常有效,适用于平面射流、圆形射流、旋转流[11]。
2.2 计算模型及方法
以双管自动迫击炮为研究对象,计算弹丸运动到炮口时即弹丸后效期的模型,身管长度L1=1 400 mm,身管壁面厚度L2=13 mm,计算域外流场为直径3 600 mm、长度2 500 mm的圆柱形流场区域。三维网格纵向切面如图3所示。

图3 部分三维网格纵向切面示意图
Fig.3 Schematic diagram of the longitudinal slice of a 3D mesh
由于后效期阶段火药气体和弹丸之间的流固耦合作用,本文中采用动网格技术方法中的层铺法模拟弹丸运动。其中,弹丸四周的网格采用四面体非结构网格划分,运动前后区域以及静态区域为六面体结构化网格,在静态区域与运动区域传输时,需对2个区域交界处的网格进行加密处理,避免由于不同大小的网格传输时出现数据间断,影响迭代收敛和等值线图。远离炮口和弹丸的网格区域采取结构网格进行划分,并可将网格放大用于提高生成速度和计算速度。
2.3 初始条件和边界条件
初始时间为弹丸到达膛口时,即后效期开始时刻,此时膛内气体的压力、速度及温度分布计算公式为[12]
身管内压力分布:
![]()
(6)
火药燃气速度分布:
![]()
(7)
膛内温度分布:
![]()
(8)
式(6)—式(8)中:px为膛内火药燃气压力沿身管轴向分布;pd为弹底压力;ω为装药质量;φ1为次要功系数;m为弹丸质量;L为身管长度;ux为火药燃气速度沿身管轴向分布;v为弹丸出炮口速度;M为火药燃气摩尔质量;ρg为膛内平均密度;R为气体常数。
初始时间身管内压力和火药燃气速度曲线如图4所示。计算区域中存在出口边界和固体壁面边界,身管的内外表面为固壁边界,弹丸区域前后表面为动网格边界面,外围流场区域定义为压力出口边界。
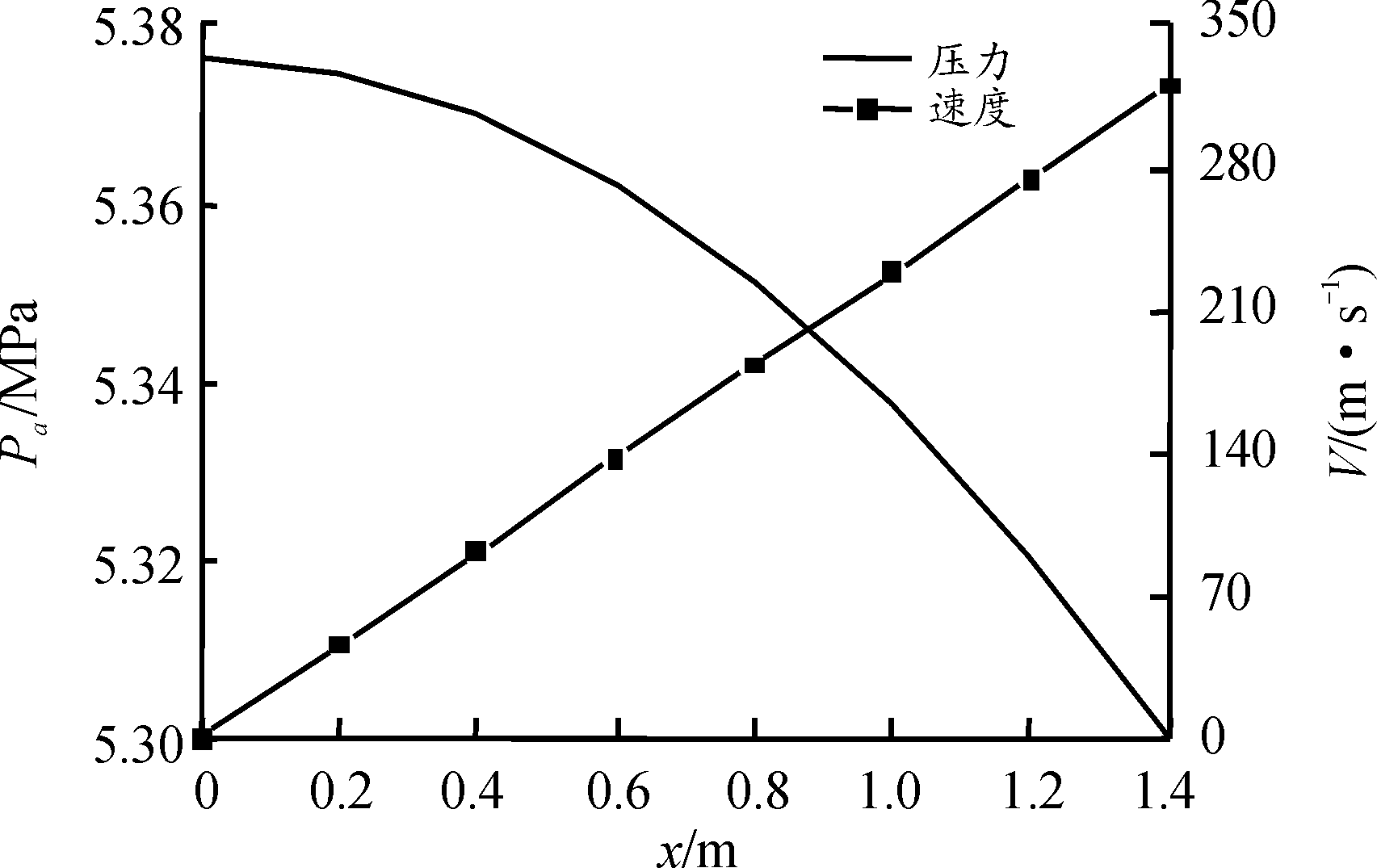
图4 初始时间身管内压力和火药燃气速度曲线
Fig.4 Initial time pressure in the tube and gunpowder gas velocity curve
3 计算结果与分析
由于膛内的高温高压气体在弹丸出炮口后急剧膨胀,会形成炮口流场复杂激波系。图5为双管迫击炮齐射时不同时刻的炮口流场纵向切面速度云图。弹丸出炮口后,高速气流冲出炮口,从炮口向周围扩散,由于炮管内气体与炮口处气体运动速度不同,从而在炮口处形成接触间断,此时火药燃气冲击波呈现球形状。如图5(a)所示,在0.5 ms前,炮管内火药燃气冲出炮口并在弹丸周围溢出,膛内火药燃气在短时间内膨胀较小,所产生2个冲击波区域彼此互不影响,2个流场独立进行发展,此时炮口附近火药燃气速度较高,速度为828.2 m/s。如图5(b)、图5(c)所示,在1 ms后,由于弹丸飞行速度小于火药燃气速度,弹丸被火药气体完全包围,随着火药燃气继续向外扩张,两身管产生的炮口流场相互叠加干扰,与此同时,高速欠膨胀气流推动弹丸向前运动,前方未受到扰动气流与弹丸相互作用而产生弹前激波。
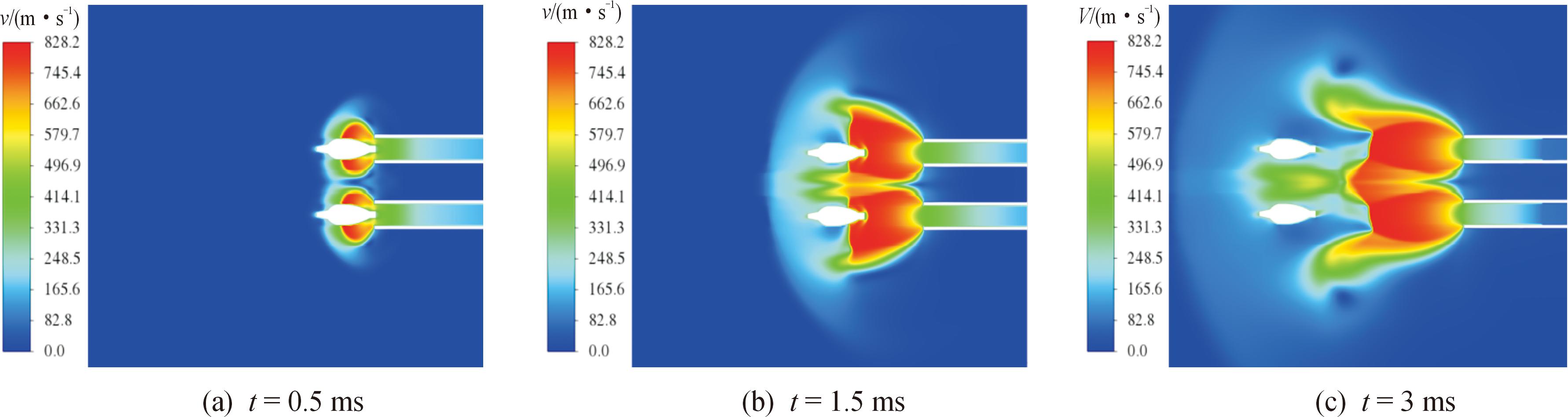
图5 不同时刻下速度云图
Fig.5 Velocity cloud at different times
图6为双管迫击炮齐射时不同时刻的炮口流场纵向切面压力云图。如图6(a)所示,在0.5 ms之前身管两侧的气流在炮口迅速膨胀形成侧向独立的冲击波,此时流场并未叠加。如图6(b)所示,在1 ms时,由于向身管两侧膨胀的火药燃气在两身管间相互叠加干扰,形成局部高压区域。如图6(c)所示,在3 ms后,弹丸运动以及高压气体不断膨胀的共同作用下,两弹丸间的火药燃气压力慢慢衰减,对两弹丸的侧向作用力逐渐减弱。

图6 不同时刻下压力云图
Fig.6 Pressure cloud at different times
在距离炮口横向0.75 m处设置了4个监测点a、b、c、d,监测点分别在距离为0.5、0、-0.5、-1 m的炮口轴向位置处。图7为监测点超压值随时间变化规律。由于炮口冲击波呈球状向外扩散,并且在扩散过程中不断衰减,根据波后和波前的压力比和来流马赫数之间的关系可知[13],冲击波波面上的压力并非均匀,表现为从右向左递减。因此,a点处的超压值大于b点,a点处的超压值为123 kPa,b点处的超压值为106 kPa。因为c、d点远离冲击波中心处,所以该2点处的超压值出现时间迟于a、b点处,且超压值小于a、b点处。
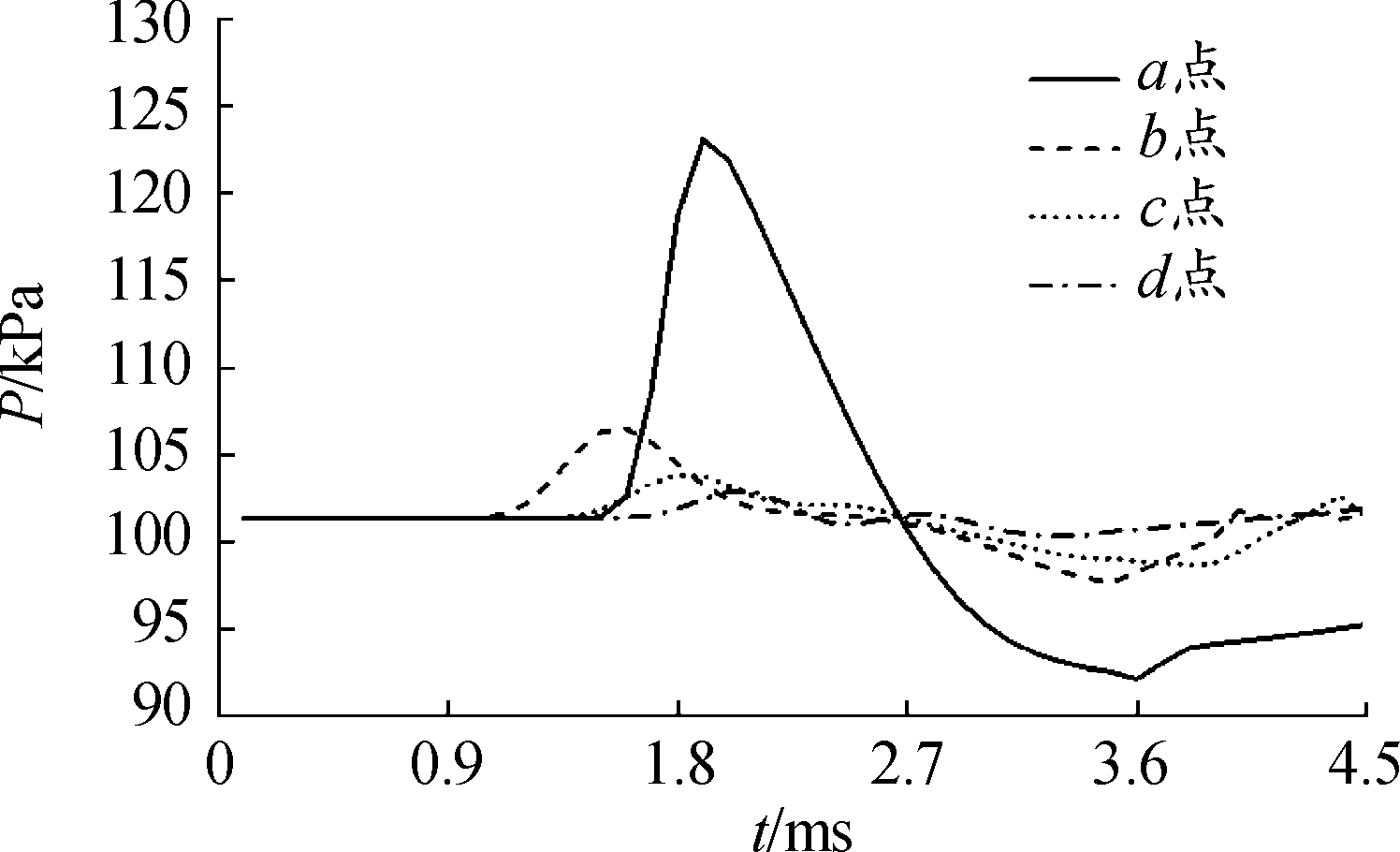
图7 监测点静压变化图
Fig.7 Graph of static pressure change at the monitoring point
图8、图9为弹丸所受轴向合力、侧向合力随时间变化情况。

图8 两弹丸轴向合力随时间变化曲线
Fig.8 Curve of the axial resultant force of the two projectiles with time
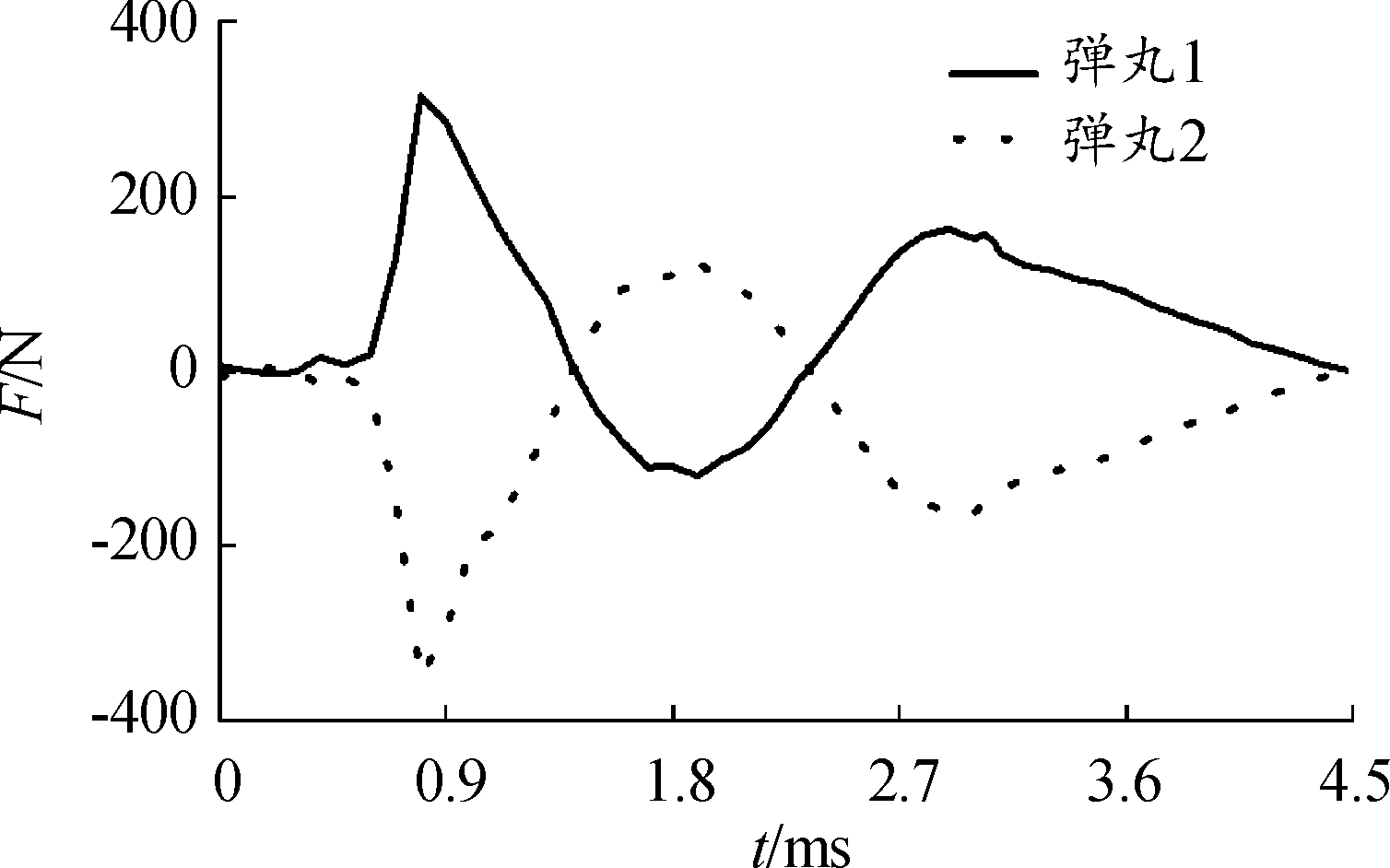
图9 两弹丸侧向合力随时间变化曲线
Fig.9 Lateral resultant force of two projectiles with time
由图8可知,当弹丸从炮口射出后,由于火药气体从身管内向外部快速扩散,从而导致弹丸受到的轴向合力也急剧下降。由图9可知,在2个流场独立发展0.5 ms之内,由于2个流场并没有相互影响,弹丸所受侧向作用几乎为零。在0.5 ms之后,火药燃气继续迅速膨胀,两身管之间的气流相遇,炮口流场相互叠加干扰,在两身管间形成局部高压区域,进一步加剧了对弹丸的影响,使弹丸受到的侧向力迅速升高,导致弹丸两侧的力不相等,弹丸内侧的力明显大于弹丸外侧受到的力,弹丸获得单向力,其最大侧向合力约为350.6 N。随着弹丸以及气流运动的影响,叠加流场所产生的高压区域压力降低,侧向合力影响逐渐减小。大约在1.4 ms时,叠加流场产生的侧向合力达到最小。在弹丸穿越马赫盘后,叠加流场所形成的高压区域对弹丸的影响逐渐减小,但由于马赫盘继续扩张,当高速气流从两弹丸之间穿过时,对弹丸再次产生影响,此时弹丸受到的侧向合力和侧向偏移速度有所增加。当弹丸逐渐远离炮口后,2发弹丸的叠加流场产生的侧向合力再次减小,在大约4.5 ms之后弹丸的侧向合力达到稳定。
4 结论
本文中基于三维Euler方程,采用动态分层技术的结构化动网格方法,对双管自动迫击炮齐射时的炮口流场进行三维数值模拟并进行超压值监测。得到如下结论:越在炮口后方的位置,超压值越小。火药燃气叠加形成的局部高压区域使弹丸受到不对称的侧向力,其最大侧向合力为350.6 N,在侧向合力的作用下导致弹丸获得侧向加速度,会导致射击精度下降。此计算结果可为身管后方设备及人员安全位置区域的确定和后续对该双管迫击炮外弹道结果计算提供依据。
[1] 张焕好,陈志华,姜孝海,等.膛口装置三维流场的数值模拟及制退效率计算[J].兵工学报,2011,32(5):513-519.ZHANG Huanhao,CHEN Zhihua,JIANG Xiaohai,et al.Numerical simulation of three-dimensional flow field and calculation of stopping and retreating efficiency of bore device[J].Acta Armamentarii,2011,32(5):513-519.
[2] ZHANG Hailong,LI Zhongxin,CAI Hongming,et al.Numerical analysis of flow field in muzzle of a pod aircraft gun[J].Journal of Ordnance Equipment Engineering,2022,43(3):73-78.
[3] LI Shanji,WANG Huiyuan,HUANG Shaobao,et al.Analysis of deflection flow fields of aircraft gun pod based on CFD[J].Journal of Ordnance Equipment Engineering,2020,41(12):118-122.
[4] 刘欣宁,岳明凯.带炮口制退器的火炮膛口流场三维数值模拟[J].四川兵工学报,2015(7):56-59.LIU Xinning,YUE Mingkai.Three-dimensional numerical simulation of gun muzzle flow field with muzzle brake[J].Journal of Sichuan Ordnance,2015(7):56-59.
[5] 汤傲,戴劲松,王茂森,等.小口径尾翼弹膛口流场数值模拟[J].兵器装备工程学报,2021,42(6):34-37.TANG Ao,DAI Jinsong,WANG Maosen,et al.Numerical simulation of the flow field of the chamber of a small-bore tail projectile[J].Journal of Ordnance Equipment Engineering,2021,42(6):34-37.
[6] 郭则庆,王杨,姜孝海,等.膛口初始流场对火药燃气流场影响的数值研究[J].兵工学报,2012,33(6):663-668.GUO Zeqing,WANG Yang,JIANG Xiaohai,et al.Numericalstudy on the influence of the initial flow field of the bore on the flow field of gunpowder gas[J].Acta Armamentarii,2012,33(6):663-668.
[7] 黄欢,何永,蔺月敬.某迫击炮炮口流场数值模拟与分析[J].火炮发射与控制学报,2012(4):63-67.HUANG Huan,HE Yong,LIN Yuejing.Numerical simulation and analysis of the muzzle flow field of a mortar[J].Journal Of Gun Launch &Control,2012(4):63-67.
[8] 钱林方.火炮弹道学[M].北京:北京理工大学出版社,2009:166-168.QIAN Linfang.Artillery ballistics[M].Beijing:Beijing Institute of Technology Press,2009:166-168.
[9] CORNER J.Theory of the interior ballistics of guns[M].New York:New York Wiley,1950.
[10] 李鸿志,姜孝海,王杨,等.中间弹道学[M].北京:北京理工大学出版社,2015.LI Hongzhi,JIANG Xiaohai,WANG Yang,et al.Inter-mediate ballistics[M].Beijing:Beijing Institute Technology Press,2015.
[11] 李子杰,王浩,陈健伟.超高速弹丸膛口流场结构分析[J].哈尔滨工业大学学报,2017,49(10):53-59.LI Zijie,WANG Hao,CHEN Jianwei.Analysis of flow field structure at the muzzle of ultra high speed projectile[J].Journal of Harbin Institute of Technology,2017,49(10):53-59.
[12] 廖振强,邱明.自动武器燃气动力学[M].北京:国防工业出版社,2015.LIAO Zhenqiang,QIU Ming.Inter-mediate ballistics[M].Beijing:National Defense Industry Press,2015.
[13] 高树滋,陈运生.火炮反后坐装置设计[M].北京:兵器工业出版社,1995:293-294.GAO Shuzi,CHENG Yunsheng.Artillery recoil mechanism design[M].Beijing:Weapon Industry Press,1995:293-294.